中国海上风能资源丰富,海上风电具有风能资源稳定、不占用土地等独特优势,发展海上风电条件十分优越[1]。然而,由于海上风电运行环境十分恶劣,风力机容易发生故障,因此导致了必要的海上运维工作,且出现专门用于海上风力机维护的风电运维船[2]。该船在运送工作人员进入风力机的方式有很多,目前比较安全的方式是在船上搭载六自由度补偿平台,该平台会补偿掉波浪引起的船体运动,使得输送通道相对稳定。因此,如果能够提前分析得知六自由度补偿平台基座位置处的姿态变化情况,不仅能够为该平台控制系统提供数据输入,而且通过运动学分析可进一步得知液压缸所需的运动位移,实现实时运动补偿。
风电运维船上搭载的六自由度补偿平台固连在甲板上,因此研究平台基座的姿态运动即为研究船舶甲板安装点处的运动响应。针对船舶在波浪中运动响应的研究,Fang C.C.等[3]根据线性频域理论,研究出一种常规波浪中双体船水动力运动响应的非线性时域方法,并与试验数据结果对比发现非线性时域方法比线性频域方法更能准确预报双体船运动响应。耿彦超等[4]用二维半理论和程序对某高速穿浪双体船在斜浪中的运动响应进行预报,并把理论计算结果与模型试验结果及其他程序计算结果比较分析,验证了文中方法和程序在预报高速双体船运动的适用性。金晨露[5]基于水动力性能软件研究了风电运维双体船在静水中的阻力性能以及在波浪中的波浪增阻和运动响应幅值,通过不断优化船型参数来降低静水阻力与运动幅值。周云司雅[6]基于三维势流理论,利用水动力分析软件AQWA对风电运维船停泊状态下横、纵摇性能分析,并通过加装喷水减摇装置进行对比分析以验证该装置的有效性。邓磊等[7]基于RANS方程和VOF模型求解船体粘性兴波流场,研究了小水线面双体船在迎浪规则波中纵向运动的非线性特性。谢云平等[8]基于CFD计算海上三体风电运维船静水阻力和规则波中迎浪增阻与运动响应,并预报不规则波中运动有义值和阻力值。Guanche等[9]运用频域下的多刚体水动力模型,给出了顶浪和横浪情况下人员可安全通过栈桥的浪高范围。但针对搭载伸缩舷梯的六自由度补偿平台安装点位置处的运动响应研究较少,张萌[10]通过处理惯性测量单元测得的信息对船舶的升沉和纵摇运动进行预报,利用运动学反解出要实现廊桥的波浪补偿,并对波浪补偿控制律的有效性进行了验证,但该单元并未对廊桥底座与甲板安装点处的运动进行测量。苏建国[11]通过动平衡原理建立并简化船舶运动模型,通过Matlab软件对船舶的运动响应进行仿真,设计并优化了风电运维船辅助登靠控制系统,但研究并未针对辅助登靠平台的安装点进行运动响应仿真。
基于以往学者对船舶运动响应以及六自由度补偿平台的研究,本文以风电运维船上六自由度补偿平台基座安装点位置为研究对象,基于三维势流理论和波浪绕射理论,建立风电运维船计算模型并分析其在特定海况下的六自由度运动响应特性,并将船舶重心处的运动响应转换为补偿平台基座安装点位置处的运动响应,分析该安装点位置处的运动响应特性,研究结果为六自由度补偿平台控制系统以及液压缸运动位移的运动学分析提供数据输入,为运维时机的选择以及平台液压机构的选型提供参考依据。
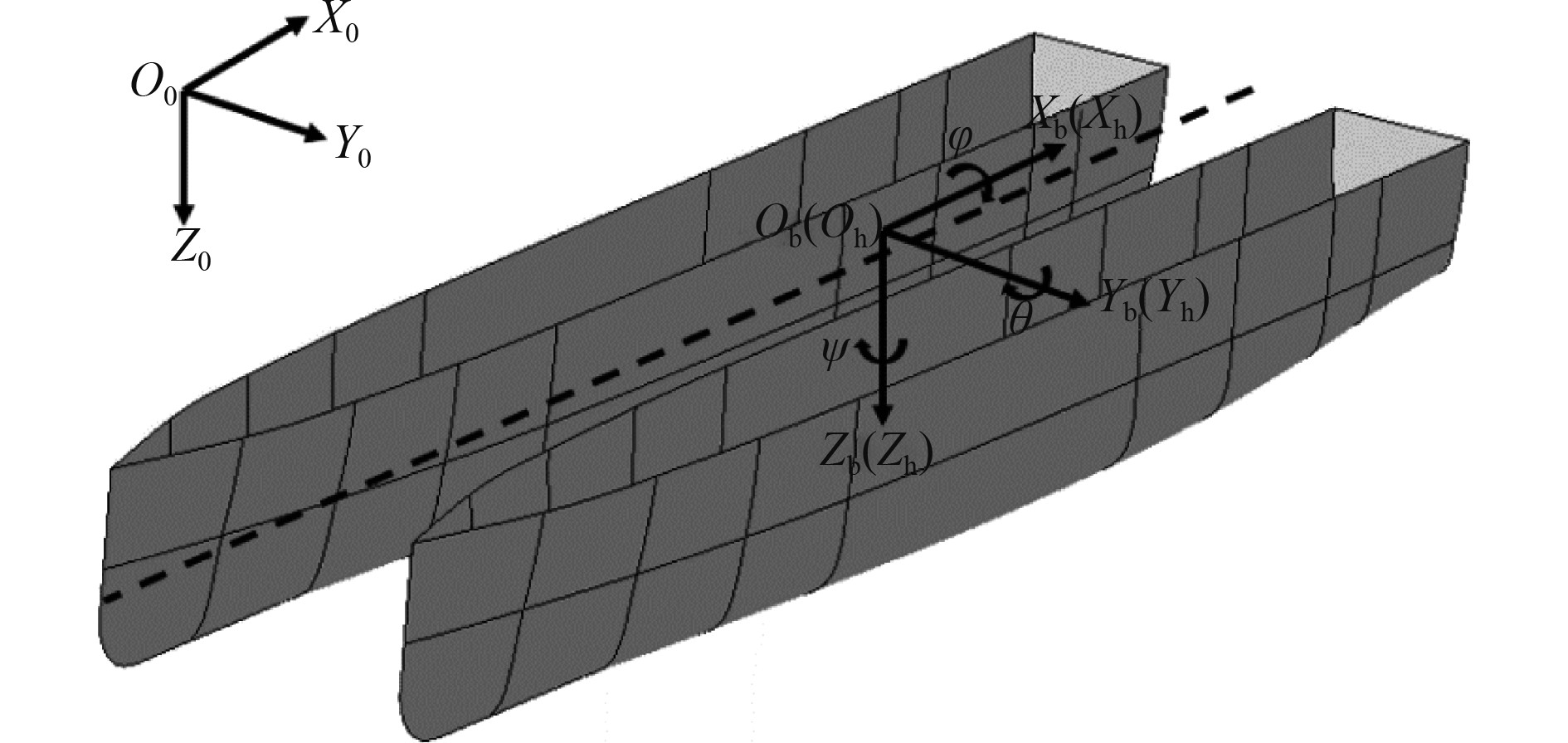
1 坐标系建立及转换 1.1 坐标系建立船舶运动由3个平移运动(横荡、纵荡和垂荡)和3个旋转运动(横摇、纵摇和首摇)表示[12],为了更好地描述船舶运动以及分析后的六自由度补偿平台运动,建立3个坐标系,如图1所示。固定坐标系O0X0Y0Z0作为参考坐标系在流场中固定,O0X0Y0平面定义为水线面,垂直于该平面的O0Z0轴。随体坐标系ObXbYbZb原点Ob与结构物重心位置重合,与船舶固连。水动力学坐标系OhXhYhZh在船舶静止时建立,原点Oh接近船体浮心。
|
图 1 船舶坐标系 Fig. 1 Establishment of ship coordinate system |
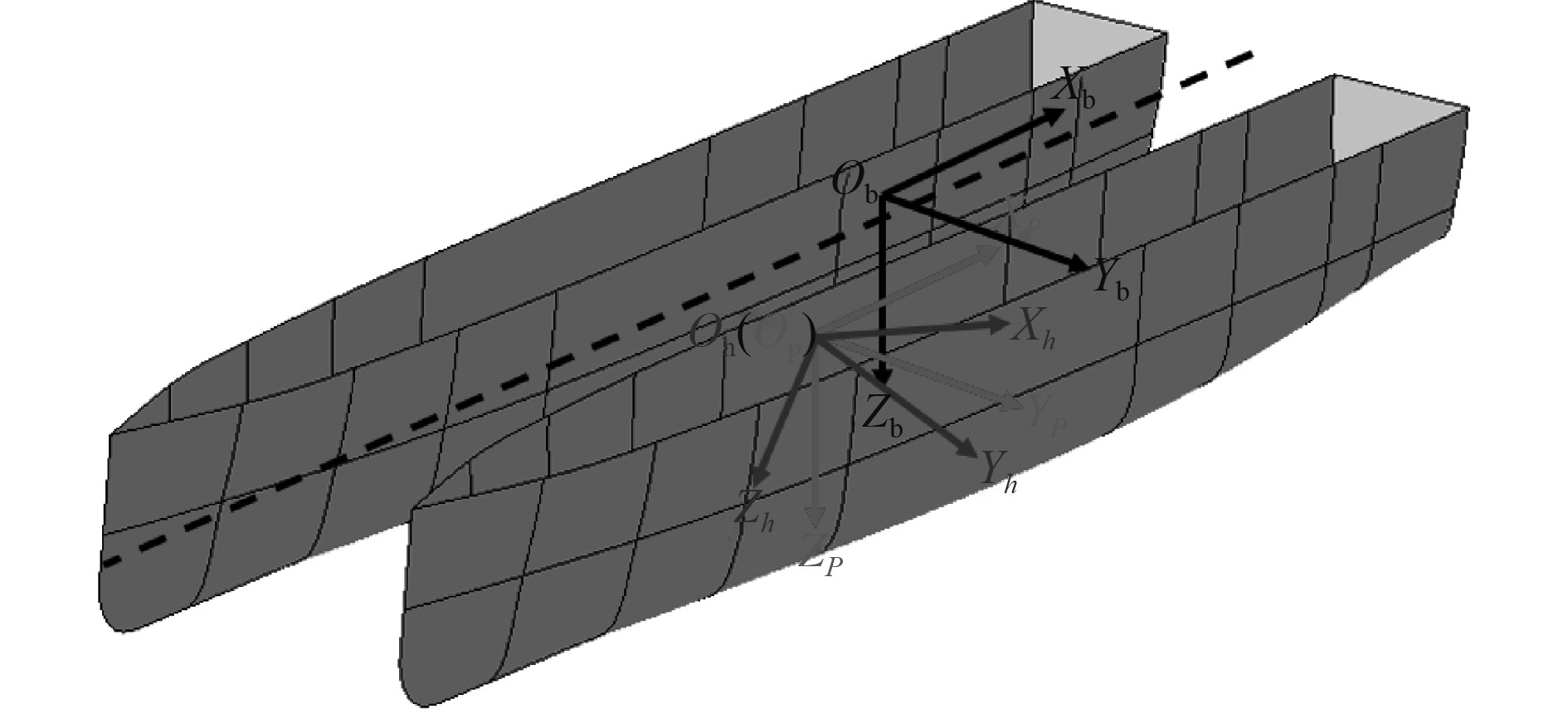
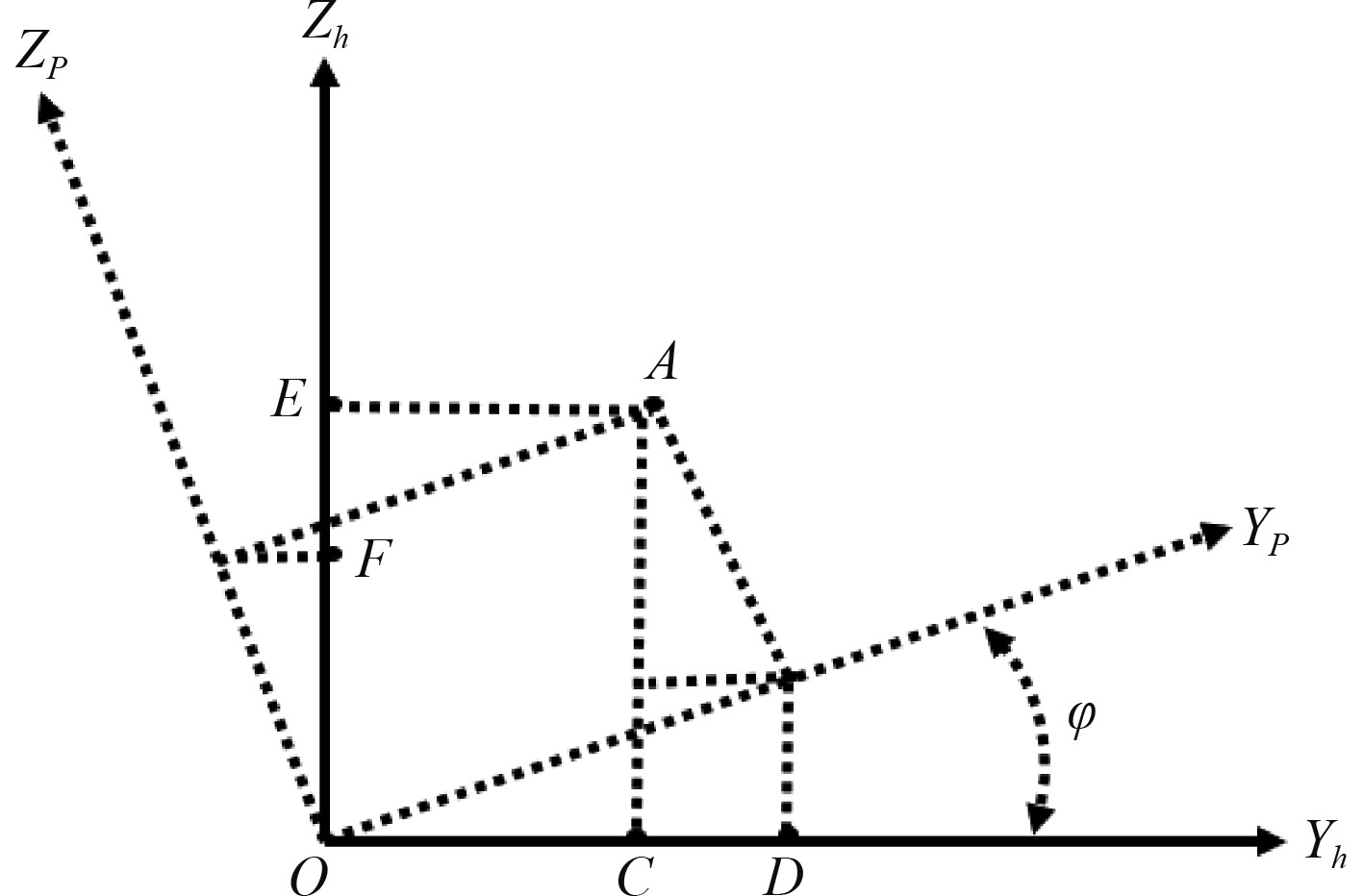
由于要知道六自由度补偿平台安装点位姿,需要将船舶在水动力学坐标下的运动响应转换为六自由度补偿平台安装点位置的运动响应,为此建立一个新的坐标系{p},它与水动力坐标系{h}原点相同、与船舶随动坐标系{b}三轴平行,如图2所示。两坐标系之间只存在旋转关系,即绕X轴的横摇转动φ、绕Y轴的纵摇转动θ和绕Z轴的艏摇转动ψ。当船舶只受横摇运动时,坐标系{p}绕坐标系{h}的X轴转动了一个横摇角度φ,如图3所示。坐标系中的一点A的X轴坐标值不变,Y轴和Z轴坐标变换为:
|
图 2 {h}和{p}坐标系之间关系 Fig. 2 The relationship between {h} and {p} coordinate systems |
|
图 3 坐标系{p}绕X轴转动 Fig. 3 The coordinate system {p} rotates around the X axis |
| $ \left\{ {\begin{array}{*{20}{c}} {{Y_{A,h}}{\text{ = }}OC = OD - CD = {Y_{A,p}}\cos \varphi - {Z_{A,p}}\sin \varphi,} \\ {{Z_{A,h}} = OE = OF + FE = {Z_{A,p}}\cos \varphi + {Y_{A,p}}\sin \varphi ,} \end{array}} \right. $ | (1) |
因此,横摇运动的坐标变换的矩阵型式为:
| $ \left[ {\begin{array}{*{20}{c}} {{X_h}} \\ {{Y_h}} \\ {{Z_h}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi }&{\cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_p}} \\ {{Y_p}} \\ {{Z_p}} \end{array}} \right],$ | (2) |
横摇运动的齐次坐标变换矩阵为:
| $ {T_X} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos \varphi }&{ - \sin \varphi }&0 \\ 0&{\sin \varphi }&{\cos \varphi }&0 \\ 0&0&0&1 \end{array}} \right],$ | (3) |
纵摇和首摇运动的齐次变换矩阵为:
| $ {T_Y} = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&0&{\sin \theta }&0 \\ 0&1&0&0 \\ { - \sin \theta }&0&{\cos \theta }&0 \\ 0&0&0&1 \end{array}} \right],$ | (4) |
| $ {T_Z} = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0&0 \\ {\sin \psi }&{\cos \psi }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] 。$ | (5) |
可知坐标系{p}相对于坐标系{h}的齐次变换矩阵为:
| $ {}_p^hT = {T_Z}{T_Y}{T_X}。$ | (6) |
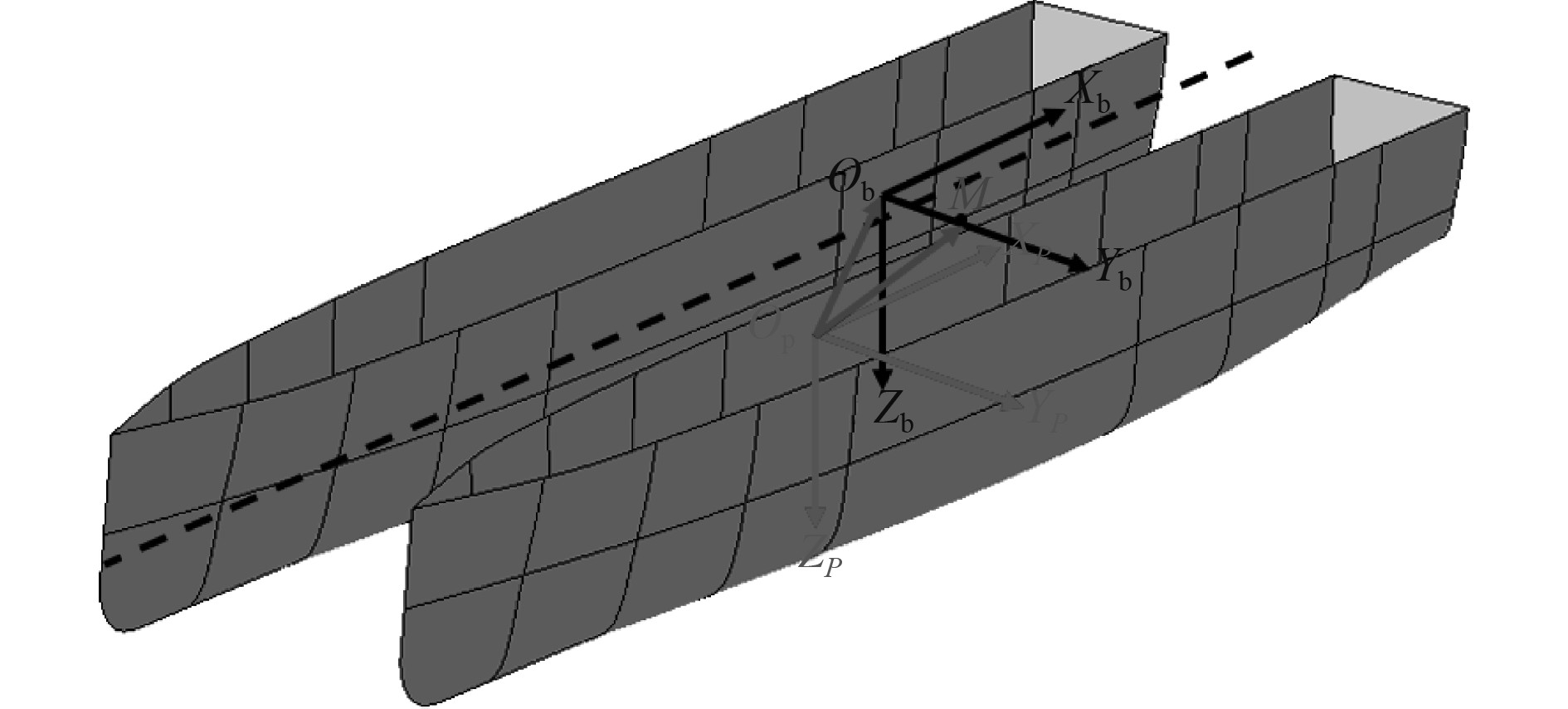
随后建立一个平移坐标系OqXqYqZq,它由船舶随动坐标系{b}平移而来,用来描述六自由度补偿平台在船舶甲板上的位置,根据船舶参数在坐标系{b}下取该位置点M。坐标系{p}和坐标系{q}之间存在一个平移变换关系,如图4所示。M点在{p}坐标系下的坐标表示为(Mx,My,Mz),其齐次变换矩阵表示为:
|
图 4 M点和{p}坐标系之间关系 Fig. 4 The relationship between Mpoint and {p} coordinate system |
| $ {T_M} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{{M_{{x}}}} \\ 0&1&0&{{M_{{y}}}} \\ 0&0&1&{{M_{{z}}}} \\ 0&0&0&1 \end{array}} \right] ,$ | (7) |
则坐标系{q}相对于坐标系{h}的齐次变换矩阵为:
| $ {}_q^hT = {T_q}{T_Z}{T_Y}{T_X} 。$ | (8) |
以某新型风电运维双体船为研究对象,具体主尺度参数如表1所示。船体主甲板上搭载六自由度补偿平台,水动力模型如图5所示。计算中坐标原点取为重心在水线面上的投影点,以船首方向为X轴正方向,左侧片体方向为Y轴正方向,竖直向上方向为Z轴正方向。
|
|
表 1 风电运维双体船主尺度 Tab.1 Main scale of wind power operation and maintenance catamaran |
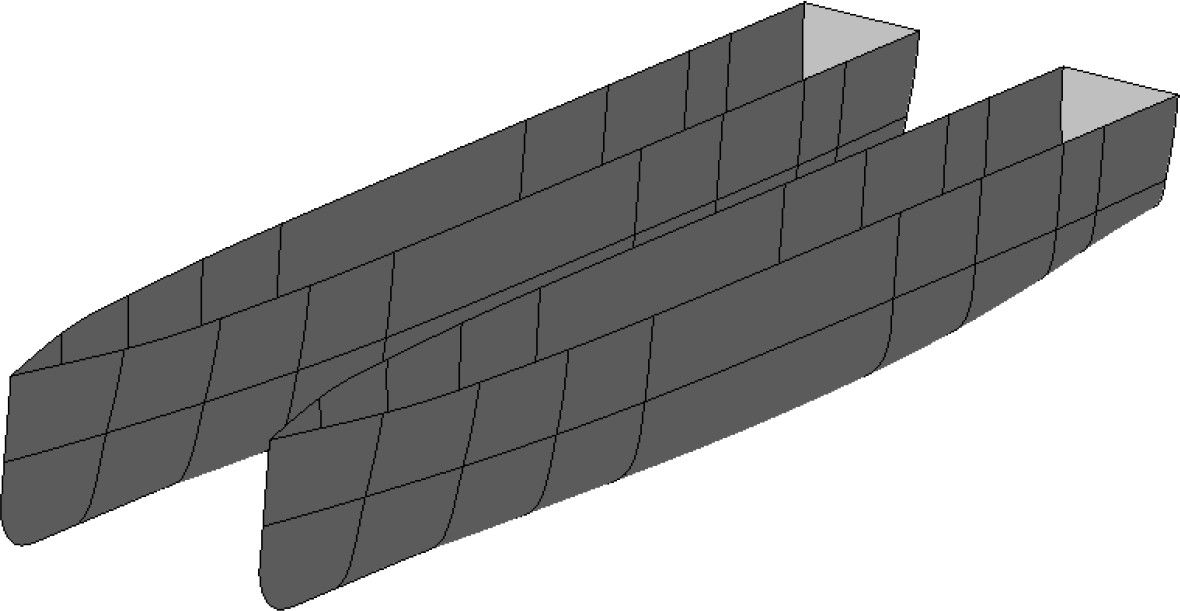
|
图 5 风电运维船湿表面模型 Fig. 5 Wet surface model of wind power operation and maintenance ship |
计算海况选用不规则波,波浪谱采用国际拖曳水池会议(Internation Towing Tank Conference,ITTC)推荐的双参数Pierson-Moskowitz谱[13],考虑到船舶的具体运维海区,有义波高为1.5 m,平均过零周期为8 s,具体计算环境如表2所示。
|
|
表 2 环境条件 Tab.2 Environmental conditions |
模型采用workbench中的默认网格划分方式进行网格划分,网格模型共有4538个节点,4350个单元,其中包括2490个绕射单元,网格模型图如图6所示。

|
图 6 网格模型图 Fig. 6 Grid model diagram |
风电运维双体船左片体主甲板处配备有六自由度补偿平台,在补偿运维过程中双体船的垂荡响应、横摇响应、纵摇响应是影响补偿运动的关键,也是保证船舶安全作业的重要参考[14]。对此,将对该船频域内6个自由度上的运动响应、附加质量以及辐射阻尼进行分析。
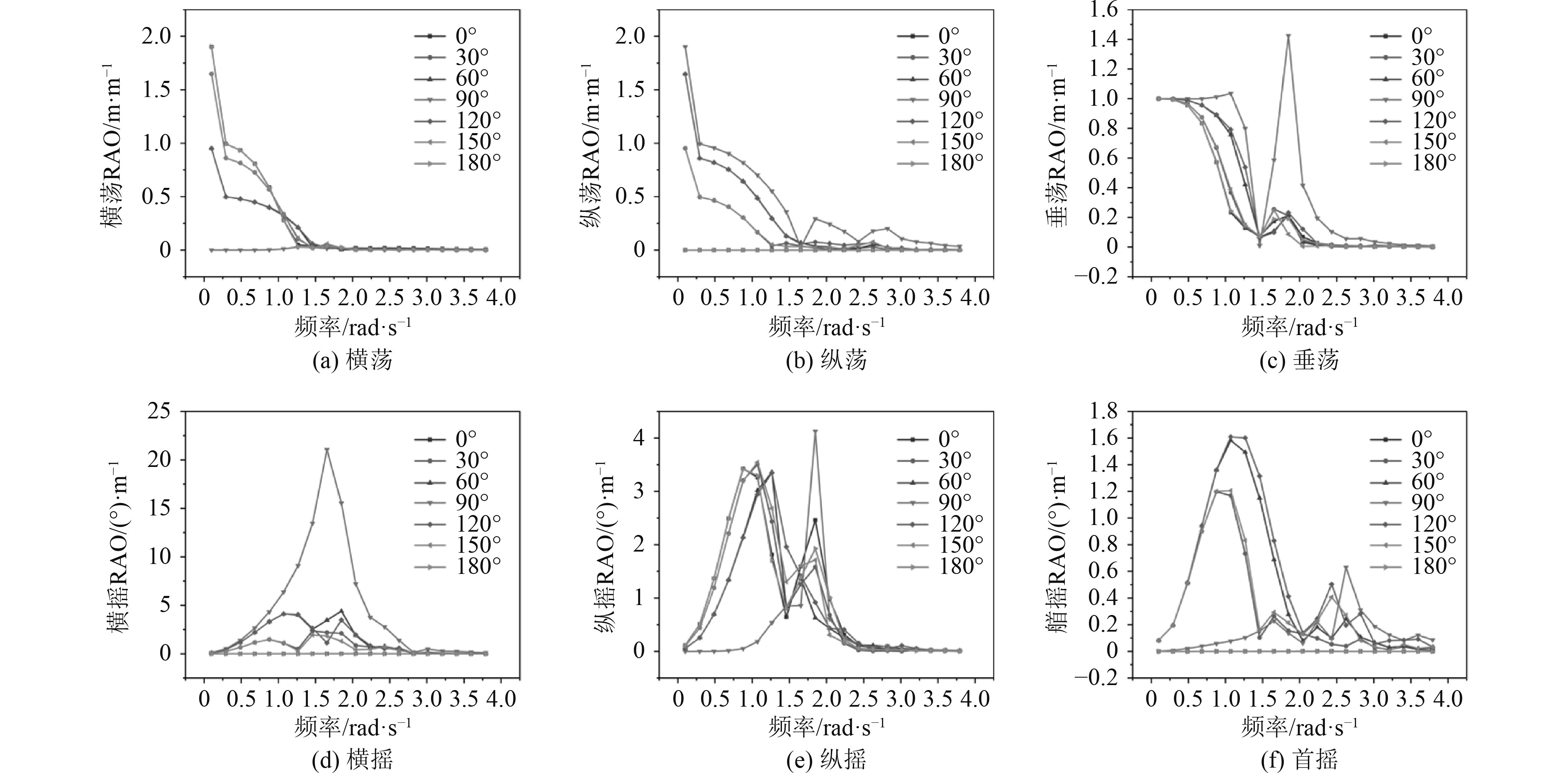
2.2.1 RAO分析运动响应谱反映了在规定海况下响应幅值与波浪频率之间的关系,图7(a)~图7(f)分别为风电运维船在不同浪向下的横荡、纵荡、垂荡、横摇、纵摇和首摇6个自由度响应谱变化曲线。由图可知,风电运维船的横荡和纵荡运动在各个浪向角下的RAO随着波浪频率的增加而下降,在1.6 rad/s后基本趋于平稳;在垂荡运动中,各个浪向角下的RAO基本随着波浪频率的增加而下降,在波浪周期为4~10 s时下降幅度最大,在1.8 rad/s时又回升至峰值,其中浪向角为90°时的峰值比其他角度都要大得多,此时的波浪周期为3.3 s;风电运维船的横摇运动在各个浪向角下的RAO基本随着波浪频率的增加而增大,在波浪周期3~7 s时运动比较剧烈,变化幅度较大,最大时出现在横浪时,此时周期为3.7 s,随后在2.3 rad/s时各自浪向角下的RAO趋于平稳;纵摇运动在各个浪向角下的RAO基本随着波浪的频率增加而增大,在1.2 rad/s附近出现了第1个峰值,即在波浪周期为6~20 s时幅值迅速增大,达到极值后迅速回落,并在1.8 rad/s附近出现第2个较小的峰值,即在波浪周期为3~4 s时又出现小幅上升,幅值最大时出现在波浪周期为5.6 s的随浪和3.3 s的横浪;首摇运动在各个浪向角下的RAO基本随着波浪频率的增加而下降,在1~1.3 rad/s时部分浪向角下的RAO达到峰值,随后在高频时基本趋于平稳。因此,若风电运维船在运维时,应尽量避免在波浪周期为3~10 s的区域内工作。
|
图 7 频域运动响应曲线 Fig. 7 Frequency domain motion response curve |
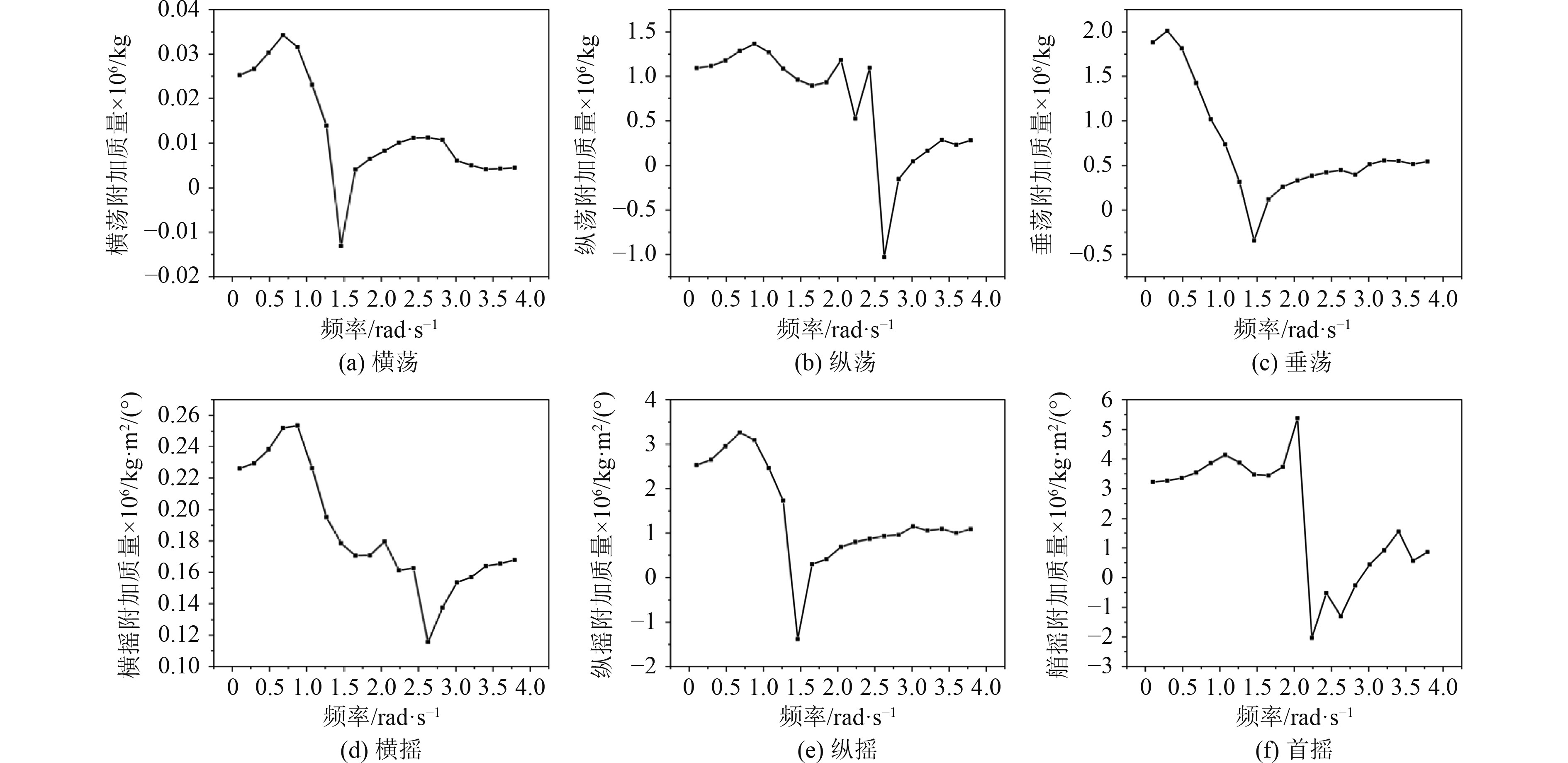
船舶的附加质量是准确预报船舶在波浪中运动性能的参数之一,图8(a)~图8(f)分别为风电运维船横荡、纵荡、垂荡、横摇、纵摇和首摇时附加质量随波浪频率变化的曲线图。由图可知,横荡、垂荡和纵摇的附加质量在高频段相对稳定,基本都在1.5 rad/s时达到波谷;纵荡和横摇的附加质量基本随着波浪频率的增加而降低,其中纵荡在低频段相对稳定,两者基本都在2.6 rad/s时达到波谷;首摇的附加质量在低频段相对稳定,在高频段逐渐增大。
|
图 8 附加质量随波浪频率变化曲线图 Fig. 8 Curve of additional mass change with wave frequency |
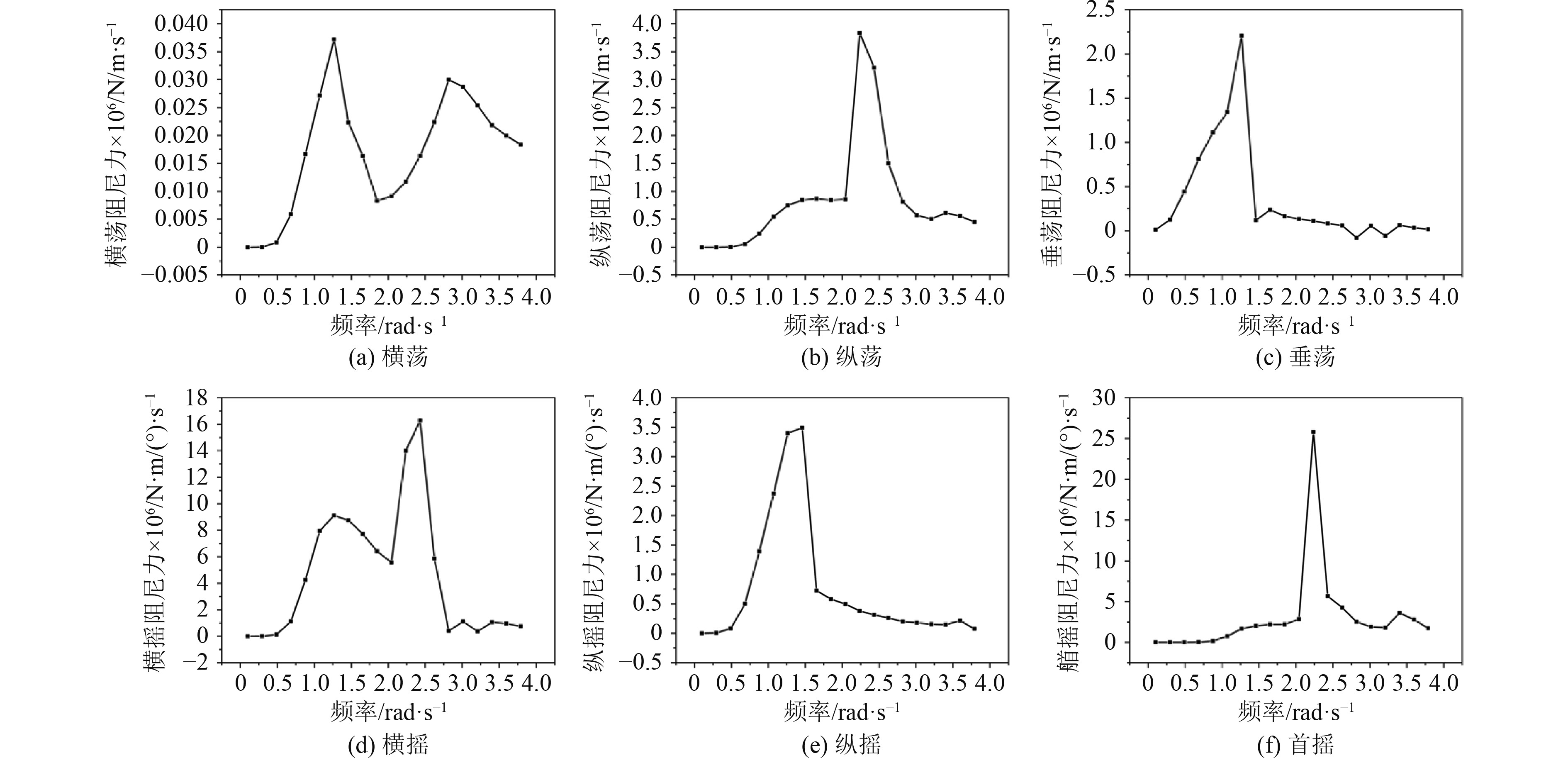
图9(a)~图9(f)分别为风电运维船横荡、纵荡、垂荡、横摇、纵摇和首摇时阻尼力随波浪频率变化的曲线图。由图可知,横荡和横摇的阻尼力在0~1.3 rad/s频段逐步上升,在经历一个短暂的下降后并分别在2.4 rad/s和2.8 rad/s达到峰值,随后下降并趋于稳定;纵荡和首摇的阻尼力在0~2 rad/s频段相对稳定,在2.4 rad/s时达到峰值,随后急剧下降并趋于稳定;垂荡和纵摇的阻尼力在0~1.3 rad/s频段逐步上升,在1.4 rad/s时达到峰值,随后急剧下降并趋于稳定。
|
图 9 阻尼力随波浪频率变化曲线图 Fig. 9 Variation curve of damping force with wave frequency |
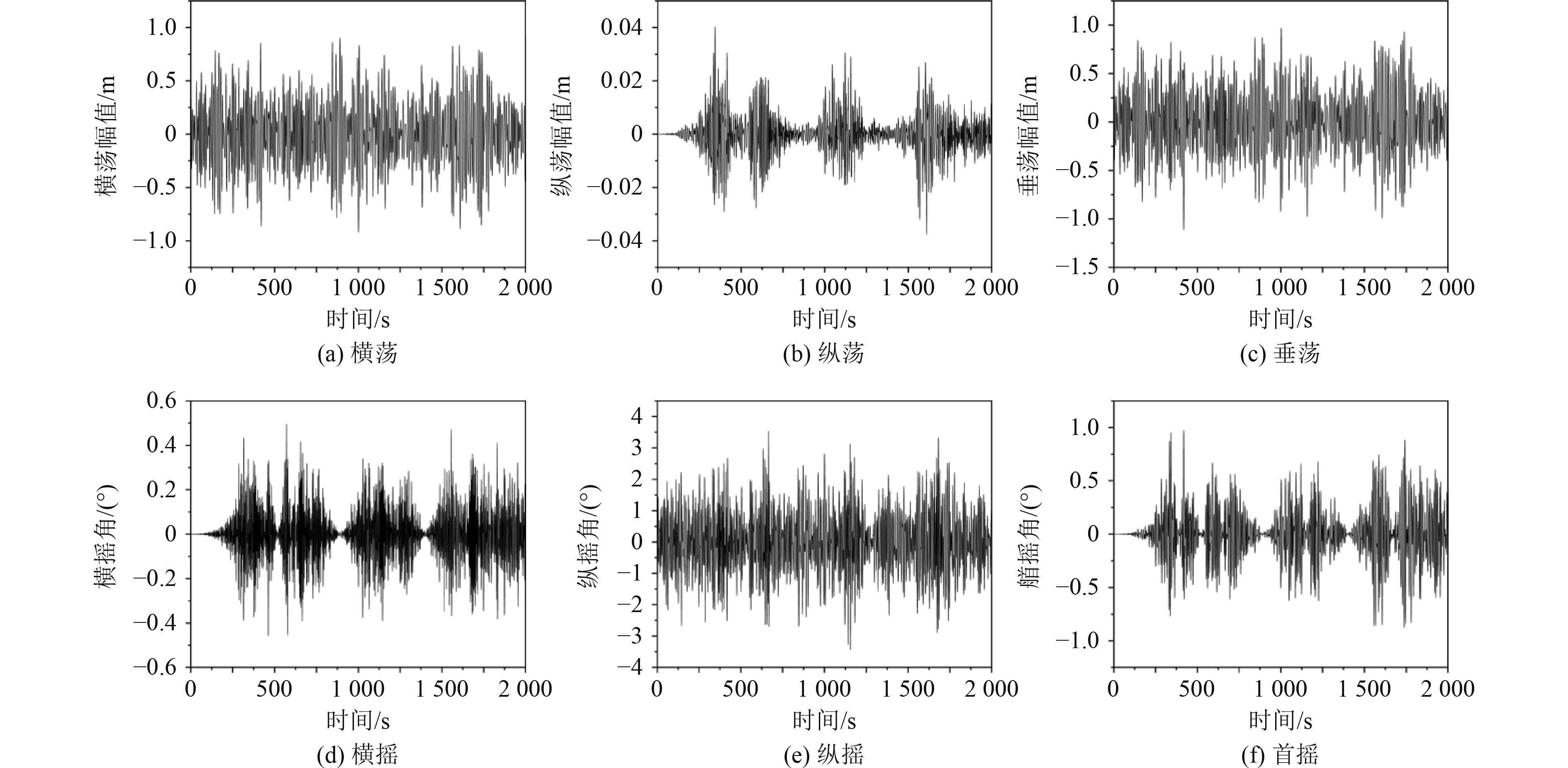
通过频域方法对风电运维船进行了水动力分析,计算得到了船舶的运动RAO、附加质量以及辐射阻尼等水动力参数。基于频域计算结果,对风电运维船在运维海况下进行时域耦合分析,设置总时长为2000 s,计算步长间隔0.1 s,计算得到船舶的运动响应历程。图10(a)~图10(f)为风、浪、流载荷作用方向为0°时船舶横荡、纵荡、垂荡、横摇、纵摇和首摇的时域计算结果。从结果可以看出,在平移运动中,风电运维船的垂荡运动幅度最大,最大幅值为1.11 m,横荡运动幅度次之,幅值为0.92 m,纵荡运动幅度最小,幅值仅为0.04 m;在转动运动中,风电运维船的纵摇运动幅度最大,最大幅度为3.53°,首摇运动幅度次之,幅度为0.98°,横摇运动幅度最小,幅度仅为0.49°。
|
图 10 时域运动响应谱 Fig. 10 Time domain motion response spectrum |
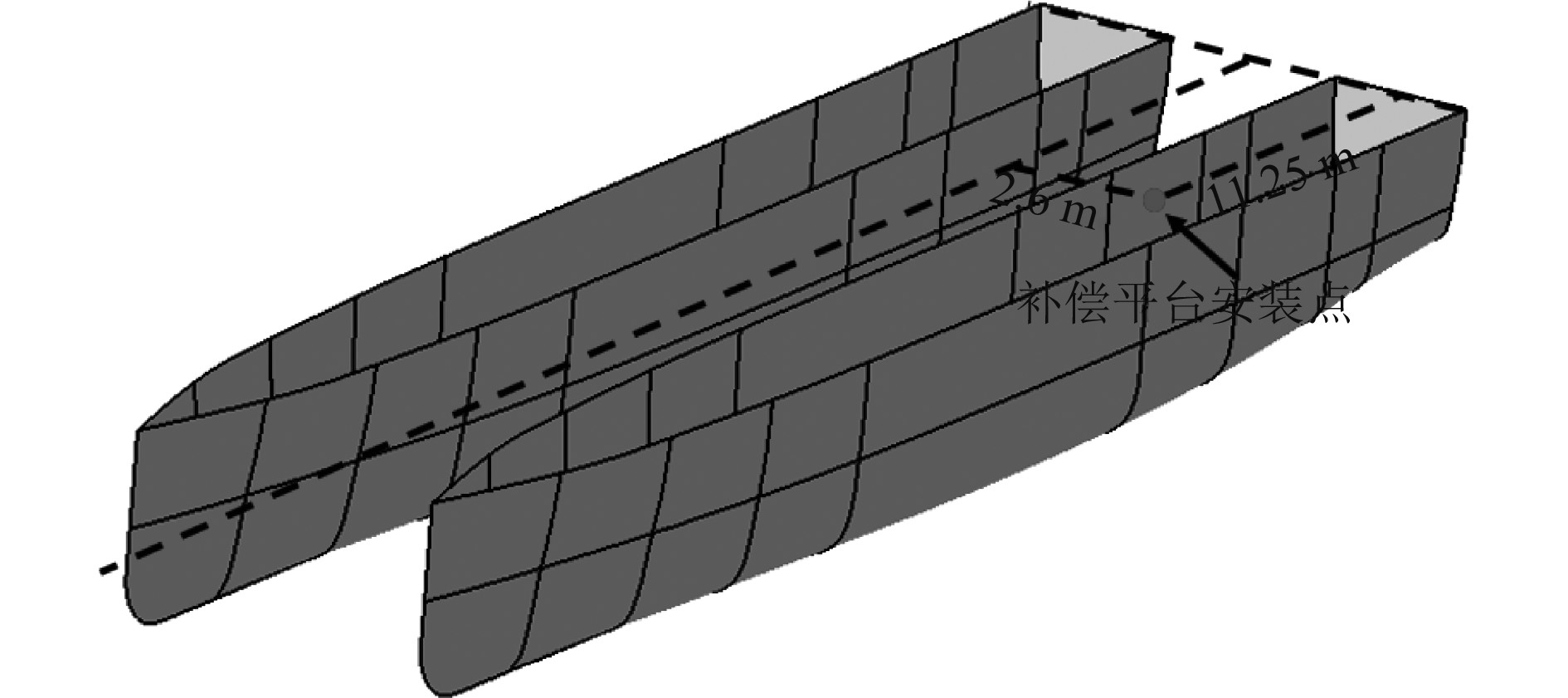
上述针对风电运维船的水动力分析是基于船舶重心的结果,但根据实际运维状态,精确的研究对象为风电运维船上搭载的六自由度补偿平台基座安装点位置处的6个自由度的运动响应,因此需要将船舶重心处的运动响应转换为基座安装点位置处的运动响应。由于该风电运维船搭载动力定位系统[15],故主要考虑此安装点处在垂荡、横摇和纵摇的运动响应。六自由度补偿平台安装于该双体船左片体上距中线2.6 m且距船尾11.25 m处的甲板位置上,如图11所示。
|
图 11 六自由度补偿平台基座安装点示意图 Fig. 11 Schematic diagram of the installation point of the 6-DOF compensation platform base |
图12(a)~图12(c)分别为六自由度补偿平台基座安装点位置处的垂荡、横摇和纵摇的运动响应曲线图。由图可知,安装位置处的垂荡最大幅值为1.702 m,横摇运动最大幅度为0.5°,纵摇运动最大幅度为3.5°。

|
图 12 基座安装点位置处垂荡、横摇和纵摇运动响应曲线图 Fig. 12 The response curve of heave, roll and pitch motion at the location of the base installation point |
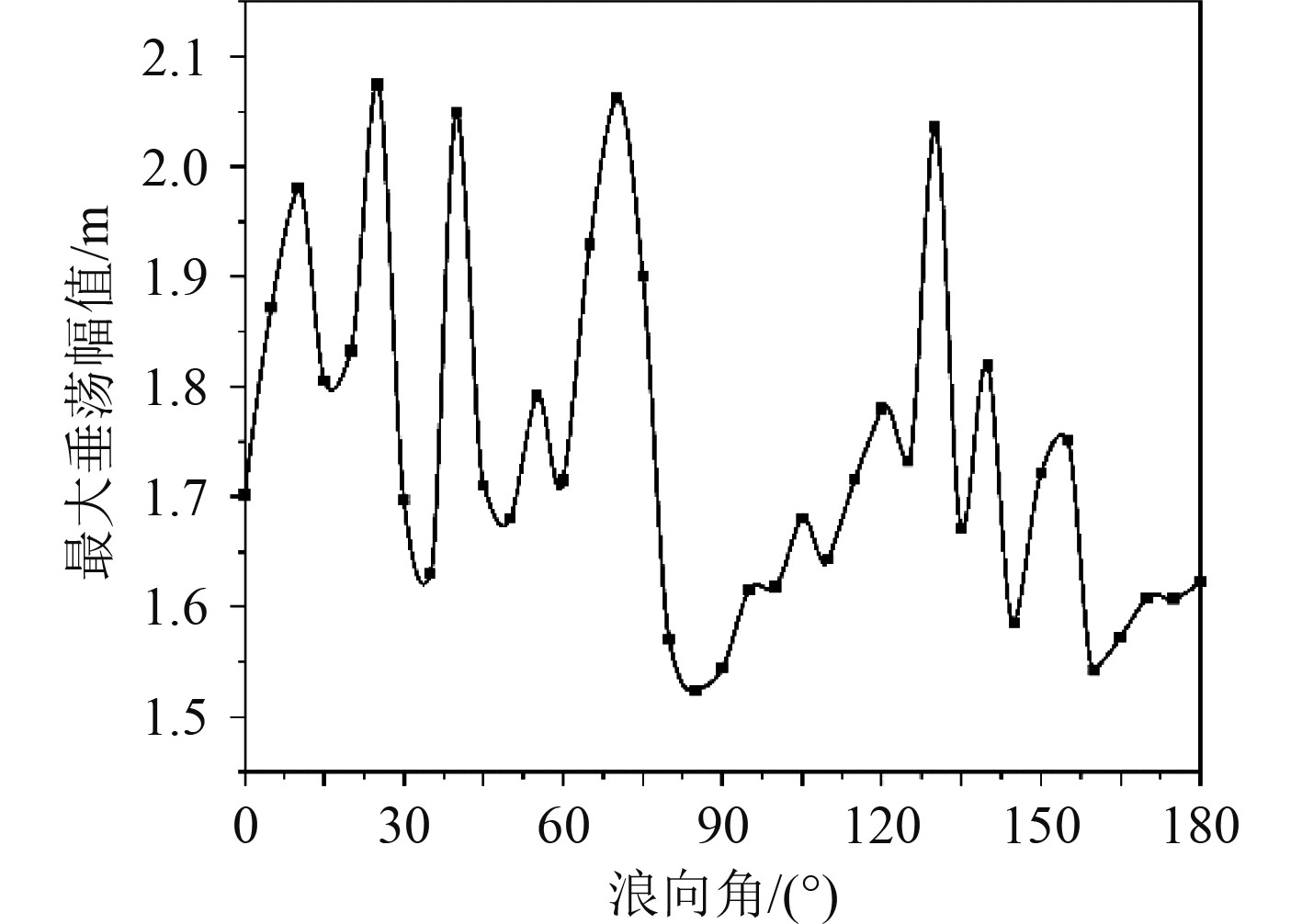
图13为补偿平台基座安装点位置处在不同浪向角下的最大垂荡幅值,从图可知,在其他环境条件不变的情况下,浪向角0°~90°区间内的最大垂荡幅值呈震荡趋势,在浪向角为25°、40°和70°时的垂荡幅值最大,在浪向角为90°时的垂荡幅值最小;在浪向角90°~180°区间内的最大垂荡幅值呈现先增大后减小的趋势,在浪向角为130°时的垂荡幅值最大。综上所述,在横浪时的垂荡幅值最小,在随浪时的垂荡幅值相对偏大。
|
图 13 基座安装点位置处在不同浪向角下的最大垂荡幅值 Fig. 13 The maximum heave amplitude at different wave angles at the location of the base installation point |
本文基于三维势流理论和波浪绕射理论,运用水动力软件AQWA计算分析了风电运维双体船在频域内的运动响应幅值、附加质量以及辐射阻尼,并基于频域计算结果,进一步通过时域耦合分析其在给定海况下的运动响应历程。此外,将风电运维船重心处的运动响应转换为六自由度补偿平台基座安装点位置处的运动响应,分析了该安装位置处垂荡、横摇和纵摇的运动响应以及在不同浪向角下的最大垂荡幅值,主要结论如下:
1)该风电运维船搭载的六自由度补偿平台基座处最大垂荡幅值是1.702 m,最大横摇幅度为0.5°,最大纵摇幅度为3.5°;
2)基于风电运维船在各个浪向下的频域运动响应特性,该船在波浪周期3~10 s时运动响应最剧烈,应避免在此波浪周期内开展运维工作;
3)基于不同浪向角下的补偿平台基座垂荡幅值对比,得出该船应选择在横浪状态下进行运维工作。
| [1] |
时智勇, 王彩霞, 李琼慧. “十四五”中国海上风电发展关键问题[J]. 中国电力, 2020, 53(07): 8-17. |
| [2] |
高巍, 周华. 风电运维船登靠作业概率评估[J]. 中国海洋平台, 2018, 33(06): 77-84. DOI:10.3969/j.issn.1001-4500.2018.06.012 |
| [3] |
FANG C C, CHAN H S A. Incecik. Investigation of motions of catamarans in regular waves—II[J]. Ocean Engineering, 1997, 24(10).
|
| [4] |
耿彦超, 顾学康, 汪雪良. 高速双体船斜浪中运动响应及连接桥波浪载荷预报[J]. 船舶力学, 2010, 14(04): 385-392. DOI:10.3969/j.issn.1007-7294.2010.04.009 |
| [5] |
金晨露. 风电双体维护船船型设计研究与水动力性能优化[D]. 镇江: 江苏科技大学, 2018.
|
| [6] |
周云司雅. 海上风电运维双体船减摇方法研究[D]. 镇江: 江苏科技大学, 2019.
|
| [7] |
邓磊, 董文才, 姚朝帮. 迎浪规则波中小水线面双体船纵向运动及波浪载荷非线性特性数值分析(英文)[J]. 船舶力学, 2017, 21(03): 249-262. DOI:10.3969/j.issn.1007-7294.2017.03.001 |
| [8] |
谢云平, 彭鹏. 海上三体风电运维船阻力和运动性能综合研究[J]. 船舶工程, 2015, 37(12): 13-17. |
| [9] |
RAÚL Guanche, MICHELE Martini, Alfonso Jurado, Iñigo J. Losada. Walk-to-work accessibility assessment for floating offshore wind turbines[J]. Ocean Engineering, 2016, 116. |
| [10] |
张萌. 海上廊桥波浪补偿控制研究[D]. 大连: 大连海事大学, 2020.
|
| [11] |
苏建国. 基于并联平台的海上风电运维船舶辅助登靠系统研究[D]. 南京: 南京理工大学, 2019.
|
| [12] |
徐佳. 具有波浪补偿功能的海上换乘舷梯设计与仿真[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [13] |
LI Ying, ZHOU Rui, LI Hao Kuan, et al. The Offshore Wave Simulation Based on the Improved P-M Spectrum and Multiple Fractal Interpolation[J]. Advanced Materials Research, 2014, 3470. |
| [14] |
戴佳莉, 陈新权, 杨启. 超大型双体船运动响应与波浪载荷研究[J]. 舰船科学技术, 2020, 42(17): 30-35. |
| [15] |
江苏大洋海装50m风电运维船试航成功[J]. 船舶工程, 2020, 42(1): 62.
|
 2022, Vol. 44
2022, Vol. 44

