舰载机由于其优秀的作战反应能力,受到各国海军的青睐,然而相对于陆基飞机而言,舰载机以有限长度的甲板起降,这必然对舰载机的着舰性能提出巨大考验。为了减少着舰距离,舰载机一般采用拦阻着舰的方式,而特殊的着舰方式也给舰载机起落架的设计提出了巨大挑战,因此准确的载荷分析对起落架的的安全至关重要。
对于飞机着舰回收技术,国外研究时间较长,大多以实验为主[1-3]。随着我国航空母舰的快速发展,舰载机着舰过程中起落架问题受到越来越多的学者关注,并取得了一定的进展[4-6],然而大多数理论中仅考虑了单体起落架落震以及起落架触地与拦阻钩勾索同时发生的状态,而忽略了自由飞行钩住的情况。
根据着舰撞击情况,每个下沉速度下总着舰次数的1/10是自由飞行钩住[7],因此研究舰载机自由飞行钩住着舰特性对于舰载机起落架设计以及飞机结构设计具有重要意义。本文以某型舰载机拦阻着舰为背景,在建立舰载机着舰仿真模型的基础上,考虑自由飞行钩住着舰时,舰上结合速度以及下沉速度对起落架动态特性的影响。
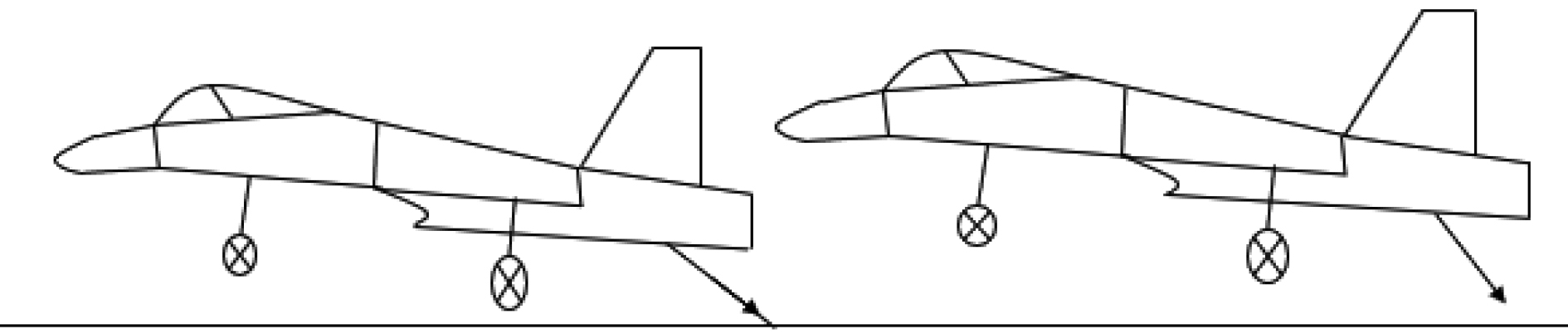
1 自由飞行钩住及说明 1.1 自由飞行钩住根据自由飞行钩住条件[8]可知,自由飞行钩住指的是舰载机起落架还未触舰时,拦阻钩已经勾住拦阻索的情况,如图1所示。
|
图 1 自由飞行钩住 Fig. 1 Free flight engagement |
根据自由飞行钩住时关于飞机重心离地高度的取值范围:由拦阻钩处于完全放下位置钩住拦阻索的状态,到拦阻钩旋转到主起落架触舰的同时拦阻钩挂索,重心高度处于这2种状态之间各值。因此为了便于分析,假设自由飞行钩住时拦阻钩以完全放下位置时挂索。如图2所示,主起落架刚好触舰,拦阻钩以完全放下位置钩锁时的飞机放置状态,相关几何参数如表1所示。

|
图 2 舰载机示意图 Fig. 2 Carrier-based aircraft diagram |
|
|
表 1 舰载机布局几何参数 Tab.1 Parameters of carrier-based aircraft |
为方便研究作出如下假设:
1)机体做刚性处理,即不考虑机体旋转部件及弹性变形的影响。
2)不考虑大气湍流、甲板运动对机体扰动的影响。
3)对于着舰过程中燃油消耗所引起舰载机质量以及质心位置的变化,则不予以考虑。
4)着舰过程中,仅考虑舰载机纵向平面内的运动。
2.2 坐标系定义由于舰载机在拦阻着舰过程中只考虑纵向平面的运动,坐标系定义如下:
1)大地坐标系(
原点
2)机体坐标系(
固定在舰载机上,原点
3)气流坐标系(
原点
4)减震支柱坐标系(
原点
舰载机着舰过程中受到的气动力表示为:
| $ \left\{ {\begin{array}{*{20}{c}} {L = \dfrac{1}{2}\rho {V^2}{S_A}{C_L}},\\ {D = \dfrac{1}{2}\rho {V^2}{S_A}{C_D}},\\ {{M_z} = \dfrac{1}{2}\rho {V^2}{S_A}l{m_z}} 。\end{array}} \right. $ | (1) |
式中:
其中总的缓冲器力
| $ {F_c} = {F_a} + {F_{oil}} + {F_f} + {F_s}。$ | (2) |
双腔缓冲器分为低压腔和高压腔,当活塞杆未进入高压腔时,缓冲器仅有低压腔工作,之后进入高压腔同时工作。空气弹簧力是由压气面积、初始压力和气体瞬时压缩比决定的,空气压力为:
| $ {F_a} = \left\{ \begin{array}{*{20}{l}} {{F_{a1}} = {A_{a1}}{P_{01}}{{\left( {\dfrac{{{V_{01}}}}{{{V_{01}} - {A_{a1}}S}}} \right)}^{{n_1}}}} ,\\ {F_{a2}} = {A_{a1}}\left[ {{P_{01}}{{\left( {\dfrac{{{V_{01}}}}{{{V_{01}} - {A_{a1}}S}}} \right)}^{{n_1}}} - {P_a}} \right] + \\ {A_{a2}}\left[ {{P_{02}}{{\left( {\dfrac{{{V_{02}}}}{{{V_{02}} - {A_{a2}}(S - {S_0})}}} \right)}^{{n_2}}} - {P_a}} \right],\end{array} \right. $ | (3) |
| $ {F_{oil}} = \frac{{\rho {A_h}^3\dot S}}{{2{{({C_d}{A_{01}})}^2}}}\left| {\dot S} \right| 。$ | (4) |
由于起落架刚性,不考虑支柱弯曲,因此有:
| $ {F_f} = \frac{{\dot S}}{{\left| {\dot S} \right|}}{\mu _{km}}{F_a} ,$ | (5) |
| $ {F_s} = \left\{ {\begin{array}{*{20}{c}} {{k_{\lim it}}S},\\ 0,\\ {{k_{\lim it}}(S - {S_{\max }})} ,\end{array}\begin{array}{*{20}{c}} {S < 0},\\ {0 \leqslant S \leqslant {S_{\max }}} ,\\ {S > {S_{\max }}} 。\end{array}} \right. $ | (6) |
式中:
当舰载机着舰时,来自甲板对轮胎的力为:
| $ {{\boldsymbol{F}}_t} = {k_t}\varepsilon + {c_t}\dot \varepsilon 。$ | (7) |
式中:
由于轮胎本身具有黏性阻尼作用而吸收功功,因此
| $ {k_t} = \frac{{6{W_{\max }}}}{{{D_{mdis}}^2}} - \frac{{2{F_{\max }}}}{{{D_{mdis}}}},$ | (8) |
| $ {c_t} = \frac{{6{W_{\max }}}}{{{D_{mdis}}^3}} - \frac{{3{F_{\max }}}}{{{D_{mdis}}^2}}。$ | (9) |
式中:
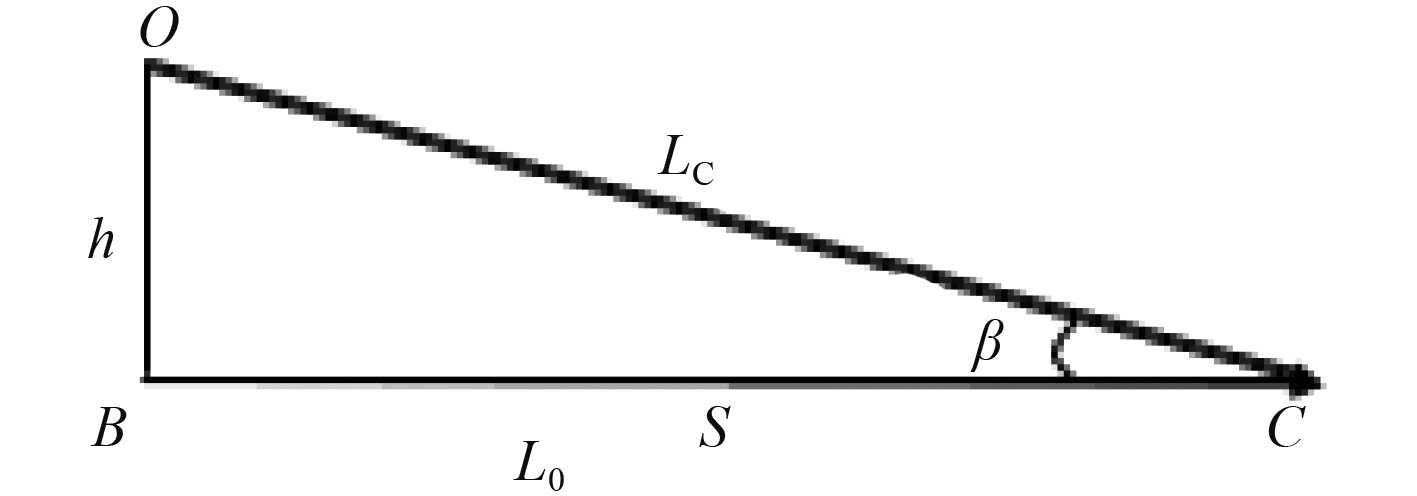
假设拦阻钩与拦阻索之间没有相对滑动,拦阻力理论模型如图3所示。
|
图 3 拦阻力力学模型 Fig. 3 Arresting force model |
图3中,
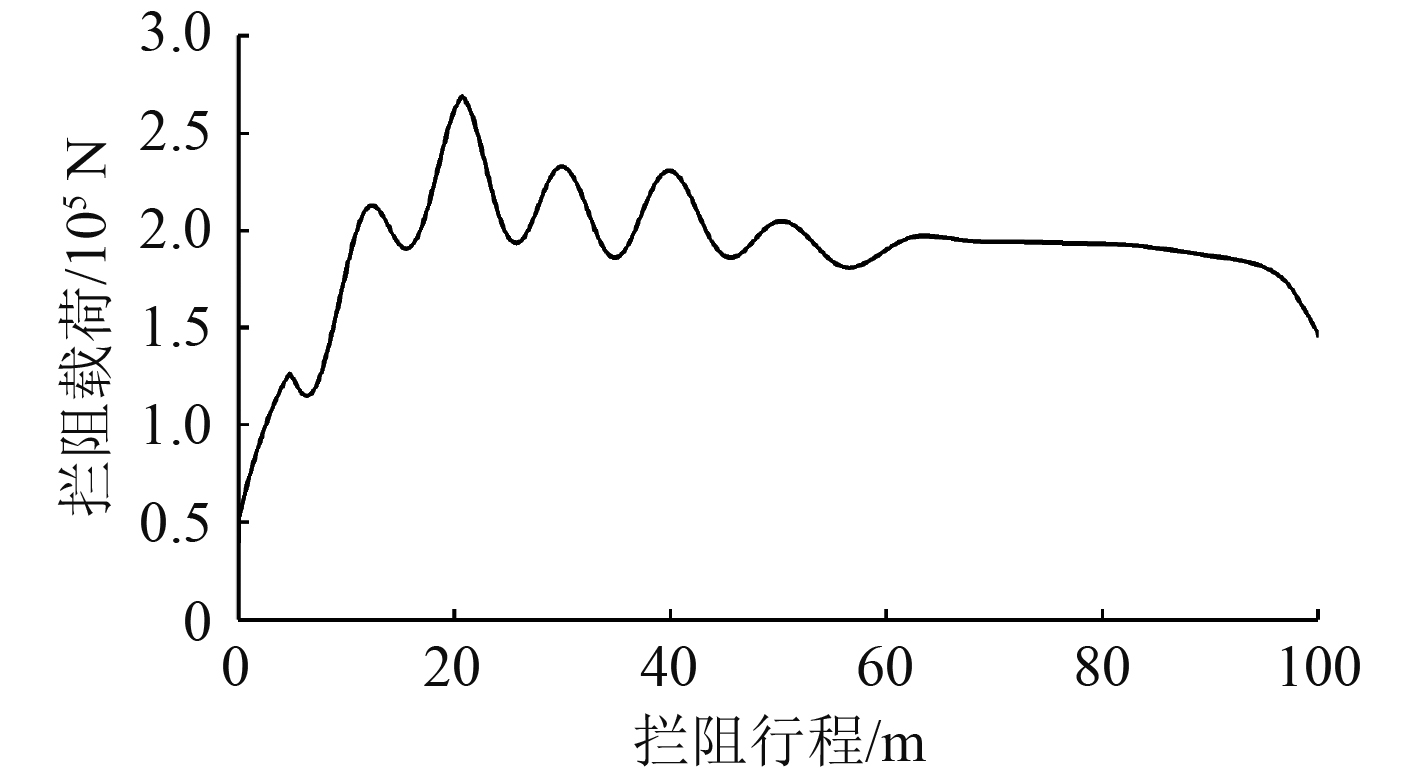
|
图 4 拦阻载荷-行程曲线 Fig. 4 Arresting force-displacement curve |
在
| $ {L_C} = \frac{{{L_0}}}{{\cos \beta }} = \frac{{{L_0}\sqrt {{h^2} + {s^2}} }}{s} 。$ | (10) |
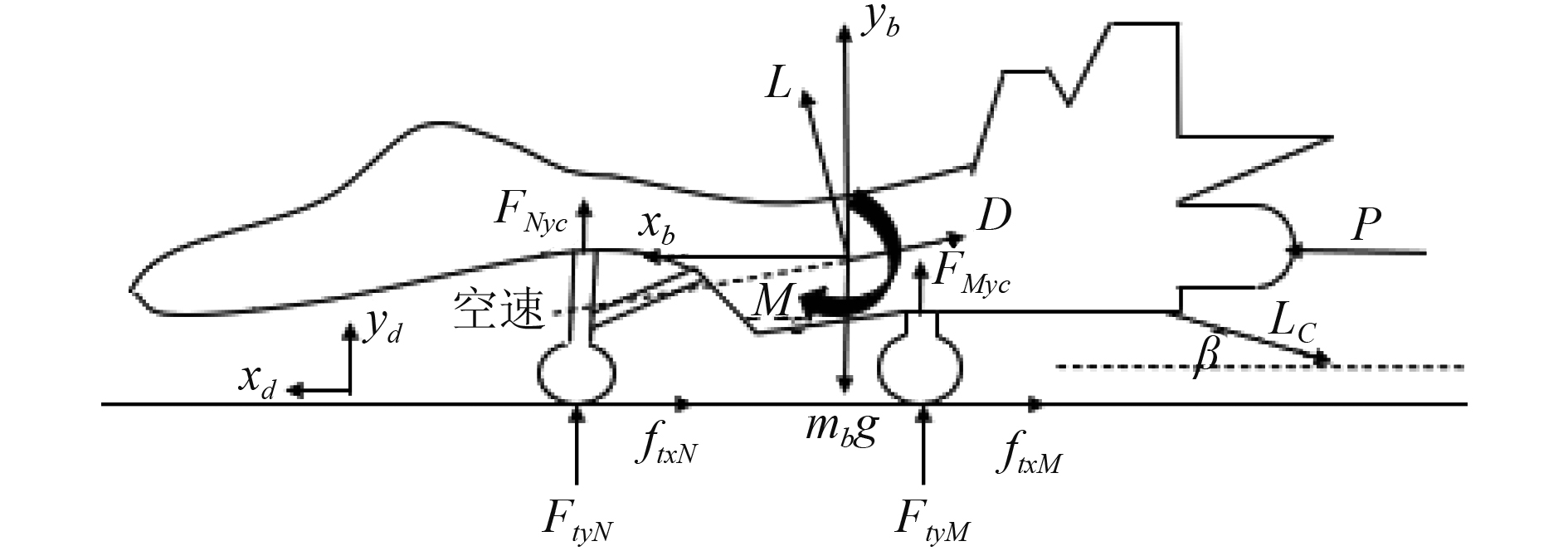
起落架采用二质量简化模型[9],舰载机机体着舰过程中受力分析如图5所示,舰载机在着舰过程中所受到的外力主要为发动机推力
|
图 5 舰载机着舰过程受力示意图 Fig. 5 Force diagram of Carrier aircraft airframe load landing process landing process |
由受力分析,可写出机体坐标系下舰载机的动力学方程,机体随质心平动方程:
| $\begin{split} & {m_b}\left( {\left[ {\begin{array}{*{20}{c}} {\dfrac{{{\text{d}}u}}{{{\text{d}}t}}} \\ {\dfrac{{{\text{d}}v}}{{{\text{d}}t}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{ - r} \\ r&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u \\ v \end{array}} \right]} \right) = \left[ {\begin{array}{*{20}{c}} {P - {L_C}\cos \beta } \\ {{L_C}\sin \beta } \end{array}} \right] + \\ & {{\boldsymbol{T}}_{ba}}\left[ {\begin{array}{*{20}{c}} { - D} \\ L \end{array}} \right] + {{\boldsymbol{T}}_{bd}}\left[ {\begin{array}{*{20}{c}} 0 \\ { - {m_b}g} \end{array}} \right] + \sum\limits_{i = N,ML,MR} {{{\boldsymbol{T}}_{bc}}\left[ {\begin{array}{*{20}{c}} {{F_{ixc}}} \\ {{F_{iyc}}} \end{array}} \right],}\end{split} $ | (11) |
机体绕质心转动方程:
| $ \begin{split} & {I_z}\dot r = {L_C}{\left[ {\begin{array}{*{20}{c}} {\sin \beta } \\ { - \cos \beta } \end{array}} \right]^{\text{T}}}\left[ {\begin{array}{*{20}{c}} {{d_x}} \\ {{d_y}} \end{array}} \right] + \sum\limits_{i = N,ML,MR} {{{\left[ {\begin{array}{*{20}{c}} {{F_{{\text{iyc}}}}} \\ {{F_{ixc}}} \end{array}} \right]}^{\text{T}}}} \left[ {\begin{array}{*{20}{c}} {{R_{xi}}} \\ {{R_{yi}}} \end{array}} \right] +\\ & \sum\limits_{i = N,ML,MR} {\left( {{f_{xi}}{\Delta _{yi}}} \right)} + {M_z},\end{split}$ | (12) |
起落架非弹性支撑部分平动与转动方程分别如下式:
| $\begin{split} & {m_q}_i\left( {\left[ {\begin{array}{*{20}{c}} {\dfrac{{{\text{d}}{u_i}}}{{{\text{d}}t}}} \\ {\dfrac{{{\text{d}}{v_i}}}{{{\text{d}}t}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{ - r} \\ r&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_i}} \\ {{v_i}} \end{array}} \right]} \right) = \\ & {{\mathbf{T}}_{bd}}\left[ {\begin{array}{*{20}{c}} { - {f_{txi}}} \\ {{F_{tyi}} - {m_q}_ig} \end{array}} \right] - {{\mathbf{T}}_{bc}}\left[ {\begin{array}{*{20}{c}} {{F_{ixc}}} \\ {{F_{iyc}}} \end{array}} \right],\end{split} $ | (13) |
| $ {I_{\omega i}}\frac{{{\text{d}}{\omega _{\omega i}}}}{{{\text{d}}t}} = {f_{txi}}\left( {{R_{0i}} - {\varepsilon _i}} \right)。$ | (14) |
式中:
针对某型号舰载机,通过LMS.Virtual. Lab Motion建立甲板模型和舰载机全机模型。舰载机拦阻着舰过程中,对舰载机着舰状态有重要影响的8个参数为:接地限制速度
已知舰载机着舰重量为7100 kg,双发发动机推力为40 kN,从拦阻钩拦阻索刚啮合时开始仿真直至1.8 s结束。
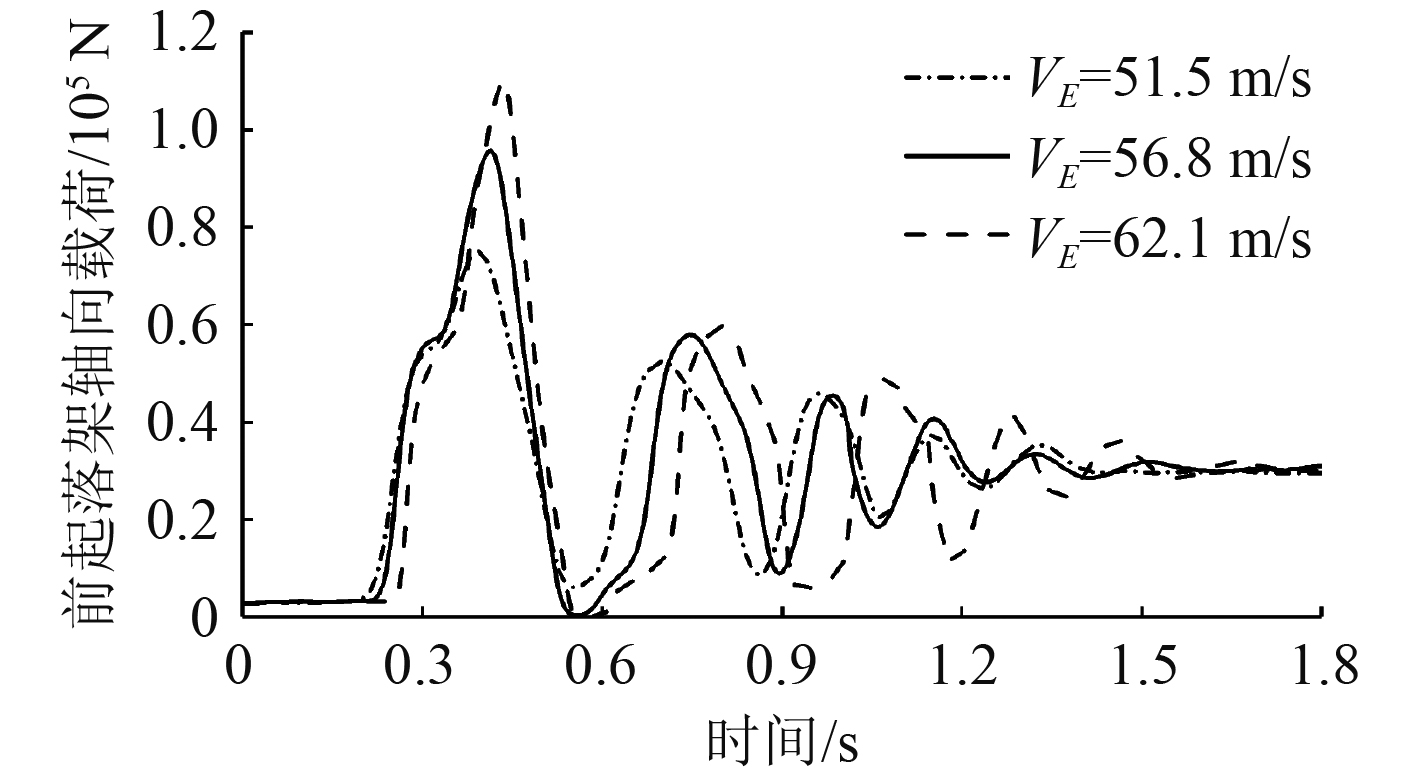
|
图 6 前起落架轴向载荷-时间曲线 Fig. 6 Axis load-time curves of nose landing gear |
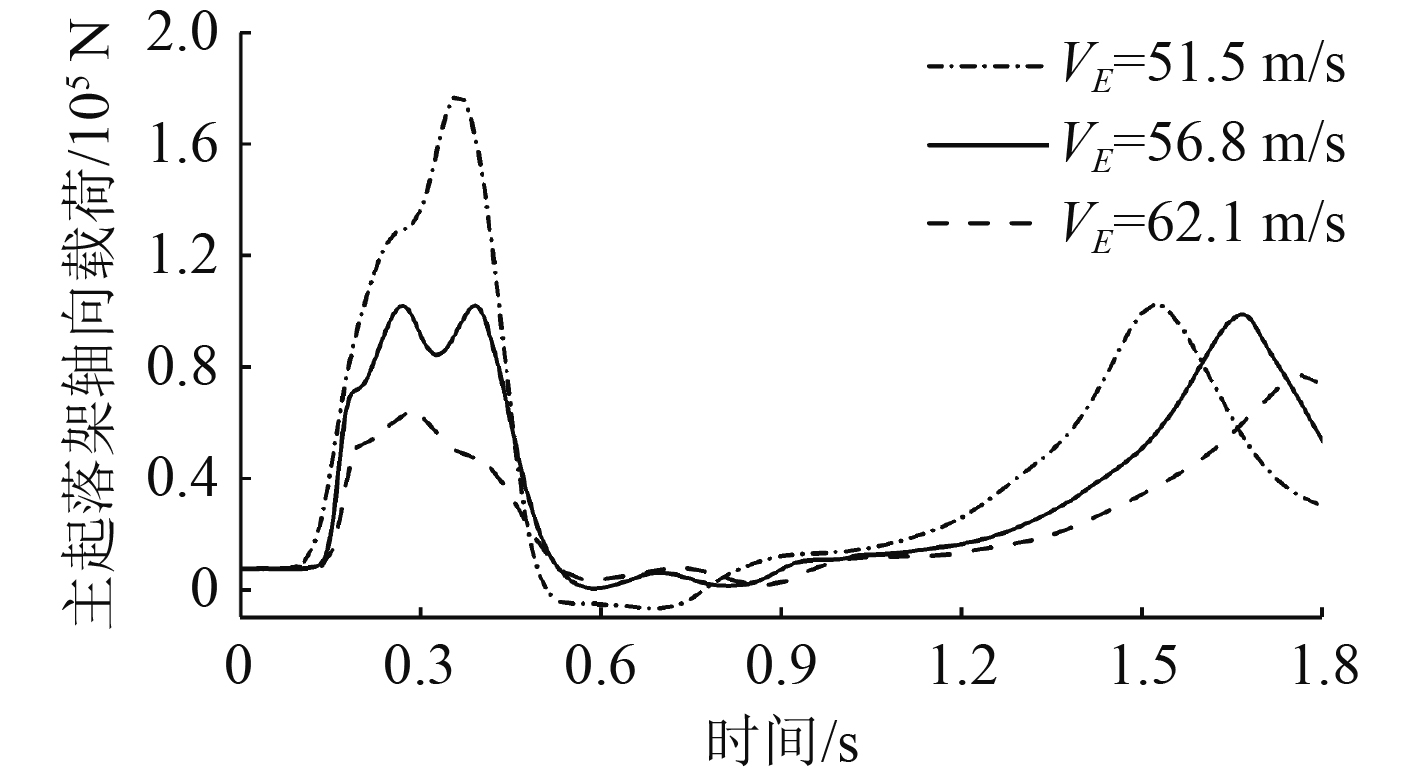
|
图 7 主起落架轴向载荷-时间曲线 Fig. 7 Axis load-time curves of main landing gear |
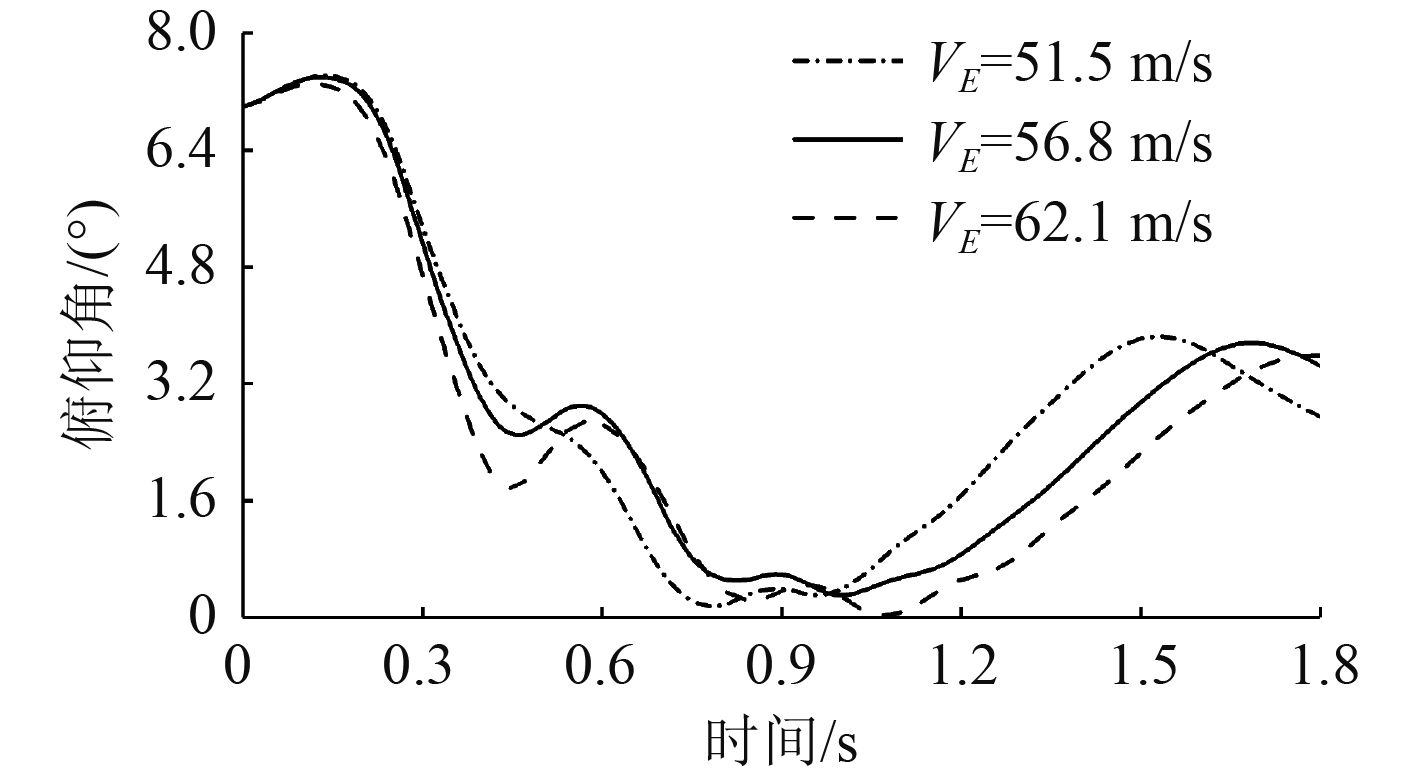
|
图 8 俯仰角变化规律 Fig. 8 Pitching angle |
由仿真结果可以看出,随着水平速度的增大,舰载机在0.4 s内低头速率逐渐增大,主要是由于升力的增大延缓了触舰的时间,拦阻力在同等时间内对机头做的功更多,从而导致在较大的水平速度下,前起落架轴向载荷更大。同等姿态时,越大的水平速度,升力越大,对主起落架受载减弱能力也越大,因此,主起落架所受载荷也就越小。
3.2 下沉速度对起落架轴向载荷的影响在
如图9所示,随着重心处下沉速度的减小,主起落架触舰时刻的下沉速度几乎与重心处下沉速度相当,而前起落架触舰时刻的下沉速度快速增大;当初始下沉速为1.2 m/s,前起落架着舰时刻的下沉速度更是达到了4.3 m/s左右。主要因为当初始下沉速度减小时,着舰速度减慢,拦阻力对机头的低头力矩作用的时间更长,从而出现前起落架着舰时的下沉速度较大的情况。
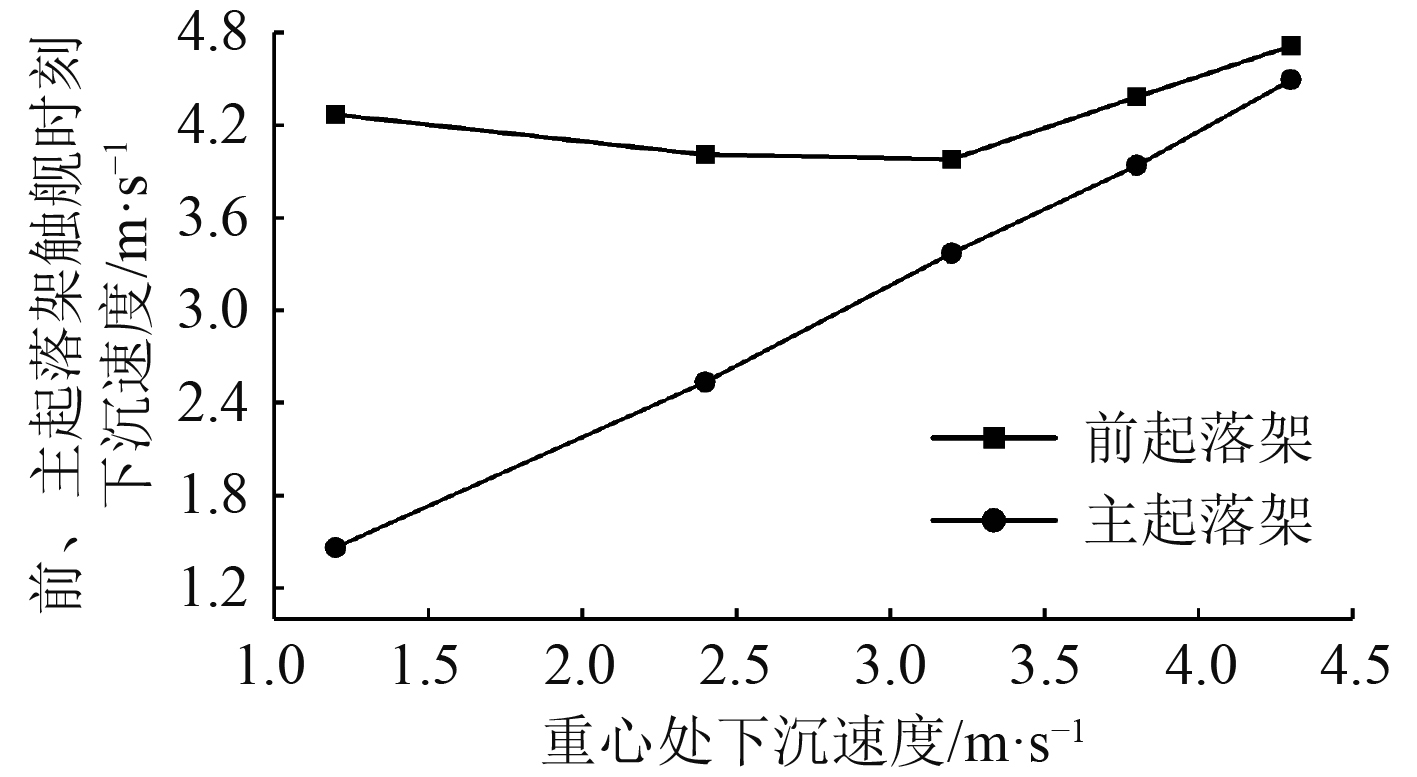
|
图 9 重心处下沉速度下前、主起落架触舰时刻的下沉速度 Fig. 9 Sink speed of nose and main gear at landing time during different sinking speed |
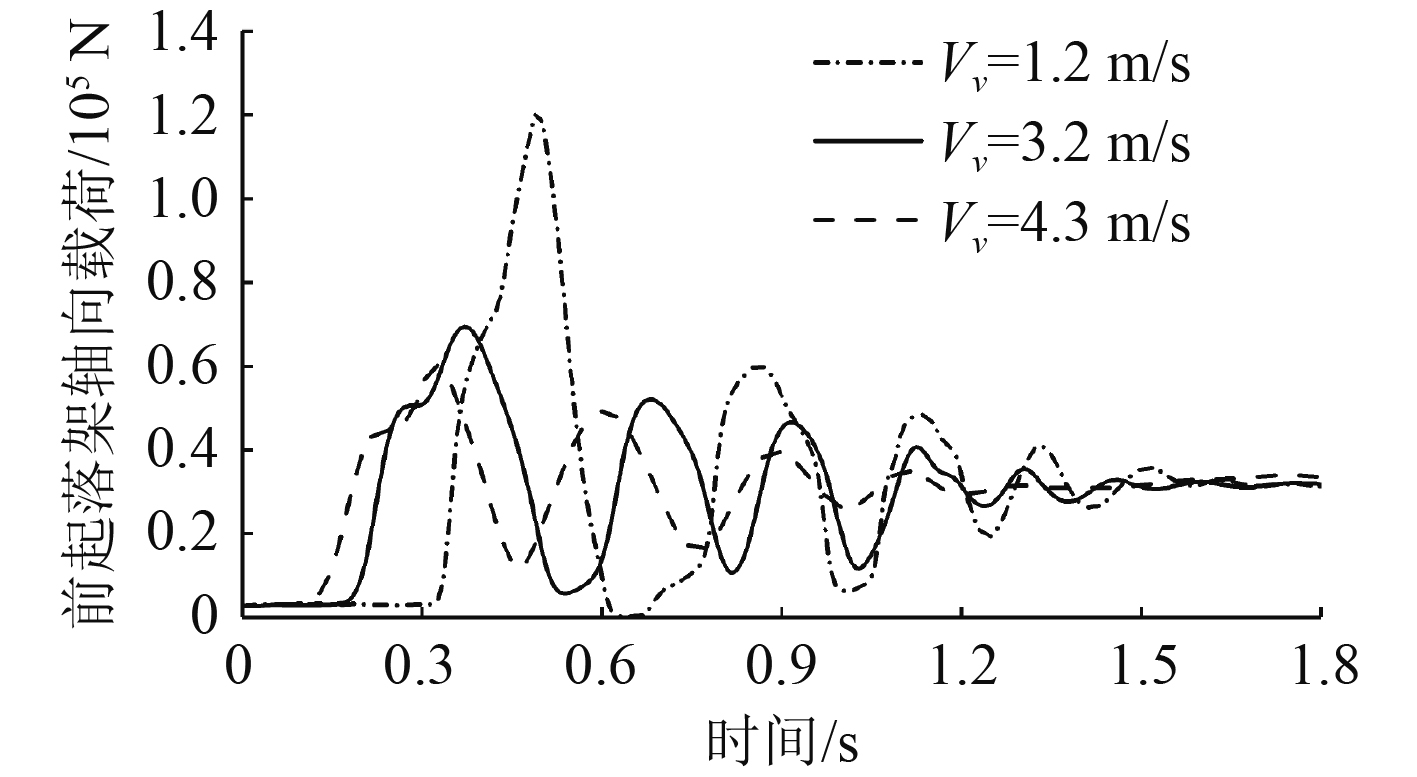
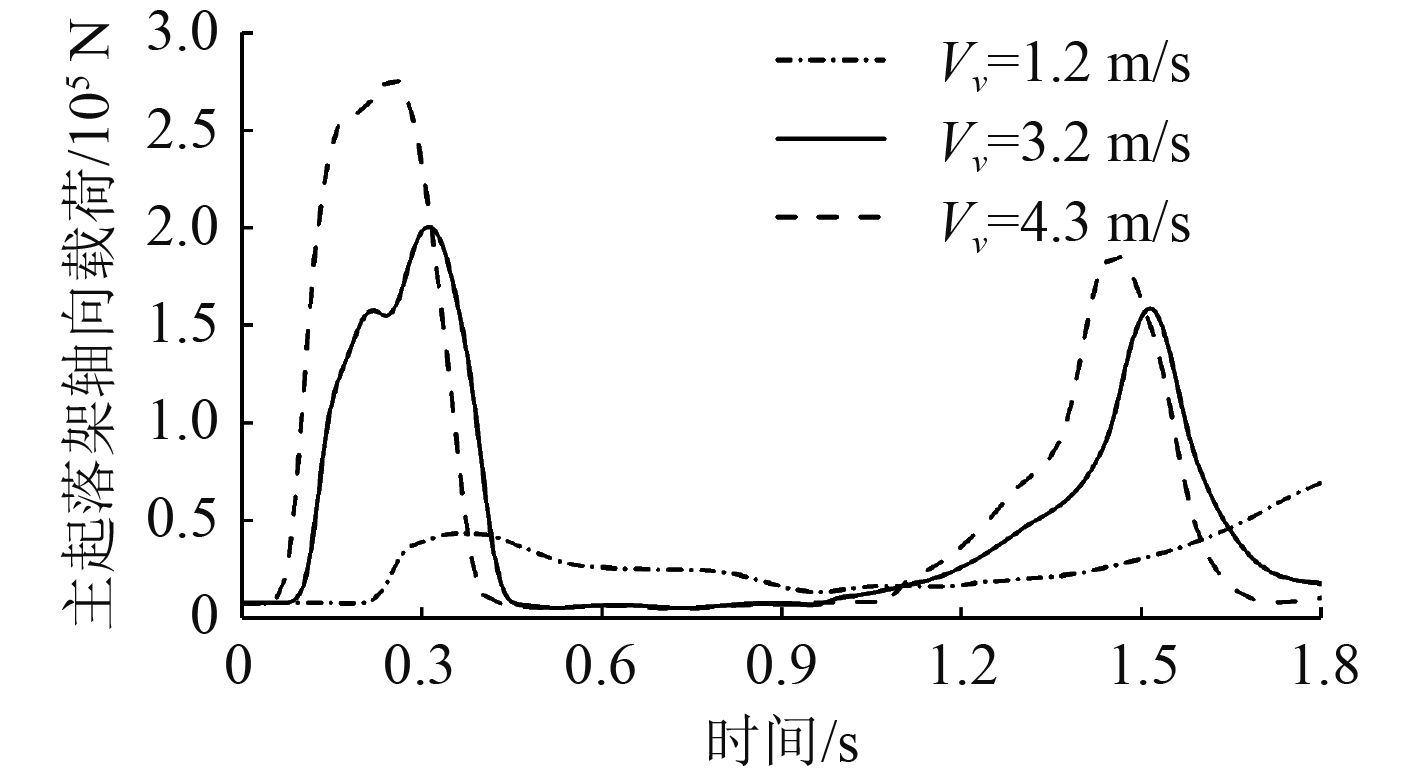
由图10和图11可以看出,随着初始下沉速度越大,主起落架轴向载荷峰值越大,而前起落架受载则与之相反。另外下沉速度越小,着舰越滞后,当初始下沉速度为1.2 m/s时,前起落架轴向载荷达到了12 kN,是以4.3 m/s着舰所受载的2倍左右,且此时前起落架作为主要承载机构。
|
图 10 前起落架轴向载荷-时间曲线 Fig. 10 Axis load-time curves of nose landing gear |
|
图 11 主起落架轴向载荷-时间曲线 Fig. 11 Axis load-time curves of main landing gear |
本文针对在拦阻钩处于完全放置状态下钩索时,舰载机以自由飞行钩住方式着舰的情况下,分析水平速度以及下沉速度对起落架轴向载荷的影响。通过仿真分析,相比于舰上结合速度,下沉速度对起落架轴向载荷影响较大,其中前起落架轴向载荷对小下沉速度较为敏感,分析结果可以为起落架结构设计提供依据。
| [1] |
SOMIESKI G. Shimmy analysis of a simple aircraft nose landing gear model using different mathematical methods[J]. Aerospace Science & Technology, 1997, 1(8): 545-555. |
| [2] |
PRITCHARD J. Overview of landing gear dynamics[J]. Journal of Aircraft, 2001, 38(1): 130-137. DOI:10.2514/2.2744 |
| [3] |
NORWOOD D S, CHICHESTER R H. Full scale aircraft drop test program for the F-35C carrier variant[J]. AIAA Journal, 2015.
|
| [4] |
贾忠湖, 郑小洪. 拦阻着舰过程中的飞机起落架动力学分析[J]. 海军航空工程学院学报, 2012, 27(1): 50-54. JIA Zhong-hu, ZHENG Xiao-hong. Analysis of the dynamic loads of aircraft's landing gear during the arresting[J]. Journal of Naval Aeronautical and Astronautical University, 2012, 27(1): 50-54. DOI:10.3969/j.issn.1673-1522.2012.01.012 |
| [5] |
魏小辉, 聂宏. 舰载机起落架落震性能动力学仿真分析[J]. 中国机械工程, 2007(5): 520-523. WEI Xiao-hui, Nie Hong. Study on landing impact force of carrier-based aircraft landing gears[J]. China Mechanical Engineering, 2007(5): 520-523. DOI:10.3321/j.issn:1004-132X.2007.05.005 |
| [6] |
田佳杰, 牟钋, 程素华, 等. 大下沉速度下的起落架落震仿真与试验[J]. 液压与气动, 2020(10): 174-180. TIAN Jia-jie, MU Po, CHENG Su-hua, et al. Drop simulation and drop test of aircraft main laning gear with high sinking speed[J]. Chinese Hydraulics & Pneumatics, 2020(10): 174-180. DOI:10.11832/j.issn.1000-4858.2020.10.029 |
| [7] |
中国人民解放军总装备部. 军用飞机结构强度规范重复载荷、耐久性和损伤容限; GJB 67.6A-2008[S]. 北京: 中国人民解放军总装备部, 2008.
|
| [8] |
MIL-A-8863C. Military specification airplane strength and rigidity ground loads for navy acquired airplanes[S].
|
| [9] |
聂宏, 魏小辉, 等. 飞机起落架动力学设计与分析[M]. 西安: 西北工业大学出版社, 2013.
|
 2022, Vol. 44
2022, Vol. 44
