2. 喷水推进技术重点实验室,上海 201100
2. Science and Technology Laboratory of Water-jet Propulsion, Shanghai 201100, China
带坞舱类运输船型在航行过程中,可通过下放尾跳板形成半开敞水域供坞舱内的浮式舟艇或泛水车辆快速进出,具有特殊的应用前景。但同时在使用过程中,坞舱内部和舱口附近区域的尾流受到下放尾跳板、推进装置以及坞舱回流的共同作用,相应的流场特性十分复杂,有着独特的变化规律。为了确保浮式舟艇和车辆进出坞作业的顺利进行,避免因坞舱内水深估计不足发生触底、搁浅等危险,需要对舱内及尾流段的流场特性及母船对其影响规律展开研究。
带坞舱船舶相较于常规船型主要有2个特点:一是尾部包含半开敞坞舱水域;二是下放的尾跳板会对船舶阻力及尾流场产生较大影响。目前国内外对带坞舱船舶的研究成果发表相对较少。2019年胡晓庆[1]就带坞舱的Wigely-III船型在不同浪向下的运动响应以及坞舱内有浮体时耦合运动响应展开研究,初步分析了波浪等特征对船体及浮体运动的影响。2020年,Xu[2]延续胡晓庆的研究工作,针对坞舱中带有浮体的Wigely-III船在规则波中运动时,母船及浮体的运动特性展开研究,工作表明坞舱对船舶水动力性能影响不大。上述研究工作中,采用的船型并非常规的带坞舱方尾船型、不包含尾跳板且坞舱外形与常规带坞舱船舶有较大不同。此外,研究工作主要侧重于船舶整体的运动,并未对细节流场进行分析。
船舶下放的尾跳板不仅在结构尺寸上远大于尾压浪板,且工作工况也有较大区别,尾跳板通常作用于船舶低速工况,而尾压浪板应用于高速船舶。但2种装置对尾流场的影响有一定的相似之处,可以作为研究参考。早在1989年,美国海军在“科普兰”号(FFG25)[3]上安装了压浪板,并通过实船试验证明了压浪有较好的减阻性能。2004年,程明道[4]研究方尾高速船加装尾板试验中发现,加装尾压浪板后,船后鸡尾流变长,从而减小船舶兴波阻力。2011年,澳大利亚对Aguisa导航艇[5]加装尾压浪板的模型试验中表明,压浪板最佳减阻攻角与航速呈一定的负相关关系,即船舶航速越高,压浪板最佳减阻攻角越小。近年来,针对压浪板相关的研究工作主要围绕压浪板的形状对所应用船型的减阻效果展开。2019年,李冬琴[6]对分段式压浪板减阻性能展开研究;陈怀远[7]对平面及曲面压浪板的减阻效果展开研究,结果表明压浪板对船尾水流有阻滞作用,改善尾流场,使鸡尾流后移。本文研究中,尾跳板下放设计的主要目的是改善尾流场,便于浮式装备进出坞操作,目前国内外相关研究工作还较少。
本文建立带坞舱、尾跳板以及推进系统的母船数值仿真模型,采用基于虚拟盘的体积力法的螺旋桨模型,依据匀速运动需求实时调整螺旋桨转速,构建船舶匀速航行时船、桨、跳板耦合作用下真实尾流场仿真模型。通过对舱内及尾流段水体精细化分析,获得舱内水体分布及运动规律,研究航速及尾跳板攻角对舱内水体及尾流的影响。
1 数值计算方法简介带坞舱船舶航行时,船舶尾流区水体运动会同时受到坞舱内外半开水域、下放尾跳板及推进装置尾流的联合作用。为充分考虑推进装置对尾流影响,准确捕捉水体运动规律,通常采用螺旋桨体积力法,其在外流场上与直接螺旋桨仿真结果基本一致[8],可足够反映船桨的相互作用,常用于船舶自航数值仿真[9] ,因此本文采用处理方便、高效的虚拟盘螺旋桨模型。
1.1 控制方程对于两相不可压绕流问题,引入体积力时,相应的连续性方程和动量方程如下:
| $ \dfrac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathit{u}\right)=0 ,$ | (1) |
| $ \frac{\partial \mathit{u}}{\partial t}+\mathit{u}\cdot \nabla \mathit{u}=-\frac{1}{\rho }\nabla p+\nabla \cdot \left({\nu }_{eff}\left(\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^{{\rm{T}}}\right)\right)+{\mathit{f}}_{\sigma }+{\mathit{f}}_{b} 。$ | (2) |
其中:
| $ \frac{\partial \alpha }{\partial t}+\nabla \cdot \left(\alpha \mathit{u}\right)+\nabla \cdot \left[\left(1-\alpha \right)\alpha {\mathit{u}}_{r}\right]=0,$ | (3) |
其中
| $ {\mathit{f}}_{bx}=\frac{105}{8}\times \frac{T}{{\text{π}} {t}_{b}\left(3{R}_{H}+4{R}_{p}\right)\left({R}_{p}-{R}_{H}\right)}\times {r}^{*}\sqrt{1-{r}^{*}} ,$ | (4) |
| $ {\mathit{f}}_{b\theta }=\frac{105}{8}\times \frac{Q}{{\text{π}} {t}_{b}\left(3{R}_{H}+4{R}_{p}\right)\left({R}_{p}-{R}_{H}\right)}\times \frac{{r}^{*}\sqrt{1-{r}^{*}}}{{r}^{*}\left({R}_{p}-{R}_{H}\right)+{R}_{H}},$ | (5) |
| $ {r}^{*}=\frac{r-{R}_{H}}{{R}_{p}-{R}_{H}}。$ | (6) |
其中:
为了模拟船舶匀速运动工况下的真实尾流场,采用依据船舶阻力实时调整螺旋桨转速的方式来保证船舶推力与阻力平衡:
| $ {R}_{T}=NT。$ | (7) |
其中:
| $ n=60\sqrt{\frac{{R}_{T}}{\rho N{D}^{4}{K}_{T}}}。$ | (8) |
其中:
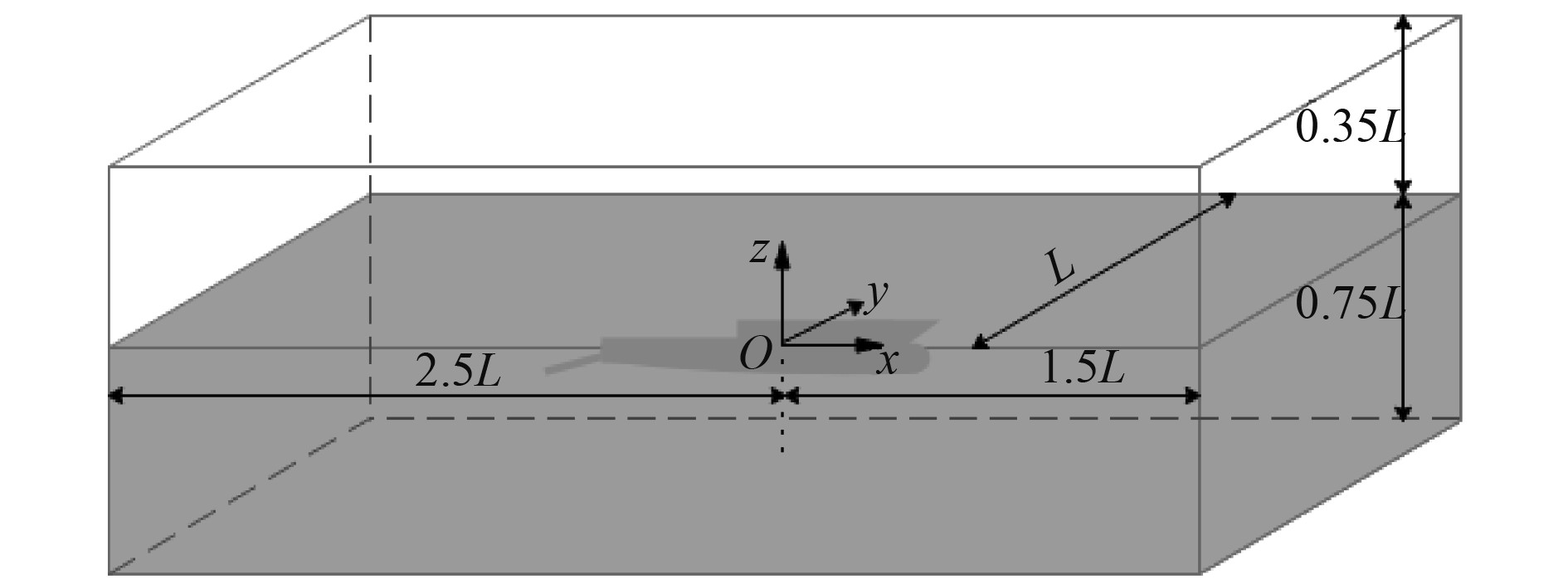
针对某典型带尾门、坞舱船型展开研究。考虑到船体、推进装置分布以及运动的对称性,引入对称面,采用半流场进行数值仿真减少计算量。计算域尺寸如图1所示。
|
图 1 带坞舱船舶仿真计算域 Fig. 1 Computation domain for ship with well deck |
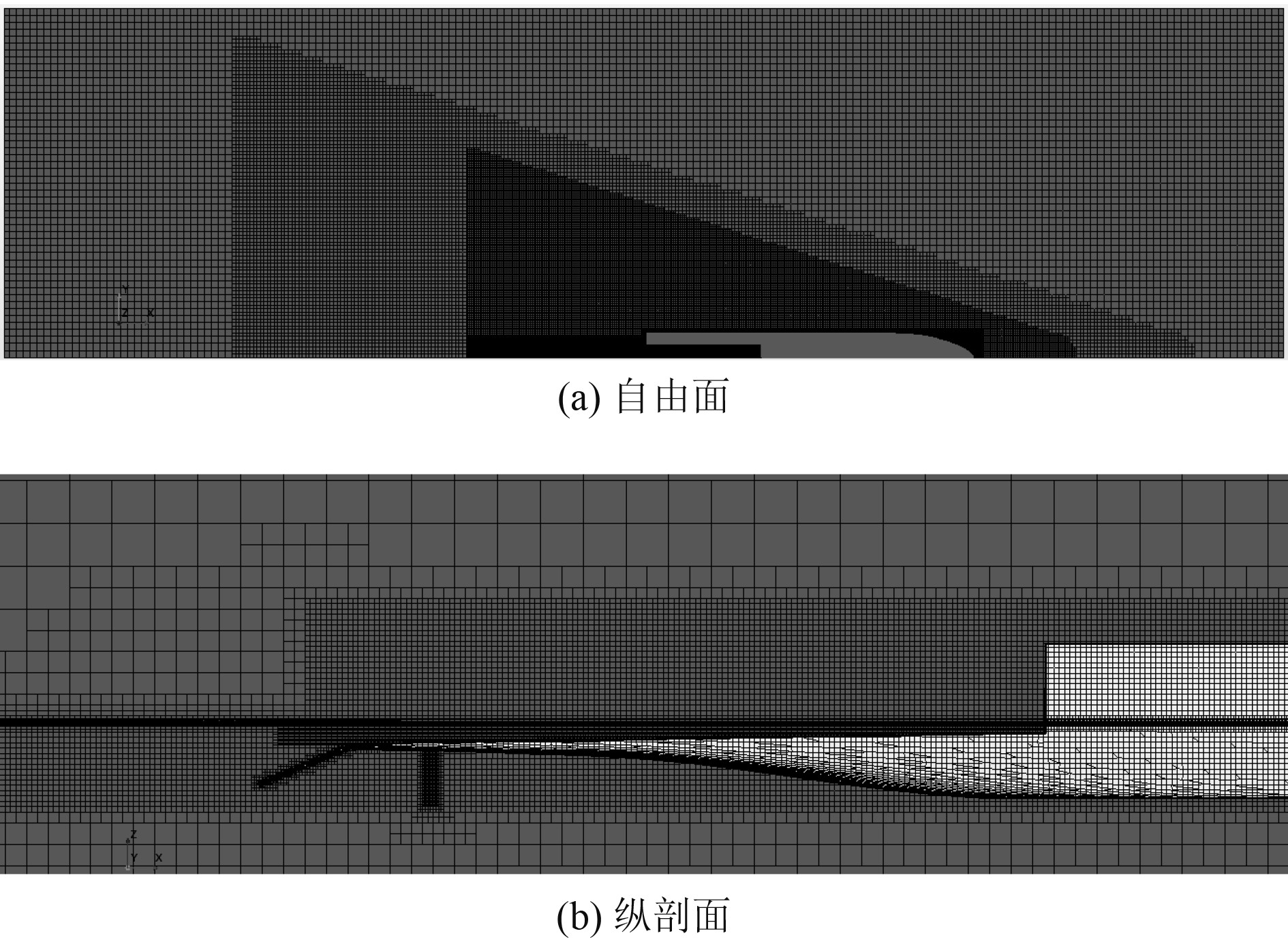
浮式舟艇装备进出坞舱作业时,母船通常处于超低速航行状态,兴波波幅较小。为精确地捕捉自由面变化,相较于常规的船舶定常兴波计算,需要采用更精细的自由面网格。此外,尾部坞舱及尾流部分的水体运动相对复杂,需要根据试算的自由面波高情况进行局部加密。另外,尾跳板及虚拟盘等关键构件区域同样需要进行加密处理,如图2所示。
|
图 2 计算网格划分 Fig. 2 Mesh of the computational domain |
由自由面及虚拟盘剖面网格图可见,计算网格采用切割体网格生成,加密区域主要位于自由面、坞舱、尾流段、虚拟盘以及尾跳板等处。船体及坞舱内第一层网格与壁面无因次距离y+为30~60左右。考虑到主要研究重点在于水体运动,自由面及坞舱附近的网格密度是精确捕捉水体运动的关键。因此,在进行网格无关性验证时,边界层网格变化不大,主要通过控制自由面及坞舱内网格密度进行网格收敛性验证,网格选取如表1所示。
|
|
表 1 网格收敛性分析 Tab.1 Mesh convergence analysis |
表1中,阻力系数
|
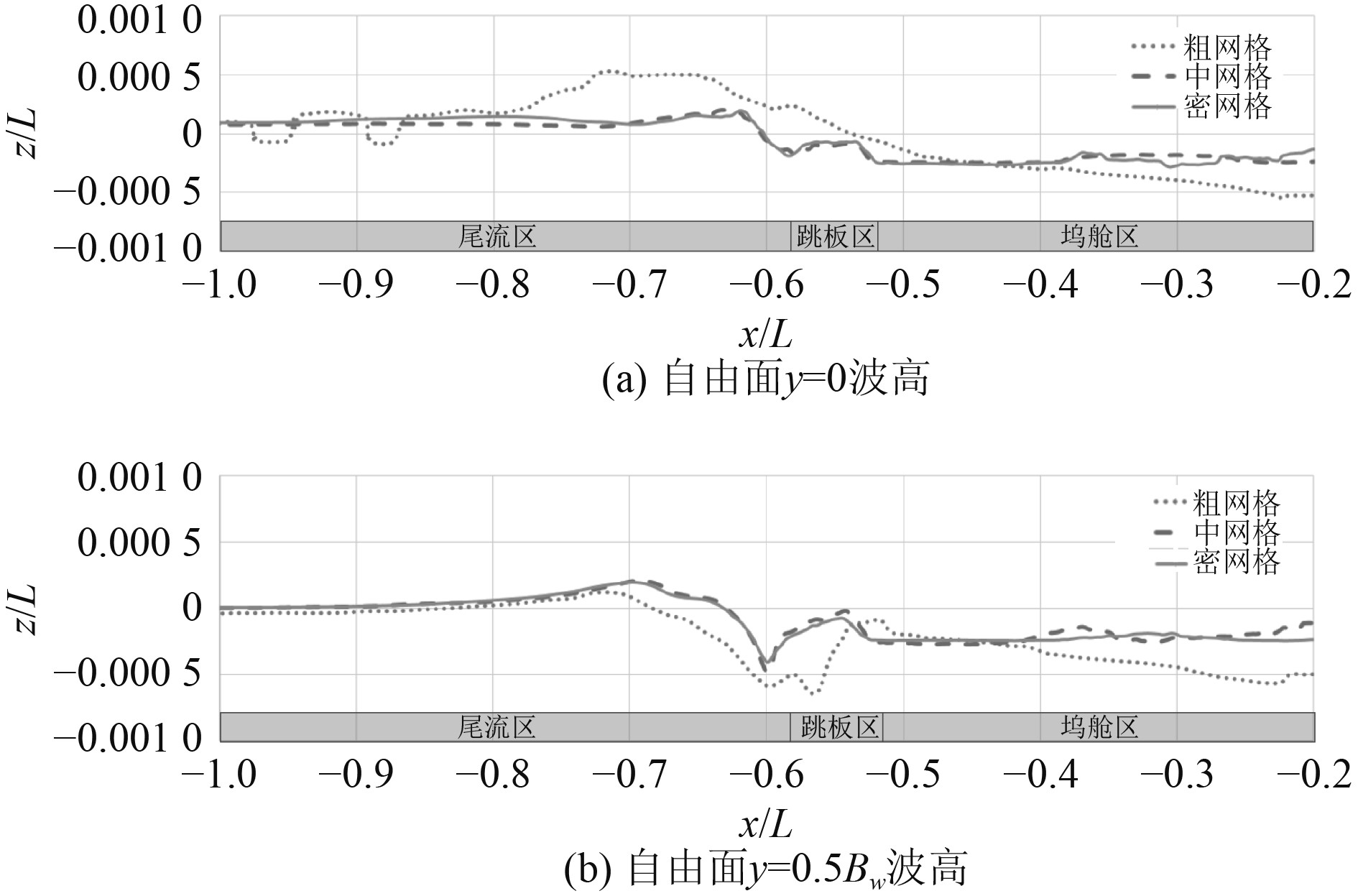
图 3 自由面监测线波高 Fig. 3 Wave elevation on monitor lines |
图3给出了自由面与中纵剖面以及坞舱y=0.5
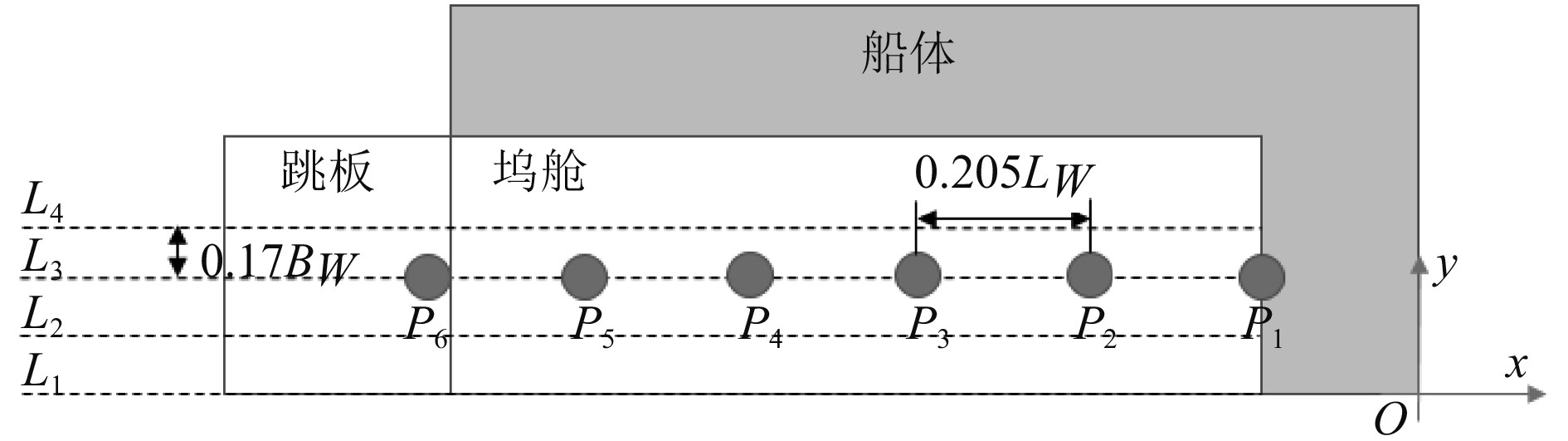
为了进一步研究匀速航行时坞舱内的水体运动情况,选取一系列检测线和监测点进行水体运动监测,相关监测线及点分布如图4所示。
|
图 4 监测位置示意图 Fig. 4 Schematic diagram of monitor position |
选取4条检测线及6处监测点,其中
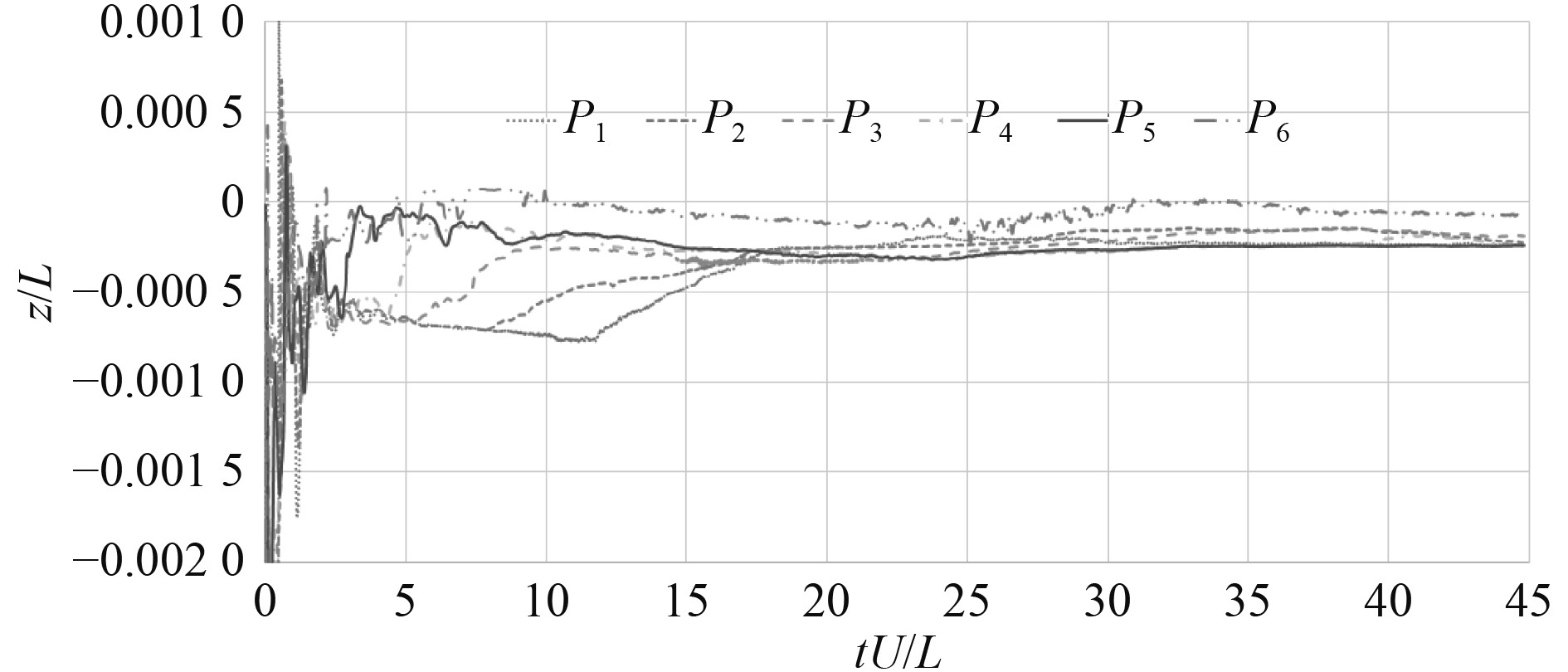
|
图 5 监测点水体运动时历 Fig. 5 Wave elevation history on monitor points |
图5中,横坐标为无因次化的时间,纵坐标为无因次自由面高度。由图5可见,除去前2个特征周期内的非稳定状态,舱内水体运动主要分为3个阶段。
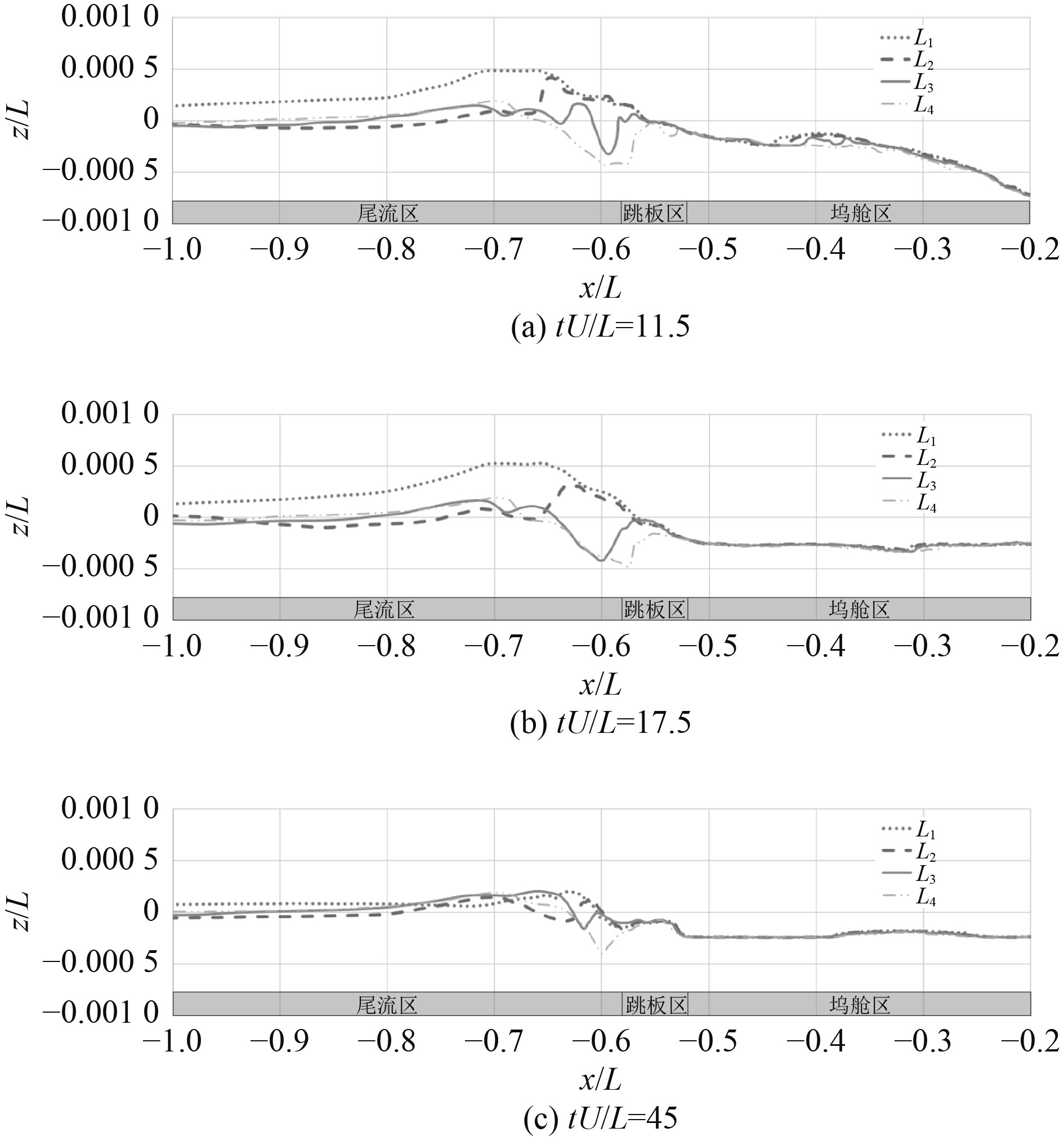
|
图 6 监测线上水体分布 Fig. 6 Wave elevation on monitor lines |
由图6可见,坞舱内的水体运动主要集中在坞舱内侧区域,在坞舱靠近尾部出口段的水体运动幅度相对较小。对比图6(b)与图6(c)可见,在水体运动第3阶段,虽然舱内水体变化不大,但跳板区及尾流区水体变化明显,鸡尾流高度变小,同时尾流区、跳板区以及坞舱区的水位呈阶梯分布。为了更直观地观察尾流区水体运动情况,给出
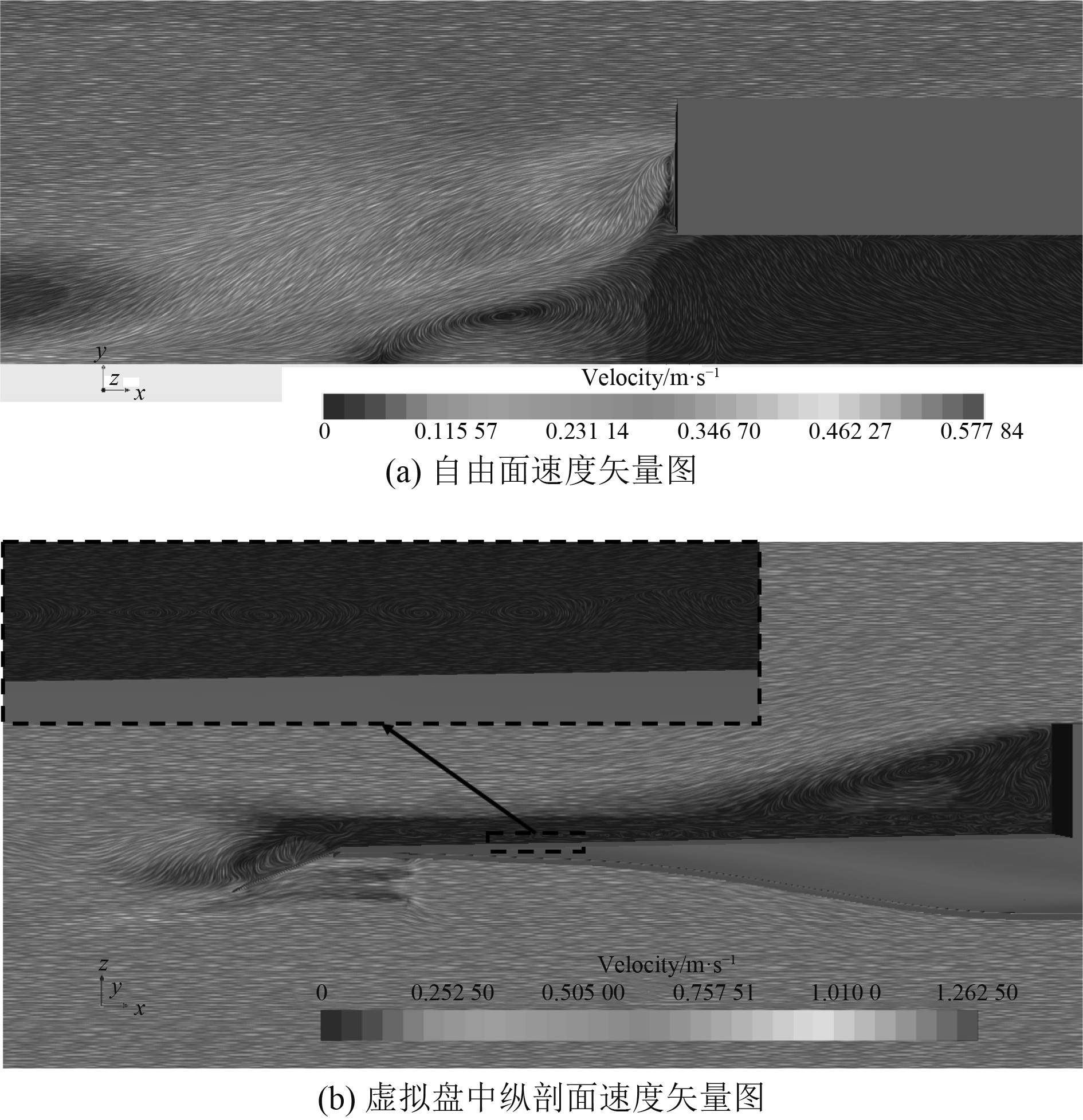
|
图 7 船尾附近流场速度云图 Fig. 7 Velocity contour around stern |
由图7(a)可见,流场稳定后,坞舱内的水流速较小接近于0,舱内低速水流与舱外高速水流在尾部交界处会形成明显的分界线。同时,在尾板上方高速流动到低速流动的过渡区域内会形成较大的涡结构。由7(b)可见,下放的尾跳板处于螺旋桨尾流中,会产生较大的阻力及纵摇力矩,从而容易影响船体的航速及稳定性。此外,由局部放大图可见,坞舱内的水体流动虽然缓慢,但存在许多细小的涡结构,一定程度上影响坞舱内浮式装备运动的稳定性。
2.3 航速对舱内水体运动影响研究考虑到浮式装备进出坞作业过程中,船舶航速会因任务需求改变,舱内及尾流区水体的运动规律也会有不同。因此,为了研究舱内水体运动随航速变化的关系,这里对船舶Fr=0.044,0.066以及0.088的3种低航速工况展开研究。坞舱及尾流区的流场如图8所示。

|
图 8 不同航速时舱内水体等值线图 Fig. 8 Velocity contour in well deck at various advancing velocity |
由图8可见,随着航速的升高,坞舱内同区域的水位逐渐降低,尾流中鸡尾流高度逐渐增加。此外,在尾流以及坞舱内水体对流的作用下,坞舱尾部的尾流中涡系结构对自由面的影响逐渐显著,这为船舶进出坞作业航向控制带来一定的挑战。为了定量地反映不同航速下水体运动情况,选取中纵对称平面上的自由面高度对比,如图9所示。
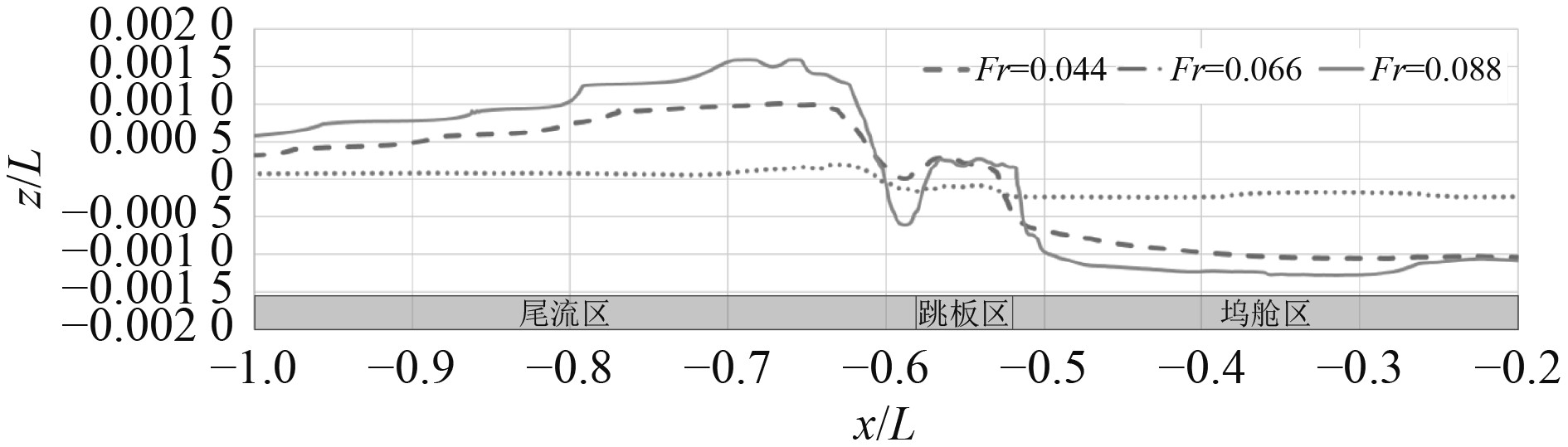
|
图 9 不同航速波高对比图 Fig. 9 Wave elevation at various advancing velocity |
由图9可见,随着船舶航速增加,尾流的基本分布趋势一致,但坞舱内水位下降,跳板上方水位升高,同时鸡尾流高度变大。该现象表明,船舶航速越高,舱口附近水面坡度越大,对浮式舟艇低速进出坞容易产生不利影响。对于坞舱内部,由于舱内通常采用斜底结构,坞舱口水深大,而舱内端水深小,在舱内水位下降时相对水深下降更为明显。给出不同航速时舱内水位降,如图10所示。
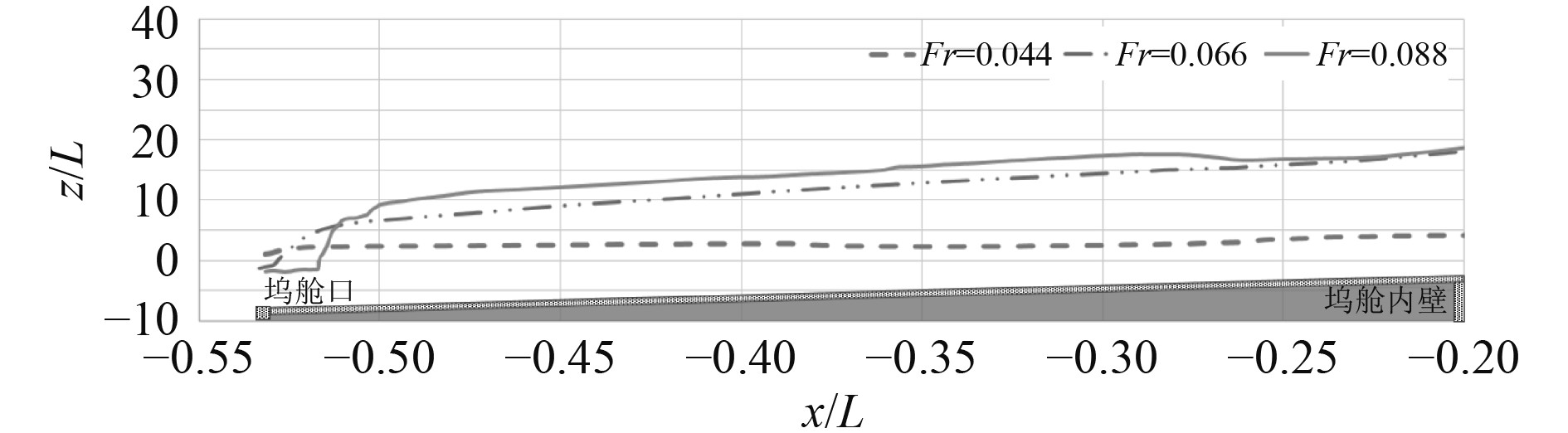
|
图 10 不同航速下舱内水深 Fig. 10 Wave depth at various advancing velocity |
图10中,水位降为坞舱内实际水深下降值占设计水深的百分比。由图可见,
由前述流场分析可见,跳板攻角越大,跳板产生的阻力越大,从而匀速运动时螺旋桨需要的转速越高,推进装置对尾流的影响越显著。为了探究跳板攻角与舱内水体分布规律,这里选取一组跳板处于不同攻角工况的船舶进行数值仿真,相应工况下图4位置监测线上自由面波高分布如图11所示。
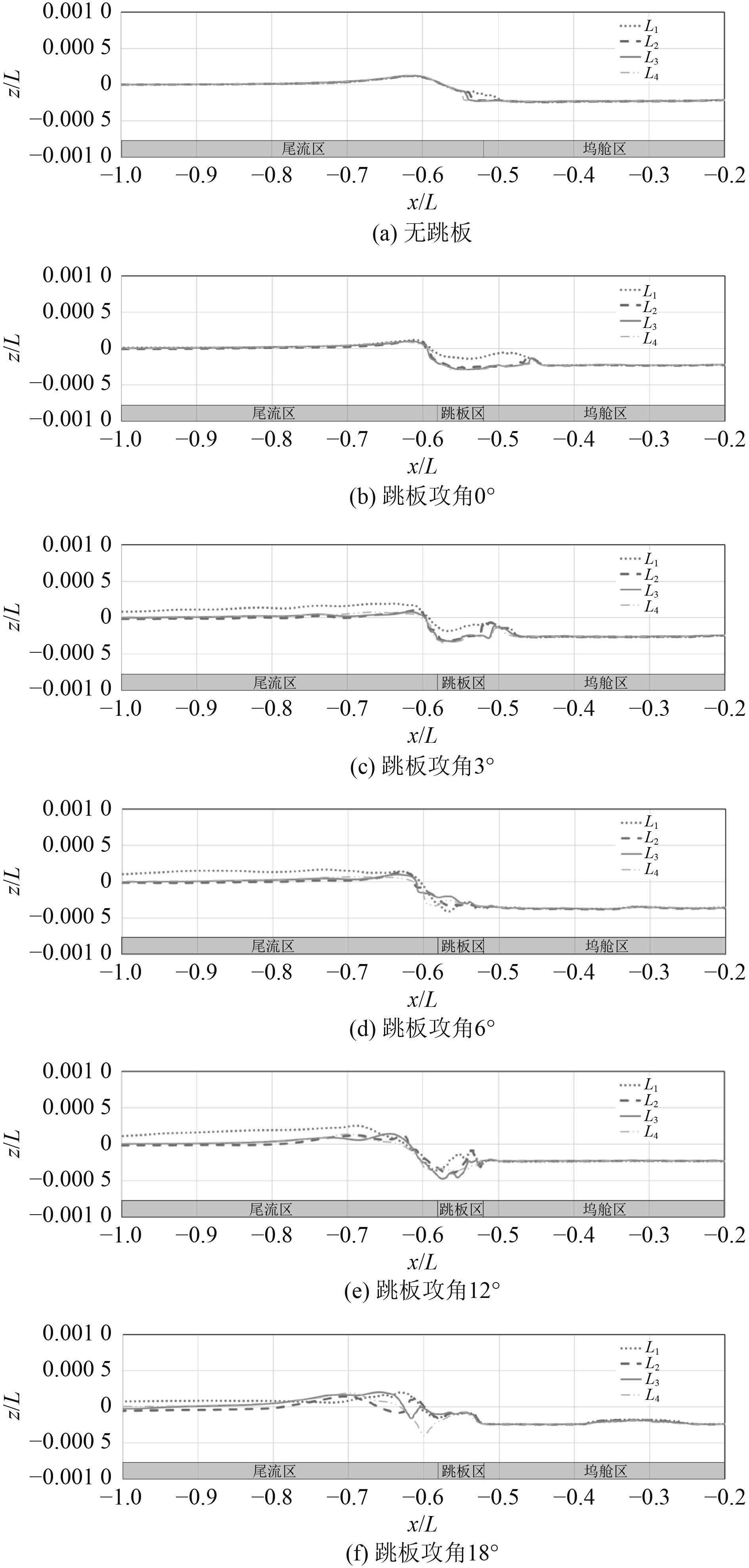
|
图 11 不同攻角跳板波高对比图 Fig. 11 Wave elevation of longitudinal section at various gangplank attack angel |
对比图11中无跳板以及有跳板自由面计算情况可见,小攻角跳板上水体分布与坞舱相似,相当于延长了坞舱范围。随着跳板攻角增加,舱内水体平稳区间略微延长,但尾跳板区域及尾流中流场逐渐混乱。为了直观地考虑坞舱及尾部流场情况,取尾流最高点、最低点以及坞舱内平均水位高度作图,如图12所示。
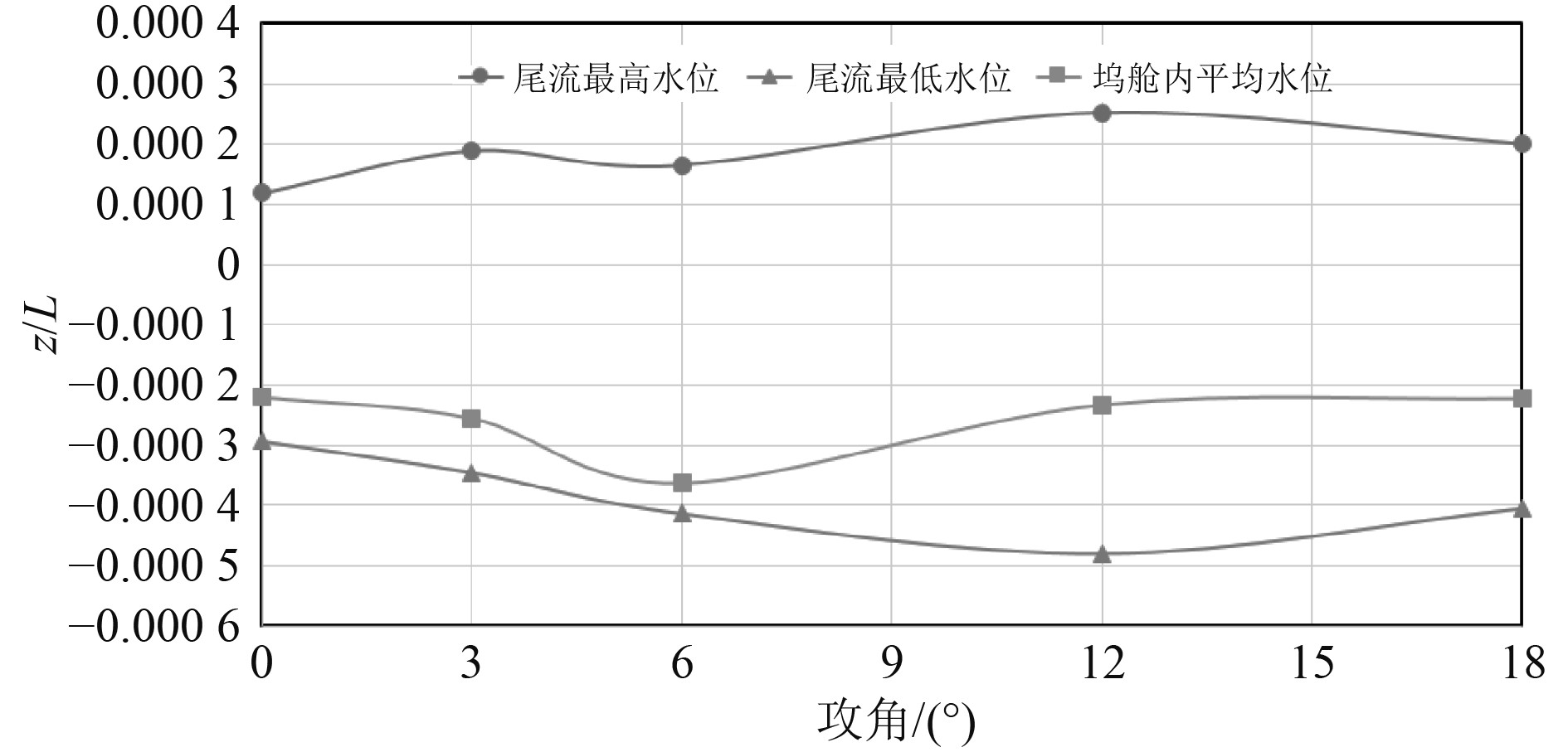
|
图 12 不同攻角下流场特征参数图 Fig. 12 Flow field characteristics at various gangplank attack angel |
由图12可见,在一定跳板攻角范围内,随着跳板攻角增大,尾流中最高点升高,最低点下降,舱口附近平均水位落差增加。当跳板攻角大于12°时,虽然尾流中水位落差减小,但水体稳定性明显下降。这里选取船体阻力达到稳定的无因次时间作为判断水体稳定程度的标准。各攻角下水体稳定的无因次时间列表如表2所示。
|
|
表 2 水体稳定时间 Tab.2 Stability time of water |
由表2可见,跳板角度小于3°时,舱内水体稳定度比无跳板略好;当跳板攻角大于6°后,舱内水体稳定性快速下降;当超过12°时,舱内水体会出现明显的倾斜回复运动。综上所述,尾跳板攻角对舱内水深影响不大,但对舱内水体的稳定性影响显著。
3 结 语本文建立考虑船、桨、尾跳板耦合作用的匀速运动数值仿真模型,主要针对带坞舱船舶匀速航行时半开敞式坞舱内水体分布特性展开研究,根据坞舱内水体分布、运动时历以及不同工况下坞舱内水体分布仿真计算结果,获得关于航速、尾跳板攻角对舱内水体运动影响分析结论,可服务于带坞舱船舶设计以及浮式装备进出坞作业安全性评估和后续的控制策略研究。结论如下:
1)半开敞坞舱内的水体与船几乎相对静止,与外流域对流较小,内外水域交接处会存在较大涡结构。
2)在船舶下放跳板后,坞舱舱内水体会经历较长周期的倾斜与回复运动,坞舱内侧水体运动幅度较大。
3)坞舱内水体稳定后,水位会低于平均自由面。且母船航速越高,舱内水位越低。
4)尾跳板攻角对坞舱内水深影响不大,但会显著地影响坞舱内水体的稳定性。
| [1] |
胡晓庆. 含有坞舱的船舶水动力性能分析[D]. 镇江: 江苏科技大学, 2019.
|
| [2] |
GANG Xu, TIAN-Rui Mei, MING-Liang Hu, et al. Hydrodynamic analysis of ship with well deck in the linear numerical wave tank[J]. Mathematical Problems in Engineering, 2020(10).
|
| [3] |
MCCALLUM D, ENGLE A H, PLATZER G P, Hydrodynamic efficiency improvements for U. S. Navy ships[J]. Naval Engineers Journal, 1991, 103(3): 74-90. DOI:10.1111/j.1559-3584.1991.tb00939.x |
| [4] |
程明道, 刘晓东, 张建武. 尾板对高速水面舰水动力影响的模型试验研究[C]// 船舶水动力学学术会议论文集, 2004.
|
| [5] |
KARAFIATH G, CUSANELLI D, LIN C W. Stern Wedges and Stern Flaps for Improved Powering - U. S. Navy Experience [J]. Military Vessels, 2011.
|
| [6] |
李冬琴, 李鹏, 章易立, 等. 分段式尾压浪板对高速船阻力性能的影响[J]. 船舶工程, 2019, 41(7): 37-43. DOI:10.13788/j.cnki.cbgc.2019.07.07 |
| [7] |
陈怀远. 船舶压浪板设计优化及应用[D]. 大连: 大连理工大学, 2019.
|
| [8] |
ARASH E, MARKO V. A body-force model for waterjet pump simulation[J]. Applied Ocean Research, 2019, 90.
|
| [9] |
傅慧萍, THAD J. MICHAEL, CARRICA P M. 一种基于体积力螺旋桨模型的自航计算方法. 船舶力学, 2015, 19(7): 791–796.
|
| [10] |
STAR-CCM+ User Guide. Simens, version 15.06[R] 2020.
|
 2022, Vol. 44
2022, Vol. 44
