高速双体船具有良好的快速性和较大的有效载荷,被广泛应用于军事领域和商业领域[1]。高速双体船两片体均为细长体,船体储备浮力严重不足,难以对抗双体船在波浪中大幅度的纵向运动。为此,在双体船中央甲板首部位置添加了穿浪首,用以增加双体船的储备浮力,进而加大了纵摇运动中的恢复力矩[2]。穿浪双体船做纵摇运动时,部分船体结构会频繁地出水、入水进而发生砰击现象。这种现象容易引起船体产生严重的颤振,使局部应力过大而破坏[3]。穿浪首作为双体船出水后最先入水的部位,其砰击现象最为严重,已逐渐成为研究的重点[4-5]。
研究穿浪首砰击问题的目的在于确定设计砰击压力载荷,合理设计穿浪首的结构,其影响因素主要包括穿浪首的入水高度、形状,以及分布位置等。目前研究砰击问题的方法主要包括理论计算,数值预报,试验3种方法[6]。
试验研究主要分为实船试验和模型试验。其中实船试验成本高,试验条件不受人为控制,数据难以准确获得,因而大多以模型试验为主[3]。Chuang曾对入水冲击问题作了系统的模型试验研究,包括楔形体、圆锥体撞水试验等,并结Wagner的二维楔形体砰击理论和Chuang的三维圆锥体砰击理论,拟合得到适用于三维船体的刚性楔形体的砰击压力系数与斜升角之间关系的砰击压力公式。Zhao[7]对斜升角 30°的 V 形楔形体以及典型的船首外飘剖面进行了落体入水冲击试验,测量了砰击压力以及砰击力,验证了其 NBE 数值计算结果。Engle 等[8]针对 10°和 20°楔形体,开展了落体模型试验,并与国际上多个典型的数值计算结果进行了对比,发现20°时结果吻合很好。Whelan等和Davis等在Tasmania大学对双体船二维剖面模型做了相关跌落试验,测量了模型入水时的速度,加速度以及压力分布,对二维剖面的中体形状做了仔细研究。总的来说,模型试验可以获得较为准确数据,但试验成本较高,耗时长,工作量大,不适宜作为前期砰击预报的主要手段。
在理论研究和数值计算方面,VON Karman[9]为分析水上飞机降落时受到的水砰击荷载最早开始对水砰击进行理论研究,对于二维楔形体撞水问题采用势流理论引入了附加质量的概念根据平板假设分析砰击压力。Doborvolskaya[10]发展了自相似Similarity 理论,采用独特的数值法求解了二维撞水问题的砰击荷载。由于砰击问题实际上是三维问题,因此需要对二维结果做一定修正,Scolan等[11]利用Wagner理论研究了三维钝物体砰击理想不可压缩液体的问题,采用Wagner反问题方法,提出了三维砰击分析理论,分析了椭圆抛物体入水砰击问题,与切片理论计算结果进行了比较。Faltinsen等[12]采用广义的 Wagner 理论,研究任意3D物体的砰击情况,分析了某中间是圆柱体,两端是半球的理想物体砰击问题,并验证了实验模型的砰击压力和砰击力结果。但是砰击本身具有的三维效应和强非线性,借鉴势流理论的方法处理该类复杂问题仍存在一定的困难和局限性。
随着计算机的飞速发展,计算流体力学软件已经被用于流固耦合现象的研究。Reddy[13]采用 PHOENICS 软件模拟了斜升30的楔形体入水的砰击载荷,控制方程用有限体积,FVM离散自由表面采用流体体积法VOF捕捉,分析了入水速度,网格大小等影响因素。Yang[14]采用Fluent软件分析了二维楔形体以及某集装箱尾部入水砰击问题。相比于传统的CFD方法,基于粒子的全拉格朗日技术的SPH方法,能将网格划分的工作完全避免,对具有复杂外形的边界条件具有很好的适应性。Whilst Veen[15]利用SPH方法对二维楔形体的跌落砰击做了模拟计算,但目前为止仅限于二维现象,尚未利用这种方法研究三维问题。
本文利用SPH方法和FVM分别模拟穿浪首的三维分段模型在跌落过程中的砰击现象,并计算模型入水时的速度和加速度随时间的衰减曲线,将现象和数值与试验值进行了对比,分析找到2种方法在解决砰击问题上的差异,目的是针对双体船穿浪首的砰击压力找到一种最合适的预报方法。
1 SPH应用理论基础 1.1 粒子点的生成在给定流体域内,采用均匀分布的方式进行粒子点的布置。在设定点的间距之前,必须事先估算算例中粒子点在一个时间步长内的行程,避免粒子点在一个时间步长内超出壁面边界,一般在解决高速撞击问题时尤为需要。
为解决此问题,可以通过设置虚粒子,此举虽然增加计算量,但保证计算的稳定性。虚粒子是边界层粒子关于边界层的镜像,虚粒子的速度也和边界层粒子的速度关于边界层对称。
布置完点后,赋予流场内每个点相同的影响域和支持域,并据此进行粒子点搜索。采用全配对搜索法。对于给定粒子i,计算粒子i到粒子j的距离rij,若rij小于粒子i的支持域半径,则粒子j为粒子i支持域内的粒子。同样,粒子i也在粒子j的支持域内。通过对所有粒子的遍历搜索,得到粒子i的支持域内所有的粒子点[16]。
1.2 光滑函数的选取在SPH方法中,光滑长度h非常重要,直接影响到求解的计算效率和精度。若h太小,则在以kh为半径的支持域中将没有足够的粒子对给定的粒子施加作用点,导致结果的精度较低。若h太大,则粒子部分信息或局部特征会“丢失”,同时也会影响结果的精度。SPH方法使用粒子近似法主要依赖于一个以kh为半径,且包含足够多的粒子的支持域。计算的效率或速度也取决于粒子的数量。若粒子所分布的栅格的光滑长度为粒子间距的1.2倍,且k=2,则在一维、二维和三维的情况下,栅格内邻近粒子的数量分别为5, 21, 57[17]。
如果光滑长度是随着时间和空间的变化而变化,则每个粒子点都具有独立的光滑长度,极易失去粒子点相互作用的对称性。保持粒子间相互作用对称性的一种可行方法就是对光滑长度的修正方案。
选取
| $ W\left( {R,h} \right) = \left\{ {\begin{array}{*{20}{l}} \dfrac{{105}}{{16{\text{π}} {h^2}}}\left( {1 + 3R} \right){{\left( {1 - R} \right)}^2},R \leqslant 1 ,\\ 0,R > 1 。\end{array}} \right. $ | (1) |
式中:
首先对流场内粒子点以及双体船进行初始化,给定其物理属性和边界条件。对流场内质点进行遍历搜索及计算,对粒子点i及其支持域内的所有粒子点j,使用SPH方法求解Navier-Stokes方程。
连续性方程
| $ \dfrac{{{\rm{d}}{\rho _i}}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^N {{m_j}\nu _{ij}^\beta \dfrac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}}, $ | (2) |
动量方程
| $ \dfrac{{{\rm{d}}\nu _i^a}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^N {{m_j}\dfrac{{\sigma _i^{\alpha \beta } + \sigma _j^{\alpha \beta }}}{{{\rho _i}{\rho _j}}}\dfrac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}}, $ | (3) |
能量方程
| $ \dfrac{{{\rm{d}}{e_i}}}{{{\rm{d}}t}} = \dfrac{1}{2}\sum\limits_{j = 1}^N {{m_j}\dfrac{{{p_i} + {p_j}}}{{{\rho _i}{\rho _j}}}\nu _{ij}^\beta \dfrac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}} + \frac{{{\mu _i}}}{{2{\rho _i}}}\varepsilon _i^{\alpha \beta }\varepsilon _i^{\alpha \beta }。$ | (4) |
在计算中,把水当做是微可压缩流体,因此引入人工压缩率。Monaghan应用水的状态方程模拟具有自由表面的流动:
| $ p = B\left( {{{\left( {\frac{\rho }{{{\rho _0}}}} \right)}^r} - 1} \right)。$ | (5) |
式中:γ为常数,建议取7;ρ0为参照密度,即初始密度;B作为初始压力;式中减去1是为了消除自由表面流动的边缘效应。在求解离散化的SPH方程时,采用三阶龙格库塔方法,为了避免粒子非物理穿透边界,采用定时间步长。
1.4 动边界在本文所做的船舶跌落算例中,船舶模型采用的是不可穿透壁面,只给船模升沉方向自由度。在计算过程中,为了避免船体表面和水发生互相非物理渗透现象,对于处于交界面的粒子点,在下一步时间步长计算前,对边界层内的粒子点做一个适当的预判,当它们趋于渗透时,赋予相应粒子点一个足够大的力来修正。当满足以下条件时,则认为渗透即将发生。
| $ pe = \frac{{{h_i} + {h_j}}}{{2{r_{ij}}}} \geqslant 1,$ | (6) |
式中:hi为壁面粒子i的影响域直径;hj为壁面粒子j的影响域直径;rij为2个粒子点的距离。
| $ P = \left\{ {\begin{array}{*{20}{l}} \dfrac{{{{10}^5}}}{{{r_{ij}}}}\left( {p{e^6} - p{e^4}} \right),pe \geqslant 1 ,\\ 0,pe < 1 。\end{array}} \right. $ | (7) |
由于SPH采用支持域对粒子点进行捕捉,因此无需像网格法中通过水和空气的交界面来构造自由面,对自由面的处理简单方便。
2 有限体积法应用基础 2.1 有限体积法理论基础有限体积法(FVM)又称为控制体积法,其基本思想是将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有一个控制积;将待求解的微分方程对每一个控制体积积分,便得出一组离散方程,其中的未知数是网格节点上因变量的数值。在求解控制体积的积分时,需要假设因变量的值在网格点之间的变化规律,属于加权余量法中的子域法,因而子域法加离散也是有限体积法的核心思想[18]。
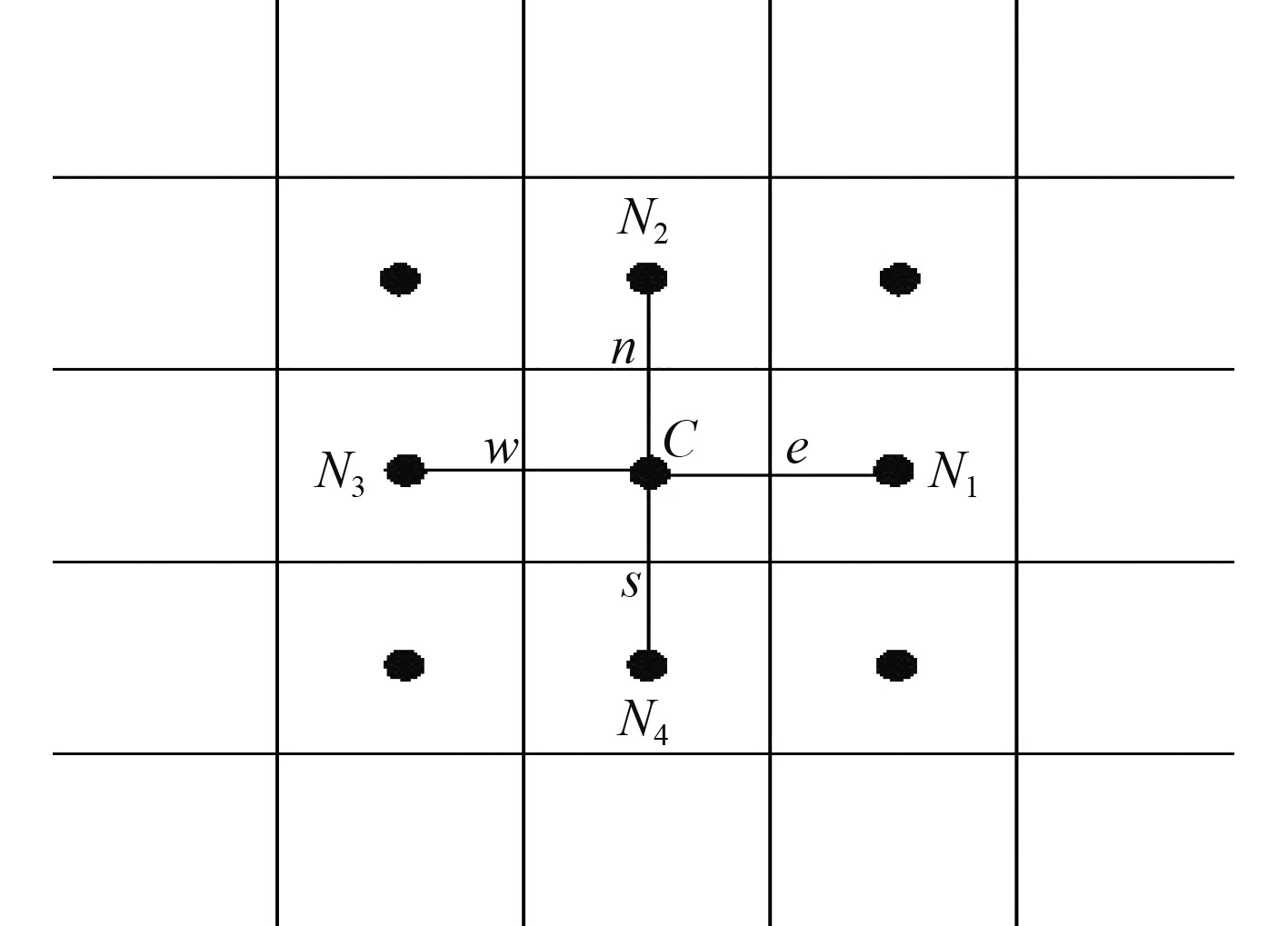
有限体积法在离散时的基本原理如图1所示。通过计算网格划分整个流体域,其中C为一个节点,N1,N2,N3,N4分别为C节点附近的相邻节点,小正方形表示单个控制体,C处得控制体积C由界面w, n, e, s所围成,宽度为小正方形的边长。在处理三维问题中,分别增加上下2个方向的控制点N5和N6。
|
图 1 离散原理图 Fig. 1 The theory of discretion |
离散方程可以写成如下通用形式:
| $ {a_p}{\varphi _p} = \sum {{a_{nb}}{\varphi _{nb}} + b}。$ | (8) |
式中:下标nb表示相邻节点;b是与源项相关的项;ap表示中心点的系数;Φ 表示节点物理量。
有限体积法主要求解步骤可以简化如下:
1)求解整个流体区域内控制单元上的积分方程;
2)运用相应的离散格式把控制体上的积分方程转化为代数方程求解,其中包括对方程对流项,扩散项,源项的离散;
3)使用设当的迭代方法求解代数方程。
其中离散格式的不同将会影响求解结果的不同。离散格式又分为一阶迎风格式,二阶迎风格式以及QUICK格式和三阶MUSCL格式,其中二阶迎风格式在保证计算精度的情况下,计算时间较快,因而采用二阶迎风格式对积分方程中的对流项进行离散。
有限体积法与有限元法和有限差分法的区别在于:有限元法需要假定物理量在网格节点之间的变化规律,即插值函数,进而求得近似解。有限差分法只考虑网格节点上物理量的值而忽略物理量在网格节点上的变化规律,而有限体积法在物理量的节点值时,又必须假定物理量在网格点之间的分布。在插值函数的使用方面,有限体积法在计算过程中插值函数只用于计算控制体积的积分,得出离散方程后,便不在使用插值函数,相对于有限元法更为简单易懂;在守恒性方面,有限体积法即使在粗糙的网格情况下,也能保证准确的积分守恒,只需花费较少的网格就可以清晰捕捉流场细节。因此,在对流体域和 RANS 方程的离散过程中,采用有限体积法是非常适用的,目前大多数CFD软件都采用该方法,如CFX,Fluent,STAR-CCM+。
2.2 计算过程 2.2.1 湍流模型的确立湍流模型的不同对数值计算结果会产生很大影响,针对不同的计算要求,需要选取不同的湍流模型,以保证计算结果的准确性。SST
| $ \dfrac{\partial }{{\partial t}}(\rho k) + \dfrac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \dfrac{\partial }{{\partial {x_j}}}\left({\Gamma _k}\dfrac{{\partial k}}{{\partial {x_j}}}\right) + {\tilde G_k} - {Y_k} + {S_k},$ | (9) |
| $ \dfrac{\partial }{{\partial t}}(\rho \omega ) + \dfrac{\partial }{{\partial {x_i}}}(\rho \omega {u_i}) = \dfrac{\partial }{{\partial {x_j}}}\left({\Gamma _\omega }\dfrac{{\partial \omega }}{{\partial {x_j}}}\right) + {\tilde G_\omega } - {Y_\omega } + {S_\omega }。$ | (10) |
其中:
| $ \begin{gathered} {\alpha _1} = 0.31, {\beta _{t,1}} = 0.075, {\beta _{t,2}} = 0.0828,\\ {\sigma _{k,1}} = 1.176,{\sigma _{\omega ,1}} = 2.0,{\sigma _{\omega ,2}} = 1.168。\\ \end{gathered} $ |
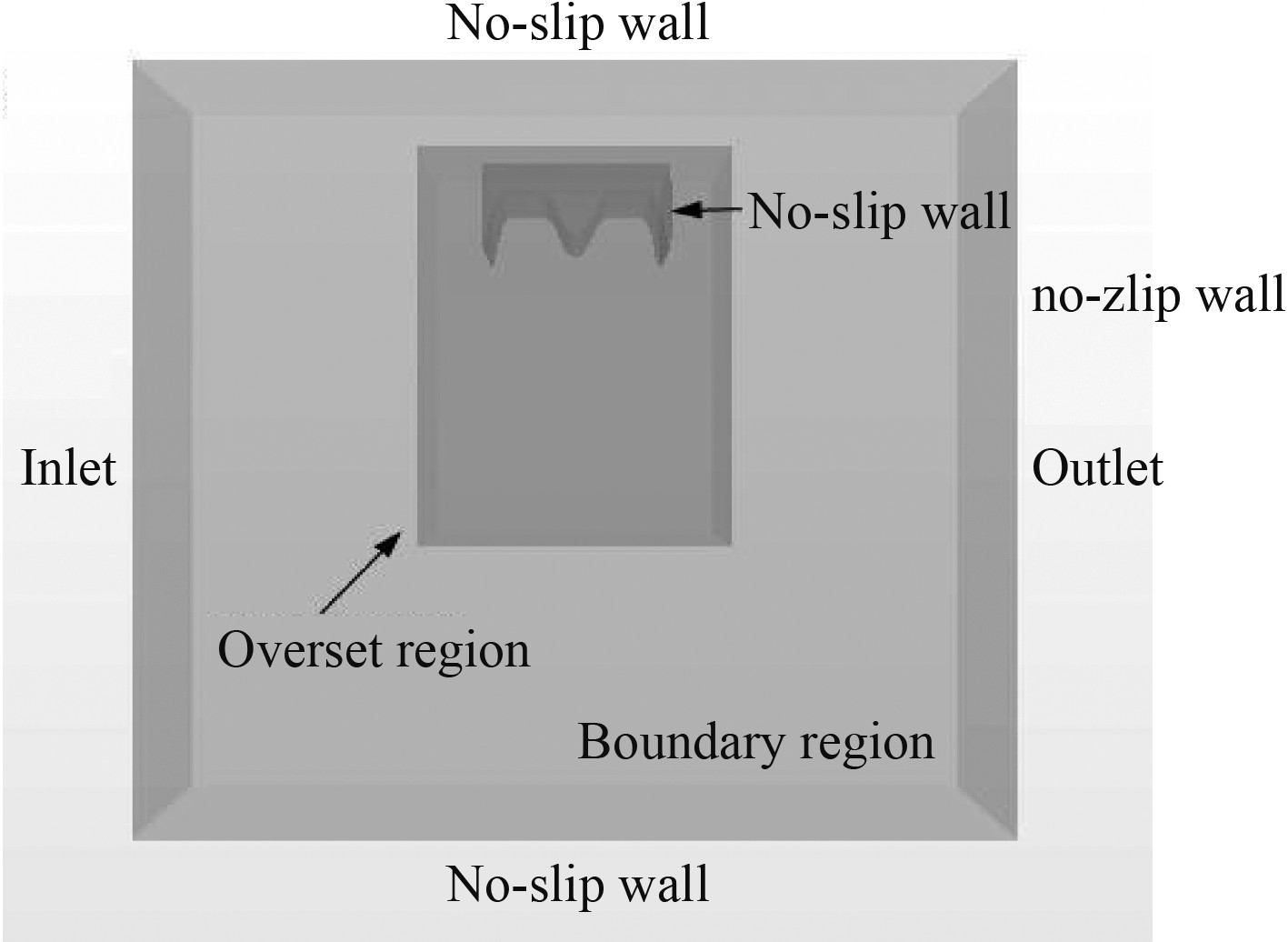
下落过程中的砰击模型边界条件如图2所示。流域的左右两侧分别设为速度入口和压力出口,为了更好模拟实验现象,流域四周的边界条件与实验水池的边界条件相同,设为刚性无滑移壁面(
|
图 2 边界条件示意图 Fig. 2 The boundary conditions |
因为物体在下落过程中,物体相对于计算域产生了移动,因而在对网格进行处理时需要用到动网格技术,即把整个流域分为2套网格,物体在周围一套网格,整个流域一套网格,物体周围的网格设为活动网格,而流域其他部分的网格为非活动网格,只在物体经过的范围内,进行重叠网格处理。利用STAR-CCM+中的Overset meshes功能对重叠网格做相应处理,得到了比较满意的效果。
在一个重叠网格中,网格单元通常被分为活动单元,非活动单元和受体单元3个部分。活动单元指变量可以在其中进行传递,只有在活动网格单元中,离散控制方程才能得到求解。非活动单元中,离散控制方程不能求解。但当重叠网格区域产生移动时,非活动单元能够相应的转化为活动单元。受体单元是存在于流体域中活动单元与非活动单元之间的网格,它依附在重叠网格区域(Overset region)的边界上,用于2个重叠网格的之间的过渡,使单个控制体单元处的变量能够得到有效解。其相应的插值形式包括,距离加权,线性插值,最小二乘法等,重叠网格附件控制体单元的分布如图3所示。

|
图 3 控制体单元分布形式 Fig. 3 The distribution form of control units |
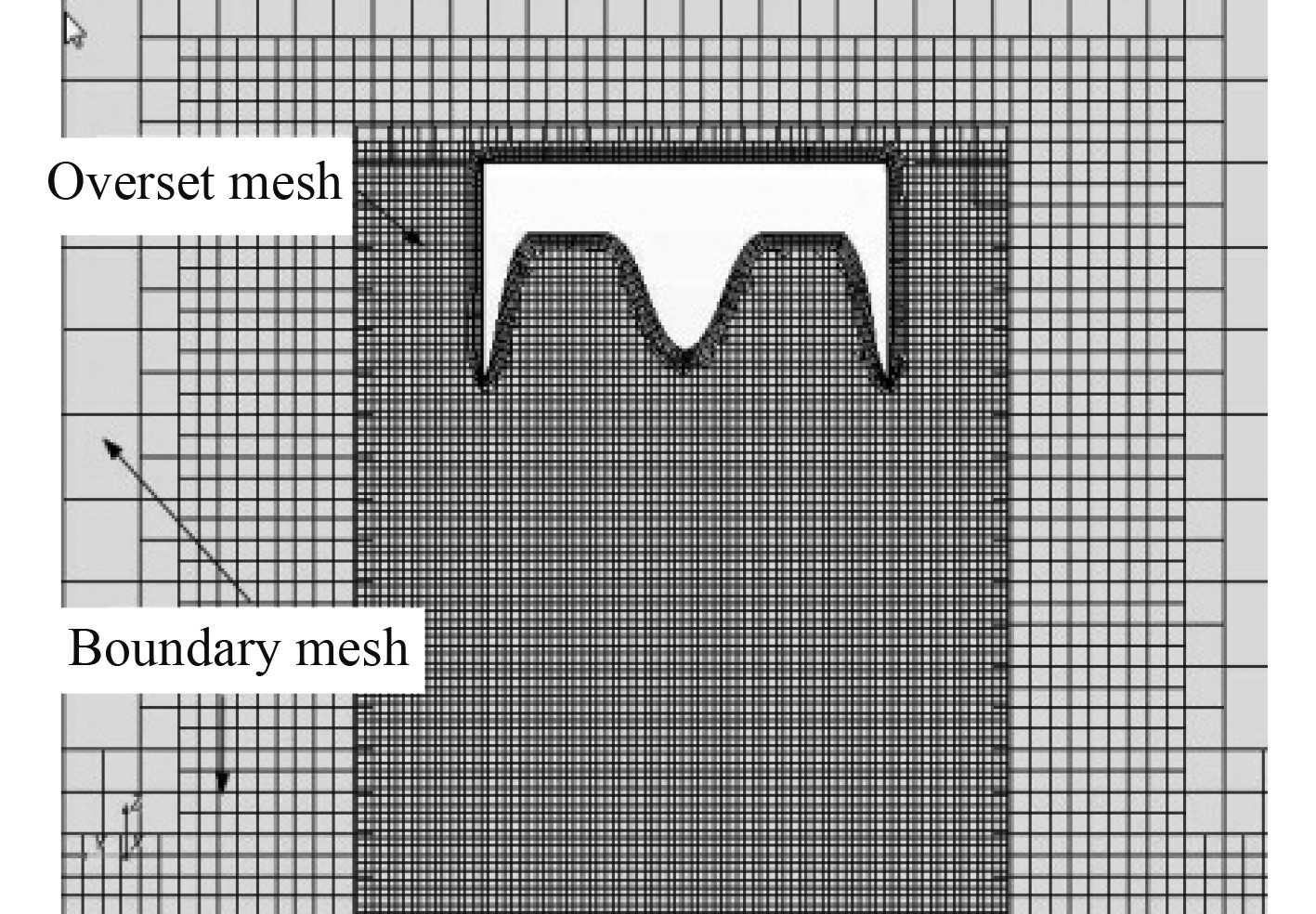
Overset meshes在设置流体区域时,需要一个能够用于完整计算的大的流体域以及一个包含物体表面的小的流体域,如图4所示。在网格划分时,首先在整个流域中设置一套大尺寸网格,再在物体周围区域设置一套尺寸较小的网格,使其包括在流域中,在网格重叠部分需要设置过渡区,目的是使物体在下落过程中,重叠区域附近的非活动单元能够有效的转为活动单元。
|
图 4 重叠网格图 Fig. 4 The overlapping grid |
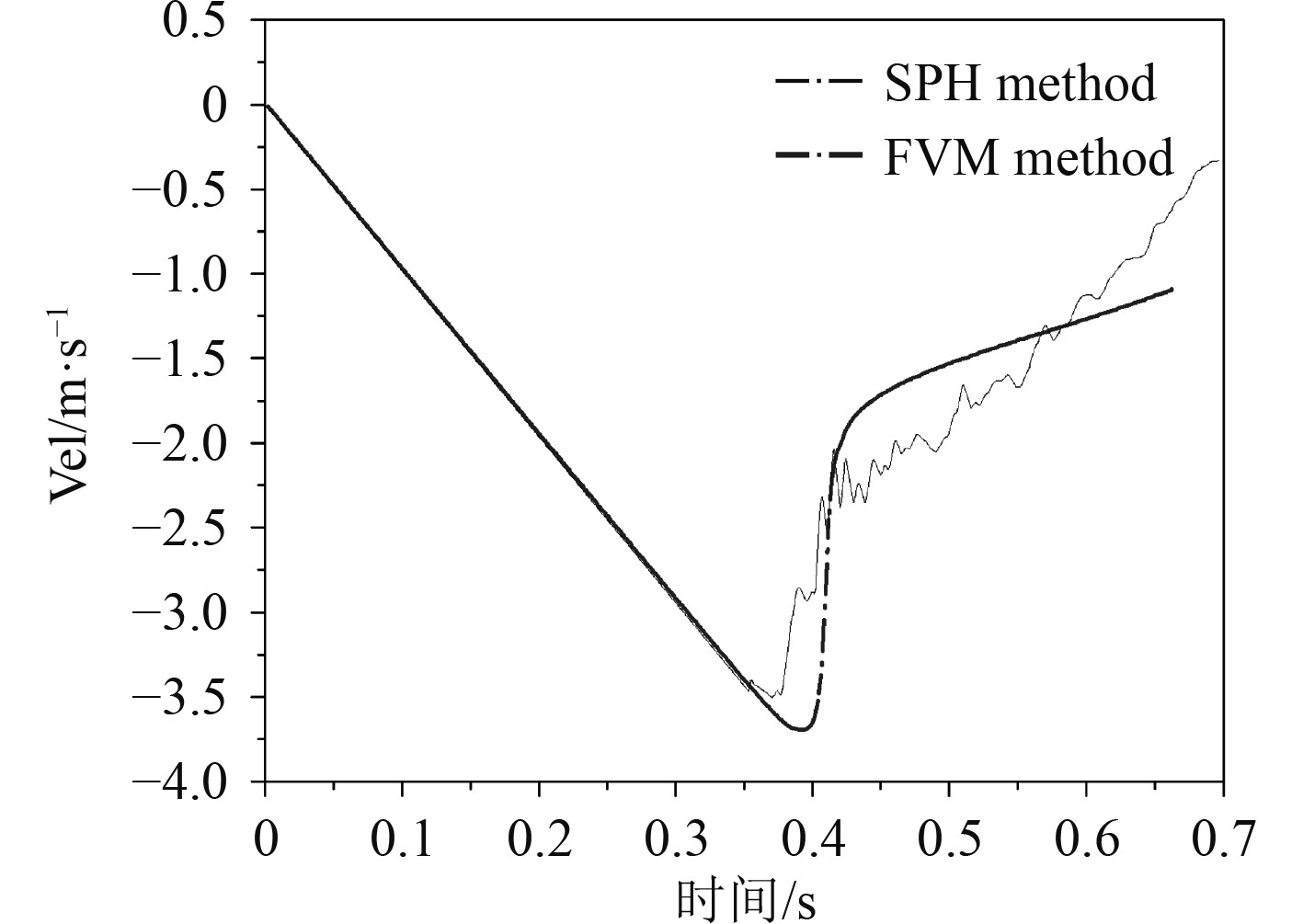
SPH方法和FVM计算结果与试验值[20]的对比如图5和图6所示。本文的试验数据来源于Michael R. Davis和James R. Whelan发表的数据。由于本文主要研究穿浪双体船跌落所受的砰击,故试验值给出的是跌落加速度的变化以表征其所受的砰击载荷,数值计算也侧重跌落速度和加速度的变化以研究穿浪双体船的跌落过程。
|
图 5 跌落速度曲线 Fig. 5 The curves of dropping velocity |
|
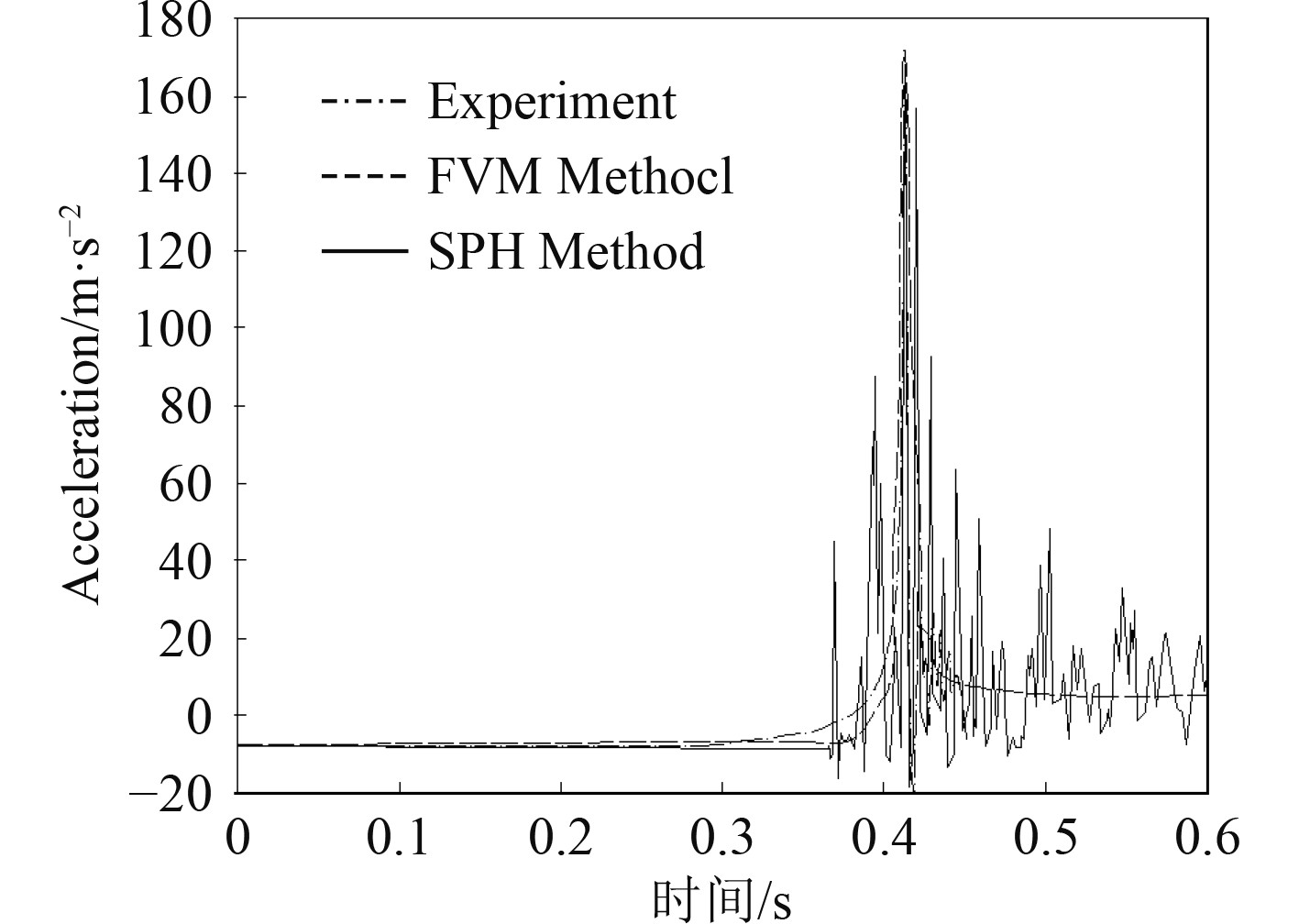
图 6 跌落加速度数值计算与试验对比曲线 Fig. 6 The comparison of numerical calculation and experiment on dropping acceleration |
从计算结果曲线上看,SPH方法计算的结果与FVM的计算结果存在一定的差异。相比之下SPH方法的震荡性比较大,在收敛过程中伴随着明显的震荡现象,而FVM则表现的平滑。由图5可知,当船体触水后,跌落的速度发生急剧变化,在一段时间内变化迅速,而后相对缓慢。SPH方法与FVM的计算结果在入水初期,两者变化趋势大体相当。而后期,SPH方法下速度的大小不断降低,比FVM更趋于速度为0。这是由于在SPH计算中,对于自由面的处理采用离散粒子点的方式,因而在下落入水后,槽道拱形顶部的空气成分能够得到及时的排除。然后FVM中的自由液面采用的是水气交界面,网格内部采用的是填充一份水或一份气的方式,在跌落时容易造成槽道内空气无法及时排除。从对水气物质的表达方式上看,SPH和FVM之间的差异能够对计算产生较大的影响。
由图6可知,SPH在跌落过程中加速度变化剧烈,这是由于SPH计算的收敛性使得其速度在小时间步长内变化剧烈,同时加速度也随之变化剧烈。但是从结果上看,并不妨碍对于最大加速度的计算和捕捉。2种计算方式的加速度的峰值近似,并且出现时刻同步,与试验值相比,误差在可接受范围内。
通过表1数据可以看出,双体船跌落受水砰击所产生的最大加速度发生的时刻在刚入水后,之前所耗费的时间主要是重力作用下落所产生的,加上跌落速度快,因而在时刻的计算上误差非常小。同时,虽然不同的计算方法与试验曲线的走势略有不同,但是其跌落加速度的峰值却相差无几,这表明在双体船跌落后,速度变化剧烈的区间基本相同,这也可以从而得出该双体船跌落后在特定吃水区间会遭遇最大加速度,其所受砰击作用力将会达到最大。
|
|
表 1 最大加速度值对比 Tab.1 The comparison on maximum acceleration |
由图7可以看出,在时间上,试验和计算的图像能够保持高度的吻合,说明数值计算方法能对试验进行准确的仿真计算。但从细节上看,SPH对于自由面的捕捉要比FVM更加精细,但是对于内部气泡的处理存在一定的失真。究其原因,SPH对于自由液面并未像FVM一样设定为水气交界面,而是粒子点边界,这就在槽道拱部不存在气泡压缩的气压差,使得水质点能都迅速充满整个槽道,气体能够及时排除,产生了与FVM不同的仿真现象。

|
图 7 跌落图像对比 Fig. 7 The comparison of drop images |
对比分析了SPH和FVM对于跌落问题的处理,在处理过程中,FVM采用了Overset Mesh的设置,使得船体运动不会引起网格的大扭曲变形,保证了计算的可行性和精度。而SPH则由于其粒子点近似的优势,在处理跌落问题时不需要对自由液面和运动的船体做特殊处理。
从计算结果上看,SPH和FVM都具有很高的计算准确性和精度。但是由于FVM采用CFL残差收敛方案,使得结果平滑收敛性好,相比之下,SPH的数值震荡比较剧烈,这也对于求解高阶导数,如加速度等带来较大影响。但是对于加速度峰值等指标参数来说,与试验值相比,数值相近并且同步。这体现了SPH和FVM用于数值仿真中有着各自的计算特点,在计算穿浪双体船穿浪首砰击压力时,需根据实际需要进行选取。当只计算最大砰击力时,建议选用SPH方法;当需要对整个砰击过程进行模拟时,FVM则表现更佳。
从跌落计算图像上来看,SPH和FVM对于计算单元的处理有较大的差异。在SPH中,拱形顶部并未形成气泡,而在FVM中,则形成了与试验现象相似的气泡现象。这也说明了在SPH中,自由液面的处理方式和FVM有较大的差别。
| [1] |
THOMAS G, WINKLER S, DAVIS M, et al. Slam events of high-speed catamarans in irregular waves[J]. Journal of Marine Science and Technology, 2011, 16(1): 8-21. DOI:10.1007/s00773-010-0105-y |
| [2] |
SHAHRAKI J R, PENESIS I, THOMAS G, et al. Prediction of slamming behaviour of monohull and multihull forms using smoothed particle hydrodymamics[C]// 9th Symposium on High Speed Marine Vehicles . 2011, 400: 1−10.
|
| [3] |
THOMAS G, DAVIS M, HOLLOWAY D, et al. Transient dynamic slam response of large high speed catamarans [C]// The 7th International Conference on Fast Sea Transportation, Ischia (Italy).
|
| [4] |
DAVIDSON G, ROBERTS T, THOMAS G. Global and slam loads for a large wave piercing catamaran design. Australian Journal of Mechanical Engineering 3 (2): 155−164.
|
| [5] |
AMIN W, DAVIS M R, THOMAS G A, et al. Slamming quasi-static Analysis of an 98m Incat high-speed wave piercing catamaran [C]// International Conference for Innovation in High Speed Marine Vessels. Fremantle, Australia.
|
| [6] |
骆寒冰, 徐慧, 余建星, 等. 舰船砰击载荷及结构动响应研究综述[J]. 船舶力学, 2010, 14(4): 439-450. |
| [7] |
ZHAO R, FALTINSEN O M, AARSNES J V. Water entry of arbitray two-dimensional sections with and without flow separation [C]// Proceeding of the 21st Symposiumon Naval Hydrodynamics, 1996: 408−423.
|
| [8] |
ENGLE A, LEWIS R. A comparison of hydrodynamic impacts prediction methods with two dimensional drop test data[J]. Marine Structures, 2003, 16(2): 175-182. DOI:10.1016/S0951-8339(02)00026-6 |
| [9] |
VON Karman T. The impact on seaplane floats during land in [R]. National Advisory Committee for Aeronatics Techinical note No. 321, 1932: 309−313.
|
| [10] |
DOBROVOLSKAYA Z N. On some problems of similarity flow of fluid with a free surface[J]. Journal of Fluid Mechanics, 1969, 36: 805-829. DOI:10.1017/S0022112069001996 |
| [11] |
SCOLAN Y M, KOROBKIN A A. Three-dimensional theory of water impact. Part1, Inverse Wagner problem[J]. Journal of Fluid Mechanics, 2001, 440: 293-326. DOI:10.1017/S002211200100475X |
| [12] |
FALTINSEN O M, CHE zhi, M. A generalized wagner method for three-dimensional slamming [J], Journal of Ship Research, 2005, 49(4): 279−287.
|
| [13] |
REDDY D N, SCANLON T, KUO Chengi. Prediction of slam loads on wedge section using computational fluid dynamics (CFD) techniques [C]// 24th Symposium on Naval Hydrodynamics. Fukuoka, Japan, July 2002: 8−13.
|
| [14] |
YANG S h, LEE H h, PARK T h, et al. Experimental and numerical study on the water entry of symmetric Wedges and astern section of modern container ship [C]// PRADS. Houston, USA, 2007: 518−526.
|
| [15] |
VEEN D J, GOURLAY T P. A 2D smoothed particle hydrodynamics theory for calculating slamming loads on ship hull sections [C]// International Conference on Marine High Speed Vessels. Fremantle, Australia, RINA: 79−84.
|
| [16] |
刘欣. 无网格方法[M]. 北京: 科学出版社, 2011.
|
| [17] |
LIU G R , LIU M B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method [M]. World Scientific Publishing Co Pte Ltd, 2003.
|
| [18] |
王福军. 计算流体动力学分析 [M]. 北京: 清华大 学出版社, 2004: 128.
|
| [19] |
MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model. [J]. Heat and Mass Transfer 2003, 4: 625−632.
|
| [20] |
MICHAEL R. D, JAMES R. W. Computation of wet deck bow slam loads for catamaran arched cross sections[J]. Ocean Engineering, 2007(34): 2265−2276.
|
 2022, Vol. 44
2022, Vol. 44
