2. 武昌船舶重工集团有限公司,湖北 武汉 430060
2. Wuchang Shipbuilding Industry Group Co., Ltd., Wuhan 430060, China
随着信息技术的发展,先进舰船综合射频系统逐渐采用模块化集成桅杆的形式[1-2]。集成桅杆的主体结构采用钢梁结构,外立面装有复合材料天线罩,形成一个封闭体,为内装设备提供保护。与传统桅杆相比,集成桅杆的结构形式差异主要体现在2个方面:一是集成桅杆结构尺寸较大,安装设备较多,结构静力复杂;二是集成桅杆所受风载荷和惯性载荷较大,载荷对结构的影响显著。针对复杂结构静力特性对桅杆结构的影响,常采用有限元分析方法,陈游洋[3],马天亮[4]等采用该方法对不同结构形式的集成桅杆进行了深入的分析,并与实船数据对比说明了该方法的有效性。针对风载荷的影响,姚熊亮[5],郭军[6],李刚[7]等,采用流体力学CFD数值计算与试验研究相结合的方法,对集成桅杆外流场的风压和流动特性问题进行理论分析和试验研究。集成桅杆实际使用时还易与振源产生共振,姚熊亮[8-9]将结构静力与风载荷相结合,研究集成桅杆在风载荷和结构重力共同作用下的结构响应,系统说明了当风压脉动频率与结构固有频率接近时会出现共振现象。
针对集成桅杆上装设备增多、体积增大的问题和结构刚强度合理平衡的需求,当前研究方向常聚焦于采用复合材料达到减重目的,而对主体结构优化设计的研究相对较少。本文针对集成桅杆的主体结构进行优化设计,采用有限元方法计算其在结构重力、风载荷及船体惯性载荷作用下的结构响应,优化后的主体结构同时满足重量、强度、刚度要求。本文为复杂舰船桅杆结构的优化设计提供了基础性的设计方法,具有普遍性的借鉴意义。
1 集成桅杆 1.1 结构形式本文所研究的集成桅杆外形采用黄金分割矩形构图法[10],造型层次感强,构成元素丰满、充实,比例关系合理、协调,整体美观、大气。整体外形呈多面体倒锥形,顶部和外立面安装雷达天线罩,内部集成射频设备。集成桅杆纵向尺寸较大,分为若干层,每层安装不同设备。主体结构整体焊接成型,是集成桅杆的关键部件,其承载了所有上装设备的重量,同时在风载荷、惯性载荷作用下满足使用要求。图1为集成桅杆及其主体结构示意图。
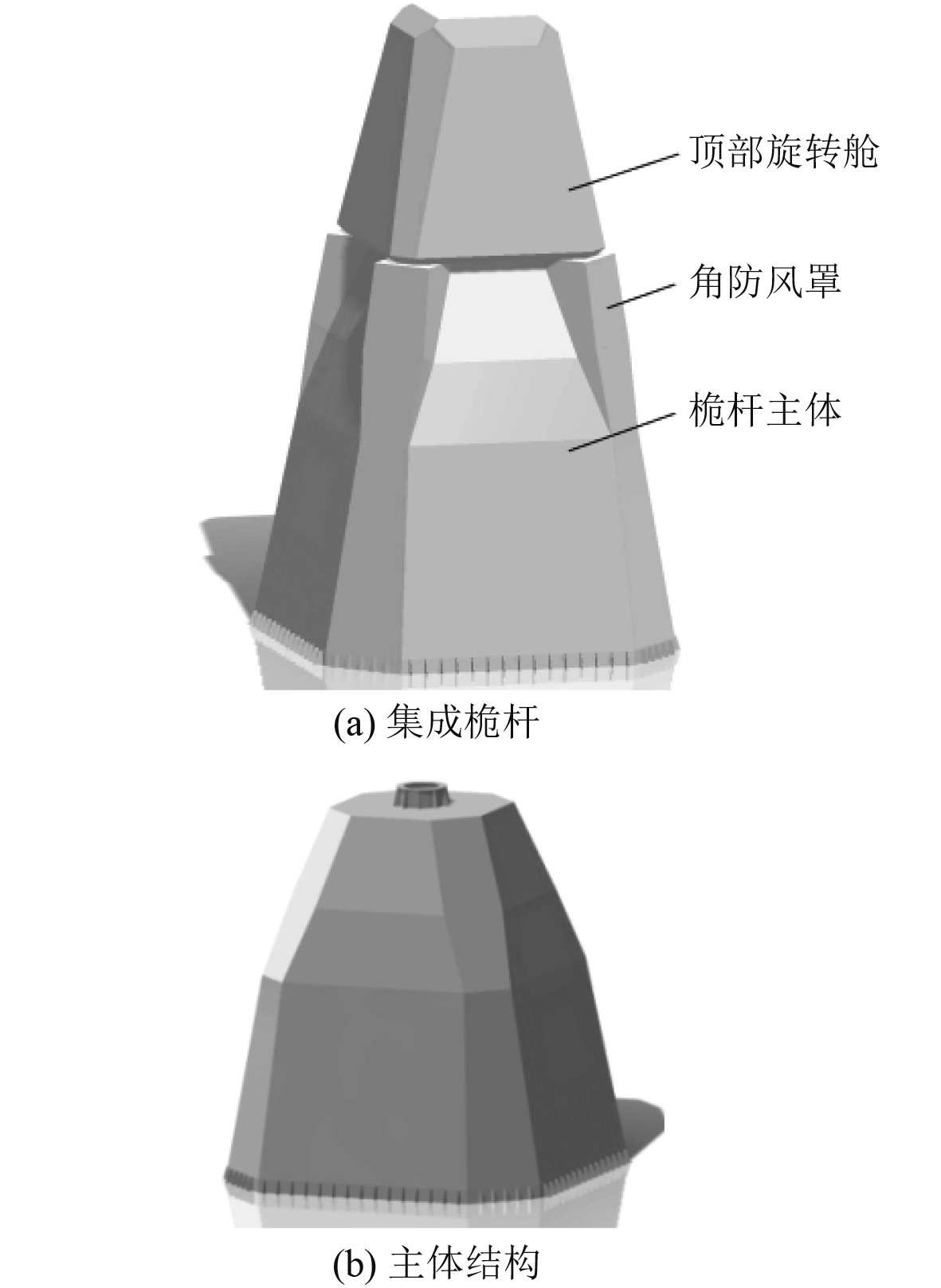
|
图 1 集成桅杆及其主体结构示意图 Fig. 1 Schematic diagram of integrated mast |
建立坐标系如图2所示。沿船长方向为纵向(X轴),舷向为横向(Y轴),垂向为Z轴。常规设计方法主要采用等厚度的外板和加强筋,结合T型材的焊接方式;该方法的特点是工艺简单,主要靠外板承载,重量较重。
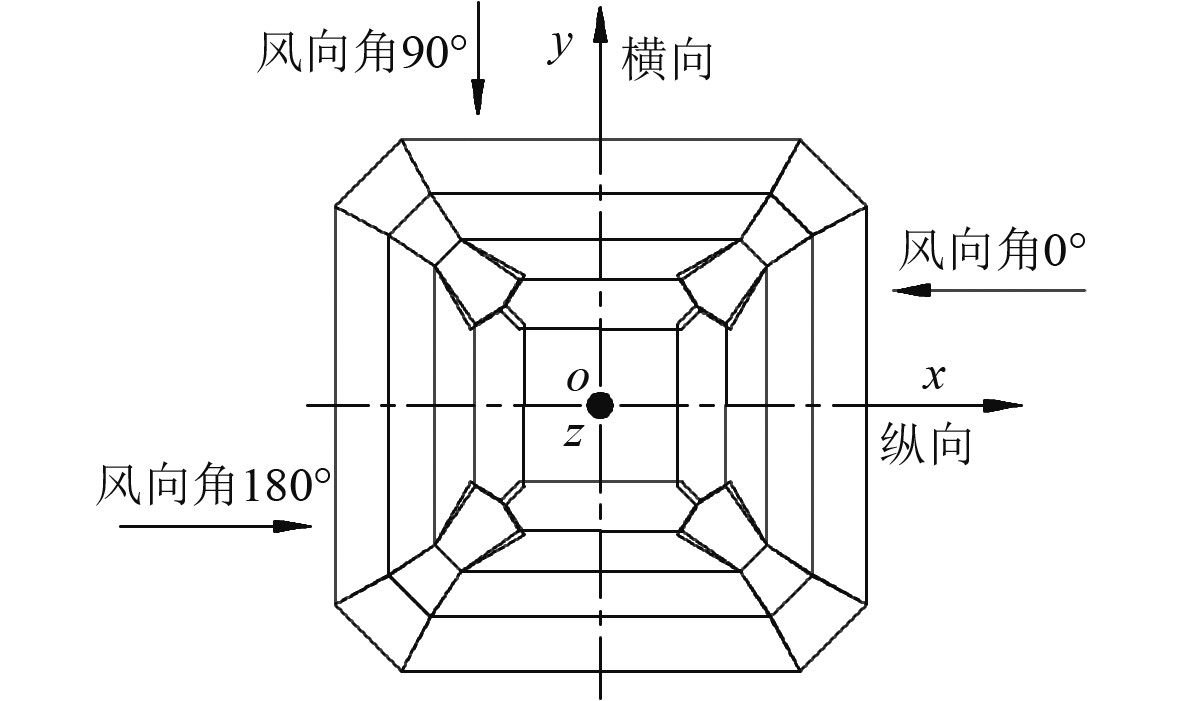
|
图 2 坐标系定义图(俯视) Fig. 2 Coordinate system definition diagram |
对常规设计方法进行优化设计,将外板厚度减薄,增加加强筋和T型材数量,以底甲板为例,优化前后对比如图3所示。优化后,主要靠加强筋和T型材承载,重量和优化前相比减轻了约53%。
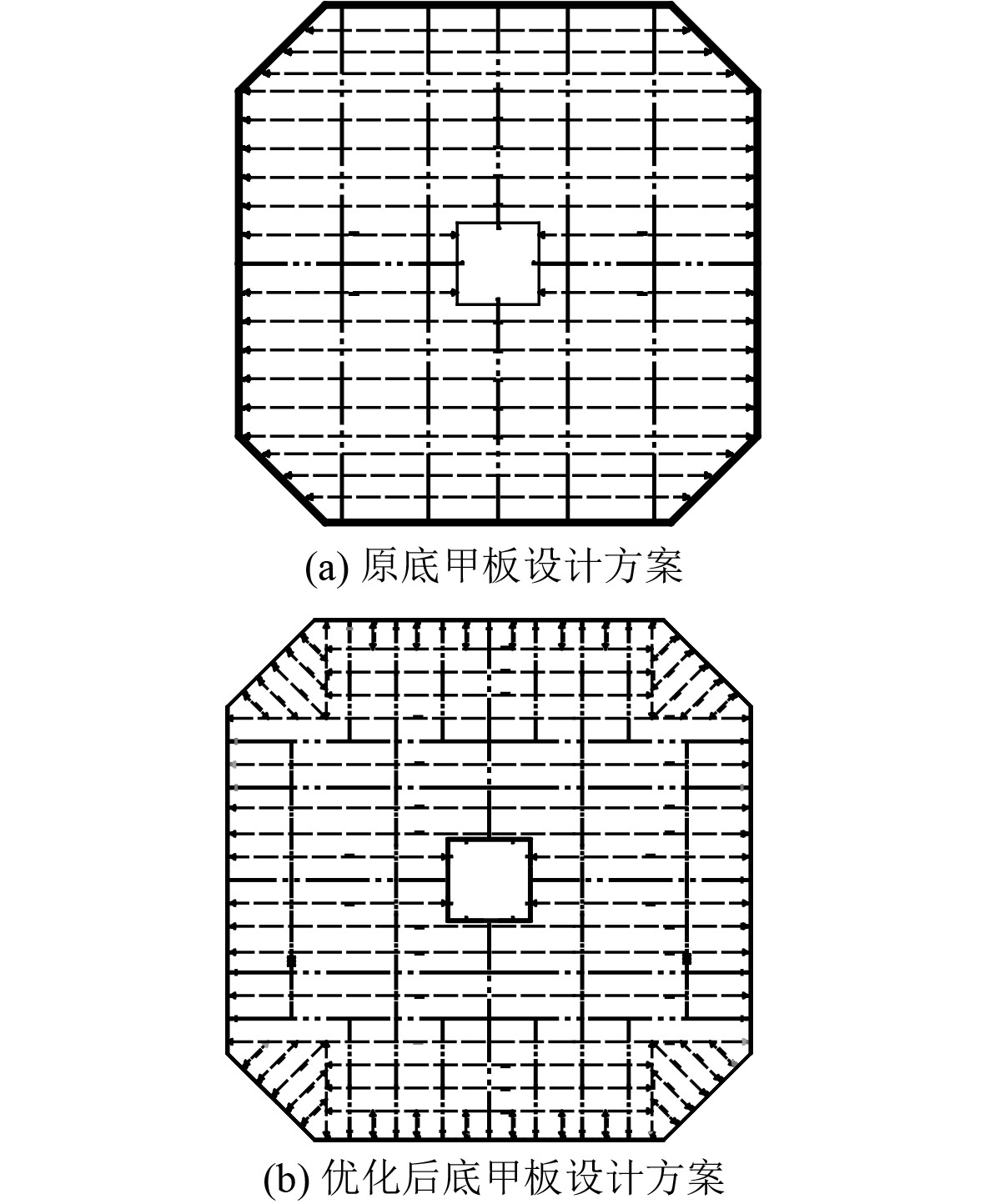
|
图 3 底甲板结构布置图 Fig. 3 Structural layout of bottom deck |
集成桅杆结构对称,工作时,弯矩作用到桅杆主体2个水平轴的概率一致;船体横摇角度大于纵摇角度,纵向弯矩略大于横向弯矩。因此在水平方向上各层甲板结构的中纵剖面惯性矩应略大于中横剖面轴惯性矩,这样设计时两个方向的抗弯效果趋于一致。优化前后,中纵剖面与中横剖面上各层甲板结构对自身水平方向轴的惯性矩如表1所示。
|
|
表 1 各层甲板惯性矩 Tab.1 Inertia moment of each deck |
优化前,中纵剖面惯性矩约为中横剖面惯性矩的3倍;优化后,中纵剖面惯性矩约为中横剖面惯性矩的1.3倍,中横剖面与中纵剖面惯性矩差异减小,纵向与横向结构抗弯能力更加合理。
2 载荷计算 2.1 风载荷理论风压力由下式计算:
| $ P = \frac{1}{2}({C_p} + {C_p}'\sin \omega t)\rho {V^2}。$ | (1) |
式中:ρ为空气密度,ρ=1.25 kg/m3;V为最大风速;Cp为平均压力系数;Cp’为脉动压力系数,ω为脉动圆频率。
流体在结构物周围高速运动时,会产生力大小随时间变化的涡流,即脉动风压。当结构物一阶固有频率与风载脉动频率接近时,脉动风压会对结构产生明显影响。根据模态分析结果,桅杆主体的一阶模态频率远离风载脉动频率,因此计算风载荷时无须计算脉动风压的影响,实际风压力为:
| $ P = \frac{1}{2}{C_p}\rho {V^2}。$ | (2) |
式中参数同式(1)。
平均压力系数Cp沿桅杆主体圆周方向各点是变量。根据图2中风向角的定义,风向角在0°~360°范围内,据参考文献[8]中对同类型集成桅杆风载荷特性的分析,平均压力系数Cp随着圆周方向角度的变化可以分为进流区(Cp=0~1)、涡激发放区(Cp=−2.2~0)及背流区(Cp=−0.5),如图4所示。分区域校核结构强度时,Cp取各自区域最大值。
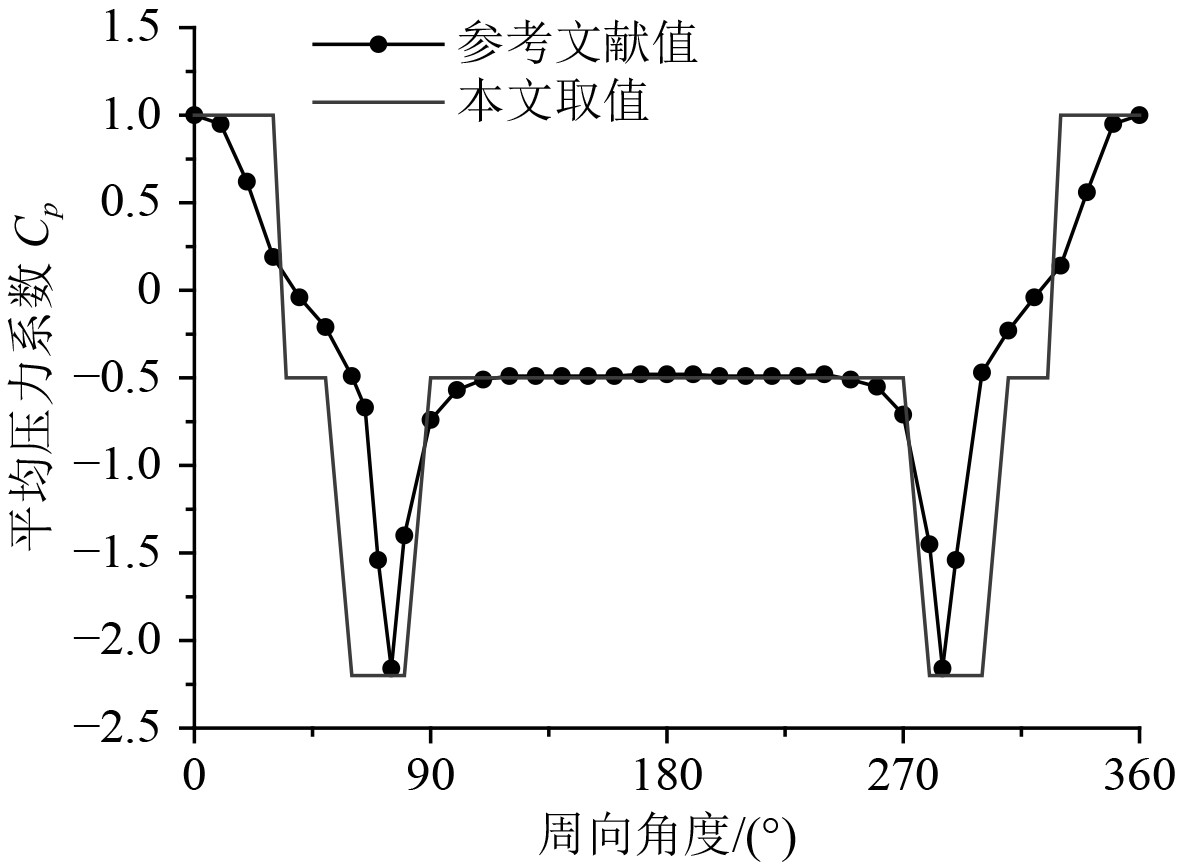
|
图 4 平均压力系数曲线 Fig. 4 Curve of average pressure coefficient |
横摇和纵摇是舰船在风浪中航行时最主要的运动形式,所产生的惯性载荷采用下式计算:
| $ \begin{split} &横摇 \left\{ {\begin{array}{*{20}{l}} {{a_x} = 0},\\ {{a_y} = g\sin {\phi _{\max }} + 4{\text{π} ^2}(Z{\phi _{\max }} + R)/T_\phi ^2} ,\\ {{a_z} = g\sin {\phi _{\max }} + 4{\text{π} ^2}(Y{\phi _{\max }} + R)/T_\phi ^2}。\end{array}} \right. \\ &纵摇 \left\{ {\begin{array}{*{20}{l}} {{a_x} = g\sin {\theta _{\max }} + 4{\text{π} ^2}Z{\theta _{\max }}/T_\theta ^2},\\ {{a_y} = 0},\\ {{a_z} = g\sin {\theta _{\max }} + 4{\text{π} ^2}X{\theta _{\max }}/T_\theta ^2}。\end{array}} \right.\end{split} $ | (3) |
式中:ax为纵向加速度;ay为横向加速度;az为垂向加速度;
求得结构所受的重力与惯性力的合加速度大小如下:
| $ 横摇 \left\{ {\begin{array}{*{20}{l}} {{a_x} = 0},\\ {{a_y} = 12.8\;{\rm{m}}/{{\rm{s}}^2}},\\ {{a_z} = 8.4\;{\rm{m}}/{{\rm{s}}^2}}。\end{array}} \right. 纵摇 \left\{ {\begin{array}{*{20}{l}} {{a_x} = 4.75\;{\rm{m}}/{{\rm{s}}^2}},\\ {{a_y} = 0},\\ {{a_z} = 13.4\;{\rm{m}}/{{\rm{s}}^2}} 。\end{array}} \right. $ |
基于有限元计算方法,进一步对主体结构的刚度和强度进行仿真分析和校核。采用有限元方法进行强度分析和模态分析的方法已非常成熟,各大船级社均有各自强度计算指南[11-12]。分析时,将主体结构底座固定约束,并赋予重力载荷、风载荷和船舶摇摆惯性载荷。
3.1 有限元建模建立优化后的主体结构有限元模型(见图5),并基于MSC.Patran/Nastran软件进行结构有限元分析与计算[13]。板单元用于模拟各层甲板、外板、围井、基座及部分关键部位T型材腹板,梁单元用于模拟加强筋、T型材及部分T型材面板,质量单元用于模拟安装于甲板或外板上的设备。边界条件为底部外板及肘板为简支。

|
图 5 有限元模型 Fig. 5 Finite element model |
为了分析不同载荷条件对主体结构的影响,共分为4种加载工况;由于结构对称,每种工况只需经历3个风向角,如表2所示。
|
|
表 2 工况定义表 Tab.2 Condition definition table |
表2中,重力包括主体结构重力和上装设备重力,根据实际大小和位置加载,上装设备按照质量点加载,假设一、二、三、四层甲板上装设备重量分别为10 t,9 t,8 t,7 t,整体释放重力加速度;风压力按照风速v=60 m/s计算;纵横摇加速度按照最大惯性加速度加载。
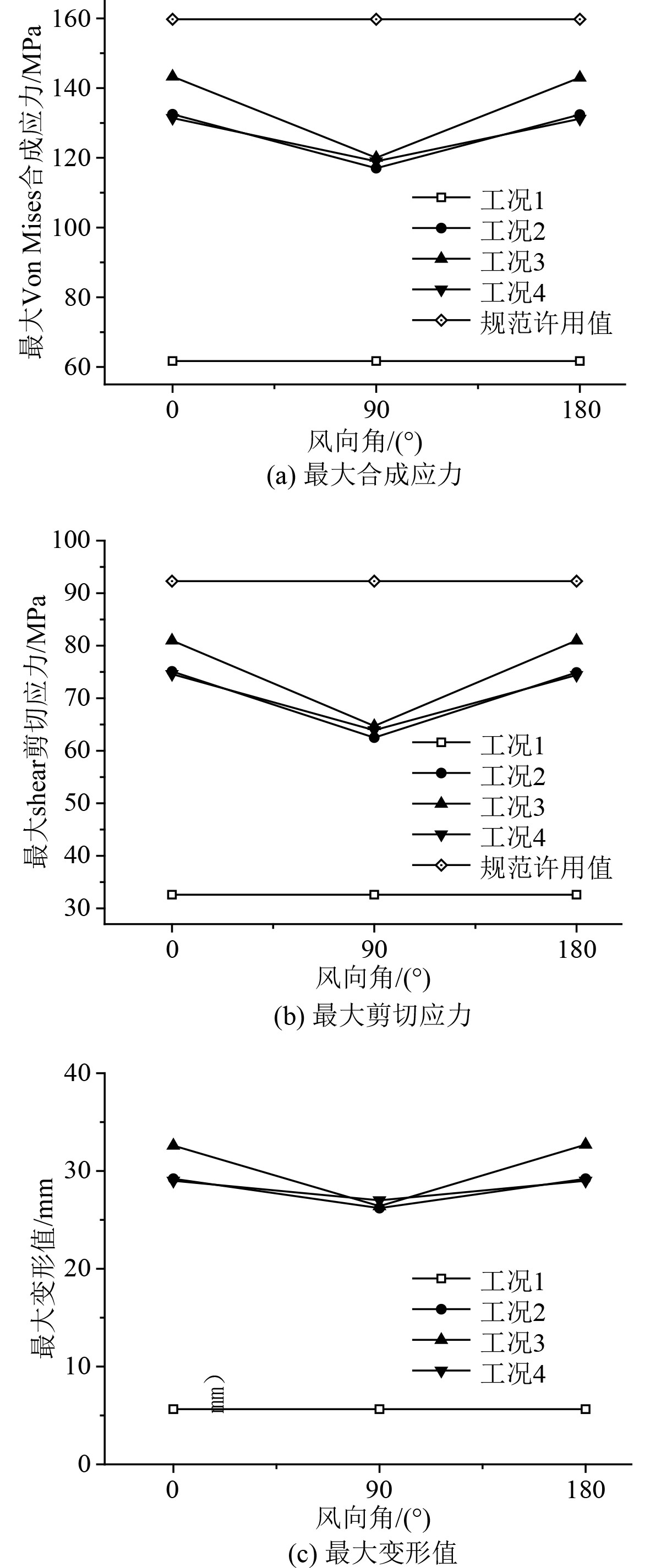
通过有限元强度计算,将主体结构在每种工况下最大合成应力、最大剪切应力与最大变形值随风向角的变化曲线汇总,如图6所示。
|
图 6 最大结构响应随风向角变化曲线 Fig. 6 Maximum structural response curve with wind direction angle |
主体结构在4种工况下的最大合成应力值为13.3 MPa,最大剪切应力值为81.1 MPa。主体结构材料为合金钢,其许用合成应力值159.75 MPa、许用剪切应力值92.3 MPa,主体结构强度满足使用要求。
同时发现,在工况2下,可变载荷仅考虑风载荷时,0°与180°风向下的结构最大合成应力分别为132.5 MPa和132.3 MPa,稍大于90°风向下的结构最大合成应力117.6 MPa,这说明本结构的横向强度稍大,纵向强度稍弱,但总体相差不大,结构强度纵横向均匀,这与表1中优化后方案的结构各层中纵剖面惯性矩值均稍大于中横剖面惯性矩值的特性相一致。
在0°风向角下,工况3的最大合成应力值和最大剪切应力为143.3 MPa与81.1 MPa,是4种计算工况中的最大值。图7为该工况在0°风向角下的结构响应云图。从图中可以发现,外板迎风面上的结构应力比较明显,最大结构应力和最大剪切应力均出现在第4层侧边外板设备开孔旁靠近迎风面的区域,即图2中风压的涡激发放区(Cp=−2.2~0),这说明风载荷对该区域具有明显的作用。同时在横摇惯性力的作用下,相同部位,一侧的最大应力值为143.3 MPa,而对称的另一侧仅为123.6 MPa,这说明横摇的水平惯性力同样对该部位有一定的影响。同时在该工况下,结构的最大变形值达到了32.6 mm,因此为增强该部位的结构刚度,实际制造过程中,第4层开孔周围均增加了加强筋。

|
图 7 结构响应云图 Fig. 7 Structure response cloud chart |
本文在风载荷的计算中仅考虑了圆周向的平均风压,未考虑脉动风压的影响,这是因为假设结构物的一阶固有频率与风载脉动频率相差较远,风场计算中可以将结构物视为一个不变形的刚体,因此需要进行结构物的一阶固有频率校核。
通过对主体结构进行模态分析,可以得到一阶固有频率为11.67 Hz,主要振动方向为沿高度方向的垂向振动,振形如图8所示。而通过文献[8]可知,对类似尺度和形状的集成桅杆风载荷时域脉动压力进行傅里叶变换可得到,风载脉动频率为2.95 Hz。船体总振动固有频率约为2~3 Hz,主机振动频率约为8 Hz,螺旋桨叶频率约为17 Hz,螺旋桨轴频率约为4 Hz。由此可以说明,主体结构一阶固有频率离上述频率较远,不会与这些振源发生共振。

|
图 8 一阶固有频率振形图 Fig. 8 First order natural frequency mode diagram |
本文首先对新型综合集成桅杆主体结构进行结构优化和轻量化设计,有效减轻了结构重量;然后建立主体结构的有限元模型,计算在不同工况和不同风向角下的结构响应,分析了结构的力学性能。最后进行结构模态分析,分析了结构的一阶固有频率。得出以下结论:
1)通过优化原集成桅杆主体结构的纵横向结构布置,减小结构和外板尺寸,在最大结构响应满足规范的前提下,本文采用的方案显著减轻了结构整体重量,纵向与横向结构抗弯能力更加合理。
2)针对本主体结构的风载荷计算,船舶相关规范与雷达规范在最大遭遇风速的取值上存在一定的差异,雷达规范取值更大,本文以雷达规范最大遭遇风速进行校核,提升了安全系数。
3)通过有限元分析,结构在0°风向角与横摇惯性力的共同作用下,结构第4层外板开孔旁区域的结构响应达到最大,该区域应进行加强,分析结果为结构特定薄弱区域的加强提供了方向。
4)通过对优化后的结构进行模态分析,其一阶固有频率值与风载脉动频率、船体总振动固有频率、主机振动频率等均明显错开,能够避免共振的发生,验证了结构优化的有效性。
| [1] |
刁瑞信, 陈豪. 国外海军集成桅杆技术发展浅析[J]. 船舶, 2015, 26(3): 97-102. DOI:10.3969/j.issn.1001-9855.2015.03.017 |
| [2] |
潘镜芙. 水面舰艇上层建筑和桅杆射频综合集成的思考[J]. 舰船科学技术, 2012, 34(5): 3-6. DOI:10.3404/j.issn.1672-7649.2012.01.001 |
| [3] |
陈游洋, 候国祥. 综合集成桅杆的简化研究[J]. 船海工程, 2014, 43(4): 29-33. DOI:10.3963/j.issn.1671-7953.2014.04.006 |
| [4] |
马天亮. 综合集成桅杆结构性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [5] |
姚熊亮, 方媛媛, 康庄. 舰船典型隐身桅杆流体动力数值实验研究[J]. 水动力学研究与进展(A辑), 2006(3): 354-362. |
| [6] |
郭军, 周维星, 杨文上, 等. 风载荷作用下综合集成桅杆动态特性实验研究[J]. 船舶工程, 2011, 33(1): 13-17. DOI:10.3969/j.issn.1000-6982.2011.01.004 |
| [7] |
李刚, 佟施宇, 丁建军, 等. 封闭式综合集成桅杆风载荷分布特性研究[J]. 船舶, 2012, 23(2): 35-40. DOI:10.3969/j.issn.1001-9855.2012.02.008 |
| [8] |
姚熊亮, 张凌江, 位莎, 等. 综合集成桅杆力学特性研究[J]. 传感器与微系统, 2010, 29(4): 45-48. DOI:10.3969/j.issn.1000-9787.2010.04.014 |
| [9] |
姚熊亮, 杨文山, 曾令玉, 等. 舰船摇摆作用下综合集成桅杆强度实验[J]. 上海交通大学学报, 2010, 44(6): 758-762. DOI:10.16183/j.cnki.jsjtu.2010.06.009 |
| [10] |
赵福燕, 杨春鹏, 陈杨. 黄金分割矩形构图方法在集成桅杆设计中的应用[J]. 雷达与对抗, 2018, 38(2): 47-58. DOI:10.19341/j.cnki.issn.1009-0401.2018.02.012 |
| [11] |
CCS集装箱船结构强度直接计算指南2005[S]. 中国船级社, 2016
|
| [12] |
ABS. Guide for safe hull-dynamic loading approach for vessels [S]. 2013.
|
| [13] |
孙丽萍. 船舶结构有限元分析[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012
|
 2022, Vol. 44
2022, Vol. 44
