钛合金材料因其良好的性能在海洋工程装备制造中有着广泛应用,随着海洋工程装备向超深海发展的趋势,高强度钛合金材料成为深海装备制造的理想选择[1]。深海装备在焊接制造和服役过程中不可避免地存在气孔、夹杂及裂纹等缺陷,其中又以裂纹缺陷最为严重。按照受力及位移特点,裂纹分为承受垂直裂纹面正应力作用的I型(张开型)、承受平行裂纹面剪应力作用的II型及承受垂直裂纹面剪应力作用的III型3种基本裂纹形式。工程实际结构裂纹位置处的复杂应力状态能分解出垂直裂纹面和平行裂纹面的应力分量,复杂应力状态下裂纹为3种基本类型裂纹中的任意2种或3种组合而成的混合型裂纹。掌握复杂应力状态下材料裂纹起裂扩展满足的力学条件及裂纹偏折规律,对于准确预测裂纹在结构中的扩展路径、合理评估结构疲劳寿命,保障结构的服役安全性具有重要意义[2]。
合理选择混合型断裂准则对于深海工程结构的安全可靠设计具有重要意义[3]。实际应用时,应根据材料混合型裂纹断裂特性试验确定适用的准则。针对深海装备用新型高强度钛合金材料Ti-6Al-2Sn-2Zr-3Mo-X[4]开展基于紧凑拉伸剪切(CTS)试样的I-II混合型裂纹断裂特性试验研究,揭示不同拉伸-剪切应力组合状态下新型钛合金裂纹起裂扩展条件和偏折规律,并将试验结果与经典的断裂准则进行对比分析,明确材料服从的断裂准则,为深海装备结构安全性评估提供支撑。
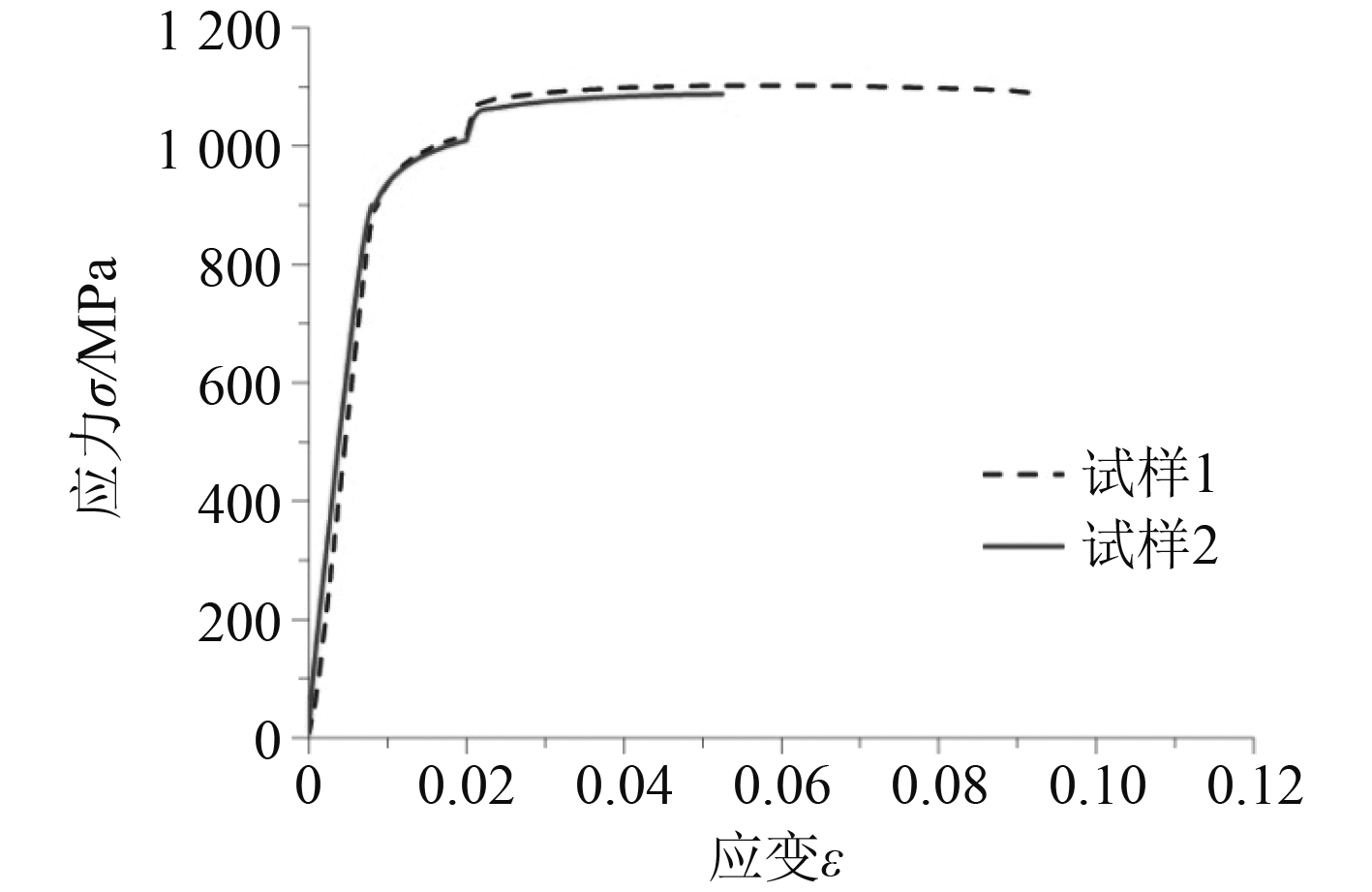
1 试样及试验方法 1.1 材料本次试验用钛合金材料取于70 mm厚锻造平板。根据GB/T 228-2010[5]测试材料基本力学性能。测试得到材料应力-应变曲线如图1所示。材料基本力学参数见表1。
|
图 1 Ti-6Al-2Sn-2Zr-3Mo-X应力应变曲线 Fig. 1 Tension stress-strain curve |
|
|
表 1 材料基本力学性能参数 Tab.1 Material basic mechanical properties |
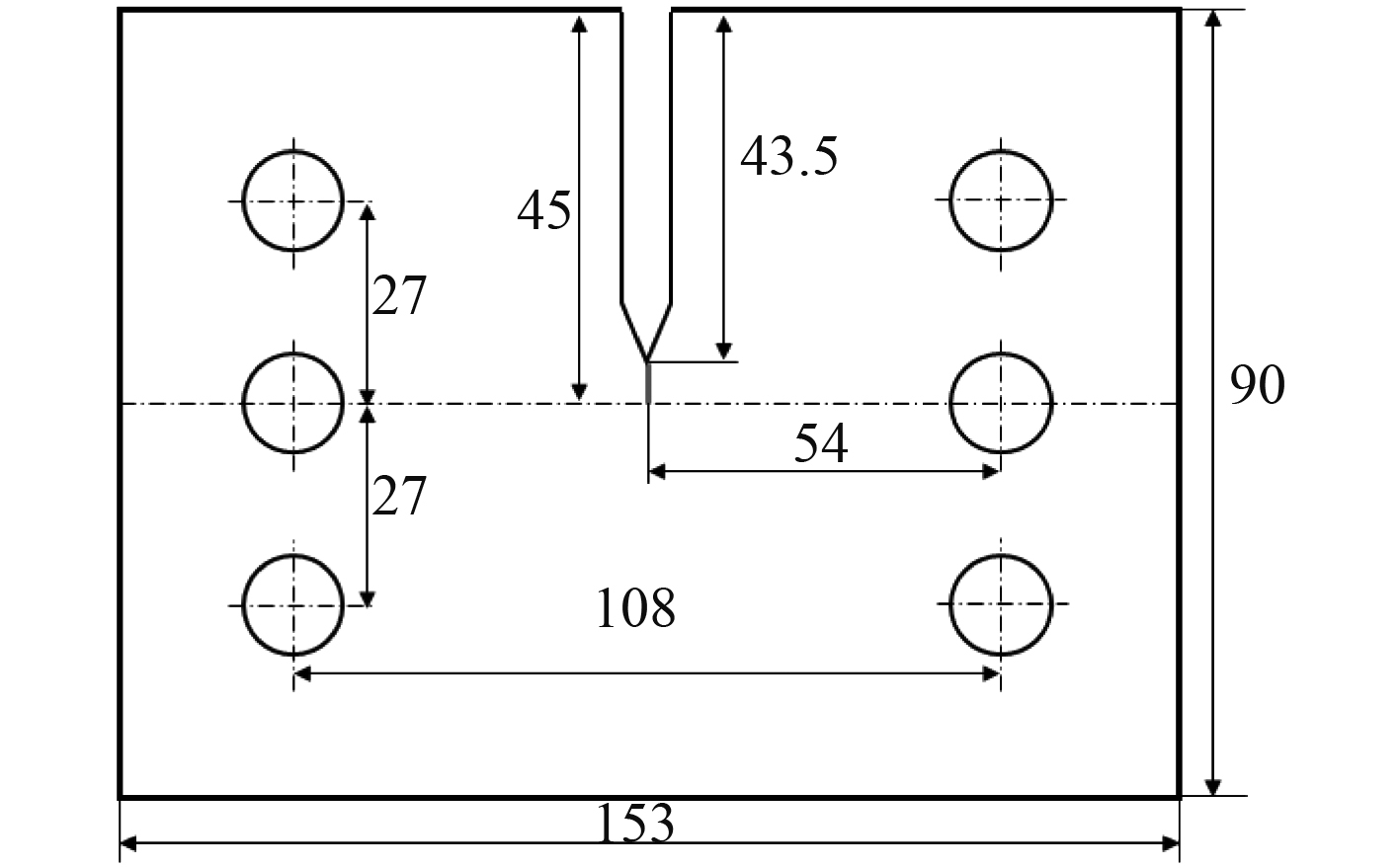
选用广泛应用于材料I-II混合型裂纹扩展特性研究中的紧凑拉伸剪切试样(CTS试样)及加载装置[6-7]开展高强度钛合金材料I-II混合型裂纹断裂特性试验研究。CTS试样示意如图2所示,试样主尺寸为153 mm×90 mm×10 mm,试样线切割缺口长度43.5 mm。CTS试样尺寸见表2(表中裂纹长度包含预制疲劳裂纹长度)。
|
图 2 CTS试样尺寸[5] Fig. 2 Sketch of CTS specimen |
|
|
表 2 CTS试样尺寸 Tab.2 Dimensions of CTS specimens |
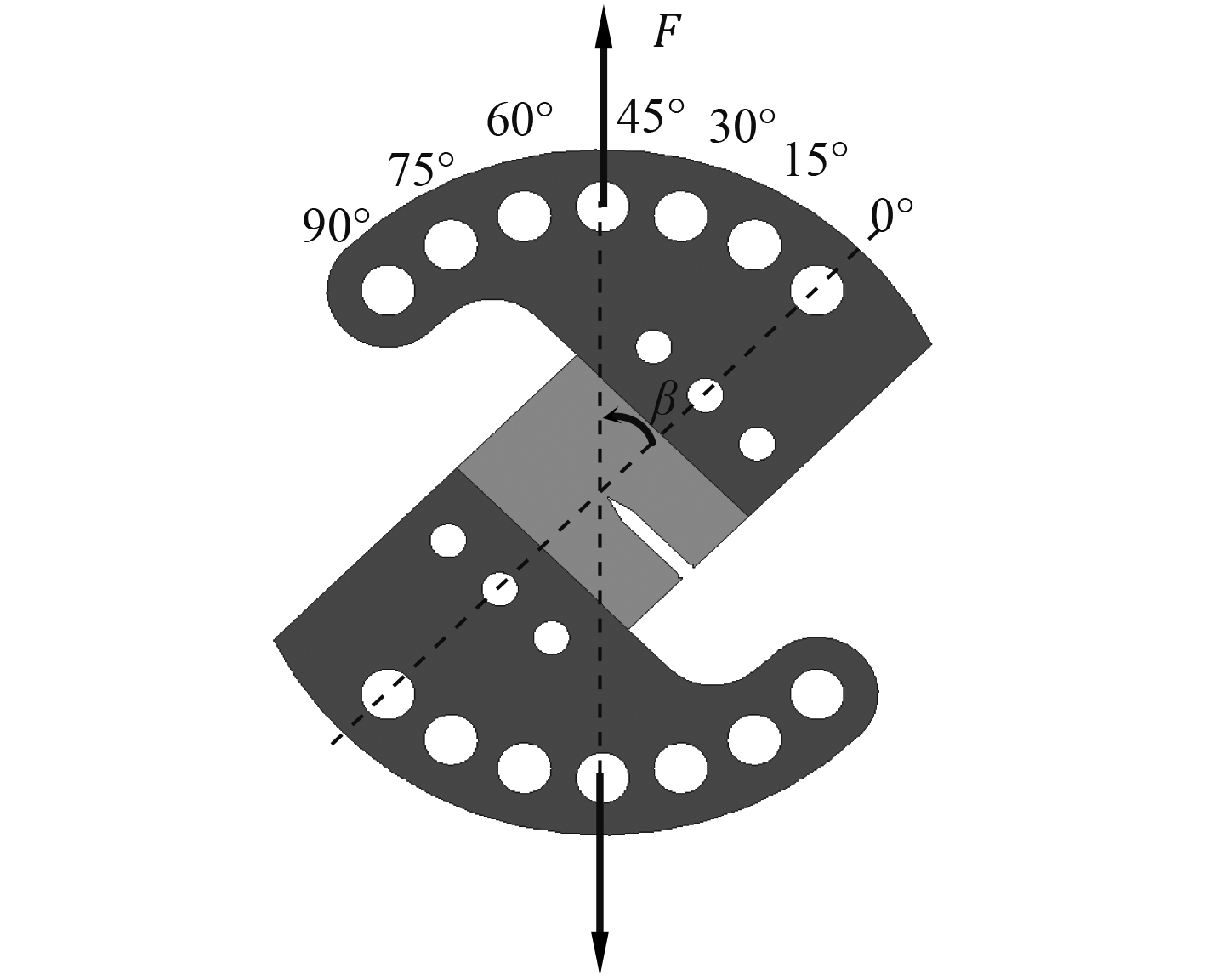
CTS试样加载示意如图3所示。通过将单轴拉伸载荷施加于不同的一对加载孔中便可以实现的不同加载角度
|
图 3
不同加载角度
|
整套系统包括walter+bai 500 kN液压伺服疲劳实验机及处理系统、夹式引伸计(精度0.001 mm)、一套CTS试样专用夹具以及CTS试样。
1.5 试验步骤参考GB/T 4161-2007标准[8]对加工完成的CTS试样进行I型加载(加载角度为0°)预制疲劳裂纹。试验环境为室温空气,加载应力比
对已预制疲劳裂纹的钛合金材料CTS试样进行不同加载角度下加载直至试样断裂。参考文献[8],应力强度因子变化范围上升速率区间为0.5 ~3.0
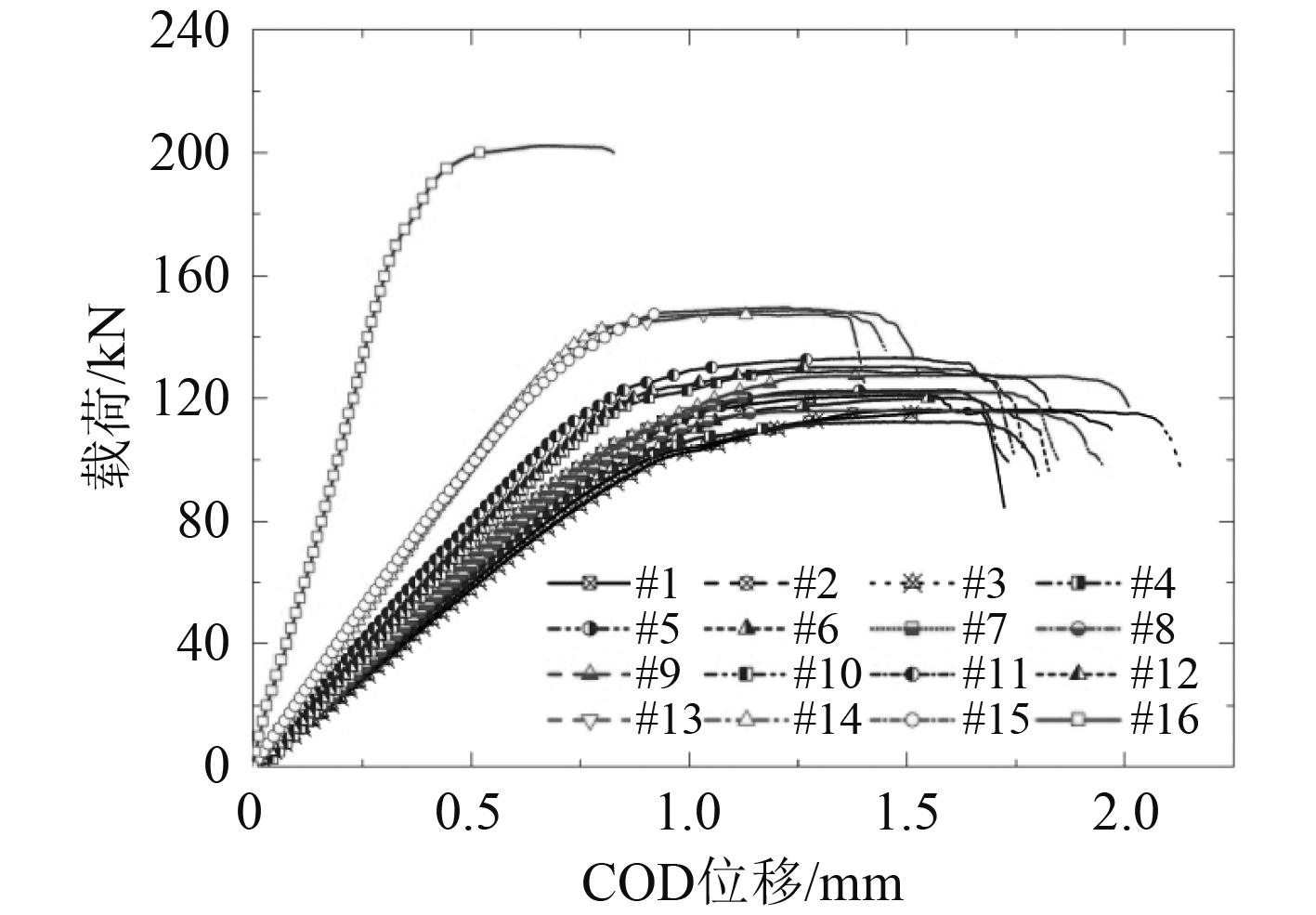
不同加载角度作用下,CTS试样断裂载荷-裂纹张开位移曲线如图4所示。
|
图 4 CTS试样载荷-位移曲线 Fig. 4 Load-displacement curves for CTS specimens |
不同加载角度下的钛合金材料CTS试样断口形貌如图5所示。

|
图 5 断裂后钛合金材料CTS试样断口形貌 Fig. 5 Fracture morphology of CTS specimens |
根据夹式引伸计(COD规)记录的载荷-裂纹张开位移确定不同加载角度CTS试样断裂载荷
|
|
表 3 CTS试样断裂试验结果 Tab.3 Test results of CTS specimens |
将不同加载角度时的断裂载荷
| $ {K}_{\mathrm{{\rm I}}}=\frac{F}{wt}\sqrt{\text{π} a}\frac{\mathrm{cos}\beta }{\left(1-\dfrac{a}{W}\right)}\sqrt{\frac{0.26+2.65\left(\dfrac{a}{W-a}\right)}{1+0.55\left(\dfrac{a}{W-a}\right)+0.08{\left(\dfrac{a}{W-a}\right)}^{2}}},$ | (1) |
| $ {K}_{\mathrm{I}\mathrm{{\rm I}}}=\frac{F}{wt}\sqrt{\text{π} a}\frac{\mathrm{sin}\beta }{\left(1-\dfrac{a}{W}\right)}\sqrt{\frac{-0.23+1.40\left(\dfrac{a}{W-a}\right)}{1-0.67\left(\dfrac{a}{W-a}\right)+2.08{\left(\dfrac{a}{W-a}\right)}^{2}}} ,$ | (2) |
式中:
将各加载角度下应力强度因子计算结果代入式(3),计算反映拉伸-剪切应力程度的I-II型裂纹混合因子
| $ {M}_{12}^{e}=\frac{2}{\text{π} }\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left|\frac{{K}_{\mathrm{I}}}{{K}_{\mathrm{I}\mathrm{I}}}\right| 。$ | (3) |
预测I-II型裂纹起裂扩展条件及偏折方向的经典断裂准则主要包括最大环向应力(MTS)准则[10]、最小应变能密度因子(SED)准则[11]、平均应变能密度(ASED)准则[12]以及Richard经验公式[13]等。分别按照MTS准则、SED准则、ASED准则和Richard经验公式对CTS试样裂纹起裂扩展条件和起裂角进行理论预测,并与试验结果进行对比分析。
表3中加载角度为0°时钛合金材料CTS试样断裂时刻I型应力强度因子
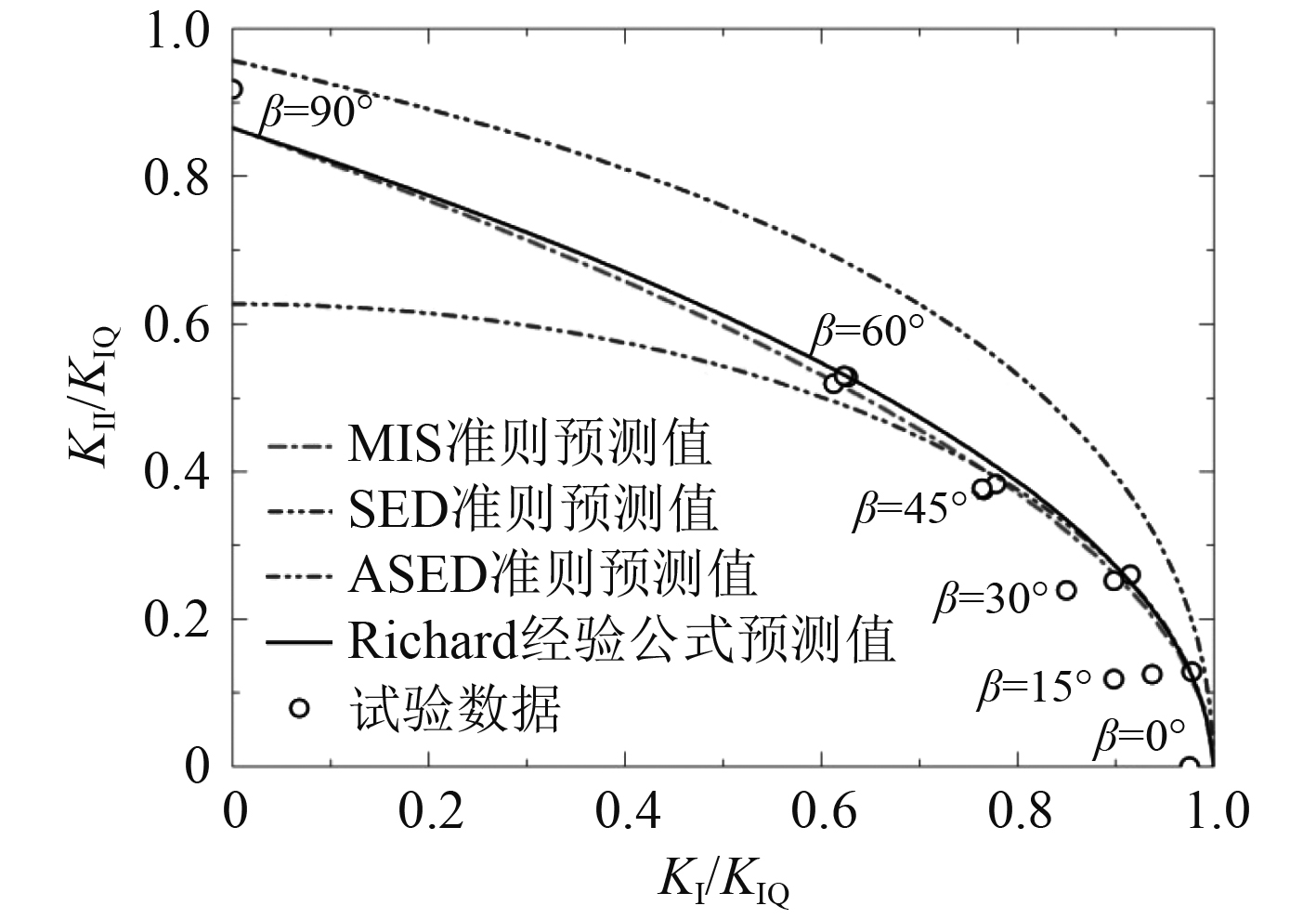
|
图 6 起裂扩展条件理论预测及试验结果 Fig. 6 Theoretical and test results for fracture limit |
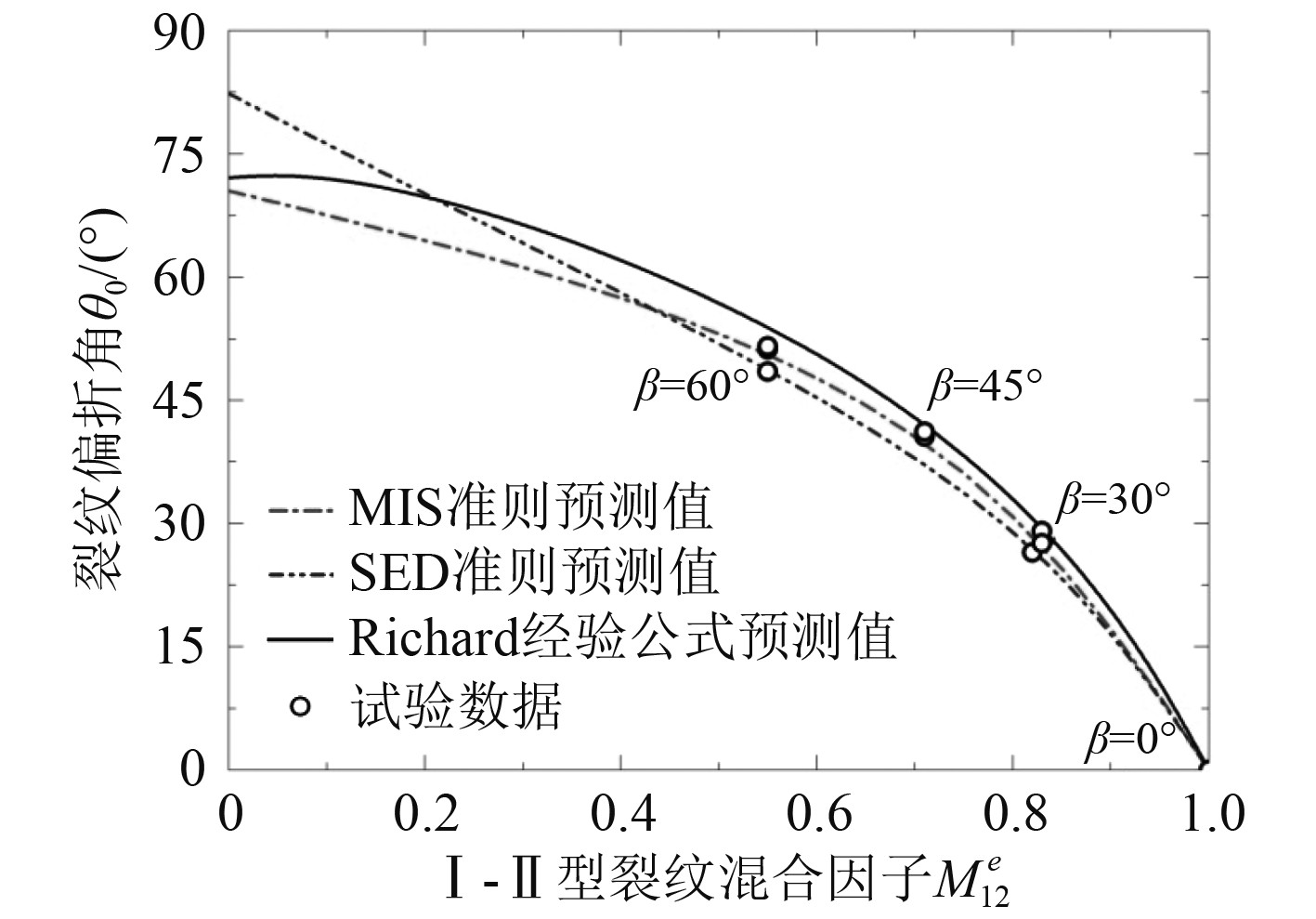
|
图 7 裂纹偏折角度理论预测及试验结果 Fig. 7 Theoretical and test results for deflection angle |
可知,Ti-6Al-2Sn-2Zr-3Mo-X材料I-II混合型裂纹起裂扩展条件及起裂偏折角可由最大环向应力(MTS)准则预测。即裂纹沿临界距离
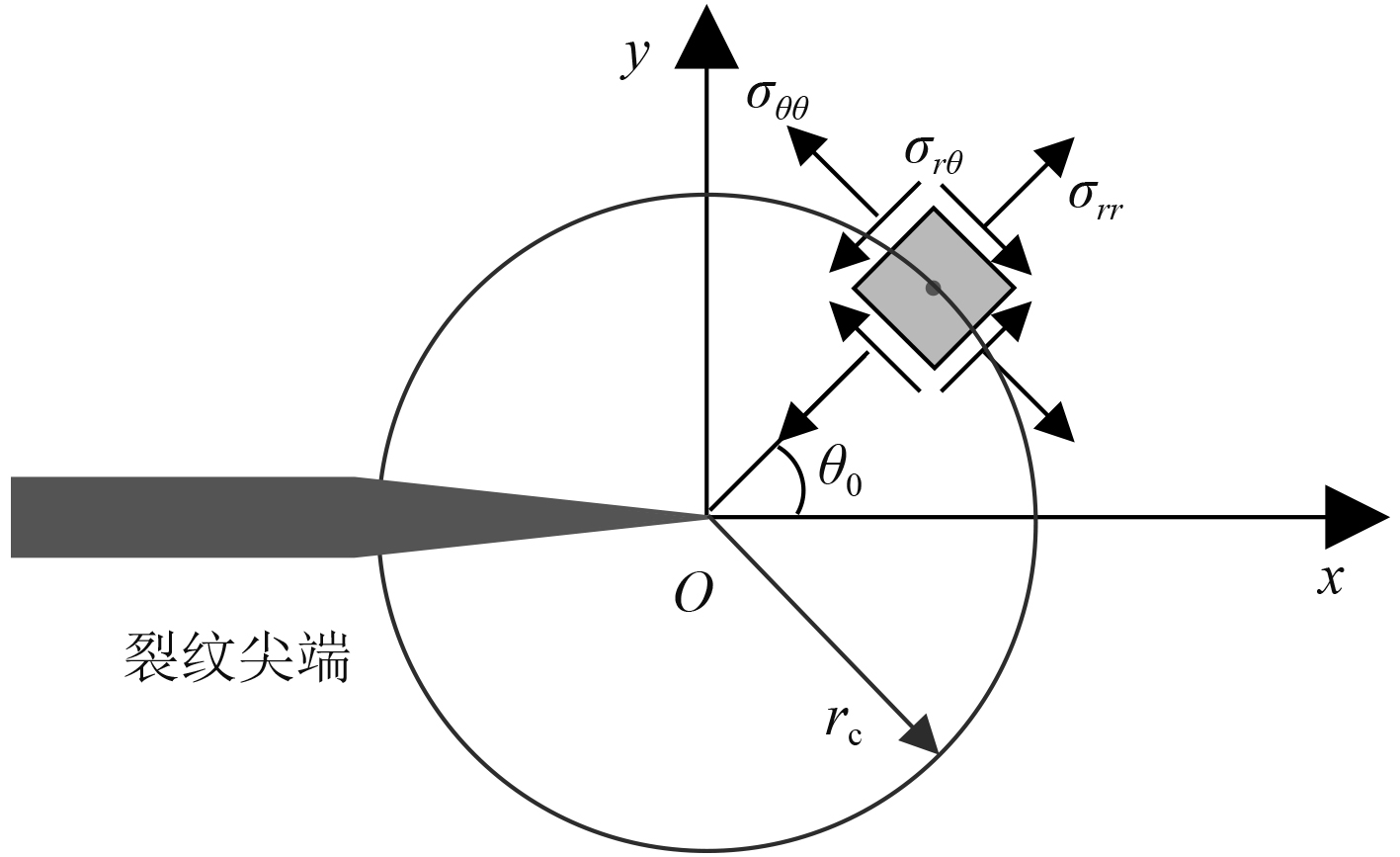
|
图 8 Ti-6Al-2Sn-2Zr-3Mo-X裂纹起裂扩展机制 Fig. 8 Fracture mechanism of Ti-6Al-2Sn-2Zr-3Mo-X |
根据MTS准则,Ti-6Al-2Sn-2Zr-3Mo-X材料I-II混合型裂纹等效应力强度因子
| $ {{K}}_{{e}{q}}=\mathrm{cos}\frac{{\mathrm{\theta }}_{0}}{2}\left({{K}}_{\mathrm{{\rm I}}}{\mathrm{cos}}^{2}\frac{{\mathrm{\theta }}_{0}}{2}-\frac{3}{2}{{K}}_{\mathrm{{\rm I}}\mathrm{{\rm I}}}\mathrm{sin}{\mathrm{\theta }}_{0}\right) ,$ | (4) |
| $ {\mathrm{\theta }}_{0}=2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{{{K}}_{\mathrm{I}}-\sqrt{{{K}}_{\mathrm{I}}^{2}+8{{K}}_{\mathrm{I}\mathrm{I}}^{2}}}{4{{K}}_{\mathrm{I}\mathrm{I}}} 。$ | (5) |
MTS准则近似可由Richard经验公式近似代替[13]。因此,Ti-6Al-2Sn-2Zr-3Mo-X材料I-II混合型裂纹等效应力强度因子和裂纹偏折角可分别采用经验公式简化计算:
| $ {K}_{{e}{q}}=\frac{{K}_{\mathrm{I}}}{2}+\frac{1}{2}\sqrt{{K}_{\mathrm{I}}^{2}+4{\left(1.115{K}_{\mathrm{I}\mathrm{I}}\right)}^{2}} ,$ | (6) |
| $ {\theta }_{0}=\mp \left[155.5°\frac{\left|{K}_{\mathrm{I}\mathrm{I}}\right|}{{K}_{\mathrm{I}}+\left|{K}_{\mathrm{I}\mathrm{I}}\right|}\right]-83.4°{\left[\frac{\left|{K}_{\mathrm{I}\mathrm{I}}\right|}{{K}_{\mathrm{I}}+\left|{K}_{\mathrm{I}\mathrm{I}}\right|}\right]}^{2}。$ | (7) |
本文针对深海装备用新型高强度钛合金材料Ti-6Al-2Sn-2Zr-3Mo-X开展了拉-剪应力复杂应力状态下I-II混合型裂纹断裂特性试验研究。研究结果表明:该高强度钛合金裂纹起裂扩展条件及裂纹偏折角服从MTS准则,当裂纹尖端临界距离
| [1] |
李艳青, 王琨, 黄进浩,等. 高强度钛合金球壳在超高压环境下的新特性[C]// 船舶结构力学会议, 中国武汉, 2016.
|
| [2] |
黄如旭, 万正权. 广义平均形状改变能密度断裂准则及应用[J]. 力学季刊, 2021, 42(01): 179-187. |
| [3] |
张少钦, 郭万林, 李禾, 等. 钛合金室温和高温三维复合型断裂实验研究[J]. 中国科学: 技术科学, 2011, 41(12): 1676-1683. |
| [4] |
SUN C Q, LI Y Q, HUANG R X, et al. Crack initiation mechanism and fatigue life of titanium alloy Ti–6Al–2Sn–2Zr–3Mo-X Effects of stress ratio and loading frequency[J]. Materials Science & Engineering A, 2020, 798: 1-13. |
| [5] |
国家质量技术监督局. 中国人民共和国国家标准: GB/T 228.1-2010金属材料拉伸试验第1部分: 室温试样方法[S]. 北京: 中国标准出版社, 2010.
|
| [6] |
RICHARD H A. A loading device for the creation of mixed mode in fracture mechanics[J]. International Journal of Fracture, 1983(22): 55-58. |
| [7] |
HUANG R X, WAN Z Q. Research on stress intensity factors for the deflected crack of CTS specimen[J]. Ship Mechanics, 2018, 22(12): 1527-1539. |
| [8] |
国家质量技术监督局. 中国人民共和国国家标准: GB/T 4161-2007金属材料平面应变断裂韧度KIC试验方法[S]. 北京: 中国标准出版社, 2007.
|
| [9] |
SMITH DJ, AYATOLLAHI MR, PAVIER MJ. The role of T-stress in brittle fracture for linear elastic materials under mixed-mode loading[J]. Fatigue Fracture Engineering Material Structure, 2001(24): 137-150. |
| [10] |
ERDOGAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineering, 1963, 85: 519-25. DOI:10.1115/1.3656897 |
| [11] |
SIH G C. Mechanics of fracture - method of analysis and solution of crack problems[M]. Leyden: Noordhoff International Publishing, 1973.
|
| [12] |
LAZZARIN P, ZAMBARDI R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches[J]. International Journal of Fracture, 2001, 112(3): 275-298. DOI:10.1023/A:1013595930617 |
| [13] |
RICHARD HA, SCHRAMM B, SCHIRMEISEN NH. Cracks on mixed mode loading – theories, experiments, simulations[J]. International Journal of Fatigue, 2014(62): 93-103. |
 2022, Vol. 44
2022, Vol. 44
