0 引　言

随着水下目标的快速发展^[1-2]，其防护能力不断提高，聚能装药水下爆炸对靶板的毁伤研究受到了更多的重视^[3-4]。聚能装药水下爆炸对靶板的毁伤主要依靠聚能效应和爆破效应。聚能侵彻体可以穿透含水层复合靶板并对后效靶板造成局部穿孔^[5-7]。爆破效应以冲击波为主，与空气中爆破效应不同^[8]，水下冲击波作用会使靶板产生大面积变形甚至撕裂破孔^[9-10]，国内外对水下爆炸冲击波进行大量研究^[11-13]，但对聚能装药水下爆炸冲击波传播和峰值压力分布规律的研究还不够深入。本文针对聚能装药水下爆炸对圆板靶毁伤实验工况，建立Autodyn仿真模型，仿真结果和实验结果进行对比验证。在仿真模型的基础上，研究聚能装药水下爆炸前向冲击波峰值压力的分布规律，拟合得到前向冲击波峰值压力的计算公式。

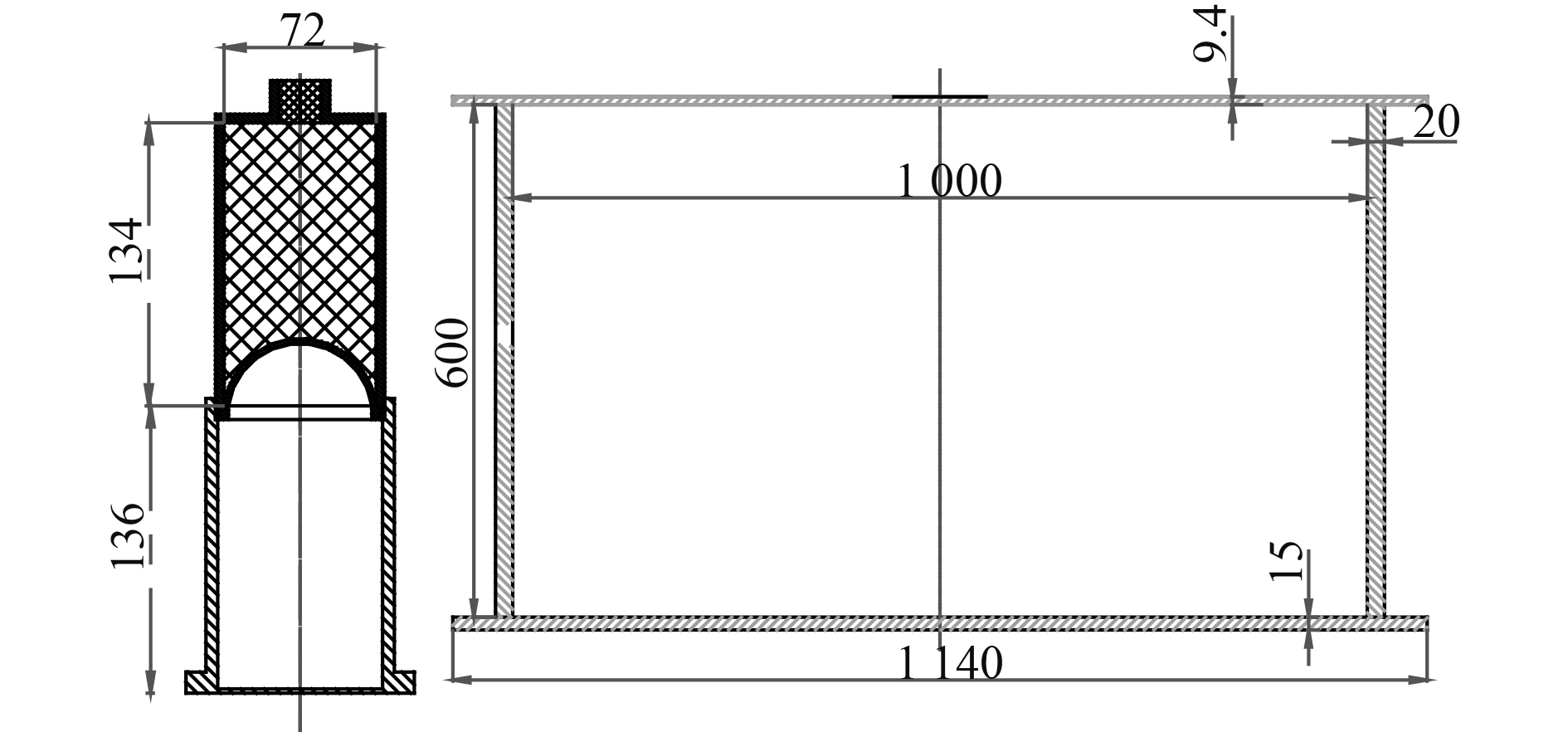
1 仿真模型 1.1 工况条件

仿真模型参考聚能装药对圆板靶毁伤实验，该实验模型如图1所示。依据典型鱼雷结构缩比设计实验战斗部，战斗部装药为B炸药，装药直径为72 mm，装药长度为134 mm，采用球缺型药型罩，罩中心厚度为2.7 mm，材料为紫铜。为研究聚能战斗部对水下单层壳体目标的毁伤效果，圆板靶设计厚度为9.4 mm，直径为1140 mm，材料为921钢。后靶厚度为为15 mm，靶标圆筒直径为1000 mm，筒壁厚度为20 mm，高度为600 mm，后靶和圆筒材料均为Q345钢。在圆板靶中心固定一个炸高筒，便于安装战斗部和模拟空气舱，设计炸高为136 mm，靶标实物如图2所示。

1.2 网格模型

利用Autodyn软件建立仿真模型，为了提高计算效率和计算精度，使用remap功能，用二维模型计算抵达靶板前冲击波、侵彻体和爆轰产物载荷，然后映射进三维模型计算靶板响应阶段。

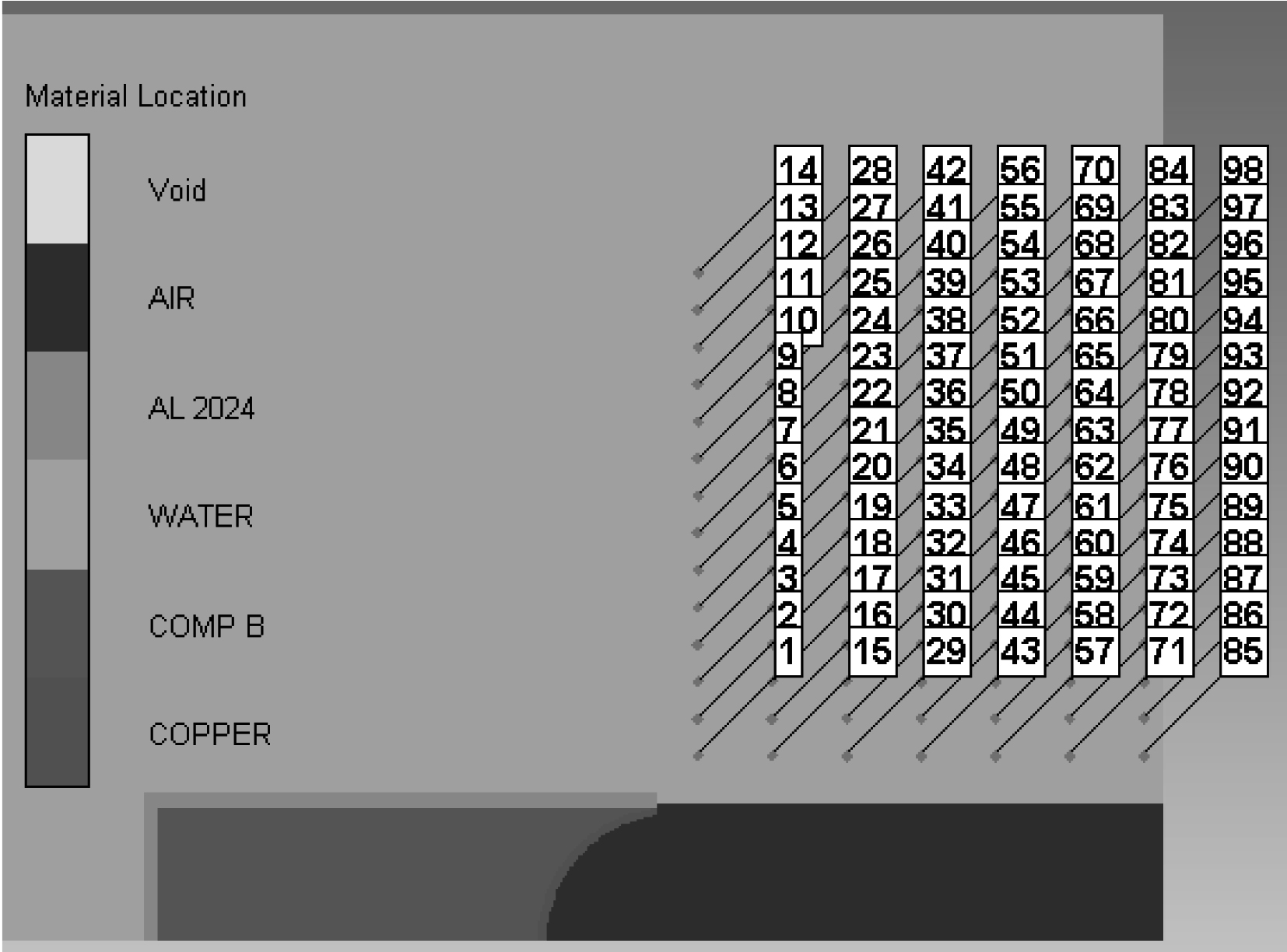
二维仿真模型如图2所示，水域长为1 m，宽为0.5 m，单个网格尺寸为0.5 mm $ \times $ 0.5 mm，装药右端面与水域右边界距离为136 mm，模拟水深为5 m。装药壳体为拉格朗日算法，其余为欧拉算法，起爆方式采用装药顶部中心点起爆。整个模型施加流固耦合条件，并在水域边界添加Flow-out流出边界。在装药右端面与水域右边界之间的区域添加观察点，观察点分为7列，对应轴向距离分别为11 mm，31 mm，51 mm，71 mm，91 mm，111 mm和131 mm，每列有14个观察点，径向距离从50 mm开始，间隔10 mm设置一个观察点。

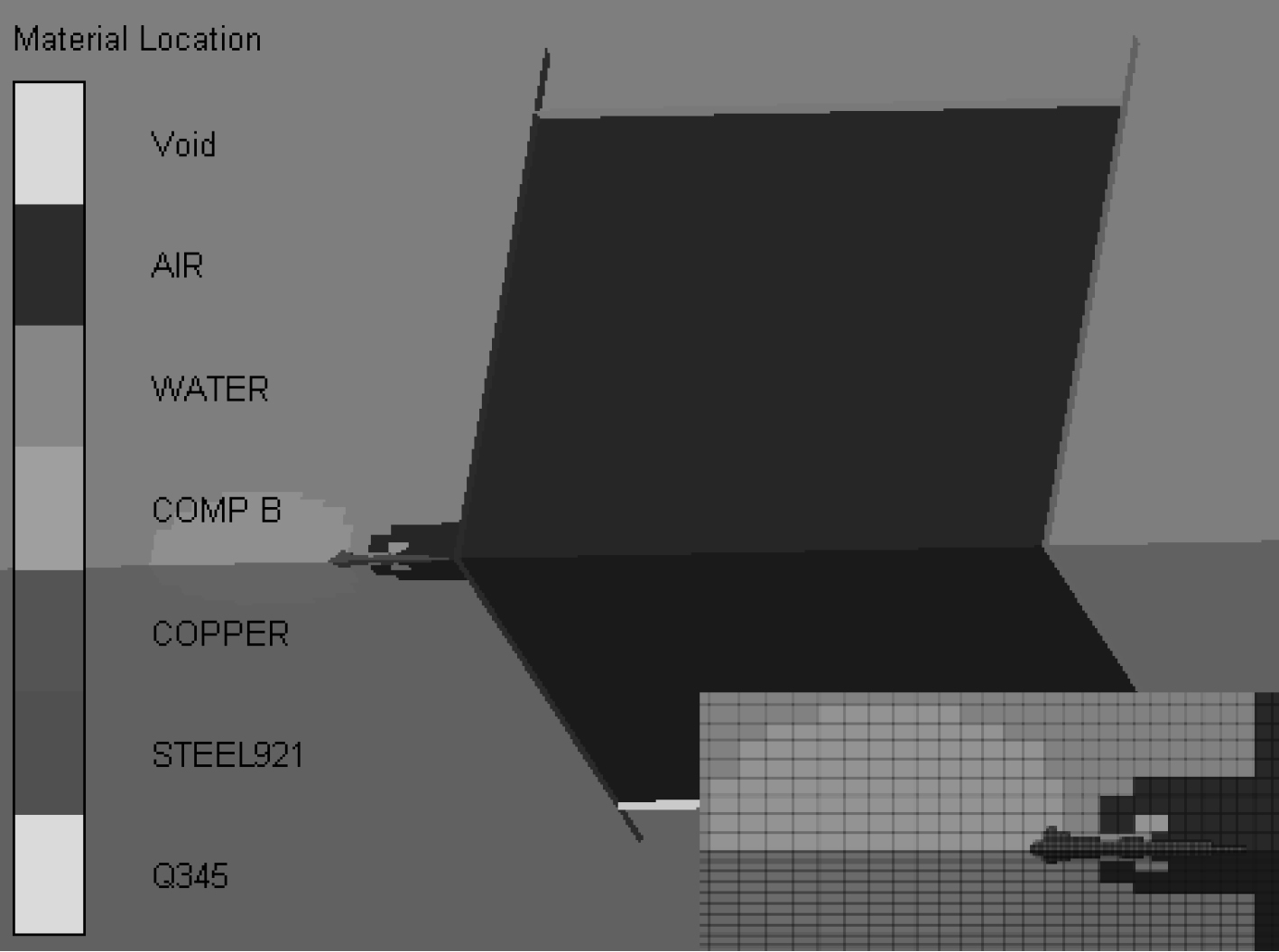
建立1/4三维模型，将二维流场映射到三维模型中，并建立靶板模型，靶标内为空气，三维模型如图3所示。靶标采用shell网格，侵彻体为拉格朗日算法，其余采用欧拉算法。三维模型中添加流固耦合条件和流出边界。

1.3 材料模型

COMP B炸药爆轰产物中的压力用JWL状态方程描述：

$ p=A\left(1-\frac{\omega }{{R}_{1}V}\right){e}^{{R}_{1}V}+B\left(1-\frac{\omega }{{R}_{2}V}\right){e}^{{R}_{2}V}+\frac{\omega E}{V}。$

(1)

式中： $ E $ 为单位质量内能； $ V $ 为爆轰产物相对比容；A，B，R₁，R₂和 $ \omega $ 为常数。状态方程各参数取值如表1所示，同时给出了炸药的密度 $ {\ \rho _{{e}}} $ 、爆轰压力 $ {P_{CJ}} $ 和爆速 $ {D_{CJ}} $ 。

水的状态方程采用多项式状态方程，当水受压时的状态方程为公式（2）；当水受拉或空化时的状态方程为公式（3）。

$ p = {A_1}\mu + {A_2}{\mu ^2} + {A_3}{\mu ^3} + \left( {{B_0} + {B_1}\mu } \right){\rho _0}e，$

(2)

$ p = {T_1}\mu + {T_2}{\mu ^2} + {B_0}{\rho _0}e。$

(3)

式中： ${A}_{1}，{A}_{2}，{A}_{3}，{B}_{0}，{B}_{1}，{T}_{1}$ 和 $ {T_2} $ 为常数， $\mu = {\rho \mathord{\left/ {\vphantom {\rho {{\rho _0} - 1}}} \right. } {{\rho _0} - 1}}$ ， $ \rho $ 为水的密度， $ {\rho _0} $ 为水的初始密度；水的比内能为 $ e = (\rho gH + {p_{atm}})/\rho /{B_0}e $ ，水深 $H{\text{ = 5}}\,\,{\rm{m}}$ ， $ {p_{atm}} $ 为大气压力。水的状态方程各参数取值如表2所示。

921钢状态方程为Linear，采用Cowper SRmonds强度模型和Plastic Strain失效模型。Q345钢的状态方程和失效模型与921钢相同，强度模型为von Mises。靶标的部分材料参数如表3所示。模型中其他材料的状态方程和部分参数如表4所示，均为Autodyn软件中的默认参数。

2 仿真与实验结果对比

实验结果如图4所示，圆板靶靶面产生整体凹陷变形，凹陷最深处为靶板中心，最大变形挠度为150.3 mm。靶板中心位置穿孔孔径为26.2 mm。实验中圆靶板边缘向上翘起并出现褶皱，靶标圆筒与圆板靶接触的位置发生内凹变形。

仿真结果如图5所示，与实验结果一样，靶板整体向内凹陷，靶板边缘向上翘起并出现褶皱，圆筒与圆板靶接触的位置向筒内弯曲变形。仿真中的靶板中心挠度为138.5 mm，相比实验结果误差为7.9%；仿真中心穿孔孔径为27.8 mm，相比实验结果误差为6.1%。仿真结果与实验结果对比，整体变形基本一致，主要特征数据误差较小，仿真模型有较高的计算精度。

3 前向冲击波特性分析

二维模型中不同时刻的压力云图如图6所示，可以看出，与射流运动方向一致的冲击波（前向冲击波）压力在传播过程中逐渐衰减。0.05 ms时刻的各向压力均很高，到0.09 ms时刻前向压力明显小于侧向压力，分析原因与药型罩和空气舱的影响有关。前向的部分爆轰能量被药型罩吸收，部分能量随爆轰产物泄入空气舱内部，并且空气舱壳体变形等也会吸收部分能量，导致前向冲击波压力明显小于侧向压力，距离空气舱位置较近的区域冲击波压力较小。观察波阵面的形状变化，贴近空气舱壁面位置的波阵面趋近于平面。同柱形装药水下爆炸冲击波均匀化一样，聚能装药水下爆炸远离空气舱的冲击波也呈现均匀化和球形化的特点。

从Autodyn软件中提取观察点压力数据，得到各观察点位置的峰值压力数值，绘制不同轴向距离下的峰值压力随径向距离变化的曲线，如图7所示。

可知，由于冲击波在水中传播的衰减作用，在同一径向距离y的峰值压力随轴向距离 $ h $ 增大而减小。水中冲击波压力衰减很快，以 $ h = {\text{11}}\,\,{\rm{mm}} $ 的曲线为例，最大峰值压力为1.48 GPa，最小峰值压力为0.59 GPa，径向距离增大110 mm，峰值压力衰减了60%。在同一轴向距离下的峰值压力曲线先上升后下降，每条曲线上都存在一个峰值压力最大值。

以峰值压力最大值为分界，对曲线中上升段和下降段分别用函数拟合。该模型下的峰值压力主要受径向距离y和轴向距离 $ h $ 影响。观察前半段峰值压力的上升趋势，在同一 $ h $ 利用Asrmptotiol函数拟合。Asrmptotiol函数如式（4）所示，利用仿真数据拟合后得到函数参数设置，如表5所示， $ h $ 为11 mm时数据较少，为减小误差不参加拟合。依据表5，得到函数参数 $ a，b，c $ 与 $ \,\,h $ 的关系，分别如式（5）～式（7）所示。

$ {p_m}(h,y) = a{{ - }}b \times {c^y}，$

(4)

$ a = 0.22 + 1.42{e^{{{ - }}h/43}}，$

(5)

$ b = 0.38 + 58{e^{{{ - h}}/23}}，$

(6)

$ c = 0.975{{ - }}0.09{e^{{{ - }}h/67}}。$

(7)

观察后半段峰值压力的上升趋势，在同一轴向距离下利用多项式Parabola函数拟合，多项式Parabola函数如式（8）所示。按照前半段的处理方式，得到后半段函数参数 $ A，B，C $ 与 $ h $ 的关系，分别如式（9）～式（11）所示。

$ {p_m}(h,y) = A + By + C{y^2} ，$

(8)

$ A = 0.28 + 3.8{e^{{{ - }}h/23.6}}，$

(9)

$ B = 4.5 \times {10^{{{ - 4}}}}{{ - 0}}{\text{.04}}{e^{{{ - }}h/15.6}} ，$

(10)

$ C = {{ - 4}} \times {\text{1}}{{\text{0}}^{{{ - 6}}}} + {\text{1}}{\text{.3}} \times {10^{{{ - 4}}}}{e^{{{ - }}h/9.2}}。$

(11)

为了得到峰值压力最大值位置规律，以二维模型为基础，在 $ h $ 和 $ y $ 为0～130 mm的范围内分区域加密观察点，获得各个 $ h $ 下的峰值压力最大值所在位置的 $ y $ 坐标，得到位置分布如图8所示。

可知，同一轴向距离 $ h $ 下，曲线下方的点的峰值压力随径向距离 $ y $ 增大而增大，曲线上方的点的峰值压力随 $ y $ 增大而减小，并且 $ h $ 越大，峰值压力最大值所在位置的 $ y $ 越大。聚能装药水下爆炸冲击波的衰减除了传播距离的影响外，空气舱附近还受到药型罩成形和装药壳体吸能等因素的影响，将这些影响因素统一称为装药结构因素。将图8中的位置连线作为一条分界线，分界线上方的峰值压力衰减主要受到传播距离的影响，分界线下方的峰值压力衰减主要受装药结构因素的影响。

对图8中峰值压力最大值位置进行线性拟合，得到该装药结构下峰值压力最大值的位置计算公式：

$ y = 0.42h + 67.27 。$

(12)

由于图7中的峰值压力曲线按找最大值位置进行分段拟合，式（12）可以用来划分曲线的上升段和下降段，最终拟合得到该模型关于轴向距离 $ h $ 和径向距离 $ y $ 的峰值压力计算经验公式：

$ {p_m}(h,y) = \left\{ \begin{gathered} 0.22 + 1.42{e^{-h/43}}-(0.38 + 58{e^{-h/23}})\times \\ {(0.975{\text{ - 0}}{\text{.09}}{e^{-h/67}})^y}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y \leqslant 0.42h + 67.27，\\ 0.28 + 3.8{e^{-h/23.6}} + (\frac{{4.5}}{{{{10}^4}}}-\frac{{4{e^{-h/15.6}}}}{{{\text{1}}{{\text{0}}^{\text{2}}}}})y+ \\ (\frac{{{\text{ - 4}}}}{{{{10}^6}}} + \frac{{1.3{e^{-h/9.2}}}}{{{{10}^4}}}){y^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y \geqslant 0.42h + 67.27 。\end{gathered} \right. $

(13)

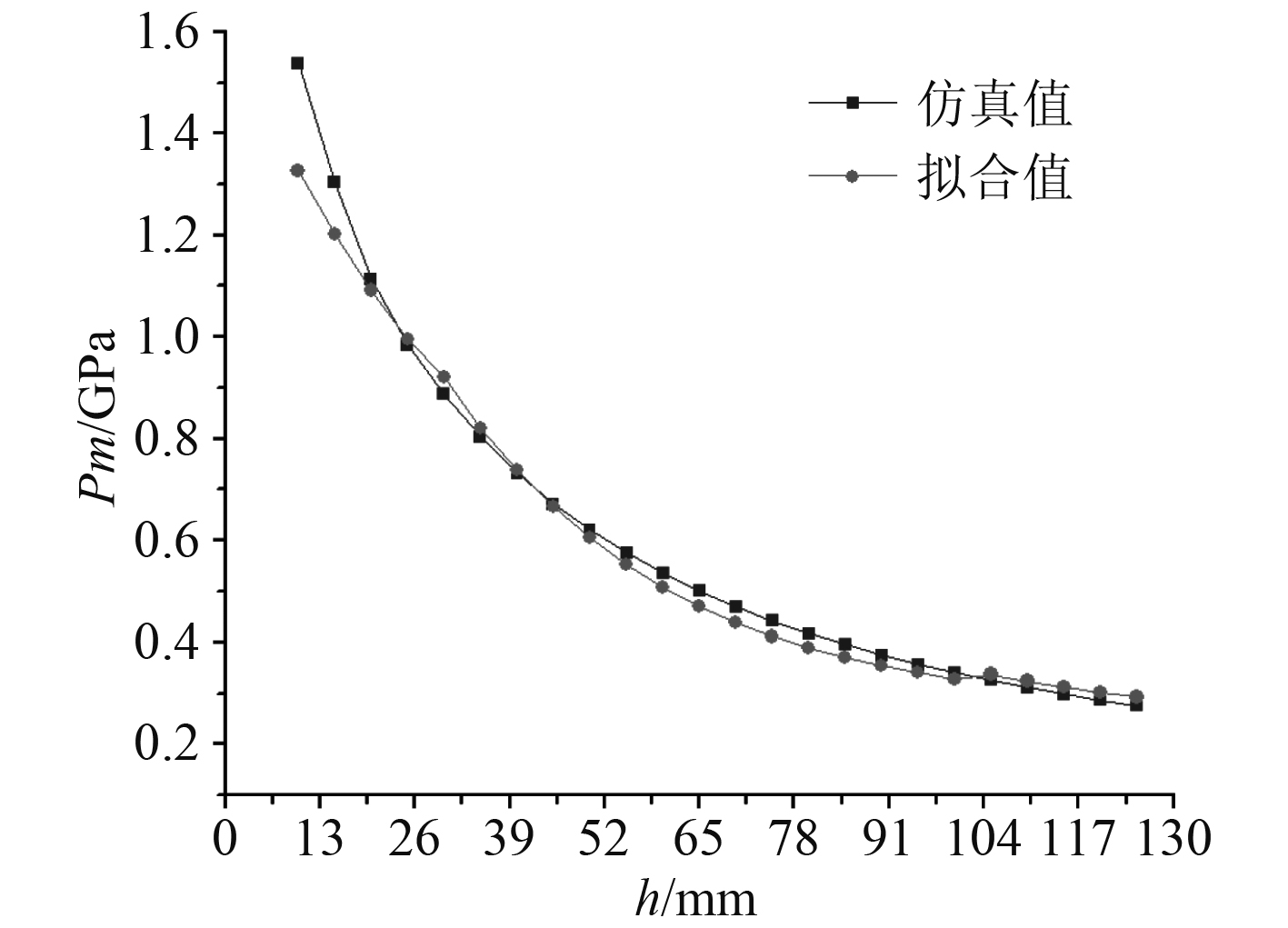
利用式（13）计算峰值压力最大值的拟合值，与仿真值进行对比，并绘制拟合值和仿真值曲线如图9所示。在 $ 50\;{\rm{mm}} < y < 180\;{\rm{mm}} $ ， $h < 136\;{\text{mm}}$ 的范围内，拟合值与仿真值的最大误差13.8%，平均误差为2.2%，拟合公式的计算精度较高，拟合效果好。

4 结　语

1）冲击波压力随传播距离的增大逐渐衰减，远离空气舱的冲击波在传播过程中呈现均匀化和球形化的特点。靠近空气舱位置的前向冲击波波阵面近似平面，空气舱附近压力明显小于侧向压力。

2）在同一轴向距离下，冲击波峰值压力随着径向距离先增大再减小，即存在一个峰值压力最大值，该最大值点的轴向与径向坐标关系呈线性分布。

3）利用冲击波峰值压力沿径向和轴向分布数据，采用分段拟合的方法，得到了峰值压力计算经验公式，平均误差率为2.2%，误差率较小，拟合效果较好。