加筋板广泛应用于航空航天、建筑、车辆和海军工程,在各个领域发挥着重要作用[1-4]。目前,仍为船舶的主要建造结构[5]。对加筋板进行抗爆设计,对于提升舰船生命力,具有十分重要的意义。
为了评估船舶结构的抗爆性,Rudrapatna[6],Zong等[7]均对爆炸荷载下加筋板的变形进行了数值研究,分析了剪应力对结构破坏的影响。Zakrissonand[8]对可变形钢板进行了近场空气爆炸载荷模拟,结果表明,爆炸载荷建模对模拟结果有很大影响。上述研究主要考虑炸药产生的近场爆炸。事实上,船舶在航行过程中也会受到远场爆炸产生的平面冲击波的威胁,研究加筋板在平面冲击波作用下的动力响应是十分必要的。
在研究中,往往使用简化的爆炸发生器来模拟空爆载荷对结构物的冲击[9-11]。早期的平面波发生器主要包括双组分炸药、多点起爆、捕鼠器和惰性材料等[12-14]。为了减少平面波发生器结构的复杂度,降低相关成本,便于实际应用,设计了一种模拟爆炸平面冲击波的简单装置。该装置由雷管、传爆药、主装药、空气-金属屏障区域以及二次装药构成[15-16]。但目前,对于该装置的分析仍停留在理论与数值层面,并未进行实际试验。同时,在进行爆炸试验时,一些选择在露天条件下进行,成本较高的同时,极易对结果产生影响与干扰,对环境也产生了较大污染[17]。因此,有必要将平面波发生器与密闭容器进行结合,并基于核爆特点,将爆炸冲击波简化为持续的平面冲击载荷,从而较好地实现试验模拟。
本文采用筒形爆炸容器,将球形冲击波转化为平面冲击波[18] ,对加筋板在平面冲击波作用下的响应进行试验研究。分析加筋板的变形、加速度和破坏模式,提出冲击波压力随标度距离和载荷持续时间的经验表达式,并利用经验公式计算的冲击波时程进行了数值模拟。结果表明,数值计算结果与试验结果吻合较好。此外,还探讨了峰值爆炸压力对加筋板响应的影响,分析了加劲肋能承受的极限载荷。
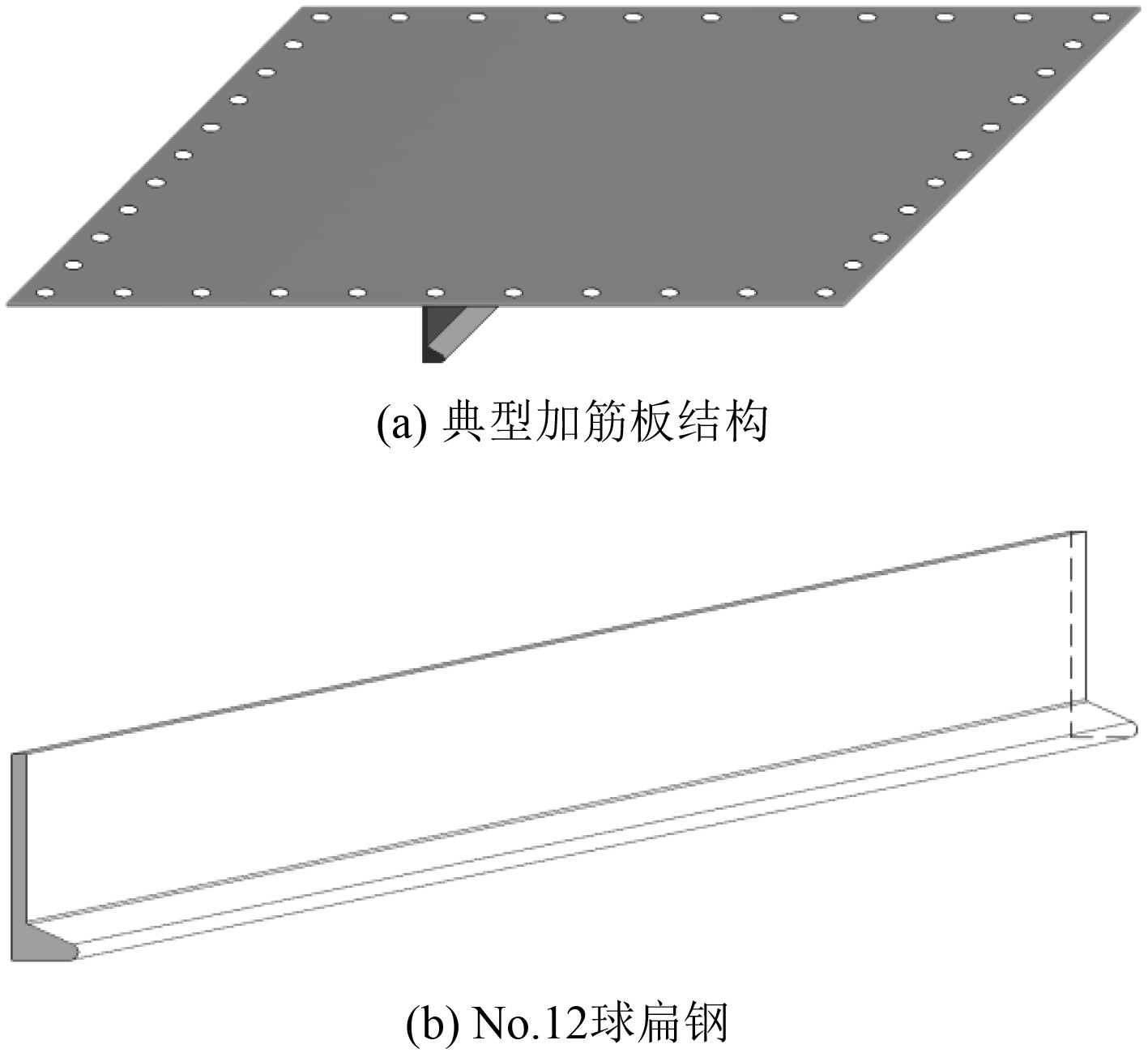
1 爆炸试验 1.1 试验模型与装置试验所用加筋板结构如图1所示。其中,加强筋采用No.12号球扁钢。主要尺寸参数为:长度L=1 160 mm,宽度B=1 160 mm,面板厚度tf=5 mm,D=26 mm,M=40,N=108 mm。其中,L为长度,B为宽度,tf为面板厚度,D为开孔直径,M为开孔总数,N为相邻开孔之间的距离。试验模型通过M24螺栓实现与固定约束工装的连接,模型材料选用Q235低碳钢。
|
图 1 试验模型 Fig. 1 Test model |
采用传统CO2气体保护焊对模型进行加工,并对模型面板以50 mm为间距进行画线,如图2所示。采用如图3所示的装置进行试验。

|
图 2 面板画线 Fig. 2 Draw line on the panel |
|
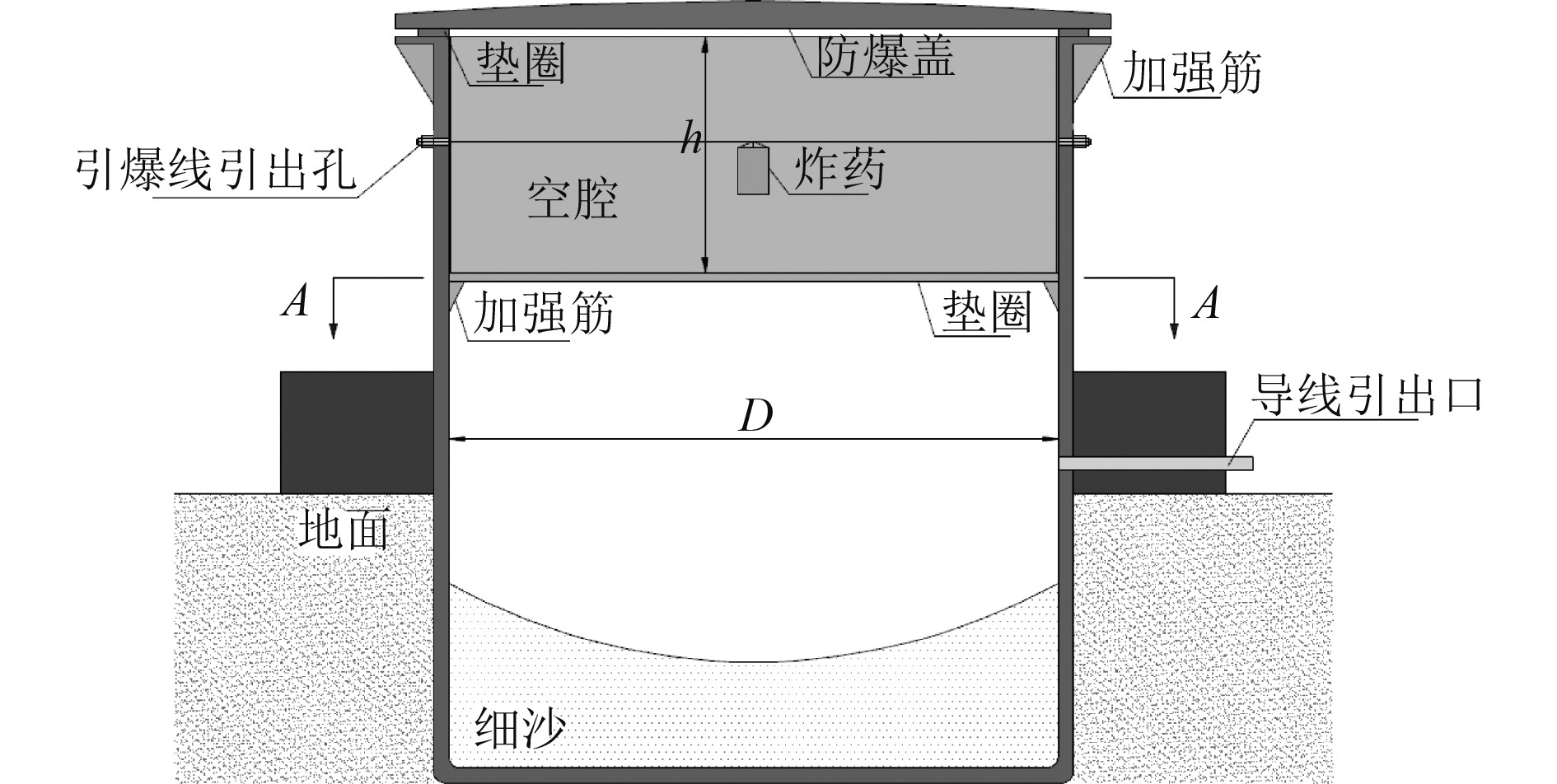
图 3 爆炸试验装置[18] Fig. 3 The test device applied to air blast |
在试验前,对爆炸载荷进行调试,并给出爆炸参数:爆距1.2 m,聚黑-2炸药质量mj=400 g时,峰值可达500 kPa,载荷持续时间可达1 s。符合《The marine environment requires the mechanical environment》[19] 对远场爆炸冲击波载荷峰值及持续时间的规定。
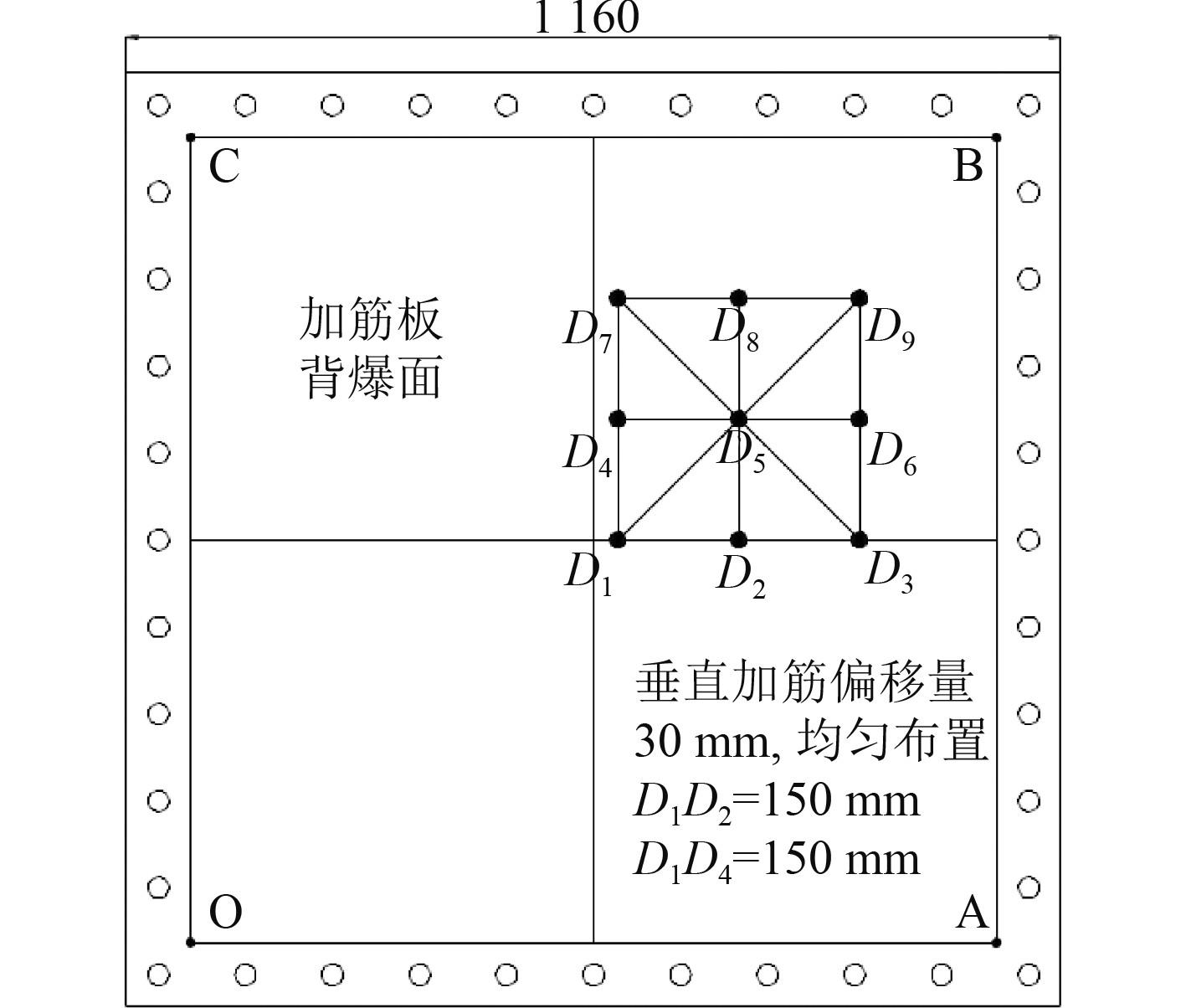
试验测点选取如图4所示。其中,D1,D3,D5,D7,D9五处位置布置应变花,用于测量应变;D1,D6,D8布置加速度传感器,进行加速度测量。
|
图 4 测点布置图 Fig. 4 Layout of measuring points |
主应力计算公式:
| $ \left\{ \begin{gathered} {\sigma _{\text{1}}}{\text{ = }}\frac{E}{2}\left[ {\frac{{{\varepsilon _0} + {\varepsilon _{90}}}}{{1 - v}} + \frac{1}{{1 + v}}\sqrt {{{({\varepsilon _0} - {\varepsilon _{90}})}^2} + {{(2{\varepsilon _{45}} - {\varepsilon _0} - {\varepsilon _{90}})}^2}} } \right] ,\\ {\sigma _{\text{2}}}{\text{ = }}\frac{E}{2}\left[ {\frac{{{\varepsilon _0} + {\varepsilon _{90}}}}{{1 - v}} - \frac{1}{{1 + v}}\sqrt {{{({\varepsilon _0} - {\varepsilon _{90}})}^2} + {{(2{\varepsilon _{45}} - {\varepsilon _0} - {\varepsilon _{90}})}^2}} } \right] ,\\ {\tau _{\max }} = \frac{E}{{1 + v}}\sqrt {{{({\varepsilon _0} - {\varepsilon _{90}})}^2} + {{(2{\varepsilon _{45}} - {\varepsilon _0} - {\varepsilon _{90}})}^2}} 。\\ \end{gathered} \right. $ | (1) |
式中:ε0,ε45,ε90分别对应着同一应变花3个不同方向的应变值。试验测量得到的极值如表1所示。
|
|
表 1 三向应变花试验测量极值 Tab.1 Extreme value of triaxial strain rosette test |
等效应力公式:
| $ {\sigma _s}{\text{ = }}\frac{1}{{\sqrt 2 }}\sqrt {{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _3} - {\sigma _1})}^2}},$ | (2) |
本次试验测得的应力为平面应力,由式(1)和式(2)可得等效应力值,公式如下:
| $ {\sigma _0}{\text{ = }}\frac{1}{{\sqrt 2 }}\sqrt {{{({\sigma _1} - {\sigma _2})}^2} + \sigma _1^2 + \sigma _2^2} ,$ | (3) |
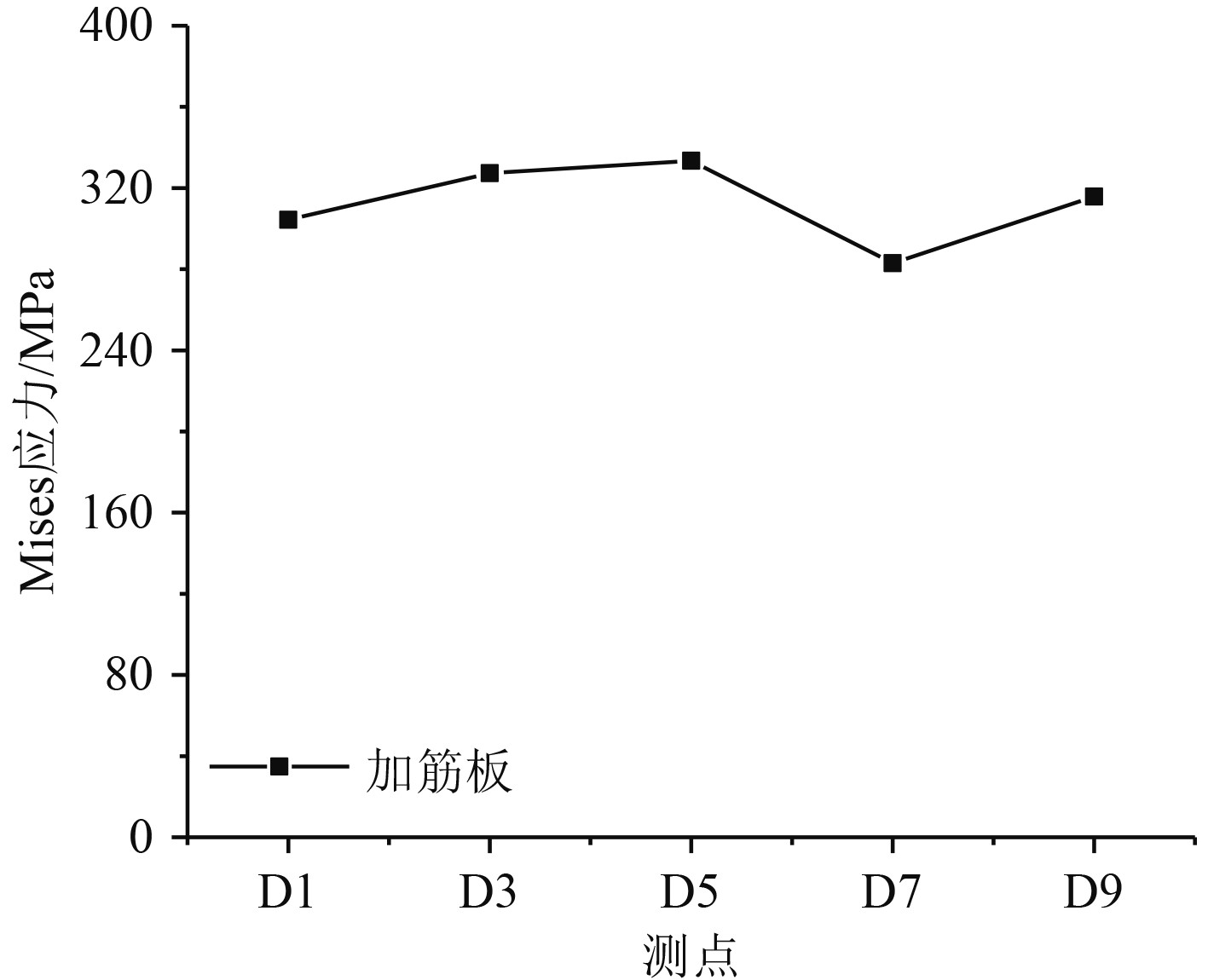
根据式(1)和式(3),及表1中的应变值求出加筋板测点处Mises等效应力值,如图5所示。
|
图 5 爆炸试件测点处应力值 Fig. 5 Stress value of explosion specimen at measuring point |
由图5可知,加筋板在测点D5处应力最大,在测点D7处应力最小,加筋板测点处的应力关系为
由于加筋板具有结构对称性,取1/2试验现象图,对加筋板爆炸之后的结构响应情况进行分析,如图6所示。

|
图 6 500 kPa载荷作用下加筋板结构响应情况 Fig. 6 Response of stiffened plate under 500 kPa load |
由图6可知,在爆炸载荷作用下,加筋板在边界区域面板上产生了明显的塑性绞线,变形主要发生在加强筋与边界之间的面板区域。加筋板与面板连接节点处出现了明显的豁口,进一步验证了上述结论。
1.3.2 加速度本试验采用压电式加速度传感器记录加速度数据。传感器的灵敏度为0.043 m/s2,采样频率100 kHz。
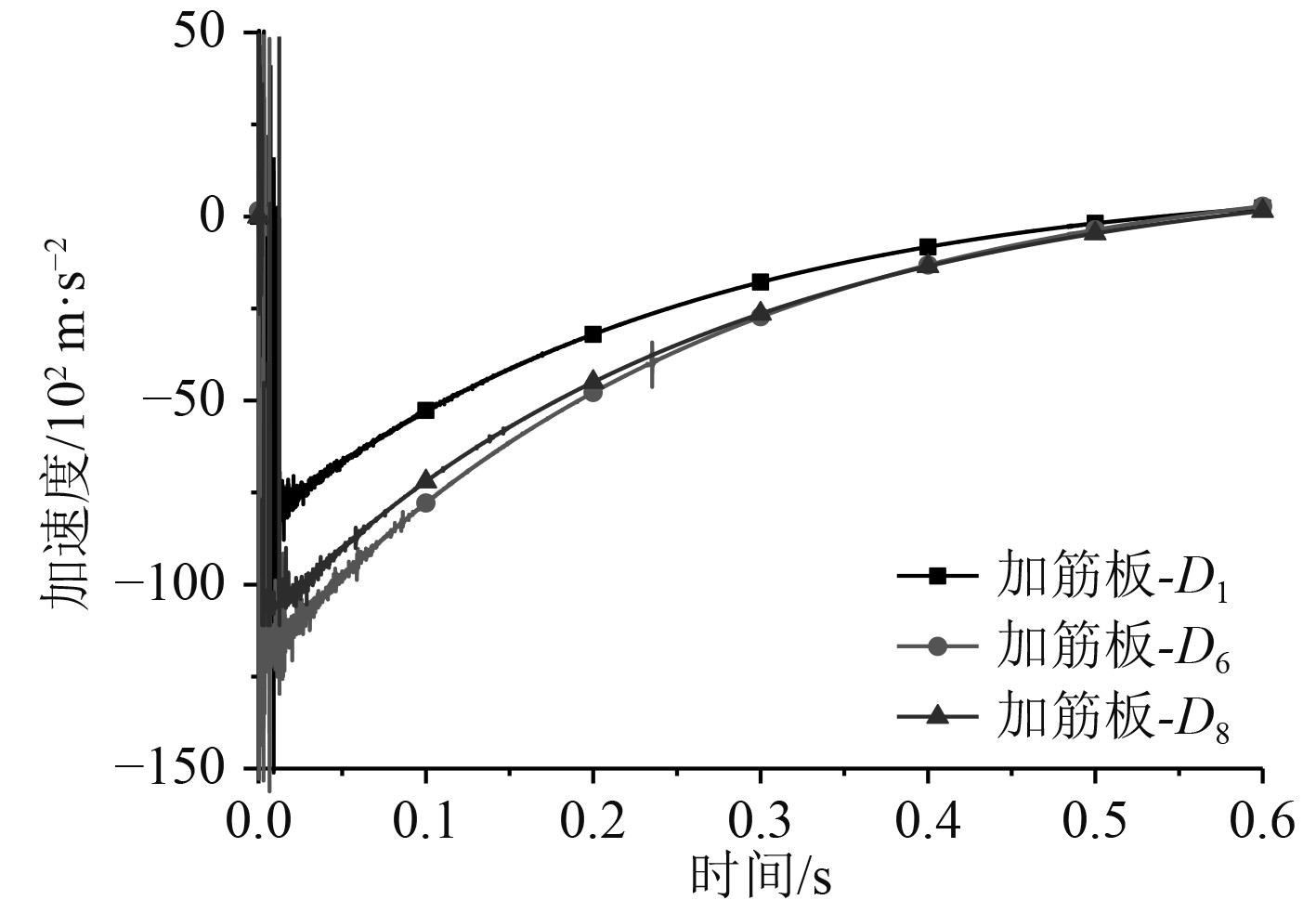
根据试验结果,在0.6 s之后,各点加速度均趋于0,故只对该时间点之前的加速度波动情况进行分析,如图7所示。整理该区间内加速度极值,如表2所示。
|
图 7 爆炸试件各点加速度值 Fig. 7 Acceleration value at different measuring point of explosive specimen |
|
|
表 2 结构测点加速度试验极值 Tab.2 Acceleration test extremum of structure measuring point |
综合图表可知,D6处的加速度与D8处较为接近,最大值稍大。D1处的加速度则小得多,这是由于D1更靠近加强筋位置,表明加强筋的存在提高了加筋板的抗冲击性能。
1.3.3 损伤变形情况500 kPa爆炸载荷作用下加筋板的结构变形情况如图8所示。

|
图 8 500 kPa爆炸载荷下加筋板结构变形情况 Fig. 8 Deformation of stiffened plate structure under 500 kPa explosion load |
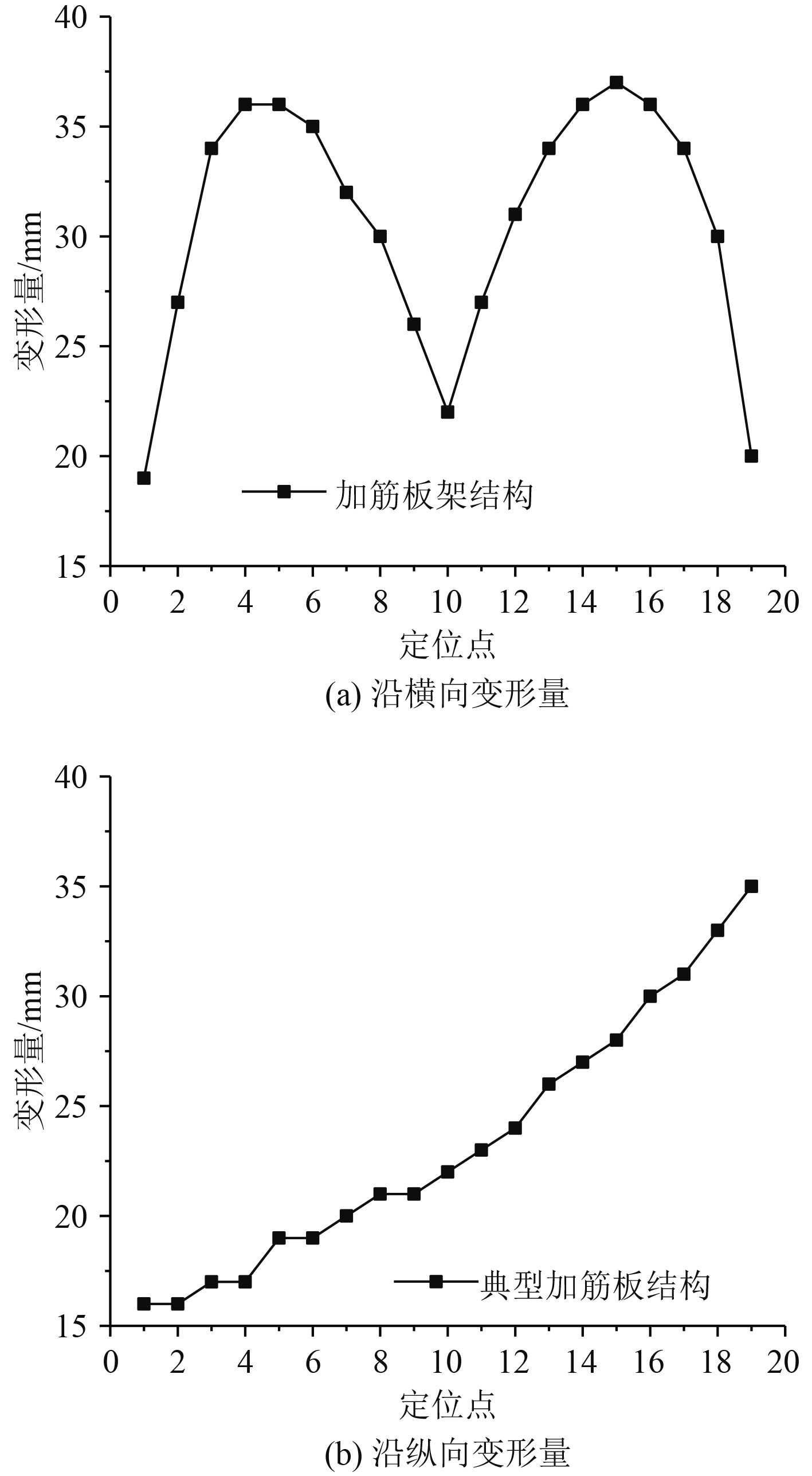
由图8可知,加筋板面板在爆炸载荷作用下变形具有明显的对称性,且在加筋区域变形很小。为了进一步研究加筋板的变形规律,将面板画线的交叉点作为定位点,并将加筋板中心位置处作为定位点10,分别沿横向和纵向进行变形量整理,如图9所示。
|
图 9 典型加筋板架结构变形情况 Fig. 9 Deformation of typical stiffened grillage structure |
由图9(a)可知,对于典型加筋板架结构中心处的横向变形量,由于加强筋的存在与边界限制的作用,变形呈现“双峰”趋势。变形量由一端边界处逐步增大到第一个峰值后,再逐步减小至中心位置处达到“谷值”,再由中心位置向另一端边界处逐渐增大到峰值后继续减小直至另一端边界处。
由图9(b)可知,相较于横向变形量,除两端变形较小外,典型加筋板架结构纵向变形量整体呈现增加趋势。这是因为在500 kPa爆炸载荷作用下,加筋板中加强筋与面板连接处某一连接节点处出现了豁口,从而导致加筋板在产生变形的同时,沿某一侧发生倾斜。由于变形主要发生在加强筋两侧,在实际应用中,可在两侧进行加固处理,从而提高结构的抗爆性能。
2 平面冲击载荷数值仿真研究 2.1 有限元模型为进一步对平面冲击波作用下加筋板的响应情况进行研究,以爆炸试验为基础,利用有限元软件Abaqus进行数值仿真计算。建立有限元模型,如图10所示。

|
图 10 加筋板有限元模型 Fig. 10 Finite element model of stiffened panel |
通过对Baker,Hetherington,Wu等研究成果[20-22] 进行总结,可得拟合公式[23]:
| $ \left\{ \begin{gathered} P = {P_s}\frac{t}{{{\tau _r}}}{\text{ }}(0 \leqslant t \leqslant {\tau _r}),\\ P = {P_s}\left(1 - \frac{{t - {\tau _r}}}{{{\tau _d}}}\right){e^{ - a\frac{{t - {\tau _r}}}{{{\tau _d}}}}}{\text{ }}({\tau _r} \leqslant t \leqslant {\tau _ + })。\\ \end{gathered} \right. $ | (4) |
式中:
| $ a = 4.228P_s^{0.38} + 9.59P_s^{0.79}{e^{ - 4.55\frac{{0.4 - {\tau _r}}}{{{\tau _d}}}}},$ | (5) |
| $ {P_s} = \mu {P_{so}} ,$ | (6) |
| $ {P_{so}} = \frac{{0.13}}{Z}{\text{ - }}\frac{{0.668}}{{{Z^2}}}{\text{ + }}\frac{{2.614}}{{{Z^3}}}{\text{ (MPa)}} 。$ | (7) |
式中,
在上述计算的基础上,作出拟合曲线并与试验测得的载荷幅值曲线进行对比,如图11所示。

|
图 11 核爆幅值曲线拟合情况对比 Fig. 11 Comparison of nuclear explosion amplitude curve fitting |
由图11可知,拟合得出的压力与试验结果吻合较好,故可将其作为模型外载荷输入曲线。
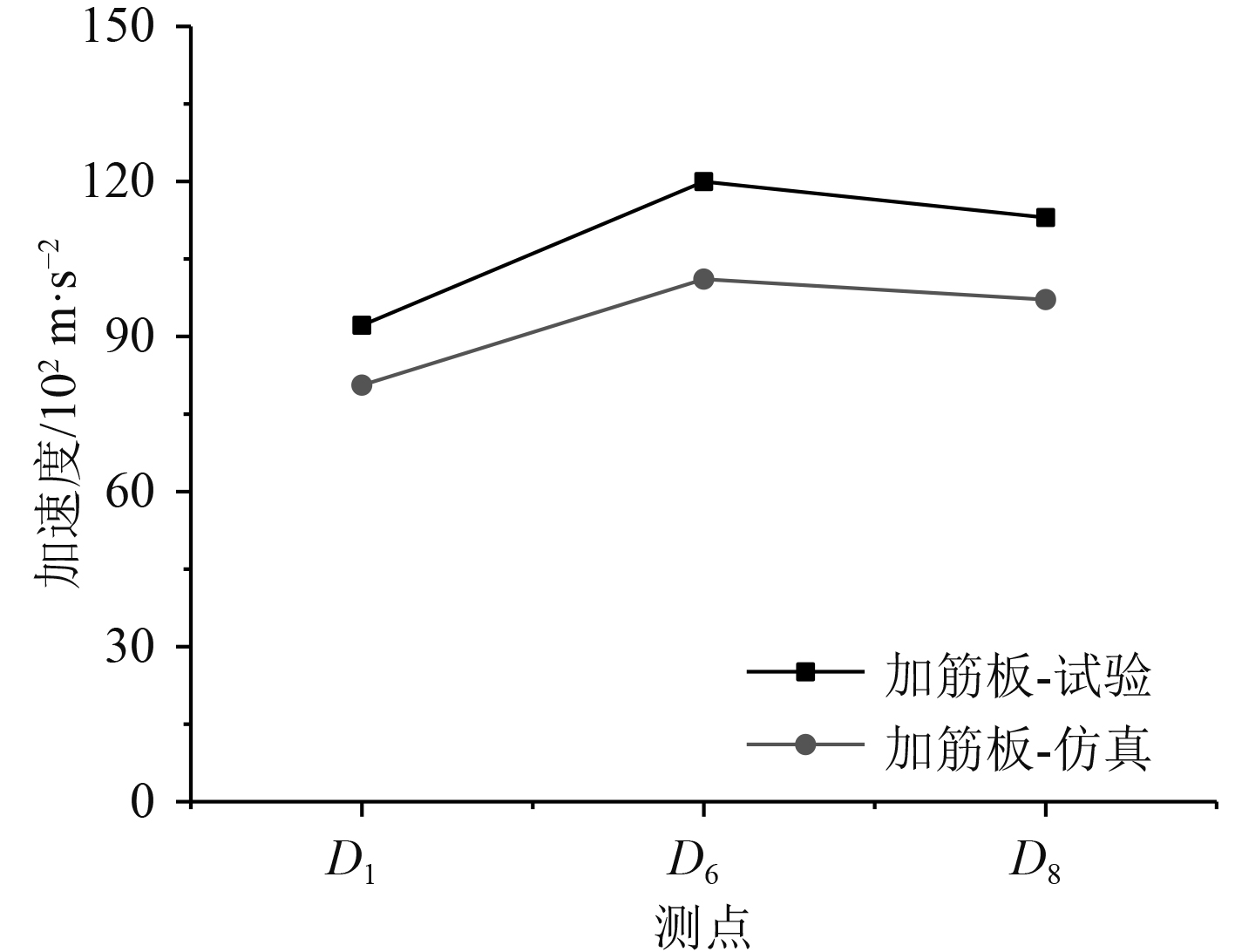
2.2 结果对比分析 2.2.1 加速度结果对比将加速度的仿真结果与试验值对比,如图12所示。
|
图 12 加速度对比(试验-仿真) Fig. 12 Comparison of accelerations(test-simulation) |
由图12可知,测点加速度的仿真值与试验值具有基本一致的变化趋势,在数值上,平均误差为14.12%。总体而言,仿真值与试验测得的加速度值较为接近,吻合较好。在靠近加劲肋的区域,加速度的幅度相对较小,而在远离加劲肋的区域,加速度较大。
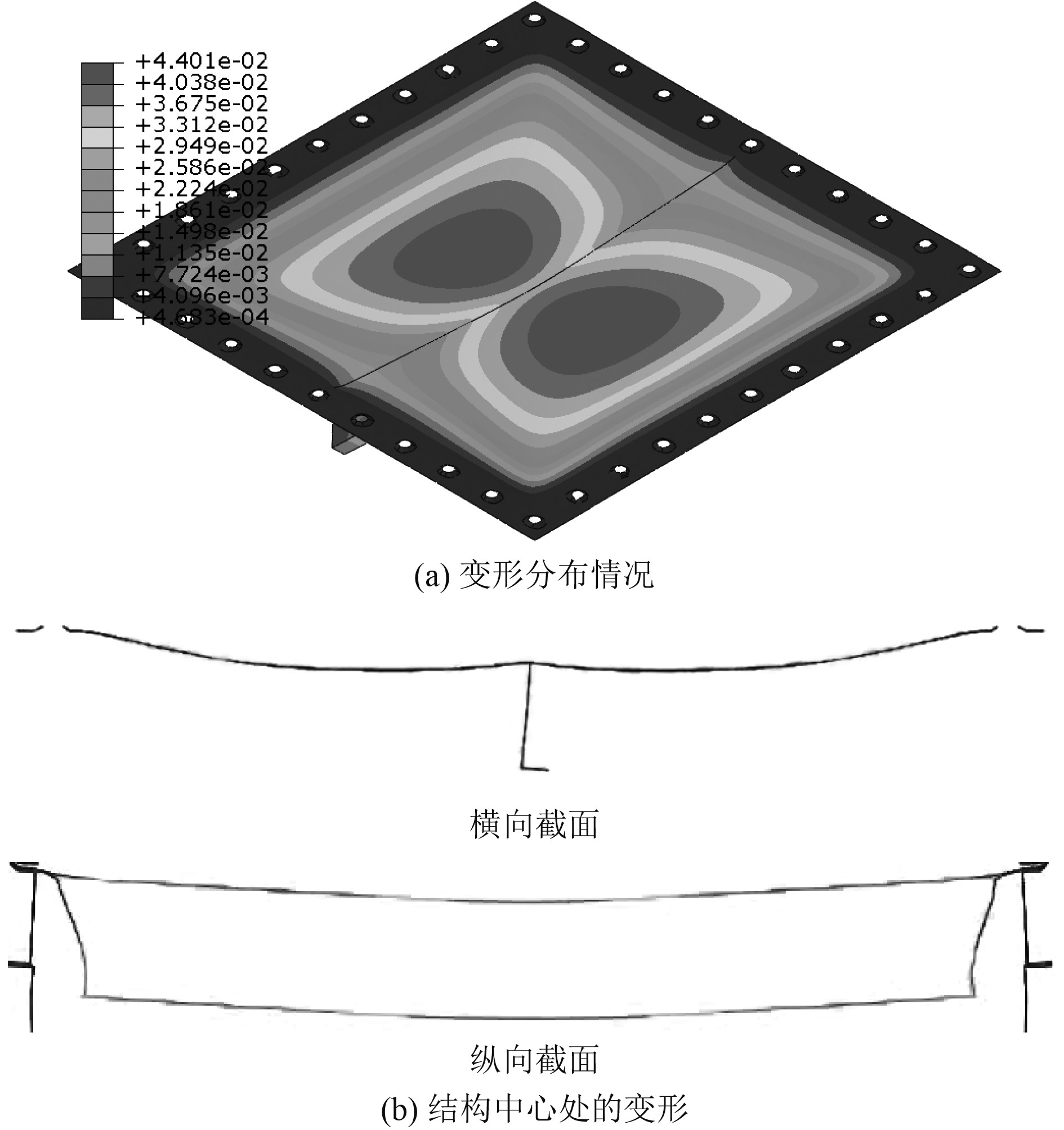
2.2.2 损伤变形结果对比结构变形的仿真结果如图13所示。
|
图 13 典型加筋结构计算云图 Fig. 13 Calculation nephogram of typical reinforced structure |
由仿真结果可知,加筋板变形主要集中在加筋板两侧区域,且变形区域呈“半圆形”。这说明横、纵方向边界的影响不同,其中,垂直加筋的横向边界影响较强,平行加筋的纵向边界影响较弱。
结合图8、图13(a),将数值模拟和试验结果进行比较可知,数值模拟得到的面板板变形与爆炸试验中的变形范围相同,横向上的“双拱形”变形也与试验结果一致。这表明,数值模型能准确地反映结构的变形和破坏模式。
为了进一步研究加筋板变形特点,分别在结构迎爆面和背爆面沿横向和纵向依次取5处测点数据,每处测点相距150 mm,其中沿横向测点3对应D1,测点4对应D2,测点5对应D3;沿纵向测点3对应D1,测点4对应D4,测点5对应D7。由此分析结构沿不同方向的变形情况。记录各测点变形数据,如图14所示。

|
图 14 典型加筋结构测点变形情况 Fig. 14 Deformation of measuring points of typical reinforced structure |
由图14可知,典型加筋结构横向、纵向变形差异性较大。对于横向变形,变形量在加筋板两端较大,在加强筋上变形急剧减小。对于纵向变形,中心位置处变形最大,边界处变形最小。
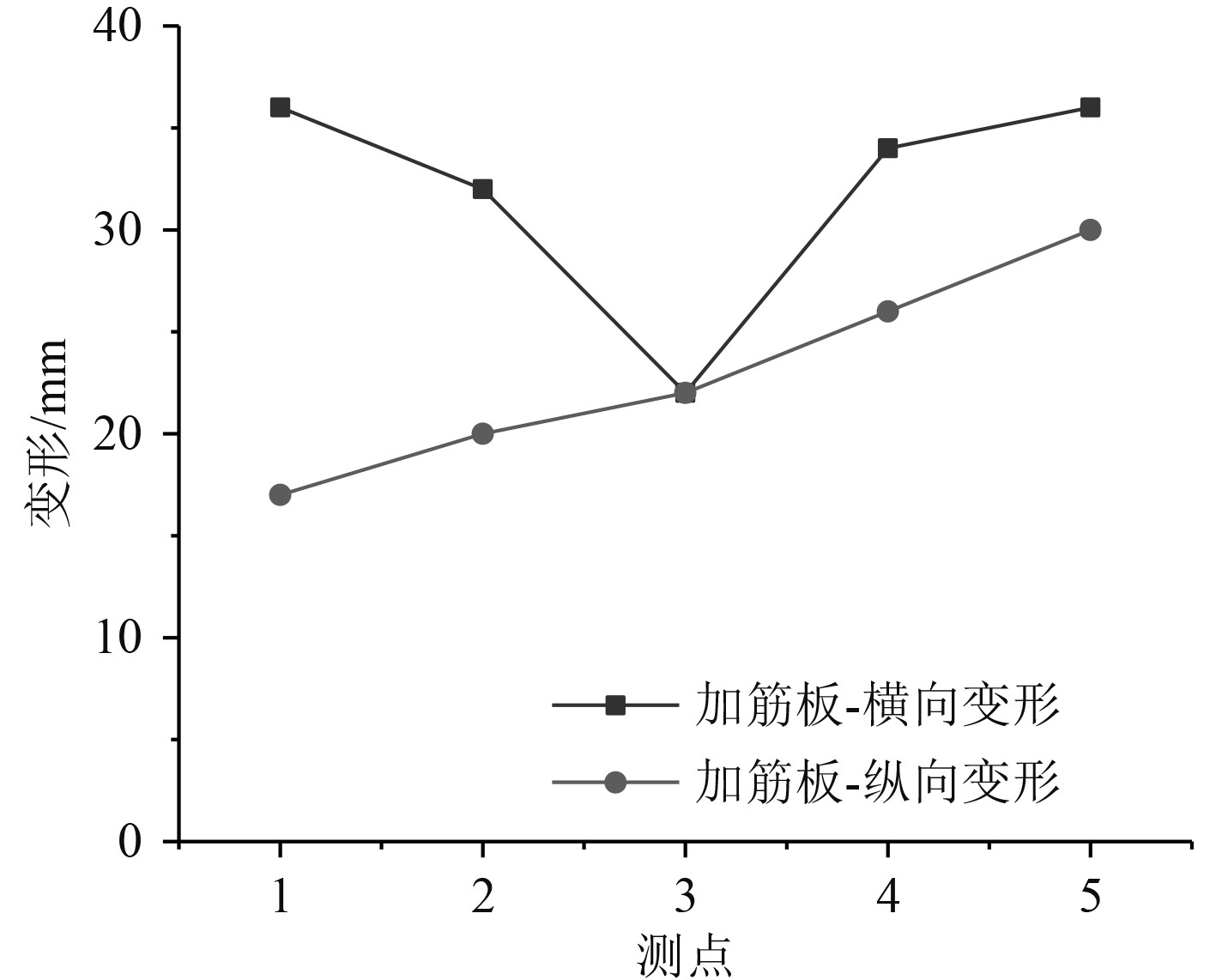
为了有效比较试验值和仿真值,选出与仿真值测点一一对应的试验测量值进行对比,如图15所示。
|
图 15 典型加筋结构测点变形情况 Fig. 15 Deformation of measuring points of typical reinforced structure |
经对比可知,测点仿真计算得到的结果与试验测得的数值变形规律具有相似性,忽略误差的影响,仿真值可以有效反映结构在爆炸载荷作用下的变形规律。
根据5处测点的试验值与仿真值,算出相对误差。沿横向,最大误差13%,最小误差3%。沿纵向,最大误差54%,最小误差1%。加筋板横向变形试验值与仿真值部分测点在横向误差较小,在纵向靠近边界处测点误差较大。总体而言,在应用固定边界条件的面板边缘附近发生相对较大的变形差异,而在加筋板附近发生相对较小的变形差异。仿真计算的加筋板最大变形点位置与试验结果一致,表明仿真能有效反映加筋板的变形趋势。
2.3 载荷峰值影响分析为了深入研究载荷峰值对加筋板结构响应的影响,选取500 kPa,650 kPa,800 kPa,1 000 kPa,1 200 kPa五种工况进行研究,如图16所示。

|
图 16 等效塑性应变情况 Fig. 16 Equivalent plastic strain |
由图16可知,随着载荷峰值的增加,加筋板变形下凹现象越发明显,并在加筋板与板的连接节点处出现等效塑性应变的最大值,且最大值不断增加。
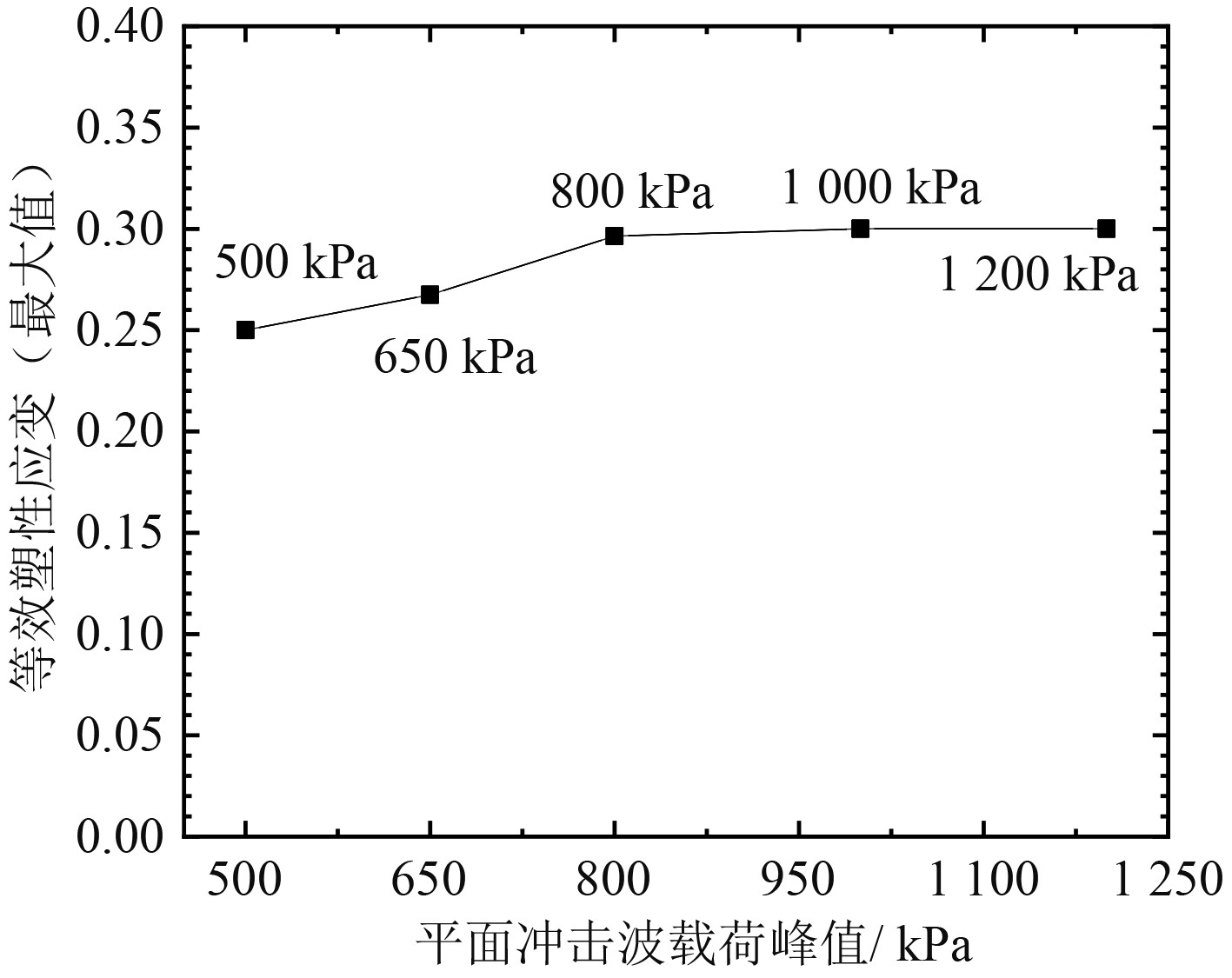
根据数值仿真计算结果,对不同载荷峰值作用下整体结构的等效塑性应变(最大值)进行整理,如图17所示。
|
图 17 不同载荷峰值下等效塑性应变 Fig. 17 Equivalent plastic strain under different load peaks |
通过分析可知,随着峰值压力的增加,加强筋的等效塑性应变增加。在1 200 kPa时,最大等效塑性应变达到临界值0.3[20] ,之后加大载荷峰值,结构会发生破坏,故加筋板发生破坏时的临界载荷峰值为1 200 kPa。峰值压力超过1 200 kPa后,加筋板的抗爆能力减弱。
同时,通过观察不同峰值载荷下的等效塑性应变等值线,可以清楚地发现加筋板的变形趋势。随着峰值压力的增大,加筋板转角处的塑性应变逐渐累积。其中,最危险的区域是加筋板与板之间的连接节点,更容易发生破坏。
3 结 语本文通过试验与数值研究,分析了平面冲击波载荷持续作用下加筋板的爆炸响应情况。同时,验证完善了结构远场爆炸数值仿真技术。讨论了峰值压力大小对加筋板响应的影响,确定了加筋板能承受的极限载荷。得出如下结论:
1)在500 kPa爆炸载荷作用下,加筋板进入塑性阶段。该结构发生破坏时的临界载荷峰值为1 200 kPa,符合国军标要求,抗爆性能较为优良。
2)不同峰值载荷下加筋板的破坏情况不同。随着峰值压力的增大,加筋板转角处的塑性应变逐渐累积,加筋板与板之间的连接节点处更容易发生破坏。
3)在加强筋的作用下,结构在不同方向的抗爆性能不同。结构变形主要发生在加强筋两侧,在实际应用中,可在两侧进行加固处理,从而提高结构的抗爆性能。
| [1] |
LYNCH C J, MURPHY A, PRICE M, et al. The computational post-buckling analysis of fuselage stiffened panels loaded in compression[J]. Thin-walled Structures, 2004, 42: 1445-1464. DOI:10.1016/j.tws.2004.04.002 |
| [2] |
CHEN Hao, LAI Hongpeng, QIU Yuliang , et al Reinforcing Distressed Lining Structure of Highway Tunnel with Bonded Steel Plates: Case Study [J]. Journal of Performance of Constructed Facilities, 2020, 34(1).
|
| [3] |
LI Yongxuan, LIU Yuqing, LIU Rong. Finite Element Analysis on Axial Compressive Behaviors of High-Performance Steel Stiffened Plates in Bridge Application [J]. International Journal of Steel Structures, 2019, 19(5).
|
| [4] |
MASOOD S N, VISHAKH R, VISWAMURTHY S R, et al. Influence of stiffener configuration on post-buckled response of composite panels with impact damages[J]. Composite Structures. 2018, 194: 433–444.
|
| [5] |
CAMPBELL J, HETEY L, VIGNJEVIC R. Non-linear idealisation error analysis of a metallic stiffened panel loaded in compression[J]. Thin-Walled Structures, 2012, 54: 44–53.
|
| [6] |
RUDRAPATNA N S, VAZIRI R, OLSON M D. Deformation and failure of blast-loaded stiffened plates[J]. International Journal of Impact Engineering, 2000, 24(5): 457–474.
|
| [7] |
ZONG Z, ZHAO Y, LI H. A numerical study of whole ship structural damage resulting from close-in underwater explosion shock[J]. Marine Structures, 2013, 31: 24–43.
|
| [8] |
ZAKRISSON B, WIKMAN B, HÄGGBLAD H Å. Numerical simulations of blast loads and structural deformation from near-field explosions in air[J]. International Journal of Impact Engineering, 2011, 38(7): 597–612.
|
| [9] |
BERNSTEIN D, GOETTELMAN R C. Generation of cylindrically symmetric implosions[J]. Review of Scientific Instruments, 1966, 37(10): 1373–1375.
|
| [10] |
BENEDICK W B. Detonation wave shaping[R]. Albuquerque, N. Mex. : Sandia Labs. , 1972.
|
| [11] |
FRITZ J N. A simple plane-wave explosive lens[R]. NM (USA): Los Alamos National Lab. , 1990.
|
| [12] |
YADAV H S, KAMAT P V, Sundaram S G. Study of an explosive-driven metal plate[J]. Propellants, Explosives, Pyrotechnics, 1986, 11(1): 16–22.
|
| [13] |
CHEN C Y, SHIUAN J H, LAN I F. Design of an inert material type plane wave generator[J]. Propellants, explosives, pyrotechnics, 1993, 18(3): 139–145.
|
| [14] |
BUCCI O M, MIGLIORE M D, PANARIELLO G, et al. On the synthesis of plane wave generators: performance limits, design paradigms and effective algorithms[C]//2012 6th European Conference on Antennas and Propagation. Institute of Electrical and Electronics Engineers, 2012: 3500–3503.
|
| [15] |
ZHANG C S, ZOU D H, MADENGA V. Numerical simulation of wave propagation in grouted rock bolts and the effects of mesh density and wave frequency[J]. International journal of rock Mechanics and Mining Sciences, 2006, 4(43): 634-639. |
| [16] |
XIONG W, ZHANG X, GUAN Z, et al. Study of simple plane wave generator with an air-metal barrier[J]. Defence Technology, 2014, 10(2): 190-197. DOI:10.1016/j.dt.2014.05.012 |
| [17] |
DING C, NGO T, GHAZLAN A, et al. Numerical simulation of structural responses to a far-field explosion[J]. Australian Journal of Structural Engineering, 2015, 16(3): 226-236. DOI:10.1080/13287982.2015.1092686 |
| [18] |
邱艳宇, 卢红标, 蔡立艮. 爆炸冲击波信号处理方法比较[J]. 爆破, 2010, 27(1): 92-95. DOI:10.3963/j.issn.1001-487X.2010.01.025 |
| [19] |
JONES N. Structural impact[M]. Cambridge University Press, 2011.
|
| [20] |
BAKER W E, COX P A , KULESZ J J , et al. Explosion hazards and evaluation[M]. Elsevier, 2012.
|
| [21] |
HETHERINGTON J, SMITH P. Blast and ballistic loading of structures[M]. Chemical Rubber Company Press, 2014.
|
| [22] |
WU C, HAO H. Modeling of simultaneous ground shock and air-blast pressure on nearby structures from surface explosions[J]. International Journal of Impact Engineering, 2005, 31(6): 699-717. DOI:10.1016/j.ijimpeng.2004.03.002 |
| [23] |
柯力. 钢质夹层板上层建筑结构防护性能优化及抗爆试验研究[D]. 镇江: 江苏科技大学, 2020.
|
 2022, Vol. 44
2022, Vol. 44
