0 引　言

声呐是船舶必不可少的一种水下探测设备，尤其对于舰船、潜艇等，声呐装载于船首的舱室结构中，可以辅助舰船进行导航、海底地貌的侦察、敌方船只探测、距离探测等。性能良好的声呐能够快速发现距离较远的敌方舰船，在作战中占据主动；能及时探测到水下的暗礁、覆冰等障碍物，避免船舶搁浅、碰撞事故的发生。因此，提升船舶声呐的设计水平，改善声呐探测精度具有重要意义。

评定船舶声呐性能的参数包括探测频率、定向精度、信号灵敏度等，由于海洋环境的复杂性，声呐的探测精度与灵敏度往往受到多种影响因素的干扰。声呐结构机械自噪声是指来自非侦测目标的噪声，这类噪声不仅包括环境噪声，也包括船体振动噪声、声呐工作噪声等，本文的研究方向是船舶声呐自噪声的传播特性分析，从声呐结构、噪声来源等方面进行研究，并基于有限元仿真软件对船舶声呐自噪声的传播特性进行了仿真分析。

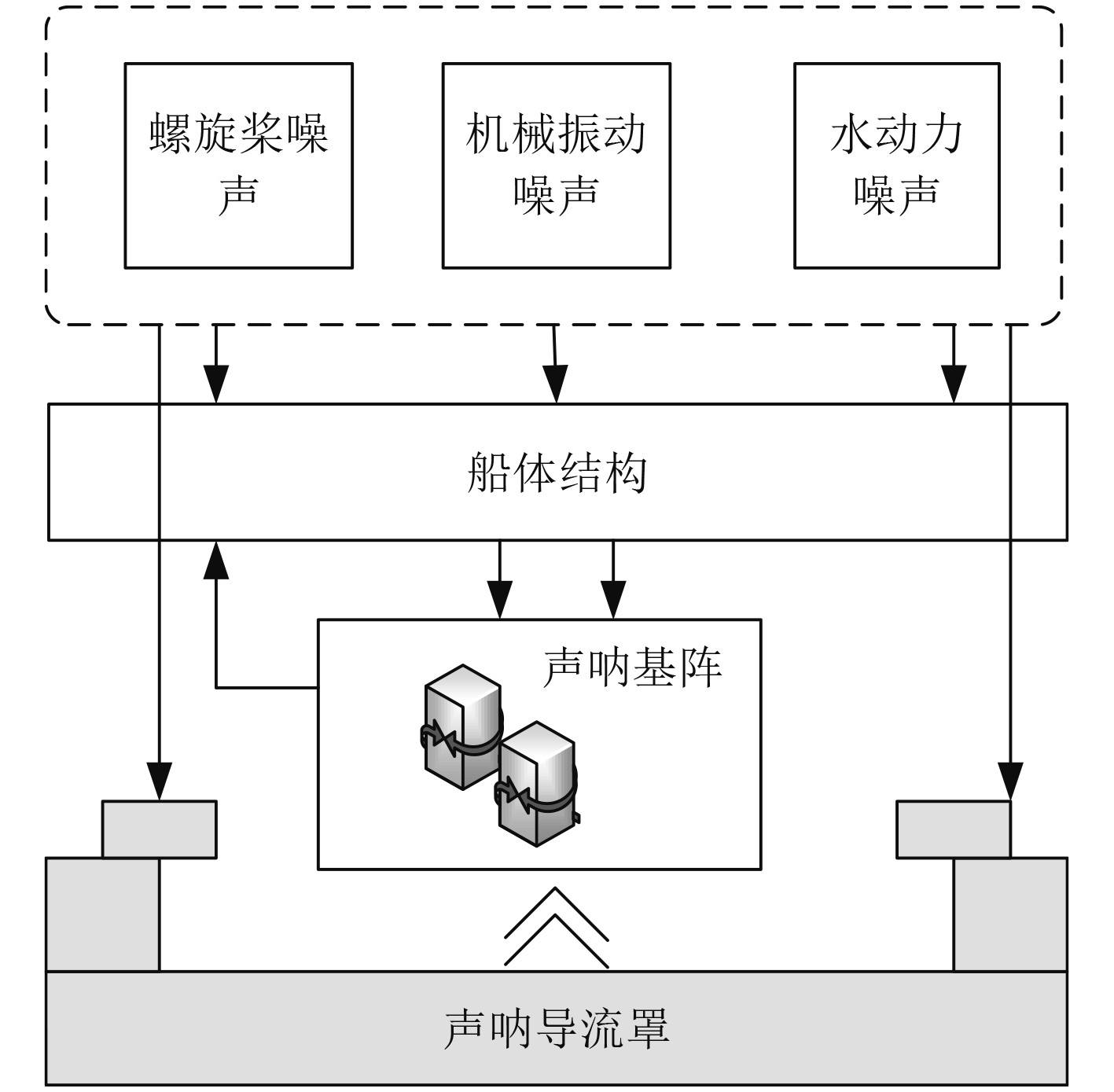
1 舰船声呐结构机械自噪声的来源与特性分析

声呐结构机械自噪声是指仅与机械结构相关的噪声，研究表明，船舶声呐结构机械自噪声的来源包括螺旋桨噪声、机械振动噪声和水动力噪声等，自噪声来源示意图如图1所示。

1）水动力噪声

水动力噪声与船艏位置声呐的导流罩结构有关，在船舶的快速航行中，海水作用于船舶声呐导流罩外表面，并在外表面生成湍流边界层，湍流进一步导致表面的粘性应力及雷诺应力增大，导致导流罩受力不均产生噪声，噪声以辐射噪声为主。水动力噪声是流体、机械结构、水声结构的耦合作用，航速越大，水动力噪声越明显^[1]。

2）螺旋桨噪声

螺旋桨作为舰船工作时的主要噪声源，对船舶声呐的影响也很明显，当螺旋桨与海水发生相互作用时，螺旋桨叶片表面同样会由于水动力特性产生湍流，加上螺旋桨叶片的空泡效应，会进一步提升螺旋桨的噪声级别。与此同时，船舶声呐与螺旋桨的距离相对较远，因此，往往声呐接收到的螺旋桨噪声是由海面、海底反射传播后进入声呐基阵的，强度有所降低。

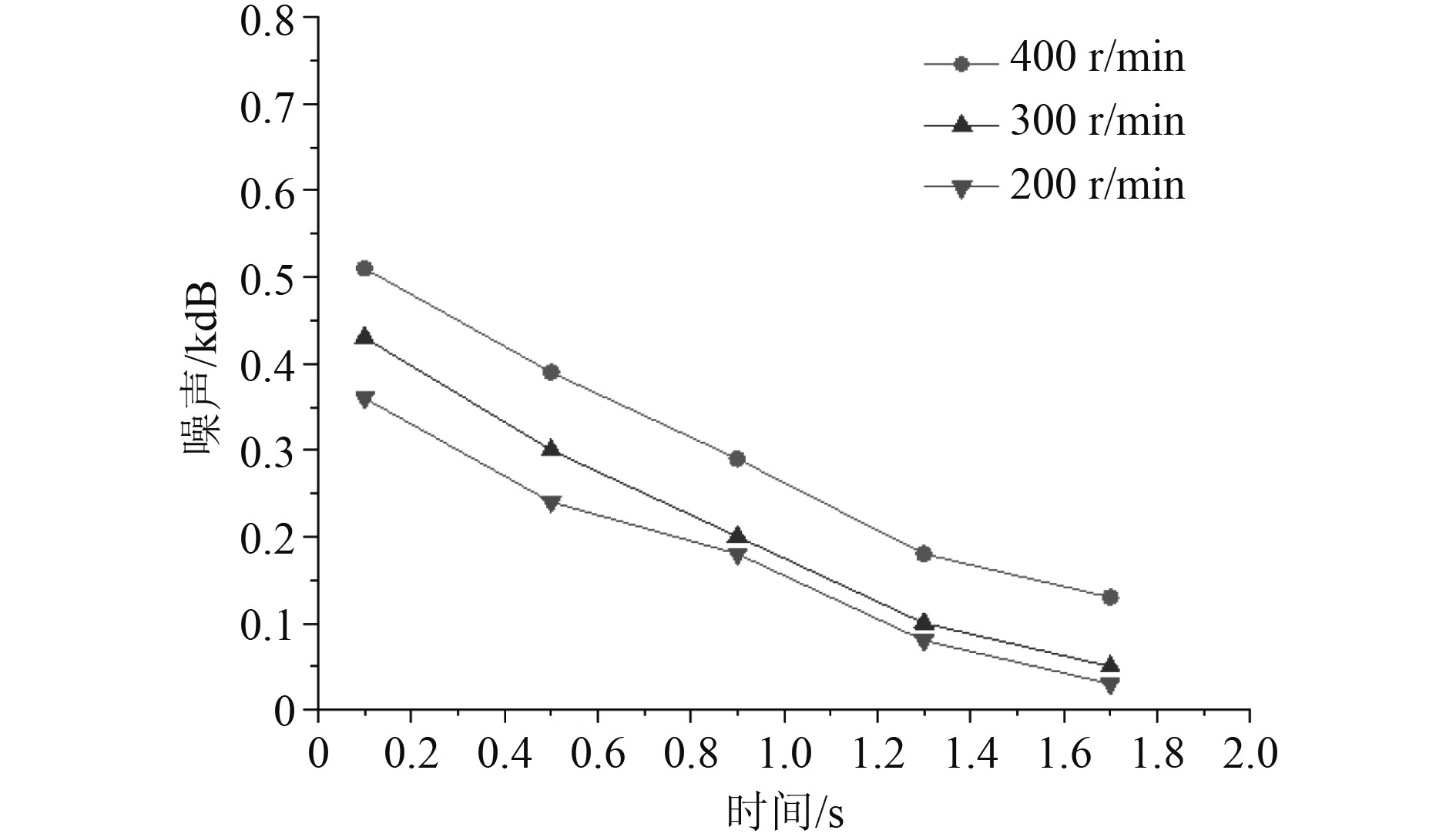
螺旋桨的转动速度为300 r/min，400 r/min和200 r/min时，螺旋桨噪声特性曲线如图2所示。

3）机械振动噪声

机械振动噪声的来源非常广泛，船上各种机械设备如主机、齿轮箱、发电机等设备的振动，会通过船体结构传递至声呐的基阵中。当船舶航行速度较慢时，机械振动噪声是船舶声呐结构机械自噪声的主要组成部分。

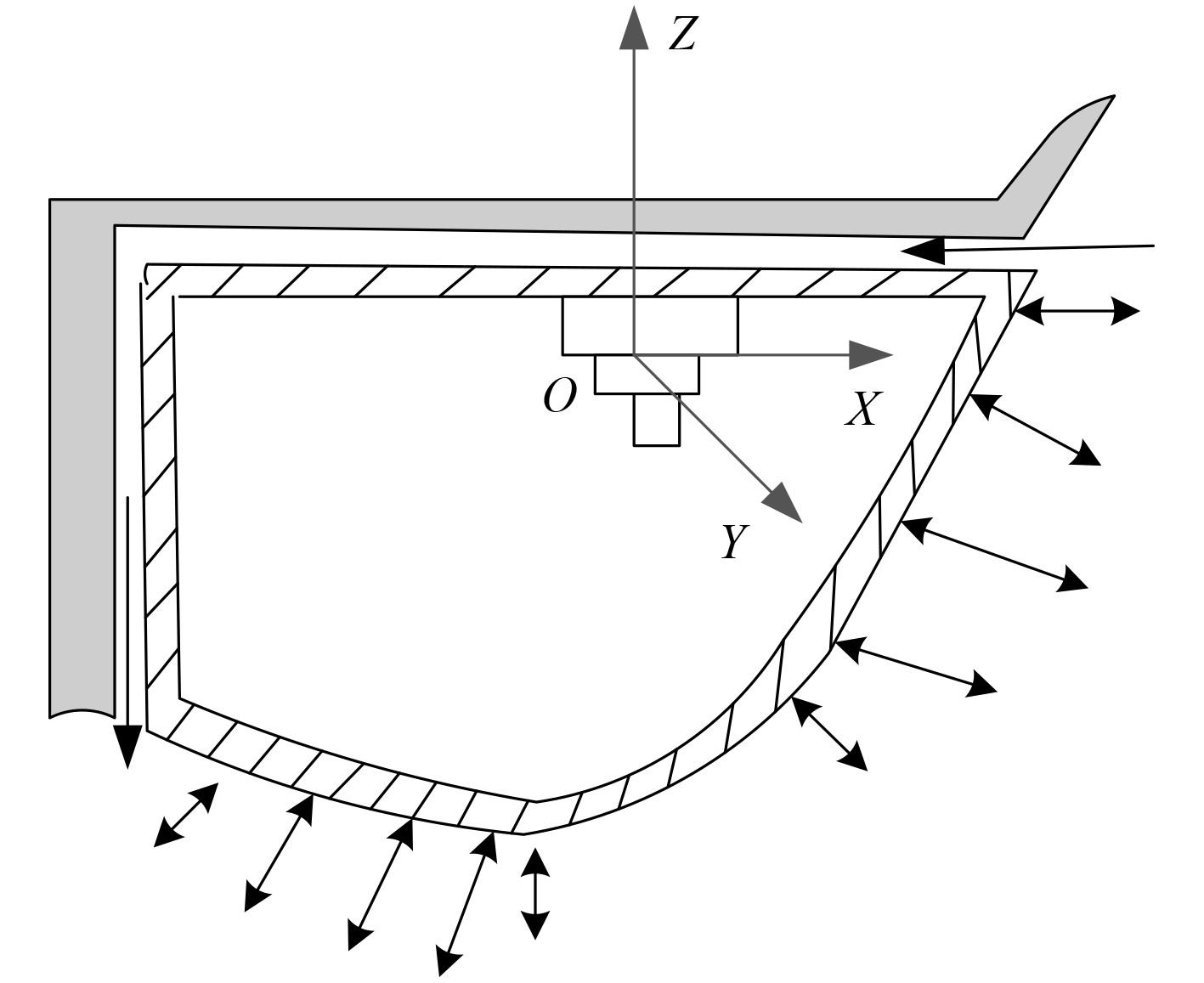
2 船舶声呐结构机械自噪声的传播分析和仿真研究 2.1 建立考虑流固耦合作用的声呐部件声学模型

船舶声呐结构自噪声是流体场和固体场耦合作用的结果，因此，本文在探究声呐结构自噪声的传播特性时，考虑了声呐导流罩位置的流固耦合作用，首先建立船舶声呐导流罩位置处的数学模型如图3所示。

声呐导流罩在激励作用下的结构振动满足波动方程^[2]，如下式：

$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{{{c^2}}}\dfrac{{{\partial ^2}{P_0}}}{{\partial {t^2}}} = {\nabla ^2}{P_0}} \;，\\ {\dfrac{{\partial {P_0}}}{{\partial s}} = - {\rho _0}jw{V_0}} \; 。\end{array}} \right. \text{} $

其中： $ {P_0} $ 为流体的任意点压力； $ c $ 为声音在流体中的传播速度； $ {V_0} $ 为导流罩流固耦合处的振动速度； $ {\rho _0} $ 为海水密度。

同时，导流罩的水动力噪声满足流固耦合边界的辐射条件^[3]，如下式：

$ \mathop {\lim }\limits_{t \to \infty } \left[ {d\left( {\frac{{\partial {P_0}}}{{\partial s}} + jk{P_0}} \right)} \right] = 0 。$

其中， $ k $ 为流体的波数^[3]。

定义流固耦合边界上的点 $ \left( {M,N} \right) $ ，利用加权法可得声呐导流罩的辐射噪声特性方程如下式：

$ \iint {\left[ {P\left( {M,N} \right)\frac{{\partial G(M,N)}}{{\partial n}} + jwG(M,N)} \right]}{\rm{d}} s= \frac{1}{2}P\left( h \right) \text{。} $

式中： $ h $ 为耦合界面位置的振动； $ G(M,N) = \dfrac{{{e^{ - jwt}}}}{{4{\text{π}} h}} $ 。

声呐导流罩的辐射噪声功率谱可以用Ecs型曲线来近似拟合，Ecs型噪声功率谱的自相关函数为：

$ \delta \left( t \right) = {e^{ - t}}\left( {\cos {w_0}t + k{\rm{sin}}{w_0}t} \right) \text{，} $

其中： $ {w_0} $ 为振动频率； $ k $ 为0~1之间的实数。

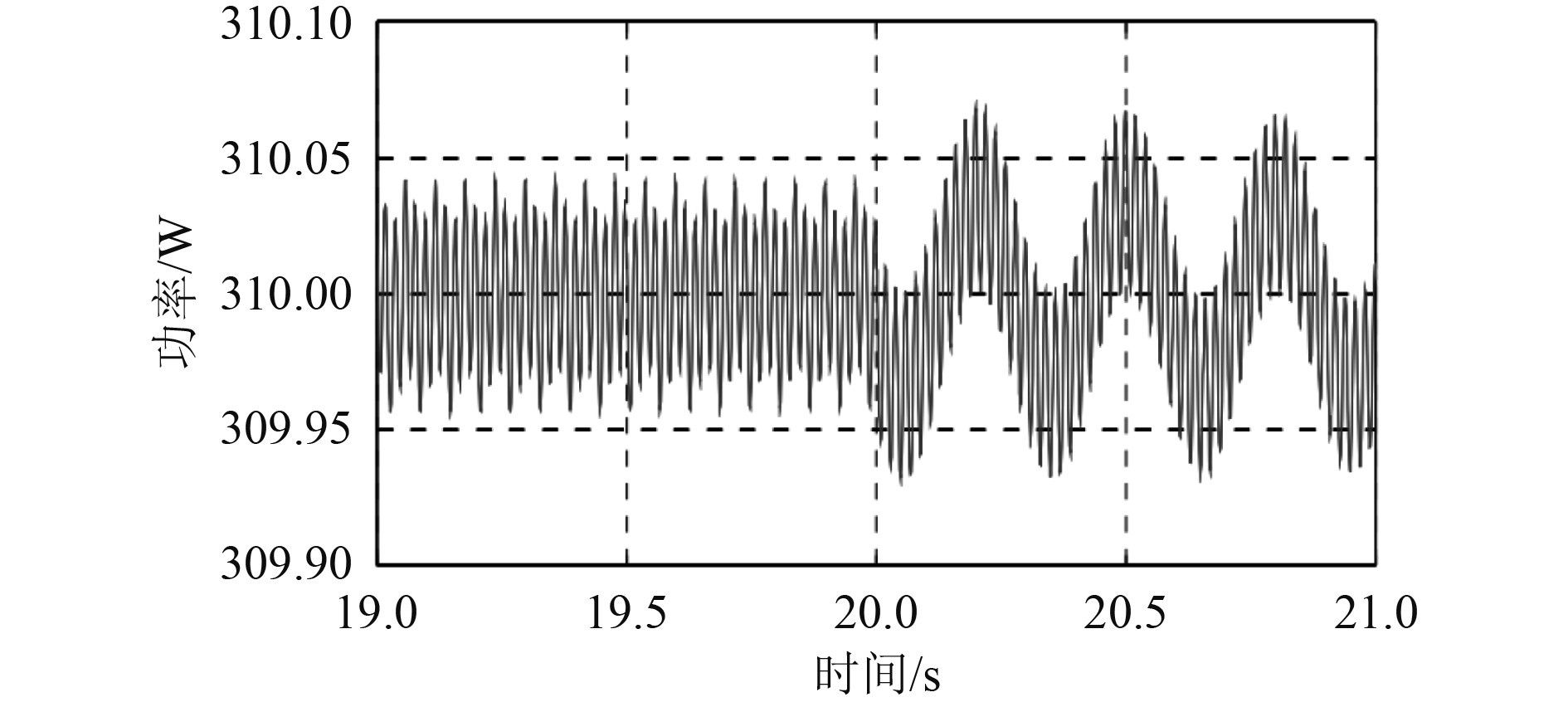
声呐导流罩辐射噪声的功率谱如图4所示。

2.2 考虑流固耦合作用的声呐机械噪声传播分析

为了探究船舶声呐结构噪声的传播特性，使用弹性薄板模拟声呐导流罩结构，以矩形腔模拟声呐的内部腔体，并对结构的振动特性进行详细的数学建模。

根据弹性薄板的克希霍夫^[4]假设，矩形薄板在受力作用下的横向振动微分方程为：

$ {D_0}\left( {\frac{{{\partial ^4}w}}{{\partial {x^4}}} + 2\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}w}}{{\partial {y^4}}}} \right) + \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = p(x,y,t) \text{，} $

也可以简化为：

$ {D_0}{\nabla ^4}w + \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = p({\text{x}},y,t) \text{。} $

式中， $ {\nabla ^4} $ 为调和算子，按下式计算：

$ {\nabla ^4} = \left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right) \text{。} $

式中： $ \rho $ 为单位体积薄板的密度； $ \rho h\dfrac{{{\partial ^2}w}}{{\partial {t^2}}} $ 为单位面积的惯性力； $ {D_0} $ 为薄板的扭转刚度； $ w $ 为薄板的位移。

薄板结构在空间中的自由振动方程为：

$ {\nabla ^4}w + \frac{{\rho h}}{{{D_0}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}} = 0 。$

建立声呐导流罩的主振型为：

$ w({{x}},y,t) = W({{x}},y)\sin (\omega t + \varphi ) \text{，} $

$W({{x}},y)$ 满足4个方向的边界条件如下：

$ \begin{gathered} {\left. W \right|_{x = 0}} = {\left. {\frac{{{\partial ^2}W}}{{\partial {x^2}}}} \right|_{x = 0}} = 0,{\left. W \right|_{x = d}} = {\left. {\frac{{{\partial ^2}W}}{{\partial {x^2}}}} \right|_{x = \infty }} = 0 ，\\ {\left. W \right|_{y = 0}} = {\left. {\frac{{{\partial ^2}W}}{{\partial {y^2}}}} \right|_{y = 0}} = 0,{\left. W \right|_{y = h}} = {\left. {\frac{{{\partial ^2}W}}{{\partial {y^2}}}} \right|_{y \to \infty }} = 0 。\\ \end{gathered} $

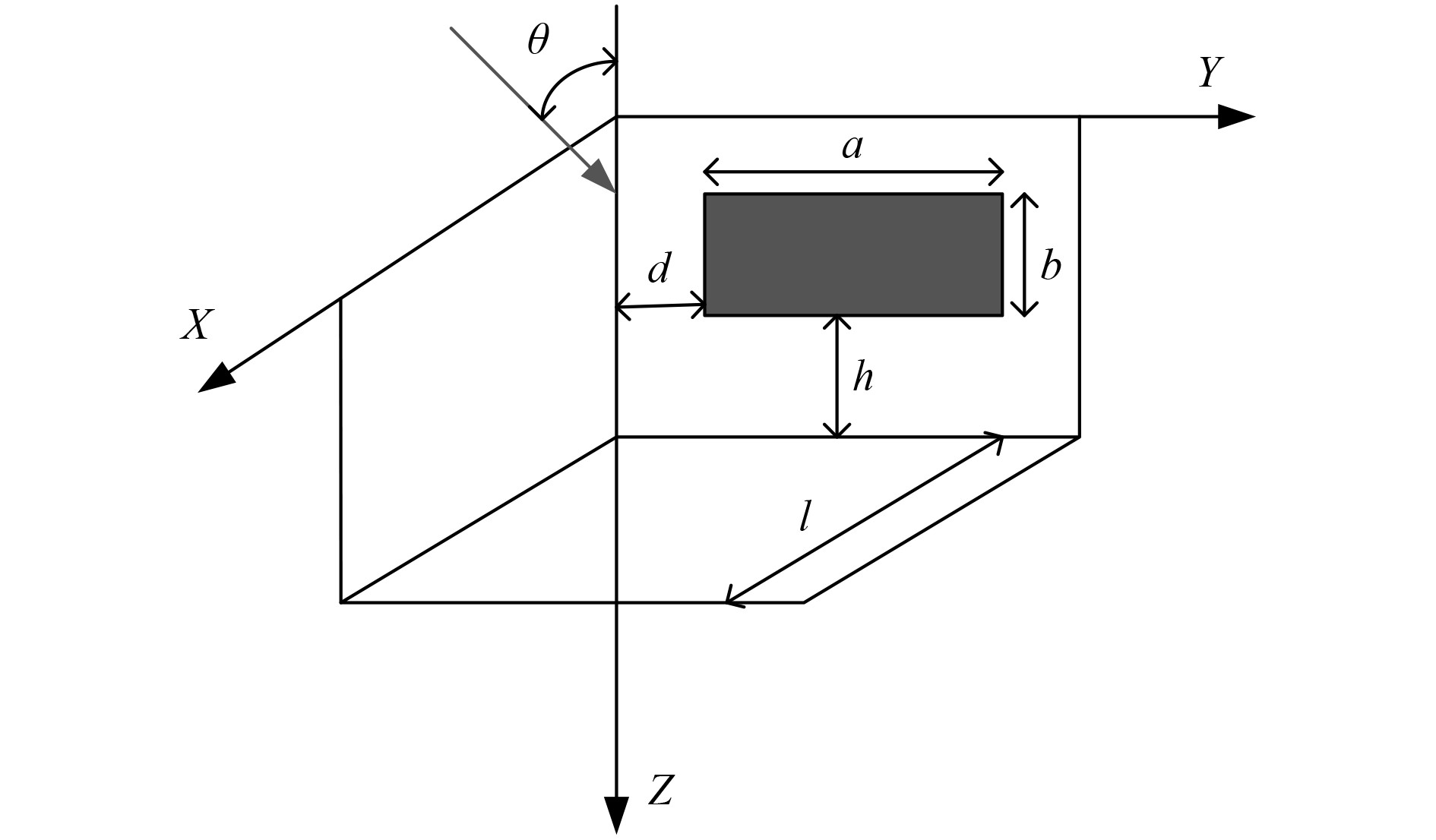
建立流固耦合作用下声呐矩形腔体的数学模型如图5所示。

根据腔体模型，建立声呐矩形腔的噪声模态模型为：

$ {F_r}(\sigma ) = \cos \left( {\frac{{l{\text{π}} x}}{a}} \right)\sin \left( {\frac{{m{\text{π}} y}}{b}} \right)\cos \left( {\frac{{n{\text{π}} z}}{d}} \right) \text{，} $

$ l/m/n $ 为自然数，腔体的振动固有频率为：

$ \omega _r^{} = {c_0}\sqrt {{{\left( {\frac{{l{\text{π}} }}{{ax}}} \right)}^2} + {{\left( {\frac{{m{\text{π}} }}{{by}}} \right)}^2} + {{\left( {\frac{{n{\text{π}} }}{{dz}}} \right)}^2}} {\text{ }} 。$

2.3 基于有限元的声呐结构机械自噪声仿真

基于有限元建模软件Ansys进行船舶声呐结构机械自噪声的仿真分析，关键步骤包括：

1）有限元模型的搭建

声呐平台结构包括上、下平台、导流罩、舱壁、腔体等，因此在仿真前需要建立合理的有限元模型，声呐平台采用一体建模，实体单元采用SOLID45单元，将所有机械结构简化为同一种材料，定义杨氏模量为 $ E = 1.2 \times {10^9}\;{\rm{N}}/{{\rm{m}}^2} $ ，密度为1080 kg/m^3[5]，局部倒角位置进行模型的细化。

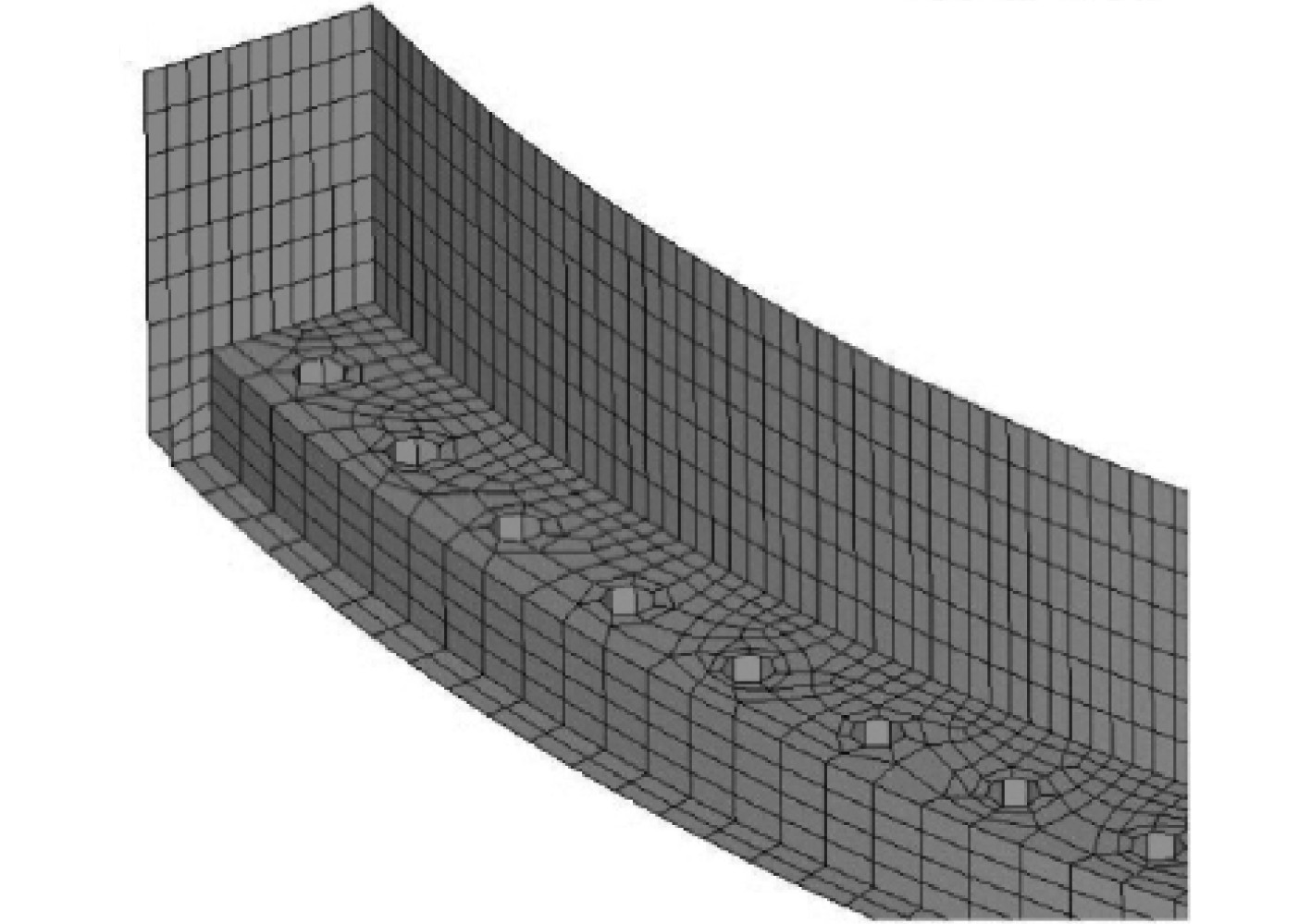
图6为声呐导流罩与舱壁结合部位的有限元模型示意图。

2）真求解

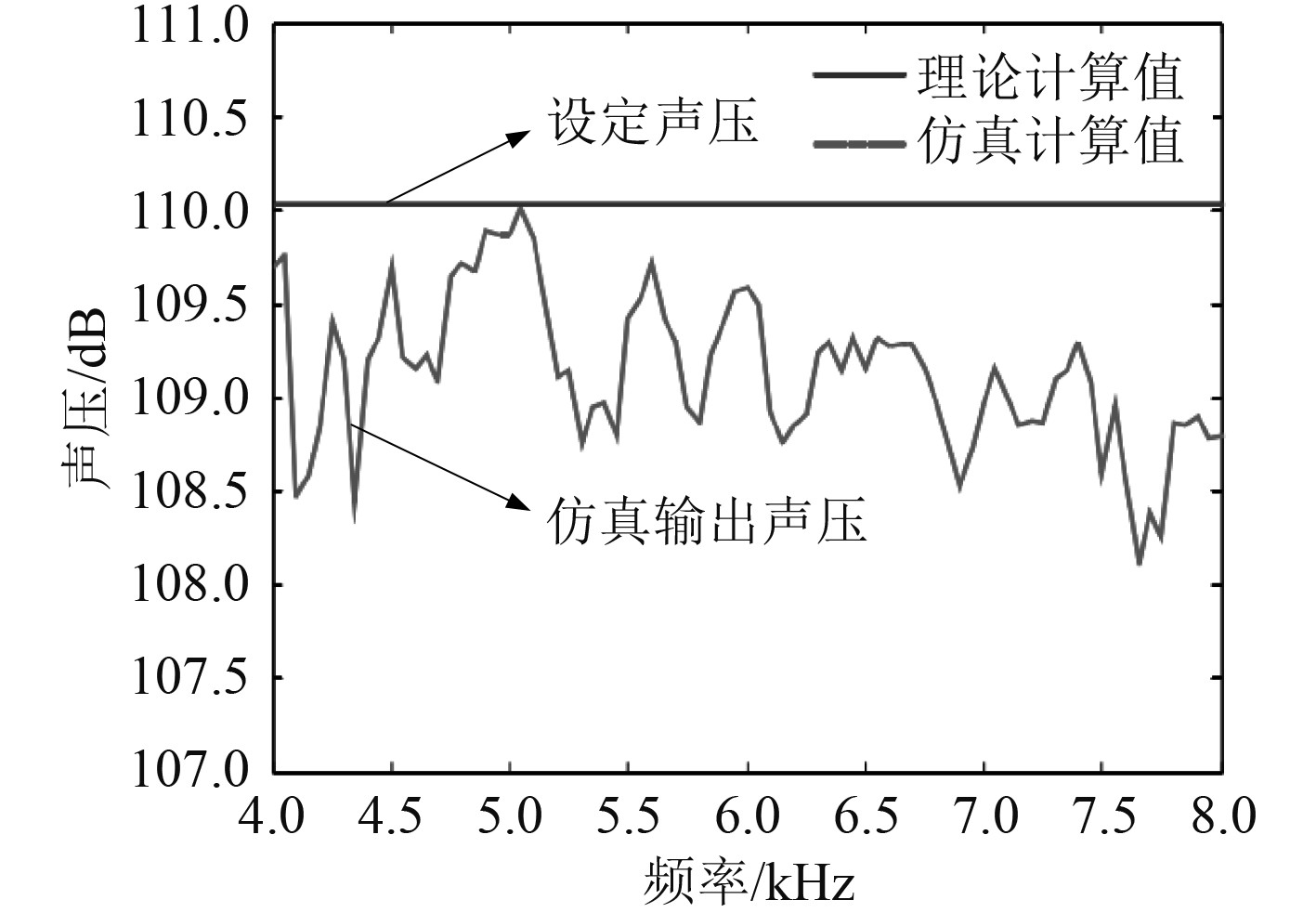
定义薄壁结构的厚度为5 mm，初始的结构声压为110 dB，进行声呐自噪声的声压求解。

图7为基于Ansys的船舶声呐机械自噪声声压仿真结果。

3 结　语

舰船声呐机械结构的自噪声由水动力噪声、螺旋桨噪声等组成，这些噪声会影响声呐的探测精度，因此，本文对船舶声呐自噪声的传播特性进行详细的数学建模和分析，并结合有限元仿真软件进行了声呐自噪声的仿真。