船舶推进轴系(简称轴系)是船舶动力装置的重要组成部分,其运行状态直接关系到船舶的航行安全。不对中是轴系常见的故障之一,严重的对中性失效可导致主机曲轴断裂、轴系振动剧烈和尾轴变形与密封破坏等恶性事故[1]。因此,开展船舶推进轴系校中状态监测研究对于保障船舶的航行安全具有重要意义。
目前,船舶轴系不对中故障研究中,多是通过测量轴的位移响应来研究不对中故障,即当轴系出现不对中故障时,会产生2倍频响应[2]。因此,2倍频响应可以作为不对中故障特征信号。然而,在实际应用中,这种2倍频位移响应往往难以测量。因此,近年来有学者通过轴承座振动来判断轴系不对中状态[3],但是在轴系振动向轴承座传递的过程中,是否存在不对中特征振动目前还不清楚。随机共振[4]是一种利用噪声能量来增强微弱特征信号的方法,在微弱特征信号检测中得到了广泛的应用,如通过随机共振成功检测出轴承和齿轮微弱特征信号[5-7]。谐波小波包具有一般正交小波包无法比拟的带通滤波性能和极强的微弱特征信号提取能力,被广泛运用于信号提取中,如谐波小波包能够提取轴承的微弱故障特征信号[8-9]。因此,本文首先利用随机共振检测轴承座振动中是否存在不对中故障特征,然后再通过谐波小波包对检测出的特征信号进行提取,实现从轴承座振动中提取船舶轴系不对中故障特征。
为了验证所提出方法的有效性,在船舶轴系实验台上进行船舶轴系不对中实验,采集实验过程中尾后轴承座处的振动信号,应用随机共振对采集的信号进行检测,然后利用谐波小波包对检测出的特征信号进行提取并分析其随校中状态的变化。
1 方 法本文提出利用随机共振对轴承座振动中的不对中故障特征进行检测并通过谐波小波包对检测出的特征信号进行提取,实现从轴承座振动中提取船舶轴系不对中故障特征的方法。
1.1 检测随机共振是指一定的非线性条件下,弱周期信号与噪声达成协同作用而使输出信号的信噪比增强的现象。因此,应用随机共振对轴承座振动中的不对中故障特征进行检测。常用的随机共振模型如下:
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = - U'(x) + s(t) + n(t)。$ | (1) |
式中:x表示系统输出;U(x)为非线性双稳态势函数,U(x)=−(ax2/2)+(bx4/4),a和b是系统参数;s(t)表示微弱周期信号;n(t)为高斯白噪声。
由于式(1)中系统参数a和b以及噪声强度都会影响到随机共振输出信噪比,从而影响微弱周期信号的检测效果,因此可以通过调节系统参数和噪声强度来达到最优信噪比。在不对中特征振动检测中,噪声强度一般是确定的。因此,通常采用系统参数a和b的最优解来保证信噪比达到最大值。本文利用粒子群算法[10]的全局寻优能力对随机共振系统参数a和b进行同步优化,实现最优随机共振,具体步骤如下:
步骤1 初始化粒子的位置x和速度v,每个位置对应1组随机共振系统参数a和b,速度为系统参数a和b的更新步长。
步骤2 采用二次采样[11]方法对振动信号进行预处理,即通过频率变换尺度R将振动信号变换为满足随机共振小参数要求的低频信号。
步骤3 将每个粒子的位置和预处理后的振动信号代入随机共振系统,选择系统输出信号的信噪比作为适应度函数,根据式(2)计算每个粒子的适应度值,粒子中适应度值最大的粒子为个体最优值pbest,种群中适应度值最大的粒子为种群最优值gbest。
| $ SNR = 10\lg \frac{{S({f_0})}}{{N({f_0})}}。$ | (2) |
式中:S(f0)为不对中特征振动信号功率;N(f0)为不对中特征振动信号背景噪声功率。
步骤4 根据式(3)和式(4)更新所有粒子的速度和位置。
| $ \begin{split} & {v_i^d = wv_i^{d - 1} + {c_1}{r_1}(pbest_i^d - x_i^d)}+ \\ & { {c_2}{r_2}(gbes{t^d} - x_i^d)} ,\end{split}$ | (3) |
| $ x_i^{d + 1} = x_i^d + v_i^d。$ | (4) |
式中:w为惯性权重;c1和c2为学习因子;r1和r2是[0,1]上的随机数;d为最大进化代数;i=1,2,···,n;n为种群数量。
步骤5 计算更新后各粒子的适应度值,通过与上一代粒子的个体和种群最优值比较,更新个体和种群最优值。判断新种群是否达到最大进化代数d,达到则输出最优系统参数,否则转到上一步。
步骤6 将最优系统参数a和b代入随机共振系统,实现轴承座振动中的不对中故障特征的检测。
1.2 提取谐波小波具有盒形紧支特性和相位保持特性等优点,作为谐波小波变换的扩展,谐波小波包不仅具有谐波小波的优点,并且还能实现对信号任意频段的任意细化。因此,应用谐波小波包对随机共振检测出的不对中特征振动信号进行提取。根据谐波小波包变换原理[12],船舶轴系振动信号的谐波小波包变换过程如下:
1)根据最高分析频率为fh和分解层数j,由式(5)和式(6)确定分析带宽B和不对中特征振动信号所在分析频带的上、下限m,n。
| $ B = {2^{ - j}}{f_h},$ | (5) |
| $\begin{split} & {m = sB,n = (s + 1)B} ,\\ & {s = 0,1,2, \cdots ,{2^{j - 1}}} 。\end{split} $ | (6) |
式中:j和s分别为谐波小波包的分解层数和频段数。
2)计算分析频带的谐波小波的频域值。
| $ \begin{array}{l} {h}_{m,n}[(n-m)\omega ]=\\ \Bigg\{\begin{array}{ll}1/[(n-m)2 \text{π} ],& 2\text{π} m \leqslant \omega < 2 \text{π} n,\\ 0,&{\rm{ others}}。\end{array}\end{array} $ | (7) |
3)对振动信号f(t)进行快速傅里叶变换,求得其频域离散值f(w)。
4)由式(8)计算不对中特征振动信号所在分析频带的谐波小波变换的频域值,进行频域特征分析。
| $ Q(m,n,w) = f(\omega ){h_{m,n}}[(n - m)\omega ]。$ | (8) |
5)对上一步得到的频域值进行逆快速傅里叶变换,得到谐波小波变换后不对中特征振动信号所在频段的时域信号,进行时域特征分析。
2 不对中状态下轴承座振动分析 2.1 实验 2.1.1 实验条件在船舶轴系实验台上进行不对中故障模拟实验,其主要由配重盘、传动轴、中间轴承、尾前轴承、尾后轴承、驱动电机等部件组成,如图1所示。其中,驱动电机采用型号为D1TP180L-6型变频调速三相异步电机,转速范围0~1000 r/min,其通过弹性联轴器与轴系连接驱动整个轴系;各轴承均安装在高度可调的蜗轮丝杠上,丝杠转动一周轴承高度可改变0.25 mm;配重盘的质量为22 kg,用来模拟螺旋桨,安装在轴系末端。

|
图 1 实验台结构示意图 Fig. 1 Schematic diagram of the experimental platform structure |
实验过程中,设定电机转速为90 r/min,通过调节尾前轴承标高来获得不同的校中状态,其中直线校中状态设定为基础状态,轴承标高为0 mm,在此基础上以0.2 mm为步长,在0~1 mm范围内不断增加尾前轴承的标高,共获得6种校中状态。
对于每一种校中状态,通过灵敏度为506.2 mV/g、量程为10 g、频响范围为0.2~8000 Hz的YA-22T型单轴加速度传感器测量尾后轴承处竖直方向的振动信号,加速度传感器安装在尾后轴承座上表面。利用NI Pxle-4499型信号采集系统连续采集30组振动信号,采样频率为2 048 Hz,采样点数为8192。
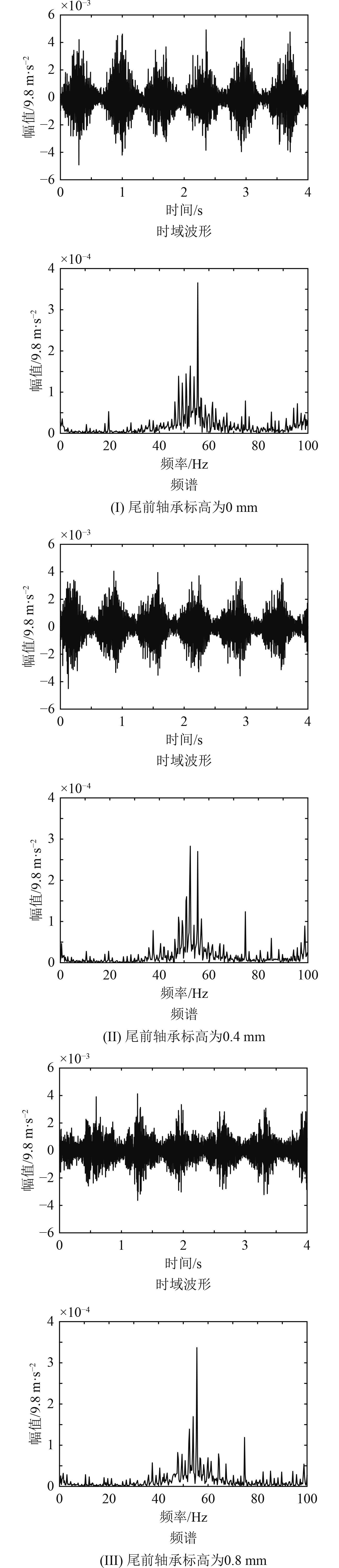
2.2 结果与讨论 2.2.1 特征振动信号检测当尾前轴承标高分别为0 mm,0.4 mm和0.8 mm时测得尾后轴承处振动信号的时域波形与频谱如图2所示。根据本文实验设计条件,轴系转速为90 r/min,因此轴系不对中故障特征响应存在于2倍转频信号上,即其特征频率为3 Hz。可以看出,不同标高情况下振动信号的时域波形比较复杂,(见图2(a))。从其频谱可以看出,信号频率成分不同,其幅值存在较大差异,频率3 Hz成分的信号幅值十分微弱,淹没在强背景噪声中难以识别,(见图2(b))。因此,从测得的轴承座振动信号中无法判断船舶轴系是否存在不对中故障。
|
图 2 不同校中状态下尾后轴承处振动信号的时域波形与频谱 Fig. 2 Time-domain waveform and frequency spectrum of the vibration signal at the stern rear bearing in different alignment conditions |
应用基于粒子群算法优化的随机共振对图2中的振动信号进行检测。根据文献[13]设置频率变换尺度R=500,同时粒子群算法的参数设置如下:种群粒子数量为n=50,系统参数a和b的搜索范围均为(0,10),系统参数a和b的最大搜索速度均取最大调整步长的20%,即vmax=2,最大进化代数d=400,求解精度为1×10-5。求解得到最优系统参数,并将最优系统参数带入随机共振系统,系统输出信号的时域波形和频谱如图3所示。

|
图 3 不同校中状态下随机共振输出信号时域波形与频谱 Fig. 3 Time-domain waveform and frequency spectrum of stochastic resonance output signal under different alignment conditions |
从图3时域波形图可以看出,随机共振处理后的振动信号时域波形中的噪声成分被极大地削弱了。从图3频谱图可以看出,不对中故障特征频率处的幅值在整个频谱图中最突出,即从轴承座振动信号中检测出了不对中特征振动信号。因此,在不同校中状态下,船舶推进轴系存在不对中振动响应,即2倍频响应。
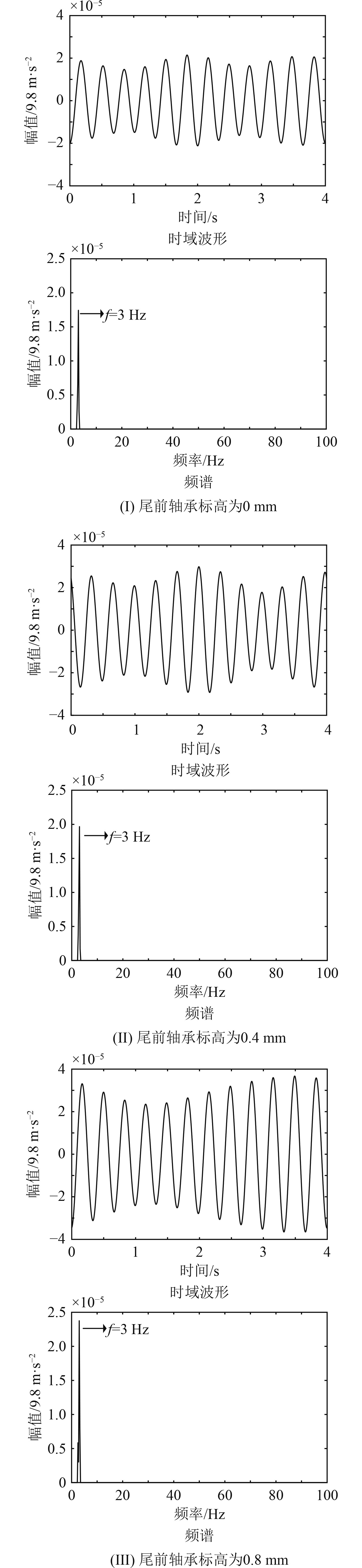
2.2.2 特征振动信号的提取及分析为了验证随机共振的检测结果,应用谐波小波包对检测到的特征振动信号进行提取。其方法是对振动信号进行11层分解,将其分解至2048个频段,每个频带的带宽为0.5 Hz,然后对包含不对中特征振动信号的频段进行提取。给出尾前轴承标高为0 mm,0.4 mm和0.8 mm时提取出的不对中特征振动信号的时域波形与频谱,如图4所示。
|
图 4 不同校中状态下不对中特征振动信号的时域波形与频谱 Fig. 4 Time-domain waveform and frequency spectrum of the characteristic vibration signal of misalignment under different alignment conditions |
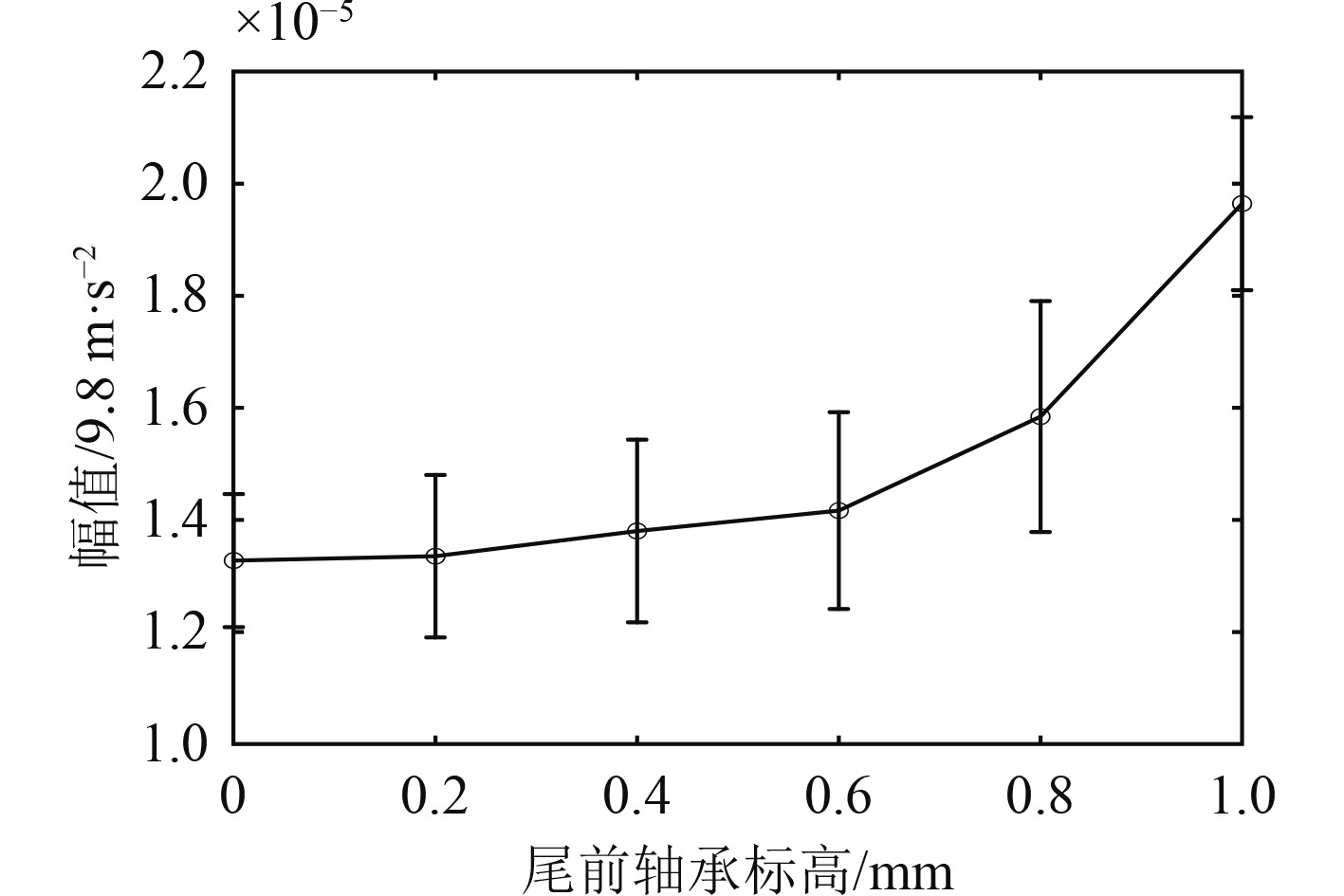
可以看出,通过谐波小波包变换可以有效剔除振动信号中的其他频率成分,成功提取出不同校中状态下不对中特征振动信号的频率,如图4频谱图所示。从图4时域波形图可以看出,不对中特征振动信号的时域波形幅值随着尾前轴承标高的增加明显增大,计算不同校中状态下特征振动信号的有效值,结果如图5所示。
|
图 5 不同校中状态下特征振动信号有效值变化趋势 Fig. 5 The change trend of the effective value of the characteristic vibration signal under different alignment conditions |
从图5可以看出,由直线校中到尾前轴承标高0.6 mm过程中,振动信号中的不对中特征振动信号的有效值缓慢增加;由尾前轴承标高0.6 mm到艉前轴承标高1 mm过程中,振动信号中的不对中特征振动信号的有效值急剧增加。这是由于在尾前轴承标高增加过程中,尾后轴承处不对中激励不断增大,轴系不对中状态逐渐恶化,从而导致不对中特征振动信号的有效值不断增加。
3 结 语本文基于轴承座振动对船舶轴系不对中故障特征进行提取,可以得出以下结论:
1)应用基于粒子群算法优化的随机共振可实现轴承座振动中的船舶轴系不对中故障特征的检测。
2)应用谐波小波包可对检测到的特征振动信号进行提取,其有效值的变化能够反映校中状态的改变。
| [1] |
毛海波. 大船集团VLOC轴系质量管理研究[D]. 大连: 大连理工大学, 2015.
|
| [2] |
杨俊, 王隽, 王刚伟. 船舶推进轴系校中对轴系振动影响分析[J]. 动力学与控制学报, 2016, 14(2): 157-164. Yang Jun, Wang Jun, Wang Gang-wei. Analysis of the influence of ship propulsion shafting alignment on shafting vibration[J]. Dynamics and Control, 2016, 14(2): 157-164. |
| [3] |
杨一舟, 蒋东翔. 概率神经网络用于机匣振动故障诊断[J]. 机械科学与技术, 2016, 35(12): 1805-1810. Yang Yi-zhou, Jiang Dong-xiang. Application of probabilistic neural network to case vibration fault diagnosis[J]. Mechanical Science and Technology, 2016, 35(12): 1805-1810. DOI:10.13433/j.cnki.1003-8728.2016.1201 |
| [4] |
BENZI R SUTERA A. The mechanism of stochastic resonance[J]. Journal of Physics A:Mathematical and General, 1981, 14(11): 447-453. |
| [5] |
田晶, 周杰, 王术光, 等. 基于自适应双稳态随机共振的中介轴承故障诊断方法[J]. 航空动力学报, 2019, 34(10): 162-170. Tian Jing, Zhou Jie, Wang Shu-guang, et al. Intermediate bearing fault diagnosis method based on adaptive bistable stochastic resonance[J]. Journal of Aeronautics and Dynamics, 2019, 34(10): 162-170. DOI:10.13224/j.cnki.jasp.2019.10.017 |
| [6] |
谢有浩, 刘晓乐, 刘后广, 等. 基于改进移频变尺度随机共振的齿轮故障诊断[J]. 农业工程学报, 2016, 32(8): 70-76. Xie You-hao, Liu Xiao-le, Liu Hou-guang, et al. Gear fault diagnosis based on improved frequency-shifted variable-scale stochastic resonance[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(8): 70-76. DOI:10.11975/j.issn.1002-6819.2016.08.010 |
| [7] |
富志凯, 邢建春, 王双庆, 等. 一种舰船辐射噪声线谱检测新方法[J]. 舰船科学技术, 2013, 35(12): 37-41. Fu Zhi-kai, Xing Jian-chun, Wang Shuang-qing, et al. A new method for detecting ship radiated noise line spectrum[J]. Ship Science and Technology, 2013, 35(12): 37-41. DOI:10.3404/j.issn.1672-7649.2013.12.008 |
| [8] |
TAO X, PEI A, YONG L. Discrimination the roller bearing faults with harmonic wavelet package, kernel principal component analysis and relevance vector machine[J]. Sensors & Transducers, 2014, 179(9).
|
| [9] |
田福庆, 罗荣. 改进的谐波小波包变换及其在弱故障特征提取中的应用[J]. 振动与冲击, 2013, 32(17): 29-34. Tian Fu-qing, Luo Rong. Improved harmonic wavelet packet transform and its application in weak fault feature extraction[J]. Journal of Vibration and Shock, 2013, 32(17): 29-34. DOI:10.3969/j.issn.1000-3835.2013.17.006 |
| [10] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//. Perth, Aust: IEEE, 1995.
|
| [11] |
冷永刚, 王太勇, 郭焱. 二次采样用于随机共振从强噪声中提取弱信号的数值研究[J]. 物理学报, 2003, 52(10): 2432-2437. Leng Yong-gang, Wang Tai-yong, Guo Yan. Numerical study of sub-sampling used for stochastic resonance to extract weak signals from strong noises[J]. Acta Phys. Sin., 2003, 52(10): 2432-2437. DOI:10.3321/j.issn:1000-3290.2003.10.014 |
| [12] |
YAN R, GAO R X. An Efficient approach to machine health diagnosis based on harmonic wavelet packet transform[J]. Robotics and Computer integrated Manufacturing, 2005, 21(4-5): 291-301. DOI:10.1016/j.rcim.2004.10.005 |
| [13] |
冷永刚, 王太勇, 郭焱, 等. 二次采样随机共振的工程应用研究[J]. 中国机械工程, 2004, 15(20): 1847-1852. Leng Yong-gang, Wang Tai-yong, Guo Yan, et al. Engineering application research of secondary sampling stochastic resonance[J]. China Mechanical Engineering, 2004, 15(20): 1847-1852. DOI:10.3321/j.issn:1004-132X.2004.20.017 |
 2022, Vol. 44
2022, Vol. 44
