2. 许昌职业技术学院,河南 许昌 461000
2. Xuchang Vocational Technical College, Xuchang 461000, China
暂态电压稳定问题是船舶电力系统研究的重要课题之一,由于暂态电压基本都是由负荷引起,而在船舶中,柴油发电机组是主要的动态负荷,所以在对暂态电压稳定仿真分析时,要充分考虑动态负荷,使选用的紧急控制方法合理、有效。本文对船用柴油发电机组暂态电压紧急控制方法仿真展开探讨。
1 船用柴油发电机组仿真模型的构建 1.1 模型构建思路电站系统是船舶不可或缺的重要系统之一,它是一个独立的电力系统,柴油发电机组是该系统的核心部分,其特点是负荷种类多、动态变化范围大且过程比较复杂[1]。在船舶电力系统中,负荷可以分为以下几类:无功功率补偿负荷、照明负荷以及感应电动机负荷等。负荷的变化会对船舶电力系统及柴油发电机组的运行稳定性产生影响,容易形成暂态电压,由此会对船舶上用电设备的安全运行造成影响[2-3],所以有必要采取适宜的方法对船用柴油发电机组暂态电压紧急控制,消除其对设备的危害。船用柴油机组暂态电压的过程中,需要对突然增加和卸掉的负荷过程进行实测,为实现这一目标要构建相应的模型。本文选用的模型为同步发电机7阶模型,重点对基于负荷的船用发电机组暂态电压控制模型进行构建。
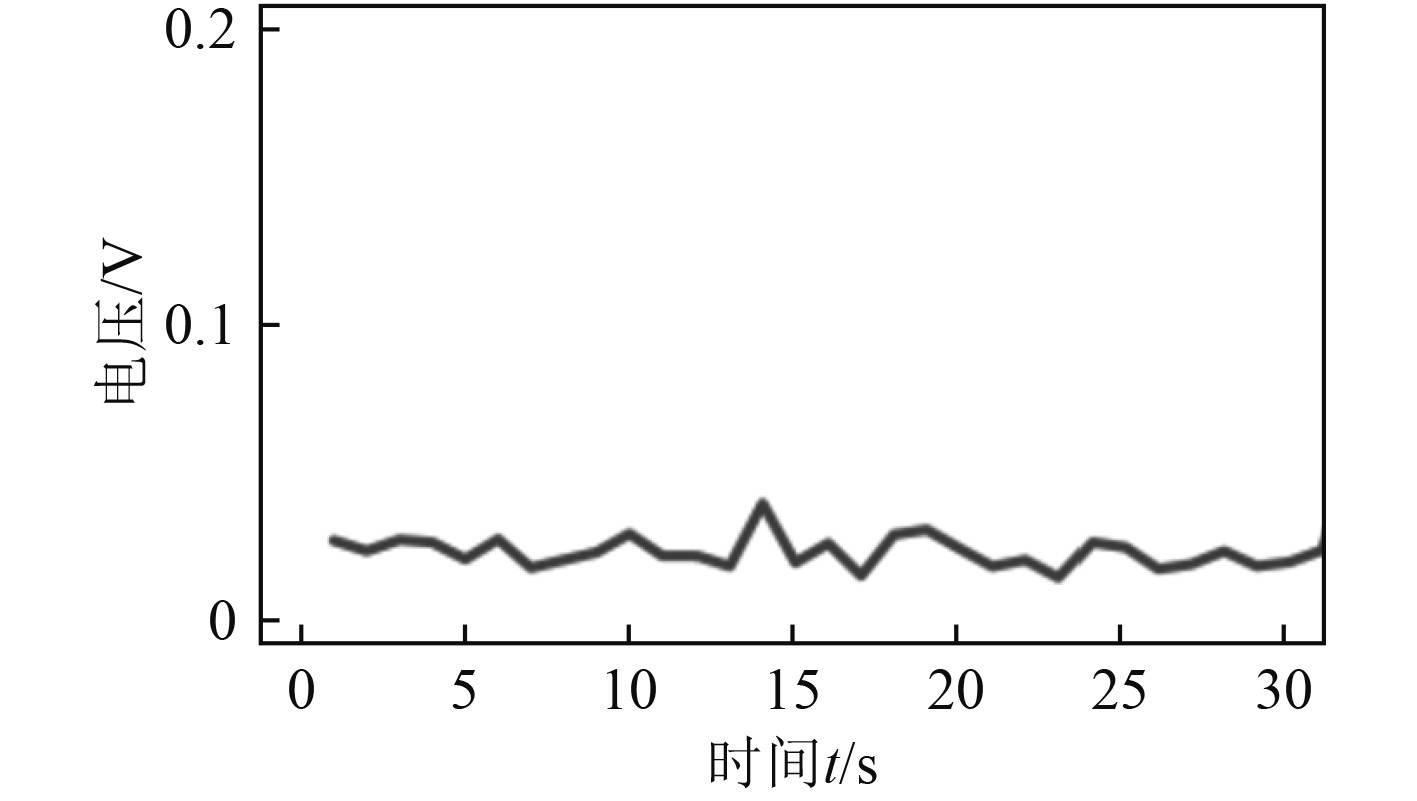
1.2 模型的构建过程柴油发电机组的功率为64 kW,额定功率因数为0.8,额定电压和电流分别为400 V和116 A。在加载的过程中,对电压实测后发现,从410 V降至395 V,大约在3 s左右,电压稳定在406 V;在卸载的过程中,电压大约在2 s左右,从406 V升高到417 V,并在1 s后稳定在415 V。电压、负荷电流、抖动频率的实测误差曲线分别如图1~图3所示。
|
图 1 船用柴油发动机组电压实测误差曲线 Fig. 1 Measured error curve of voltage of marine diesel engine set |
|
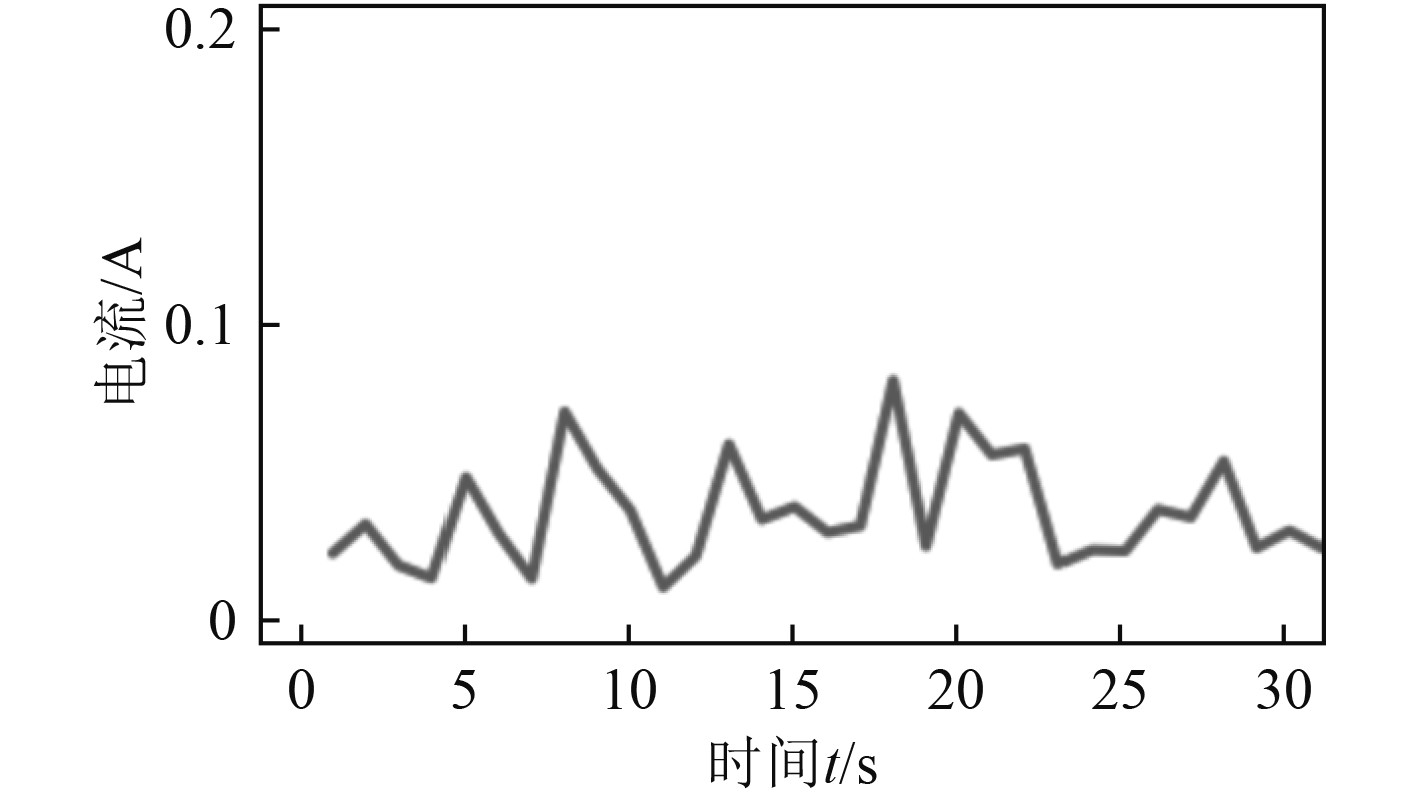
图 2 船用柴油发动机组负荷电流误差实测曲线 Fig. 2 Measured curve of load current error of marine diesel engine set |
|
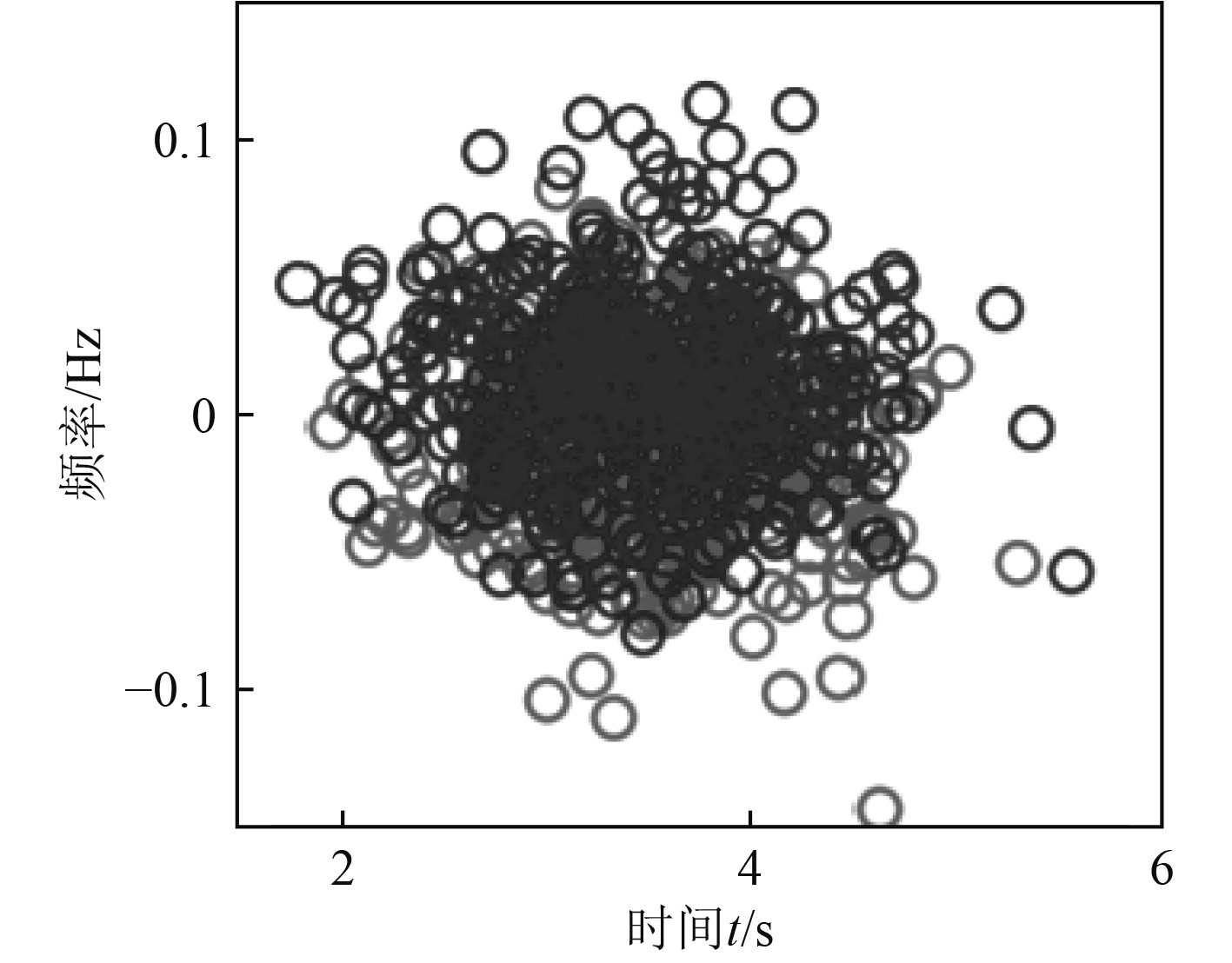
图 3 船用柴油发动机组抖动频率误差实测曲线 Fig. 3 Measured curve of jitter frequency error of marine diesel engine set |
对于船用发电机组而言,输出电压的频率与转速相关,当频率发生变化时,转速也会随之发生改变。在对发电机组加载时,船舶电网的频率有所下降,大约在2 s左右下降了3.0 Hz,即从50.4 Hz降至47.4 Hz,在49.5 Hz时达到稳定状态。卸载过程中,船舶电网的频率在大约2 s内升高1.6 Hz,从49.5升高到51.1 Hz,最终稳定在50.8 Hz。通过图1~图3的对比可以发现,变化趋势具有相同的特点,并且数值也比较接近。由此表明,本次的建模具有一定的合理性和可行性,构建的模型可以用于船用发电机组暂态电压稳定分析。
2 船用柴油发电机组暂态电压紧急控制方法仿真 2.1 暂态电压的稳定时域在研究船用柴油发电机组暂态电压控制问题时,比较常用的方法为稳定分析法,如时域仿真、能量函数等[4-5]。在船舶电力系统暂态电压稳定过程的分析中,可将时域仿真作为首选方法。具体应用的过程中,要保证所选模型的适用性,以便借助常规的仿真程序分析暂态电压的稳定问题。在船舶电力系统中,柴油发电机由转子运动与回路2个部分组成,前者主要与输入的机械功率有关,转速的偏差可以借助调速器控制。当柴油发电机输出的电磁功率发生变化时,会造成转子输入与输出的功能不平衡,由此严重影响转子的速度与角度。柴油发电机组的暂态电压稳定过程可以用下式表示:
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}y}} = f(x,y) \text{。} $ |
式中:x为系统状态的变量,如暂态电动势等;y为代数变量,如电压幅值等。在船舶电网中,负荷的种类相对较多,这些负荷之间存在相互影响的关系,由此导致船用柴油机发电机组暂态电压稳定分析过程的复杂性。由于系统模型多样,加之暂态电压的稳定分析过程复杂,为此,研究分析时,可根据实际情况作出一系列假设,以此来简化计算。假设船用发电机组的机械动态过程比暂态过程慢,且输入的机械功率为恒定不变,负荷采用阻抗模型,占比为65%。
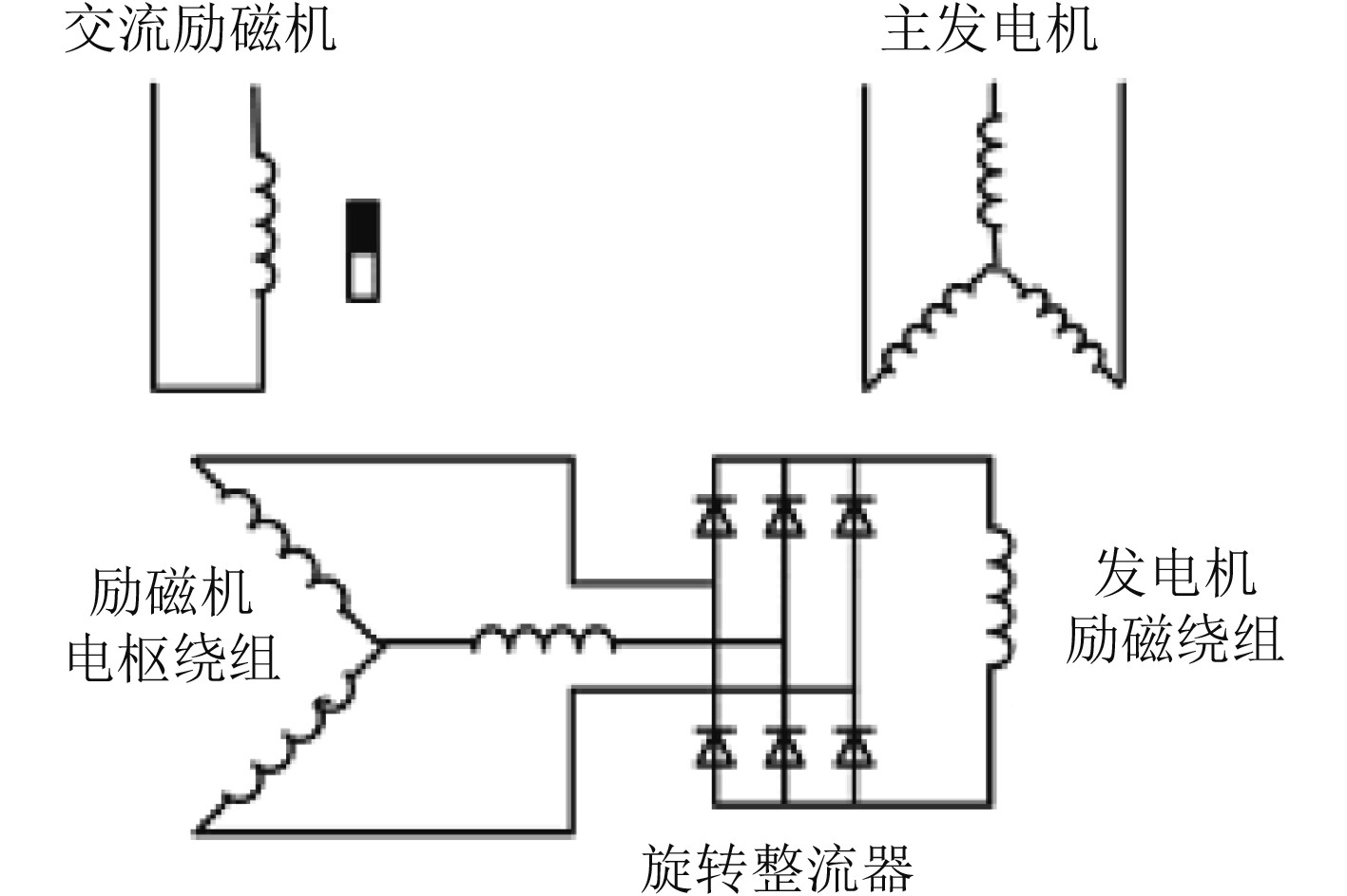
在船舶电力系统中,柴油发电机组的励磁功率主要是由励磁系统负责提供,它对于发电机组电压的调节与保持具有重要作用。不仅如此,励磁系统还能对柴油发电机无功功率的分配进行控制,由此使其对发电机的动态行为产生较大的影响。在大容量的柴油发电机组中,半导体励磁系统比较常见,其特点是可靠性高、响应速度快、便于维修等。船用柴油发电机组经典励磁系统结构情况如图4所示。
|
图 4 船用柴油发电机组经典励磁系统结构示意图 Fig. 4 Structural diagram of classical excitation system of marine diesel generator set |
由于时间常数比较小,所以在测量环节中,可将其忽略。通常情况下,可以用超前滞后和惯性放大2个环节表示电压调节器,其中惯性放大的时间常数为
在分析船用柴油发电机组暂态电压稳定问题前,要先计算初值,具体包括柴油发电机状态变量初值、导出参数、励磁系统状态变量初值、负荷状态变量初值等,以上的这些量均以潮流计算作为基础,利用稳态方程求解。对于船用柴油发电机组暂态电压控制而言,故障的处理是一个较为重要的环节,当暂态故障发生后,船舶电力系统的拓扑结构会在短时间内发生改变,对此应及时修正网络导纳阵。对暂态电压开展稳定计算操作时,虽然系统的状态量并不会发生突然改变的情况,但与其相关的数量却发生突变,如果涉及动态负荷,则状态方程也会随之变化。所以要对故障引起的变化做修正处理。在暂态电压稳定分析中,求取时刻变量,并在故障发生时做出相应的处理。微分与代数方程组是暂态电压稳定分析求解的关键,对重要元件的微分方程进行转化,使其变为差分方程,用牛顿法求解非线性方程组。由此能够得到某个时刻的状态量与代数量的准确值。暂态电压稳定分析的具体流程如下:
步骤1 首先开展初始化工作,具体包括清零、预设值等;
步骤2 对船舶柴油发电机组的原始数据、稳态工况、扰动过程的信息以及控制信息等进行读入;
步骤3 按潮流计算结果,依据柴油发电机组的稳态相量关系,对初值加以计算,据此形成导纳阵,随后将负荷的恒定阻抗并入其中;
步骤4 对系统的运行状态进行判断,看是否存在故障或是操作,如果有,则需要对导纳阵加以修改,并按代数方程求解该时刻的代数量;
步骤5 将柴油发电机组的转子运动方程及绕组暂态方程转化为差分方程,利用牛顿法联立求解,从而得到状态量和代数量;
步骤6 根据结果判断是否达到仿真时间,达到仿真过程结束,未达到,重新转入步骤4。
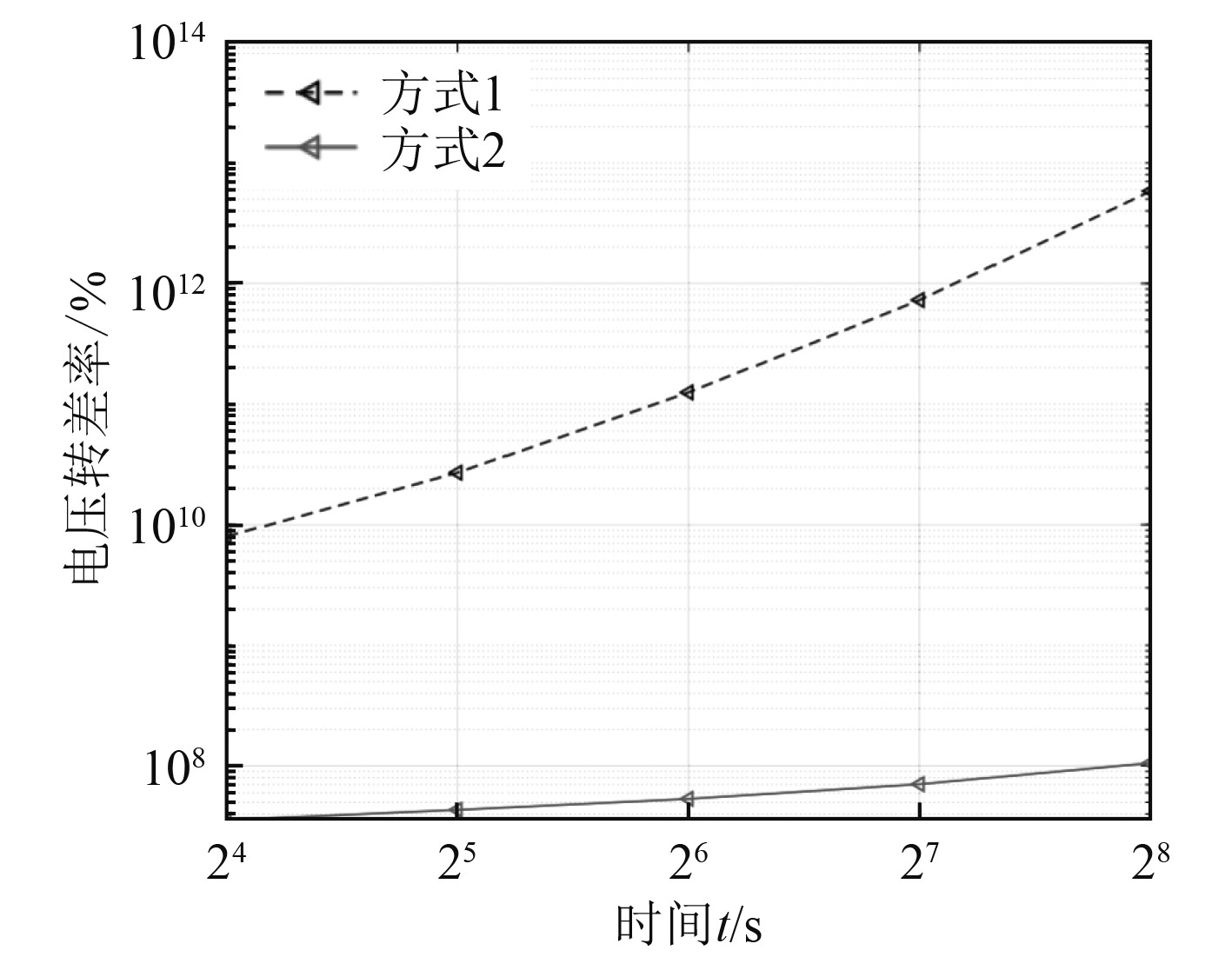
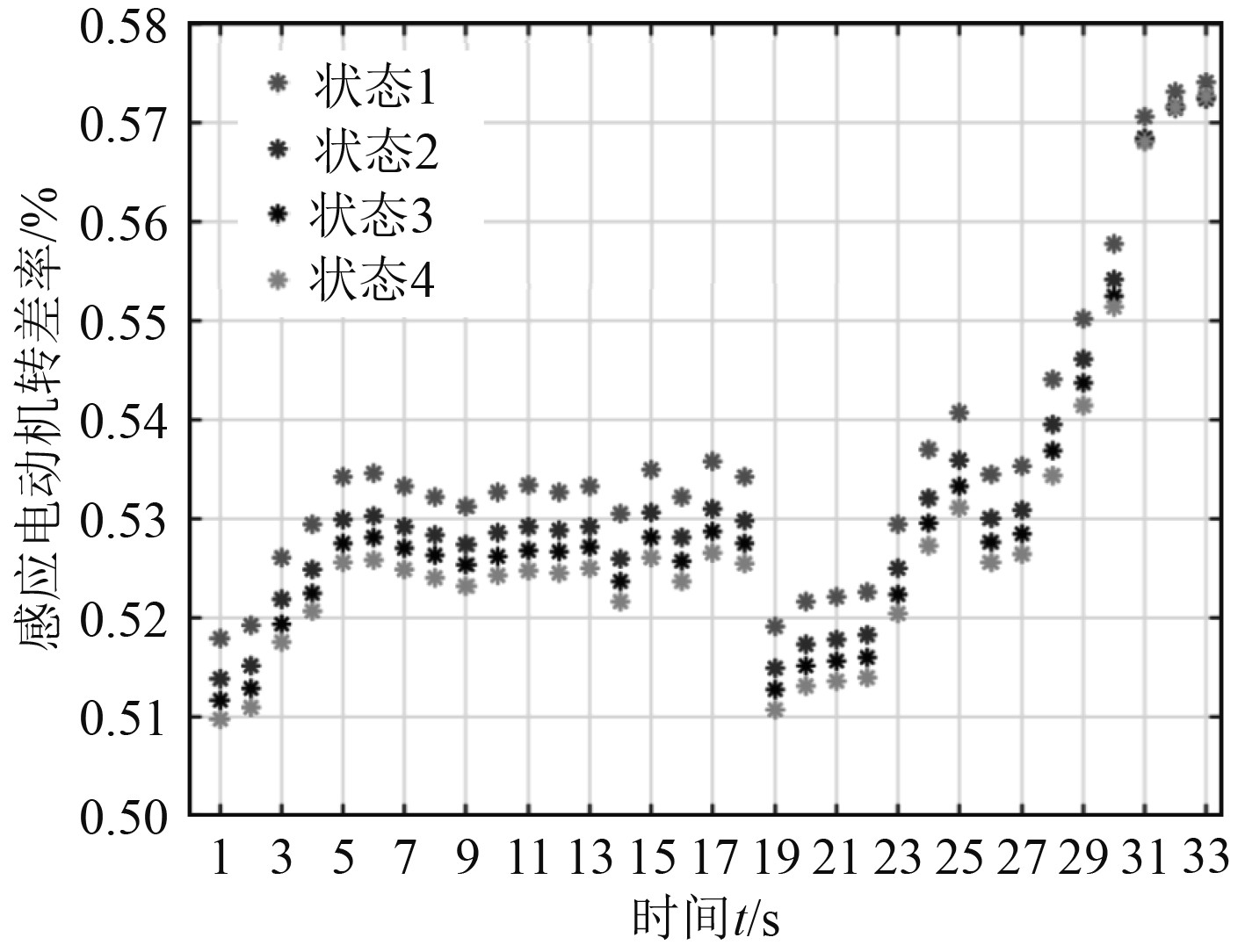
2.3 暂态电压紧急控制对于船用柴油发电机组而言,暂态电压稳定问题的研究主要是系统发生扰动后10 s左右的电压稳定性。基于这一前提,常规的控制模式及方法,很难发挥出应有的效果。所以在监测到扰动后,要及时启动紧急控制模式,以此来应对突发情况下的暂态电压稳定问题。为便于研究,暂态电压紧急控制模式的仿真模型使用7阶模型,时间常数变更为5 s。用时域仿真法分析船用柴油发电机组暂态电压稳定问题时,紧急控制模块与时域仿真模块之间的信息可以通过静止型动态无功补偿装置来传递。暂态电压稳定仿真可在相应的环境中完成,其中柴油发电机组选用的是7阶模型,微分方程为隐式梯形积分法求解,代数方程以牛顿法求解。假设船舶电力系统在1 s时发生故障,1.5 s控制中心监测到扰动,随后立即启动紧急控制模式。紧急控制模块与时域仿真模块之间便会开始数据交互,具体情形如下:时域仿真模块完成初值计算后,以隐式梯形积分法计算时步数值,若是监测到某个节点的电压出现跌落的现象时,紧急控制模块便会做出响应。通过获取该节点的相关数据,如电压、有功及无功功率等,按实际需要,对电压无功控制的灵敏度加以计算,经求解后获得柴油发电机组的输出量,并求出励磁系统的极端电压参考值的改变量,将数据传给时域仿真模块,计算代数量的值,并完成时步仿真,实现模块间的数据交互。采用本文提出的紧急控制模式,将控制时间常数设定为5 s,对船用柴油发电机组暂态电压稳定仿真,获得故障后的电压和感应电动机转差率变化曲线,2种不同方式下系统故障后的电压转差率变化曲线示意图如图5所示。4种不同状态下系统故障后的感应电动机转差率变化曲线示意图如图6所示。
|
图 5 两种不同方式下系统故障后的电压转差率变化曲线示意图 Fig. 5 Schematic diagram of voltage slip change curve after system failure in two different ways |
|
图 6 四种不同状态下系统故障后的感应电动机转差率变化曲线示意图 Fig. 6 Schematic diagram of the change curve of induction motor slip after system failure under four different states |
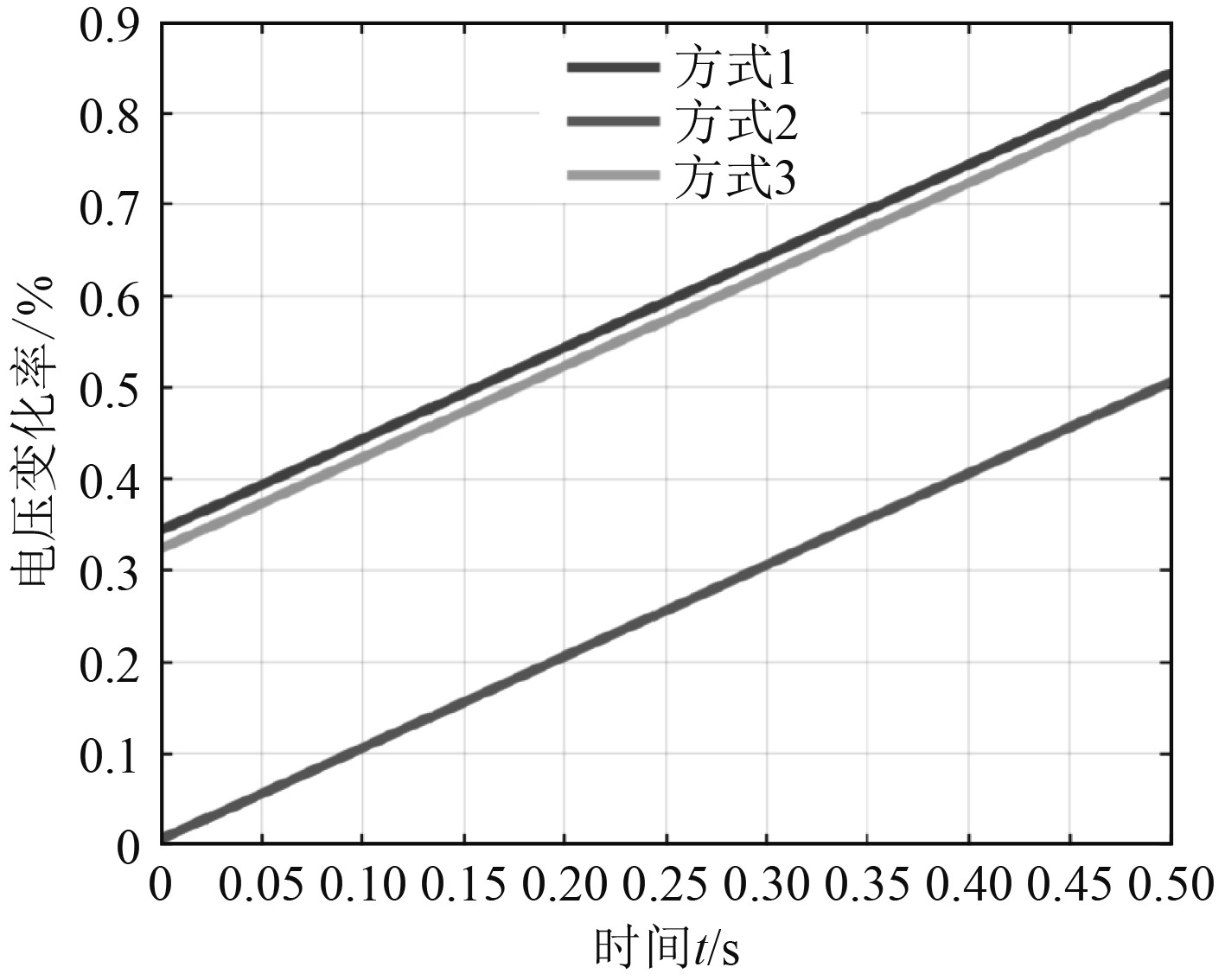
方式1为二级电压控制模式,时间常数为50 s;方式2与方式1的控制模式相同,时间常数为5 s。采用方式1控制暂态电压,当故障从线路中切除后,感应电动机的转差率随之上升,由此可以判断为电压失稳导致;在方式2下,将故障从线路中切除后,恢复的电压值比方式1有所提高,但转差率上升,说明依旧存在电压失稳的情况。2种控制方式中,方式1的时间常数为50 s,故障发生后的10 s内,电压控制并未动作,由此说明,在这个时间段内的发电机无功调节量为0。可见,方式2达到预期中的控制效果,能够满足船用柴油发电机组暂态电压紧急控制的要求。方式1的时间常数过长,无法满足实际应用。图7为3种不同控制方式下的故障节点电压曲线。
|
图 7 三种不同控制方式下的故障节点电压曲线示意图 Fig. 7 Schematic diagram of fault node voltage curve under three different control modes |
方式1为稳态电压紧急控制模式,时间常数为5 s;方式2为紧急控制与切负荷协调控制结合的模式,方式3为正常情况下的控制模式。在方式1的控制中,故障线路切除后,电压随之恢复,通过电压曲线能够判断出发生了电压失稳的现象。在方式2的控制中,故障切除后,电压恢复,且电压值保持稳定,由此判断出暂态电压稳定。可见,紧急控制后,暂态电压并不能恢复到稳定状态,需要采取切负荷等技术手段,使暂态电压恢复稳定。
3 结 语船用柴油发电机组的运行情况,直接关系到整个电力系统的运行。所以必须保证发电机组的运行稳定、可靠。基于此,应针对暂态电压,采取紧急控制方法,消除其对发电机组的影响,使船舶电力系统始终保持良好的状态。
| [1] |
钱振环, 谢辉, 佟强, 等. 基于模型的船用柴油机双泵协同共轨压力控制方法研究[J]. 内燃机工程, 2021(3): 100-108. QIAN Zhen-huan, XIE Hui, TONG Qiang, et al. Research on a model-based dual-pump collaborative common rail pressure control method for marine diesel engines[J]. Internal Combustion Engine Engineering, 2021(3): 100-108. DOI:10.13949/j.cnki.nrjgc.2021.03.015 |
| [2] |
王德民, 王恒, 王起硕, 等. 基于层次分析法的船用柴油发电机组综合健康评估[J]. 机电设备, 2020(3): 53-58. WANG De-min, WANG Heng, WANG Qi-shuo, LIU Hai-yang. Comprehensive health assessment of marine diesel generator sets based on AHP[J]. Electromechanical Equipment, 2020(3): 53-58. DOI:10.16443/j.cnki.31-1420.2020.03.013 |
| [3] |
余永华, 沈叶磊, 王勤鹏, 等. 船用低速柴油机缸压闭环控制硬件在环仿真技术研究[J]. 内燃机工程, 2019(5): 86-92. YU Yong-hua, SHEN Ye-lei, WANG Qin-peng, YANG Jian-guo. Research on hardware-in-the-loop simulation technology of closed-loop control of marine low-speed diesel engine cylinder pressure[J]. Internal Combustion Engine Engineering, 2019(5): 86-92. DOI:10.13949/j.cnki.nrjgc.2019.05.013 |
| [4] |
王正祥, 刘威, 丁艳, 等. 船用柴油机电控高压共轨燃油喷射系统研究[J]. 内燃机, 2022, 38(3): 16-21. WANG Zheng-xiang, LIU Wei, DING Yan, et al. Research on marine diesel electronically controlled high pressure common rail fuel injection system[J]. Internal Combustion Engine, 2022, 38(3): 16-21. DOI:10.3969/j.issn.1000-6494.2022.03.004 |
| [5] |
陈爱志, 马怀腾, 周昊. 船用柴油发电机组负荷突变轴系瞬时扭转振动研究[J]. 电机与控制应用, 2020(5): 6-63,69. CHEN Ai-zhi, MA Huai-teng, ZHOU Hao. Research on instantaneous torsional vibration of marine diesel generator set with sudden load change of shafting[J]. Motor and Control Application, 2020(5): 6-63,69. DOI:10.12177/emca.2020.022 |
 2022, Vol. 44
2022, Vol. 44
