防波堤系统是保障船舶或者浮式结构物安全使用的重要技术措施之一。随着海洋的开发逐渐迈向深海,传统的坐底式防波堤建设成本较高,建造较困难。在这种情况下,浮式防波堤是一种很好的替代选择,其造价更加低廉,对海底地形的依赖性更小,拆装方便,对周边海洋环境生态系统影响较小,更加环保[1]。因此,浮式防波堤在港口工程和海洋养殖等领域的应用也逐渐增多。浮式防波堤应当具有结构较简单,耐用性好,能够长期稳定在某个海域运行的特点[2]。国内外专家学者对此进行了大量研究,提出了多种类型的浮式防波堤,主要有浮箱形、浮筒型和浮筏型[3]。
浮式结构物长时间在海洋环境中工作,长期经受风、浪、流等载荷,海浪通常受海域与季节的影响具有不规则性和随机性,这使得浮式结构物的载荷计算变得相对困难[4]。刘海霞等[5]计算分析了半潜式平台的波浪载荷,在结合莫里森方程与势流理论时,计算波浪载荷可以得到满意结果。王言英等[6]推荐使用线性波理论与三维源汇分布法来计算较大型结构在波浪中的运动与载荷响应。工程上通常采用设计波法来计算浮式结构物的载荷响应[7]。为了减少作用于结构剖面上的载荷,采用模块化的建造方式,各单元模块以某种方式连接而成。Dayun等[8]基于三维水弹性理论,分别计算了多模块与单模块浮体的运动响应及其连接器上的载荷,通过对比发现,不同的连接器连接方式能较大影响浮体的运动响应和连接器载荷,对模块间的水动力相互影响效果较小。刘超等[9]采用多模块超大型浮体运动理论及RMFC模型理论,分析了连接器刚度、海况、模块的个数以及浪向角度对超大型浮体运动以及连接器载荷所产生的影响。
受有效掩护区域和服役地区的地形影响,浮式防波堤有时采用非直线型布局,需要根据不同地形及掩护区域采取不同的布局方式。与直线型浮式防波堤相比,弧型布置的浮式防波堤对多浪向的掩护效果更好,对地形的适应性也更好,但波浪载荷特性更加复杂。本文针对6模块双浮筒型浮式防波堤,将弧型布置和同尺度下直线型浮式防波堤的波浪载荷特性进行对比分析。
1 基本理论 1.1 三维势流理论三维势流理论[10]是研究浮式结构物水动力性能的方法之一,三维势流理论可用于计算大型结构物的一阶波浪载荷。对于较大的浮式结构物,入射波会发生严重的反射和绕射,在计算波浪载荷的时候,绕射力通常不可被忽略,为简化问题,使用势流理论来描述流动状态。三维势流理论假设流体是理想流体,其具有无粘性,无旋,不可压缩的特性。流体的运动可以通过拉普拉斯方程来描述:
| $ {\nabla ^2}\phi (x,y,z) = 0 z \leqslant 0 ,$ | (1) |
浮式防波堤在波浪中的流场速度势主要包括入射势、绕射势和辐射势:
| $ \phi (x,y,z,t) = {\phi _I}(x,y,z,t) + {\phi _d}(x,y,z,t) + {\phi _R}(x,y,z,t)。$ | (2) |
式中:
| $ \frac{{\partial \phi }}{{\partial n}} = V, \quad 在物面上 ,$ | (3) |
| $ \frac{{\partial \phi }}{{\partial t}} = g\frac{{\partial \phi }}{{\partial z}},\quad z = 0 ,$ | (4) |
| $ \frac{{\partial \phi }}{{\partial n}} = 0 ,\quad z = - \infty,$ | (5) |
| $ \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{{\partial \phi }}{{\partial y}} + ik\phi } \right) = 0, \quad z = 0 。$ | (6) |
式中:
通过在湿表面分布源汇来确定流场速度势,通过格林公式解出边界条件可得到总速度势,通过离散化数值计算可求得作用在浮式防波堤上的压强分布,这样就可以求得作用在浮式防波堤的一阶波浪力与力矩。
1.2 浮式防波堤波浪载荷计算方法在海洋环境中,浮式防波堤由于随机波浪的压力场的存在将受到波浪激励载荷作用,对于大尺度的结构物主要包括惯性力和绕射力[11]。一阶波浪力和力矩可以用频域方法进行求解,其与波高成线性关系,而且与波浪在相同频率。利用Cummins脉冲响应,设
| $ {F_i}^{wave(1)}(t) = \int_{ - \infty }^t {{h_i}(t - \tau )} \eta (\tau ){\rm{d}}\tau ,$ | (7) |
式中:
| $ \left\{ \begin{gathered} {f_{\omega i}}(\omega ) = \int_{ - \infty }^\infty {{h_i}(t){e^{ - i\omega t}}{\rm{d}}t} ,\\ {h_i}(t) = \frac{1}{{2 \text{π} }}\int_{ - \infty }^\infty {{f_{\omega i}}(\omega ){e^{ - i\omega t}}{\rm{d}}t} 。\\ \end{gathered} \right. $ | (8) |
已知频率响应
浮式防波堤除了受到一阶波浪力之外,还受到二阶波浪漂移力,二阶平均和低频波浪力与波高的平方成正比[12]。根据波浪在不同频率及浪向下的传递函数,利用Fourier变换可得二次脉冲响应函数
| $ g({\tau _1},{\tau _2}) = {\left( {\frac{1}{{2 \text{π} }}} \right)^2}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {G_i^{(2)}({\omega _1},{\omega _2}){e^{\left( {i{\omega _1}{t_1} - i{\omega _2}{t_2}} \right)}}{\rm{d}}{\omega _1}{\omega _2}} },$ | (9) |
| $ G_i^{(2)}({\omega _1},{\omega _2}) = P({\omega _1},{\omega _2}) + iQ({\omega _1},{\omega _2})。$ | (10) |
式中:
| $ {F_i}^{wave(2)}(t) = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{g_i}({\tau _1},{\tau _2})\zeta \left( {t - {\tau _1}} \right)\zeta \left( {t - {\tau _2}} \right)d{\tau _1}{\tau _2}} }。$ | (11) |
在求得浮式防波堤在规则波作用下的响应后,可结合达朗贝尔原理求出剖面上波浪诱导的水平剪力、垂向剪力、轴向力、扭矩、垂向弯矩和水平弯矩[13]。取单位长度浮式防波堤,假设其质量为
| $ \left[ {\bar M} \right] = \int_{{x_a}}^x {\left[ {\bar m} \right]{\rm{d}}x} 。$ | (12) |
式中:
| $ \left\{ Q \right\} = \left\{ \begin{gathered} N \\ S{F_y} \\ S{F_z} \\ TM \\ B{M_y} \\ B{M_z} \\ \end{gathered} \right\} = - \iint\limits_{{S_x}} {p\left( {x,y,z} \right)\left\{ {{n_j}} \right\}}{\rm{d}}s - {\omega ^2}\left[ {\bar M} \right]\left\{ \eta \right\}。$ | (13) |
式中:
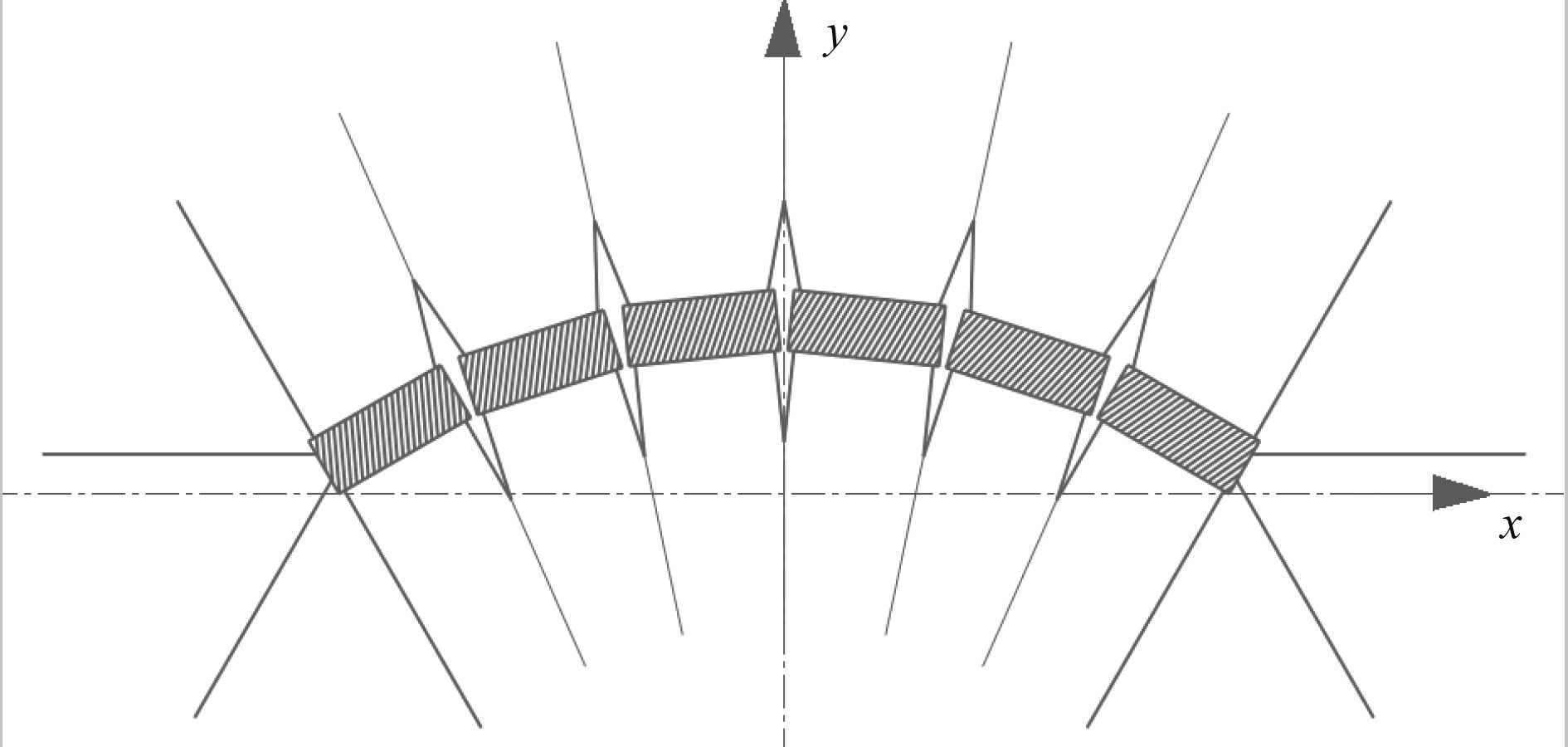
弧型布局浮式防波堤总布置示意图如图1所示。弧型布局浮式防波堤共由6个模块组成,两端模块的夹角为60°,相邻两模块之间的夹角为12°,弧长为322.6 m,在X轴上的投影总长度为312.7 m。模型整体关于YOZ面对称,由X轴负方向到X轴正方向分别编号为模块1到模块6。结合弧型布局浮式防波堤的特点,采用张紧式系泊方案,由10组Y型系泊线和8根系泊缆组成。
|
图 1 弧型布局总布置示意图 Fig. 1 Schematic diagram of the arc layout |
本文采用的浮式防波堤单模块构型为双圆筒型[14],每个浮筒半径为4 m,长50 m,2个浮筒间用7组宽为2 m的横舱相连接,防波堤的总长为50 m,总宽为20 m,型深为8 m,吃水为4 m,排水量为2 904 t。
2.2 设计海况条件服役海域选择南海某典型岛礁附近,根据其服役海域的相关资料,平均海水深度取45 m,海水密度取1.025×103 kg/m3,波浪采用JONSWAP谱,有义波高取6 m,周期为9 s。由于风、流引起的环境载荷较为稳定,这部分载荷暂不予考虑。
2.3 波浪力计算结果及分析 2.3.1 一阶波浪力一阶波浪力由入射波浪力(F-K力)和波浪绕射力及力矩组成,在规则波作用下,一阶波浪力幅值与入射波的波幅成正比,因此,一阶波浪力通常以频率响应函数来表示。对弧型布局浮式防波堤进行水动力频域分析,得到结构在规则波作用下一阶波浪力响应幅值。
由图2的计算结果可知,在纵荡、纵摇和首摇方向上,弧型布局在横浪作用下的一阶波浪力较小;在横荡与横摇方向上,横浪作用下的一阶波浪力比斜浪下的大,且随着波浪频率的增加总体呈现先增大后减小的趋势;在垂荡方向,一阶波浪力总体呈现递减趋势。

|
图 2 弧型布局在不同浪向下的一阶波浪力 Fig. 2 F-K+diffraction force of arc layout in different waves |
二阶波浪力可以分为定常项、差频项和合频项,其中水平方向的定常力又称为漂移力。二阶波浪力的存在会使得浮式防波堤产生大幅度的运动,所以对二阶波浪力的分析同样不可或缺。求解二阶波浪力主要有远场法和近场法,近场法是对湿表面进行积分来求解,而远场法是用动量定理来求解[15]。由于近场法可以求解出6个方向上的二阶波浪力及力矩,所以本文采用近场法来计算。
由图3的计算结果可知,在纵荡、纵摇和首摇方向上,弧型布局在横浪作用下的二阶波浪力较小;在横摇方向上,斜浪作用下的二阶波浪力比横浪工况下的更为剧烈;在横荡与垂荡方向上,横浪下的二阶波浪力峰值约为斜浪下的1.31~1.36倍。

|
图 3 弧型布局在不同浪向下的二阶波浪力 Fig. 3 Second order wave force of arc layout in different waves |
由于弧型布局模型关于YOZ面对称,选取模块1~3的中横剖面分别命名为截面1~3并进行分析。
图4为弧型布局在横浪与斜浪(−60°)工况下的剖面载荷。随着波浪频率的增加,各剖面载荷均呈先增大后减小的总体趋势,截面1在斜浪下的各剖面载荷均小于横浪工况;截面2在斜浪下的横向力和水平弯矩小于横浪工况,其余载荷的峰值是横浪工况下的1.3~1.6倍;截面3在斜浪下的水平弯矩小于横浪工况,其余载荷的峰值是横浪工况下的1.2~4.2倍。

|
图 4 弧型布局在不同浪向下的剖面载荷 Fig. 4 Section loads of arc layout in different waves |
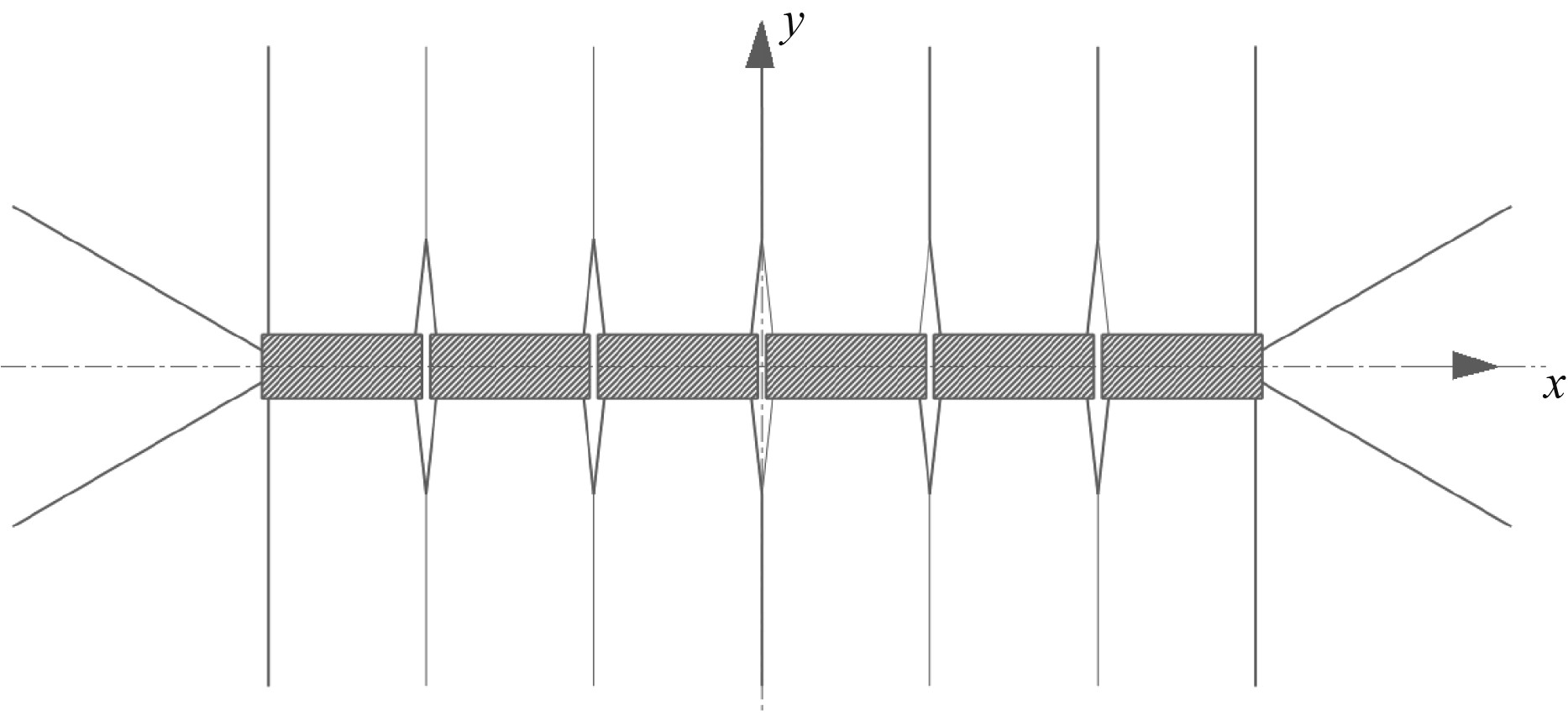
为了比较弧型布局的优缺点,选用2种直线型布局来与弧型布局做对比,直线1型的总长度与弧型布局在X轴投影长度相等,即为312.7 m;直线2型的总长度与弧型布局弧长总长度相等,即为322.6 m。2种布局均采用和弧型布局相同的单模块构型与系泊方式。直线2型与直线1型布局类似,只有浮式防波堤间的距离有所不同。直线1型如图5所示。
|
图 5 直线1型总布置示意图 Fig. 5 Schematic diagram of the linear I layout |
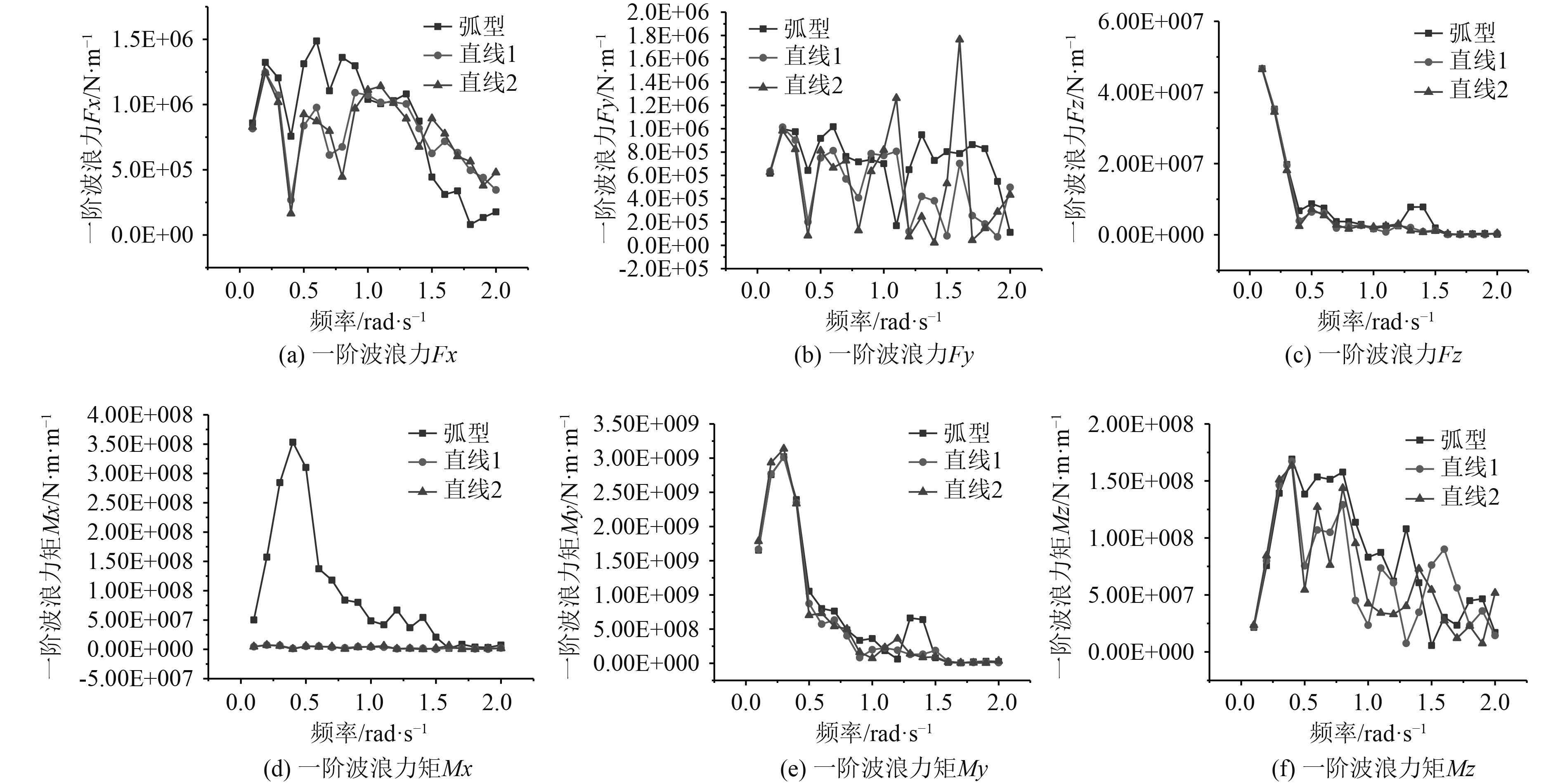
图6为横浪工况下3种不同布局浮式防波堤一阶波浪力的对比结果。3种布局的一阶波浪力总体趋势一致,随着波浪频率的增加,除垂荡和首摇方向外,其余4个方向上的一阶波浪力或力矩总体都呈先增大再减小的趋势。除横摇和纵摇方向外,弧型布局在其余4个方向上的一阶波浪力和力矩上均明显小于直线型布局,且直线2型布局在首摇方向上的峰值是弧型的15.9倍。

|
图 6 横浪工况下3种布局浮式防波堤一阶波浪力 Fig. 6 F-K+diffraction force of three layouts in transverse waves |
图7为斜浪(−60°)工况下3种不同布局浮式防波堤一阶波浪力的对比结果。3种布局浮式防波堤在纵荡、垂荡和纵摇方向上的一阶波浪力和力矩均在波浪频率较低时幅值较大,并且在这3个方向上的变化趋势总体一致。除横摇方向外,弧型布局在其余5个方向上的一阶波浪力和力矩上均与2种直线型布局总体相差不大;在横荡方向上直线2型的一阶波浪力大于弧型布局,峰值约是弧型布局的2.2倍。
|
图 7 斜浪工况下3种布局浮式防波堤一阶波浪力 Fig. 7 F-K+diffraction force of three layouts in oblique waves |
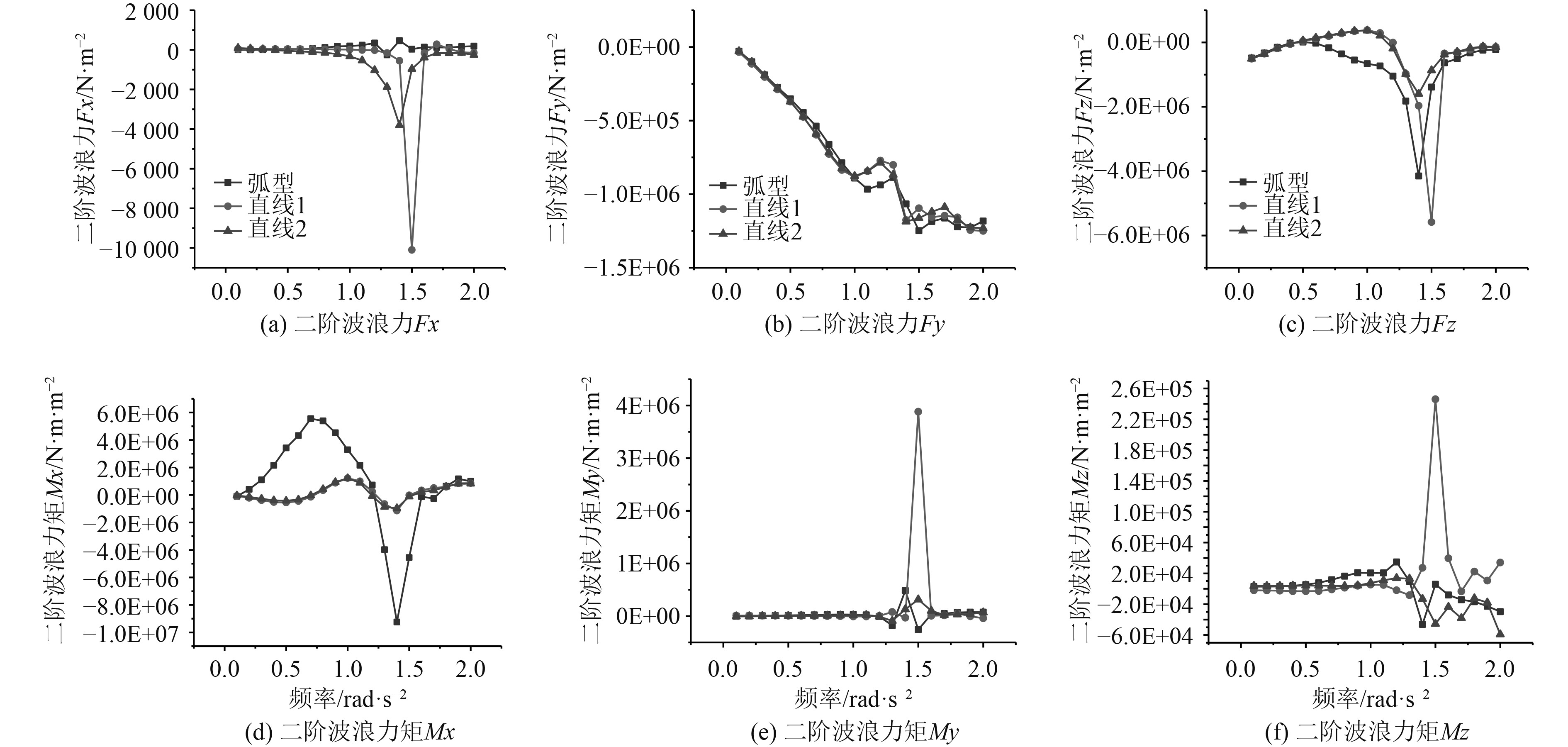
图8为横浪工况下3种不同布局浮式防波堤的二阶波浪力的对比结果。在横荡方向上,3种布局的二阶波浪力相差不大,随着波浪频率的增加总体呈下降趋势;在纵荡、垂荡、纵摇和首摇方向上,直线1型的二阶波浪力或力矩显著大于弧型布局,均在波浪频率为1.5 rad/s时达到最大值,且在首摇方向上的峰值约是弧型布局的42倍。
|
图 8 横浪工况下3种布局浮式防波堤二阶波浪力 Fig. 8 Second order wave force of three layouts in transverse waves |
图9为斜浪(–60°)工况下3种不同布局浮式防波堤的二阶波浪力的对比结果。在纵荡、横摇和首摇方向上,弧型布局的二阶波浪力在波浪频率较低时与2种直线型布局相差不大,但在波浪频率较高时弧型布局的二阶波浪力明显高于直线型局部方式;在横荡、垂荡及纵摇方向上,直线1型的二阶波浪力或力矩较大,在波浪频率为1.4~1.5 rad/s时达到最大值。

|
图 9 斜浪工况下3种布局浮式防波堤二阶波浪力 Fig. 9 Second order wave force of three layouts in oblique waves |
图10为直线型布局在不同浪向下的剖面载荷,与弧型布局相似,随着波浪频率的增加,各剖面载荷均呈先增大后减小的总体趋势,且2种直线型布局方式的剖面载荷相差并不是很大。直线型布局在斜浪下只有水平弯矩小于横浪工况,其余载荷均显著大于横浪工况,斜浪下的垂向力、纵向扭矩和垂向弯矩的峰值是横浪工况下的4.7~9.1倍,而弧型布局在斜浪下各剖面载荷峰值最大只有横浪工况下的1.2~4.2倍。
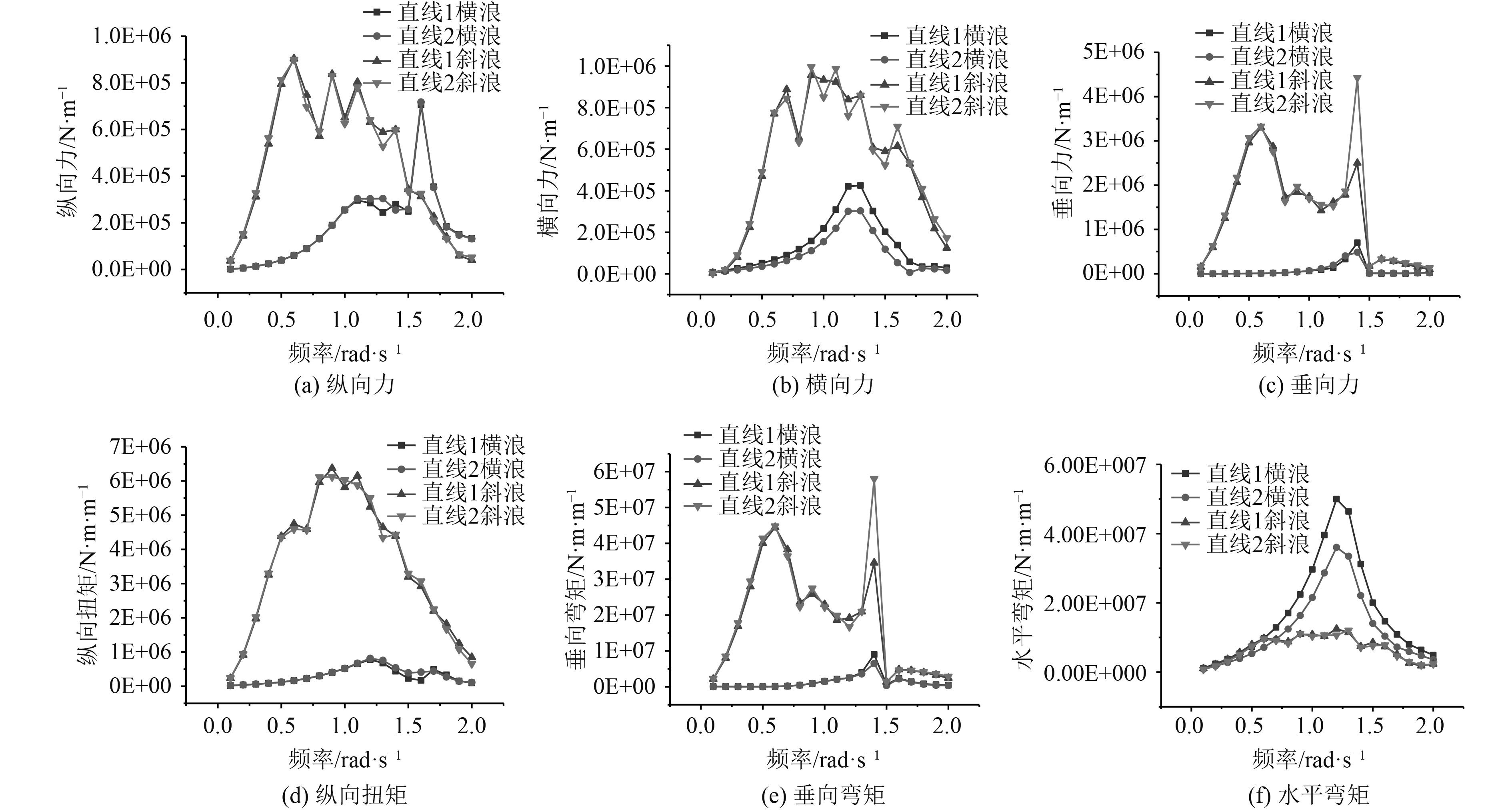
|
图 10 直线型布局在不同浪向下的剖面载荷 Fig. 10 Section loads of linear layout in different waves |
本文提出一种浮式防波堤的弧型布局方案,并以2种直线型布局的浮式防波堤为对比对象,分析了横浪与斜浪工况下的一阶波浪力、二阶波浪力与关键剖面载荷,通过不同布局下的计算结果,得到以下结论:
1)在横浪工况下,除横摇和纵摇方向外,弧型布局在其余4个方向上的一阶波浪力和力矩上均明显小于直线型布局,且直线2型布局在首摇方向上的峰值是弧型的15.9倍。在纵荡、垂荡、纵摇和首摇方向上,直线1型的二阶波浪力或力矩显著大于弧型布局,且直线1型在首摇方向上的峰值约是弧型布局的42倍。采用弧型布局能够显著降低结构在横浪下的一阶与二阶波浪力。
2)在斜浪工况下,除横摇方向外,弧型布局在其余5个方向上的一阶波浪力和力矩上与2种直线型布局总体相差不大。在横荡、垂荡及纵摇方向上,直线1型的二阶波浪力或力矩较大,在波浪频率为1.4~1.5 rad/s时达到最大值。
3)弧型布局能够显著降低位于两端的模块在斜浪下的剖面载荷,位于中间的模块在斜浪下的剖面载荷约是横浪工况下的1.2~4.2倍,而直线型布局在斜浪下的剖面载荷显著大于横浪工况,斜浪下的垂向弯矩达到了横浪工况下的8.9倍。采用弧形布局能够降低结构剖面载荷受浪向角的影响。
| [1] |
JI C Y , CHEN X , CUI J , et al. Experimental study on configuration optimization of floating breakwaters[J]. Ocean Engineering, 2016, 117(may 1): 302-310.
|
| [2] |
WANG Na, XING L , GANG W , et al. Stress analysis of anchor chain on the floating breakwater structure with cage culture function[J]. IOP Conference Series: Earth and Environmental Science, 2020, 567(1): 012008 (7pp).
|
| [3] |
卞向前. 新型水轮机式浮式防波堤设计与分析[D]. 镇江: 江苏科技大学, 2019.
|
| [4] |
曹剑锋, 李良碧, 顾海英, 等. 基于Ansys/AQWA的极大型浮式结构总体强度分析[J]. 舰船科学技术, 2015, 37(9): 30-34+39. CAO Jian-feng, LI Liang-bi, GU Hai-ying, et al. The global strength analysis of VLFS based on Ansys/AQWA[J]. Ship Science and Technology, 2015, 37(9): 30-34+39. DOI:10.3404/j.issn.1672-7649.2015.09.007 |
| [5] |
刘海霞, 肖熙. 半潜式平台结构强度分析中的波浪载荷计算[J]. 中国海洋平台, 2003(02): 3-6. LIU Hai-xia, XIAO Xi. The wave load calculation in the analysis of structural strength of a semi-submersible[J]. China Offshore Platform, 2003(02): 3-6. DOI:10.3969/j.issn.1001-4500.2003.02.001 |
| [6] |
王言英, 李芳. 浮式结构物在波浪中的运动响应计算[J]. 水动力学研究与进展(A辑), 1995(6): 571-580. |
| [7] |
夏风, 黄东, 滕洪园, 等. 船体结构强度评估的线性设计波法研究[J]. 舰船科学技术, 2019, 41(7): 34-38. XIA Feng, HUANG Dong, TENG Hong-yuan, et al. Research on linear design wave method of structure strength evaluating of hull[J]. Ship Science and Technology, 2019, 41(7): 34-38. DOI:10.3404/j.issn.1672-7649.2019.04.007 |
| [8] |
DAYUN, RIGGS H R, ERTEKIN R C. Three-dimensional hydroelastic response of a very large floating structure[J]. International Journal of Offshore and Polar Engineering, 1991, 1(4): 307-316. |
| [9] |
刘超. 超大型浮体多模块柔性连接结构响应研究[D]. 北京: 中国舰船研究院, 2014.
|
| [10] |
朱仁庆, 杨松林, 王志东. 船舶流体力学[M]. 北京: 国防工业出版社, 2015.
|
| [11] |
FALTINSEN O M. 船舶与海洋工程环境载荷(第二版)[M]. 上海: 上海交通大学出版社, 2013.
|
| [12] |
徐胜. 半潜式平台运动耦合分析方法及水动力模型试验研究[D]. 镇江: 江苏科技大学, 2012.
|
| [13] |
王松波. 六边围圈型浮式平台连接器载荷特性及结构响应研究[D]. 武汉: 武汉理工大学, 2019.
|
| [14] |
JI C Y, CHENG Y, YANG K, et al. Numerical and experimental investigation of hydrodynamic performance of a cylindrical dual pontoon-net floating breakwater[J]. Coastal Engineering, 2017, 129: 1-16. |
| [15] |
杨田祥. 通用抗流动力浮标平台运动特性及阻力研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
 2022, Vol. 44
2022, Vol. 44

