0 引　言

随着海洋战略的实施和快速推进，我国的海洋科技发展迅猛，以水面无人艇/船为代表的海洋高端装备成为助力透明海洋、智慧海洋建设的重要手段。无人艇已成为船舶科学中的新兴课题，其在作业时有应对恶劣海况的可能，因此，高性能无人艇运载平台需要具备良好的水动力性能。

无人艇船型的发展从大型船只演变而来，早期阶段多以单体船为主。美国海军开发了一种更高速度的气垫式单体无人艇Spartan Scout号^[1]；以色列研制了高速无人艇Protector系列^[2]和中型USV Silver Marlin号，可使用船岸间的通信系统以及岸上基站的监测系统，USV通过各主要性能指标和传感器的传回数据进行监测^[3]；Elbit公司正在研制具备目标辨识、主动巡航等多项功能的Stingary型无人艇^[3]。国内根据无人艇高速、容易移动的特性也进行了有益的探索，王保明^[4]加入水翼艇的设计思想，研发了一种小水线的建筑型单体水翼复合艇；霍聪等^[5]设计了可转换航态的高速无人船型。

近年来,穿浪船也因其在海浪中作业时具有较好的迅捷度与耐波性而被着重研究^[6]。英国研制了双体穿浪无人艇C-Enduro系列^[7]，意大利研发了双体无人艇Charlie号^[8]，英格兰普利茅斯大学研发了Springer号^[9]，德国联邦科技部所支持了水面无人艇计划^[10]，法国波尔多工程研究院自主开发了ROAZ号^[11]。杨显原等^[12]用数值仿真对双体无人船迎浪航行进行分析，并选出阻力较小较设计方案。以上无人船型均采用双体船型,可以看出双体船型对尺度较小的无人艇来说具有较好的穿浪性。同时,由于双体穿浪船水线面积更小,有良好的耐波性^[13]，是海洋综合科考、水文观测的首选船型。

本文以一种双体无人艇为例，说明RANS模型在测量无人艇稳性中的应用方法，对其在不规则波（P-M谱）中航行状态进行数值模拟，并做出分析与预报。

1 模型分析

在海洋科考中，母船往往携带若干无人艇，当母船行驶至特定海域，科考人员将无人艇放至海面，由无人艇完成测绘任务。本文以一个船体由2个充气式浮筒构成的无人艇（见图1）为例，其技术参数见表1。

2 无人艇数值分析方法 2.1 控制方程

粘性、不可压缩流体应满足连续方程和N-S方程，表达式为：

$ {\rm{div}}\;u=0 ,$

(1)

$ \frac{\partial u}{\partial t}+{\rm{div}}(u \mathop {u}\limits^ \rightharpoonup)=-\frac{1}{\rho}\frac{\partial p}{\partial x}+v\;{\rm{div}} (grad\;u), $

(2)

$ \frac{\partial v}{\partial t}+{\rm{div}}(v \mathop {u}\limits^ \rightharpoonup)=-\frac{1}{\rho}\frac{\partial p}{\partial y}+v\;{\rm{div}} (grad\;v), $

(3)

$ \frac{\partial u}{\partial t}+{\rm{div}}(w \mathop {u}\limits^ \rightharpoonup)=-\frac{1}{\rho}\frac{\partial p}{\partial z}+v\;{\rm{div}} (grad\;w) 。$

(4)

式中： $u,\;\;v$ 和 $ w $ 分别为速度矢量 $ \mathop {u}\limits^ \rightharpoonup$ 在 $ x,\;\;y $ 和 $ z $ 方向上的分量； $ \nu $ 为流体的运动粘度。

本文模拟产生波浪的方法是：在入口处输入波形函数产生一阶入射波，规则波的波面方程可以表达为：

$ \eta = H\cos {\text{(}}mx - \omega t{\text{)}}，$

(5)

而规则波的速度场为：

$ \left\{ \begin{gathered} U = \omega H{e^{kz}}\cos {\text{(}}mx - \omega t{\text{)}} ，\\ V = 0 ，\\ W = \omega H{e^{kz}}\sin {\text{(}}mx - \omega t{\text{)}}。\\ \end{gathered} \right. $

(6)

式中： $ H $ 为波幅； $ m $ 为波数； $ \omega $ 为波浪圆频率。 $ X $ 轴正方向是相速度方向， $ Z $ 轴为波动方向，通过波的叠加即可产生不规则波。

不规则波选取Pierson-Moskowitz谱，其表达式为：

$ {S_{PM}}\left( \omega \right){\text{ = }}\frac{{\text{5}}}{{{\text{16}}}}\left( {H_S^{\text{2}}\omega _P^{\text{4}}} \right){\omega ^{{{ - 5}}}}\exp \left( { - \frac{5}{4}{{\left( {\frac{\omega }{{{\omega _P}}}} \right)}^{ - 4}}} \right)。$

(7)

式中： ${\omega _P} = \left( {2\text{π} } \right){\text{/}}\left( {{T_P}} \right)$ ，代表谱峰频率。

2.2 模型建立

本文基于STAR-CCM+进行数值仿真计算，采用雷诺平均方法（SST k-ω）求解控制方程，设置方法如表2所示。

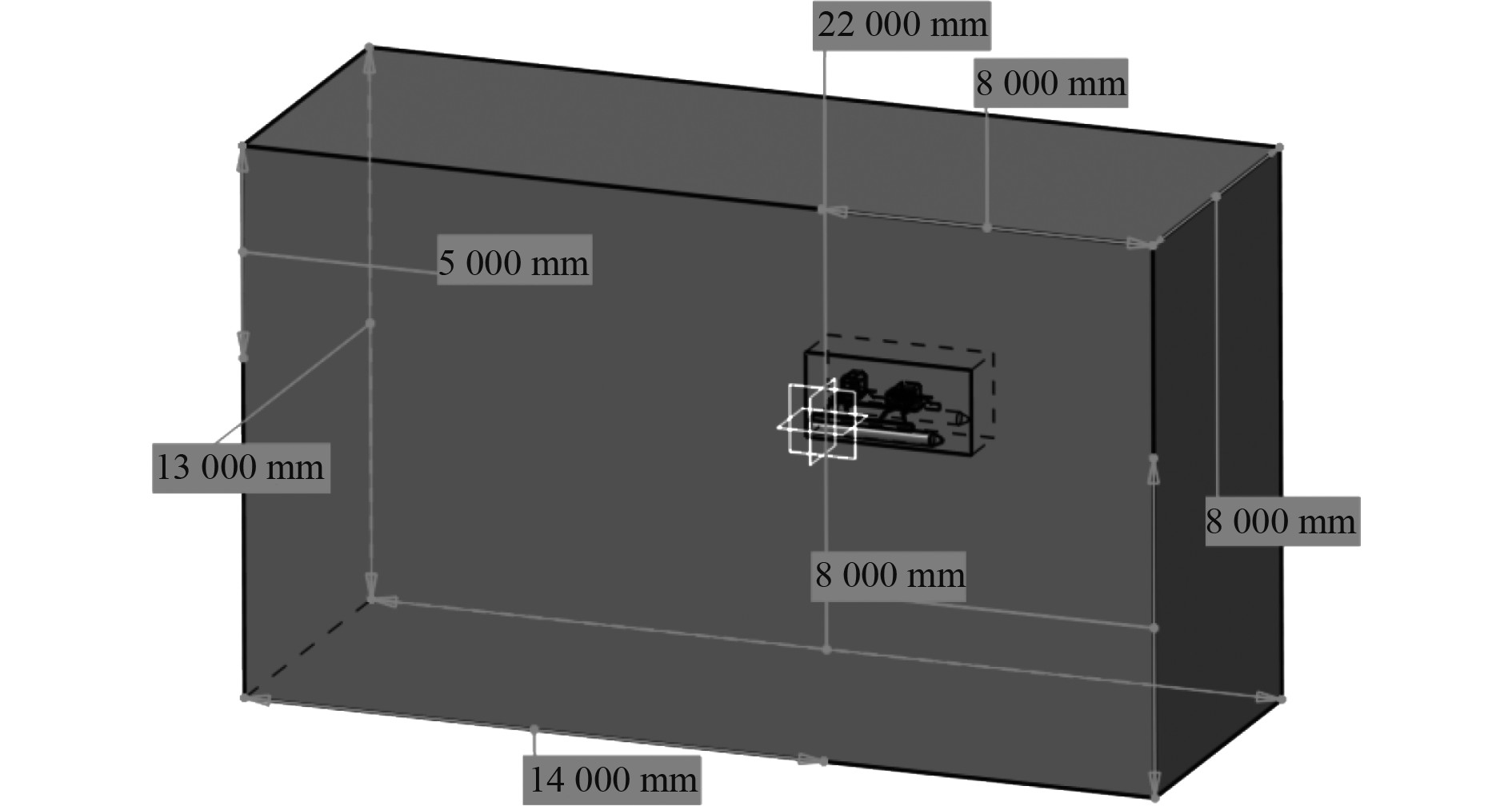
如图2所示，计算域为：流域入口边界条件采用Velocity-Inlet，流域出口边界条件采用Pressure-Outlet，侧壁采用对称边界条件。网格数量为1.37×10⁷，三维网格划分和壁面周围网格分布如图3和图4所示。

3 结果分析

选取5 kn，8 kn，11 kn三种航速，0.5 m，1 m，1.5 m三种有效波高的不规则波，对无人艇进行仿真计算（见表3），分析无人艇的水动力特性。

3.1 升沉与纵倾

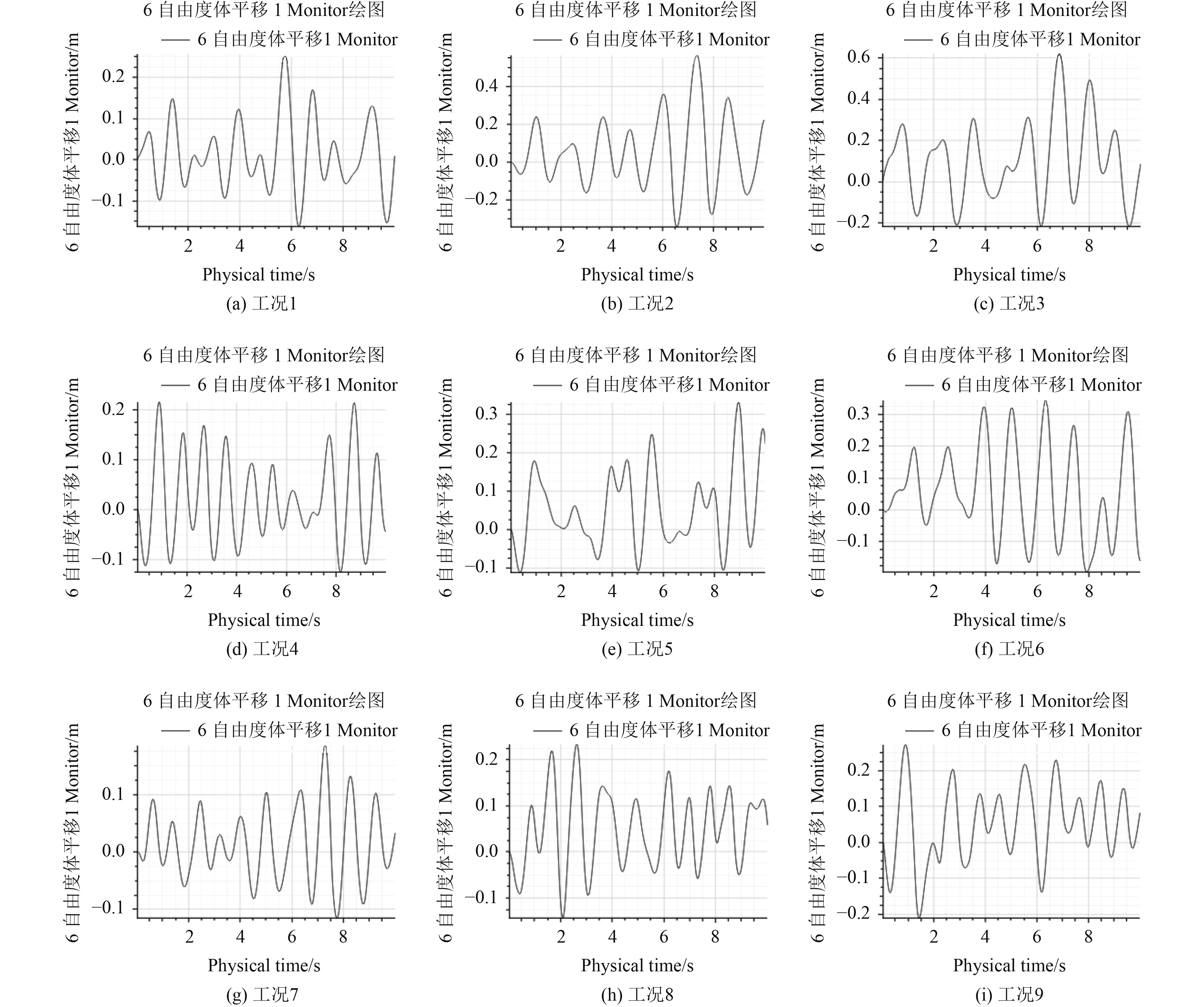
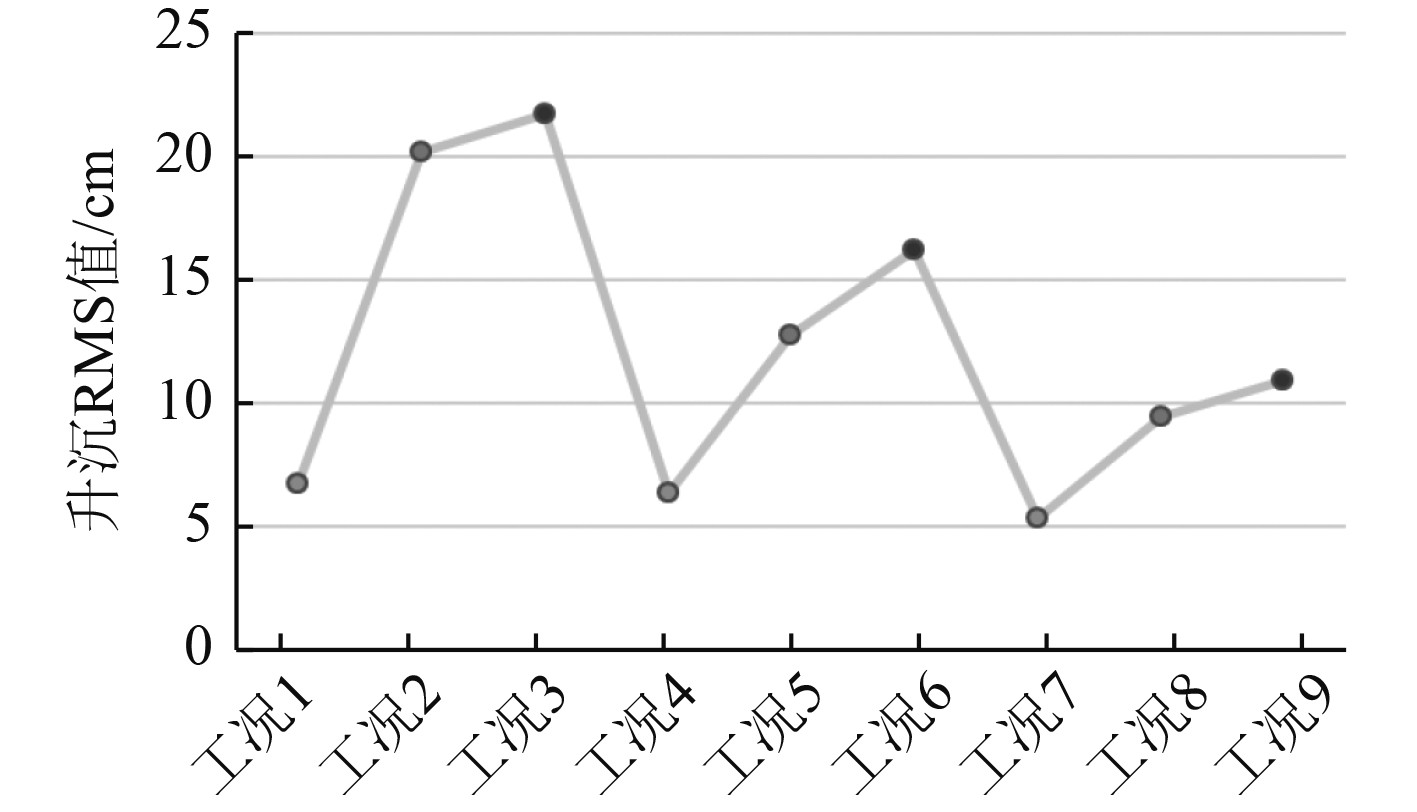
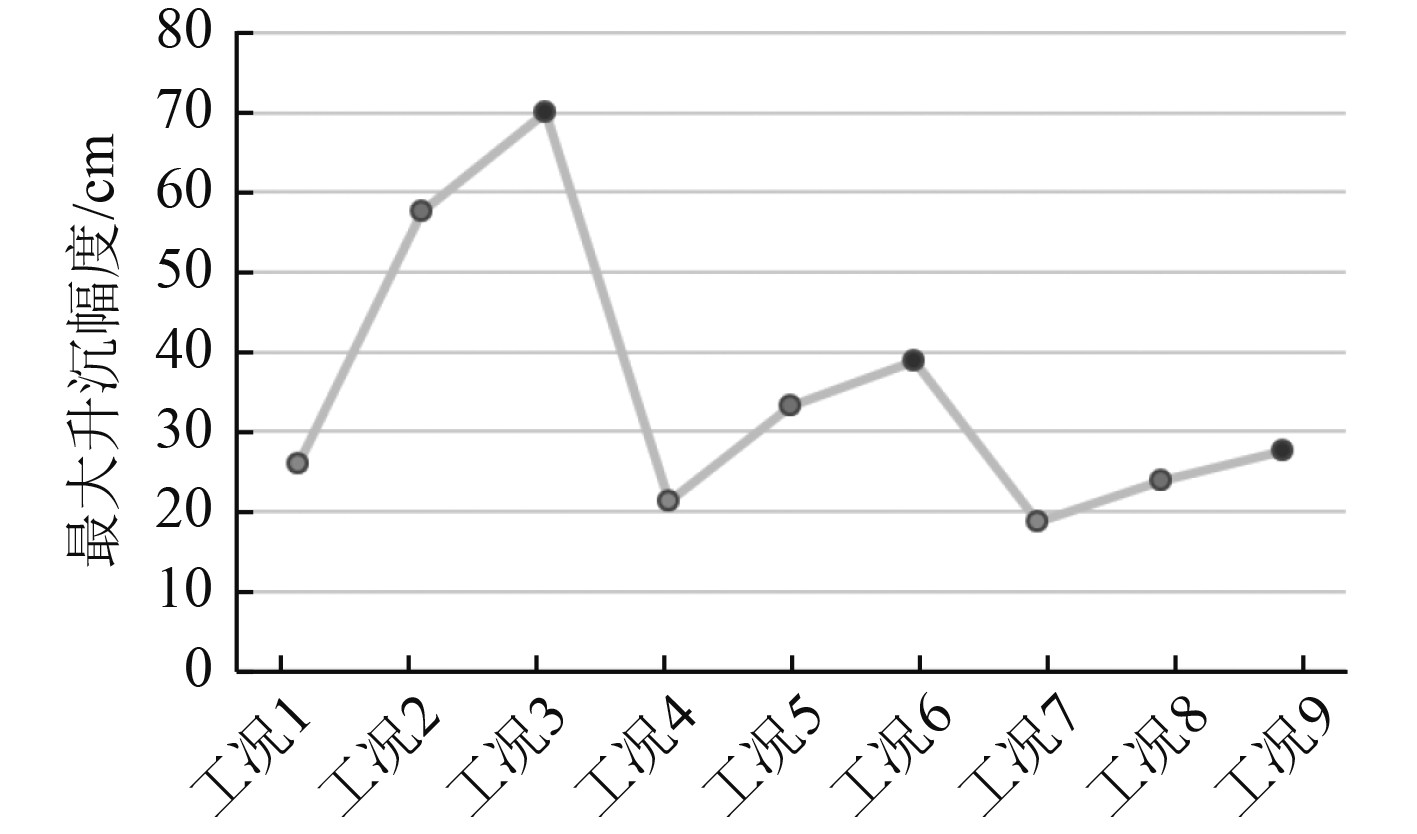
无人艇通常吃水较小，但作业时如遇水下暗礁或浅滩等特殊地形，由于限制水域的阻塞效应^[14]，使船体表面形成压力分布差，将增加船体触礁、触岸的风险。如图5所示，由于航速的增加，无人艇的升沉运动出现了缓和态势。航速为11 kn时升沉曲线波动稳定程度较航速为5 kn时有较大程度的提高。如图6所示，无人艇平均吃水随航速提高而降低，随波高的增加而上升。升沉幅度最大均方根值出现在航速5 kn，有效波高1.5 m时，为0.22 m。航速为8 kn和11 kn时，升沉的均方根值分别减少25.7%和58.2%。如图7所示，在航速为5 kn，有效波高为1.5 m时，升沉幅度范围较大，最大值为0.7 m。

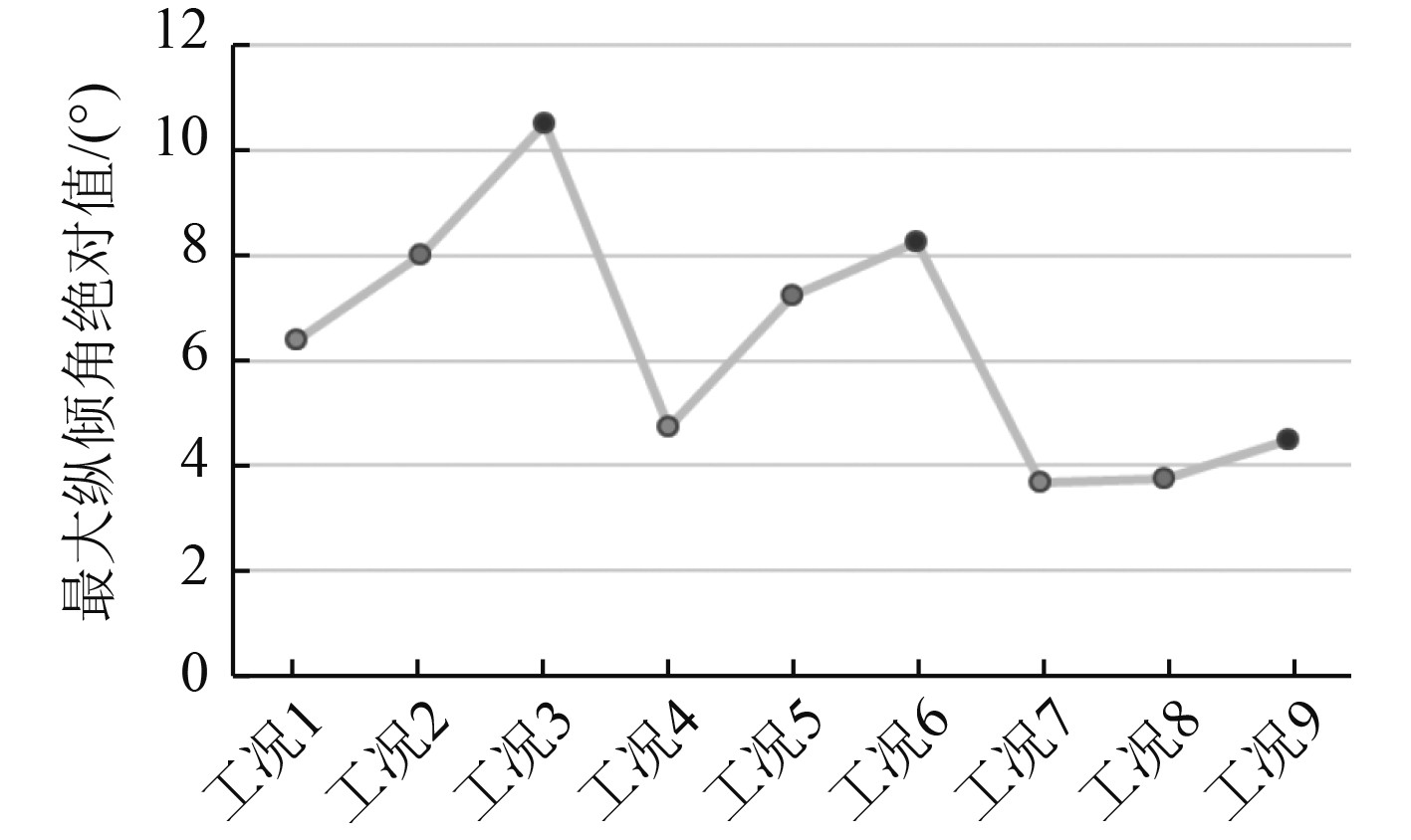
航行中船体的稳定性极大影响搭载设备的测绘质量，例如多波束测深仪和侧扫声呐若搭载在纵倾较大的无人艇平台上，则难以保证测绘数据的可靠性。如图8所示，船体纵倾程度随着最大航速和有效波高的增加反而减小，表明增加航速后船体可在较大海浪中航行变稳定。如图9所示，最小纵倾角出现时的航速和有效波高均高于最大纵倾角出现时的航速和有效波高，说明此种结构的船体有较好的穿浪性能。

3.2 航行阻力

无人艇因克服环境阻力而对外界做功，因此无人艇受到的阻力增大其能耗随之增大。通过对阻力计算结果进行分析，可选择合理的航行速度和航行区域，达到节约能耗、提升无人艇续航能力的目的^[15-16]。

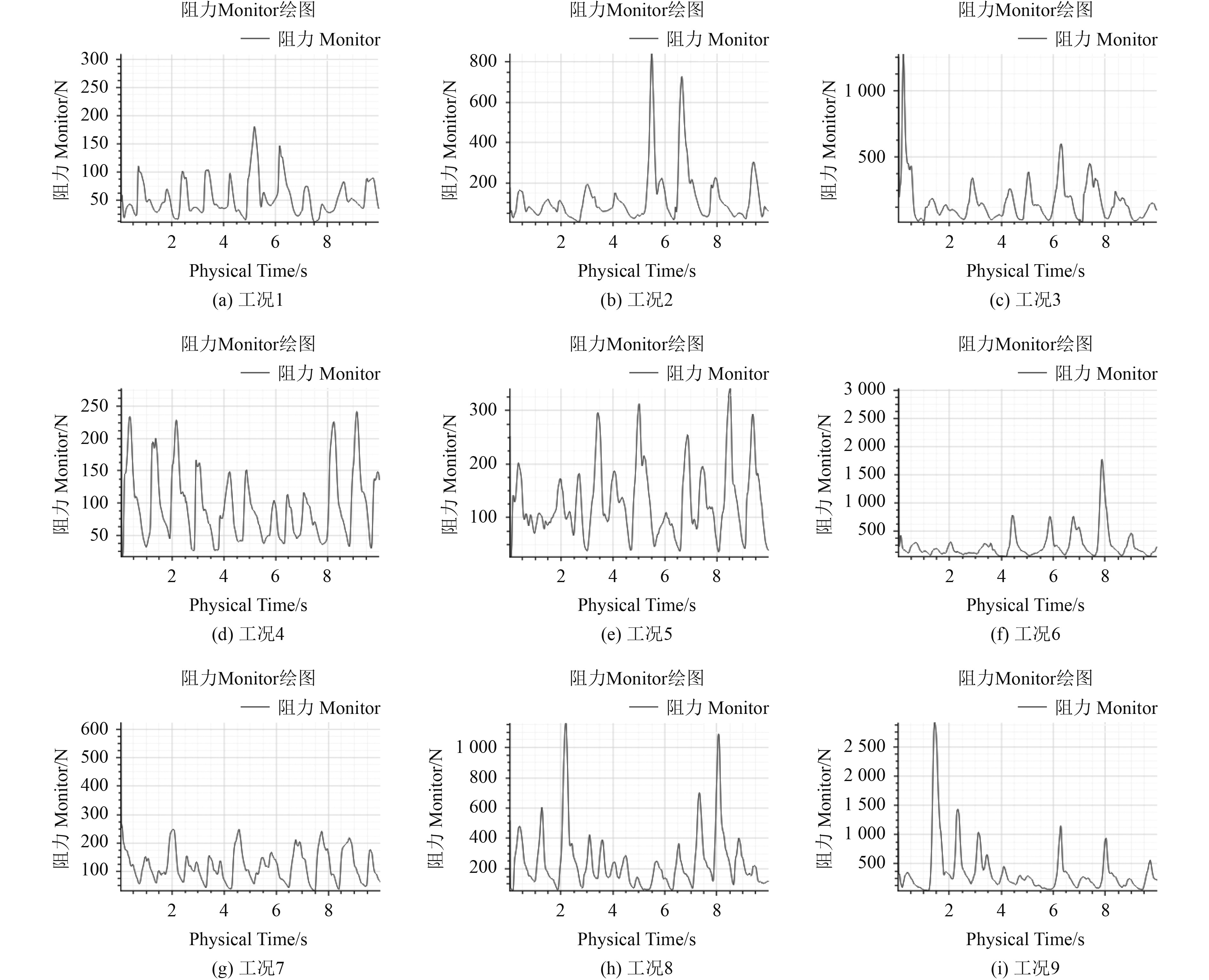
如图10和图11所示，无人艇航行速度一定的情况下，航行阻力随着有效波高递增。无人艇以5 kn速度航行，当有效波高从0.5 m变为1 m时，航行平均阻力增大200.28%；当有效波高达到1 m后，随着波高的增加，航行阻力增大15.14%。当航速为8 kn，有效波高从0.5 m增大为1 m时，航行阻力增加36.23%；有效波高从1 m增大为1.5 m时，增加99.85%。当航速为11 kn，有效波高从0.5 m增加到1 m时，平均阻力增加94.73%；有效波高从1 m增长到1.5 m时，平均阻力增加55.86%。

当有效波高为0.5 m时，航行平均阻力随航速的增大而增大。航速由5 kn增大到8 kn时，容积傅汝德数 $ {F_{r\nabla }} $ 由0.42增长至0.63，在有效波高为1 m和1.5 m的工况下，平均阻力下降。当航速增大到11 kn时， $ {F_{r\nabla }} $ = 0.84，平均阻力大幅度的增加。说明当有效波高达到1 m以上时，无人艇在低速航行中摩擦阻力占主要成分。随着航速增大，艇体有所上抬，飞溅阻力增加故而平均阻力增大。以能耗最优为约束条件的无人艇运动规划需根据航行海域波高情况选择合适的航行速度，也可选择波高较小的区域航行以减小航行阻力进而达到节约航行能耗的目的。因此在浪高较大时应选择8 kn航速可以使能耗降至最低。

4 结　语

海道测量无人艇平台的航行稳定性和能耗是考察其性能的重要指标，具有航行状态平稳、低能耗特性的无人艇可较好完成海洋测绘的工作，为搭载的设备提供良好的作业平台。本文对一种小尺度双体无人艇进行数值模拟计算，预报其在不规则波中的航行状态，得到如下结论：

1）该结构无人艇具有较好的航行稳定性和穿浪性，可在较高海况下平稳作业，为测绘工作提供良好的作业平台。

2）无人艇在有效波高为0.5 m的海况中航行，航速为5 kn时耗能最低；在有效波高1 m和1.5 m的海况中航行，航速为8 kn时耗能最低；有效波高1.5 m时，航速11 kn时无人艇耗能最高。

通过研究可以看到该种充气浮筒式的无人艇具有良好的水动力性能，可完成水文要素测量的工作。以上结论可为无人艇作业水域的选择和航行路线规划提供指导，并用于进一步提高无人艇航行稳定性和续航力的研究。