2. 船舶振动噪声重点实验室,湖北 武汉 430033;
3. 海军工程大学 舰船与海洋学院,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China;
3. College of Ship and Ocean, Naval University of Engineering, Wuhan 430033, China
在浮筏结构变形测量中,传统方法主要依靠位移传感器进行测量,然而,浮筏隔振装置工作条件多样,结构复杂,位移传感器布置困难,很多关键地方不能布置位移传感器,将其应用于弹性较大的大型浮筏时,往往导致变形监测不全面[1-3]。光纤光栅传感器,布置方法简单,体积小,精度高,越来越广泛应用于结构变形监测领域[4]。理论上讲,越多的测点,其获取的结构信息越全面,越能判别筏架姿态变化,但由于实际因素的影响,在具体测试中都应用尽可能少的测点得到尽可能多的结构变形信息[5]。因此,本文目的是实现利用有限测量的应变信息,重构结构在任意静态载荷下的位移。
基于应变数据的结构感知方法有很多种,目前广泛应用于各种结构变形重构有模态法,Ko位移法,逆有限元法和曲率重构法等[6]。Li等[7]介绍了基于模态法的结构形状重建理论,并对传感器位置和数量进行了布局优化,通过实验验证了重构位移的准确性。袁慎芳等[8]利用Ko位移理论对翼梁结构表面进行重构,并通过简单悬臂梁结果验证了Ko位移理论的有效性,但其理论是建立在经典梁方程的基础上,应用范围小,受测量误差影响较大。Mingyao Liu[9]提出一种基于逆有限元法的龙门机床结构变形重构方法,通过有限元分析对龙门结构单元进行划分得到形状函数,解决了传统有限元分析方法主要针对一些简单梁结构的缺陷,但该方法构造复杂结构的形函数困难。Zhang等[10]介绍了一种基于正交应变数据的空间曲面形状重构算法,通过曲率曲面转换方法重构。试验表明,该方法对纯弯曲变形,扭转变形和低频动态振动形状具有良好的重构性能,但该方法会累加重构误差,稳定性差。
当前国内外对桥梁,悬臂梁,平板等约束边界简单的结构研究较多,对复杂约束边界条件如两边为多弹性支撑的板状结构研究较少。本文以浮筏筏架为研究对象,利用光纤光栅测量系统获取结构表面应变信息,通过建立应变-位移转换方程,重构筏架位移曲面,达到准确监测筏架结构位移的目的。
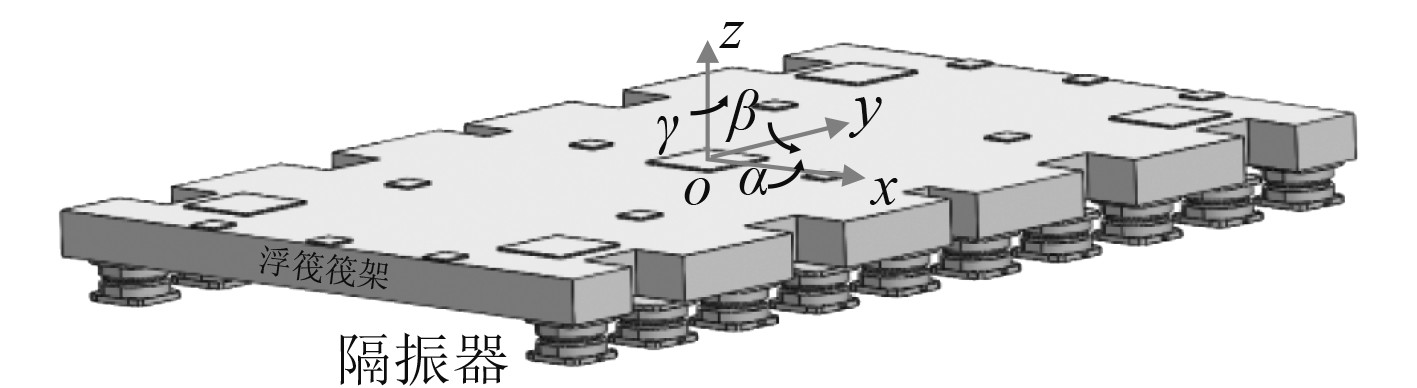
1 结构建模浮筏隔振装置主要由隔振器和筏架组成,如图1所示。
|
图 1 浮筏气囊隔振系统示意图 Fig. 1 The sketch of floating raft air spring isolation device |
作为本文主要研究对象的筏架结构外壳主要由结构钢构成,其下由气囊隔振器支撑,通过控制气囊充放气调整筏架姿态,筏架尺寸为10 555 mm×6500×437 mm,采用壳单元建模,在筏架下表面布置20个气囊隔振器,气囊隔振器简化为具有三向刚度的弹簧阻尼单元,模拟均匀承载,同时在筏架上表面施加面载荷模拟系统载荷变化。材料属性设置为钢材,密度为7850 kg/m3。该装置设备及筏架总重量为43.8 t,满载载荷为312 t,半载为249.5 t,空载187 t,在Workbench中将系统载荷简化为力,设置浮筏实际工作中满载工况(312 t)时需输入的力2 627 380 N。重力加速度g取9.8 m/s2,方向为-Z。
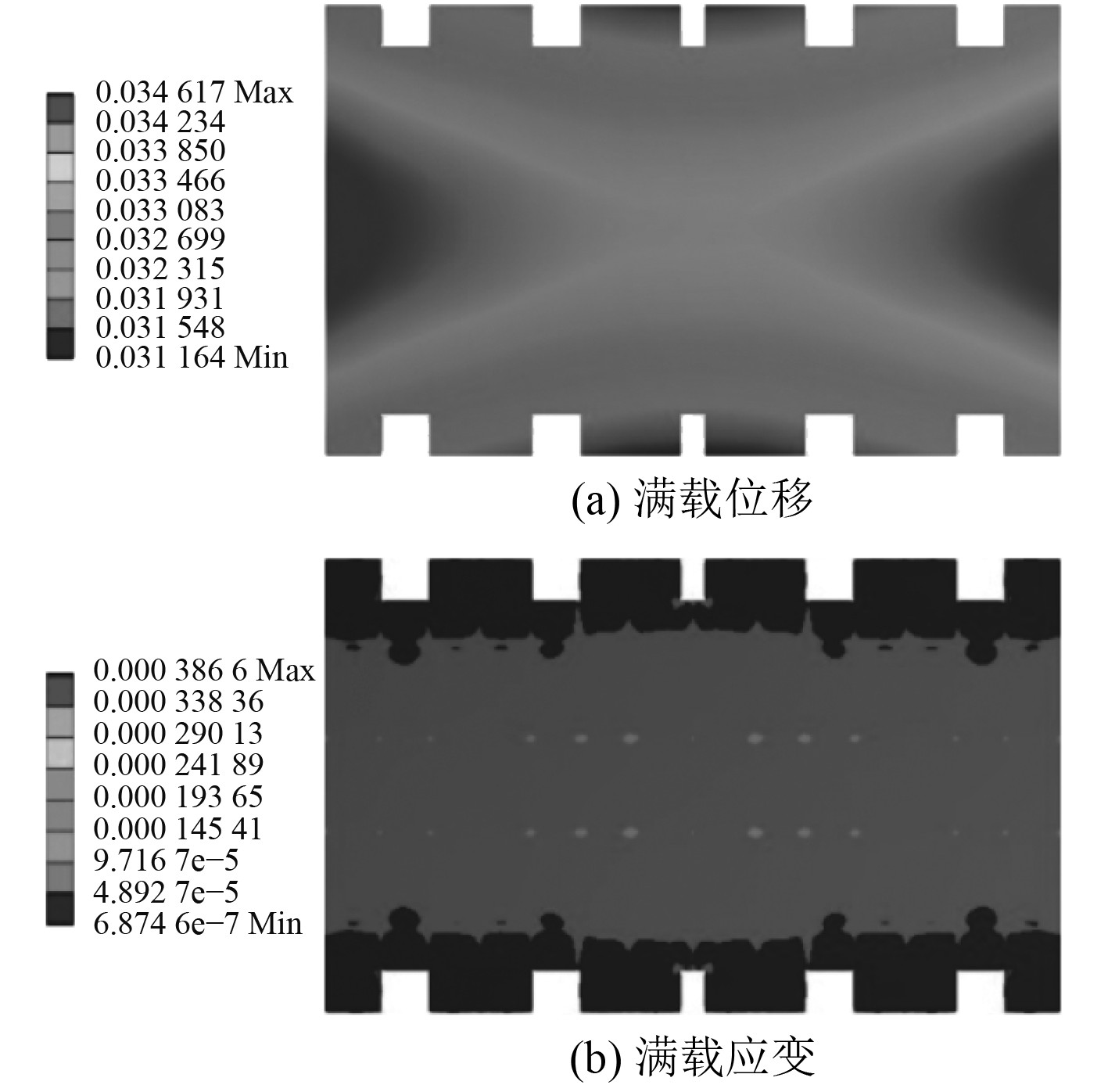
首先对筏架进行静力学分析,得到不同载荷工况下结构的变形特征,实现传感器初步布局。图2为筏架在满载工况下的位移云图与应变云图,从中可以看出筏架变形主要以Z方向为主,应变分布均匀,从中间依此向两舷减小。因此初步选取传感器布局为均匀分布。
|
图 2 浮筏结构有限元分析图 Fig. 2 Floating raft finite element analysis |
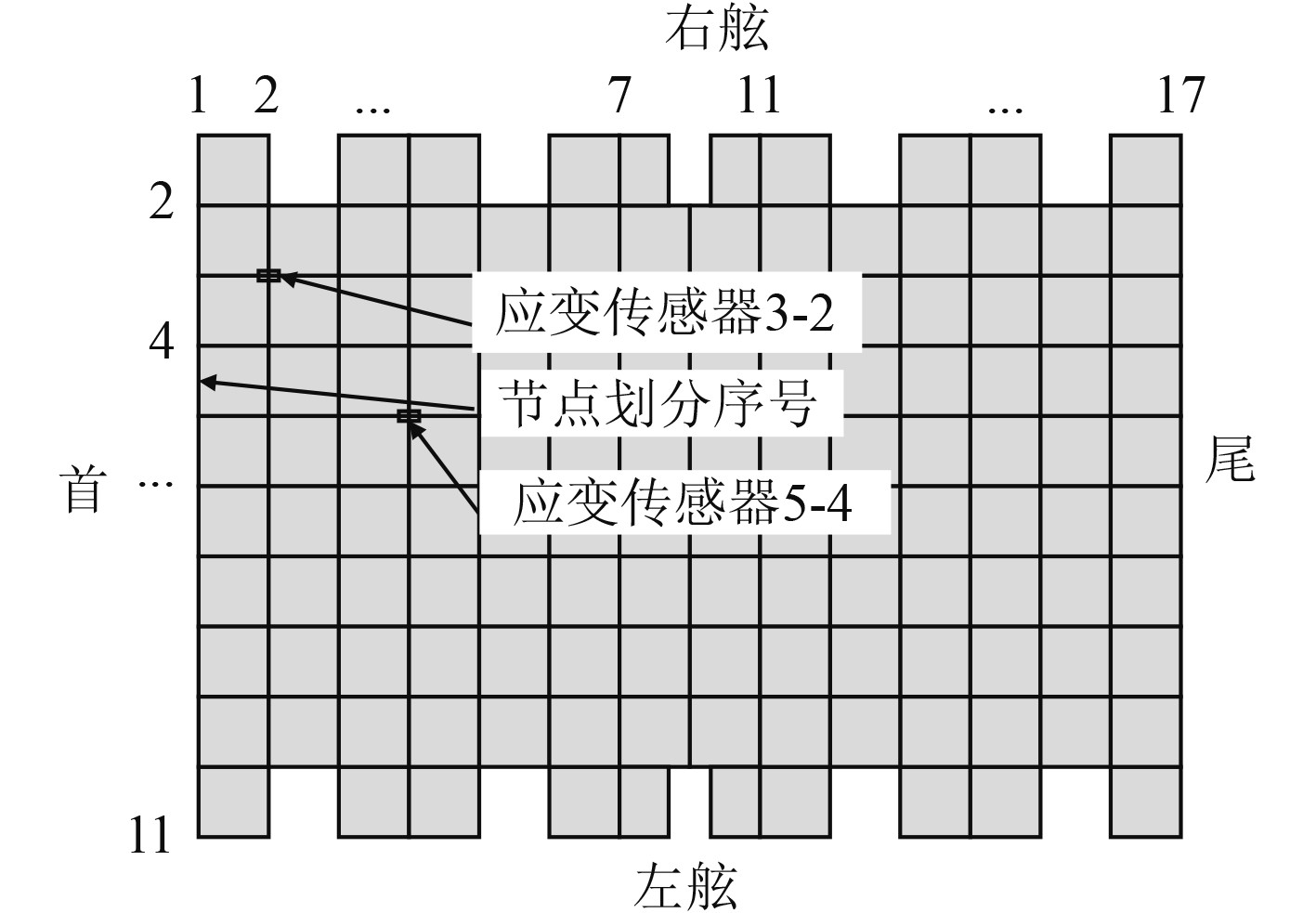
综合以上分析,为了提取筏架表面应变数据,将筏架按照均匀分为132个单元,筏架结构空缺处不设置节点,有限元计算结果可以作为参考位移场,并提供重构算法所需的模拟应变数据,依此由首到尾从右舷到左舷编号1-1,1-2…,如图3所示,从而实现结构全局变形监测。
|
图 3 光纤光栅传感器网络划分示意图 Fig. 3 FBG sensor metwork divided schematic |
由结构动力学知识可知,浮筏隔振系统可以描述为一个外载荷作用下的有阻尼多自由度系统,其动力学方程可以表示为:
| $ M\ddot{\delta} + C\dot{\delta} + K\delta = Q。$ | (1) |
式中:
设
| $ K\varPhi - {\omega ^2}M\varPhi = 0 。$ | (2) |
在获取结构的固有频率
| $ \delta (t) = \sum\limits_{i = 1}^n {{\varPhi _i}} {q_i} = \varPhi q 。$ | (3) |
式中:
将式(3)代入式(1),可得耦合的动力学方程为:
| $ M\varPhi \ddot q + C\varPhi \dot q + K\varPhi q = Q,$ | (4) |
同时由应变和位移基本转换关系[11]可知:
| $ \left\{ {\boldsymbol{\delta}} \right\} = \left[ {{{\boldsymbol{\phi _d}}}} \right]\left\{ {\boldsymbol{q}} \right\},$ | (5) |
| $ \left\{ {\boldsymbol{\varepsilon }} \right\} = \left[ {{{\boldsymbol{\phi _s}}}} \right]\left\{ {\boldsymbol{q }}\right\} 。$ | (6) |
其中:
由式(5)和式(6)可以推出:
| $ \left\{ {\boldsymbol{\delta}} \right\} = \left[ {{{{\boldsymbol{\phi}} _{\boldsymbol{d}}}}} \right]{\left[ {{{\boldsymbol{\phi _s}}}} \right]^{ - 1}}\left\{ {\boldsymbol{\varepsilon }} \right\}。$ | (7) |
式中
| $ {\left[ {{{\boldsymbol{\phi _s}}}} \right]^{\rm{T}}}\left\{ {\boldsymbol{\varepsilon }} \right\} = {\left[ {{{\boldsymbol{\phi _s}}}} \right]^{\rm{T}}}\left[ {{{\boldsymbol{\phi _s}}}} \right]\left\{ {\boldsymbol{q}} \right\},$ | (8) |
| $ \left\{ {\boldsymbol{q}} \right\} = {\left[ {{{\left[ {{{\boldsymbol{\phi _s}}}} \right]}^{\rm{T}}}\left[ {{{\boldsymbol{\phi _s}}}} \right]} \right]^{ - 1}}{\left[ {{{\boldsymbol{\phi _s}}}} \right]^{\rm{T}}}\left\{ {\boldsymbol{\varepsilon}} \right\},$ | (9) |
将(9)代入式(5)可得:
| $ \left\{{\boldsymbol{ \delta}} \right\} = \left[ {{{\boldsymbol{\phi _d}}}} \right]{\left[ {{{\left[ {{{\boldsymbol{\phi _s}}}} \right]}^{\rm{T}}}\left[ {{{\boldsymbol{\phi _s}}}} \right]} \right]^{ - 1}}{\left[ {{{\boldsymbol{\phi _s}}}} \right]^{\rm{T}}}\left\{ {\boldsymbol{\varepsilon }} \right\},$ | (10) |
设
| $ {\left\{ {\boldsymbol{\delta}} \right\}_{N \times 1}} = {\left[ {\boldsymbol{T}} \right]_{N \times M}}{\left\{{\boldsymbol{ \varepsilon}} \right\}_{M \times 1}},$ | (11) |
| $ {\left\{ {\boldsymbol{T}} \right\}_{N \times M}} = {\left[ {{{\boldsymbol{\phi _d}}}} \right]_{N \times n}}{\left[ {{{\left[ {{{\boldsymbol{\phi _s}}}} \right]}_{n \times M}}^{\rm{T}}{{\left[ {{{\boldsymbol{\phi _s}}}} \right]}_{M \times n}}} \right]^{ - 1}}{\left[ {{{\boldsymbol{\phi _s}}}} \right]^{\rm{T}}}_{n \times M} 。$ | (12) |
其中,
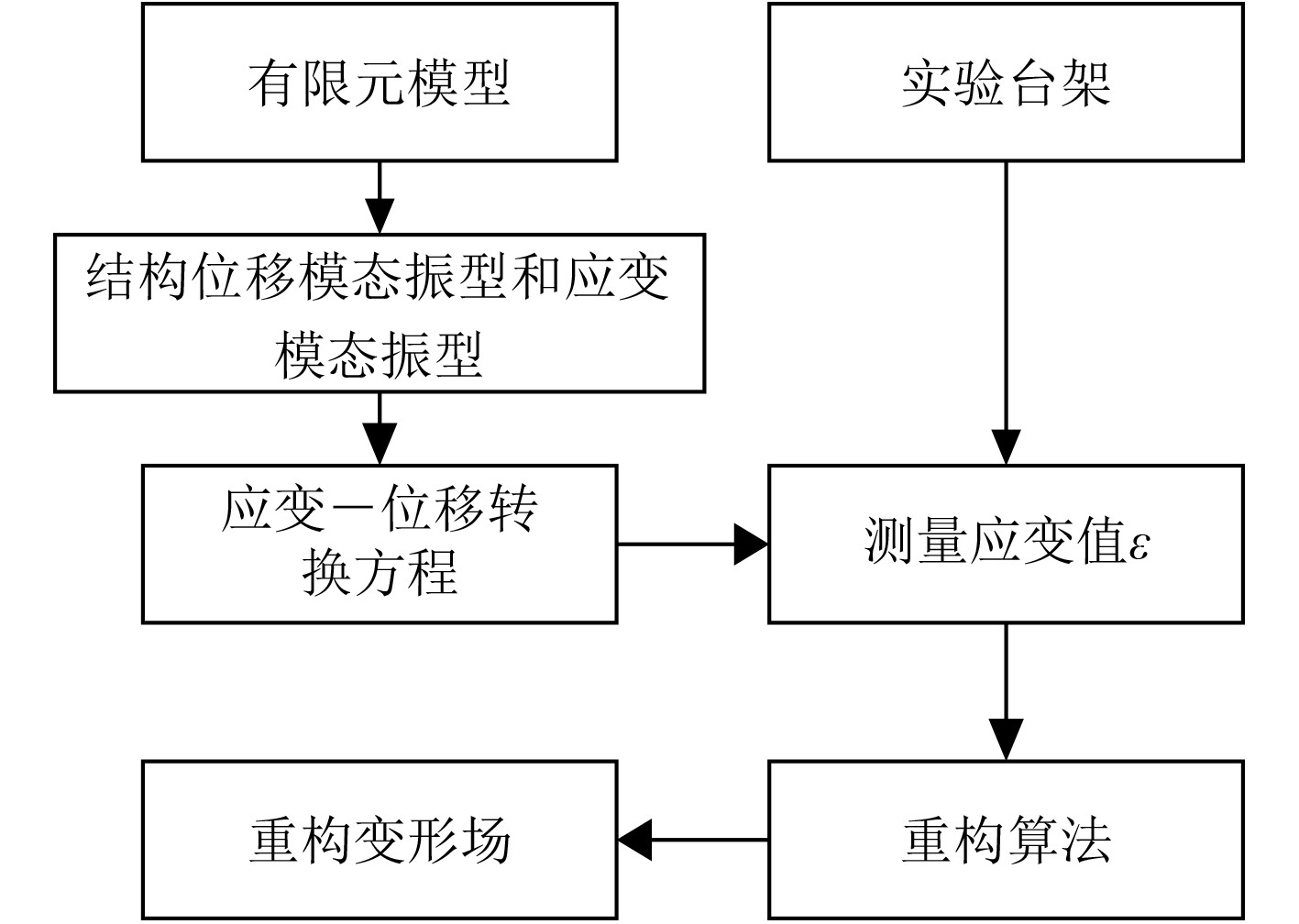
综上所述,基于模态法的筏架结构形状感知流程图如图4所示。首先基于有限元模型获取结构位移模态振型
|
图 4 基于模态法的筏架结构形状重构流程 Fig. 4 Flow chart of shape reconstruction of raft structure based on modal method |
由上述结构建模可知,本文筏架运动认为是准静态过程,筏架静态变形主要以弯曲和扭转变形为主,基于模态法的结构变形重构方法,传感器的数量至少等于模态法的模态阶数的数量[12]。这里分析选取最小传感器数量,即与模态法的模态阶数数量一致,因此需要研究截断模态选取策略。为了减小传感器位置和方向对本文方法的干扰,将传感器位置点正交化布置,各测点位置均布。结合筏架有限元静力学分析可知,该结构柔性较强。模态前6阶以刚体模态为主,因此模态分别选取前9阶,前12阶,前15阶,前17阶模态进行分析,讨论截断模态选取原则,测点布置及各模态下重构位移如图5所示。
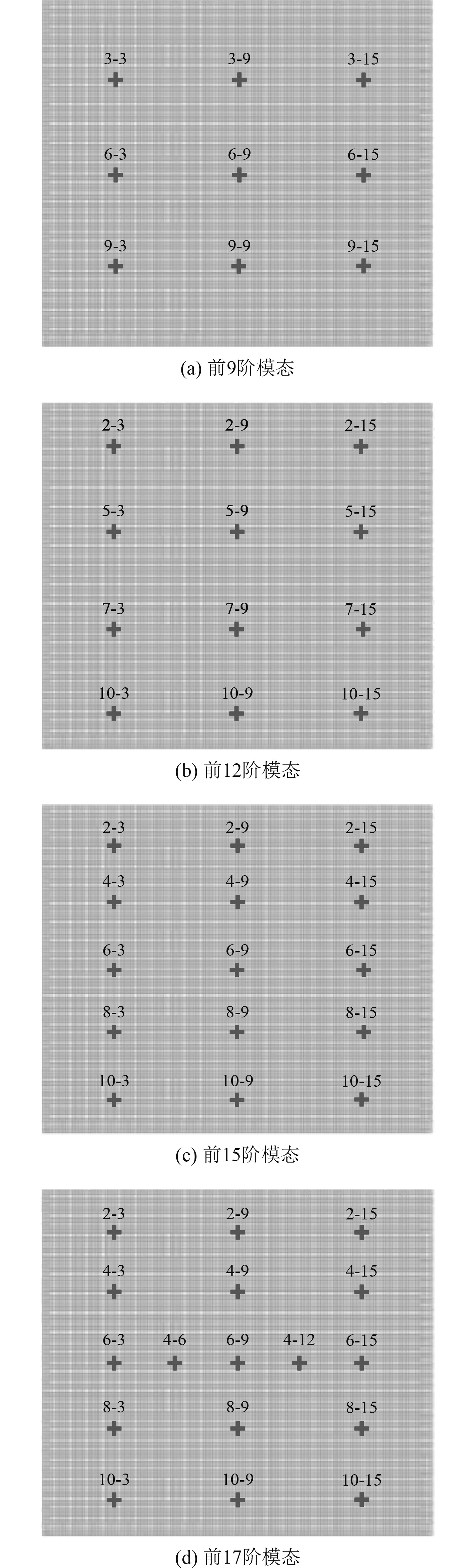
|
图 5 各截断模态应变传感器分布示意图 Fig. 5 Schematic diagram of the distribution of strain sensors in each truncated mode |
对于二维情况,定义误差e作为评判各节点的重构位移与参考位移之间的优劣,如下式:
| $ e = \dfrac{{\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\left| {{f_i} - {y_i}} \right|} }}{{\max (\left| {y\max } \right|)}} \times 100 \text%。$ | (13) |
式中:
图6给出了不同截断模态下筏架重构位移图。图6(a)为筏架在载荷施加2 627 380N时的参考位移曲面图,可以看出截断模态到前15阶时,筏架参考位移曲面与重构曲面形态基本一致。截断模态为9阶及12阶时,筏架重构曲面结果误差e分别为3.81%和3.78%,两者误差相差不大。截断模态到15阶和17阶时,误差e为2.01%和1.98%,截断模态数量增多,误差e减小但相差不大,这可能是这几阶高阶模态包含的总体变形信息较筏架整体变形较少,对结构位移重构曲面影响不大。当模态超过12阶时,误差由3.78%减小为2.01%,误差减小了46.8%,说明后几阶高阶模态对结构位移曲面重构影响较大,当截断模态增大到17阶时,误差e变化不大,这可能是后续高阶模态对结构曲面重构的贡献较小。前9阶截断模态到前17阶截断模态的误差e均小于4%,重构精度较高。
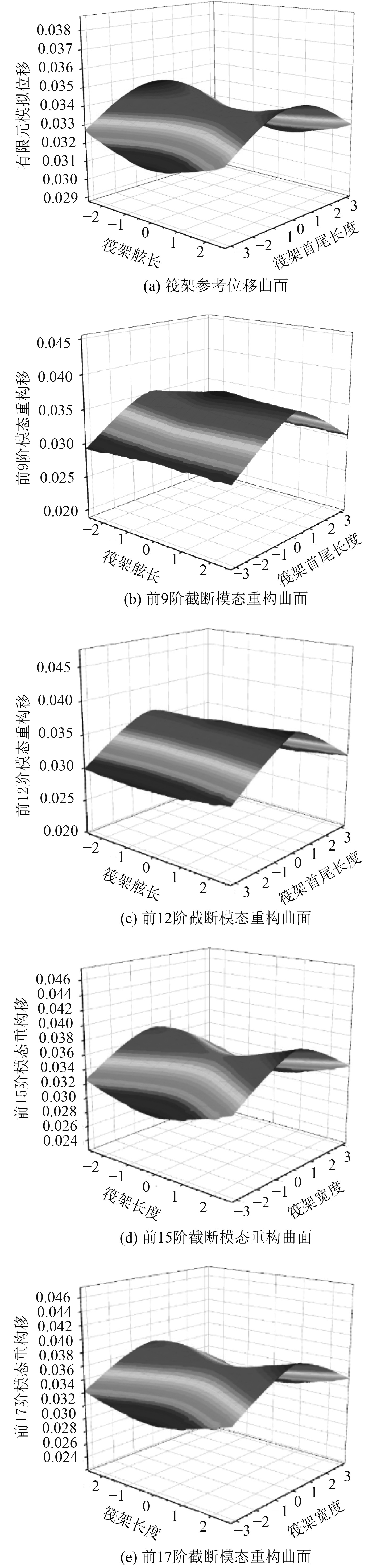
|
图 6 筏架重构曲面图 Fig. 6 Raft reconstruction surface |
以上重构结果从整体上给出了重构精度的好坏,但很难看出重构曲面的具体细节,因此,可以沿筏架不同部位截取等高线剖图,同时采用参考有限元进行归一化,如图7所示。
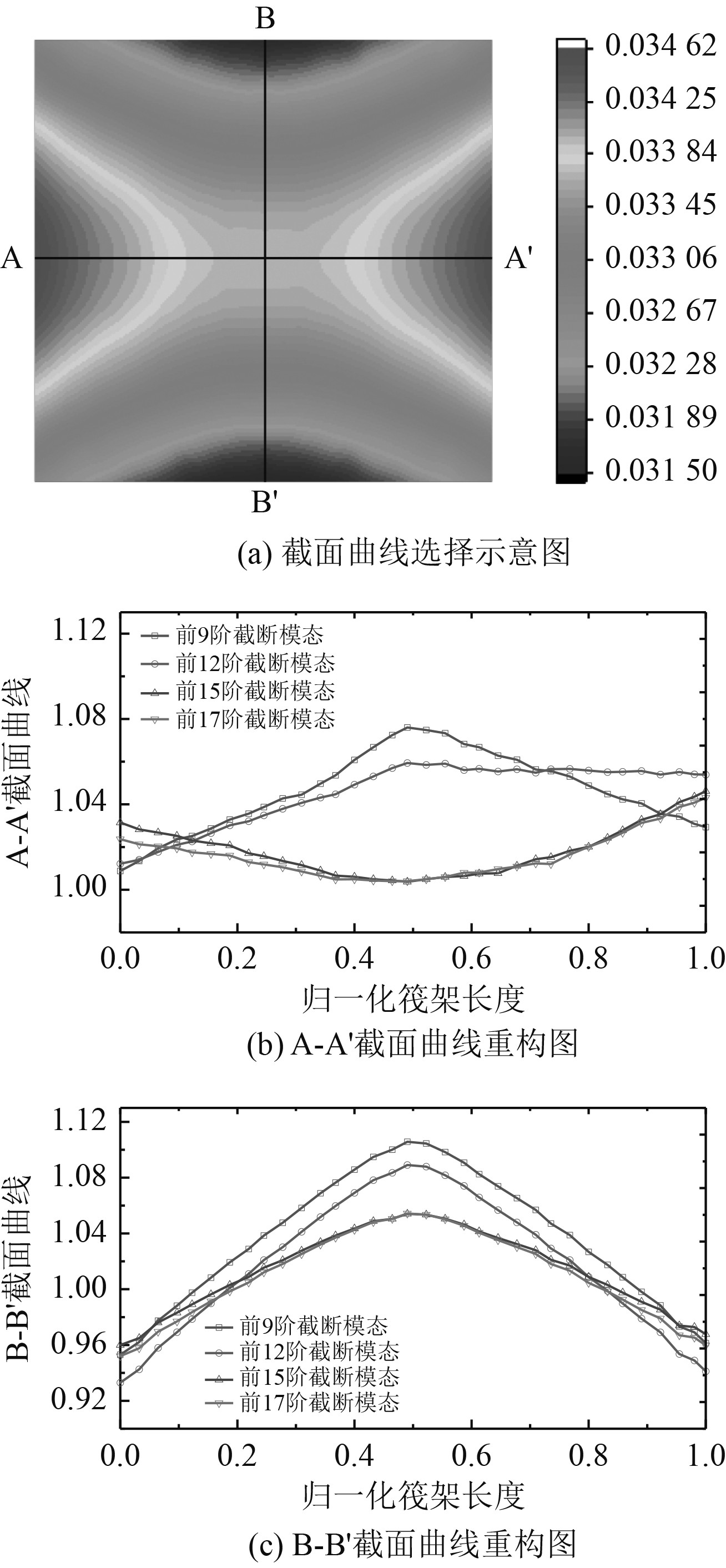
|
图 7 截面曲线选择及重构图 Fig. 7 Schematic diagram of cross-section surface selection and reconstruction curve diagram |
图7(a)为筏架变形等高线图,筏架在中间剖面处的位移变化较大,因此选择截面A-A'与B-B'进行分析。将各阶截取模态重构的筏架曲面沿A-A'与B-B'截面与有限元参考截面比较,如图7(b)和图7(c)所示。将参考截面挠度作为标准进行归一化处理,可以看出在A-A'截面处前9阶截断模态重构曲面的截面曲线最大误差为7.4%,最小误差为1.8%;前12阶最大误差为5.9%,最小误差为1.2%;前15阶最大误差为4.6%,最小误差为0.37%;前17阶最大误差为4.3%,最小误差为0.40%。前9阶截断模态和前12阶截断模态的截面曲线最大误差均发生在中间位置,最小误差均发生在曲线两侧,而对于前15阶截断模态和前17阶截断模态截面曲线而言,其最大误差发生在曲线两侧,最小误差发生在中间部位。
同理,对于B-B'截面,前9阶截断模态重构曲面的截面曲线最大误差为10.5%;前12阶最大误差为8.9%;前15阶最大误差为5.4%;前17阶最大误差为5.2%,各阶截面曲线最小误差均接近0,且最大误差均发生在曲线中间位置。
综上所述,A-A'截面曲线在截断模态较少时在筏架的外边界处更精确,截断模态较多时在曲线中点处误差较小;B-B'截面曲线则在靠近筏架的外边界处更精确,在曲线中点处误差较大,这可能是因为应变传感器布局沿截面的密集程度有关(见图5)。对截面A-A'而言,从传感器布局图5(a)和图5(b)可以推测出,沿截面处均匀布置应变传感器与沿截面两侧均布传感器对截面曲线重构的影响不大,分析传感器布局图5(a)~图5(c)可知,沿截面处及截面两侧均匀布置应变传感器时重构效果要好于传感器分别沿截面处均匀布置和沿截面两侧均布传感器;分析传感器布局图5(c)和图5(d)可知,同一截面均匀布置传感器时,布置一定数量后,增加传感器数量对截断曲线重构效果影响不大。对截面曲线B-B'来说,分析图5(a)~图5(d)可知,同一截面均匀布置传感器时,随传感器数量增加,截面曲线重构效果增强。因此,若想得到某个节点精确位移,必须在该点位置处多布置应变传感器,准确重构该节点处位移。
4 结 语本文针对弹性支撑浮筏结构变形监测问题,利用结构测点应变信息,通过有限元模型得到筏架的位移模态矩阵和应变模态矩阵,与相应的模态坐标一起推导了应变-位移转换方程,建立了基于模态法的筏架变形监测方法。在仿真中,对测点布局及截断模态选取测量进行研究,得到了各截断模态重构曲面,并进行误差分析。结果表明,前15阶截断模态形状可以有效重构出筏架复杂变形。对于前9阶结果,虽然部分截面点误差较大为10.5%,但总误差小于4%,在实际工程中依旧可以接受,因此本文方法是在有限测点及无法直接测量位移条件下重构结构位移的有效方法,方便快捷,在浮筏变形监测领域中具有很好的发展前景。
| [1] |
吕志强, 施 亮, 赵应龙. 气囊浮筏隔振装置姿态控制问题[J]. 噪声与振动控制, 2013(1): 40-44. LV Zhi-qiang, SHI Liang, ZHAO Ying-long. Attitude control of air spring raft isolation system[J]. Noise and Vibration Control, 2013(1): 40-44. |
| [2] |
秦文政, 施亮. 浮筏气囊隔振系统弹性变形控制研究[J]. 舰船科学技术, 2020, 42(17): 67-70. QIN Wen-zheng, SHI Liang. Research on elastic deformation control of air spring raft isolation system[J]. Ship Science and Technology, 2020, 42(17): 67-70. DOI:10.3404/j.issn.1672-7649.2020.09.012 |
| [3] |
ZHANG Yang, LIU Peng, ZHAO Xue-feng. Structural displacement monitoring based on mask regions with convolutional neural network[J]. Construction and Building Materials, 2020.
|
| [4] |
朱晓锦, 陆美玉, 樊红朝, 等. 光纤光栅机敏结构振动形态感知与重构试验研究[J]. 仪器仪表学报, 2009, 30(1): 65-70. DOI:10.19650/j.cnki.cjsi.2009.01.013 |
| [5] |
HAO Xu, et al. Reconstruction of full-field complex deformed shapes of thin-walled special-section beam structures based on in situ strain measurement[J]. Advances in Structural Engineering, 2020, 23(15): 3335-3350. DOI:10.1177/1369433220937156 |
| [6] |
冯荻. 基于光纤光栅应变传感的结构变形重构技术研究[D]. 大连: 大连理工大学, 2020.
|
| [7] |
LI Li, ZHONG Ben-shan, LI Wu-qian, et al. Structural shape reconstruction of fiber Bragg grating flexible plate based on strain modes using finite element method[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(4).
|
| [8] |
袁慎芳, 闫美佳, 张巾巾, 等. 一种适用于梁式机翼的变形重构方法[J]. 南京航空航天大学学报, 2014, 46(6): 825-830. DOI:10.3969/j.issn.1005-2615.2014.06.001 |
| [9] |
LIU Ming-yao, ZHANG Xiong, SONG Han, et al. Inverse finite element method for reconstruction of deformation in the gantry structure of heavy-duty machine tool using FBG sensors[J]. Sensors, 2018, 18(7).
|
| [10] |
ZHANG He-sheng, ZHU Xiao-jin, GAO Zhi-yuan, et al. Fiber bragg grating plate structure shape reconstruction algorithm based on orthogonal curve net[J]. Journal of Intelligent Material Systems and Structures, 2016, 27(17).
|
| [11] |
杨坤, 李强. 基于模态转换算法的结构变形监测的关键技术研究[J]. 科技信息, 2011(24): 726+728. DOI:10.3969/j.issn.1001-9960.2011.24.643 |
| [12] |
BANG Hyung-Joon, KIM Hong-Il, LEE Kang-Su. Measurement of strain and bending deflection of a wind turbine tower using arrayed FBG sensors[J]. International Journal of Precision Engineering and Manufacturing, 2012, 13(12).
|
 2022, Vol. 44
2022, Vol. 44
