2. 武汉第二船舶设计研究所,湖北 武汉 430205
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
推进轴系是船舶尾部重量最大、长度最长的旋转设备,推进器及主轴自身的各种激励作用下引起的轴系振动通过轴承及基座传递至尾部船体,并传递至水中形成辐射噪声。推进轴系尾轴承是推进器激励力经轴系向船体振动传递的主要途径,其主要功能是支撑并保证较长纵向跨度下轴系的安全运行,因而尾轴承是影响推进系统声学性能,甚至船体尾部声辐射的关键设备[1]。
在推进器的悬臂载荷作用下,轴承会出现“边缘负荷”效应,导致轴承载荷分布不均匀,即负荷主要集中在轴承尾部,而首部载荷很小甚至脱空,由此带来的影响包括:1)局部过载加速轴承磨损,降低轴承使用寿命;2)轴承出现偏磨,造成轴承不对中,影响轴系振动;3)局部过载使橡胶轴承容易出现摩擦噪声[2-6]。为了解决该问题,需要通过轴承均载技术来提高轴承内载荷分布的均匀性。通常,以轴系静态校中计算结果为依据,通过倾斜轴承的措施使轴承顺应轴端的弯曲变化,以实现均载[7-9]。但在船舶轴系实际运行过程中,轴系对中状态受船体变形、水温变化、装载量不同及转速变化等动态因素的影响而不断变化,基于静态校中理论倾斜轴承的方法未能考虑动态效应,均载效果有限。因此,如何改善推进器轴承的支撑界面特性,降低边缘负荷对轴承及轴系的不利影响,并在此基础上进行减隔振设计,是提高轴承寿命并优化推进轴系振动研究的重要方向之一。
本文针对水润滑尾轴承承载状态,提出了一种兼具静态均载与动态减振于一体的自适应水润滑轴承结构,可以有效提高尾轴承的静态与动态均载性能,改善尾轴承的边缘效应,使其接触压力沿轴向分布均匀,并通过轴系动力学性能分析其隔振性能。
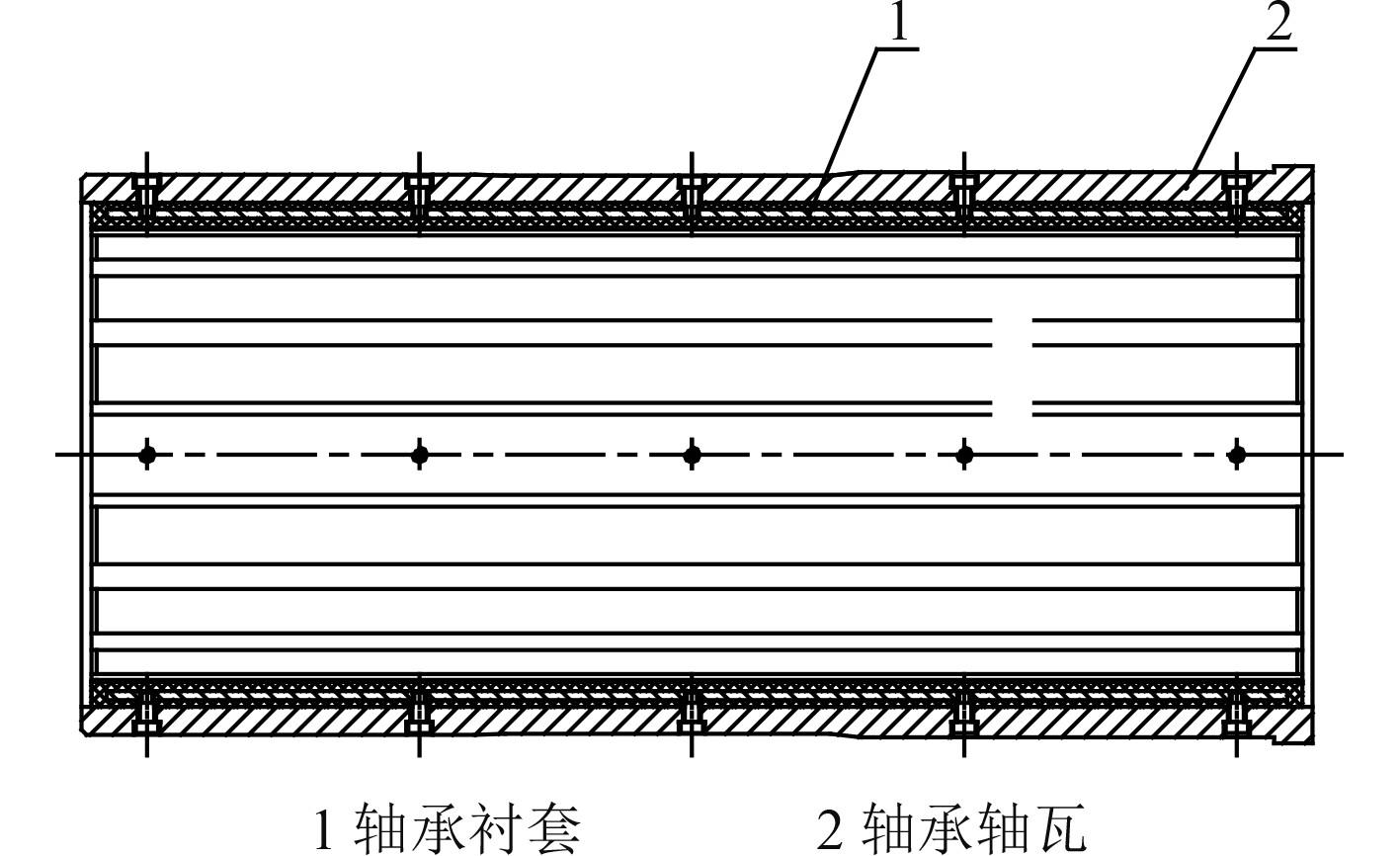
1 新型水润滑尾轴承结构设计 1.1 传统水润滑轴承结构传统的水润滑支承轴承结构如图1所示,由外侧的轴承衬套及内侧的轴承轴瓦构成,内侧轴瓦材料一般由橡胶或高分子材料组成,紧固在衬套内侧起支撑轴系作用,轴承通过外侧衬套安装在船体结构上,轴系运行的横向振动会通过轴瓦-衬套-结构传递到船体上形成辐射噪声。
|
图 1 传统水润滑尾轴承结构 Fig. 1 The conventional structure of water lubricated stern bearing |
在船舶实际航行过程中,螺旋桨产生的推力传递至推进轴系,受航行环境和运行工况影响,轴线在不同运行状态下呈现不同弯曲形式,而目前舰船推荐传统水润滑尾轴承设计长径比大于3,加上尾部螺旋桨的悬臂载荷作用,使得尾轴承内呈现较为明显的偏载现象,即边缘效应,并不能确保尾轴承在不同运行状态下的润滑良好,使得局部润滑状态恶化,甚至发生局部碰摩,加剧尾轴承的磨损(如图2所示)。同时也会加剧尾轴承摩擦振动,产生异常噪声,影响推进轴系运行安全性及隐身性能。
|
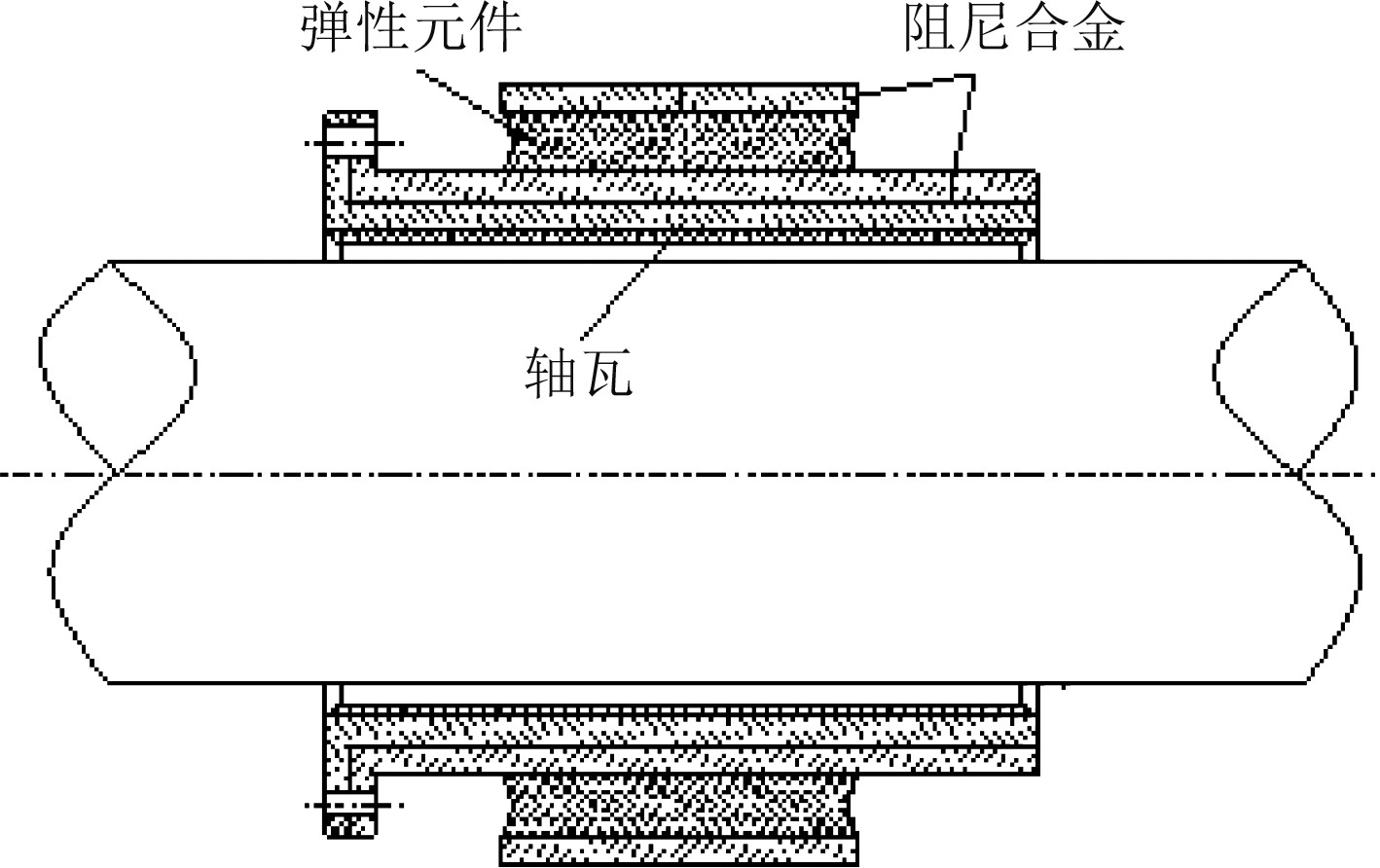
图 2 自适应尾轴承结构 Fig. 2 The structure of adaptive stern bearing |
为了解决上述传统轴承的偏磨问题,需要通过轴承均载技术来提高轴承内载荷分布的均匀性。因而本文根据实船运行需求,设计一种自适应尾轴承。该尾轴承结构主要由轴瓦、弹性元件和阻尼合金3部分构成,如图2所示。弹性元件用于实现尾轴承的静态与动态均载,减少尾轴承的边缘效应,使其接触压力沿轴向分布均匀,从而提高轴承的使用寿命和降低轴承的摩擦激励,阻尼合金用于衰减轴系振动经轴承向基础的振动传递,从而实现振动的传递特性优化。此自适应尾轴承的承载状态可随推进轴系实际轴线挠曲状态变化而变化,最终达到各运行工况下尾轴承均能实现均载,改善轴承润滑性能,减少摩擦,降低振动。
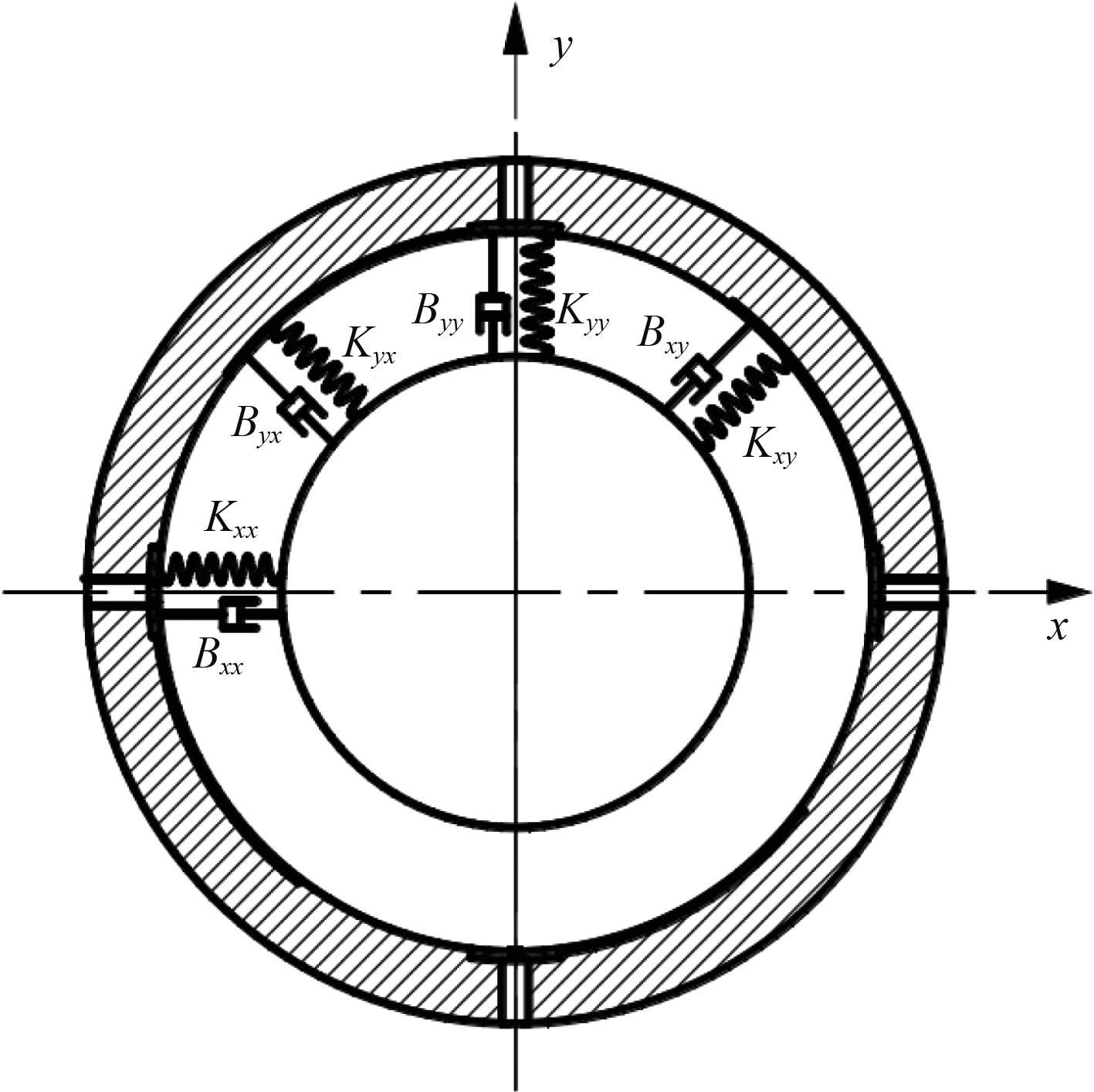
2 考虑润滑的尾轴承动参数计算分析液膜的刚度和阻尼(轴承动参数)是轴承动力学性能的主要参数,也是影响轴系振动特性的重要影响因素。本文将基于微扰动法[10]给出水润滑尾轴承动参数计算方法。基于线性理论建立起来的轴承的动力学模型如图3所示,轴承的刚度系数由K表示,分别由主刚度和交叉刚度 组成,阻尼系数由C表示,分别由主阻尼和交叉阻尼 组成。
|
图 3 液膜动力学模型 Fig. 3 The model of water lubricated bearing |
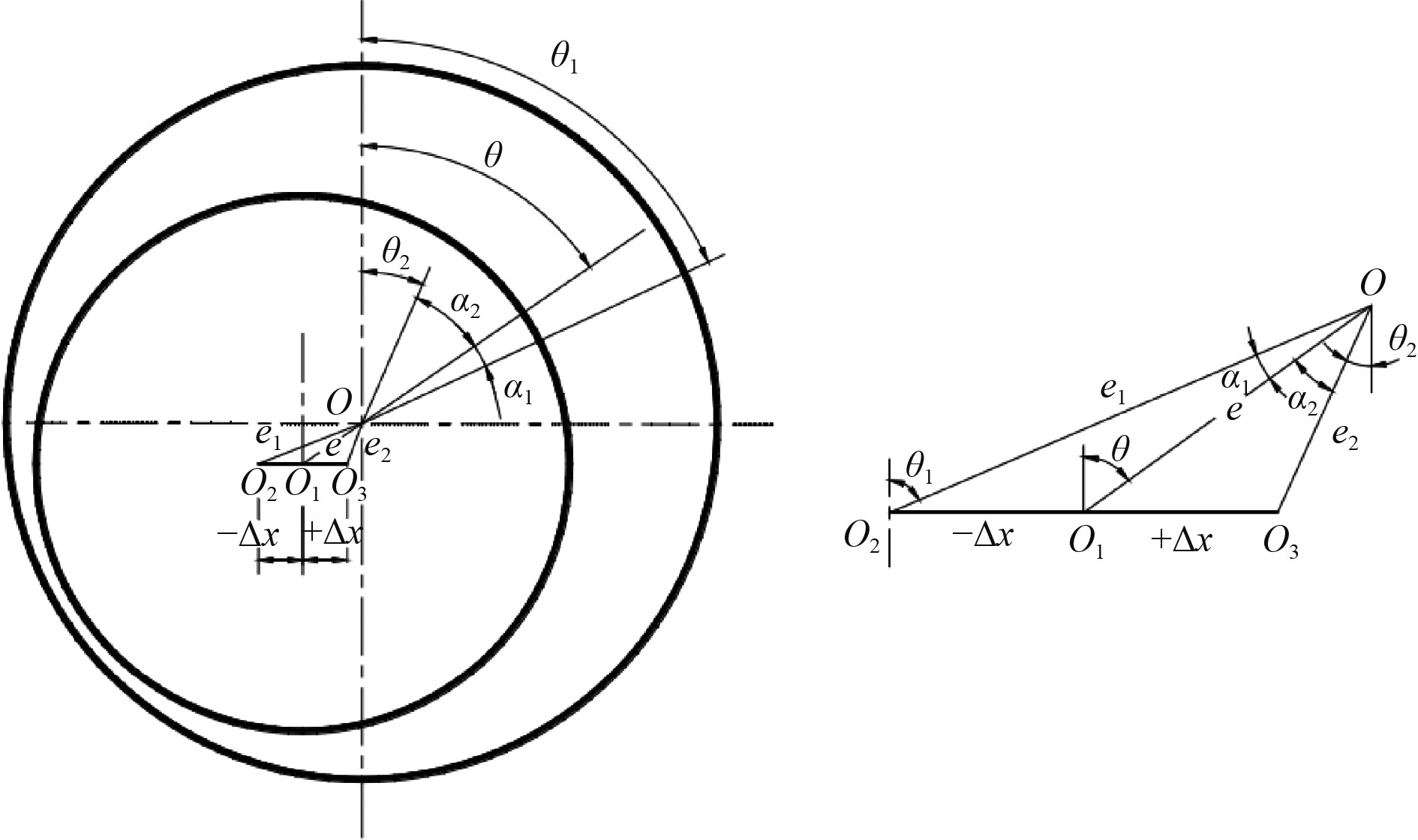
在轴系运行过程中,轴颈在轴承中的相对位置如图4所示。其中O为滑动轴承的中心位置,O1为某运行工况下当主轴处于受力平衡状态是轴径中心位置,θ和e分别表示此时轴径截面相对与轴承中心的偏位角和偏心距。此时当主轴受到微小扰动,产生运动∆x位移,达到新的平衡位置O2点,此时的偏心距和偏位角分别为e1和θ1,此时的液膜力分别为Fx1和Fy1,e1和θ1与e和θ的关系式为:
|
图 4 扰动法示意图 Fig. 4 Schematic diagram of disturbance method |
| $ \left\{ \begin{gathered} {e_1} = \sqrt {{e^2} + {{\left( {\Delta x} \right)}^2} - 2e\Delta x\cos \left( {{{90}^ \circ } + \theta } \right)},\\ \frac{{{e_1}}}{{\sin \left( {{{90}^ \circ } + \theta } \right)}} = \frac{{\Delta x}}{{\sin {\alpha _1}}},\\ {\theta _1} = \theta + {\alpha _1} 。\\ \end{gathered} \right. $ | (1) |
在轴心处于O1时再对主轴施加一个微小扰动,使得新的轴心位置运动∆x处于O3点,此时的轴承液膜力分别为Fx2和Fy2,根据图4所示坐标系,建立此时偏心距与偏位角的关系如下式:
| $ \left\{ \begin{gathered} {e_2} = \sqrt {{e^2} + {{\left( {\Delta x} \right)}^2} - 2e\Delta x\cos \left( {{{90}^ \circ } - \theta } \right)},\\ \frac{{{e_2}}}{{\sin \left( {{{90}^ \circ } - \theta } \right)}} = \frac{{\Delta x}}{{\sin {\alpha _2}}},\\ {\theta _2} = \theta + {\alpha _2}。\\ \end{gathered} \right. $ | (2) |
结合受力和位移变化,液膜刚度Kxx和Kyx计算式为:
| $ \left\{ \begin{gathered} {K_{xx}} = \frac{{{F_{x1}} - {F_{x2}}}}{{2\Delta x}},\\ {K_{yx}} = \frac{{{F_{y1}} - {F_{y2}}}}{{2\Delta x}}。\\ \end{gathered} \right. $ | (3) |
按照微扰动理论,此时在y方向上对主轴施加微小扰动,使得轴心产生∆y的位移分别运动到新的平衡位置O4和O5,则可计算得到Kxy和Kyy。其中Fx3和Fy3,Fx4和Fy4分别表示轴心处于O4和O5时的液膜力分量。
| $ \left\{ \begin{gathered} {K_{x{\text{y}}}} = \frac{{{F_{x3}} - {F_{x4}}}}{{2\Delta y}} ,\\ {K_{yy}} = \frac{{{F_{y3}} - {F_{y4}}}}{{2\Delta y}} 。\\ \end{gathered} \right. $ | (4) |
微扰动法求解轴承动刚度与实际刚度值的误差取决与微小扰动位移∆x和∆y,在编写的分析程序中,为提高计算精度,减小误差,扰动位移与最小液膜厚度间的比值不能大于0.01。
2.2 液膜阻尼计算与液膜刚度求解方式类似,基于微扰动法,分别对轴径施加+
| $ \left\{ \begin{gathered} {C_{xx}} = \frac{{{F_{x5}} - {F_{x6}}}}{{2\Delta \dot x}} ,\\ {C_{yx}} = \frac{{{F_{y5}} - {F_{y6}}}}{{2\Delta x}} 。\\ \end{gathered} \right. $ | (5) |
类似分别对轴径施加+
| $ \left\{ \begin{gathered} {C_{yy}} = \frac{{{F_{y7}} - {F_{y8}}}}{{2\Delta \dot y}},\\ {C_{xy}} = \frac{{{F_{x7}} - {F_{x8}}}}{{2\Delta \dot y}}。\\ \end{gathered} \right. $ | (6) |
同样,为保证计算精度,扰动速度
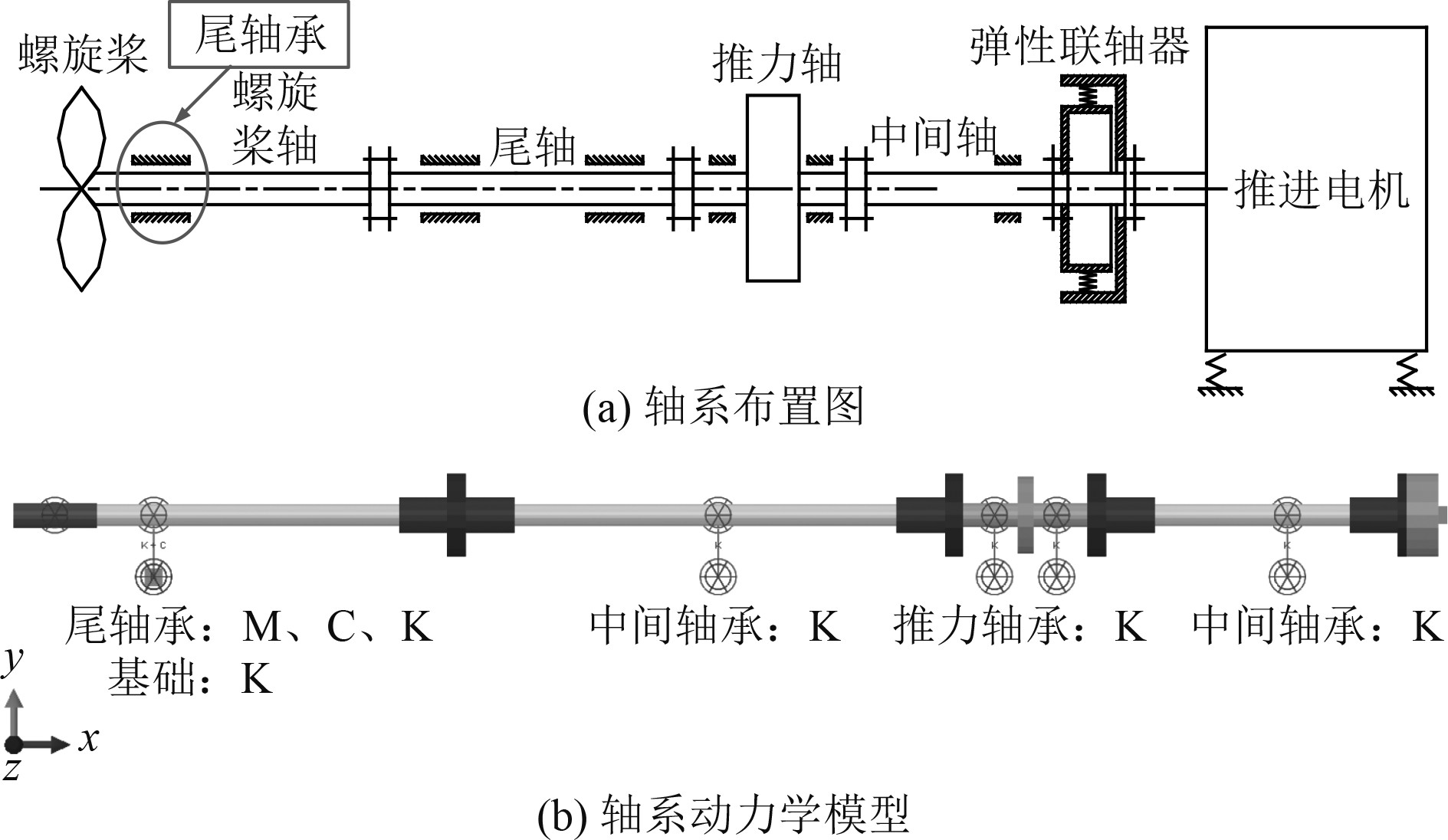
针对如图5所示的轴系振动特性进行计算分析,轴系由推进电机驱动,经由弹性联轴器、中间轴、推力轴、尾轴、螺旋桨轴及轴间连接法兰,将动力传递至螺旋桨,其结构参数如表1所示。其中尾轴承采用自适应结构(见图3),其外层为实测阻尼比为0.03的阻尼合金。
|
图 5 轴系模型 Fig. 5 The EF model of the propulsion shafting |
|
|
表 1 轴系试验台架参数 Tab.1 Parameters of bearing in analysis |
采用文献[11]所建立的挠曲状态下轴承润滑模型对自适应尾轴承和传统轴承的润滑状态进行对比分析。转速为100 r/min时2种轴承的液膜压力分布如图6所示。可知,与传统轴承相比,自适应尾轴承的液膜压力分布更加对称,最大液膜压力由0.059 MPa减小到0.03 MPa,出现的位置也由距中间截面0.25 L的地方移动至轴承轴向中间截面处,对应的最小液膜厚度由20 μm增大至25 μm。结果表明,传统水润滑轴承由于悬臂支承导致轴径倾斜,使得轴承尾端出现局部承载大,产生边缘效应,从而加剧轴承尾部磨损,降低轴承寿命。而自适应尾轴承的边缘效应减弱,轴承润滑状态改善明显,有助于提升轴承使用寿命,降低轴承磨损。

|
图 6 两种轴承的液膜压力分布 Fig. 6 The difference of film pressure in two type bearings |
针对图5所示的轴系台架,基于文献[11]所建立的尾轴承润滑模型,并结合所推导的液膜刚度与阻尼的表达式,建立轴系的动力学模型。各部分材料属性如表2所示。
|
|
表 2 自适应尾轴承材料属性 Tab.2 Material Properties of bearing parts |
首先分析自适应尾轴承的对于轴系回旋振动临界转速的影响,计算结果如表3所示,各阶振型如图7所示。结果表明,自适应轴承对于临界转速的影响主要集中在一阶轴频与叶频次,分别由1406.85 r/min和182.96 r/min降至1346.81 r/min和176.93 r/min,降幅为4.3%和3.3%,对于回旋振动各阶振型的影响相对较小。
|
|
表 3 采用自适应轴承前后轴系回旋振动轴频与叶频临界转速(r/min) Tab.3 Critical speed of axial frequency and blade frequency of cyclotron vibration with adaptive stern bearing |

|
图 7 采用不同轴承结构对轴系回旋振动前3阶振型 Fig. 7 Influence of bearing structure on the first three modes of cyclotron vibration of shafting |
在螺旋桨重心处加载横向单位激励力,分析频率范围为1~100 Hz,提取尾轴承位置处的振动速度响应,用于评价推进器至尾轴承的振动传递特性。
图8为采用不同轴承结构在尾轴承节点的速度响应。可知,尾轴承处的振动响应以1阶和3阶回旋振动固有频率为主,且采用自适应尾轴承之后,1阶固有频率处的响应由0.0056 mm/s下降到0.003 mm/s,降幅为46.43%,即向基础传递的振动能量减小。

|
图 8 采用自适应轴承前后尾轴承速度响应 Fig. 8 Speed response of fore and aft stern bearing with adaptive bearing |
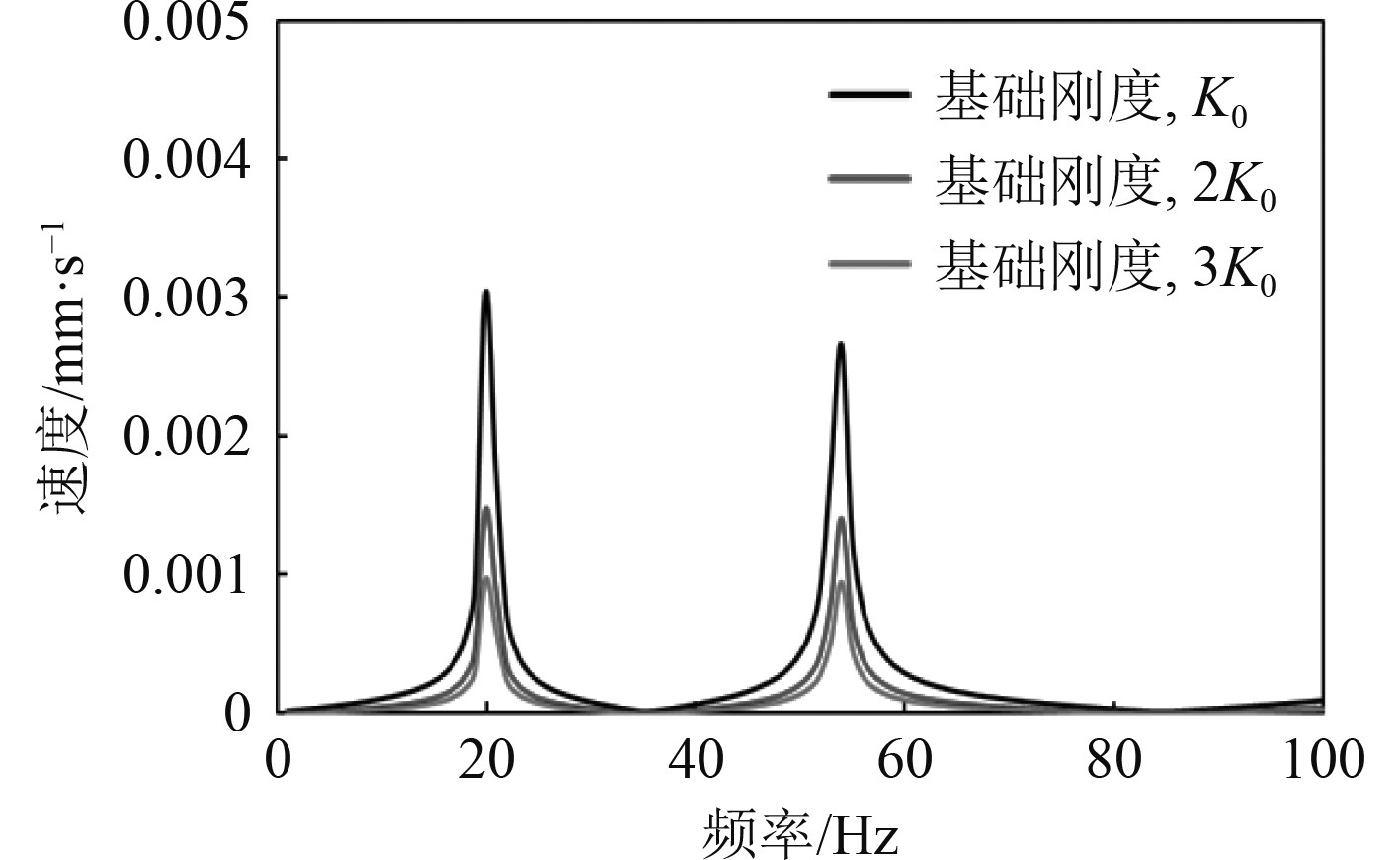
此外,计算结果表明基础刚度也是影响轴承振动响应的关键因素。令基础的原始支撑刚度为K0,分别调整基础刚度至2K0和3K0,不同刚度下的尾轴承速度响应如图9所示。结果表明,随着基础刚度的增加,尾轴承的振动响应逐步降低,20 Hz附近的振动响应降幅依次为51.13%和67.66%。因此,在采用自适应尾轴承的基础上,适度提高船体结构的支撑刚度,可进一步减小轴承振动响应,从而更利于轴承的稳定运行。另外不同的基础刚度几乎没有影响固有频率偏移,主要是因为轴承的刚度要弱于基础刚度,二者串联,综合刚度以轴承刚度为主。
|
图 9 不同基础刚度下的尾轴承速度响应 Fig. 9 Speed response of Stern bearing under different foundation stiffness |
本文以实现水润滑尾轴承动态均载为目标,设计一种具有自适应能力的尾轴承结构,并对自适应尾轴承润滑性能及轴系振动特性进行了理论分析,结果表明:
1)相比于传统水润滑轴承结构,采用自适应结构的尾轴承可随着轴系的倾斜状态而改变轴承偏转角以达到轴承均载,最大液膜压力明显降低,轴承润滑状态改善明显,可有效降低轴承磨损,提升轴承运行寿命;
2)采用自适应尾轴承轴承之后,螺旋桨激励至轴承节点处的振动传递特性得到了优化,1阶固频处的振动响应降幅为46.43%。同时,如适当提高尾轴承处船体结构的支撑刚度,尾轴承振动响应会进一步降低。
| [1] |
CHERTOCK G. Forces on a submarine hull induced by the propeller[R]. David Taylor Model Basin Washington DC Acoustics and Vibration Lab, 1965.
|
| [2] |
姚世卫, 杨俊, 张雪冰, 等. 水润滑橡胶轴承振动噪声激励分析与试验研究[J]. 振动与冲击, 2011, 30(2): 214-216. DOI:10.3969/j.issn.1000-3835.2011.02.043 |
| [3] |
QIN Hong-lin, ZHOU Xin-cong, ZHAO Xin-ze, et al. A new rubber/UHMWPE alloy for water-Lubricated stern bearing[J]. Wear, 2015, 328/329: 257-261. DOI:10.1016/j.wear.2015.02.016 |
| [4] |
DONG Cong-lin, SHI Li-Chun, LI Lyu-zhou, et al. Stick-slip behaviours of water lubrication polymer meterials under low speed conditions[J]. Tribology International, 2017, 103: 55-61. |
| [5] |
ZHANG Zhen-guo, ZHANG Zhi-yi, HUANG Xiu-chang, et al. Stability and transient dynamics induced by nonlinear friction action on bearing-shaft contact interface[J]. Journal of Sound and Vibration, 2014, 333(12): 2608-2630. DOI:10.1016/j.jsv.2014.01.026 |
| [6] |
欧阳武, 程启超, 王磊, 等. 偏载下水润滑尾轴承分布式动力学特性[J]. 交通运输工程学报, 2019, 19(2): 92-100. DOI:10.3969/j.issn.1671-1637.2019.02.009 |
| [7] |
周瑞平. 超大型船舶推进轴系校中理论研究[D]. 武汉: 武汉理工大学, 2005.
|
| [8] |
蒋平, 朱汉华, 严新平, 等. 船体大变形对轴系校中的影响[J]. 船舶工程, 2013(1): 35-38. DOI:10.13788/j.cnki.cbgc.2013.01.011 |
| [9] |
李泽远, 汪骥, 刘玉君. 考虑船体变形的轴系动态校中算法[J]. 船舶工程, 2018, 40(10): 59-63. DOI:10.13788/j.cnki.cbgc.2018.10.059 |
| [10] |
QIU Z. L. A theoretical and experimental study on dynamic characteristics of journal bearings [D]. PhD thesis. University of Wollongong, Wollongong, 1995.
|
| [11] |
王攀. 超高速磨削电主轴液体动静压轴承动力学问题研究[D]. 洛阳: 河南工业大学, 2018.
|
| [12] |
HE Zhen-peng, ZHANG Jun-hong, XIE Wei-song, et al. Misalignment analysis of journal bearing influenced by asymmetric deflection, based on a simple stepped shaft model[J]. Journal of Zhejiang University - Science A (Applied Physics & Engineering). 2012, 13(9): 647-664.
|
 2022, Vol. 44
2022, Vol. 44
