随着减振降噪技术的不断发展,潜艇辐射噪声已经大幅减小。根据有关资料报告,美国潜艇的自噪声已经接近海洋的背景噪声[1-2]。这表明,依靠传统的声学为主的单一反潜手段已经不能满足当前的实际需求。在众多的非声探潜技术中,基于水动力尾迹的遥感探测,以其全天候、全天时对海洋高分辨率成像观测的能力引起越来越多国家的重视[3]。
水动力尾迹主要包括:伯努利“水丘”,内波尾迹、卡尔文尾迹、湍流尾迹等[4-5]。卡尔文尾迹是潜艇航行方向的后方呈现的V型尾迹,其包络在19.5°夹角内,典型的潜艇水下运动对远场水面产生的影响如图1所示。伯努利“水丘”和卡尔文尾迹都与潜艇潜深和航速密切相关,随着航速的降低以及潜深的增加会迅速减小。同时,随着潜深的增加,湍流尾迹也很难在海洋自由表面形成可探测的水动力特征,所以均不适合用作广域的监视对象。

|
图 1 合成孔径雷达检测的尾迹 Fig. 1 Wake detected by SAR |
内波尾迹是潜艇水动力尾迹的主要研究内容之一,是层化海洋环境中,潜艇在水下航行扰动密度(温度)跃层引起的物理现象。当潜艇在密度分层海洋中航行时,它产生的内波会引起海洋自由表面的辐聚辐散流动(散度场),这种海洋表面散度场流动的信号特征很容易成为机载或星载SAR(合成孔径雷达)的追踪目标,从而暴露潜艇的航行踪迹[6]。因此,对密度分层流体中水下航行体激发内波形成内波尾迹的研究,不仅具有重要的科学意义还具有重要的军事价值。
层化环境下,潜艇激发的表面散度场的研究,主要包含数值模拟和水池实验2种方法。随着计算机技术的迅猛发展和计算流体力学(CFD)软件的日益完善,在内波尾迹领域中CFD数值模拟所占比重和所起作用也越来越大,成熟的商业CFD软件如STAR CCM+,Fluent等已经在流场计算、船舶设计中获得大量应用[7-10]。陈雄等[11]采用Fluent中的VOF模型,对存在正温度梯度海水中无螺旋桨、有螺旋桨转动和排放冷却水3种情况的潜艇尾流进行数值模拟,获得了潜艇在不同情况下的水面兴波,并分析了海面和其他截面的温度场及流场分布。研究结果表明水面兴波主要受艇身影响。万鹏程等[12]同样以Fluent为平台,采用VOF两相流及k-ε湍流模型,对舰船气泡尾流进行了数值模拟研究,结果表明将自由液面法向速度梯度相关的空气卷吸模型用于舰船气泡尾流的模拟是可行的。
作为数值模拟技术的重要补充,PIV技术具有非接触式、二维或三维高精度测量等优势[13-14] 。近些年,随着PIV技术迅猛发展,国内外的学者利用PIV技术对船舶和潜艇尾流特性进行了大量的研究[15-18]。Felli等[19]用PIV技术对某潜艇艇体流场进行了测量。王志博等[20]人进行了指挥台围壳对潜艇尾流影响的计算研究,得出围壳外形与潜艇尾流场特征的关系。李茂华等[21]将三维PIV应用于船舶尾流场的精细测试研究,并详细阐述了SPIV技术近些年的进展。
本文针对层化海洋环境下,Suboff模型激发的内波尾迹自由面散度场特性开展数值模拟与水池实验研究,并获得内波尾迹表面散度场的尾迹开角及最大散度场强度随傅汝德数的变化关系。
1 数值模拟方法 1.1 计算模型为了与水池实验相互对比,本文数值模拟采用的Suboff模型长度为80 cm,直径为10 cm,计算域的长度为500 cm,宽为75 cm,深度为45 cm。采用STAR CCM+的切割体网格单元生成器生成网格,并同时进行网格重构与自动表面修复。层化海洋中潜艇的数值网格划分结果,如图2所示。为了尽可能捕获跃层处的尾迹特征,网格模型在密度跃层及自由液面处进行了网格加密,同时在模型的舰艏和舵面处也进行了网格加密。上层介质为空气,密度为ρ1=1 kg/m3;中间流体为淡水,密度为ρ2=1 000 kg/m3;下层流体为盐水,密度为ρ3=1 020 kg/m3或1 040 g/m3。上层流体深度为h1=15 cm,下层深度为 h2=30 cm。

|
图 2 潜艇与跃层的网格划分 Fig. 2 Meshing of submarine and thermocline |
本文采用标准的k-ε模型进行湍流模拟[22],标准的k-ε湍流模型是基于湍流动能的输运方程(k)和耗散速率(ε)。式(1)和式(2)对k和 ε 进行了定义:
| $ \begin{split}\frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] +\\ &{G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k},\end{split} $ | (1) |
| $ \begin{split}\frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +\\ &{C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {C_{3\varepsilon }}{G_b}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon }。\end{split} $ | (2) |
式中:Gk代表了平均速度梯度产生的湍流动能,在计算中用来表述k-ε模型中湍流的产生;Gb代表浮力产生的湍流动能,用于计算k-ε模型中浮力的影响;YM 代表可压缩湍流到全部耗散速率中颤振耗散项的影响,是k-ε模型中可压湍流影响的计算。C1ε,C2ε, 和C3ε 为常数;
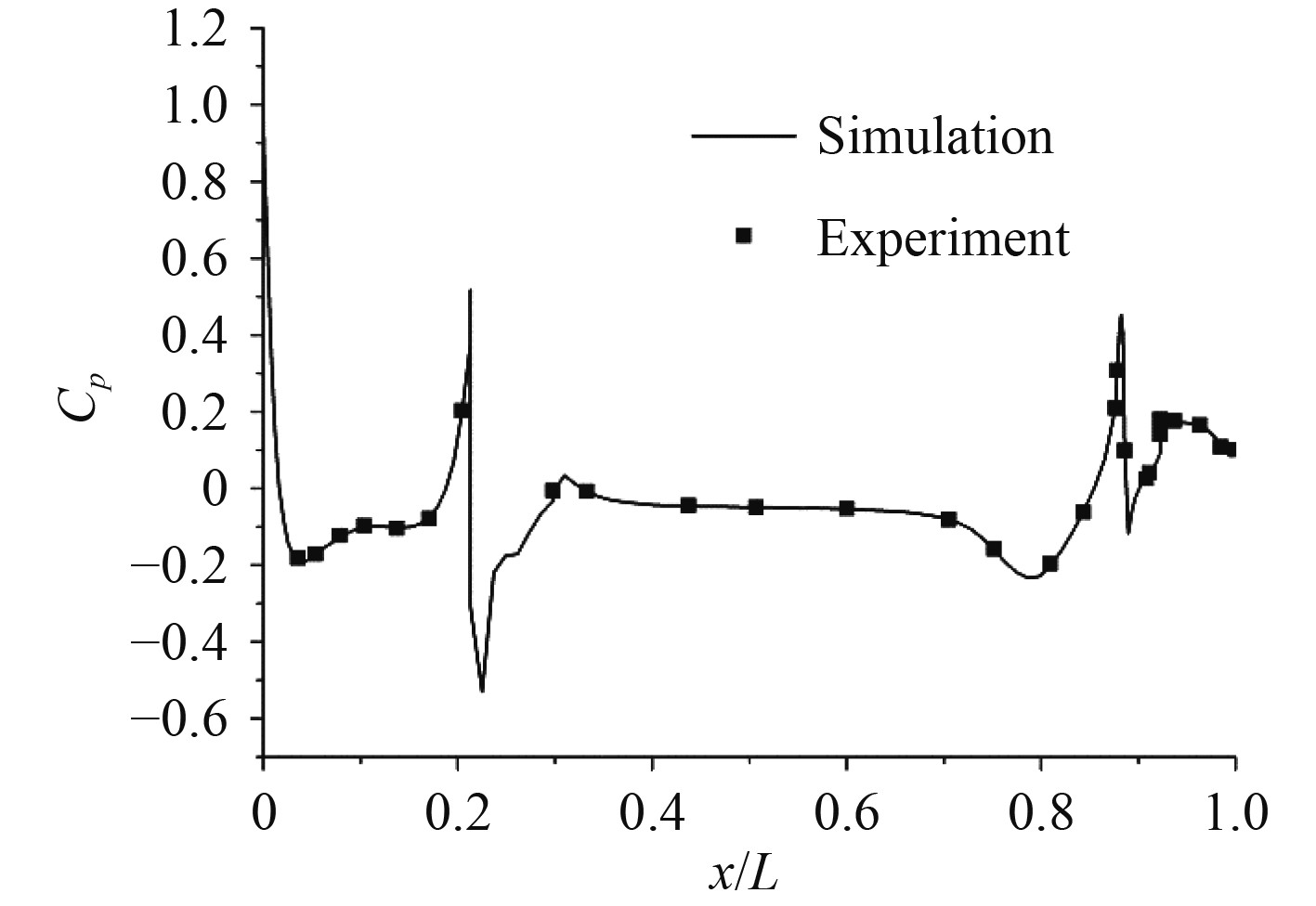
当流体密度为1000 kg/m3,来流速度为3 m/s时,图3给出了Suboff对称截面处的表面压力系数(Cp)计算结果与实验值[23]的比较,从而验证数值方法的准确性。可以看出:仿真与实验结果几乎完全重合。Cp在潜望塔及尾舵处的颤振是由于附体处强涡和流场脱落引起的。在压力系数验证的基础上,根据潜艇激发的自由液面散度场的尾迹开角以及最大强度的水池实验结果进一步验证数值模拟的准确性,并给出尾迹开角及最大散度强度随傅汝德数的变化规律。
|
图 3 潜艇对称截面处的压力分布(Cp ) Fig. 3 Pressure distribution at symmetric section (Cp) of submarine |
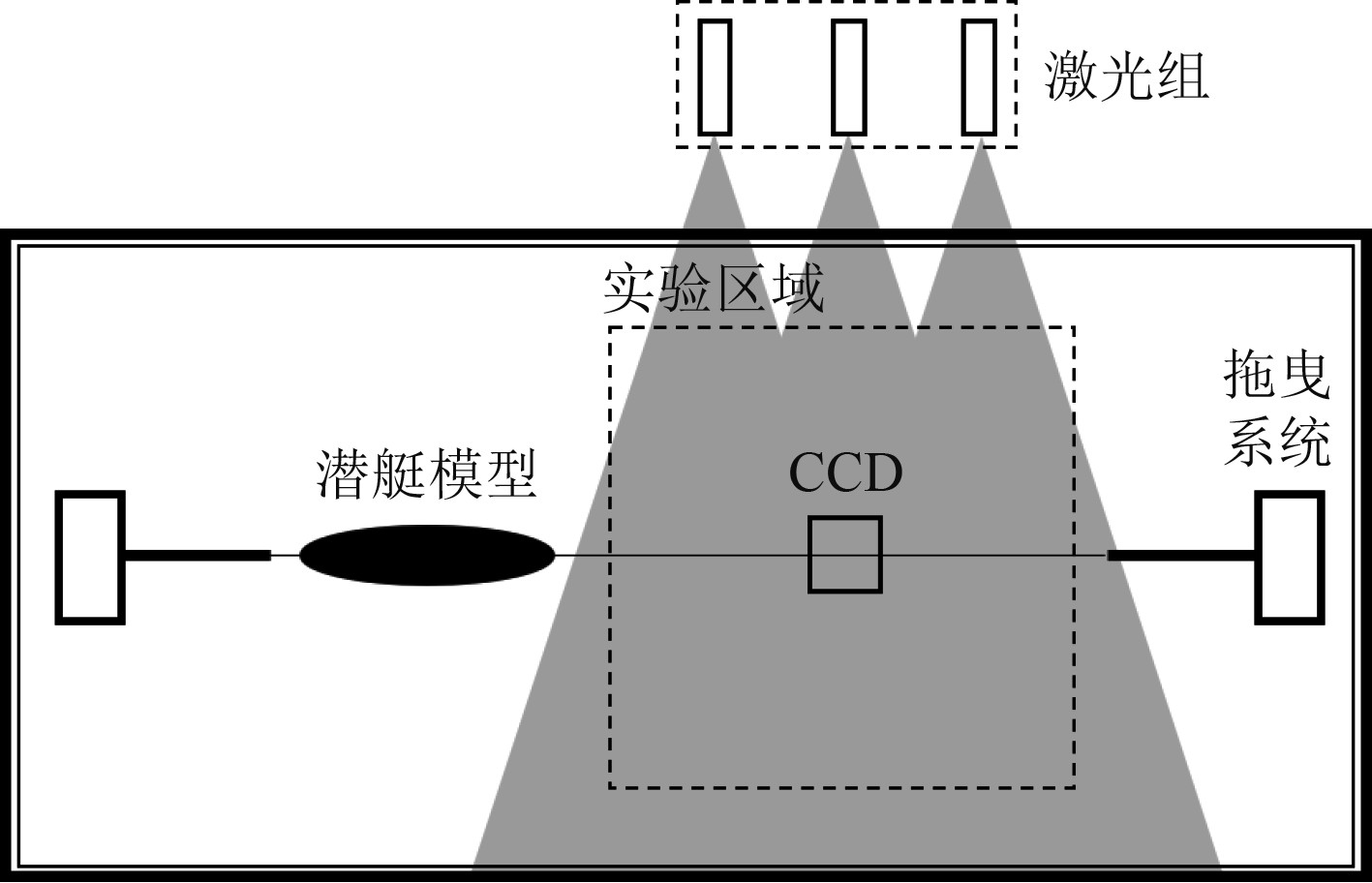
图4为水池PIV实验PIV的示意图。在水槽侧方设置激光组,激光覆盖水槽光学测量区域表层,通过拖曳系统拖动模型前进,在流场上方设置CCD进行实验图像采集。本实验PIV测量系统包括532 nm片光系统、CCD图像采集系统及数据分析系统。激光器作为点光源,其发射的激光通过柱形凹透镜展片后被展成1.5 mm厚的片光。在每次实验前利用标尺确定相机像素点和实际距离的对应关系,并利用密度计监测密度跃层的变化。
|
图 4 PIV测量系统采集示意图 Fig. 4 schematic diagram of PIV experiment |
当潜艇模型拖曳向前产生扰动,在跃层处由于山后波机制形成尾迹内波,内波的存在使表面呈现出散度场。本文的表面散度场开角通过获取该区域散度极值并拟合出直线与水平直线的夹角获得。当拖曳速度33 cm/s时,水下5 cm处水平截面的散度场PIV与数值模拟结果如图5所示。

|
图 5 表面散度场(下层,ρ3=1040 kg/m3,U=33 cm/s) Fig. 5 Divergence field(bottom, ρ3=1040 kg/m3,U=33 cm/s) |
实验重复5次并根据拟合曲线进行散度极大值的重复性验证,其中当Y=0.15 m位置处误差最小。因此水池实验与数值仿真均选择Y=0.15 m处作为监控点,进行表面散度场的获取与分析。图6给出了数值模拟中表面散度场尾迹夹角及散度极值的取值范围。

|
图 6 散度取样位置及表面散度角 Fig. 6 Divergence sampling position and surface divergence Angle |
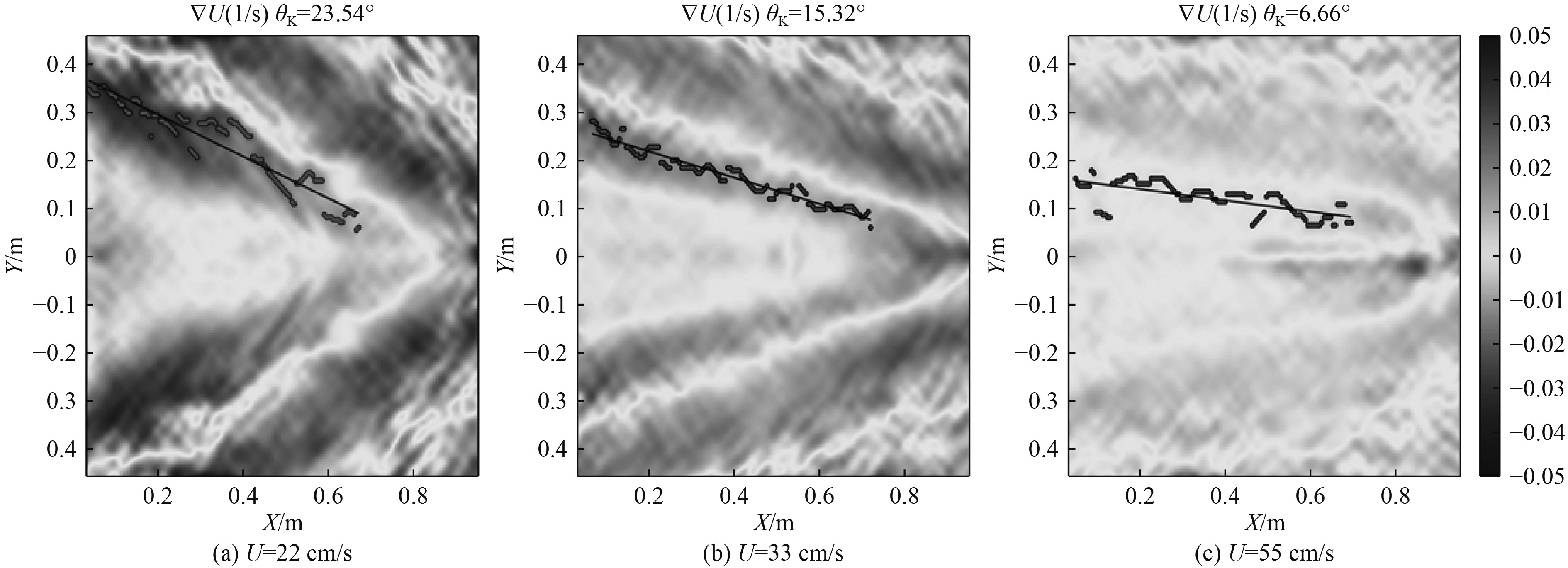
对不同的拖曳速度进行系统的水池实验,当最底层流体密度ρ3=1 040 kg/m3,拖曳速度分别为22 cm/s、33 cm/s和55 cm/s,对应的Fr数分别为0.56,0.84和1.72。拖曳实验获得的表面散度场及尾迹角度的获取边界如图7所示。此时,尾迹开角分别为23.54°,15.32°和6.66°。可以看出,随着拖曳速度的增加,尾迹的开角逐渐减小。
|
图 7 不同速度表面散度场水池实验结果(ρ3=1 040 kg/m3) Fig. 7 Pool experiment results of surface divergence field at different velocities (ρ3=1 040 kg/m3) |
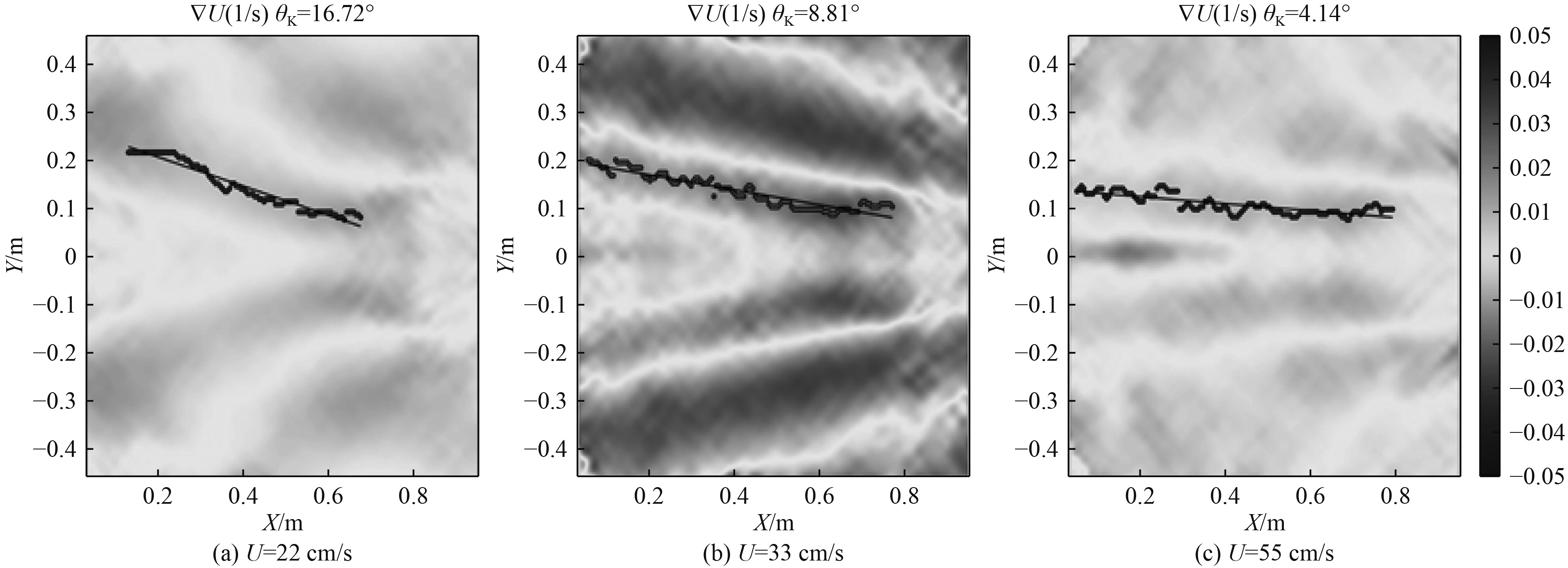
当最底层流体密度ρ3=1 020 kg/m3时,拖曳速度分别为22 cm/s、33 cm/s和55 cm/s,对应的Fr数分别为0.87,1.38和2.20。经过拖曳实验获得的表面散度场及尾迹角度的获取边界如图8所示。此时,尾迹开角分别为16.72°,8.81°和4.14°。类似于强分层的实验结果:随着拖曳速度的增加,尾迹的开角逐渐减小。
|
图 8 不同速度表面散度场水池实验结果(ρ3=1 020 kg/m3) Fig. 8 Pool experiment results of surface divergence field at different velocities (ρ3=1 020 kg/m3) |
比较图7(b)和图8(a)以及图7(c)和图8(b)可以看出:当Fr数比较接近时,内波尾迹的开角也比较接近。
当ρ3=1040 kg/m3,拖曳速度分别为33 cm/s和55 cm/s时,表面散度场极值及尾迹开角的水池实验结果与数值模拟结果的比较如表1所示。
|
|
表 1 表面散度场的比较(ρ3=1040 kg/m3,U=33 cm/s) Tab.1 Comparison of the numerical simulation results |
经过对不同的拖曳速度进行系统实验,得到表面散度场尾迹开角随Fr数的变化拟合曲线,如图9所示。当Fr数在0.3~1.5范围内,各层结工况表面散度场开角与Fr成递减关系。二者关系满足双e指数拟合,拟合公式为
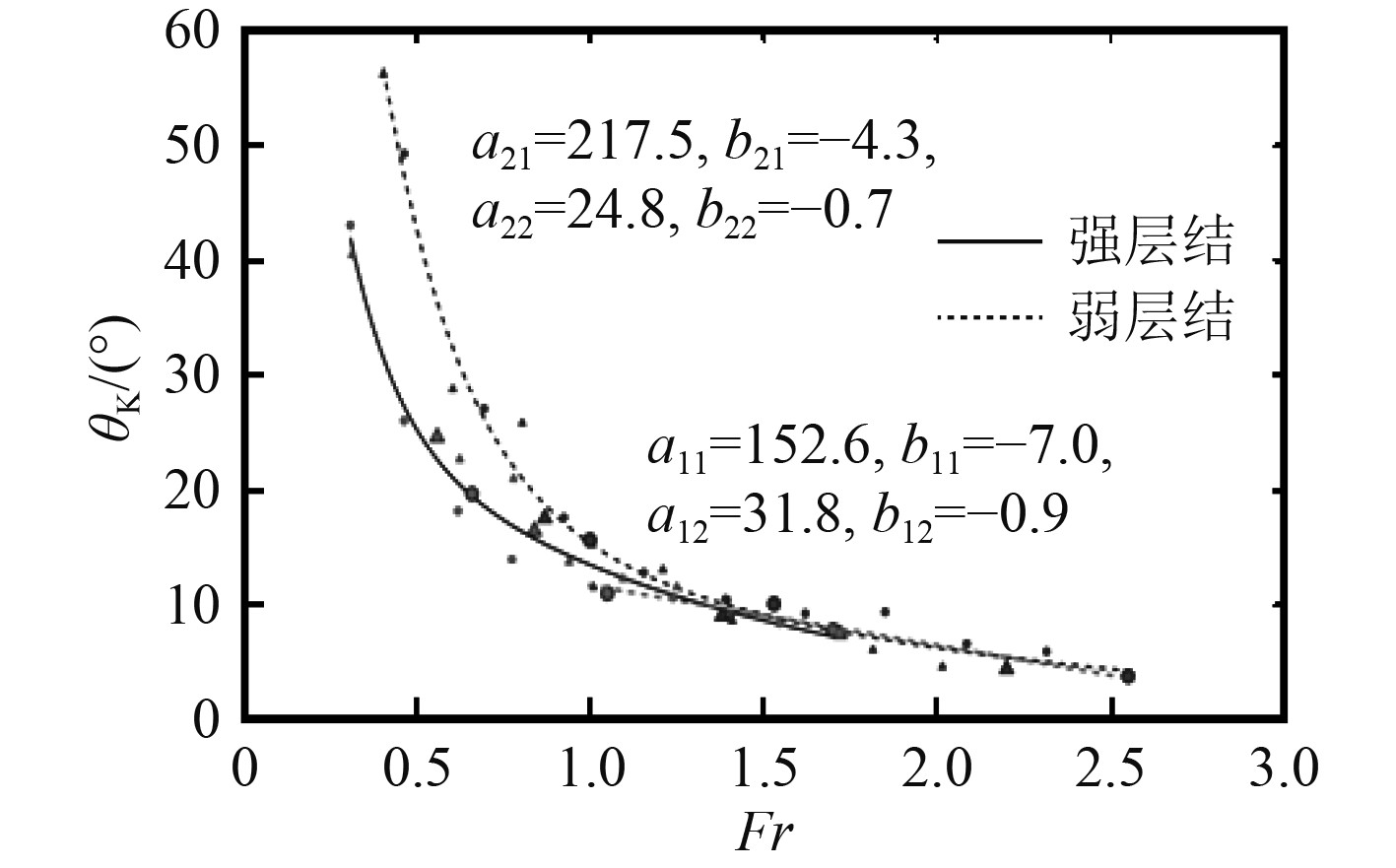
|
图 9 表面散度拟合曲线 Fig. 9 Fitting curve of surface divergence |
通过实验,Fr数在0.3~2.6范围内,表面散度场最大值的变化规律如图10所示。实验结果表明,散度最大值的变化规律呈现单峰结构,并在0.8<Fr<1.1范围内,散度最大值会达到极大值。
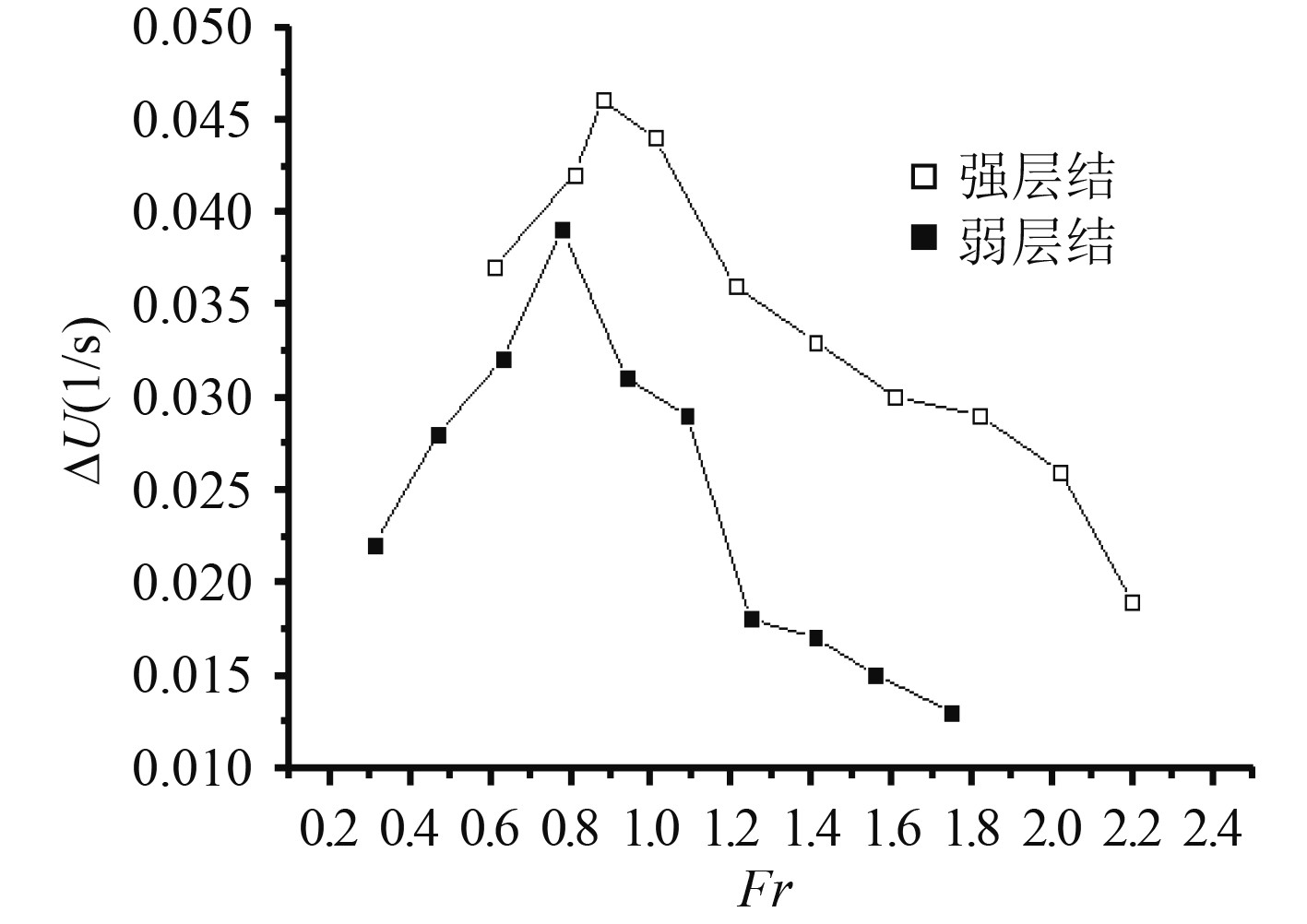
|
图 10 拖曳速度与最大散度关系 Fig. 10 Relationship between drag velocity and maximum divergence |
计算采用全尺度模型进行,Suboff模型是标准模型的20倍,模型长度为80 m,水下排水量为5600 t。上层流体的深度为15 m,下层流体深度为30 m,下游长度为900 m,上游长度为100 m,宽度为400 m,同样采用切割体网格技术进行网格划分,网格总数为1000万,网格形式可以参考图2。来流速度分别为4 m/s、5 m/s和6 m/s。
为了进一步研究速度对实际潜艇目标激发的海洋表面尾迹流场特征的影响,图11给出了自由表面散度场随速度的变化情况。

|
图 11 表面散度随时间的变化情况(实际目标) Fig. 11 Variation of surface divergence with time (actual target) |
表面V型尾迹的散度值随航速的变化如图12(a)所示。与前面的水池尺度散度值的取值方法类似,图12(a)中的散度取值为水下0.5 m与潜艇对称面外侧15 m处2个截面的交界线上X坐标在34~36 m之间网格点上散度的平均值。表面V型尾迹的夹角随速度的变化如图12(b)所示。
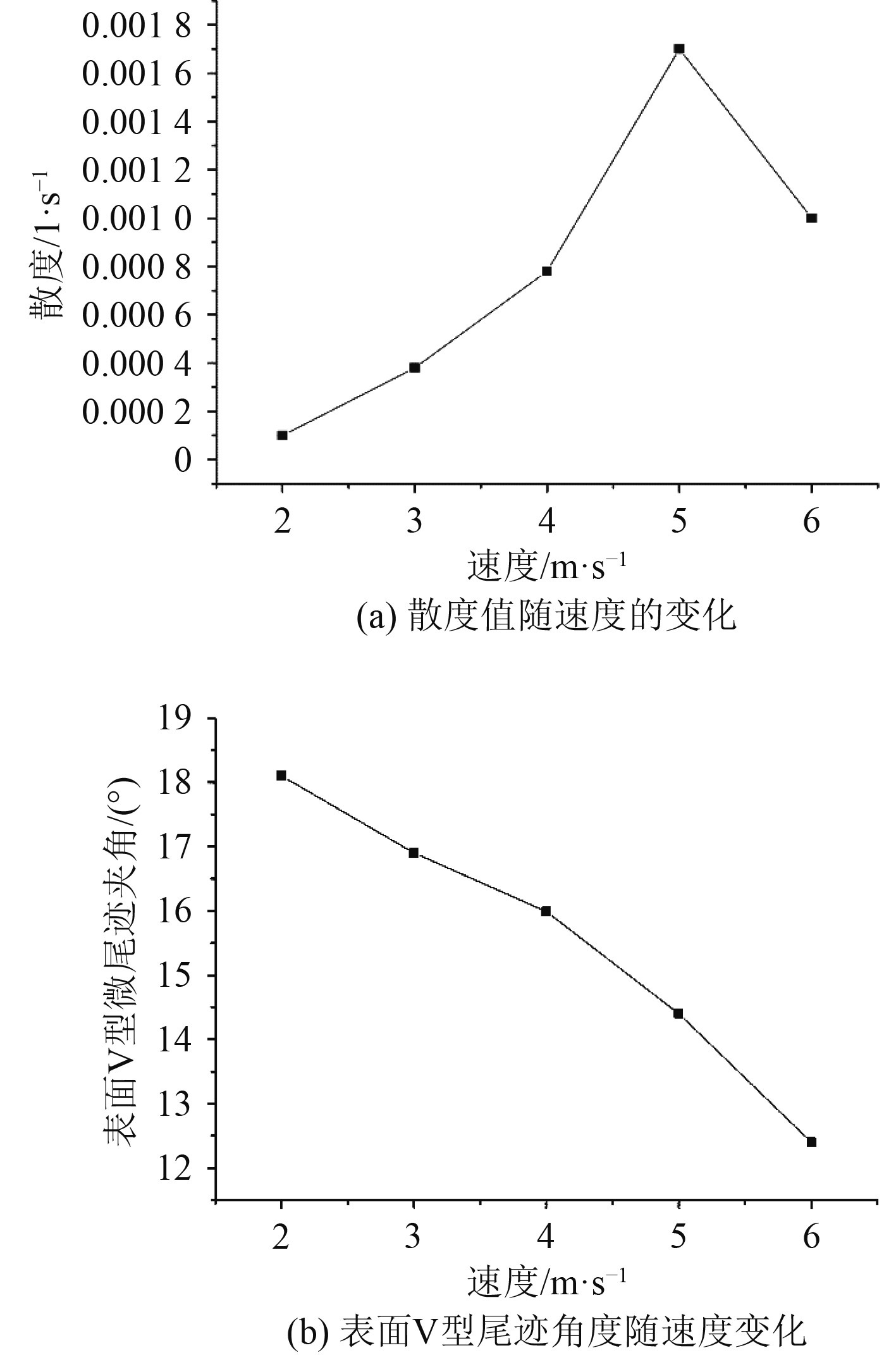
|
图 12 表面流场特性随航速的变化(实际目标) Fig. 12 Variation of surface flow field characteristics with speed (actual target) |
可以看出,表面尾迹的散度值随来流速度是先增大后减小的,表面V型尾迹的夹角随来流速度是逐渐减小的,这些研究结论与水池实验研究结果保持一致。
5 结 语本文采用的数值模拟方法很好捕获了层化条件下潜艇激发的表面散度场。无论是内波尾迹的开角还是表面散度场的最大值,二者的误差都在10%以内。在水池实验中,当Fr数在0.3~1.5范围内,各层结工况表面散度场开角与Fr数都成递减关系,而且满足双e指数拟合;当Fr大于1.5后,满足直线拟合递减关系。数值研究表明:层化海洋环境下,实际尺寸的潜艇激发的表面散度场的尾迹开角,随着航速的增大而逐渐减小;表面散度场的最大强度随着航速的增大呈现先增大后减小的变化趋势。这些研究结论与水池实验研究结果保持一致。
| [1] |
崔国恒, 于德新. 非声探潜技术现状及其对抗措施[J]. 火力与指挥控制, 2007, 32(12). CUI Guoheng, YU Dexin. Status quo of non-acoustics antisubmarine detecting technology and its countermeasures[J]. Fire Control and Command Control, 2007, 32(12). |
| [2] |
韩晶, 赵朝方. 海洋遥感技术在探测潜艇中的应用[J]. 装备环境工程, 2008, 5(3): 67-70. |
| [3] |
陈允锋, 刘伟. 非声探潜新技术浅析[J]. 光纤与电缆及其应用技术, 2016, 6(6): 29-36. |
| [4] |
张军, 张效慈, 赵峰. 源于水动力学的潜艇尾迹非声探测技术研究进展[J]. 船舶力学, 2003, 7(2): 121-128. |
| [5] |
WREN G G, MAY D. Detection of submerged vessels using remote sensing techniques[J]. Australian Defense Force, 1997, 127: 8-15. |
| [6] |
REED A M. MILGRAM J H.. Ship wakes and their radar images[J]. Annu Rev Fluid Mech, 2002(34): 469-502. |
| [7] |
GONG B, HUANG W G, CHEN P. Study on the SAR imaging simulation of Kelvin ship wake[J]. Marine Science Bulletin, 2013, 32(2): 208-213. |
| [8] |
YEUNG R W, NGUYEN T C. Waves generated by a moving source in a two-layer ocean of finite depth[J]. Journal of Engineering Mathematics, 1999(35): 85-107. |
| [9] |
GAYEN B, TAYLOR R J, and SARKAR S. Large eddy simulation of a stratified boundary layer under an oscillatory current. Journal[J]. Journal. Fluid Mech, 2010, 643: 233-266. |
| [10] |
陈圣涛, 王慧丽, 王运鹰, 等. 舰船气泡尾流特性的数值模拟和实验研究[J]. 船舶力学, 2012, 16(4): 342-348. |
| [11] |
陈雄, 杨智惠, 韩玉阁. 温度分层海水中潜艇尾流数值模拟[J]. 声学技术, 2016, 35(3): 118-121. |
| [12] |
万鹏程, 傅慧萍. 舰船气泡尾流数值模拟[J]. 上海交通大学学报, 2013, 47(2): 193-197. |
| [13] |
BUICK J M, MARTIN A J, COSGROVE J A, et al. Comparison of a lattice Boltzmann simulation of steep internal waves and laboratory measurements using particle image velocimetry[J]. European Journal of Mechanics B/Fluids, 2003, 22: 27-38. |
| [14] |
KRAFT W N. Experimental investigation of a stratified buoyant wave. [M]. United Sates: Texas A & M University, 2004.
|
| [15] |
李广年, 李磊, 谢永和. PIV技术在旋转流场测试中的应用[J]. 中国造船, 2011, 52: 145-149. |
| [16] |
李广年, 张国平, 陆林章. 大型空泡水筒中螺旋桨尾流场2D-PIV测量[J]. 船舶力学, 2009(5): 682-687. |
| [17] |
黄少锋, 张志荣, 赵峰. 自由面肥大船粘性绕流场的数值模拟[J]. 船舶力学, 2008(1): 46-53. |
| [18] |
代钦, 赵莉莉. 近自由表面翼型尾流速度场的PIV测量及POD分析[J]. 水动力学研究与进展A辑, 2008, 23(2): 196-203. |
| [19] |
FELLI M, PEREIRA F, CALCAGNO G. A modular Stereo-PIV probe for underwater applications configurations and measurement performance[C] // Proceedings of 5th International Symposium on Particle Image Velocimetry. Busan, Korea, 2003.
|
| [20] |
王志博, 姚惠之, 张楠. 指挥台围壳对潜艇尾流影响的计算研究[J]. 船舶力学, 2009, 13(2): 197-202. |
| [21] |
李茂华, 龚杰. 三维PIV应用于船舶精细流场测试研究进展[J]. 中国舰船研究, 2015, 10(1): 58-67. |
| [22] |
熊莉芳, 林源, 李世武. K-ε湍流模型及其在FLUENT软件中的应用
[J]. 工业加热, 2007, 4(36): 13-15. |
| [23] |
ALIN N, BENSOW R E, FUREBY C. Current capabilities of DES and LES for submarines at straight course[J]. Journal of Ship Research, 2010, 54(3): 184-196. |
 2022, Vol. 44
2022, Vol. 44

