自然界中流动的流体大多为粘性流体,因此无论是空中飞行的飞行器亦或是水下的航行器都不可避免地会受到粘性流体施加的阻力,从而使得飞行器和航行器的能耗加大,阻力降低以及产生噪声和振动等[1-2]。因此减阻技术是飞行器和航行器设计的关键技术,也是节能的重要途径。美国NASA早在2001年就将减阻技术列为21世纪的关键技术[3]。减阻控制技术也因此成为水动力学领域的研究热点。
目前的减阻技术主要有五类:沟槽仿鲨鱼表皮减阻法、疏水表面隔离减阻法、柔性表皮减阻法、微气泡减阻法以及减阻剂减阻法等[4]。根据数值计算和试验结果表明,在满足特定的参数条件下,上述减阻技术均可获得不同程度地减阻效果,但是同时也都存在一些局限性。除了上述5种减阻技术外,光滑平板的展向周期振动也可以有效减少阻力。Jung等[5]于1992年首先借助直接数值模拟技术证实了这种减阻方法的有效性。国内的黄乐萍[6],葛铭纬[3],朱兰[7]以及黄伟希[8]等同样开展了类似地研究。上述研究大多采用DNS方法对低雷诺数下(Re < 10 3)平板周期性振动的减阻特性进行研究,在高雷诺数下的研究则较少涉及。鉴于此,本文借助Fluent软件中的动网格技术对光滑平板在实际可应用雷诺数范围下的周期振动减阻特性进行研究,系统分析各个运动参数对减阻效果的影响。本文研究成果可为后期模型试验提供技术参考。
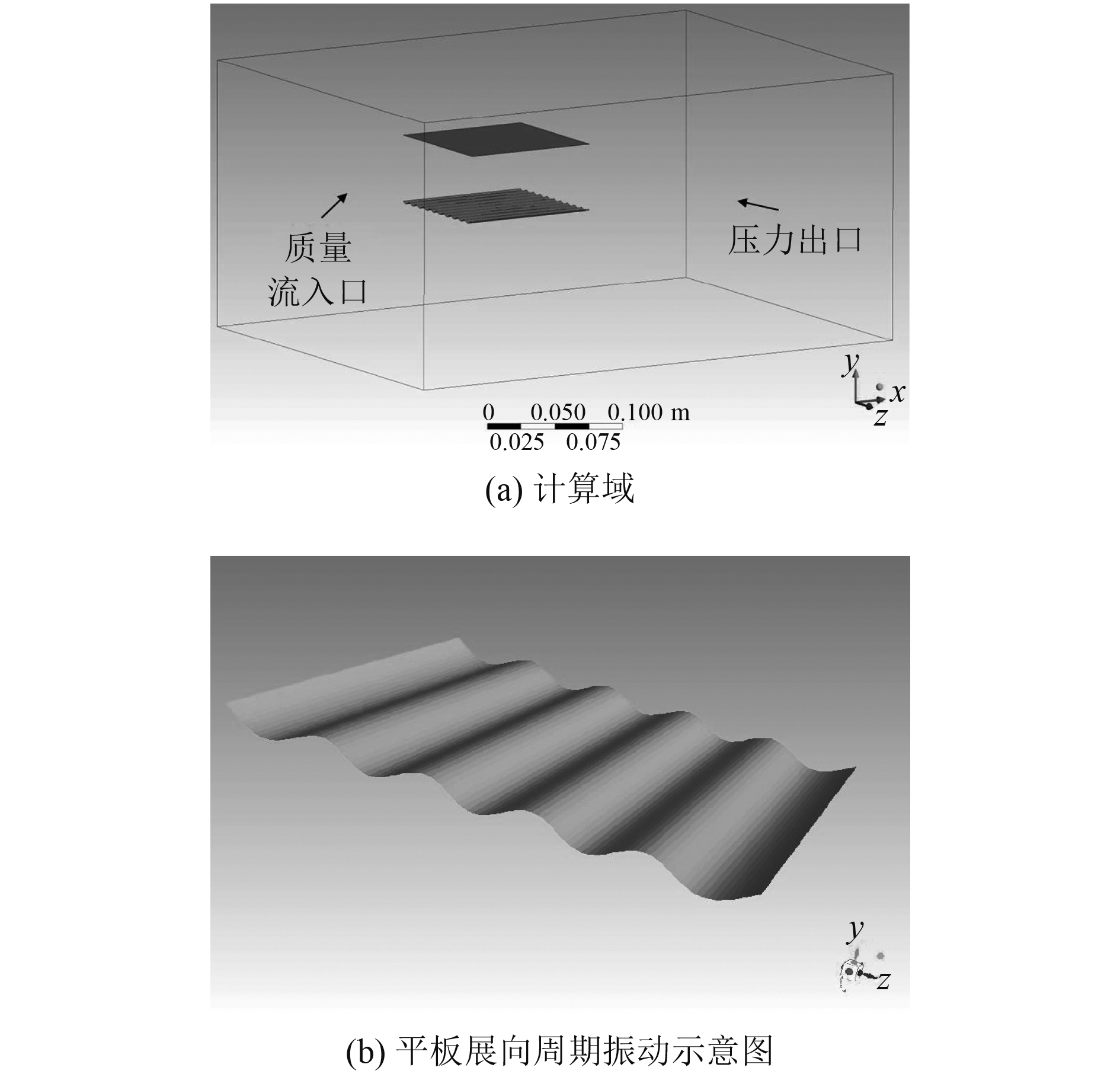
1 计算模型及网格本文选取的计算模型如图1(a)所示,该模型由2块完全相同的零厚度正方形平板组成,平板的边长为0.1 m,记为特征长度C。两块平板沿着垂向(Y方向)平行布置,上面平板保持静止,下面的平板做展向周期振动,运动示意图如图1(b)所示。
|
图 1 计算模型 Fig. 1 Diagram of computation domain |
2块平板间距设为ΔY = 1.5 C以消除两块平板之间的相互干扰。本文选取的计算域为长方体计算域,具体尺寸为(x, y, z)= (10 C, 7 C, 7C )。其中,平板前段至计算域上游(负X方向)距离为2C,平板上表面至计算域顶部(正Y方向)距离2.0 C,运动方程如下式:
| $ y(x,t) = {h_{\max }} \cdot \sin (\omega t - kz) = {h_{\max }} \cdot \sin \left(2{\text{π}} ft - \frac{{2\text{π} }}{\lambda }z\right)。$ | (1) |
式中:hmax 表示Y 方向的行波运动幅值;f 表示行波频率;k 表示行波波数;λ 表示行波波长。
采用纯六面体网格进行计算,并对平板表面附近进行局部加密,以保证y+ ≤ 1。以 Re = 6×104为例,全局网格共计700万左右。其中Re表示特征雷诺数,其具体表达式为:

|
图 2 平板运动时附近网格 Fig. 2 Grid distribution of the plate during the motion process |
平板周围的流场为不可压缩流体,采用N-S方程作为控制方程,其表达式为:
| $ \nabla \cdot {{{\boldsymbol{u}}}} = 0,{\text{ }}\dfrac{{\partial {{{\boldsymbol{u}}}}}}{{\partial t}} + ({{{\boldsymbol{u}}}} \cdot \nabla ){{{\boldsymbol{u}}}} = - \frac{1}{\rho }\nabla p + \frac{\mu }{\rho }{\nabla ^2}{{{\boldsymbol{u}}}}。$ | (2) |
式中:u为流体速度,ρ为流体密度,P为压力。Μ为粘性系数。采用通用商业软件Ansys Fluent求解,采用 SST k-ω 湍流模型对方程进行封闭处理。
针对运动壁面的捕捉,采用Fluent中的动网格技术进行处理。具体来说,仅采用弹性广顺模型进行网格变形处理以保证网格的质量和计算的精度。
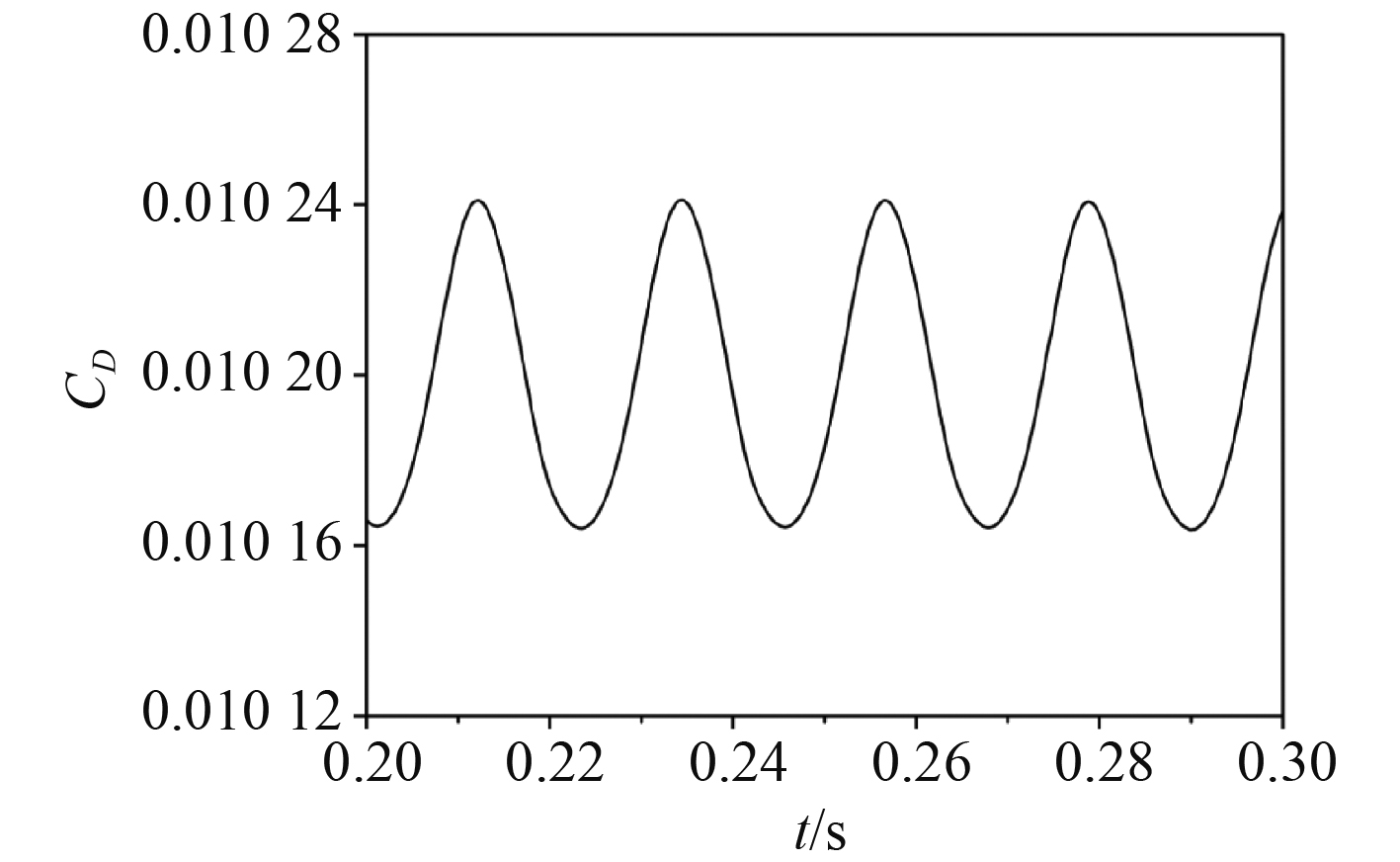
3 计算结果及分析 3.1 水动力的瞬时值变化研究平板做展向运动时,其阻力系数值随时间的变化规律。如图3所示,取 hmax = 0.001 m,f = 45 Hz,λ = 0.05 m,计算得到平板X方向上的水动力系数在四个周期内瞬时值随时间的变化。其中CD表示阻力系数,定义如下式:
|
图 3 平板运动时阻力系数随时间变化曲线 Fig. 3 Variation curves of drag force during the motion process |
| $ {C_D} = {F_x}/(0.5 \cdot \rho \cdot {V^2} \cdot {C^2})。$ | (3) |
式中:Fx表示平板X方向的阻力,V表示特征来流速度,C表示平板长度,ρ表示流体密度。
可以看出平板展向周期振动时其阻力系数随时间呈现周期性变化,且变化周期为运动周期一致,实际中表现为平板的阻力在一个运动周期内2次取得极大值,这与运动运动的对称性规律是相一致的。
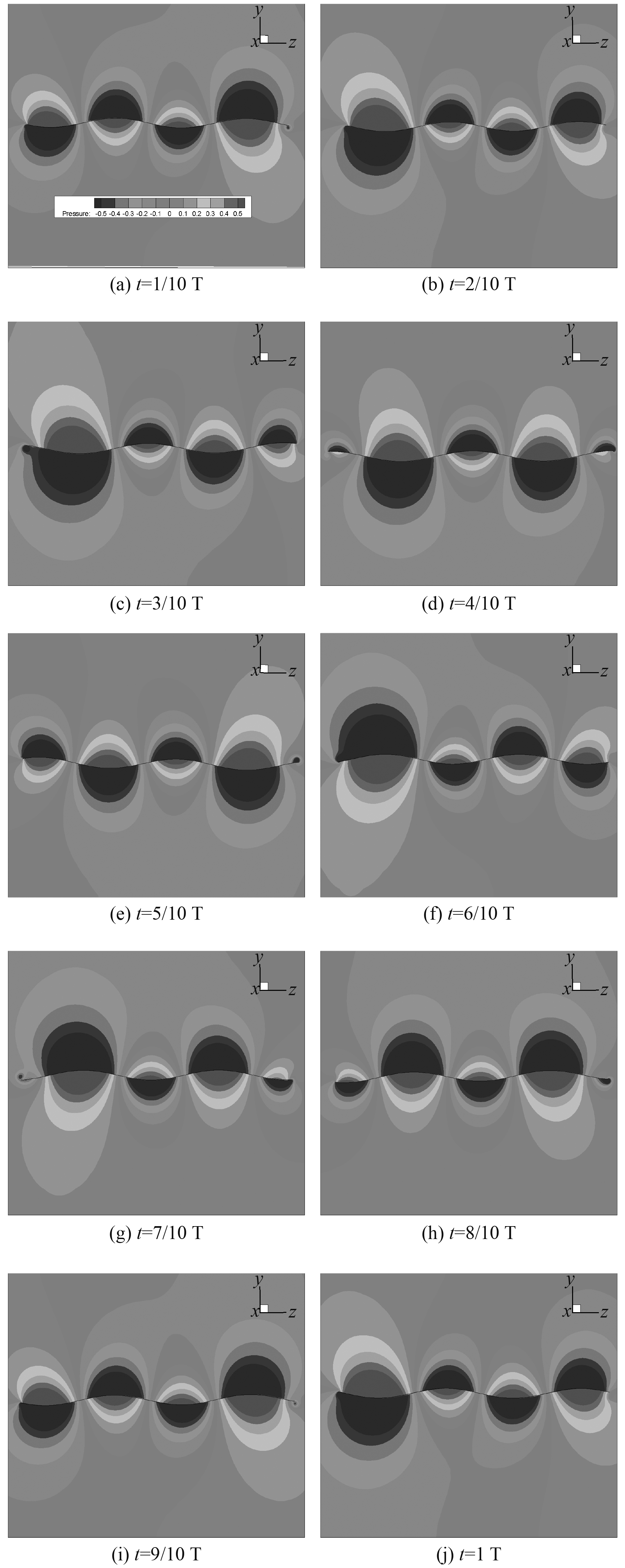
3.2 压力分布规律对垂直于X 轴的一个平面上压力分布进行研究,尝试揭示平板展向振动减阻的原因。图4 为一个运动周期内截面周围的压力分布变化。可以看出,平板在做展向振动时,在平板的正反两面形成数个交替变化高压区和低压区,从而形成压力差并产生与流动方向相反的推力,平板表面的压力随着时间的推移不断向展向传播。
|
图 4 一个周期内截面周围的压力分布变化 Fig. 4 Pressure distribution on the section plane during the whole motion process. |
研究各个运动参数对减阻效果的影响规律,分别取运动频率f = 40 Hz,50 Hz,60 Hz、80 Hz和100 Hz,运动振幅hmax = 0.000 2 m,0.000 4 m,0.000 6 m,0.000 8 m,0.001 0 m和 0.000 15 m,定义特征波数Kx = L / λ ,用以表征展向宽度上所具有的行波个数,Kx 的值分别设置为0.2,0.5,1.0,3.0,5.0和10.0。计算得到系泊条件下减阻率随运动参数的变化关系如图5所示。其中减阻率Dr定义如下:

|
图 5 减阻率随运动参数的变化规律 Fig. 5 Variation law of drag reduction rate with motion parameters. |
| $ \begin{split}{D}_{r}=&\dfrac{\overline{{f}_{平板}}-\overline{{f}_{波动板}}}{\overline{{f}_{平板}}}\times 100\text{%}=\left(1\text-\dfrac{\overline{{f}_{波动板}}}{\overline{{f}_{平板}}}\right)\times 100\text{%}= \\ &\left(1\text-\dfrac{\dfrac{1}{T}{\displaystyle \int _{{\text{t}}_{0}}^{{{\text{t}}_{0}+T}}{f}_{波动板}dt}}{\dfrac{1}{T}{\displaystyle \int_{{\text{t}}_{0}}^{{{\text{t}}_{0}+T}}{f}_{平板}dt}}\right)\times 100\text{%}。\end{split} $ | (4) |
其中,
对于图5(a)主要研究减阻率与特征波数之间的关系,其他参数设置为f = 50 Hz, hmax = 0.001 0 m。由图中可以看出,平板减阻率随着特征波数的增加呈现出先增大后减小的趋势,特征波数大于1.0后逐渐有了减阻的效果,且在Kx =3.0附近达到最大减阻率。这即意味着在平板上至少形成一个完整的行波才可以产生减阻效果,且存在最佳完整行波个数对应最大减阻率,这一结论可为后续试验提供理论指导。
对于图5(b)主要研究减阻率与运动幅值之间的关系,其他参数设置为f = 50 Hz, Kx =3.0。由图中可以看出,平板减阻率随着运动幅值的增加呈现出逐渐增加的趋势,且运动幅值越大对应的减阻率增加愈发缓慢,这一结论与通过参考文献[7]中的结论是相一致。考虑到主要研究微变形运动对减阻效果的影响,因此运动幅值仅限制在0.02 L以内。
4 结 语本文以简化的二维平板为计算模型,使得平板采取沿着展向周期振动运动的方式进行减阻效果探索研究。相关结论如下:
1)在系泊状态下,平板做展向周期振动时的阻力系数变化频率等于振动频率,实际中表现为平板的阻力在一个运动周期内2次取得极大值,这与运动运动的对称性规律是相一致的;平板截面周围的压力分布和其随相位的变化规律表明,在平板的两侧形成的高压区和低压区产生的压差是平板做展向周期振动减阻的主要原因。
2)平板展向周期振动的减阻率随着运动幅值和特征波数的增加而相应增大,且存在最佳特征波数对应最大减阻率。
| [1] |
王晋军. 沟槽面湍流减阻研究综述[J]. 北京航空航天大学报, 1998, 24(1): 31-34. |
| [2] |
许春晓. 壁湍流相干结构和减阻控制机理研究[J]. 力学与实践, 2015, 37(3): 460-467. |
| [3] |
葛铭纬. 基于近壁相干结构的湍流减阻主动控制研究[D]. 清华大学, 2011.
|
| [4] |
刘宝胜, 吴为, 曾元松. 鲨鱼皮仿生结构应用及制造技术综述[J]. 塑性工程学报, 2014, 21(4): 56-62. DOI:10.3969/j.issn.1007-2012.2014.04.012 |
| [5] |
JUNG WJ, AKHAVAN R. Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations[J]. Physics of Fluids, 1992, 4(8): 1605-1607. DOI:10.1063/1.858381 |
| [6] |
黄乐萍, 范宝春, 董 刚. 槽道湍流壁面展向周期振动减阻机理研究[J]. 南京理工大学学报(自然科学版), 2010, 34(3): 361-366. |
| [7] |
朱兰. 基于展向壁面振动控制的槽道湍流结构研究[D]. 南京理工大学, 2008.
|
| [8] |
黄伟希, 许春晓, 崔桂香, 等. 壁面展向周期振动的槽道湍流减阻机理的研究田. 力学学报, 2004, 36(1).
|
 2022, Vol. 44
2022, Vol. 44
