0 引　言

船舶阻力性能的优劣直接决定了船舶的航速、运输效率及经济性能的好坏。由于自由液面的影响，兴波阻力对船舶的影响不可忽略，其大小取决于船舶外形结构及航行工况^[1]。因此，获得船舶在不同航行工况下的阻力特性、水面兴波特性可为船型优化提供重要依据^[2]。

Deng等^[3]研究了流域网格参数对双体船阻力特性的影响，得到了在计算双体船阻力特性时双体船表面网格尺寸、y⁺、流域网格分布规律的选取标准，并通过与实验数据对比验证了数值模型及计算结果的合理性。在研究自由液面航行的高速船体流体动力时，通常采用基于VOF多流体模型和雷诺时均的N-S方程（RANS）处理自由液面，为了加速计算的收敛性及计算速度，Alban等^[4]提出了2种数值控制策略，可在保证计算精度的前提下提高约4倍的计算速度。刘富强等^[5]基于STAR-CCM+流体计算软件对小尺度回转体静水面滑行进行了数值模拟，得到了航速及浸没深度对航行体流体动力特性的影响。

为了研究某特大型水面船舶在静水面以不同航速、侧向角航行时的流体动力特性及流场分布规律，本文基于STAR-CCM+仿真软件，考虑自由液面的影响，建立了特大型船舶静水面航行的数值模型。分别基于粘性理论和试验数据^[6]，对数值模型的计算精度进行校核，获得了特大型船舶在不同航行工况下的流体动力特性。

1 数值模型的建立

采用欧拉多相流模型处理多相流问题，采用VOF波中的平波模型处理自由液面，考虑重力作用的影响。特大型船舶水面航行时不引起流场温度的显著变化，数值模型忽略了能量方程^[5]。因此，流场控制方程包括连续性方程、动量方程和相体积分数方程。

特大型船舶水面高速航行时涉及大逆压梯度引起的流动分离，Menter提出的SST湍流模型考虑湍流剪切力的传输，可以精准预测流动的开始及分离。SST湍流模型关于湍动能及湍动能耗散率的控制方程如下：

$ \dfrac{\partial }{\partial t}\left(\rho \kappa \right)+\dfrac{\partial }{\partial {x}_{i}}\left(\rho \kappa {u}_{i}\right)=\dfrac{\partial }{\partial {x}_{j}}\left({\mathrm{\varGamma }}_{\kappa }\dfrac{\partial \kappa }{\partial {x}_{j}}\right)+{G}_{\kappa }-{Y}_{\kappa }+{S}_{\kappa } ，$

(2-1)

$ \dfrac{\partial }{\partial t}\left(\rho \omega \right)+\dfrac{\partial }{\partial {x}_{i}}\left(\rho \omega {u}_{i}\right)=\dfrac{\partial }{\partial {x}_{j}}\left({\mathrm{\varGamma }}_{\omega }\dfrac{\partial \omega }{\partial {x}_{j}}\right)+{G}_{\omega }-{Y}_{\omega }+{S}_{\omega }。$

(2-2)

式中： ${\mathrm{\varGamma }}_{\kappa }$ 和 ${\mathrm{\varGamma }}_{\omega }$ 分别表示 $ \kappa $ 和 $ \omega $ 的有效扩散率； $ {G}_{\kappa } $ 表示由于平均速度梯度产生的湍流动能； $ {G}_{\omega } $ 表示特殊湍流动能耗率 $ \omega $ 的产生； $ {Y}_{\kappa } $ 和 $ {Y}_{\omega } $ 分别表示由于湍流 $ \kappa $ 和 $ \omega $ 的耗散； $ {S}_{\kappa } $ 和 $ {S}_{\omega } $ 为源项，本文此项取0。

2 数值模型验证

为了验证本文建立的船舶水面高速航行数值模型的计算精度，采用Moctar等^[7]基于DTC船模开展的航行试验数据进行模型校正和计算精度评估。DTC船模的主要几何参数包括：总长5976 mm，水线宽859 mm，淹深244 mm，排水量0.827 m³。

为了精准地获得船体的阻力特性，在船模附近进行多层加密。流域尺寸、边界条件及流动工况完全匹配试验工况。采用所建立的数值仿真方法对系列速度下的船模水面航行工况进行数值模拟，从船模摩擦阻力和总阻力2个指标对数值模型的计算精度进行定量校核，对比结果见表1。对于船模总阻力，仿真结果和试验结果的最大相对偏差不超过4%，摩擦阻力的最大相对偏差不超过1.5%。表明本文建立的数值模型是合理的，能够较精准预测船舶在水面航行时的流体动力特性。

3 计算模型及仿真过程 3.1 船体模型

特大型船舶的结构外形如图1所示，其几何尺寸详见表2。图1中X正方向表示船舶航行方向，Y正方向为垂直X轴沿船左舷方向，Z方向由笛卡尔坐标系右手定则确定，其垂直于甲板向上。坐标原点为纵剖面与水线在船首处交点。

3.2 计算域及网格划分

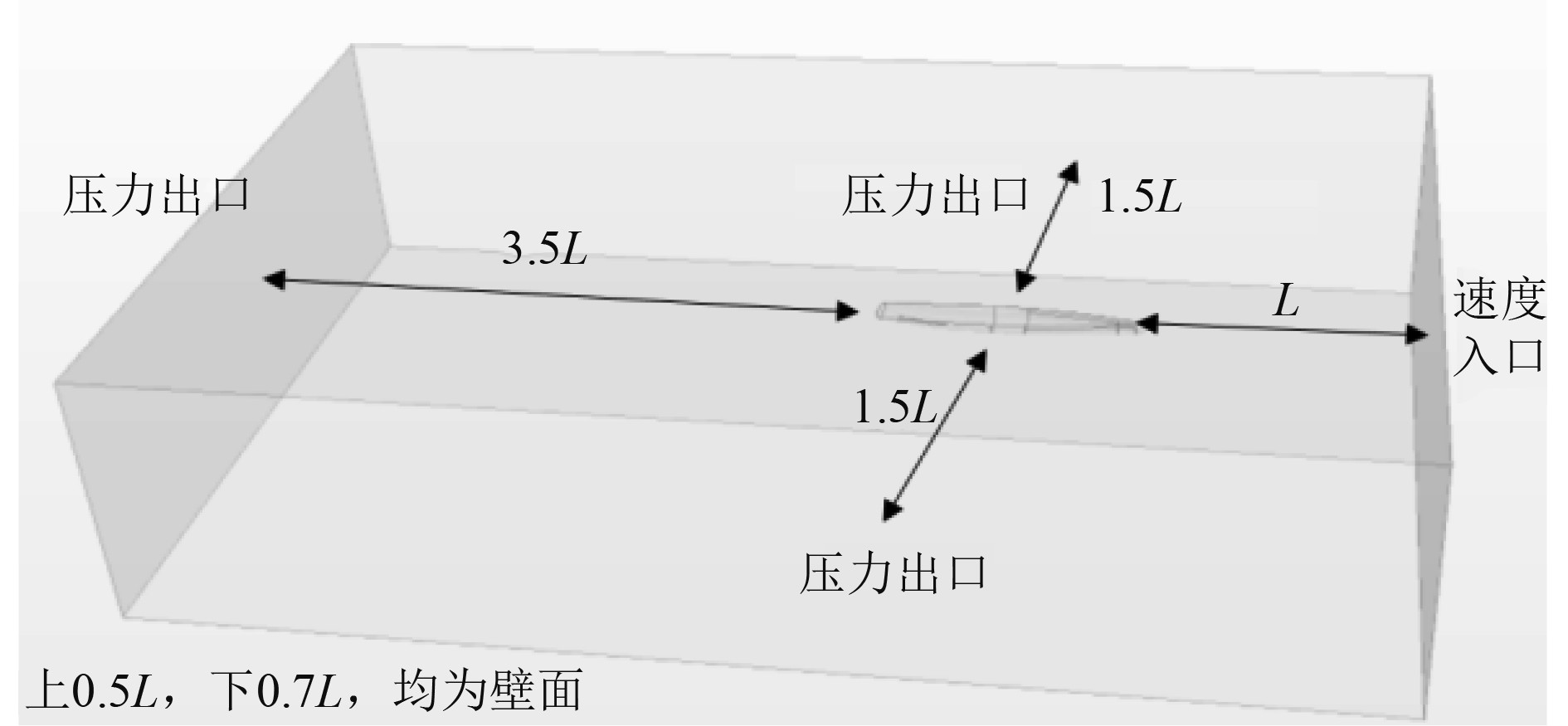
计算域结构外形及尺寸如图2所示。以船体长度L为基准，计算域全长为5.5L，计算域宽为3.0L。计算域前、后面均设置为压力出口；计算域上边界距离自由液面0.5L，下边界距离自由液面0.7L，2个边界均设置为无滑移壁面；船体表面设置为无滑移壁面边界条件，计算域左边界为压力出口，其距离船尾3.5L；计算域右边界为速度入口，其距离船首1.0L，速度大小由航速决定。

4 仿真结果 4.1 水面兴波特性

水面兴波在不同航速时呈现不同的流场特性，如图3所示。其差别主要体现在波高与波宽方面，船体周围兴波由初始时呈现的凯尔文波形逐渐发展成遍布水面的兴波。船尾波主要由横波和两波系的散波，横波逐渐向两侧发展，且随着平台以相同的航行速度前进。船行波的波长随着航速提高而增大，理论波长 $ \mathrm{\lambda } $ 计算公式如下：

$ \lambda =\frac{2\text{π} {v}^{2}}{g} 。$

(5-1)

式中： $ v $ 表示航速； $ \mathrm{g} $ 表示重力加速度。以此计算得到航速10 kn，20 kn，30 kn时波长分别为16.97 m，67.86 m，152.65 m。

水面平台船首横波的第1个波峰和船尾横波的第1个波峰之间的距离 $ mL $ 与航行速度的关系可以表示为：

$ mL=n\lambda +q\lambda 。$

(5-2)

式中： $ L $ 表示船长； $ n $ 为正整数； $ q $ 为正分数。

不同的 $ q $ 值可以反映出船舶航行时波浪对船体航行的影响，当 $ q $ =0.5时，船首波与船尾波相位差为 $\text{π}$ ，两波相抵消，船舶受波浪影响最小；当 $ q $ =0时，船首波与船艉波相位差为0，两波相叠加，船舶所受波浪影响最大，即所受兴波阻力越大，不同船舶会根据船舶尺度设计其对应的最佳航速。以上不同航速 $ n+q $ 分别为15.77，3.94，1.75，自由液面兴波仿真结果基本符合计算结果。理论分析表明，当航速为20 kn时，船体受兴波阻力影响最小。

4.2 阻力特性

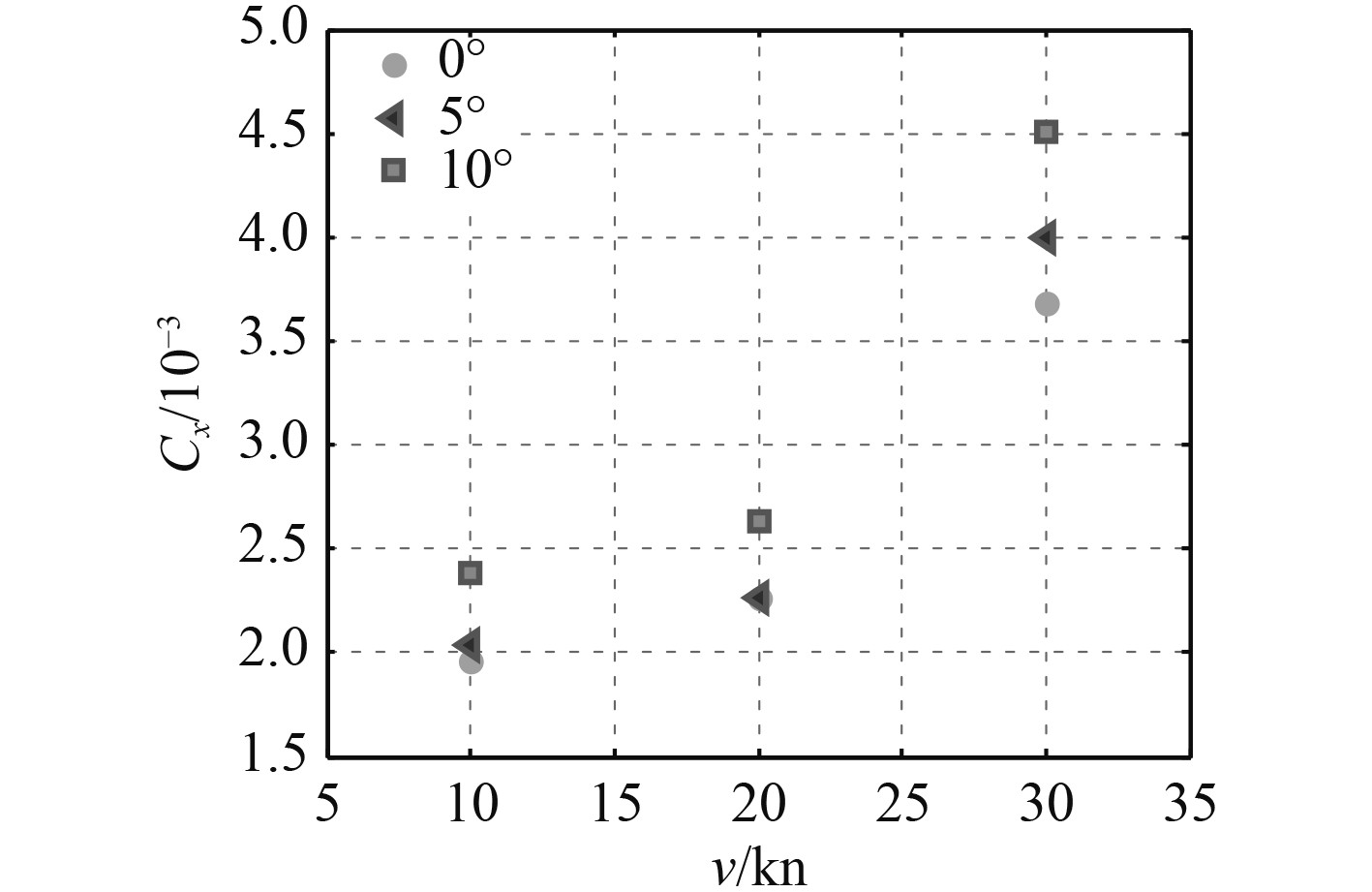
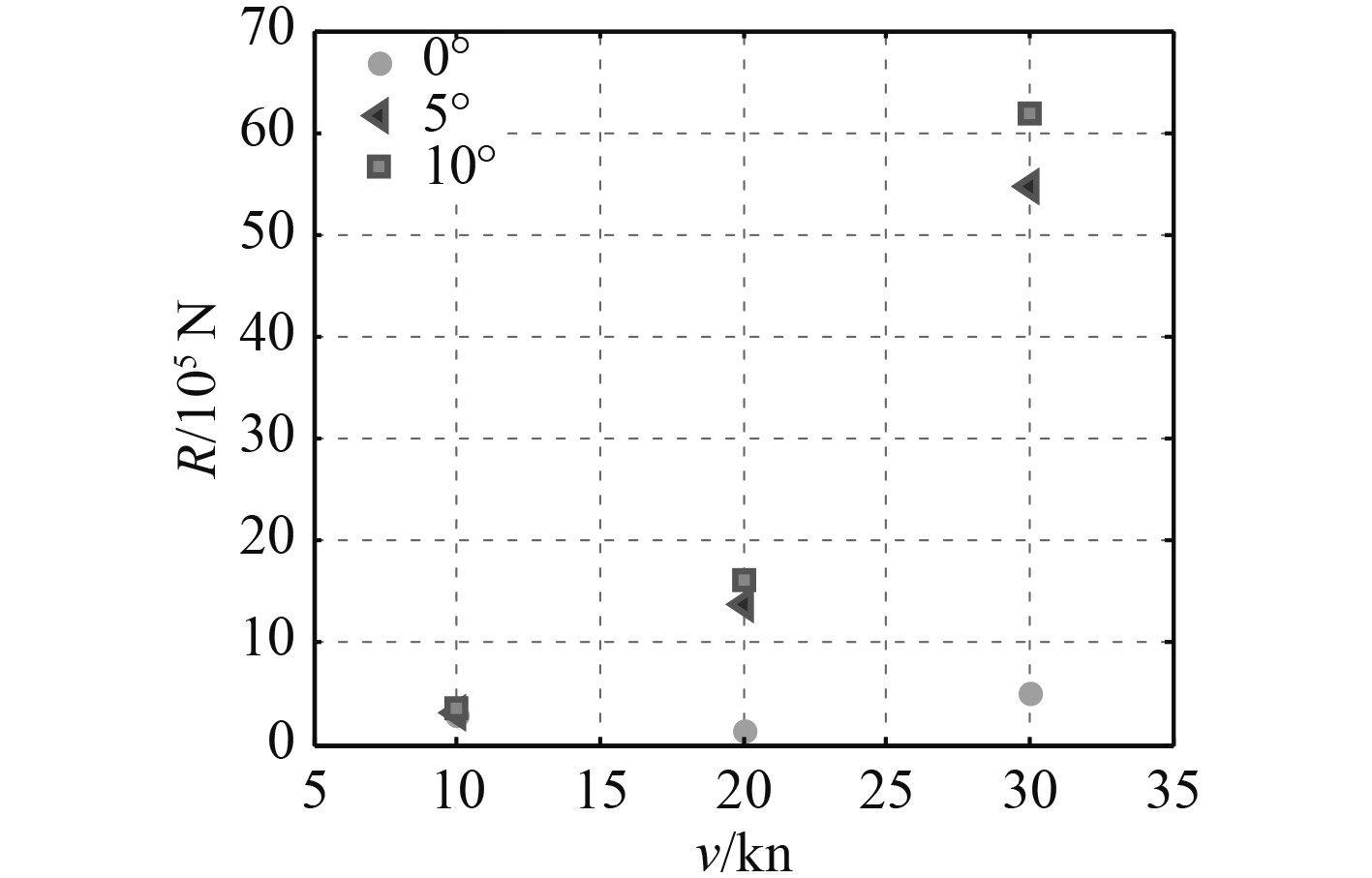
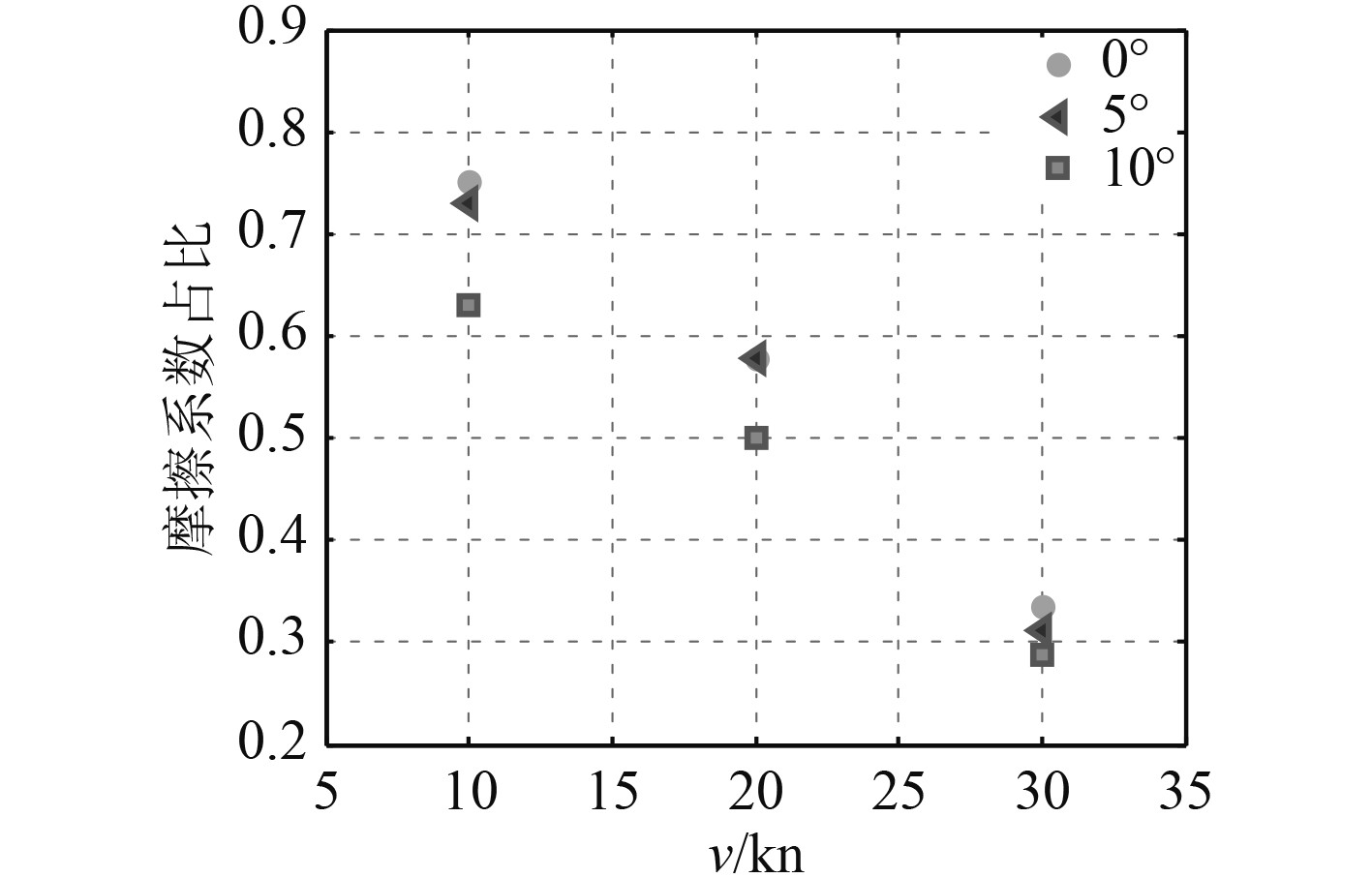
为了获得特大型船舶在不同航行工况下的阻力特性，图4及图5分别展示了阻力系数及阻力随航速、航向角的变化规律。为了研究水面兴波对船体阻力的影响特性，图6给出了不同工况下摩擦阻力占比，以分析不同航行工况下兴波阻力对船体的影响特性。

由图4及图5可知，随着航速及航向角的增大，船体总阻力显著增加。在无航向角、航速20 kn时船体总阻力明显小于其他航速工况，该航速为船体设计经济巡航速度，仿真结果进一步验证了该船体外形结构的合理性。由图6可知，摩擦阻力占比随着航速增大而显著减小，因为在以一定航向角航行时随着航速增大，船体兴波阻力和黏压阻力增大，而摩擦阻力仅与航速与沾湿面积相关。因此在航向角不变情况下，随着航速的增加，摩擦阻力占比减小。此外，在航速不变情况下，小航向角时，由于航向角改变而引起的沾湿面积变化较小，摩擦阻力占比几乎不随航向角（小角度范围内）而改变。

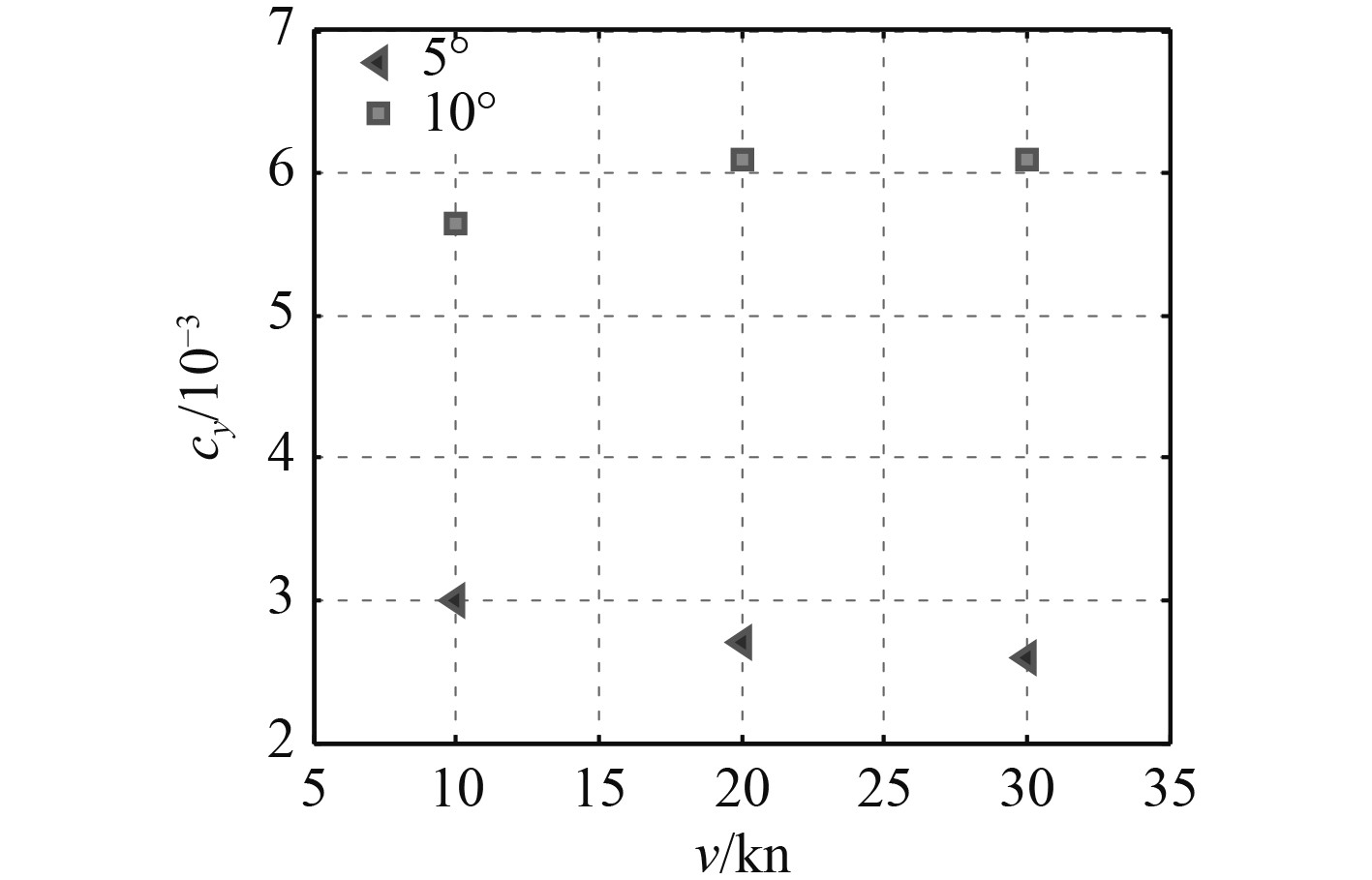
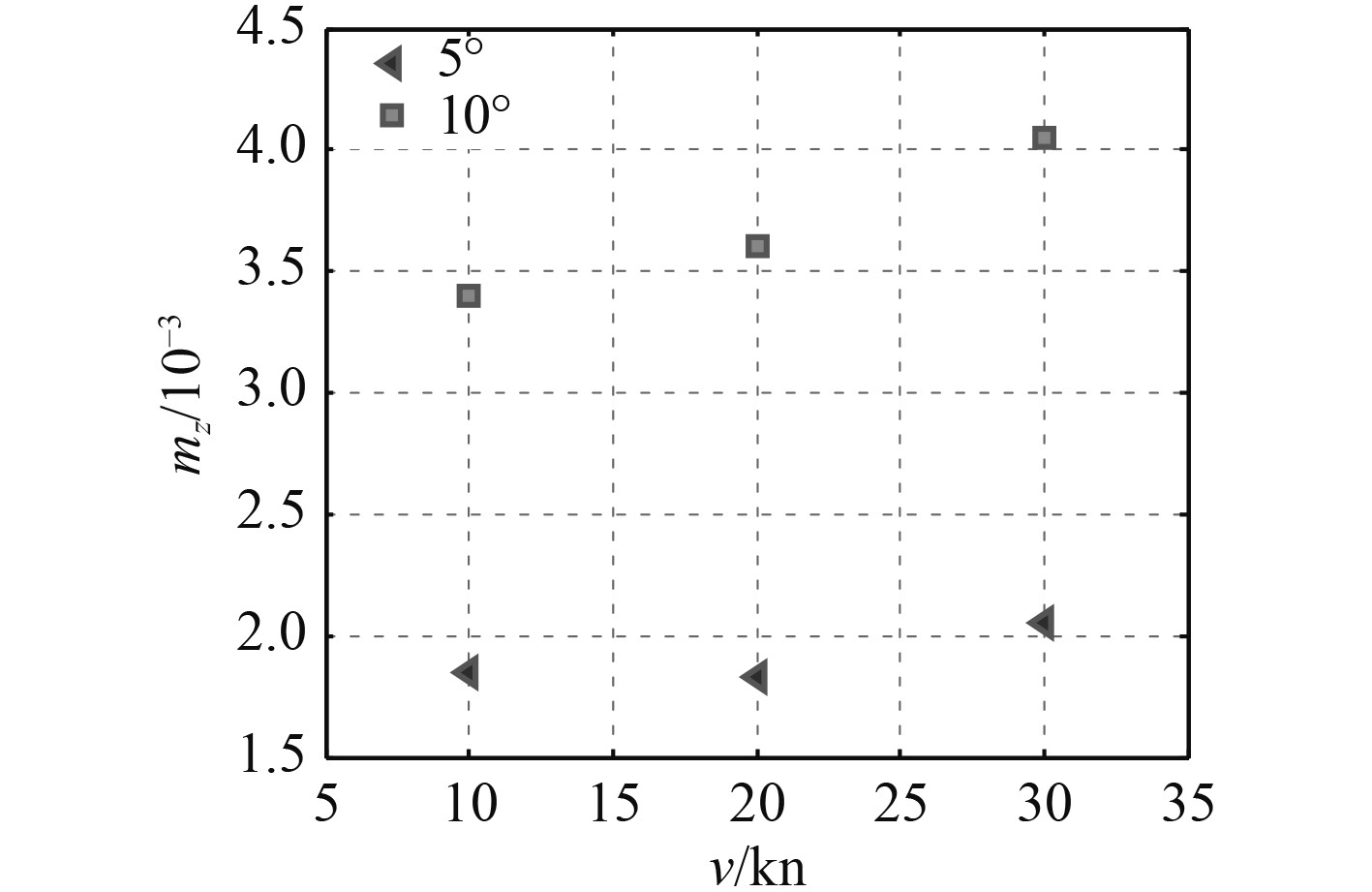
4.3 侧向力及力矩特性

为了研究船体的侧向力及侧向力矩特性，提取数值计算结果，并对数据进行处理，得到了不同航向角、航速对侧向力及力矩的影响特性，结果如图7和图8所示。当航向角为0时，船体周围流场呈现很好的对称性，随着航向角度的增加，船体周围流场不对称性逐渐加剧。航向角为正值时，左舷为迎流面，船艏区域左舷液面高于右舷，而船尾右舷压力略高于左舷，这一趋势随着偏航角增大而增大，引起两舷侧压力差值增加，其总侧向力也随之增大。

5 结　语

本文主要采用CFD软件STAR-CCM+对某特大型水面船舶在静水面以不同航速、航向角航行的流体动力特性开展了数值研究，主要结论如下：

1）获得了不同航速下流场兴波变化特性，对比理论计算和数值仿真，发现航速为20 kn时，船体受兴波阻力影响最小；

2）随着航速的增大以兴波阻力为主的黏压阻力的逐渐增加，使得船舶总航行阻力逐渐增大，且其中摩擦阻力占比逐渐减小；

3）随着船舶航向角的增加船体周围压力场分布规律会发生显著变化，导致船舶所受侧向力与侧向力矩随之增大，其主要由于船体周围压力场的变化引起。

本文研究结果可为大型水面平台的总体设计及船型优化工作提供参考。