涡激振动是土木工程、风工程和海洋工程中常见的流致振动现象。涡激振动通常是在非流线型断面交替脱落的漩涡及其脉动力的作用下发生的,当脉动力频率和结构固有频率接近时会产生涡激共振。Geller[1]分别采用格子玻尔兹曼法、有限元法和有限体积法计算了层流流动,并对3种方法所得到的结果进行比较,讨论了LBM算法的有效性。Sohankar[2]研究了低雷诺数下,计算了不同入射角下方柱绕流的涡脱形态以及边界条件对流场的影响。Arumuga[3]用格子玻尔兹曼法计算了二维不可压缩稳态和非稳态下的钝体绕流,研究了雷诺数、阻塞比和流场长度对方柱和圆柱绕流的影响。Regulski[4]等用格子玻尔兹曼法和谱元法对比研究了钝体绕流流场中的涡街特性。Namuro[5]等采用离散涡方法分析了钝体在空气动力学中的不稳定性,并模拟了方形截面柱体的驰振现象。Khalak[6]等研究了圆柱涡激振动中质量比和阻尼因子对振动幅值的影响。Okajima[7]通过实验研究了不同截面纵横比的矩形截面柱体在一定雷诺数(Re=70~20000)范围内斯托罗哈数St与雷诺数Re的关系。本文对低雷诺数下方柱的流致振动进行数值研究,重点研究了方柱的振动幅值等振动响应特性随折减速度的变换规律。
1 数值方法 1.1 流体控制方程采用格子玻尔兹曼法(lattice Boltzmann method, LBM)对流场部分进行求解。基于分子动理论的格子玻尔兹曼法属于介观方法,考虑的是大量微观粒子的平均运动状态。本文采用的是单松弛时间格式的二维九速度(D2Q9)模型,通过Boltzmann-BGK方程计算格子点上流体质点的速度分布函数,从而得到整个流场的宏观物理量。
| $ \begin{split}& {f_\alpha }\left( {{{\boldsymbol{r}}_i} + {{\boldsymbol{e}}_\alpha }{\delta _t},t + {\delta _t}} \right) = {f_\alpha }\left( {{{\boldsymbol{r}}_i},t} \right) - \frac{1}{\tau }\left[ {f_\alpha }\left( {{{\boldsymbol{r}}_i},t} \right) - \right.\\&\left.f_\alpha ^{eq}\left( {{{\boldsymbol{r}}_i},t} \right) \right] + \quad {\delta _t}F\left( {{{\boldsymbol{r}}_i},t} \right) 。\end{split}$ | (1) |
其中:ri表示某一时刻流体质点的位置;
对流固边界用浸入边界法计算,具体可参考文献[8]。流场采用欧拉网格,固体采用拉格朗日网格,欧拉网格点上的速度传播到附近的拉格朗日网格点的过程可以表示为:
| $ \dot X(t) = \int {{d^3}x{\boldsymbol{u}}({\boldsymbol{x}},t){{\Delta }}({\boldsymbol{x}} - {\boldsymbol{X}}(t))} ,$ | (2) |
拉格朗日力传播到附近流体欧拉点上的过程可表示为:
| $ {\boldsymbol{f}}({\boldsymbol{x}},t) = \int {{d^2}X{\boldsymbol{F}}({\boldsymbol{X}}(t),t)\delta ({\boldsymbol{x}} - {\boldsymbol{X}}(t))} 。$ | (3) |
物理模型如图1所示的弹簧质量模型,方柱为弹性支撑,可横向振动,来流速度为U,柱体纵向宽度为D,高度为H,雷诺数定义为
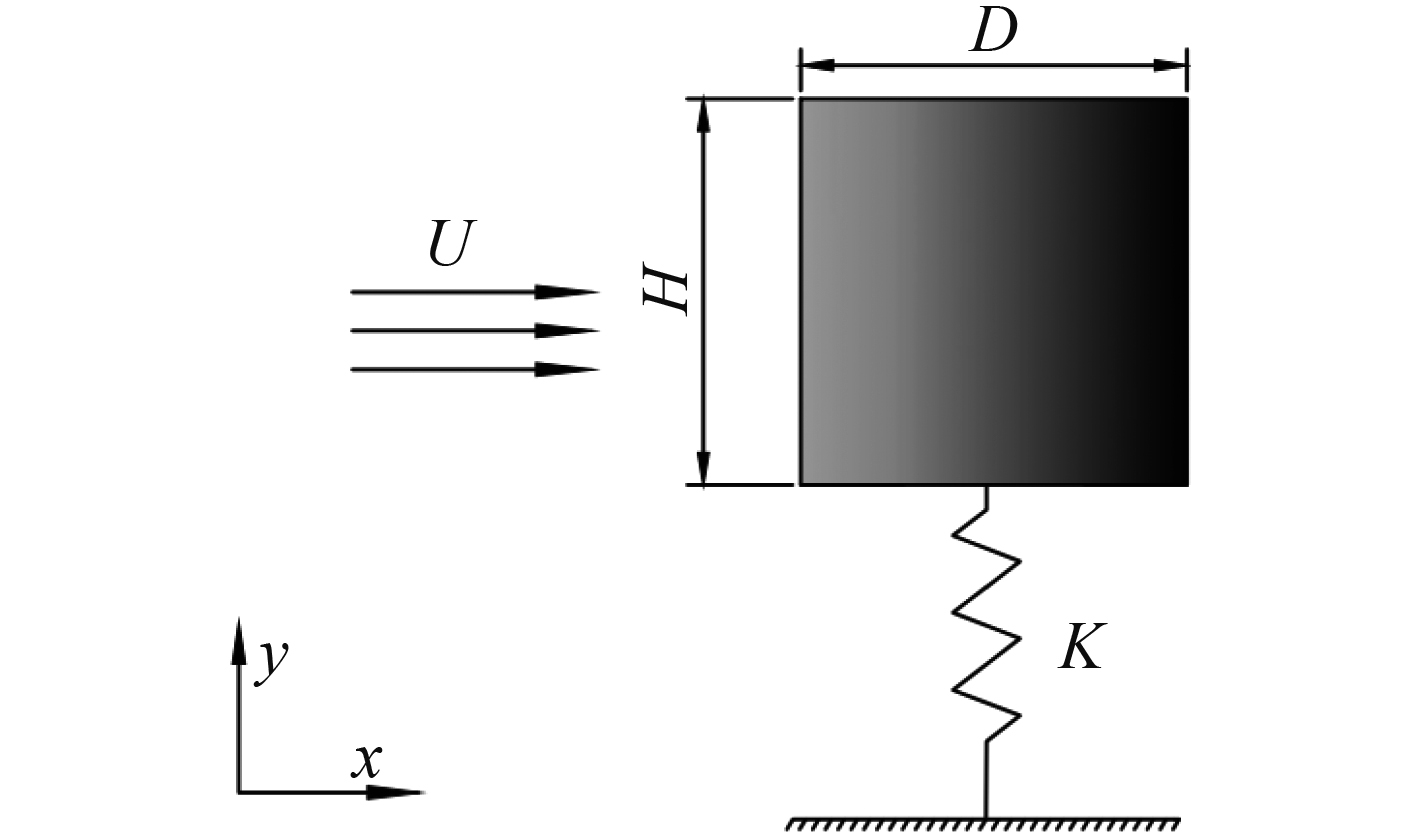
|
图 1 计算模型 Fig. 1 Calculation model |
| $ m\dfrac{{{\partial ^2}Y}}{{\partial {t^2}}} + kY = {F_y} 。$ | (4) |
式中:m为刚体质量;k为弹簧系统刚度;
假定计算模型在均匀来流、无壁面边界约束条件的流场中运动,将远场边界条件作为入口、上下边界;Neuman边界条件作为出口边界。为了避免流体穿越固体边界,拉格朗日网格节点间距应小于欧拉网格间距。为保证程序求解的有效性及计算效率,对不同计算区域下,均匀来流中方柱振动幅值以及对应的St数进行对比。
由表1结果可知:流场计算区域大小为
|
|
表 1 不同计算域下方柱的振动响应 Tab.1 Vibration responses of square cylinder in different computational domains |
为了考核程序的可靠性,利用Ansys-Fluent软件计算相同物理参数下的算例,并将横向位移时程曲线与LBM程序计算得到的结果对比。Fluent中流体采用的是SSTk-ω模型,在流固耦合的每一个时间步内,先求解流体控制方程,得到速度场、压力场以及作用在柱体上的升力,采用Newmark-β方法求解柱体动力学方程,将柱体速度通过Fluent动网格宏进行传递使网格获得速度。从图2可看出,2种计算得到的结果大致吻合。
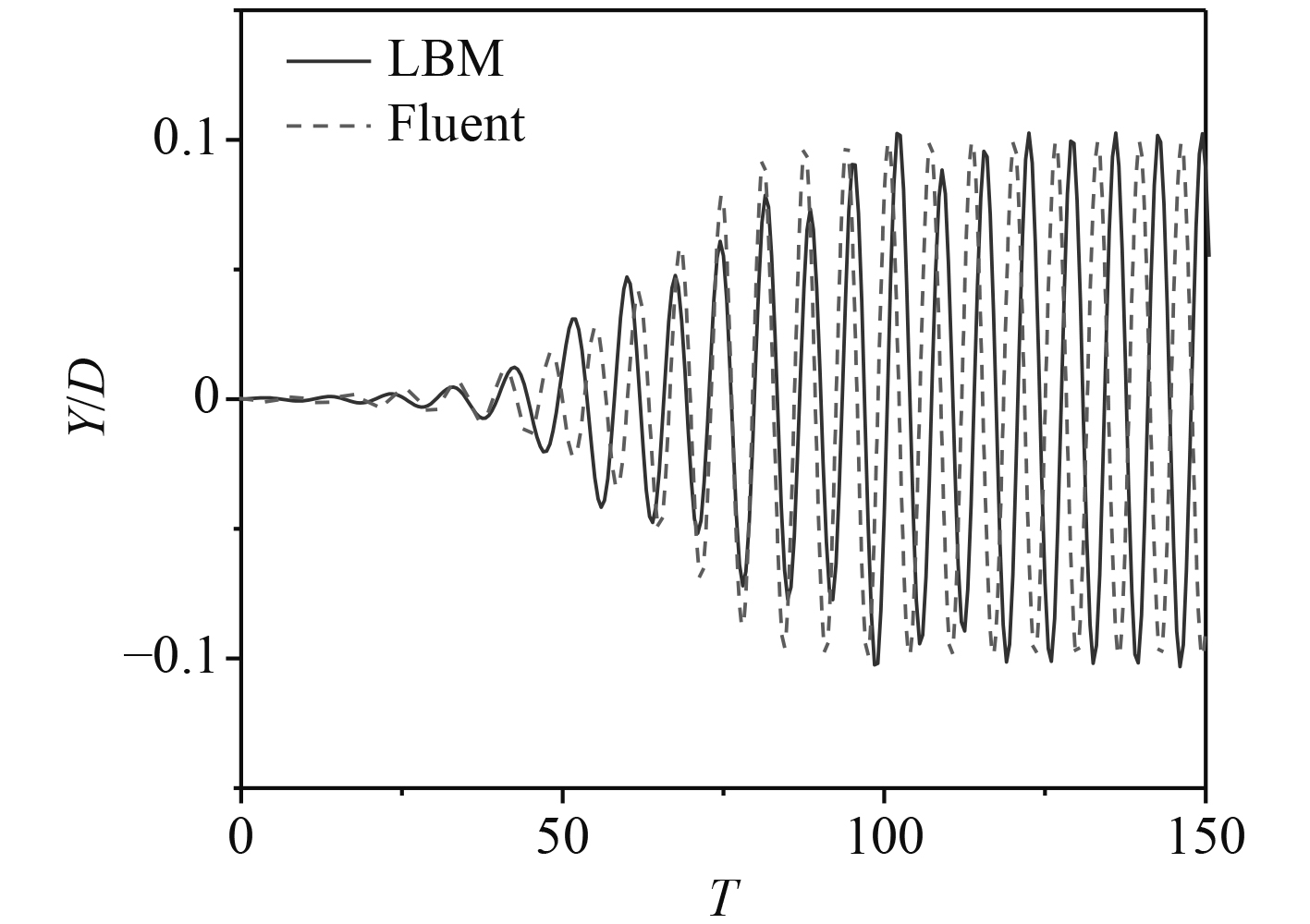
|
图 2 方柱振动位移曲线对比 Fig. 2 Comparison of vibration displacement curves of square column |
在对柱体的横向振动参数设置中,需要将LBM程序中的格子单位转换成物理单位。已知的物理量有流体密度ρf=1000 kg/m3,流体运动粘度υ=10−6m2/s。因此可得到对应的转换系数:Cρ=1000 kg/m3,Cυ=2.5×10−5m2/s。再根据给定仿真参数D=0.01 m,可得长度转换系数CL=2.5×10−4 m,因此质量转换系数和时间转换系数均可得到:CM=Cρ∙CL3=1.562×10−8 kg,Ct=CL2/ Cυ=0.0025 s。实际物理问题的各参数和对应转换系数如表2所示。
|
|
表 2 实际物理值及格子单位值 Tab.2 Physical value and LBM value |
计算在

|
图 3 静止方柱绕流涡量图 Fig. 3 Vorticity of flow around stationary square column |
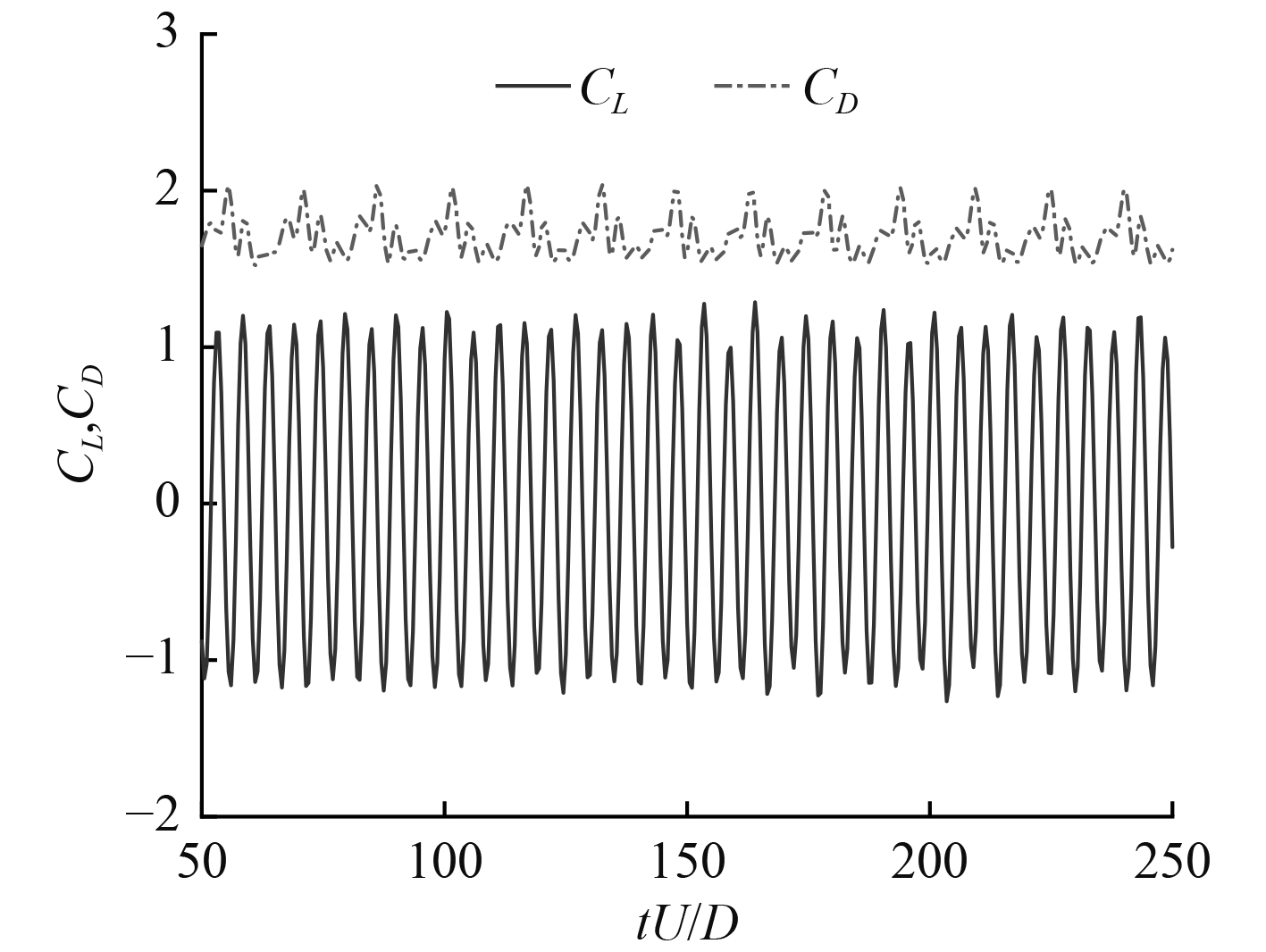
|
图 4 升阻力系数曲线图 Fig. 4 Curve of lift and drag coefficient |
| $ {C_L} = {F_y}/\left( {0.5\rho {U^2}D} \right),{C_D} = {F_x}/\left( {0.5\rho {U^2}D} \right) 。$ | (5) |
对升力系数做快速傅里叶变换(FFT)可得到方柱的涡脱频率
|
|
表 3 计算结果与已有文献对比 Tab.3 Calculated results compared with previous literature |
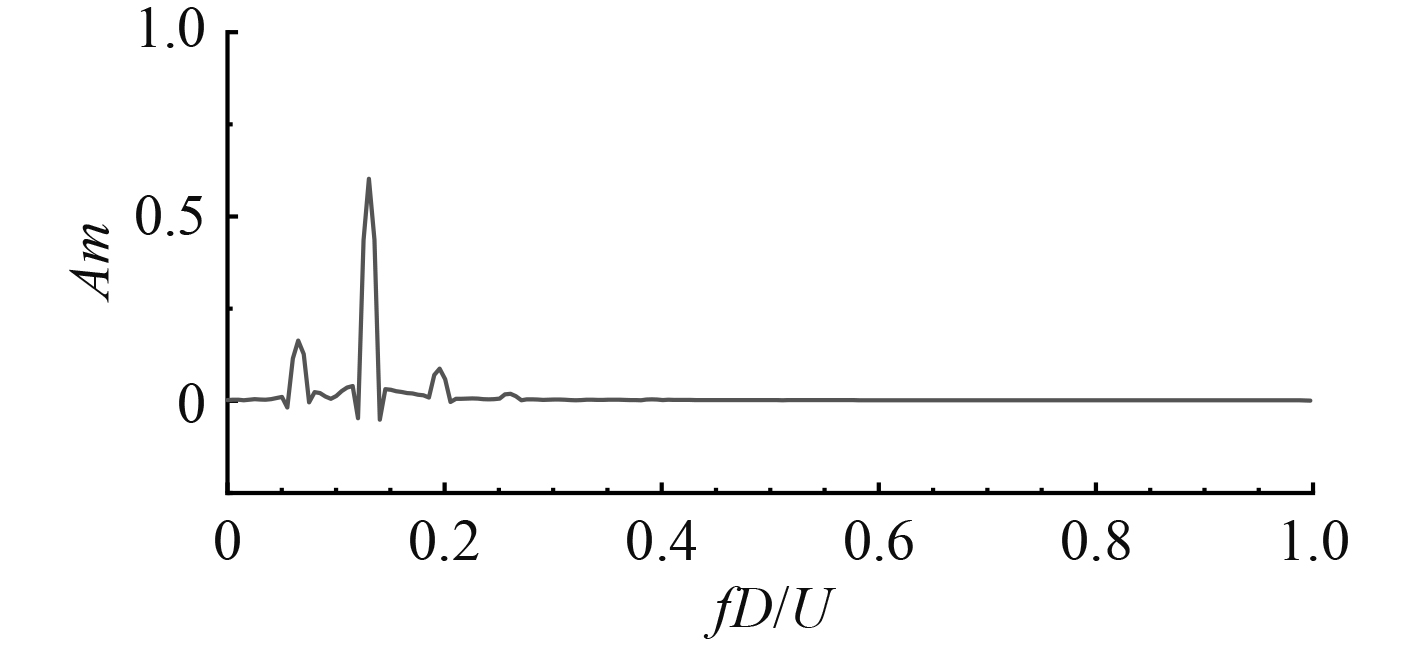
|
图 5 升力系数频谱 Fig. 5 Spectrum of lift coefficient |
为了讨论弹簧支撑的刚体梁振动响应特性与折减速度Ur的关系,折减速度定义为Ur=U/fnD。选取参数为Re=100,D=40,Mr=3进行数值模拟。矩形方柱运动的初始条件为位移和速度为0。
从图6可以看出,随着Ur的增加,方柱的振动幅度出现了明显的锁定区,在锁定区内,方柱振动的频率与其固有频率相接近,方柱发生共振,因此振幅较大。随后随着Ur的增加,方柱的振动频率比出现明显增大。
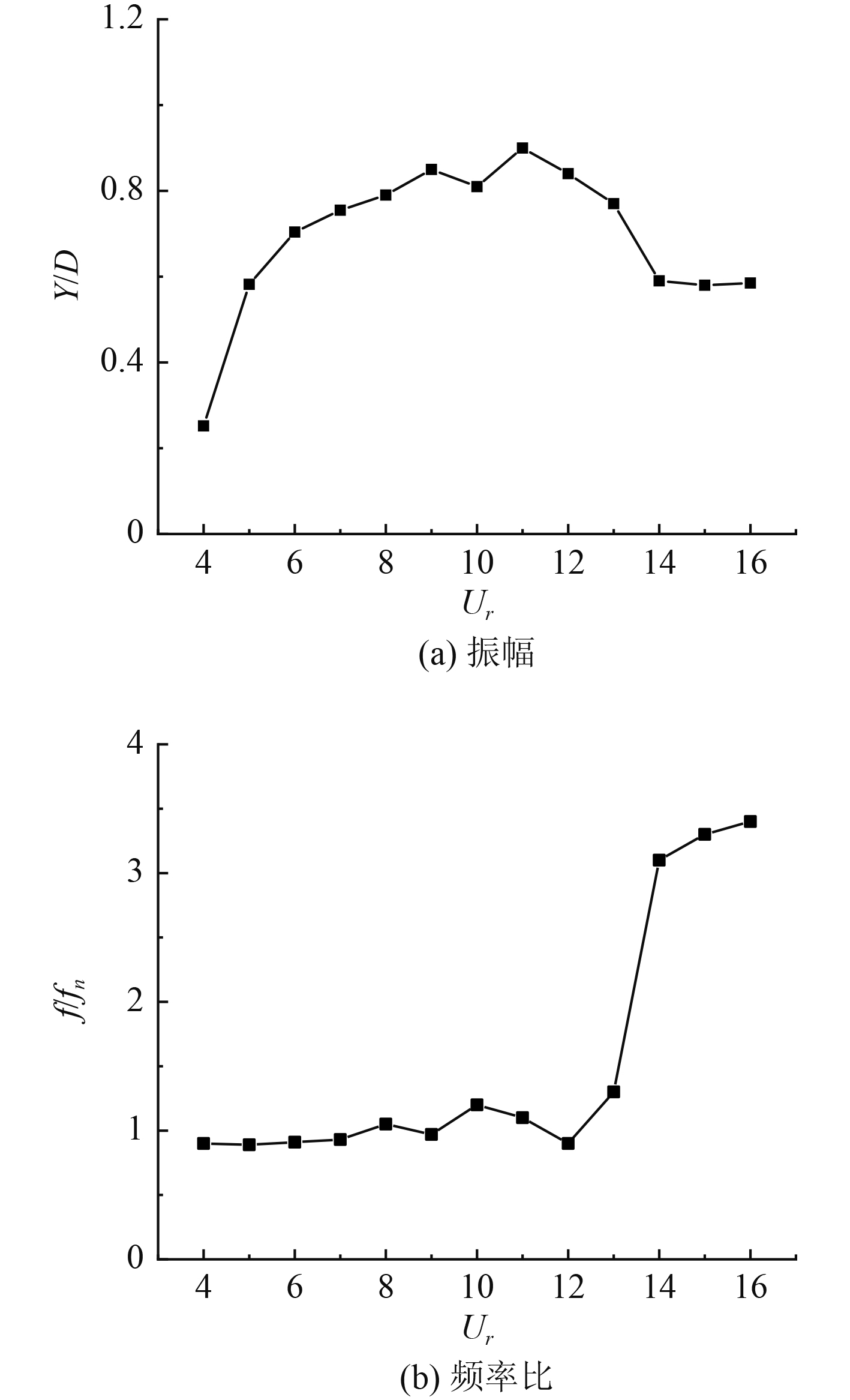
|
图 6 不同折减速度Ur下方柱的振幅比和频率比 Fig. 6 Amplitude and frequency ratios of square cylinder under different Ur |
图7为方柱不同折减速度下的位移与升力系数时程图。可以看出,在振动锁定区内,方柱存在2种振动状态,当Ur=7时,方柱平均升力系数不为零,此时方柱振动为驰振。当Ur=11时,方柱平均升力系数为零,驰振消失,由于此时振动频率接近固有频率,这是导致其振幅较大的主要原因。在锁定区外,Ur=16此时方柱为有规律的周期性振动,平均升力系数为0,振幅及脉动力系数周期恒定且上下对称,且相位一致,此时振幅较小。
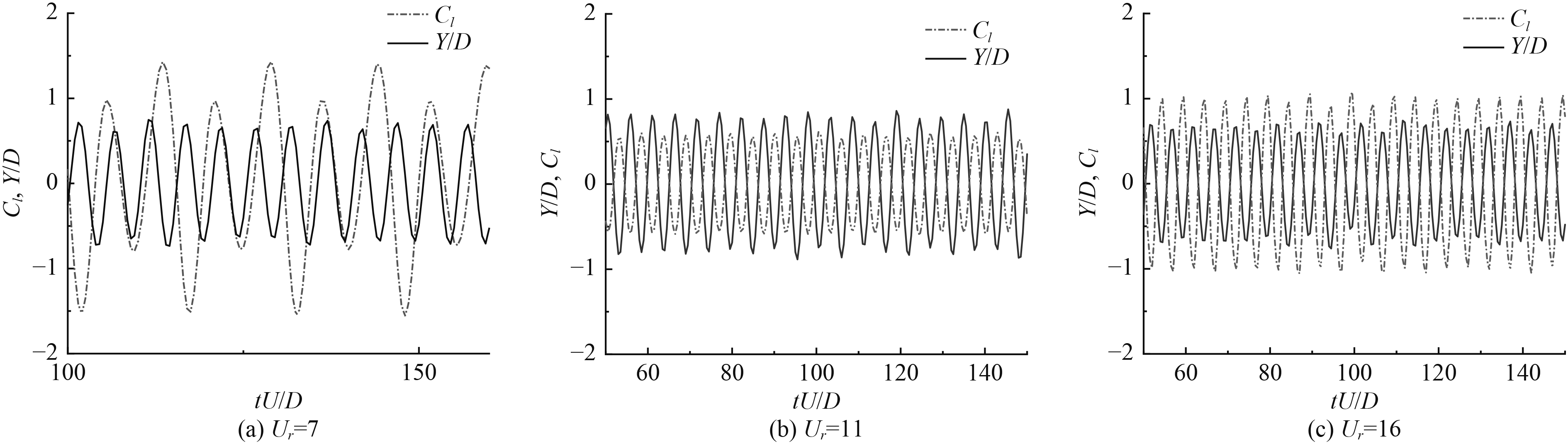
|
图 7 位移/升力系数时程曲线 Fig. 7 Displacement and lift coefficient time history curve |
图8显示了在某时刻所得的涡量图,当Ur=7,11时,此时的流态均为涡的相互作用模态,涡脱均发展为“2P”模式。当Ur=16时,出现“P+S”模式,即每个周期涡脱落一对符号相反的涡和一个单涡,由于方柱的振动,脱落下的涡被分裂或者合并形成的复杂模态。

|
图 8 弹性支撑方柱涡量图 Fig. 8 Vortex pattern in wake of elastic cylinder |
本文采用浸入边界-格子Boltzmann方法对弹性支承的方柱流固耦合问题进行了数值模拟,并将结果与基于有限体积法的Fluent软件计算结果进行对比,验证了程序的可靠性,得出以下结论:振动锁定区存在2种振动状态,一种是平均升力系数不为0导致方柱出现驰振,从而使振幅较大,一种是振动频率接近固有频率导致的振幅较大;随着折减速度Ur的增加,尾涡由“2P”模式发展为“P+S”模式。
| [1] |
GELLER S, KRAFCZYK M, TÖLKE J, et al. Benchmark computations based on Lattice-Boltzmann, finite element and finite volume methods for laminar flows[J]. Computers & Fluids, 2006, 35(8): 888-897. |
| [2] |
SOHANKAR A, NORBERG C, DAVIDSON L. Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition[J]. International Journal for Numerical Methods in Fluids, 1998, 26(1): 39-56. DOI:10.1002/(SICI)1097-0363(19980115)26:1<39::AID-FLD623>3.0.CO;2-P |
| [3] |
PERUMA D A, KUMAR G, DASS A K. Numerical Simulation of Viscous Flow over a Square Cylinder Using Lattice Boltzmann Method[J]. ISRN Mathematical Physics, 2012, 2012: 1-16. |
| [4] |
REGULSKI W, SZUMBARSKI J. Numerical simulation of confined flows past obstacles–the comparative study of Lattice Boltzmann and Spectral Element Methods[J]. Archives of Mechanics, 2012, 64(4): 423-456. |
| [5] |
INAMURO T, ADACHI T, SAKATA H. Simulation of aerodynamic instability of bluff body[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 46: 611-618. |
| [6] |
KHALAK A, WILLIAMSON C. Dynamics of a hydroelastic cylinder with very low mass and damping[J]. Journal of Fluids and Structures, 1996, 10(5): 455-472. DOI:10.1006/jfls.1996.0031 |
| [7] |
OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 2006, 123: 379-398. |
| [8] |
杨旖旎. 基于进入边界-格子玻尔兹曼方法的水下二维结构流固耦合计算研究[D]. 中国舰船研究院, 2021.
|
| [9] |
DAVIS R W, MOORE E F A. numerical study of vortex shedding from rectangles[J]. Journal of Fluid Mechanics, 1982, 116: 475-506. DOI:10.1017/S0022112082000561 |
 2022, Vol. 44
2022, Vol. 44

