2. 北方工业大学 机械与材料工程学院,北京 100144
2. School of Mechanical and Material Engineering, North China University of Technology, Beijing 100144, China
近年来,利用圆柱涡激振动从流动中获取能量的方法受到了学者们的大量关注和研究,其中包括了从风能中获取能量为城市传感器供电[1, 2],以及代替水平轴涡轮从河流或潮流流中获取能量[3-5]。虽然圆柱涡激振动问题的研究已经发展了几十年,对于圆柱涡激振动中的运动特征与受力特征都进行了深入的研究,但这些研究大多集中在低、中Re数范围内,而高Re数范围的研究较少。
从已有研究来看,决定弹性支撑圆柱涡激振动特征的主要因素是圆柱尾涡的结构特征,Williamson等[6]在2004年对圆柱涡激振动尾涡模式进行了较详细的总结,而影响圆柱尾涡结构特征的因素又包括了质量比m*、折合频率U*和Re数等,及春宁等[7]在2015年对这些参数的影响进行了较系统的汇总。
对较高Re数下的研究多集中在利用涡激振动提取流动动能方面。Bernitsas等[3-4, 8]对圆柱涡激振动潮流能装置进行了一系列实验研究,工作Re数在105左右,实现了发电功能,并对Re数、质量比、阻尼系数及折合速度等的影响进行了探讨。Chang等[9]在Bernitsas的基础上模拟了最高Re=1.2×105的圆柱涡激振动现象,加入了被动湍流控制方式,获得了最高达2.9的振幅比。Ding等[10]则对Chang的工作进行了数值仿真分析,发现了更多复杂的尾涡结构。Zhu等[11]采用数值方法模拟了带鳍型突起圆柱的涡激振动现象,同样起到控制湍流的目的,其工作Re数最高达到了1.5×105,得到了较高的振荡幅度,且振幅随折合速度的增大而持续增大。此外,还有诸多面向其他钝型结构及多自由度的流固耦合现象研究。
从以上研究来看,高Re数弹性支撑圆柱的流固耦合现象十分复杂,目前还没有较统一的认识。为了丰富高Re数圆柱涡激振动的研究基础,以及指导后续的涡激振动潮流能装置研究,本文对Re数为105量级圆柱涡激振动现象进行数值模拟研究。
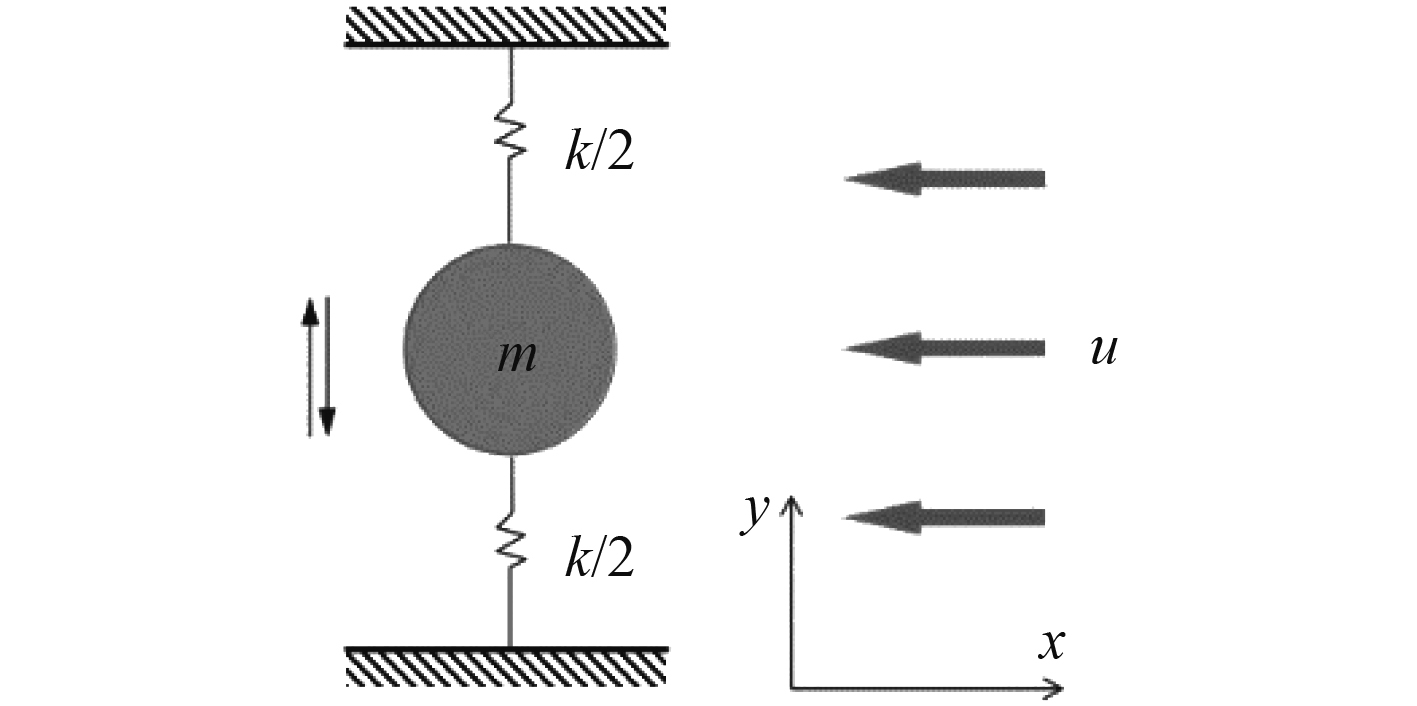
1 数值方法 1.1 数值模型本文采用二维弹性支撑圆柱模型,如图1所示。圆柱直径D=0.2 m,来流速度u=0.2~1.4 m/s,对应Re数约为0.4×105~2.8×105之间。圆柱在Y方向受弹簧支撑,单位长度圆柱上的弹簧刚度系数设定为k=1000 N/m。圆柱在X方向运动和绕Z轴方向旋转运动通过数值方法约束固定不动。
|
图 1 弹性支撑圆柱简化模型 Fig. 1 Simplified model of elastic supported model |
在有来流情况下,圆柱后产生周期性脱离涡,圆柱升力(即Y方向受力)也会周期性的变化,因而驱动圆柱在Y方向产生振动,而圆柱振动又改变圆柱受到的水动力。最终,弹性支撑圆柱在水流中形成一个自激振荡系统。设定系统阻尼为0,系统动力学方程可表示为:
| $ \left(m+{m}_{a}\right)\ddot{y}+ky={F}_{h}\left(t\right)。$ | (1) |
式中:Fh为圆柱受到的水动力作用;m为圆柱质量;ma为圆柱附加质量;
通过联立求解流体动力学方程和弹性支撑圆柱的动力学方程,可以得到圆柱涡激振动流场,及其受力与运动曲线。其中,圆柱动力学方程前文已经介绍,这里给出流体动力学方程。采用积分型不可压粘性流体动力学方程,不考虑重力因素,连续方程和动量方程分别为:
| $ \underset{S}{\oint }\overrightarrow{v}\cdot {\rm{d}}\overrightarrow{S}=0,$ | (2) |
| $ \dfrac{\partial }{\partial t}\underset{\varOmega }{\int }{\nu }_{i}{\rm{d}}\varOmega +\underset{S}{\oint }{v}_{i}\overrightarrow{v}\cdot {\rm{d}}\overrightarrow{S}=\dfrac{1}{\rho }\underset{S}{\oint }{\tau }_{ij}{\rm{d}}{S}_{j}-\frac{1}{\rho }\underset{S}{\oint }p{\rm{d}}\overrightarrow{S} 。$ | (3) |
式中:Ω表示单元体积;Sj表示单元面积矢量S的各个分量;vi表示速度矢量v的各个分速度;τij为总粘性应力张量的各个分量;p为压强。
采用FINE/Marine求解器,能够实现本文中流体动力学方程和圆柱动力学方程的联立求解,该求解器在一个时间步长内采用内部隐式迭代来保证较强的流动/运动耦合。采用Menter的SST k-ω 湍流模型,以精确模拟圆柱分离情况。
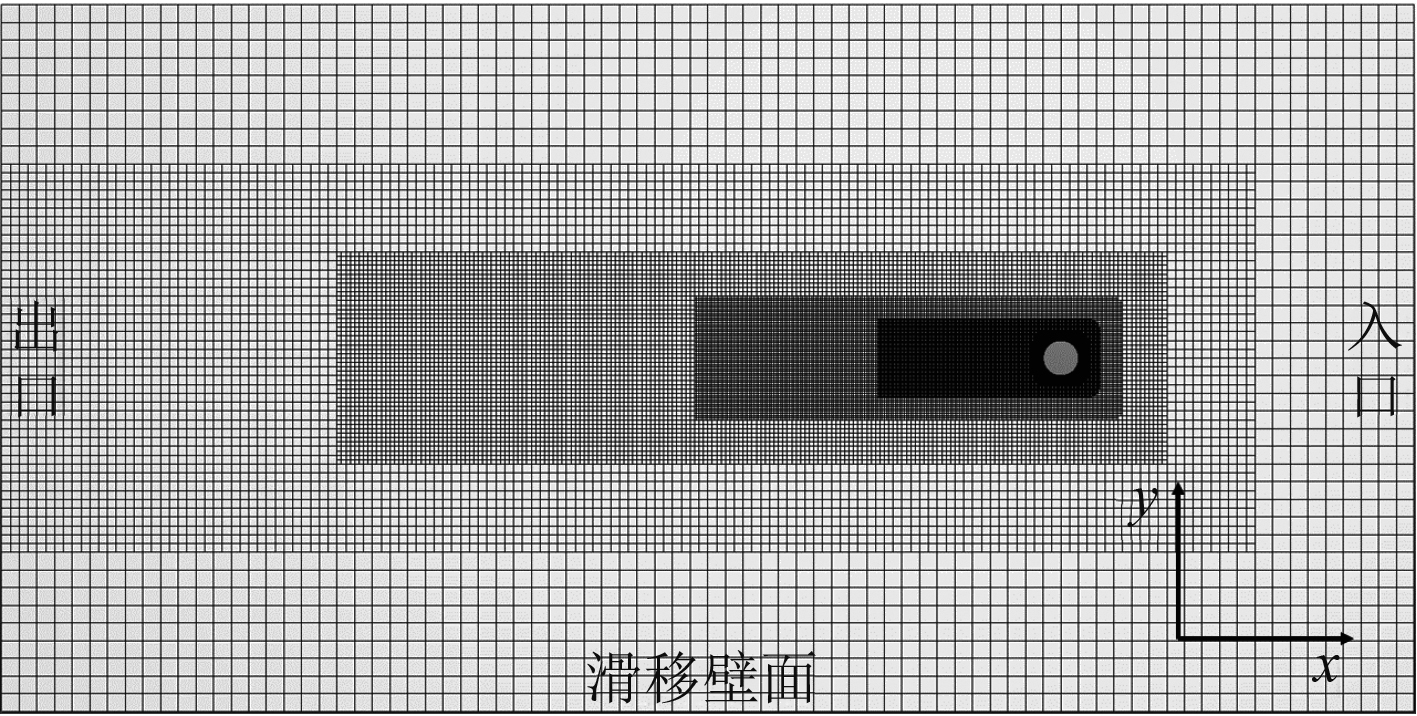
1.3 流域网格及边界条件流域如图2所示,模拟循环水池中的流动情况,上下边界给定为滑移壁面,右侧给定来流速度作为入口,左侧压力与速度外推作为出口。当圆柱在Y方向发生振动,网格随圆柱刚性运动,即在相对坐标系下对方程进行求解。
|
图 2 计算域及逐次加密的网格 Fig. 2 Computational domain and the grid of progressively increasing density |
流域总尺寸为20 D×40 D,圆柱处于流道中心、距进口10D的位置。流域的堵塞率为5%,与现有研究对比,如Raghavan等[8]的实验研究,已经足够小。并经过数值验证,该流域大小不会对圆柱的涡激振动现象产生影响。
网格采用逐次加密的方式,最终形成四边形为主的混合网格。在圆柱尾迹中进行逐次加密能够保证在分离的初始发展阶段进行更精确的模拟,而在后续发展阶段,当漩涡尺寸逐渐增大,降低网格密度以减少工作量。在需要精确分辨漩涡的情况下,增大加密区域,并不会影响圆柱的振动特征。
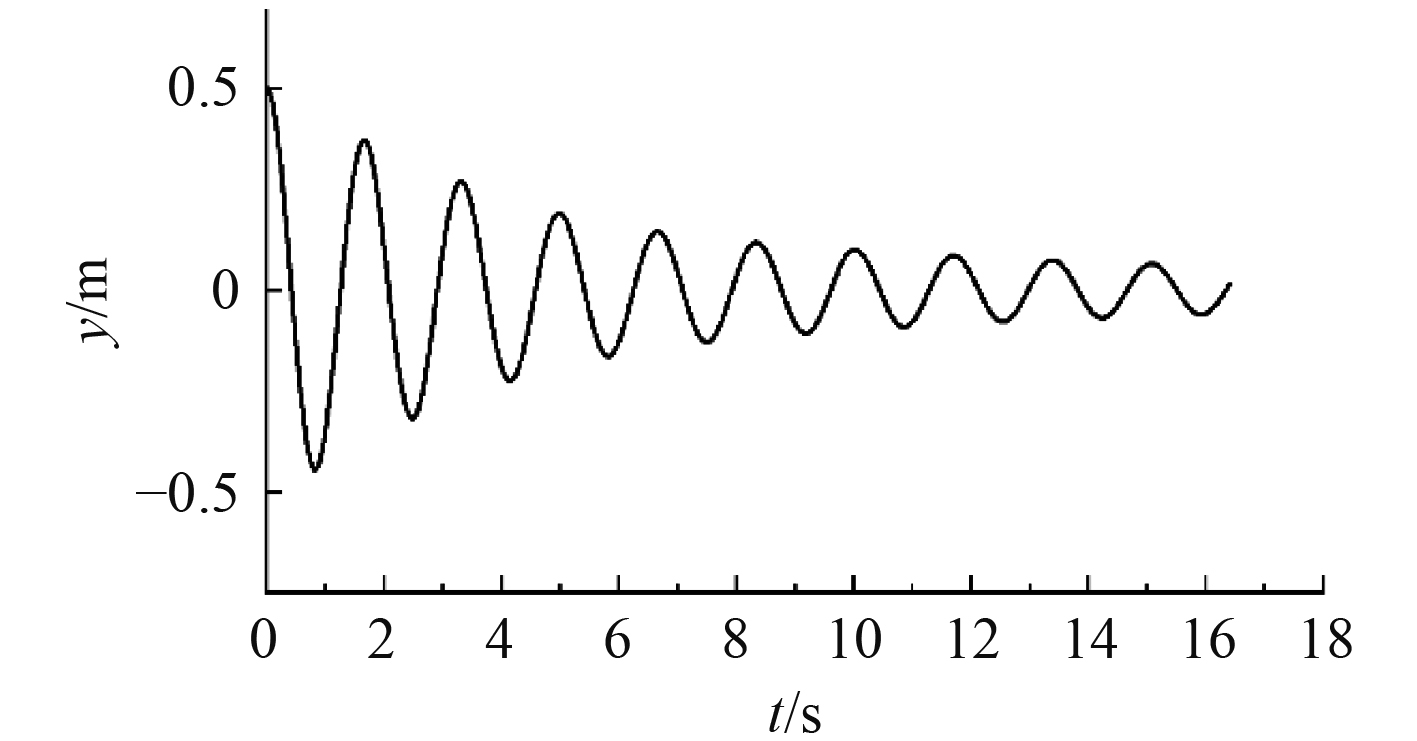
1.4 数值方法验证首先模拟圆柱在静止水域中的自由衰减运动。Y方向初始位移为1.5 D,即0.3 m,单位长度质量40 kg。其运动曲线如图3所示。通过对运动曲线的分析,可得圆柱自由衰减运动的周期T=1.67 s,这与理论解几乎是一致的。理论解计算公式为:
|
图 3 圆柱自由衰减运动曲线 Fig. 3 Free decaying motion curve of cylinder |
| $ T=2\text{π} \sqrt{\frac{m+{m}_{a}}{k}} 。$ | (4) |
而后与Raghavan等[8]的实验结果进行了对比。Raghavan采用的圆柱直径为127 mm,长914.4 mm,其工作Re数、质量比m*及折合速度U*的范围都与本文都十分接近。质量比和折合速度的定义分别为:
| ${m}^{*}=\frac{m}{{m}_{a}},{U}^{*}=\frac{u}{{f}_{N}D} ,$ | (5) |
其中,fN为圆柱在水中的自由振荡频率,即1/T。
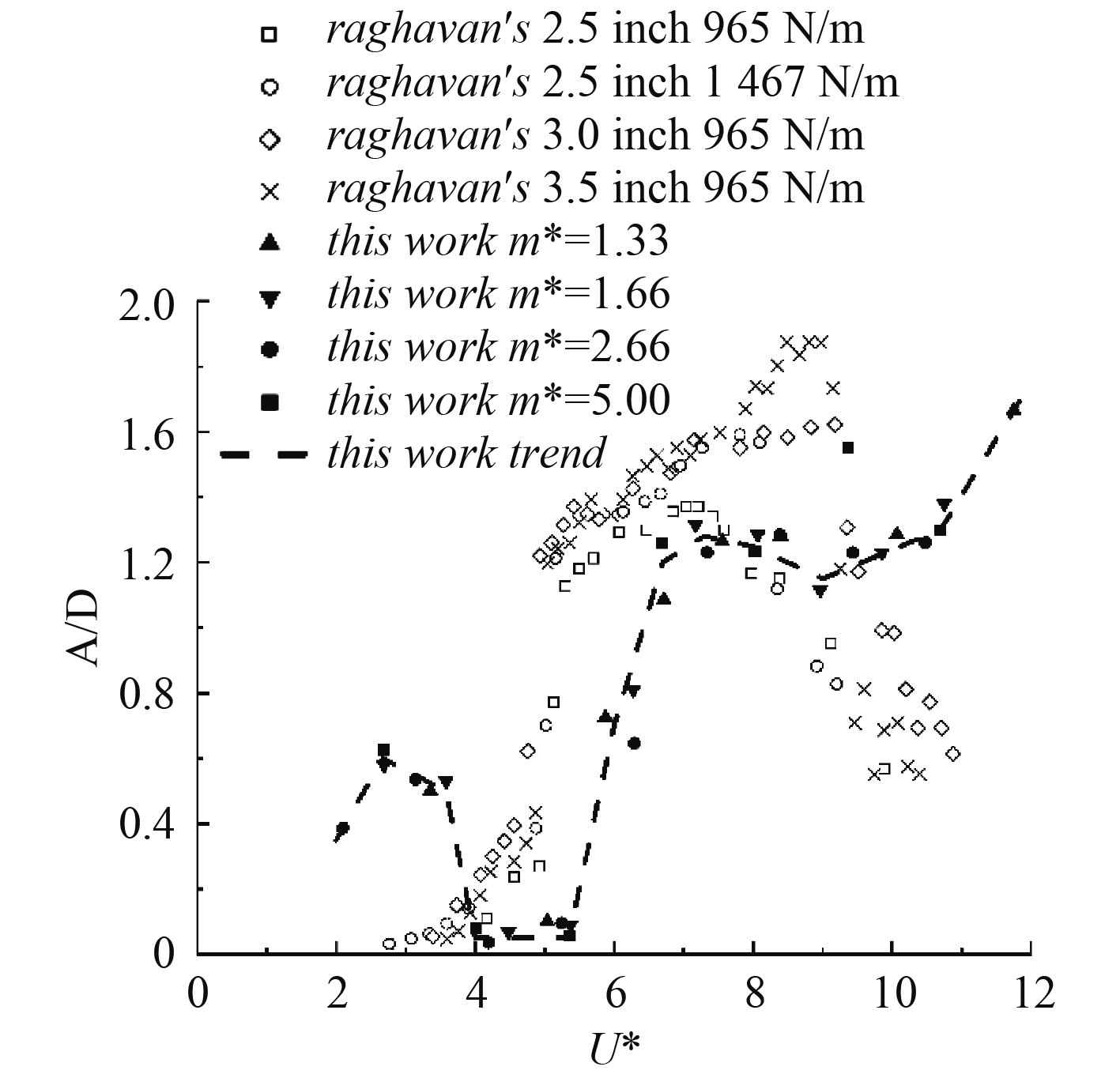
本文模拟圆柱在4个质量比m*,不同折合速度U*下的振幅曲线,与Raghavan等[8]的测量结果进行了对比,如图4所示,A为振幅。由于圆柱每次振荡的幅度都不完全相同,有时甚至2次振荡之间的幅度差别较大,定义振幅A为N次振荡幅度的平均值,表示为:
|
图 4 本文数值结果与Raghavan[8]实验结果的对比 Fig. 4 Comparison between the numerical results and Raghavan's experimental results[8] |
| $ A=\frac{1}{N}\sum _{N}\Delta y 。$ | (6) |
其中,Δy为圆柱一次振荡中从一侧极限位置运动到另一侧极限位置的位移。
从图中可以看出,在二者都存着初始分支和上分支,2个分支之间存着跳跃现象,并且振幅相当;二者都没有明显的下分支。可以初步判断本文采用的数值方法是较为可靠的。
2 结果及分析 2.1 振幅特征分析分析4组质量比情况下振幅随折合速度的变化趋势散点图,并拟合了4组数据的趋势线,如图4所示。相比于Raghavan[8]的实验结果,本文结果的不同之处体现在以下几个方面:
1)从初始分支到上分支之间的跳跃位置不同。在Raghavan的结果中,初始分支到上分支的跳跃范围大致在U*=4.7~5.5之间,而本文模拟结果中的跳跃范围大致在U*=5.4~6.7之间,相比之下,前者的跳跃更陡峭,并且本文数值结果中跳跃对应的折合速度U*略微偏大。
2)在较低的折合速度U*,本文的结果中出现了新的分支,这里称之为“左分支”,其振幅比在0.55附近,出现区间大致在折合速度U*=3.0附近。尽管这一现象在现有的研究中还十分少见,但通过湍流控制,如Ding[10]和Zhu[11]工作,能够实现在较低折合速度下的明显振荡。考虑到数值模拟圆柱分离有一定的局限性,还需要进一步的实验来验证。
3)在较高的折合速度U*区间,圆柱振幅没有如低Re情况下出现的下分支,这一点与Raghavan的实验结果是一致的。但Raghavan的实验结果在较高折合速度时振幅迅速降低,而本文数值结果在较高折合速度时出现了上翘的现象,这一点也与Ding和Zhu的湍流控制圆柱涡激振动特征类似。
针对图4中出现的几个分支现象,分别对其尾涡与受力特征进行对比分析。
2.2 初始分支分析结果中初始分支对应的折合速度在U*=4.0~5.4范围,对应Re数在0.8~1.2×105范围。分别在4个质量比下各选取了一个工况进行了对比,各工况参数如表1所示,其尾涡如图5所示。
|
|
表 1 初始分支不同质量比下的4个工况 Tab.1 Four working conditions with different mass ratios of initial branches |

|
图 5 初始分支不同质量比下的尾涡结构 Fig. 5 Wake vortex structures with different mass ratios of initial branches |
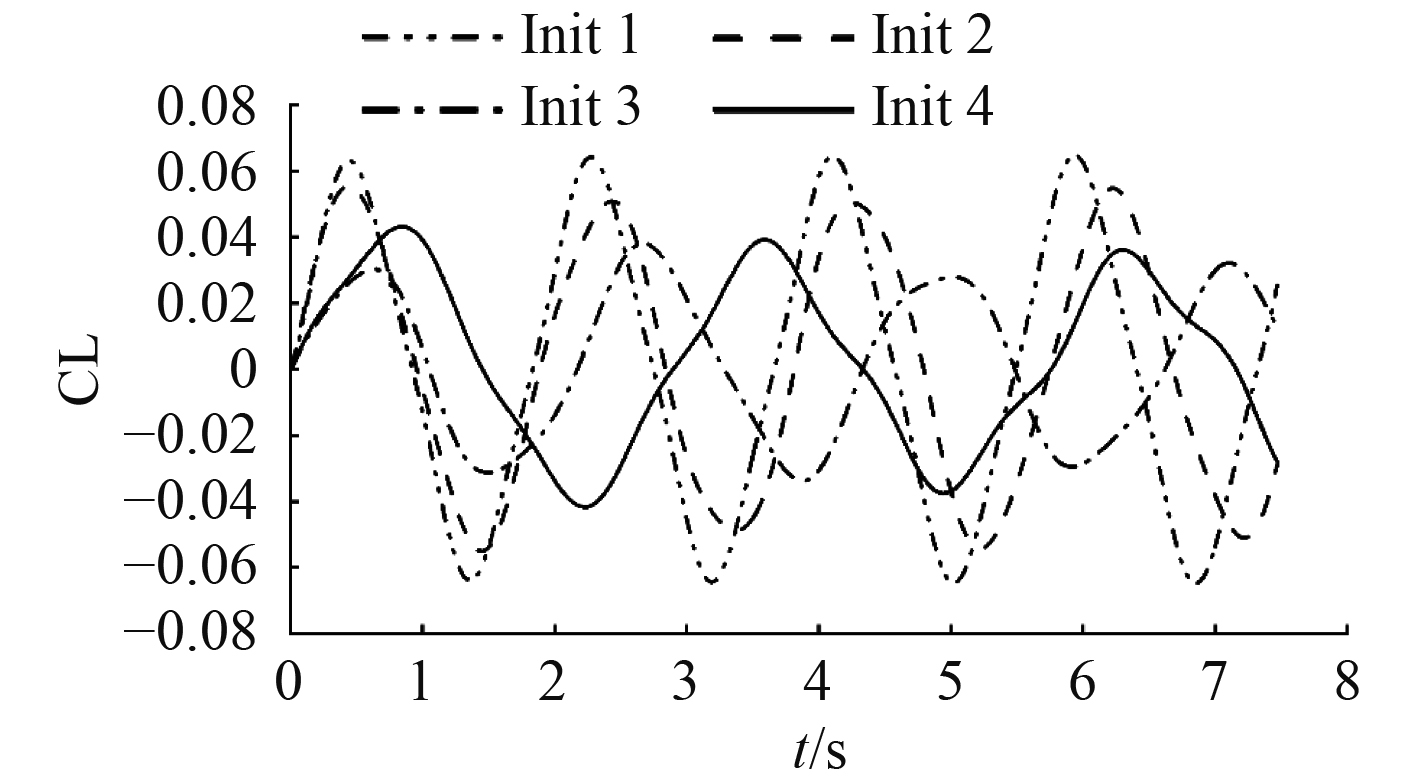
从图中可以看出,各工况下的圆柱尾涡都呈现2S(一个周期内正反各一个涡)结构,尾涡范围较窄。图6给出了对应的升力系数曲线,可以看出,此时升力系数普遍较低,最大升力系数只有约0.06。随质量比的增大,升力的波动周期逐步增大,但无量纲频率都集中在0.91~0.96范围内,如表2所示。由此可以判断,导致初始分支振幅较小的主要原因是圆柱升力波动幅度过小。
|
图 6 初始分支不同质量比下的升力系数曲线 Fig. 6 Lift coefficient curves under different mass ratios of initial branch |
|
|
表 2 初始分支不同质量比下的无量纲频率对比 Tab.2 Dimensionless frequency comparison at different mass ratios of initial branch |
考虑到质量比对上分支的影响较小,选取质量比m*=1.33情况下4个工况进行对比分析,对应折合速度分别为U*=7.56,8.40,10.1,11.8。
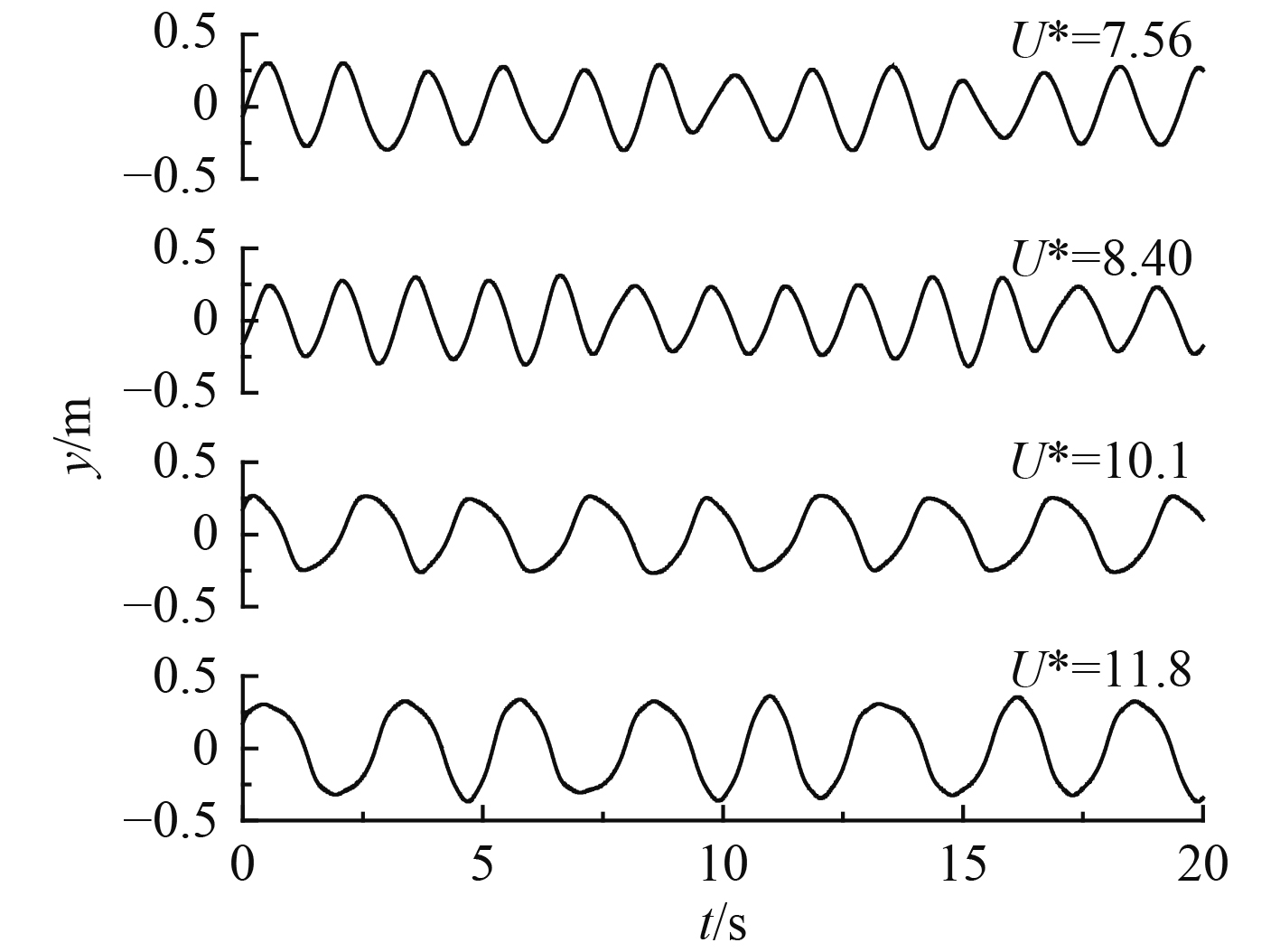
首先观察弹性支撑圆柱在4个折合速度下的Y向运动曲线,选取各自充分发展后的一段时间,如图7所示。可以看出,圆柱在U*=7.56和U*=8.40两个工况下的振荡频率明显较高,而在U*=10.1和U*=11.8两个工况下的振荡频率较低。通过分析,得到4个工况下的无量纲频率f*,如表3所示。相比前两者,后两者的无量纲频率出现明显的向下跳跃。对比现有研究结果,在较高Re下,大多数研究探讨的是圆柱脱落频率[3, 8],而少有分析圆柱运动频率,这一点需要进一步研究以证实。
|
图 7 上分支四个折合速度下的运动曲线(m*=1.33) Fig. 7 Motion curves at four reduced velocities of upper branch |
|
|
表 3 上分支不同折合速度下的无量纲频率(m*=1.33) Tab.3 Dimensionless frequencies at different reduced velocities of upper branch(m*=1.33) |
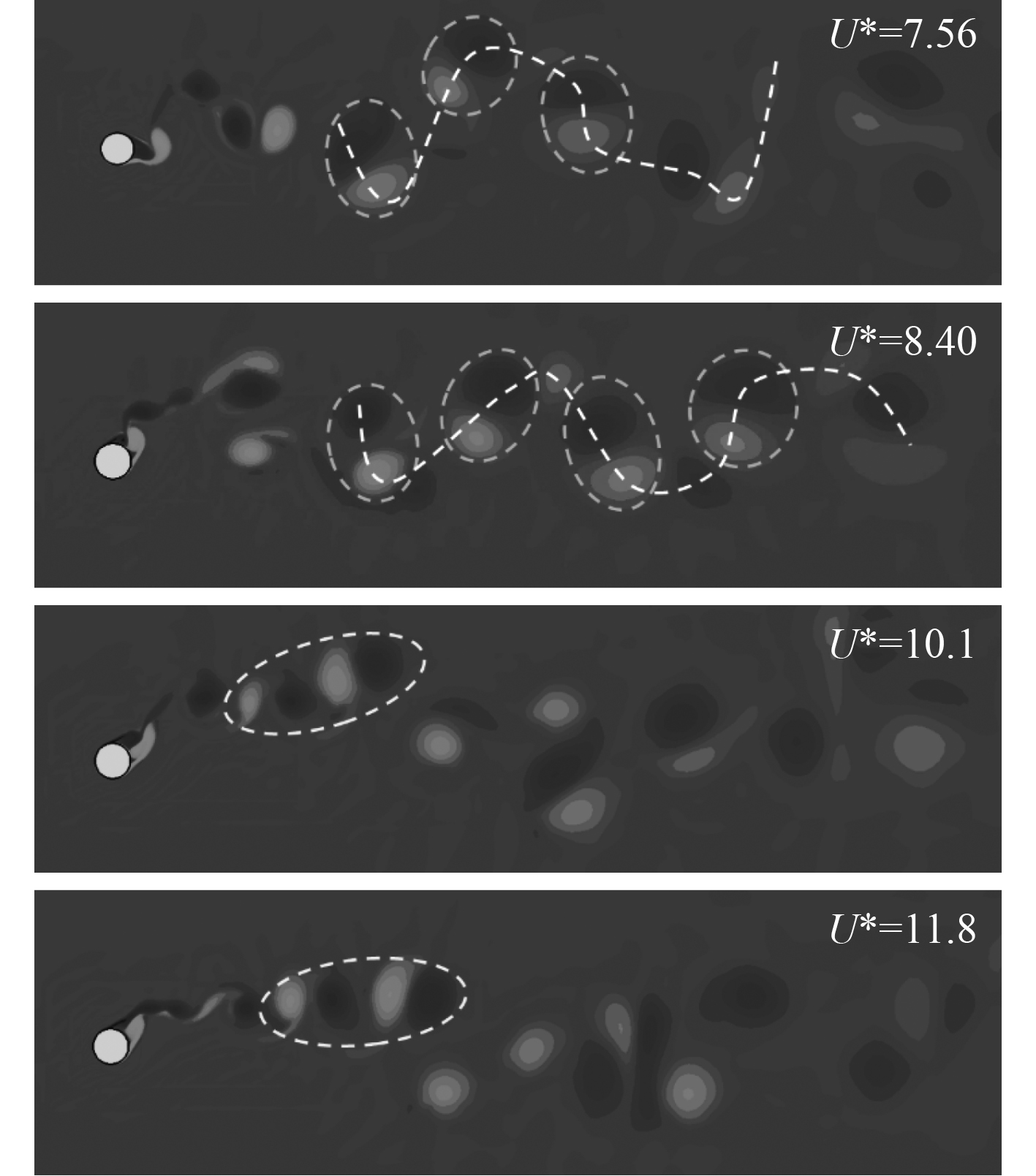
为了分析前2个折合速度和后2个折合速度下圆柱振荡频率差异的原因,观察4个工况下的尾涡结构,如图8所示。可知:
|
图 8 上分支不同折合速度下的尾涡结构(m*=1.33) Fig. 8 Wake vortex structures at different reduced velocities of upper branch(m*=1.33) |
1)在U*=7.56和U*=8.40情况下,尾涡刚刚生成时比较混乱,但随着向后发展,其轨迹逐渐表现为波动曲线形状,并且交替出现反向涡;相比前者,U*=8.40情况下的尾涡结构更具有规律型,每个周期存在6个涡,而U*=7.56情况下,每个周期存在大致5~6个涡。此外,还可以大致看出,涡的强度是有一定规律分布的,即每对强涡之间分布着一个较弱的涡,这一现象在U*=8.40情况下更为明显。
2)在U*=10.1和U*=11.8的情况下,尾涡刚刚生成时都表现为2S模式,并呈现线状分布,但随着发展逐渐变的混乱。
从这些现象来看,前2个折合速度和后2个折合速度下振荡圆柱尾涡存在明显的结构差异,这也是2组结果中频率差异的证据。
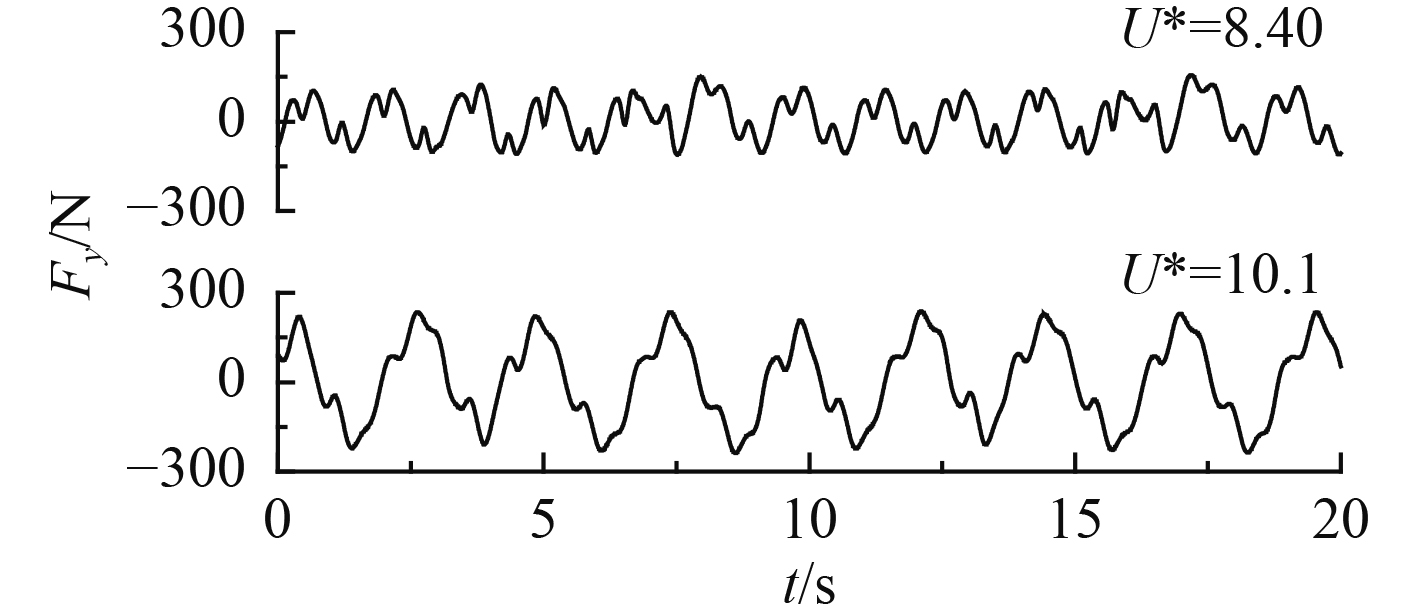
此外,还存在一个共同的现象是,在一个圆柱振荡周期内,圆柱都发生了多次漩涡脱落,这一点也在圆柱受力曲线中体现,在此仅列出了U*=8.40和U*=10.1的情况,如图9所示。可以大致看出,二者的波动分量存在较大的差异,前者存在明显的高频分量,而后者存在明显的低频分量,这也与频率特征和尾涡结构的差异相对应。
|
图 9 上分支不同折合速度下的圆柱受力(m*=1.33) Fig. 9 The force on the cylinder at different reduced velocities of upper branch |
根据图4可以发现,在初始分支的左侧存着一个振幅较明显的分支,这里称之为左分支。在4个质量比下,都存在该分支,选取质量比m*=1.33进行分析,对应折合速度U*=3.36。
首先观察m*=1.33,U*=3.36工况下的尾涡结构,如图10所示。在尾涡形成之初,可以看到明显的2P模式尾涡;而后经历一段较混乱的发展后,尾涡逐渐合并,形成狭长形状的弱涡,并排列为波形结构,且波形宽度明显大于圆柱振荡幅度,即在发展初期,尾涡成扩张式发展。

|
图 10 振荡圆柱后的尾涡结构(左分支,m*=1.33,U*=3.36) Fig. 10 Wake vortex structure behind oscillating cylinder (the left branch,m*=1.33,U*=3.36) |
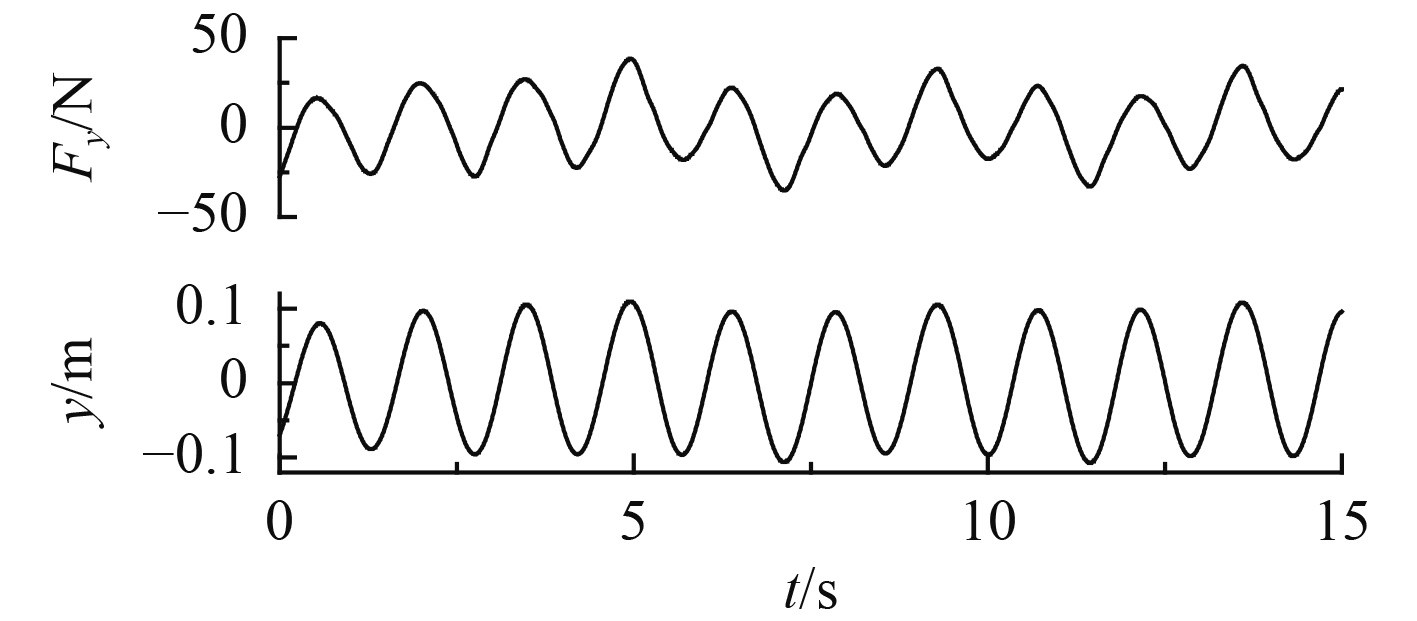
而后观察了圆柱受力和运动曲线,如图11所示。可以看出,该工况下圆柱的受力和运动曲线都表现出明显的有规律的周期性波动特征,分析可知,其无量纲频率f*=1.16,没有明显的锁频现象,其分支出现的机理也有待进一步研究。
|
图 11 振荡圆柱的受力及运动曲线(左分支,m*=1.33,U*=3.36) Fig. 11 Force and motion curve of oscillating cylinder (the left branch,m*=1.33,U*=3.36) |
本文采用数值方法模拟单自由度弹性支撑圆柱的涡激振动现象,Re数范围在0.4×105~2.8×105之间,大部分结果处于较高的Re数范围,对高Re数圆柱涡激振动问题的研究具有一定的参考意义。
本文的圆柱涡激振动模拟结果与Raghavan[8]等的实验测量结果进行了对比,主要结论如下:
1)二者的振幅特性曲线中都能够明显的观察到初始分支和上分支,且振幅大小相当;
2)对不同质量比下的振幅特性曲线进行了对比,在本文的研究范围内,质量比的影响几乎可以忽略;
3)对不同折合速度下的尾涡特征进行了分析,初步得到了一些高Re数下尾涡的特征规律。
尽管如此,本文结果与Raghavan[8]等的实验结果仍存在一些差异,需要更进一步的研究。主要表现在以下几个方面:
1)在初始分支的左侧出现了一个新的分支,其对应的折合速度范围较小,振荡幅值相比上分支较小,但振荡现象仍十分明显;
2)从初始分支到上分支的跳跃过程所对应的折合速度范围略有不同,本文结果对应的跳跃位置偏右;
3)上分支向右的发展中没有跌落过程,也没有明显的下分支,随折合速度的增加,圆柱振幅仍有上升的趋势。
| [1] |
LAI Zhihui, et al. A hybrid piezo-dielectric wind energy harvester for high-performance vortex-induced vibration energy harvesting[J]. Mechanical Systems and Signal Processing, 2021, 150: 107212. DOI:10.1016/j.ymssp.2020.107212 |
| [2] |
WANG Shuyun, et al. Development of a novel non-contact piezoelectric wind energy harvester excited by vortex-induced vibration[J]. Energy Conversion and Management, 2021, 235. |
| [3] |
BERNITSAS MICHAEL M. et al. VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A New Concept in Generation of Clean and Renewable Energy From Fluid Flow[J]. Journal of Offshore Mechanics and Arctic Engineering, 2008, 130(4).
|
| [4] |
BERNITSAS MICHAEL M. et al. The VIVACE converter: model tests at high damping and Reynolds number around 105[J]. Journal of Offshore Mechanics and Arctic Engineering, 2009, 131(1)
|
| [5] |
STAPPENBELT B , JOHNSTONE A D , ANGER J . Vortex-induced vibration marine current energy harvesting[J]. Springer Berlin Heidelberg, 2016.
|
| [6] |
WILLIAMSON C, GOVARDHAN R. Vortex-induced vibrations. Annual Review of Fluid Mechanics, 2004. 36(1): 413-455.
|
| [7] |
及春宁, 李非凡, 陈威霖, 等. 圆柱涡激振动研究进展与展望[J]. 海洋技术学报, 2015, 34(1): 106-118. |
| [8] |
RAGHAVAN K, BERNITSAS M M.. Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports[J]. Ocean Engineering, 2011, 38(5/6): 719-731. |
| [9] |
CHANG C, KUMAR R A, BERNITSAS M M. VIV and galloping of single circular cylinder with surface roughness at 3.0×104≤ Re≤1.2×105[J]. Ocean Engineering, 2011, 38(16): 1713-1732. DOI:10.1016/j.oceaneng.2011.07.013 |
| [10] |
LIN Ding, et al. Numerical simulation and experimental validation for energy harvesting of single-cylinder VIVACE converter with passive turbulence control[J]. Renewable Energy, 2016, 85: 1246-1259. DOI:10.1016/j.renene.2015.07.088 |
| [11] |
ZHU Hongjun, GAO Yue.. Hydrokinetic energy harvesting from flow-induced vibration of a circular cylinder with two symmetrical fin-shaped strips[J]. Energy, 2018, 165: 1259-1281. DOI:10.1016/j.energy.2018.10.109 |
 2022, Vol. 44
2022, Vol. 44

