空调系统的许多故障,可能是由设备或执行器故障引起的,也可能是由传感器或控制器故障引起的。采用数据挖掘的方法分析运行数据,及时发现空调系统可能发生的潜在故障,将有助于维持系统稳定运行,保证船舱内良好的热舒适性。虽然已有许多故障检测与诊断方法,已经被成功应用于机械或能源系统中,但是针对实际舰船空调通风系统的在线故障检测的研究不多,这个领域有必要开展深入研究。
国内外已有许多学者进行了基于主元分析的故障检测与诊断技术研究。Hassanpour等[1] 采用热力学第一定律结合主元分析方法研究陆用空调系统故障检测。Wang等[2]采用主元分析来检测办公建筑空调箱传感器故障,并采用贡献法和专家规则隔离和诊断故障。Jin等 [3]采用角度分析法改进主元分析,来检测变风量空调系统中具有固定和漂移偏差的多个传感器故障。Bakdi等[4]基于改进的指数加权移动平均控制图统计数据,开发了一种新的自适应阈值方案,增强主元分析过程监测性能。Li等[5] 结合模式匹配对训练数据进行预处理,以提高主元分析的故障检测性能。Zhang等[6]采用主元分析结合聚类方法,进行水源热泵空调传感器故障检测与诊断。许多研究[7-9]中采用故障检测率、故障检测精度、误报警率、故障检测占比等指标来评价故障检测结果。
作为一种数据挖掘方法,主元分析(principal component analysis,PCA)根据主成分的累计贡献率方法,确定出最优主成分数[10]。通过协方差矩阵正交分解的过程变量,给出最大的数据变化方向,将多个变量变换为少量数据,实现多维数据的降维[11]。当前的研究主要针对主元分析及其组合方法应用于故障检测与诊断,大多还是在理论应用阶段,采用模拟数据或部分现场测试数据,很少考虑空调系统对外界负荷变化的滞后性和延迟性。并且,针对实际系统在线故障检测的研究也较少,尤其是针对舰船空调的在线故障检测。
本文考虑空调系统对外部负荷的响应时变性,采用当前时刻和前59个时间点(共60个时间点)的数据作为1个计算滑动窗口。针对某舰船实际空调系统,基于能量守恒和压力—流量守恒模型,研究采用滑动窗口和主元方法的在线故障检测方法,测试了11天无故障和11天人工故障,验证方法的故障检测结果。
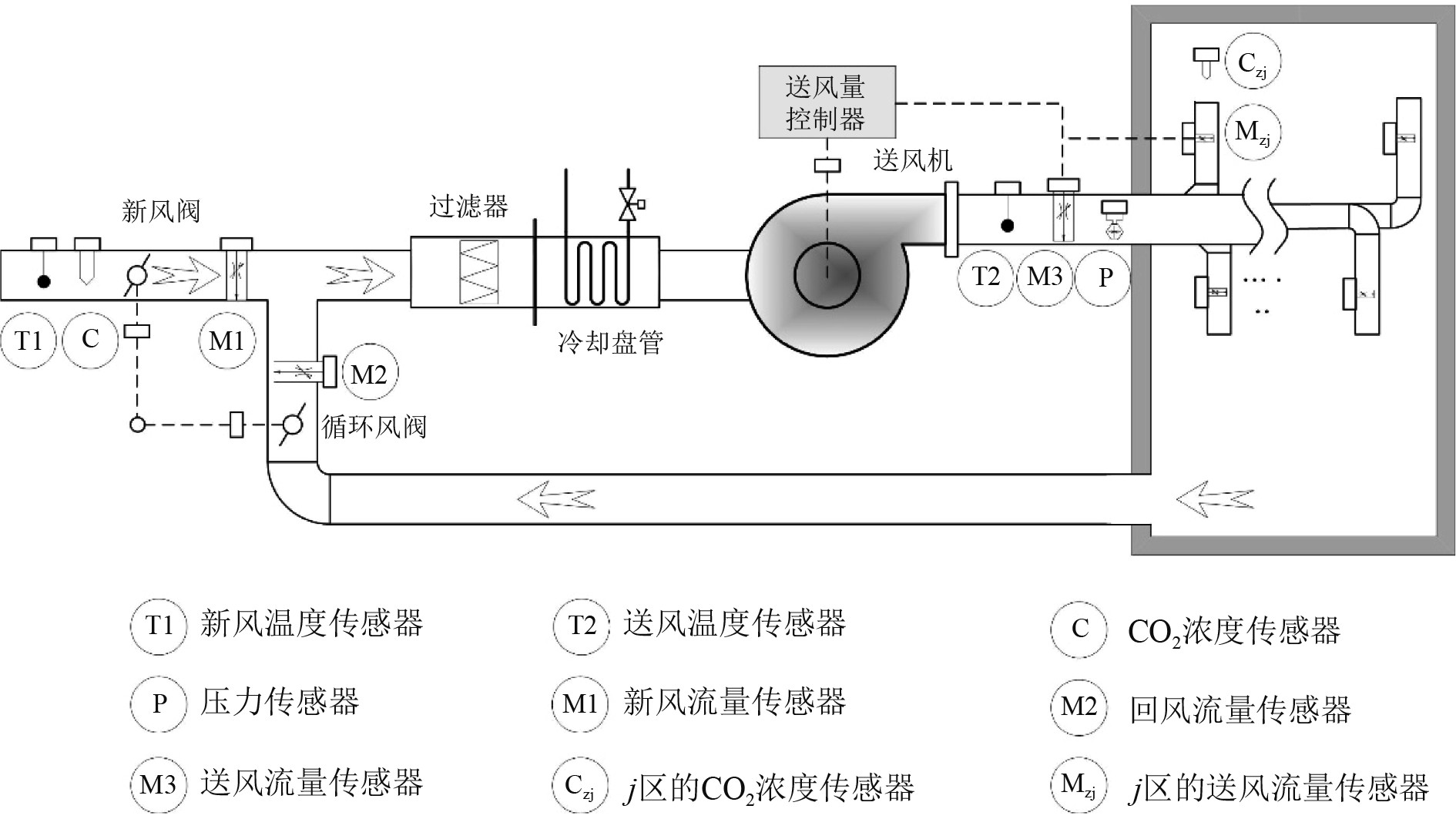
1 空调与性能参数 1.1 典型船用变风量空调系统简介图1为空调箱主要设备与控制系统。新风与循环风混合后,流经过滤器、冷却盘管后,由送风机送入多个送风末端。送风量的调节,由各个送风末端的风量需求之和来调整风机频率和转速来实现。
|
图 1 典型船用变风量空调通风设备与控制系统 Fig. 1 Schematic program of main components and control system of marine VAV system |
在主元分析计算过程中,关键运行性能参数的选取直接影响计算结果的准确性。舰船空调系统的运行性能参数变化,通常具有典型的非线性特征,参数与参数之间很难建立清晰的数学物理关系。但是,空调系统又是一个典型的能量系统,许多参数之间满足质量、能量、流动和压力的守恒。因此,舰船空调箱的测量数据分成满足热量守恒的参数组和满足压力-流量守恒的参数组,2个参数组构成的总参数集合,用于主元分析的输入数据。
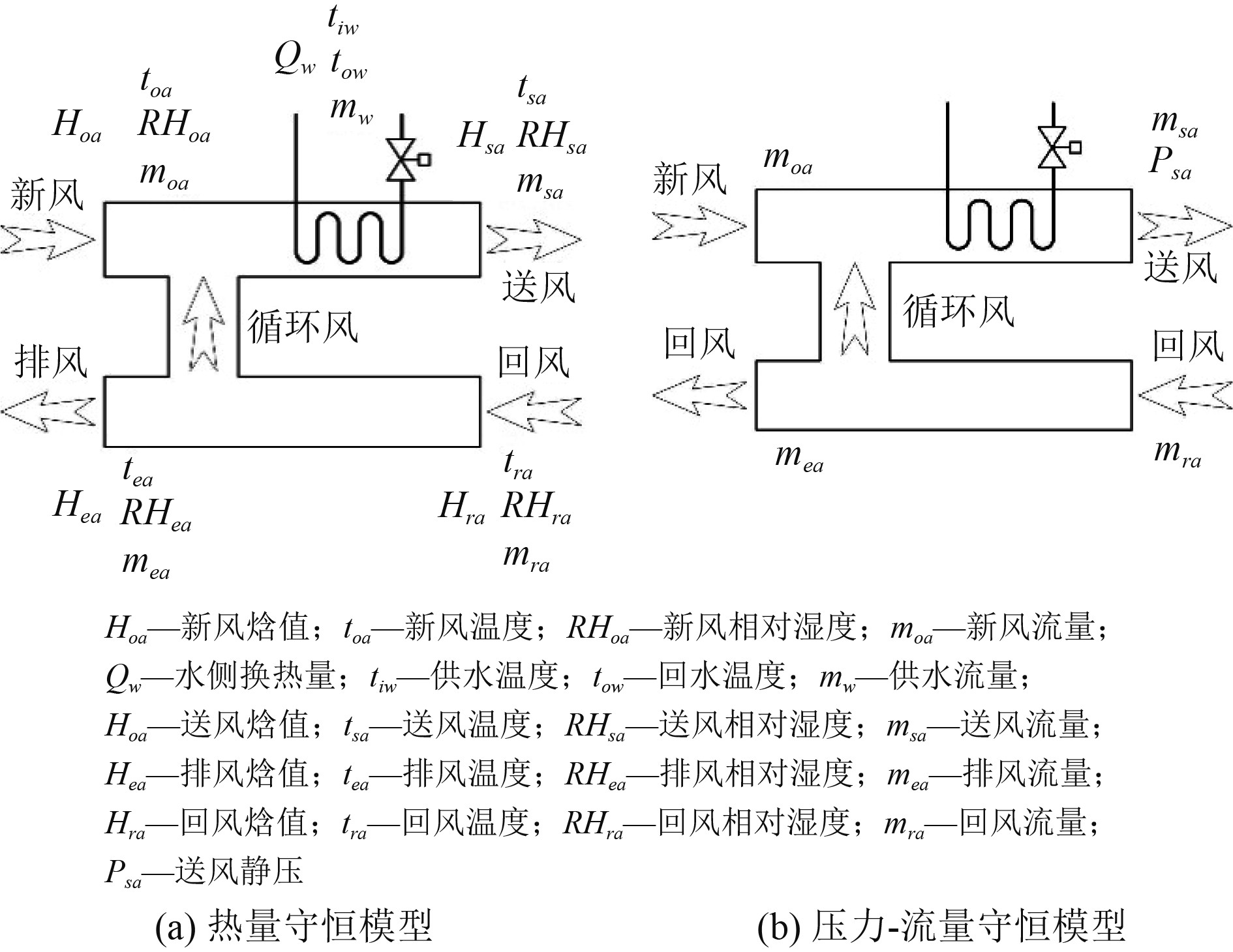
如图2所示,综合热量守恒模型和压力-流量守恒模型,空调运行性能参数选取为18个变量:新风温度、新风湿度、新风量、进水温度、出水温度、水阀开度、水流量、盘管进风温度、盘管出风温度、送风温度、送风湿度、送风静压、实测总风量、需求总风量、风机电流、风机频率、回风温度和回风湿度。
|
图 2 典型船用变风量空调系统运行性能参数的选择依据 Fig. 2 Selection baseline for operating performance parameters of marine VAV system |
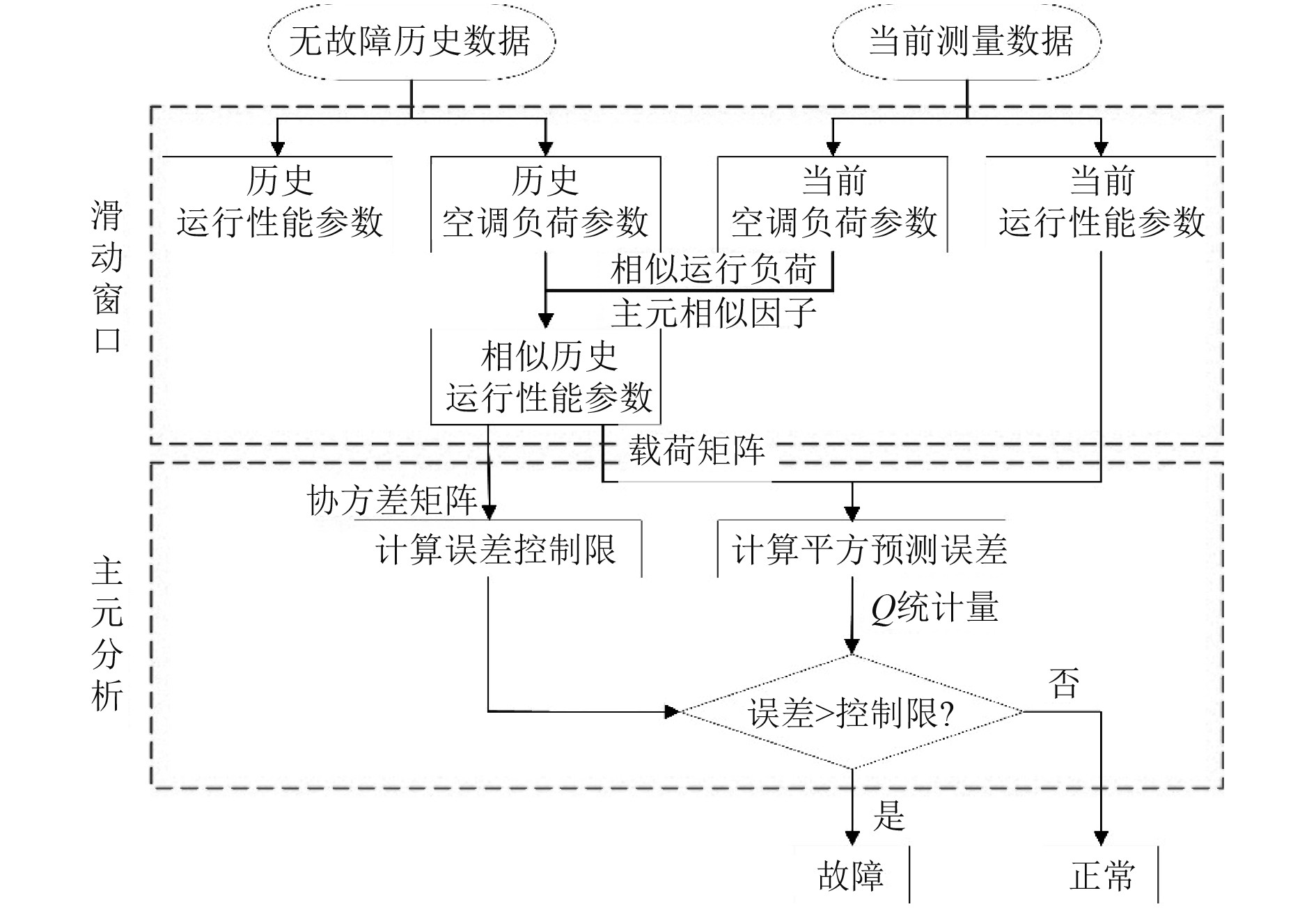
图3为滑动窗口和主元分析故障检测的计算流程。理论上来讲,相似的运行负荷下,空调系统应具有相似的运行性能表达。采用滑动窗口来表征空调系统外部和内部负荷变化的动态响应时变性。采用主元相似因子计算当前测量与历史空调负荷参数的相似程度,选取无故障历史运行性能参照数据。通过比较平方预测误差和控制限,检测空调系统是否发生故障。
|
图 3 基于滑动窗口和主元分析的故障检测计算流程 Fig. 3 Calculating flow chart of the fault detection method based on moving window and principle component analysis |
空调系统不是即时全部响应外部和内部负荷的变化,而是具有一定的时间延迟和波峰衰减。如果只用当前某个时间点的数据来表征空调系统的实时运行性能状态,不能准确地反映空调系统对外界负荷变化的动态响应。采用一段时间点内的数据,组成1个数据滑动窗口,用一组数据表征空调系统真实运行时随外界负荷变化的时变性。
当前测量数据和历史无故障数据被划分为空调负荷参数组和运行性能参数组。滑动窗口主要用于:
1)当前测量的空调负荷参数构成的滑动窗口,用于在历史数据库中寻找相似的历史空调负荷运行状态,找出相似的历史运行性能数据。
2)当前测量的空调运行性能参数组构成的滑动窗口,与历史运行性能数据滑动窗口计算得到的荷载矩阵,计算平方预测误差。
滑动窗口的参数取值如表1所示。滑动速度是指在历史无故障数据库中寻找相似空调负荷运行状态时,滑动窗口移动的速度,单位为时间点数据个数。寻找出的15倍滑动窗口大小的数据构成历史参照数据池,根据累计贡献率计算无故障历史参照的荷载矩阵。
|
|
表 1 滑动窗口的参数取值 Tab.1 Assignment of the parameters used in moving window strategy |
主元分析的计算过程为:对数据进行标准化处理后,计算协方差矩阵R的特征分解,利用主成分贡献率确定最优主成分数,根据累计贡献率确定最优主成分数并构造荷载矩阵,最后计算投影矩阵。采用平方预测误差(squared prediction error,SPE)表征残差空间中的变化量。
采用主元相似因子计算当前在线采集数据与无故障历史数据之间的相似程度。在线采集运行负荷定义为S、无故障历史运行负荷定义为H,均由n个连续时间点和m个变量组成。定义k1和k2分别是S和H的主成分,选取前k个主成分组成空间为L和M的特征向量矩阵,则相似因子计算式为:
| $ {S}_{PCA}=\frac{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({L}^{\mathrm{T}}M{M}^{\mathrm{T}}L\right)}{k}。$ | (1) |
式中:SPCA为主元相似因子;trace为用于求二维方阵的迹,即该方阵对角线元素之和;L为当前测量数据的主成分空间;M为历史运行参照数据的主成分空间;k为主成分个数。
协方差用于表征各个空调运行性能参数偏离其均值的程度,如果为正值表明2个参数是正相关,如果为负值则为负相关。可由下式进行计算:
| $ Cov(x,y)=\frac{1}{n-1}\sum _{i=1}^{n}({x}_{i}-\stackrel-{x})({y}_{i}-\stackrel-{y})。$ | (2) |
式中:Cov为协方差矩阵;n为连续时间点的个数;x和y分别为2个空调运行性能参数;
标准化后的n×m维运行性能参数矩阵X可以分解为:
| $ X = \hat X + E = \hat T{\hat P^{\rm{T}}} + \tilde T{\tilde P^{\rm{T}}}。$ | (3) |
式中:X为n×m维运行性能参数矩阵;
平方预测误差,反映了在测量的每一时刻里,测量值x对主成分模型的偏离程度的大小,可表示为:
| $ SPE = {x_i}^{\rm{T}}\left( {I - \hat P{{\hat P}^{\rm{T}}} - \hat P{{\hat P}^{\rm{T}}} + \hat P{{\hat P}^{\rm{T}}}\hat P{{\hat P}^{\rm{T}}}} \right){x_i} 。$ | (4) |
式中:SPE为平方预测误差矩阵;I为单位矩阵;上角标T为转置矩阵。
正常运行状态下,空调性能参数测量值x,通常服从多元正态分布规律。平方预测误差的控制限δ由下式计算:
| $ {\delta _\alpha } = \left[\frac{{{c_\alpha }\sqrt {2{\theta _2}h_0^2} }}{{{\theta _1}}} + 1 + \frac{{{\theta _2}{h_0}\left( {{h_0}{{ - }}1} \right)}}{{\theta _1^2}}\right]^{\frac{1}{{{h_0}}}},$ | (5) |
| $ {\theta _1} = \sum\limits_{j = 1 + l}^m {{\lambda _j}},\; {\theta _2} = \sum\limits_{j = 1 + l}^m {\lambda _j^2}, \; {\theta _3} = \sum\limits_{j = 1 + l}^m {\lambda _j^3} ,$ | (6) |
| $ {h_0} = 1 - \frac{{2{\theta _1}{\theta _3}}}{{3\theta _2^2}} 。$ | (7) |
式中:
如果平方预测误差大于控制限,则判定为空调系统发生故障。故障检测率为:
| $ \eta =\frac{{N}_{f}}{N}\times 100\text{%} 。$ | (8) |
式中:η为故障检测率;Nf为当前数据窗口的故障数;N为总测量个数。
3 在线故障检测采用滑动窗口和主元分析故障检测方法,在线测试了11天无故障和11天人工故障。表2为无故障和故障测试日的故障检测率。为了观察平方预测误差和控制限随时间的变化,分别选取3天无故障和3天故障(冷水阀卡死故障、新风温度传感器+2ºC固定偏差、AHU送风机前风管泄漏)测试,结果如图4和图5所示。
|
|
表 2 无故障和故障测试日的故障检测率 Tab.2 Fault detection ratio of fault-free and fault tests |

|
图 4 无故障测试日平方预测误差随时间的变化 Fig. 4 Change of squared prediction error under fault-free tests |
|
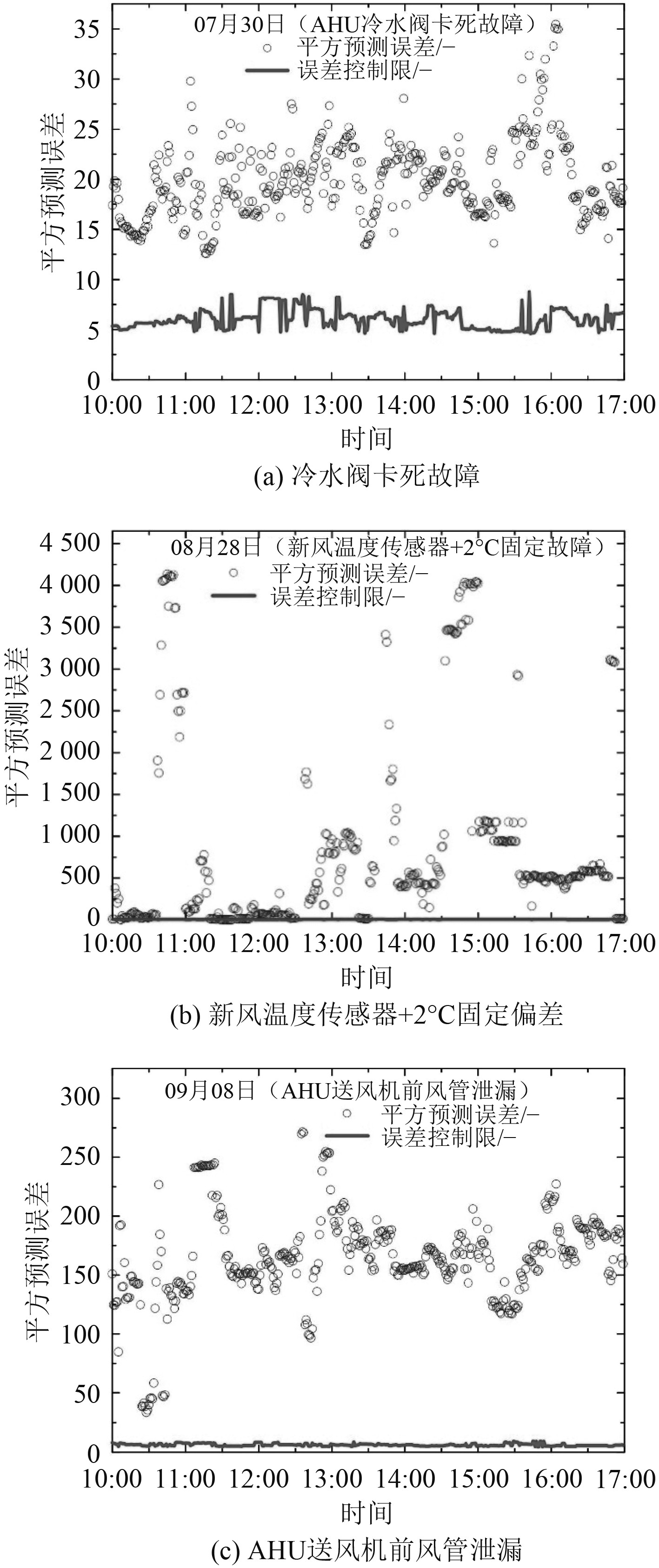
图 5 故障测试日平方预测误差随时间的变化 Fig. 5 Variation of squared prediction error on failure test over time |
当平方预测误差小于控制限时,判定为系统正常运行。从图4可以看出,控制限的值基本在4.50~8.50。表征空调系统运行性能特征变化的平方预测误差,在大部分时间点上均低于控制限。8月14日、8月20日、8月29日的无故障检测率分别为99.22%,96.31%,91.31%。如表2所示,无故障测试日的平均故障检测率为2.71%。一共有9天的故障检测率低于3.69%,只有2天的较高,分别为8.69%和8.00%。
3.2 故障测试平方预测误差的值越大,表征故障对空调系统运行性能特征的变化越明显。
如图5所示,故障测试日的平均故障检测率75.97%。11天中,有9天的故障检测率高于60.60%。7月27日(供水温度传感器+1ºC固定偏差)和8月26日(送风温度传感器+2ºC固定偏差),2天的故障检测率分别为51.54%和38.29%。
7月27日冷水机组冷媒水温度出现频繁波动,导致+1ºC固定偏差对系统运行性能的特征变化影响不明显,故障检测率较低。造成这种情况的原因可能是,受到外界干扰导致系统处于非稳定运行状态,空调箱冷媒水供水温度处于频繁的波动状态。
8月26日(送风温度传感器+2ºC固定偏差)的故障检测率只有38.29%。如表3所示,送风温度传感器出现+2ºC固定偏差的故障,相同相对湿度下,比焓值的变化约为10%左右。
|
|
表 3 送风温度固定偏差±2°C下的湿空气状态参数 Tab.3 Psychrometric properties of supply air temperature under fixed bias fault with ±2°C |
针对典型船用变风量空调系统,采用滑动窗口和主元分析检测空调系统可能发生的故障。一段时间内的滑动窗口数据能够反映空调系统对外部和内部负荷变化的动态响应时变性。采用主元相似因子寻找与当前测量空调负荷参数相似的无故障历史参照数据。比较平方预测误差和控制限的大小,作为判定系统是否发生故障的依据。采用该故障检测方法测试了11天无故障和11天人工故障,得到以下结论:
1)采用主元分析法时,反映某舰船实际空调系统运行性能特征变化的误差控制限,其值大部分在4.50~8.50。如果平方预测误差低于控制限,表明空调运行性能特征变化接近无故障正常运行时的状态。
2)无故障测试日的平均无故障检测率为97.29%。人工故障测试日的平均故障检测率75.97%。对于不能明显引起系统运行性能参数特征变化,采用数据挖掘的方法很难检测出发生的故障。
3)数据挖掘过程中发现,数据的测量精度对故障检测结果的影响很大。如果测量误差较大或者外界的扰动使空调系统处于非稳定状态,导致故障检测方法很难识别出系统运行性能特征变化,导致故障检测率较低。
| [1] |
HASSANPOUR H, MHASKAR P, HOUSE J M, et al. A hybrid modeling approach integrating first-principles knowledge with statistical methods for fault detection in HVAC systems[J]. Computers & Chemical Engineering, 2020, 142: 107022. |
| [2] |
WANG S, XIAO F. AHU sensor fault diagnosis using principal component analysis method[J]. Energy and Buildings, 2004, 36(2): 147-160. DOI:10.1016/j.enbuild.2003.10.002 |
| [3] |
JIN X, DU Z. Fault tolerant control of outdoor air and AHU supply air temperature in VAV air conditioning systems using PCA method[J]. Applied Thermal Engineering, 2006, 26(11): 1226-1237. |
| [4] |
BAKDI A, KOUADRI A. A new adaptive PCA based thresholding scheme for fault detection in complex systems[J]. Chemometrics and Intelligent Laboratory Systems, 2017, 162: 83-93. DOI:10.1016/j.chemolab.2017.01.013 |
| [5] |
LI S, WEN J. Application of pattern matching method for detecting faults in air handling unit system[J]. Automation in Construction, 2014, 43: 49-58. DOI:10.1016/j.autcon.2014.03.002 |
| [6] |
ZHANG H, CHEN H, GUO Y, et al. Sensor fault detection and diagnosis for a water source heat pump air-conditioning system based on PCA and preprocessed by combined clustering[J]. Applied Thermal Engineering, 2019, 160: 114098. DOI:10.1016/j.applthermaleng.2019.114098 |
| [7] |
CHINTALA R, WINKLER J, JIN X. Automated fault detection of residential air-conditioning systems using thermostat drive cycles[J]. Energy and Buildings, 2020, 36: 110691. |
| [8] |
EBRAHIMIFAKHAR A, KABIRIKOPAEI A, YUILL D. Data-driven fault detection and diagnosis for packaged rooftop units using statistical machine learning classification methods[J]. Energy and Buildings, 2020, 225: 110318. DOI:10.1016/j.enbuild.2020.110318 |
| [9] |
WANG H, FENG D, LIU K. Fault detection and diagnosis for multiple faults of VAV terminals using self-adaptive model and layered random forest[J]. Building and Environment, 2021, 193: 107667. DOI:10.1016/j.buildenv.2021.107667 |
| [10] |
KAZEMI P, BENGOA C, STEYER J P, et al. Data-driven techniques for fault detection in anaerobic digestion process[J]. Process Safety and Environmental Protection, 2021, 146: 905-915. DOI:10.1016/j.psep.2020.12.016 |
| [11] |
LI W, PENG M, WANG Q. Improved PCA method for sensor fault detection and isolation in a nuclear power plant[J]. Nuclear Engineering and Technology, 2019, 51(1): 146-154. DOI:10.1016/j.net.2018.08.020 |
 2022, Vol. 44
2022, Vol. 44
