0 引　言

舰炮系统是重要的海军武器装备，为了让舰炮能顶用、好用，对舰炮设备的检测很重要。目前，通过大量设置机内检测点（built in test，BIT）等方式，实现了舰炮设备健康状况的实时掌握。舰炮设备性能指标的检测信息包含了大量的可靠性信息，利用这些检测信息不仅可以及时判断当前设备是否处于良好状态，而且可以根据设备性能指标的变化趋势预测设备的剩余寿命，更好地确定设备的预防性维修（或报废）时机^[1]。合理利用设备性能指标变化规律开展可靠性评估已成为近年来可靠性评估研究的重要方向。

与基于故障信息的设备可靠性评估^[2-3]不同，用设备性能指标变化规律开展可靠性评估，实际上是通过分析产品的性能指标退化机理，建立基于性能指标的设备可靠性模型^[4-5]，并以产品性能指标的检测信息为基础得到产品剩余寿命的预测方法。目前，基于性能指标的可靠性评估方法主要分为两大类。一类是基于产品性能指标退化规律的可靠性评估方法，这类方法的核心是研究产品性能指标的退化模型，以实现设备的可靠性评估。性能指标退化模型的构建主要包括物理动力学模型^[4]、比例风险模型^[5]、随机过程模型^[6-9]、时间序列模型^[10]等。在确定性能指标退化规律的基础上，该方法基于较少的性能指标检测数据就可以较精确地评估产品可靠性。但是，这类方法具有一定的局限性，其性能指标的退化规律^[1,11]通常比较复杂，简单的退化规律不能准确反映性能指标的变化。另一类是完全不考虑设备退化轨迹的基于退化散布特征的可靠性评估方法，如文献[12-13]利用退化量的散布特征直接将产品退化信息转化为产品寿命信息，实现产品可靠性评估。这类方法实际上基于检测信息的分布特征进行评估，尤其是在性能观测数据较多的情况下，可以较准确地拟合产品寿命分布，其评估结果具有较好的鲁棒性。但该方法也有其局限性，如在产品性能指标的变化趋势不明显的情况下，这种方法将难以准确预测产品的剩余寿命。上述方法均是针对设备性能退化信息而言的，并未考虑设备的故障信息。如何综合利用设备故障信息与性能退化信息评估设备的可靠性是工程上需要解决的重要问题。

本文通过分析舰炮设备的可靠性影响因素，确定舰炮设备主要性能指标的退化演变规律，建立综合性能退化信息与故障信息的可靠性模型，通过分析故障率变化特点，说明该模型刻画舰炮设备可靠性规律的适应性。在此基础上，给出基于性能指标检测信息和故障信息的舰炮设备可靠性评估方法，并通过实例说明该评估方法的有效性。

1 舰炮设备可靠性影响因素分析

舰炮是最典型的舰载武器系统，影响其设备可靠性的因素不仅包括使用环境因素，而且与舰炮设备的使用方式和维修保障活动等因素密切相关。

舰炮武器系统的使用环境条件极为复杂，这些环境条件既包括海洋环境、气候环境、生物环境、机械环境和电磁环境等外部因素，也包括舰炮设备自身使用过程中的内部因素（如运行温度、振动等）。这些环境条件对舰炮设备可靠性的影响通常是一个渐变过程，如海浪通过浸溅导致伺服随动系统、光电传感器等设备的金属表面慢慢损坏，高温容易致使元器件出现物理损伤、化学侵蚀、腐蚀等，潮湿将直接造成装备内部元器件、印制板、接插件绝缘电阻阻值下降甚至短路、断路等。这些内外因素的共同作用通常会使舰炮设备的性能指标不断退化或性能下降，如舰炮瞄准精度下降，伺服随动系统反应慢等。尽管此时设备还能开机工作，但通常会由于设备性能指标达不到规定的精度要求而导致系统任务执行失败。

除受上述使用环境条件的影响外，舰炮设备的可靠性还受到其使用过程中各种过载负荷冲击的影响，这些冲击对舰炮设备常常是致命的，通常会造成设备的部分组部件损伤，从而导致设备故障，传统的可靠性理论研究中所指的冲击均为这类致命冲击或强烈冲击^[2]。相对而言，使用环境因素对舰炮设备的影响也可以看做是各种冲击，只是这些冲击对舰炮设备的正常使用并不会造成显著影响，甚至影响甚微，即这些冲击并不会造成设备组部件的致命损伤，但这些非致命冲击具有累积响应，当各种微小冲击累积到一定程度时，就表现出设备性能指标退化，此时设备会因性能指标退化而导致任务执行失败^[14]，为区别起见，将这类导致任务失败的故障称为软故障，而导致组部件损伤的故障称为硬故障。

2 舰炮设备可靠性模型 2.1 模型假设

在舰炮正常服役期间，其设备随时会受到各种冲击的影响，从作用效果来看，这些冲击可分为致命冲击和非致命冲击，不同作用效果对设备可靠性的影响是不同的。因此，在建立舰炮设备可靠性模型时，不仅要考虑这些冲击的发生机理，而且还要考虑这些冲击的作用效果。为此，给出如下假设：

假设1　设备在正常使用过程中受到各种各样的冲击，这些冲击分为致命冲击和非致命冲击。记 ${N_1}(t)$ 和 ${N_2}(t)$ 分别表示在时间 $\left[ {0,t} \right]$ 内受到的致命冲击流和非致命冲击流，其中致命冲击流 ${N_1}(t)$ 服从累积强度为 $\lambda t$ 的Poisson过程：

$ P\left( {{N_1}(t) = n} \right) = \frac{{{{\left( {\lambda t} \right)}^n}}}{{n!}}\exp \left( { - \lambda t} \right)\text{，}n = 1,2, \cdots，$

(1)

非致命冲击流 ${N_2}(t)$ 服从累积强度为 $at$ 的Poisson过程：

$ P\left( {{N_2}(t) = n} \right) = \frac{{{{\left( {at} \right)}^n}}}{{n!}}\exp \left( { - at} \right)\text{，}n = 1,2, \cdots 。$

(2)

式中： $a,\lambda $ 为常数。

假设2　致命冲击将直接导致设备发生硬故障。

假设3　非致命冲击将造成设备性能指标退化，且每次冲击对设备性能指标的影响十分微小。每次非致命冲击造成设备性能指标的退化量 ${Y_i}$ 是相互独立且服从均值为 $\mu $ 方差为 ${\sigma ^2}$ 的正态分布，其中均值 $\mu $ 常常接近于零。

假设4　设备在一定时间内所受到的非致命冲击具有累积响应，即各种非致命冲击对设备性能指标的影响具有可加性。

假设5　设备所受到的两类冲击流 ${N_1}(t)$ 和 ${N_2}(t)$ 与设备性能指标改变量 ${Y_i}$ 之间相互独立。

2.2 舰炮设备寿命及其分布

由假设可知，舰炮设备寿命主要由2类冲击决定。

1）考虑致命冲击流导致的设备硬故障。

设致命冲击出现时间为 ${T_1}$ ，由假设1可知， ${T_1}$ 的分布函数为：

$ \begin{split} {F_1}(t) = P\left( {{T_1} \leqslant t} \right) & = 1 - P\left( {{T_1} > t} \right) = 1 - P\left( {{N_1}(t) = 0} \right) =\\ & 1 - \exp ( - \lambda t) 。\\[-10pt] \end{split} $

(3)

2）考虑非致命冲击流对设备性能指标的影响

由于设备在时间 $\left[ {0,t} \right]$ 内受到的非致命冲击次数为 ${N_2}(t)$ ，则设备性能指标的退化量 $X(t)$ 可表示为 ${N_2}(t)$ 次冲击造成设备性能变化量 ${Y_i}$ 的累加和：

$ X(t) = \sum\limits_{i = 1}^{{N_2}(t)} {{Y_i}}。$

(4)

显然， $X(t)$ 是一个复合Poisson过程^[7]，这个过程的分布函数较为复杂，在工程实际中，为了使用方便，根据中心极限定理，可认为 $X(t)$ 近似服从正态分布，即

$ X(t) \sim N\left( {{\mu _t},\sigma _t^2} \right)。$

(5)

式中： ${\mu _t} = at\mu $ ； $\sigma _t^2 = at\left( {{\mu ^2} + {\sigma ^2}} \right)$ 。

设舰炮设备性能指标的退化量允许上限为 ${X_{cu}}$ ，则设备退化量首次超出允许上限的时间为：

$ {T_2} = \min \left( {t:\inf \left\{ {t:X(t) = {X_{cu}},t \geqslant 0} \right\}} \right) ，$

随机变量 ${T_2}$ 的分布函数为：

$ \begin{split} {F_2}\left( t \right) = P\left\{ {{T_2} \leqslant t} \right\} & = 1 - P\left\{ {{T_2} > t} \right\} = 1 - P\left\{ {\;X(t) \leqslant {X_{cu}}} \right\} = \\ & 1 - \Phi \left( {\frac{{{X_{cu}} - {\mu _t}}}{{{\sigma _t}}}} \right) 。\\[-20pt] \end{split} $

(6)

显然，舰炮设备的寿命应满足 $T = \min \left\{ {{T_1},{T_2}} \right\}$ ，因此，舰炮设备的寿命分布为：

$ \begin{split} F\left( t \right) = P\left\{ {T \leqslant t} \right\} &= P\left\{ {\min ({T_1},{T_2}) \leqslant t} \right\} = 1 - P\left\{ {{T_1} > t,{T_2} > t} \right\} =\\ & 1 - \left[ {1 - {F_1}(t)} \right]\left[ {1 - {F_2}(t)} \right] =\\ & 1 - \exp \left( { - \lambda t} \right)\varPhi \left( {\frac{{{X_{cu}} - {\mu _t}}}{{{\sigma _t}}}} \right) 。\\[-20pt] \end{split} $

(7)

2.3 舰炮设备可靠性模型

利用舰炮设备的寿命分布式（7），就可以得到舰炮设备在任意时刻 $t$ 的可靠度函数为：

$ \begin{split} R\left( t \right) = P\left\{ {T > t} \right\} &= P\left\{ {\min ({T_1},{T_1}) > t} \right\}= \\ & \left[ {1 - {F_1}(t)} \right]\left[ {1 - {F_2}(t)} \right] =\\ & \varPhi \left( {\frac{{{X_{cu}} - {\mu _t}}}{{{\sigma _t}}}} \right)\exp \left( { - \lambda t} \right) 。\\[-10pt] \end{split} $

(8)

利用上式，可以得到舰炮设备的故障率函数为：

$ \begin{split} {\lambda _s}\left( t \right)& = - \frac{{R'(t)}}{{R(t)}} = \lambda - \frac{{{\rm{d}}\varPhi \left( {({X_{cu}} - {\mu _t})/{\sigma _t}} \right)}}{{{\rm{dt}}}}{\varPhi ^{ - 1}}\left( {\frac{{{X_{cu}} - {\mu _t}}}{{{\sigma _t}}}} \right) =\\ & \lambda + \left( {\frac{{{X_{cu}}}}{{2t}} + \frac{{a\mu }}{2}} \right){e^{ - \frac{{{{\left( {{X_{cu}} - a\mu t} \right)}^2}}}{{2a({\mu ^2} + {\sigma ^2})t}}}}{\left[ {\int_{ - \infty }^{{X_{cu}}} {{e^{ - \frac{{{{\left( {{X_{cu}} - a\mu t} \right)}^2}}}{{2a({\mu ^2} + {\sigma ^2})t}}}}} {\rm{d}}x} \right]^{ - 1}} 。\\[-20pt] \end{split} $

(9)

由式（9）可知，设备的故障率函数 $ {\lambda _s}(t) $ 是 $t$ 的增函数，当工作时间趋向于无穷大时具有如下极限：

$ \begin{split} & \mathop {\lim }\limits_{t \to + \infty } {\lambda _s}\left( t \right)=\\ &\;\; \lambda + \mathop {\lim }\limits_{t \to + \infty } \left( {\frac{{{X_{cu}}}}{{2t}} + \frac{{a\mu }}{2}} \right){e^{ - \frac{{{{\left( {{X_{cu}} - a\mu t} \right)}^2}}}{{2a({\mu ^2} + {\sigma ^2})t}}}}{\left[ {\int_{ - \infty }^{{X_{cu}}} {{e^{ - \frac{{{{\left( {{X_{cu}} - a\mu t} \right)}^2}}}{{2a({\mu ^2} + {\sigma ^2})t}}}}} {\rm{d}}x} \right]^{ - 1}} =\\ &\;\; \lambda + \frac{{a\mu }}{{2\sqrt {a({\mu ^2} + {\sigma ^2})} }}{e^{\frac{{a\mu {X_{cu}}}}{{({\mu ^2} + {\sigma ^2})}}}}\mathop {\lim }\limits_{t \to + \infty } \frac{{{e^{ - \frac{{a{X_{cu}}}}{{({\mu ^2} + {\sigma ^2})}}}}}}{{\sqrt t \int_{ - \infty }^{\frac{{{X_{cu}} - a\mu t}}{{\sqrt {a({\mu ^2} + {\sigma ^2})t} }}} {{e^{ - \frac{{{x^2}}}{2}}}} {\rm{d}}x}} ，\end{split} $

由此可得舰炮设备的故障率

$ {\lambda _s} = \mathop {\lim }\limits_{t \to + \infty } {\lambda _s}\left( t \right) = \lambda + \frac{a}{2}\left( {\frac{{{\mu ^2}}}{{{\mu ^2} + {\sigma ^2}}}} \right)。$

(10)

由此可见，随着工作时间 $ t $ 增大，非致命冲击导致的设备性能指标退化量也随机增大，但当工作时间 $ t $ 较大时，设备性能指标退化量的方差 $\sigma _t^2 = at\left( {{\mu ^2} + {\sigma ^2}} \right)$ 也越来越大，从而使非致命冲击导致的设备失效，呈现出无记忆性，即设备故障规律整体服从指数分布，其渐进故障率为 $ {\lambda _s} $ ，这与实际相符。

3 舰炮设备可靠性评估

舰炮设备可靠性模型式（8）中的参数，可以采用舰炮设备的故障数据和性能指标的退化数据分别进行估计得到。

3.1 可靠性信息结构

设备在实际使用过程中能够收集到的可靠性信息主要有（硬)故障信息与性能退化信息两类。其中硬故障信息实际上是因设备的部分组部件损坏而导致的，这是目前最为常用的可靠性信息；性能退化信息实际上是设备性能指标的退化轨迹。显然，可靠性信息结构不同，其统计处理方法也不相同。

假设共有 $ m $ 台舰炮设备参与试验，收集到这 $ m $ 台舰炮设备的故障数据为 $ (T,r) $ ，其中 $ T $ 为这些设备的总工作时间， $ r $ 为故障次数。

故障信息反映了设备受到的致命冲击强度。在实际使用过程中，一般定期对设备性能指标进行检测，观察其性能指标的退化情况。此时得到的性能退化信息如下：

$ \left( {{t_i},{X_{ij}}} \right),i = 1,2, \cdots ,m,j = 1,2, \cdots ,n 。$

(11)

式中： $ {t_j}(j = 1,2, \cdots ,n) $ 为性能指标的测量时刻； ${X_{ij}}(i = 1,2, \cdots ,m,j = 1,2, \cdots ,n)$ 为第 $i$ 个试验设备在测量时刻 $ {t_j} $ 的退化量测量值。

3.2 模型参数估计

对于舰炮设备的故障数据 $ (T,r) $ ，可以利用极大似然估计方法对致命冲击强度 $ \lambda $ 进行估计：

$ \hat \lambda = \left\{ \begin{gathered} \frac{T}{r},\quad \quad r > 0 ，\\ T,\quad \quad r = 0 。\\ \end{gathered} \right. $

(12)

同样，利用性能退化数据式（11），就可以对退化模型式（6）中的性能退化参数进行估计。为方便起见，记 $u = a\mu $ ， $v = a\left( {{\mu ^2} + {\sigma ^2}} \right)$ ，则式(5)转化为：

$ X\left( t \right) \sim N\left( {ut,vt} \right)，$

(13)

由于样本数据的独立性，则在测量时刻 ${t_j}(j = 1,2, \cdots , n)$ 参数的似然函数为：

$ {L_j}\left( {b,u,v} \right) = \prod\limits_{i = 1}^m {\frac{1}{{\sqrt {2\text{π} vt_j^{}} }}\exp \left( { - \frac{{{{\left( {{X_{ij}} - ut_j^{}} \right)}^2}}}{{2vt_j^{}}}} \right)}。$

对于不同测量时刻的样本观测值，可以利用极大似然估计方法得到性能退化参数 $u$ 和 $v$ 的估计为：

$ \left\{ \begin{gathered} \hat u = {{\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^m {{X_{ij}}} } } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^m {{X_{ij}}} } } {\sum\limits_{j = 1}^n {mt_j^{}} }}} \right. } {\sum\limits_{j = 1}^n {mt_j^{}} }}，\\ \hat v = \frac{1}{{mn}}\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^m {\frac{{{{\left( {{X_{ij}} - t_j^{}u} \right)}^2}}}{{t_j^{}}}} } 。\\ \end{gathered} \right. $

(14)

3.3 可靠性指标估计

在得到舰炮可靠性模型中的参数估计后，将其代入式（8）可以得到任意时刻 $ t $ 设备的可靠度估计值

$ {\hat R^*}(t) = \varPhi \left( {\frac{{{X_{cu}} - \hat ut}}{{\sqrt {\hat vt} }}} \right)\exp \left( { - \hat \lambda t} \right)，$

(15)

相应地，舰炮设备的渐进故障率的估计为：

$ {\hat \lambda _s} = \hat \lambda + \frac{{{{\hat u}^2}}}{{2\hat v}}。$

(16)

4 实例分析

以某传感器零位电压漂移数据处理与故障数据处理为例，说明舰炮设备可靠性模型的应用过程，并通过分析其失效率特点说明模型的适应性。该传感器是保证舰炮射击精度的主要设备，要求其电信号的零位电压一般小于40 mV。在实际使用过程中，其零位电压会产生漂移，当其超出规定精度要求时需要进行标校处理。现收集到3个装置使用36天、每3天检测一次的零位电压检测数据，同时，在设备长期工作期间收集到其故障次数3次，累积工作时间共6 450 h。

1）致命冲击参数 $ \lambda $ 的估计。

利用故障数据据（6450,3），由式（12）可以得到参数 $ \lambda $ 的极大似然估计为 $ \hat \lambda = 4.6512 \times {10^{ - 4}} $ 。

2）退化数据的预处理

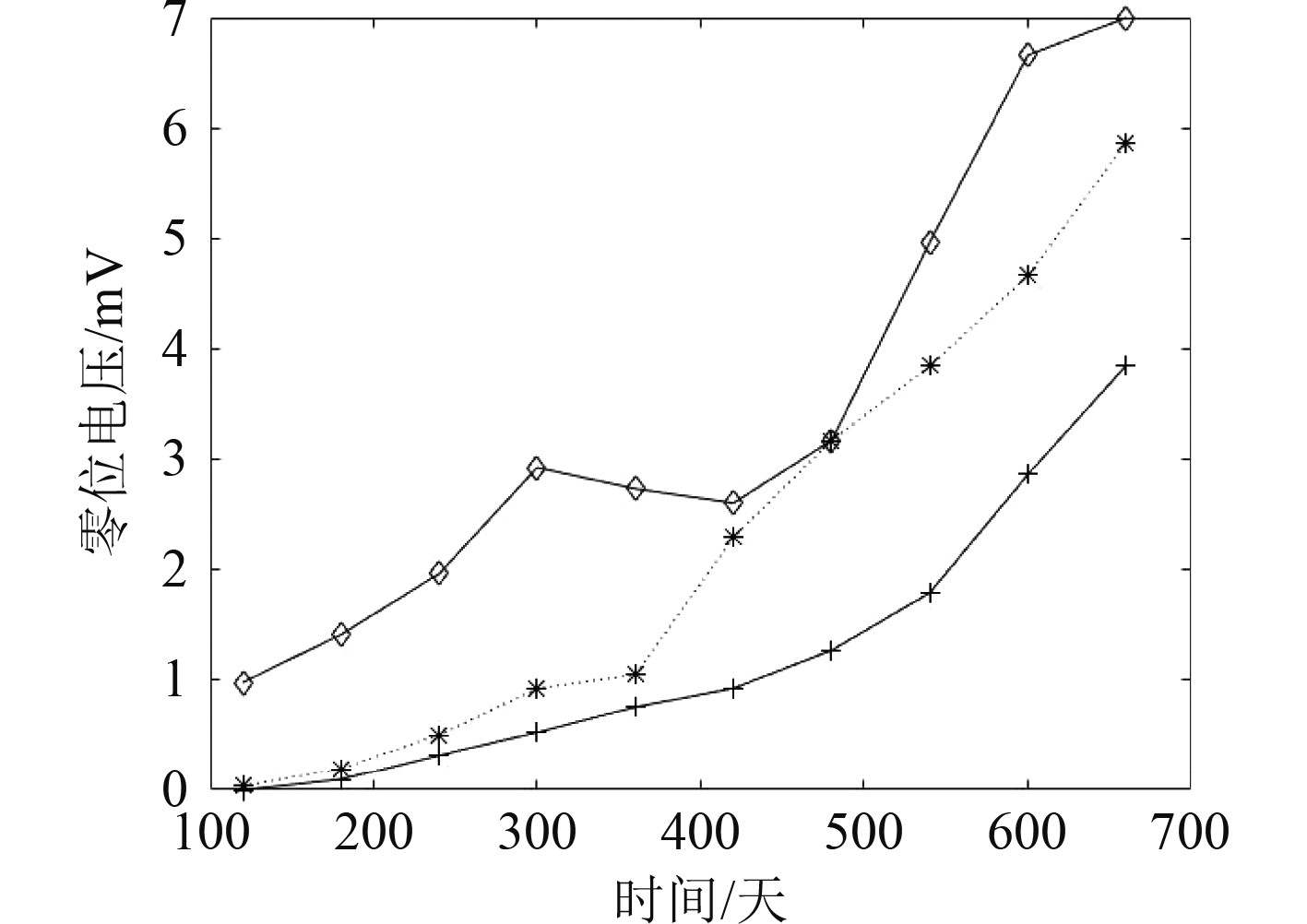
由收集到的零位电压退化数据可知前3个数据检测点对应的性能指标值存在突变的情况，从不影响其退化可靠性规律的角度，将前3个时间点和性能指标值进行平移，此时性能指标上限值为9.96 mV，电压变化趋势如图1所示。

3）退化模型参数估计

利用性能退化数据，由式（14）可以得到性能退化参数 $u$ 、 $v$ 的极大似然估计为 $ \hat u = 3.7917 \times {10^{ - 4}} $ ， $ \hat v = 7.0833 \times {10^{ - 5}} $ 。

4）可靠度与故障率的估计

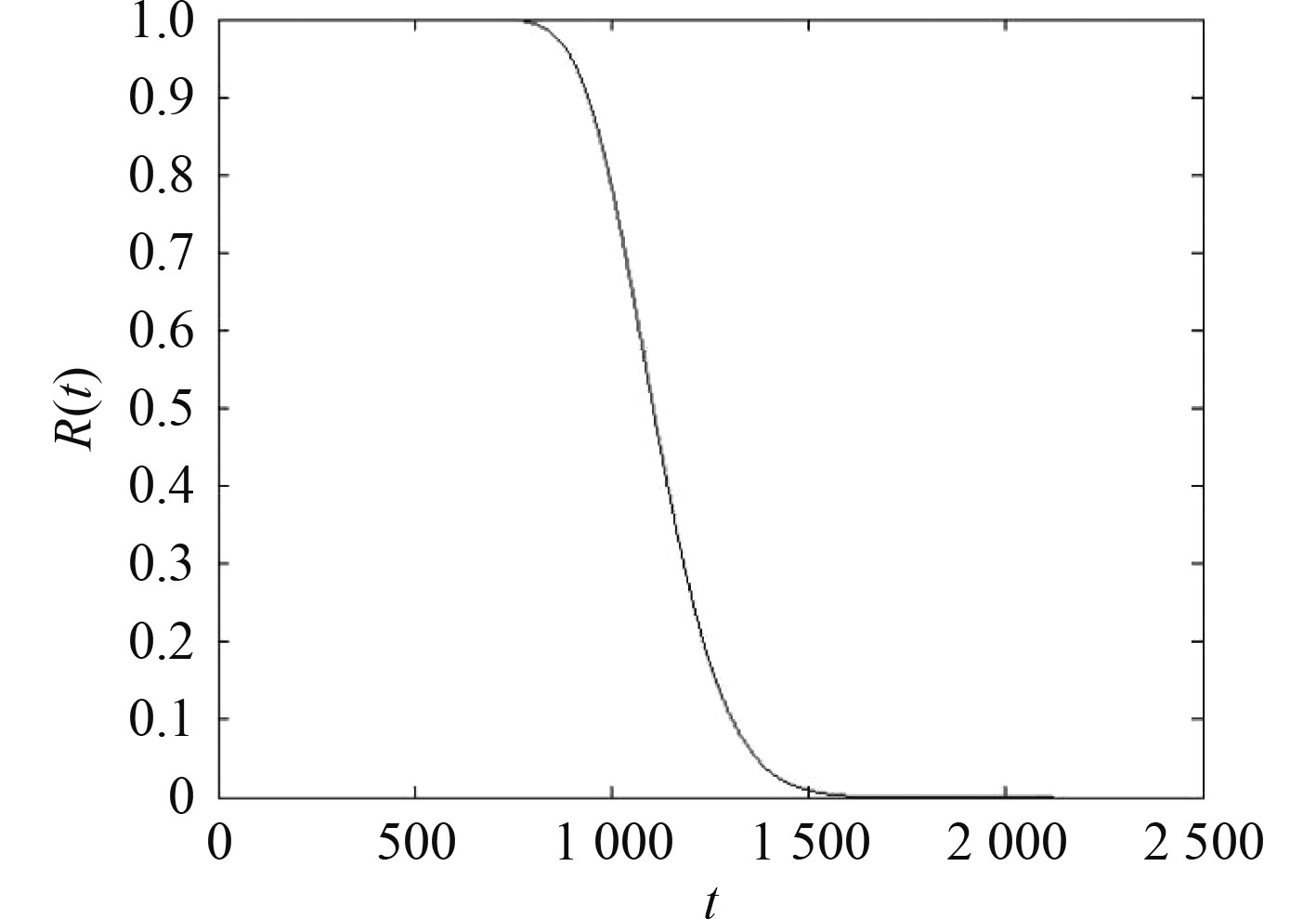
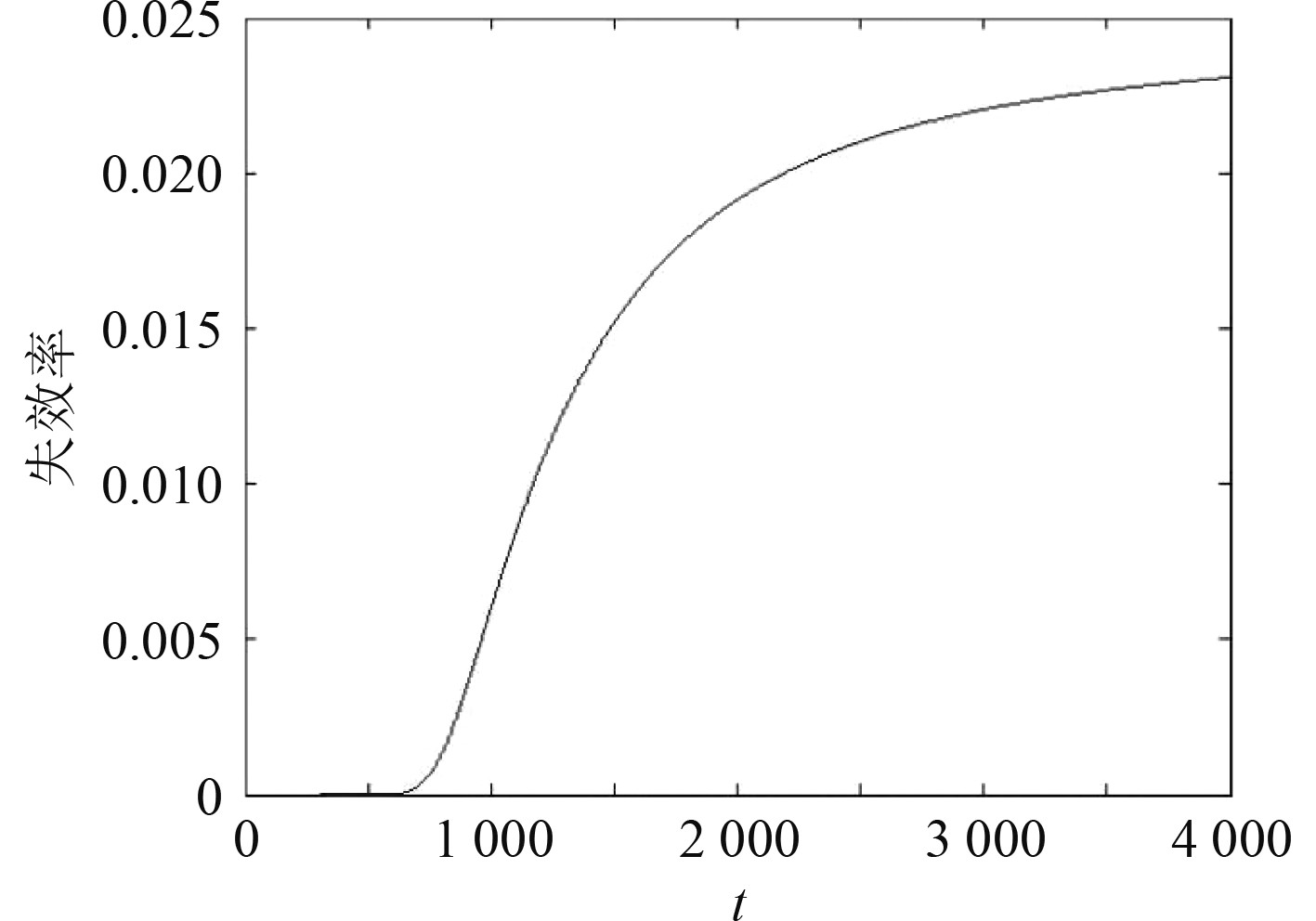
将上述参数估计代入到式（13），就可以得到传感器的可靠度估计，其可靠度曲线如图2所示。同样，由式（9）可以得到传感器的故障率估计，其故障率曲线如图3所示。其渐进故障率估计为：

$\begin{split} {\hat \lambda _s} =& \hat \lambda + \frac{{{{\hat u}^2}}}{{2\hat v}} = 4.6512 \times {10^{ - 4}}+ \\ &{(3.7917 \times {10^{ - 4}})^2}/(2 \times 7.0833 \times {10^{ - 5}})=\\ & 1.4798 \times {10^{ - 3}} 。\end{split}$

由此可计算得到硬故障在该传感器总故障的比例约为 $ \hat \lambda /{\hat \lambda _s} = 0.314 $ ，即在传感器的工作过程中，性能指标退化是影响传感器使用的重要因素，约占68.6%，这也从一个侧面说明定期开展性能指标检测对保持传感器的战备完好性具有重要意义。

5 结　语

舰炮设备可靠性演变规律不仅可以通过故障情况反映，还可以通过其性能指标值反映，而性能指标的退化过程常常可以利用冲击理论进行描述。本文在分析舰炮设备可靠性影响因素基础上，将舰炮设备所受的冲击分为致命冲击和非致命冲击，以方便地解释舰炮设备主要性能指标的退化演变规律。本文综合利用设备性能退化信息和故障信息建立了设备的可靠性模型，给出了舰炮设备可靠性评估方法。将本文提出的方法用于实例的结果说明，该可靠性评估方法是有效的。下一步需要开展舰炮设备可靠性与维修策略优化研究，进一步提高舰炮战备完好性水平。