0 引　言

船舶航行使用的重要设备是船舶电气系统，该系统包含电站、电力网与电气负载^[1]。船舶电气系统负责将各种形式的电能变更为电能，为船舶各设备分配电能。船舶电气系统内各模块的繁琐程度均较高^[2]，且具备较高的集成性，当发生故障时，维修人员无法快速、精准诊断故障，导致船舶出现大规模停电事故，造成不可估量的损失^[3-4]，及时制定相关的解决方案，提升船舶供电的连续性。臧旭等^[5]通过经验模态分解法，提取振动信号模态函数，求解其近似熵值，该方法具备较优的信号频率成分提取效果，有效实现故障诊断。张育炜等^[6]利用小波包变换降低信号内的噪声，该方法可有效诊断故障，提升供电可靠性。上述方法无法为维修人员提供精准故障诊断结果，影响供电的连续性与可靠性。为此研究船舶电气系统绝缘故障自适应诊断技术，利用核主成分分析法降低样本数据维度，提升绝缘故障自适应诊断效果，确保船舶航行安全。

1 船舶电气系统绝缘故障诊断 1.1 核主成分分析的船舶电气系统绝缘故障特征降维

核主成分分析是以主成分分析为基础，引入核函数的一种方法。利用核主成分分析，降维处理船舶电气系统绝缘故障特征值，在支持向量机内输入降维后的特征值，输出绝缘故障诊断结果。

令船舶电气系统绝缘故障变量为 $ X = \left[ {{x_1},{x_2}, \cdots ,{x_n}} \right] $ ，X为一个 $ d \times n $ 矩阵，船舶电气系统绝缘故障变量样本数量是n，样本维数是d， $ k \leqslant d $ 。中心化X，令其符合 $ \displaystyle\sum\limits_i {{x_i}} = 0 $ 。

令协方差矩阵E的公式如下：

$ E = \frac{{\displaystyle\sum\limits_i {{x_i}x_i^{\rm{T}}} }}{n} = \frac{{X{X^{\rm{T}}}}}{n} 。$

(1)

式中，T表示转置次数。

特征值分解C，获取：

$ EZ = \sum\limits_a {{\lambda _a}\gamma {z_a}z_a^{\rm{T}}} 。$

(2)

式中： $ Z = \left[ {{z_1},{z_2}, \cdots ,{z_d}} \right] $ 为船舶电气系统绝缘故障特征向量矩阵； $ \Lambda = diag\left( {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _d}} \right) $ 为d维方阵的常数；E的特征值需符合 $ {\lambda _1} \text{≥} {\lambda _2} \text{≥} \cdots \text{≥} {\lambda _d} \text{≥}0 $ 。

降维船舶电力系统绝缘故障特征向量过程中，仅选择前k个特征向量 $ {Z_k} = \left[ {{z_1},{z_2}, \cdots ,{z_k}} \right] $ ，便可完成在k维主成分方向内d维 $ {x_i} $ 的投影，公式如下：

$ \left\{ \begin{gathered} {y_1} = \gamma z_1^T{x_1}，\\ {y_2} = \gamma z_2^T{x_2}，\\ \mathop {}\nolimits_{} \mathop {}\nolimits_{} \vdots \\ {y_k} = \gamma z_k^T{x_k} 。\\ \end{gathered} \right. $

(3)

式中， $ {z_i} $ 均为d维，属于一个投影方向，同时符合 $ z_i^{\rm{T}}{z_i} = 1, $ ， $ {y_1},{y_2}, \cdots ,{y_k} $ 为彼此独立的关系，且 $ {y_i} $ 的方差为 ${\lambda _i}\left( {0 \leqslant i \leqslant k} \right)$ ，因此，船舶电气系统绝缘故障的第1、第2、…、第k个主分量是 $ {y_1},{y_2}, \cdots ,{y_k} $ 。选择前k个主分量，替换原始船舶电气系统绝缘故障特征数据展开分析，完成绝缘故障特征数据降维处理。

通过上述操作完成船舶电气系统绝缘故障特征值的降维处理，得到降维后的特征向量 $ {Z_k} $ ，输入支持向量机内，完成船舶电气系统绝缘故障自适应诊断。

1.2 基于支持向量机的船舶电气系统绝缘故障诊断

利用支持向量机，自适应诊断船舶电气系统绝缘故障，将 $ {Z_k} $ 作为支持向量机的训练样本集，通过训练学习搜索分类机 $ f\left( z \right) $ 模式，令输出值符合 $ {y_i} = f\left( {{z_i}} \right) $ 。

在 $ {y_i} \in \left\{ { - 1,1} \right\} $ 情况下，属于二类划分问题，在 $ {y_i} \in \left\{ {1,2, \cdots ,k} \right\} $ 情况下，属于k类划分，船舶电气系统绝缘故障自适应诊断属于k类划分问题。在 $ f\left( z \right) $ 是线性函数情况下，属于线性分类，反之，属于非线性分类。

对船舶电气系统绝缘故障特征训练样本集的线性分类问题，就是搜索函数问题，表达式如下：

$ {y_i} = f'\left( {{z_i}} \right) = {\rm sgn} \varphi \left( {{z_i}} \right)\left( {\left( {w \cdot {z_i}} \right) + b} \right) 。$

(4)

式中：sgn为符号函数； $ i = 1,2, \cdots ,k $ ； $\varphi \left( {{z_i}} \right) $ 为隐函数；w为法向量；b为偏置； $ \left( {w \cdot z} \right) + b = 0 $ 是划分超平面。

以边际最大化为原则，解决式（4）的线性可分离问题。边际即间隔代表 $ {Z_k} $ 至 $ \left( {w \cdot z} \right) + b = 0 $ 的距离，即全部训练样本点至 $ \left( {w \cdot z} \right) + b = 0 $ 的垂直距离内的最小者，公式如下：

$ \min \left( {\left\| {\varphi \left( z \right) - \varphi \left( {{z_i}} \right)} \right\|:z,\left( {w \cdot z} \right) + b = 0} \right)。$

(5)

边际最大化是搜索令间隔达到最大，即对w和b展开寻优，获取最大间隔：

$ \mathop {\max }\limits_{w \cdot b} \left( {\min \left( {\left\| {\varphi \left( z \right) - \varphi \left( {{z_i}} \right)} \right\|:z,\left( {w \cdot z} \right) + b = 0} \right)} \right) 。$

(6)

式（6）的划分超平面即最优划分超平面，可确保全部船舶电气系统绝缘故障特征向量训练样本，按照最大间隔分类的准确性。为此，构造线性支持向量机的问题即求解二次凸规划问题，公式如下：

$ \left\{ \begin{gathered} \min \frac{{{{\left\| w \right\|}^2}}}{2}，\\ {y_i}\left( {\left( {w \cdot {z_i}} \right) + b} \right) \geqslant 1 。\\ \end{gathered} \right. $

(7)

按照最优化原则，式（7）的问题仅包含唯一一个全局最小解。

利用粒子群算法优化支持向量机的参数σ，提升支持向量机的自适应绝缘故障诊断精度，优化步骤如下：

步骤1　初始化粒子群算法的参数，设置σ的取值范围；

步骤2　将两维搜索空间中，目前粒子位置坐标，当成支持向量机的参数σ，构建分类模型，共构建H个模型，求解这H个模型的分类准确率，计算H个模型的分类准确率均值，将其当成粒子的适应度函数值；

步骤3　以粒子目前位置为粒子的初始个体极值 $ {P'_{best}} $ ，选择步骤2中适应度函数值最优粒子相应的 $ {P'_{best}} $ ，当成初始种群极值 $ {G'_{best}} $ ；

步骤4　更新粒子位置与速度，依据步骤2求解粒子适应度值；

步骤5　判断是否达到最大迭代次数，若达到，则输出最佳适应度函数值，即σ的取值，反之，返回步骤2。

2 实验分析

以某船舶电气系统为实验对象，利用本文技术自适应诊断该船舶电气系统绝缘故障。实验过程中共设置7种绝缘故障，分别是操作过电压、母线电压波动、绝缘体受潮、操动机构脱扣过软、操动机构脱扣卡滞、电路过热、放电。

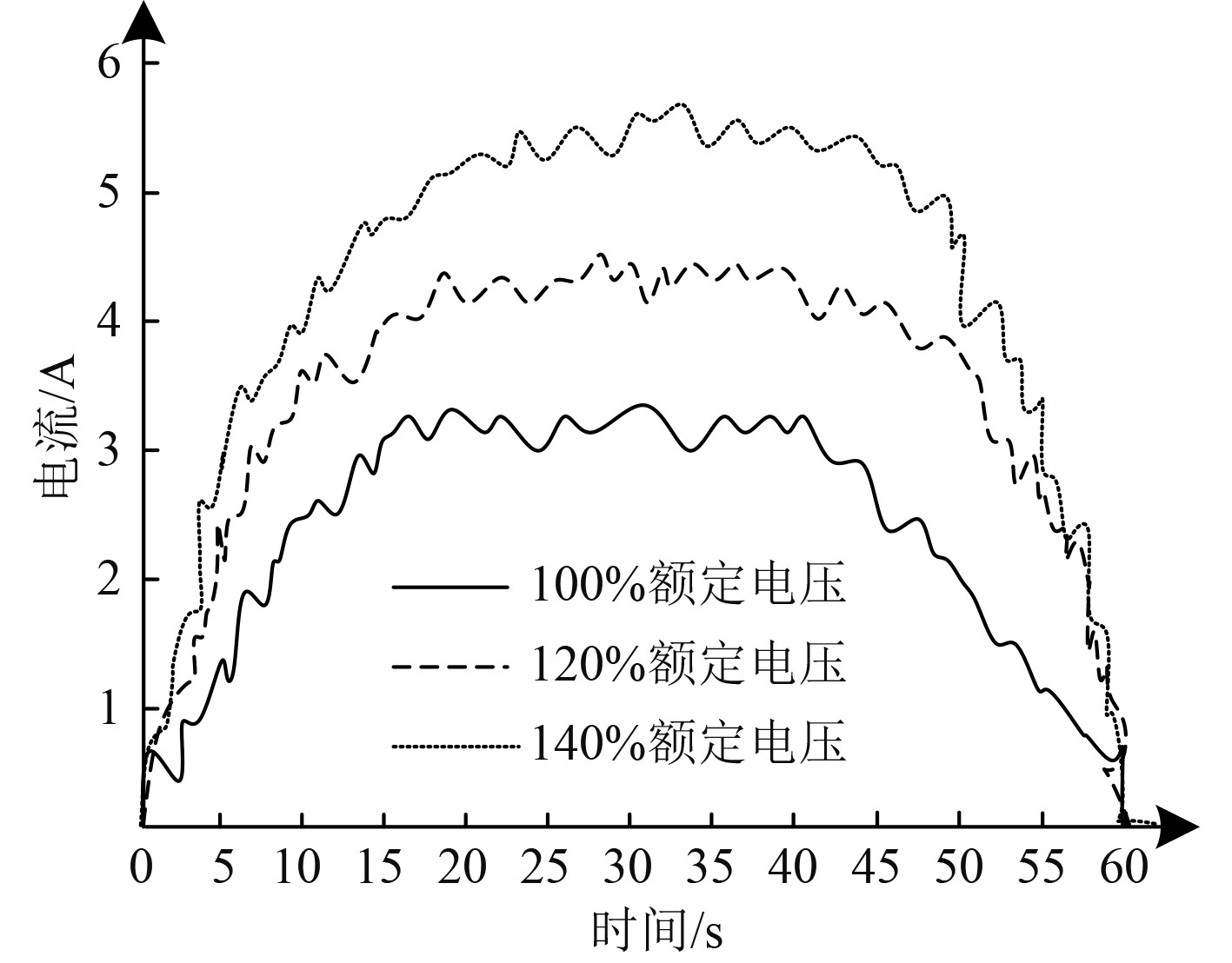
以操作过电压绝缘故障为例，利用本文技术降维处理不同额定电压时的绝缘故障特征量，不同额定电压时的电流数据如图1所示，特征向量降维处理结果如表1所示。当特征向量的累积方差贡献率超过98%时，则超过98%的之前的特征向量，便可代表全部特征向量。

可知，3种额定电压情况下，各特征向量的累计方差贡献率，均在第10个组成成分时，超过98%，因此，选择前10个组成成分作为船舶电气系统绝缘故障自适应诊断的特征向量，有效实现绝缘故障特征向量的降维处理。实验证明，本文技术可有效降维处理特征向量，减少后续船舶电气系统绝缘故障自适应诊断的计算量。

设置7种绝缘故障，利用本文技术自适应诊断，该船舶的电气系统绝缘故障，自适应诊断结果如图2所示。

可知，本文技术可有效自适应诊断，船舶电气系统绝缘故障，自适应在诊断结果共包含7种故障，与实际设置故障情况一致，仅有极少数样本分类结果错误，其余样本分类基本正确，说明本文技术具备较高的绝缘故障自适应在诊断精度。实验证明，本文技术可有效自适应诊断绝缘故障，为船舶电气系统维修人员提供精准的绝缘故障信息，利于维修人员及时维修绝缘故障，确保船舶运行安全。

本文技术内的惩罚系数，直接影响船舶电气系统绝缘故障自适应诊断效果，分析本文技术在不同惩罚系数下，各绝缘故障自适应诊断的故障可信度，分析结果如图3所示。

可知，随着惩罚系数的提升，本文技术自适应诊断各绝缘故障的故障可信度，均呈先上升后下降的趋势，当惩罚系数为1.5时，各绝缘故障自适应诊断的故障可信度最高，最高故障可信度为0.99。实验证明：为提升船舶电气系统自适应绝缘故障诊断的故障可信度，惩罚系数需取值为1.5。

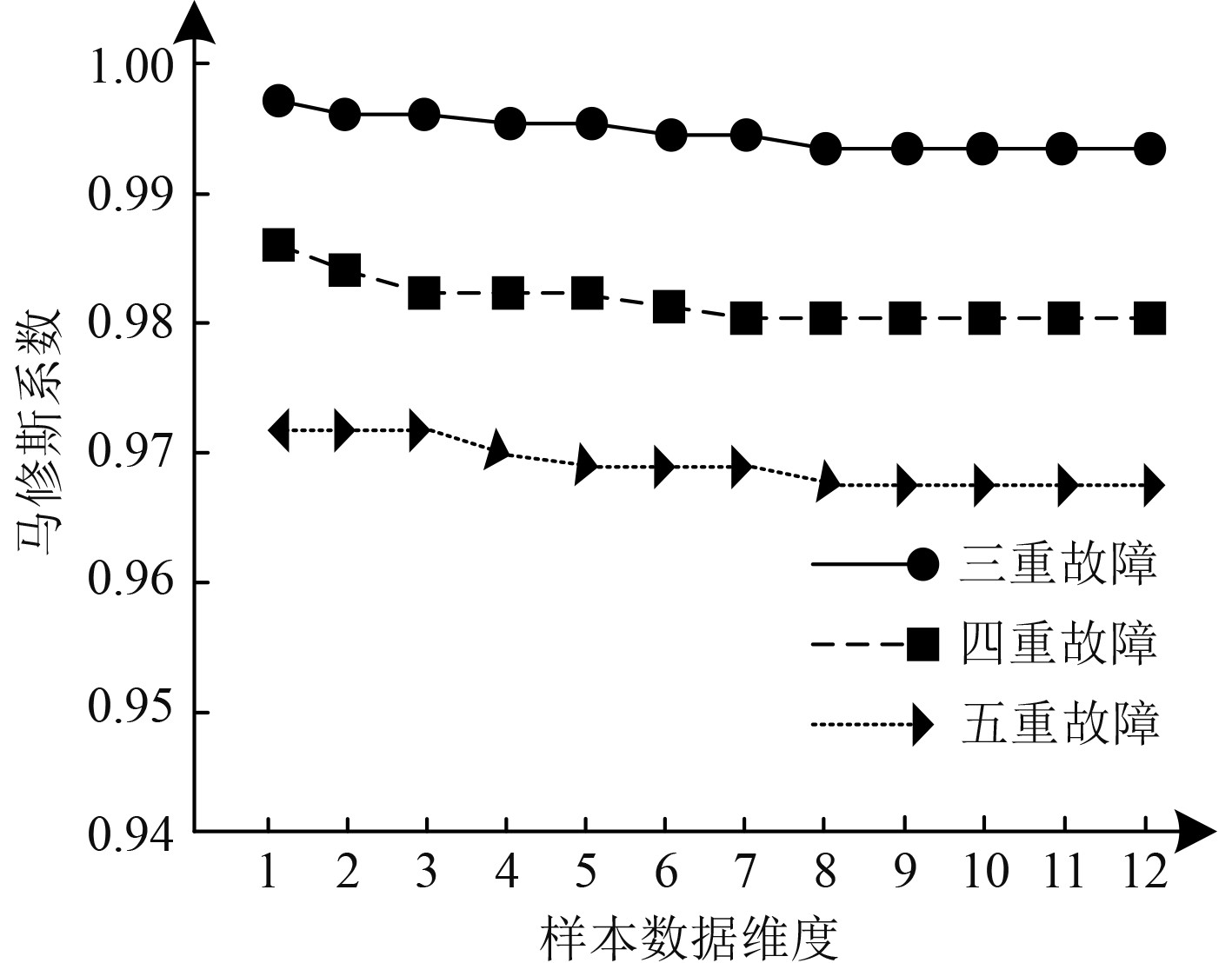
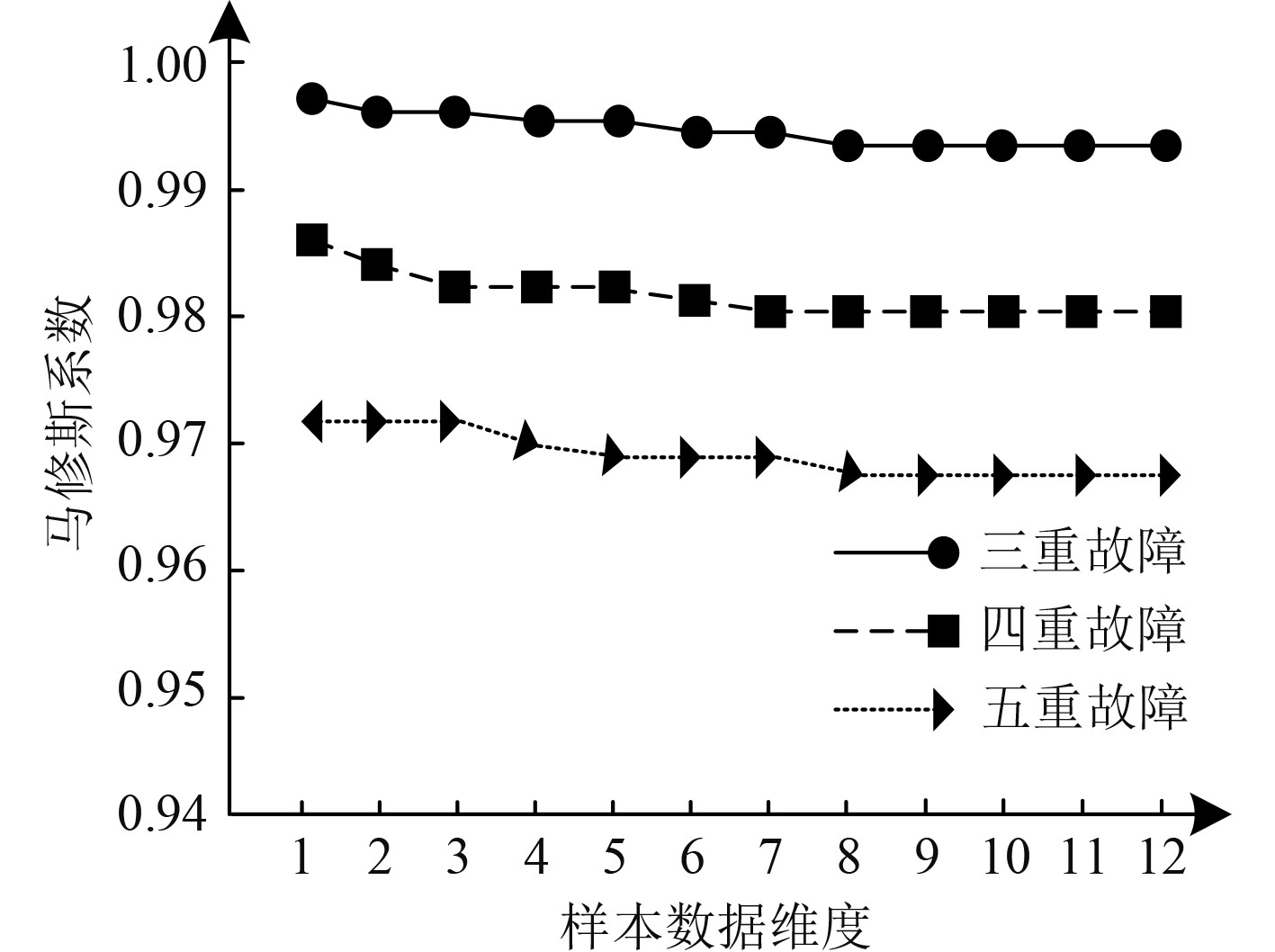
利用马修斯系数衡量本文技术绝缘故障自适应故障诊断的精度，马修斯系数代表实际结果与诊断结果二元分类间的相关系数，该值越接近1，绝缘故障自适应诊断精度越高，该值越接近−1，绝缘故障自适应诊断结果与实际结果差距越大，分析不同样本数据维度及绝缘故障规模时，本文技术自适应故障诊断精度，分析结果如图4所示。

可知，不同绝缘故障规模下，随着样本数据维度的提升，本文技术自适应绝缘故障诊断的马修斯系数仅有微小程度的下降趋势，且当样本数据维度为8维时，马修斯系数便不再发生改变，最低马修斯系数高于0.96，与1非常接近，说明样本数据维度对本文技术的马修斯系数基本无影响，原因是本文技术内利用核主成分分析法降维处理绝缘故障特征向量，可有效降低样本数据维度对绝缘故障自适应诊断的影响；故障规模越大，本文技术的马修斯系数越低，但最低马修斯系数依旧与1较为接近。实验证明，在不同样本数据维度及故障规模时，本文技术的马修斯系数均较高，即自适应绝缘故障诊断精度较高，可有效提升船舶行驶的安全性与可靠性。

3 结　语

船舶航行环境导致船舶电气系统稳定性差，易发生绝缘故障。为保证船舶行驶的安全性，研究船舶电气系统绝缘故障自适应诊断技术，通过核主成分分析法降维处理绝缘故障特征数据，降低绝缘故障特征数据维度对绝缘故障自适应诊断的影响，利用支持向量机完成绝缘故障的自适应诊断。实验证明，本文技术可精准自适应诊断绝缘故障，为船舶维修人员提供精准绝缘故障诊断结果，提升船舶供电的连续性，确保了船舶航行的安全性。