0 引　言

随着集群式AUV在海洋环境监测、资源勘探、搜索救援、侦察监视等民用和军用领域得到了日益广泛的应用，作为AUV集群关键技术之一的协同控制已成为研究热点^[1-3]。通常，AUV集群的协同行为分为：1）组群，随机分布于一定范围内的AUV能无碰聚集并以编队形式执行任务；2）分群，AUV集群在各类分群诱因下分裂为若干个子群的行为^[4]。在AUV集群实际分群应用中，只有可控的分群行为才能满足多目标跟踪、自动避险/避障等分群任务要求，否则集群易陷入无序分裂或无法分裂等非期望不可控状态，因此，分群可控性是分群控制研究中最值得深入研究的问题之一^[5]。分群可控性是指集群能在分群控制算法作用下分裂成多个子群，且各子群中所有个体行为均可达到期望状态（如期望速度、位置以及子群数量和规模等）^[6]。

文献[7-9]研究了基于C-S模型的分群控制方法，但所实现的分群是速度方向相反、大小相同的二分群集。文献[4,10-11]提出了基于信息耦合度的自组织分群控制方法，但该类方法要求个体具有一定记忆能力，实现了对称外界刺激下的等规模分群行为，子群数量、规模和速度不可控。文献[12]设计了基于个体异构特性和多个虚拟领导者的分群控制算法，但子群规模的可控是事先按异构特性通过集中分配实现的。文献[13]通过对两类异构智能体分别设计控制律实现分群，但需事先为I型个体分配所跟踪的II型个体，即子群需事先集中分配。文献[14]提出融合注意力机制和改进拟态物理法的分群控制律，实现多目标环境下分群行为。但注意力机制的引入要求个体具备识别能力，而且子群的规模和速度均不可控。文献[15-16]基于多个虚拟领导者实现了子群数量、规模、速度可控的多分群，但仅限于期望速度恒定的情况。此外，文献[15]中的分群策略不仅需要智能体与领导者的距离、领导者对应的子群规模，还需获得全局个体的子群选择信息，即个体与虚拟领导者之间需要具备双向通信能力。文献[16]则是需要虚拟领导者到智能体的单向通信和邻居智能体之间的双向通信进行分群，且由于分群决策时未考虑个体所在位置，导致过多打乱了已稳定的集群结构，进而使得集群结构调整和速度振荡较大，各个子群形成稳定群集所需时间较长。

本文针对无集中分配且仅有单向通信的AUV集群协同分群可控性问题，提出一种基于蚁群算法的分群控制算法。利用群目标到AUV单向通信的期望子群规模和AUV与群目标的相对距离信息，设计基于蚁群算法的分群策略；基于该策略设计了一种分布式协同分群控制算法，在多个速度时变的群目标导航作用下使AUV运动行为产生分化，从而使AUV集群产生结构调整和速度振荡较小且可控的分群行为。最后，利用仿真实验验证了所提算法的分群可控性。

1 问题描述 1.1 图论基础

若将AUV看成顶点，则集群中个体间相互作用可用无向拓扑图 $G = \left( {V,E,{\boldsymbol{A}}} \right)$ 表示，其中 $V = \left\{ {1,2,\cdots,N} \right\}$ 为顶点集， $E{\text{ = }}\left\{ {\left( {i,j} \right) \in V \times V,j \ne i} \right\}$ 为表示顶点间连接关系的边集，A=[α_ij]为图G的邻接矩阵，若AUV中 i与j互为邻居，α_ij=1，否则α_ij=0。可见，A为N阶对称矩阵。相应的拉普拉斯矩阵为L=D-A，其中，D=[diag(d_ii)]为度矩阵， ${d_{ii}} = \displaystyle\sum\nolimits_{j = 1}^N {{a_{ij}}} $ 为A的第 $i$ 行元素之和。

1.2 问题描述

考虑 ${{\boldsymbol{p}}_{\boldsymbol{i}}}$ 个同构AUV组成的集群， ${{\boldsymbol{p}}_{\boldsymbol{i}}}$ ， ${{\boldsymbol{v}}_i}$ 和 $ {{\boldsymbol{u}}_i} $ 分别为AUV $i$ 的位置、速度向量和控制输入，AUV $i$ 的动力学模型为：

$ \left\{ \begin{gathered} {{{\boldsymbol{\dot p}}}_i}{\kern 1pt} ={\kern 1pt} {\kern 1pt} {{\boldsymbol{v}}_i} \\ {{{\boldsymbol{\dot v}}}_i}{\kern 1pt} ={\kern 1pt} {{\boldsymbol{u}}_{\boldsymbol{i}}} \\ \end{gathered} \right.,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,\cdots,N。$

(1)

假设所有AUV通过自身配备的相同传感器获得周围邻居的速度和位置信息，故AUV $ i $ 的邻居集为：

$ {N_i} = \left\{ {j:\left\| {{{\boldsymbol{p}}_j} - {{\boldsymbol{p}}_i}} \right\| < R,j \ne i,j = 1,2,\cdots,N} \right\} 。$

(2)

其中， $ \left\| {{{\boldsymbol{p}}_j}_i} \right\| = \left\| {{{\boldsymbol{p}}_j} - {{\boldsymbol{p}}_i}} \right\| $ 为AUVi和j之间的欧式距离， ${{\boldsymbol{p}}_{{\text{t}}k}}$ 为传感器探测半径。

假设AUV集群中有 $K\left( t \right)$ 个需要一定规模AUV进行跟踪的群目标，其数量、速度取决于实际任务要求的期望子群数量、速度和规模，且仅有群目标到AUV的单向通信，群目标k可根据目标任务需要广播自身位置 ${{\boldsymbol{p}}_{{{t}}k}}$ 、速度 ${{\boldsymbol{v}}_{{{t}}k}}$ 、控制规律 ${{\boldsymbol{f}}_{{{t}}k}}$ 和需要的AUV个数 ${\tau _k}$ （ ${\tau _k} > 0$ ， $\displaystyle\sum\nolimits_{k = 1}^{K\left( t \right)} {{\tau _k}} = N$ ）。群目标k的动力学模型为：

$ \left\{ \begin{gathered} {{{\boldsymbol{\dot p}}}_{{{t}}k}}{\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} {{\boldsymbol{v}}_{{{t}}k}} \\ {{{\boldsymbol{\dot v}}}_{{{t}}k}}{\kern 1pt} {\text{ = }}{\kern 1pt} {{\boldsymbol{f}}_{{{t}}k}} \\ \end{gathered} \right.,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,2,\cdots,K\left( t \right) 。$

(3)

分群时有多个群目标要跟踪，按AUV选择的群目标是否相同，邻居集可写为：

$ {N}_{i}=\Bigg\{\begin{array}{l}{N}_{i}^{\text{s}}=\left\{j|j\in {N}_{i}且与i群目标相同\right\}，\\ {N}_{i}^{\text{d}}=\left\{j|j\in {N}_{i}且与i群目标不同\right\}。\end{array} $

(4)

在无集中分配且不额外增加个体通信能力情况下，通过建立基于蚁群算法的分群策略实现自主就近分群决策，以在满足目标任务需求前提下减少集群结构调整和速度振荡，并设计具有多个速度时变群目标的分群控制算法，实现AUV集群的可控分群运动。

2 基于蚁群算法的协同分群控制算法 2.1 基于经典蚁群算法的就近分群策略

蚂蚁m在节点 $ {{\boldsymbol{u}}_i} = {\boldsymbol{u}}_i^p + {\boldsymbol{u}}_i^v + {\boldsymbol{u}}_i^t $ 处选择下一个节点 $ {{\boldsymbol{u}}_i} = {\boldsymbol{u}}_i^p + {\boldsymbol{u}}_i^v + {\boldsymbol{u}}_i^t $ 是依据残留信息τ_ij（t）和启发信息η_ij（t）大小进行的，其选择概率为：

$ {P}_{ij}^{m}=\left\{\begin{array}{ll}\frac{{\left({\tau }_{ij}\left(t\right)\right)}^{\alpha }{\left({\eta }_{ij}\left(t\right)\right)}^{\beta }}{{\displaystyle {\sum }_{s\in {J}_{m}\left(i\right)}{\left({\tau }_{is}\left(t\right)\right)}^{\alpha }{\left({\eta }_{is}\left(t\right)\right)}^{\beta }}},&j\in {J}_{m}\left(i\right)，\\ 0\text{，} &j\notin {J}_{m}\left(i\right)。\end{array}\right. $

(5)

其中：η_ij（t）=1/d_ij表示蚂蚁从节点i转移j的期望程度，d_ij为两节点距离； $ \alpha $ 为信息素启发因子，该值越大，说明蚂蚁越趋向于选择多数蚂蚁走过的路径； $\; \beta $ 为能见度启发因子，其值越大，说明蚂蚁越趋向于选择距离近的节点； $ {J_m}\left( i \right) $ 为节点 $i$ 处蚂蚁m可选择节点集合。将多AUV集群系统分群时个体选择群目标的过程看成蚁群选择路径的过程，参照式（5），设计出子群规模可控的就近分群策略， $ t $ 时刻AUV $i$ 选择群目标k的概率公式为：

$ {P_{i,k}} = \frac{{{{\left( {{\tau _k}} \right)}^\alpha }{{\left( {{\eta _{i,k}}} \right)}^\beta }}}{{\displaystyle\sum\nolimits_{k = 1}^{K\left( t \right)} {{{\left( {{\tau _k}} \right)}^\alpha }{{\left( {{\eta _{i,k}}} \right)}^\beta }} }} 。$

(6)

其中：τ_k为群目标k对应的期望子群规模，该项保证分裂的子群规模满足任务需求；η_i,k=1/d_i,k，d_i,k为个体i与群目标k的距离，此项保证在基本满足子群规模需求条件下尽量实现按与群目标的距离进行就近分群；α和β与式（5）中相应参数含义相同。AUV i按式（6）计算选择概率并用轮盘赌选择法来确定跟踪的群目标，分群决策流程为① $sum{\text{ = }}0$ ， $k{\text{ = }}1$ ，生成[0,1]内随机数 $ r $ ；②按照式（6）计算 $ {P_{i,k}} $ ；③计算累积概率 $s{\text{ = }}s + {P_{i,k}}$ ；④若 $r < s$ ，则AUV $i$ 选择目标 $k$ ，算法结束；⑤否则， $k{\text{ = }}k + 1$ ，转到步骤2。

2.2 协同分群控制算法设计

基于蚁群算法协同分群策略设计分群控制器：

$ {{\boldsymbol{u}}_i} = {\boldsymbol{u}}_i^{{p}} + {\boldsymbol{u}}_i^{{v}} + {\boldsymbol{u}}_i^{{t}}。$

(7)

式中：

$ {\boldsymbol{u}}_i^{\text{p}}= \displaystyle\sum\limits_{j \in {N_i}} {{f_{ji}}{{\boldsymbol{e}}_{ij}}} $ 为位置协调项，通过AUV内部之间的交互作用保证个体间避碰、同子群个体聚集和不同子群个体分离，实现无碰撞的分群行为。 $ {{\boldsymbol{f}}_{ji}} $ 是邻居个体之间的相互作用力函数：

$ {f}_{ji}=\left\{ \begin{array}{l}{f}_{{r}}\left(\Vert {p}_{ji}\Vert \right),j\in {N}_{i}^{\text{s}}且\Vert {p}_{ji}\Vert < {d}_{{e}}，\\ 0,j\in {N}_{i}^{{s}}且\Vert {p}_{ji}\Vert ={d}_{{e}}，\\ {f}_{{a}}\left(\Vert {p}_{ji}\Vert \right),j\in {N}_{i}^{{s}}且{d}_{{e}} < \Vert {p}_{ji}\Vert \leqslant R,\\ {f}_{{r}}{}^{\prime }\left(\Vert {p}_{ji}\Vert \right),j\in {N}_{i}^{{d}}。\end{array} \right.$

(8)

其中： ${d_{{e}}}$ 为同子群邻居个体间的期望距离； ${f_{{r}}}\left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right)$ 为同子群邻居个体距离过近时的相互排斥力， ${f_{{a}}}\left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right)$ 为同子群邻居个体距离过远时的相互吸引力， ${f_{{r}}}^\prime \left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right)$ 为不同子群邻居个体间的相互排斥力； $ {{\boldsymbol{e}}_{ji}} = {{{{\boldsymbol{p}}_{ji}}} \mathord{\left/ {\vphantom {{{{\boldsymbol{p}}_{ji}}} {\sqrt {1 + \lambda {{\left\| {{{\boldsymbol{p}}_{ji}}} \right\|}^2}} }}} \right. } {\sqrt {1 + \lambda {{\left\| {{{\boldsymbol{p}}_{ji}}} \right\|}^2}} }} $ ， $F\left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right) = \int_{{d_{\text{e}}}}^{\left\| {{{\boldsymbol{p}}_{ij}}} \right\|} {{f_{ji}}} {\rm{d}}s$ 为 $ F\left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right) = $ $\int_{{d_{\text{e}}}}^{\left\| {{{\boldsymbol{p}}_{ij}}} \right\|} {{f_{ji}}} {\rm{d}}s$ 的固定常数。AUV i和j之间的势能函数为 $F\left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right) =\int_{{d_{\text{e}}}}^{\left\| {{{\boldsymbol{p}}_{ij}}} \right\|} {{f_{ji}}} {\rm{d}}s$ ，AUV i的总势能为 $ {F_i} = \displaystyle\sum\limits_{j \in {N_i}} {F\left( {\left\| {{{\boldsymbol{p}}_{ji}}} \right\|} \right)} $ 。

$ {\boldsymbol{u}}_i^{\text{v}}{\text{ = }} \displaystyle\sum\limits_{j \in N_i^{\text{s}}} {{{\boldsymbol{v}}_j}_i} $ 为速度协同项，保证同子群邻居AUV的速度协调一致，其中， $ {{\boldsymbol{v}}_j}_i $ 为AUV i和j之间的相对速度。

$ {\boldsymbol{u}}_i^t{\text{ = }}\displaystyle\sum\limits_{k = 1}^{K\left( t \right)} {{b_{ik}}} \left( {{c_1}{{{\boldsymbol{\tilde p}}}_{ki}} + {c_2}{{{\boldsymbol{\tilde v}}}_{ki}} + {{\boldsymbol{f}}_{{\text{t}}k}}} \right) $ 为群目标导航项，是AUV集群产生分群的诱因，并实现子群速度动态可控。其中， $ {{\boldsymbol{\tilde p}}_{ki}} = {{\boldsymbol{p}}_{{\text{t}}k}} - {{\boldsymbol{p}}_i} $ ， $ {{\boldsymbol{\tilde v}}_{ki}} = {{\boldsymbol{v}}_{{\text{t}}k}} - {{\boldsymbol{v}}_i} $ ， $ {c_1} $ 和 $ {c_2} $ 为正常数，依据分群策略，若AUV $ i $ 选择群目标k， $ {b_{ik}} = 1 $ ，否则， $ {b_{ik}} = 0 $ 。

2.3 稳定性分析

对于子群k，选择能量函数为：

$ {Q_k} = \frac{1}{2}\sum\limits_{i = 1}^{{\tau _k}} {{F_i}} + \frac{1}{2}\sum\limits_{i = 1}^{{\tau _k}} {{c_1}{{{\boldsymbol{\tilde p}}}_{ki}}^{\text{T}}{{{\boldsymbol{\tilde p}}}_{ki}}} + \frac{1}{2}\sum\limits_{i = 1}^{{\tau _k}} {{{{\boldsymbol{\tilde v}}}_{ki}}^{\text{T}}{{{\boldsymbol{\tilde v}}}_{ki}}}。$

(9)

对式（9）求时间的导数得

$ {\dot Q_k}{\boldsymbol{ = }}\frac{{\text{1}}}{{\text{2}}}\sum\limits_{i = 1}^{{\tau _k}} {{{\dot F}_{\boldsymbol{i}}}} {\boldsymbol{ + }}\sum\limits_{i = 1}^{{\tau _k}} {{c_1}{{{\boldsymbol{\tilde p}}}_{k{\boldsymbol{i}}}}^{\text{T}}{{{\boldsymbol{\tilde v}}}_{k{\boldsymbol{i}}}}} {\boldsymbol{ + }}\sum\limits_{i = 1}^{{\tau _k}} {{{{\boldsymbol{\tilde v}}}_{k{\boldsymbol{i}}}}^{\text{T}}{{{\boldsymbol{\dot {\tilde v}}}}_{k{\boldsymbol{i}}}}}。$

(10)

因 $ {\nabla _{{{{\boldsymbol{\tilde p}}}_{ji}}}}{F_{ji}}\left( {\left\| {{{{\boldsymbol{\tilde p}}}_{ji}}} \right\|} \right) = {\nabla _{{{{\boldsymbol{\tilde p}}}_{ki}}}}{F_{ji}}\left( {\left\| {{{{\boldsymbol{\tilde p}}}_{ji}}} \right\|} \right) = - {\nabla _{{{{\boldsymbol{\tilde p}}}_{kj}}}}{F_j}_i\left( {\left\| {{{{\boldsymbol{\tilde p}}}_{ji}}} \right\|} \right) $ 得

$ \frac{1}{2}\sum\limits_{i = 1}^{{\tau _k}} {{{\dot F}_i}} = \sum\limits_{i = 1}^{{\tau _k}} {{{{\boldsymbol{\tilde v}}}_{ki}}^{\text{T}}{\nabla _{{{{\boldsymbol{\tilde p}}}_{ki}}}}{F_i}} 。$

(11)

又 $ {{\boldsymbol{\dot {\tilde v}}}_{ki}} = {{\boldsymbol{u}}_i} - {{\boldsymbol{f}}_{{\text{t}}k}} $ ，得

$\begin{aligned}[b] {{\dot Q}_k} =& \sum\limits_{i = 1}^{{\tau _k}} {{{{\boldsymbol{\tilde v}}}_{ki}}^{\text{T}}{\nabla _{{{{\boldsymbol{\tilde p}}}_{ki}}}}{F_i}} + \sum\limits_{i = 1}^{{\tau _k}} {{c_1}{{{\boldsymbol{\tilde p}}}_{ki}}^{\text{T}}{{{\boldsymbol{\tilde v}}}_{ki}}}+ \sum\limits_{i = 1}^{{\tau _k}} {{{{\boldsymbol{\tilde v}}}_{ki}}^{\text{T}}\left( {{{\boldsymbol{u}}_i} - {{\boldsymbol{f}}_{{\text{t}}k}}} \right)} = \\ & -{{{\boldsymbol{\tilde v}}}^{\text{T}}}\left[ {\left( {{\boldsymbol{L}} + {c_2}{{\boldsymbol{I}}_{{\tau _k}}}} \right) \otimes {{\boldsymbol{I}}_2}} \right]{\boldsymbol{\tilde v}} 。\end{aligned} $

(12)

其中： ${\boldsymbol{\tilde v}} = {\left[ {{\boldsymbol{\tilde v}}_1^{\text{T}},{\boldsymbol{\tilde v}}_2^{\text{T}},\cdots,{\boldsymbol{\tilde v}}_{{\tau _k}}^{\text{T}}} \right]^{\text{T}}}$ ； $ \otimes $ 为克罗内克积；L为上文定义的拉普拉斯矩阵； $ {{\boldsymbol{I}}_{{\tau _k}}} $ 和 $ {{\boldsymbol{I}}_2} $ 分别为相应维度的单位阵。显然，L和 $ {{\boldsymbol{I}}_{{\tau _k}}} $ 为半正定矩阵，又因为 $ {c_1}{{\boldsymbol{\tilde p}}_{ki}}^{\text{T}}{{\boldsymbol{\tilde p}}_{ki}} \leqslant $ $2{Q_k}\left( 0 \right) $ ，所以 $ {\boldsymbol{L}} + {c_2}{{\boldsymbol{I}}_{{\tau _k}}} $ 为半正定矩阵，进而可得 $ {\dot Q_k} \leqslant 0 $ 。由此可得 $ {Q_k} $ 是非增函数，即对于任意时间t， $ {Q_k}\left( t \right) \leqslant {Q_k}\left( 0 \right) $ 。

因此，集合

$ \varOmega = \left\{ {\left( {{{{\boldsymbol{\tilde p}}}^{\text{T}}},{{{\boldsymbol{\tilde v}}}^{\text{T}}}} \right)\left| {{Q_k}\left( t \right) \leqslant {Q_k}\left( 0 \right)} \right.} \right\} 。$

(13)

是紧集。根据LaSalle不变性原理可确定子群中所有AUV起始于 $ \Omega $ 的轨迹将会收敛于最大不变集：

$ {\boldsymbol{S}} = \left\{ {\left( {{{{\boldsymbol{\tilde p}}}^{\text{T}}},{{{\boldsymbol{\tilde v}}}^{\text{T}}}} \right)\left| {{{\dot Q}_k}\left( t \right) = 0} \right.} \right\}。$

(14)

由公式（12）可得

$ {\dot Q_k} = - {{\boldsymbol{\tilde v}}^{\text{T}}}\left[ {{\boldsymbol{L}} \otimes {{\boldsymbol{I}}_2}} \right]{\boldsymbol{\tilde v}} - {c_2}{{\boldsymbol{\tilde v}}^{\text{T}}}{\boldsymbol{\tilde v}} 。$

(15)

其中 $ {\boldsymbol{L}} \otimes {{\boldsymbol{I}}_2} $ 是半正定矩阵，当且仅当 $ {{\boldsymbol{\tilde v}}^{\text{T}}}{\boldsymbol{\tilde v}}{\text{ = }}0 $ 且 $ {{\boldsymbol{\tilde v}}^{\text{T}}}\left[ {{\boldsymbol{L}} \otimes {{\boldsymbol{I}}_2}} \right]{\boldsymbol{\tilde v}}{\text{ = }}0 $ 时， $ {\dot Q_k}{\text{ = }}0 $ ，可得 $ {{\boldsymbol{\tilde v}}_{ki}} = {{\boldsymbol{v}}_i} - {{\boldsymbol{v}}_{{\text{t}}k}} = {\text{0}} $ ，即子群中AUV的速度矢量与相应群目标的速度矢量一致： ${{\boldsymbol{v}}_i} = {{\boldsymbol{v}}_{{\text{t}}k}},i = 1,2, \cdots ,{\tau _k}$ 。

3 仿真实验

为验证所设计的可控分群控制方法有效性，设计50个AUV组成的集群在Matlab下的仿真实验。参考文献[16]设定个体i和j之间相互作用力函数为：

$ {f}_{ji}=\left\{\begin{array}{l}\dfrac{5{k}_{1}{d}_{ji}}{\sqrt{1+{d}_{ji}{}^{2}}}{\rho }_{h}\left(\frac{{\Vert {p}_{ji}\Vert }_{\sigma }}{R}\right)\text{，}j\in {N}_{i}^{{s}}，\\ \dfrac{5{k}_{2}{R}_{ji}}{\sqrt{1+{d}_{ji}{}^{2}}}{\rho }_{h}\left(\frac{{\Vert {p}_{ji}\Vert }_{\sigma }}{R}\right)\text{，}j\in {N}_{i}^{{d}}。\end{array}\right. $

(16)

其中： $ {k_1} $ ， $ {k_2} $ 为任意正常数； ${d_{ji}} = \left\| {{{\boldsymbol{p}}_{ji}}} \right\| - {d_{{e}}}$ ； ${R_{ji}} = $ $ \left\| {{{\boldsymbol{p}}_{ji}}} \right\| - R $ ； $ {\left\| z \right\|_\sigma } = \dfrac{1}{\varepsilon }\left( {\sqrt {1 + \varepsilon {{\left\| z \right\|}^2}} - 1} \right) $ ， $ \varepsilon > 0 $ 。

$ {\rho _h}(z) = \left\{ {\begin{array}{*{20}{c}} {1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;z \in [0,h)}，\\ {0.5\left[ {1 + \cos \left( {\text{π} \dfrac{{z - h}}{{1 - h}}} \right)} \right],\;{\rm{if}}\;z \in [h,1]}，\\ {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}}}。\end{array}} \right. $

每个AUV的初始位置在40×40 m²范围内随机给定，初始速度在0~1 m/s内随机给定。组群时，集群中只有1个群目标1，其初始位置在40×40 m²内随机给定，分群时，原群目标消失，出现3个新的群目标。在保证速度方向发生不交叉和位置不重合的前提下，3个群目标的初始位置在距离原群目标当前位置40 m内随机给定， ${{\boldsymbol{v}}_{{{t}}1}}{\kern 1pt} {\text{ = }}\left[ {5,4} \right]$ m/s， ${{\boldsymbol{v}}_{{{t2}}}}{\kern 1pt} {\text{ = }}\left[ { - 3,8\sin t} \right]$ m/s， ${{\boldsymbol{v}}_{{{t3}}}}{\kern 1pt} {\text{ = }}\left[ {6,4\sin t} \right]$ m/s。在满足总和为50的条件下，随机给定各个子群的期望规模。其余参数设置： $ R = 8 $ m， ${d_{\text{e}}}{\text{ = }}7.4$ m， $ \varepsilon = 0.1 $ ， $ {k_1}{\text{ = 30}} $ ， $ {k_2}{\text{ = 10}} $ 。

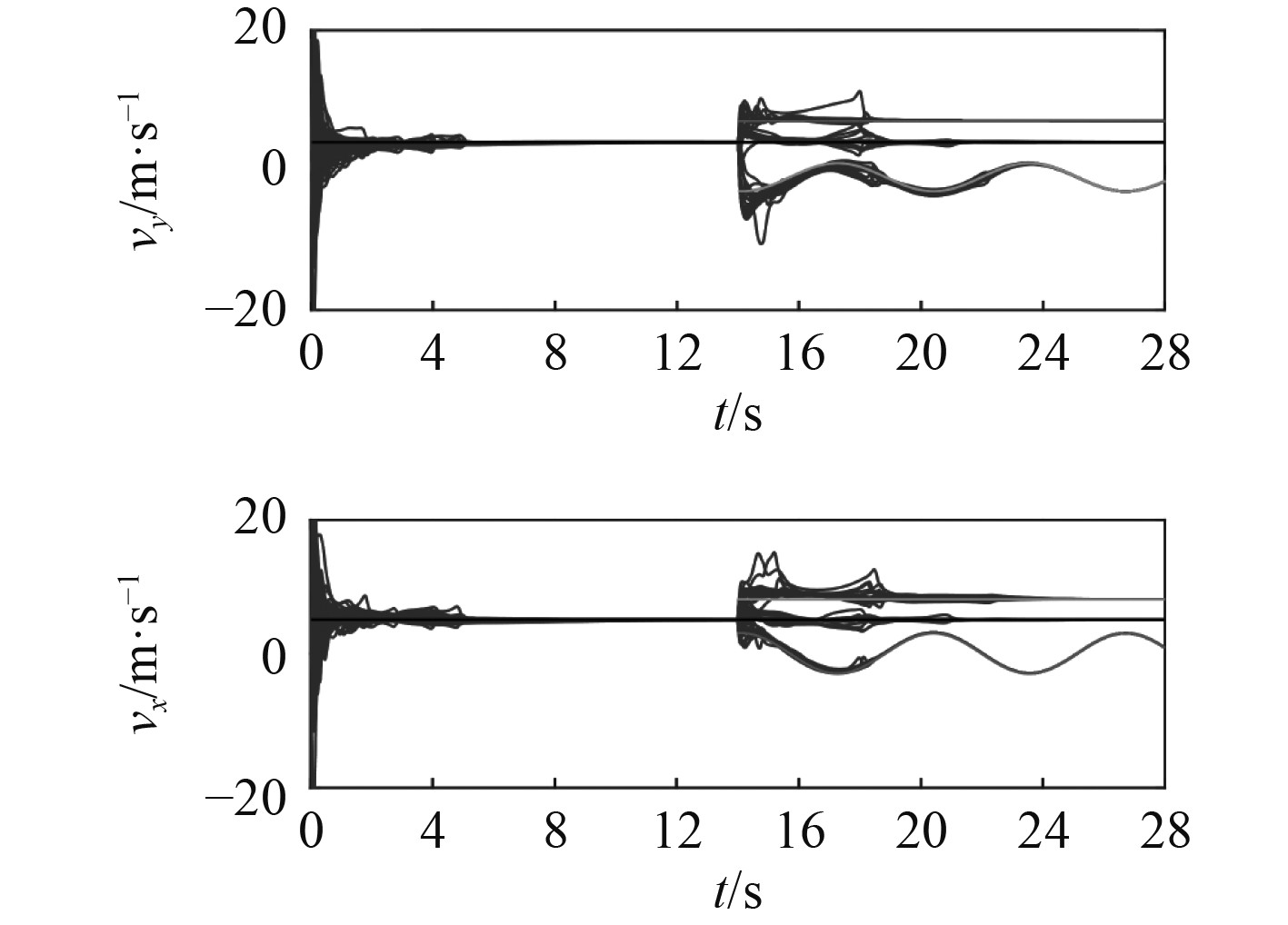
AUV集群和群目标的运行轨迹和速度曲线分别如图1和图2所示。图1中，“*”、“○”、“◇”和“☆”分别为AUV集群和3个群目标的终点，可见，集群在最初一个群目标导航作用下完成了组群，并在出现3个群目标后完成了协同分群。由图2可知，无论组群还是分群运动，各子群速度均与对应的群目标速度趋于一致，且分群时集群速度振荡较小。

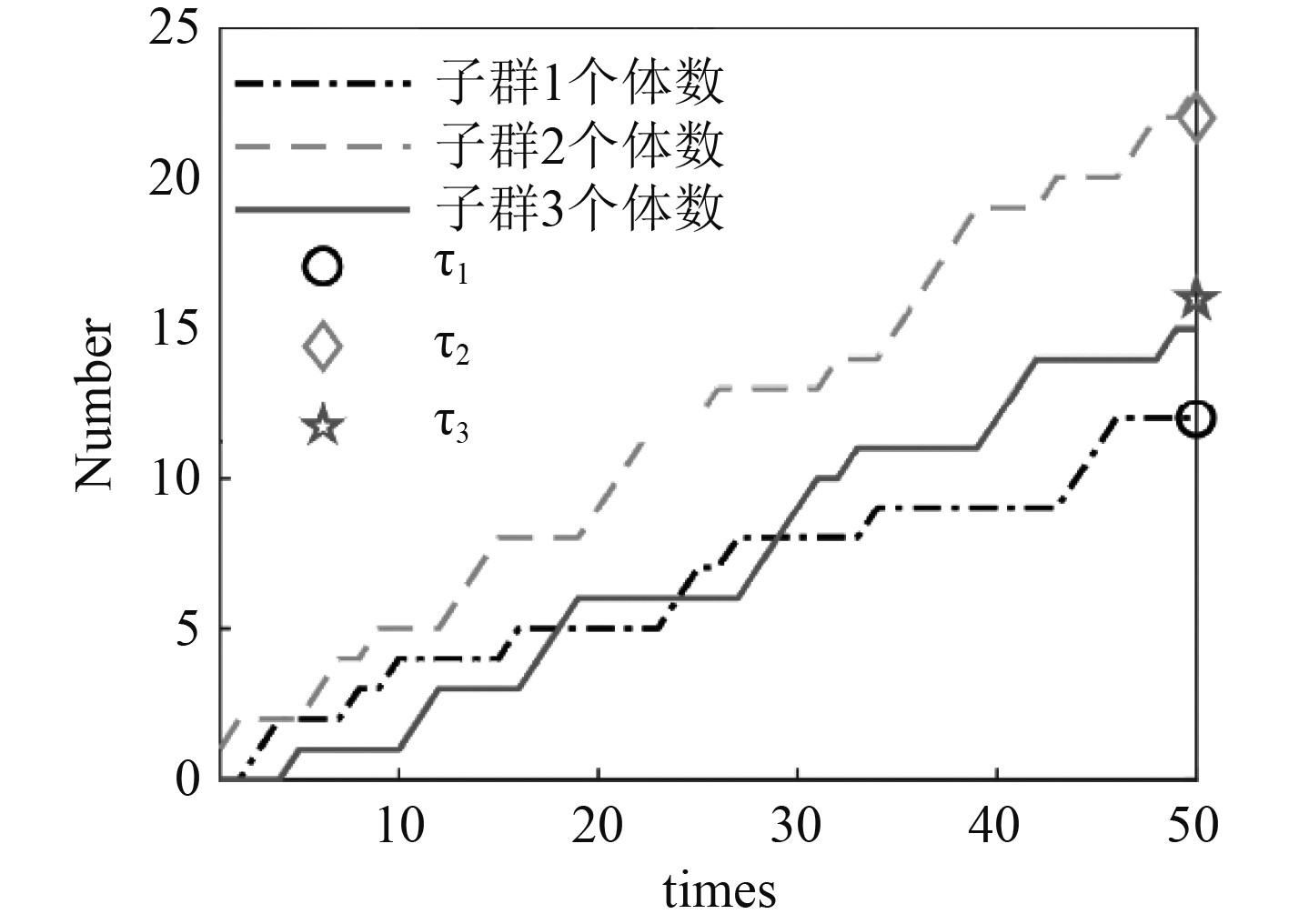
子群规模变化如图3所示。可见，3个子群分别有12，23，15个个体，与相对应的期望子群规模12，22，16基本吻合。

图4为分群过程中AUV集群结构变化。图4中小“○”为AUV位置，大“○”、“◇”和“☆”分别为群目标位置。可见，14 s时AUV集群已处于一个群目标作用下的稳定结构，并出现3个群目标；14.8 s时有部分个体分离，15.6 s时大部分个体完成了分离，16.4 s时分化成3个子群。可见，在所设计的分群控制算法作用下，AUV集群实现了按AUV与群目标距离的就近分群，且未打乱已稳定的邻居结构。

为进一步判断AUV集群是否形成稳定结构及分群过程中的结构调整大小，构造结构势能函数：

$ E = \frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{j \in {N_i}} {{{\left( {\left\| {{{\boldsymbol{p}}_j}_i} \right\| - {d_{\text{e}}}} \right)}^2}} }。$

(17)

可知，当个体间距达到期望距离时，此结构势能E最小。

AUV集群结构势能曲线如图5所示。可见，在分群过程中结构能量并没有出现大幅度增加现象，结构能量趋于稳定状态，这进一步表明所设计的就近分群策略可避免分群过程中过大的结构调整，使各个子群形成期望的稳定结构。

4 结　语

针对AUV集群在协同分群过程中出现的子群数量、规模、速度不可控问题，提出一种基于蚁群算法的可控分群控制算法。在无集中分配且仅具备单向通信能力的条件下，利用期望子群规模和AUV与群目标的相对距离，设计基于蚁群算法的分群策略，并在此基础上设计一种分布式协同分群控制算法，在多个速度时变的群目标导航作用下使AUV集群产生结构调整和速度振荡较小的可控分群行为。最后，利用理论分析和仿真实验验证了所提算法的有效性。未来将进一步探索适用于存在阻尼、障碍物等复杂环境下的分群控制算法。