无人船和无人机具有广阔的发展空间和应用前景,已成为学者的研究热点[1-2]。单无人船或者单无人机在执行任务时存在效率相对较低以及无法保证安全性等问题,且无法满足越发复杂的任务需求,所以多无人船和多无人机的协同控制已逐渐成为完成海上复杂行动的主要方式,并且该方式在军事和民事领域得到了广泛应用[3-4]。其中编队控制问题作为多智能体运动协同控制的研究热点问题之一,备受关注[5-6],实现异构多智能体编队控制具有重要的科学意义和实用价值。
多智能体编队控制问题的思路是设计有效的控制策略,使编队中的各无人船以及无人机最终形成期望的编队队形。一致性问题作为多智能体协同控制的基础问题研究已取得许多成果[7],相关成果应用于编队控制[8]。
在实际应用中,无人船和无人机之间的通信通常会受到很多因素的限制,例如有限的通信带宽以及有限的通信资源等,并且各个智能体之间进行连续通信,不仅会导致网络拥塞,造成资源浪费,还会对系统控制性能产生影响。因此引入事件触发机制[9-11],通过设计事件触发条件函数进行判断,只有超过该函数设定的阈值,才进行信息交互,从而减少通信次数和控制器更新次数来达到节约能量的目的。文献[12]首次将事件触发控制技术引入到多智能体系统中,并详细分析和讨论了事件触发控制技术在多智能体系统一致性问题中的应用。文献[13]基于事件触发函数设计分布式控制器,实现多智能体系统时变编队,将编队控制问题转化为一致性问题。文献[14]针对二阶多智能体系统的环形编队控制问题,分别设计了基于事件触发的集中式和分布式控制律。文献[15]针对具有定向拓扑的多智能体系统密闭控制问题,提出一种基于模型的边缘事件触发控制住协议。文献[16]设计了一种基于事件触发策略的有限时间一致性算法,通过定义的状态误差设计分布式控制协议,多智能体系统仅在达到触发条件时才更新控制器,从而减少了网络消耗,降低能耗。已有众多学者将事件触发机制应用在多智能体的协同控制问题中,但将多智能体协同控制与事件触发相结合的研究还相对较少,异构多智能体编队控制结合事件触发机制的研究更是屈指可数。
本文主要研究异构多智能体编队控制问题,提出一种基于事件触发机制的多智能体分布式编队控制协议,可有效节约通信资源。设计基于事件触发的状态观测器对位置信息进行估计,再分别设计纵向推进力控制律、转向力矩控制律对各智能体进行控制,系统仅需要间歇性通信,从而减低系统的通信资源消耗,更好适应于实际系统。
1 预备知识及问题描述 1.1 图论本文只考虑无向图(用图
图1中
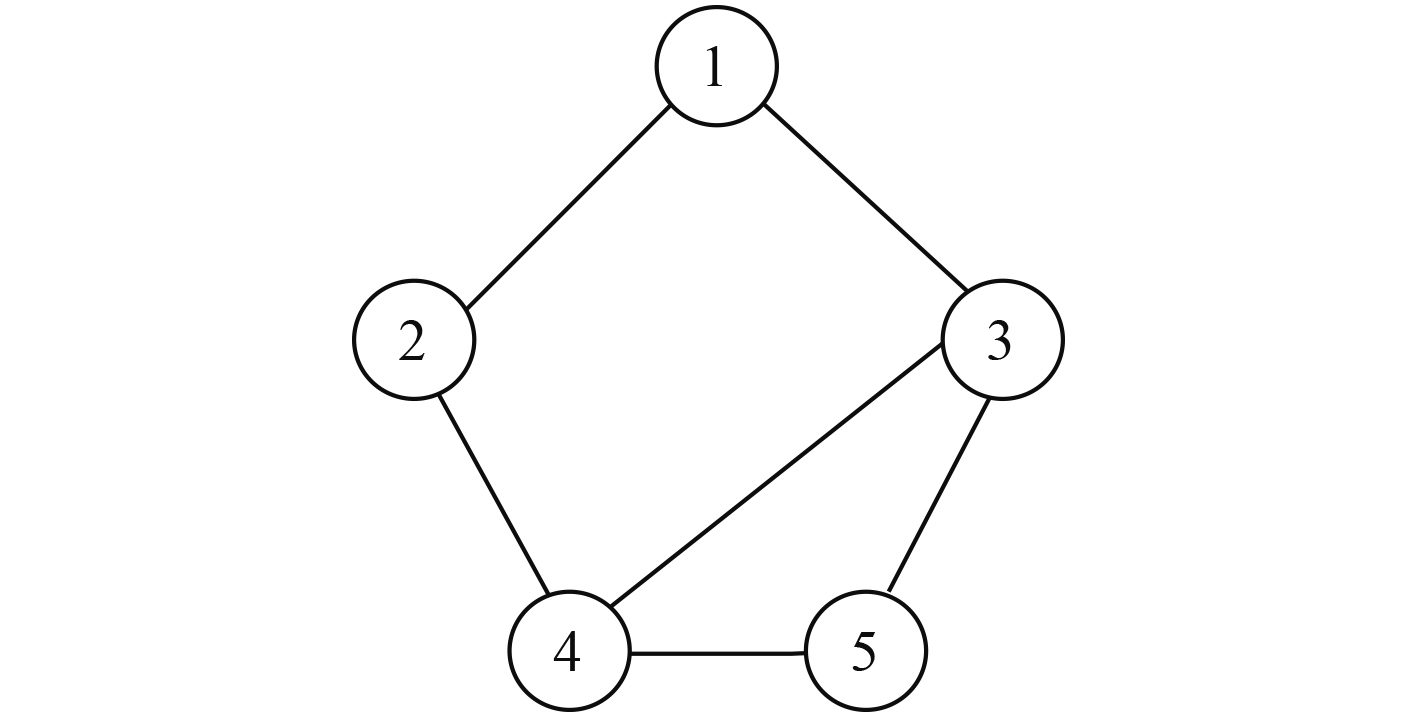
|
图 1
无向图
|
| $ \begin{split} & V\left({G}_{1}\right)=\left\{{v}_{1},{v}_{2},{v}_{3},{v}_{4},{v}_{5}\right\};\\ &\varepsilon \left({G}_{1}\right)=\left\{{e}_{12},{e}_{13},{e}_{23},{e}_{34},{e}_{35},{e}_{45}\right\}。\end{split} $ |
其中,
关联于同一条边
在图1中,2个顶点相同的边被称为环;若一对顶点
考虑
| $ \left\{\begin{split} &{\dot{x}}_{i}={u}_{i}\cos{\varphi }_{i}-{v}_{i}\sin{\varphi }_{i},\\ &{\dot{y}}_{i}={u}_{i}\sin{\varphi }_{i}+{v}_{i}\cos{\varphi }_{i},\\ &{\dot{\varphi }}_{i}={r}_{i},\\ &{\dot{u}}_{i}=\frac{{m}_{22}}{{m}_{11}}{v}_{i}{r}_{i}-\frac{{d}_{11}}{{m}_{11}}{u}_{i}+\frac{{\tau }_{ui}}{{m}_{11}},\\ &{\dot{v}}_{i}=-\frac{{m}_{11}}{{m}_{22}}{u}_{i}{r}_{i}-\frac{{d}_{22}}{{m}_{22}}{v}_{i},\\ &{\dot{r}}_{i}=\frac{{m}_{11}-{m}_{22}}{{m}_{33}}{u}_{i}{v}_{i}-\frac{{d}_{33}}{{m}_{33}}{r}_{i}+\frac{{\tau }_{ri}}{{m}_{33}}。\end{split}\right. $ | (1) |
无人船模型示意图如图2所示。其中
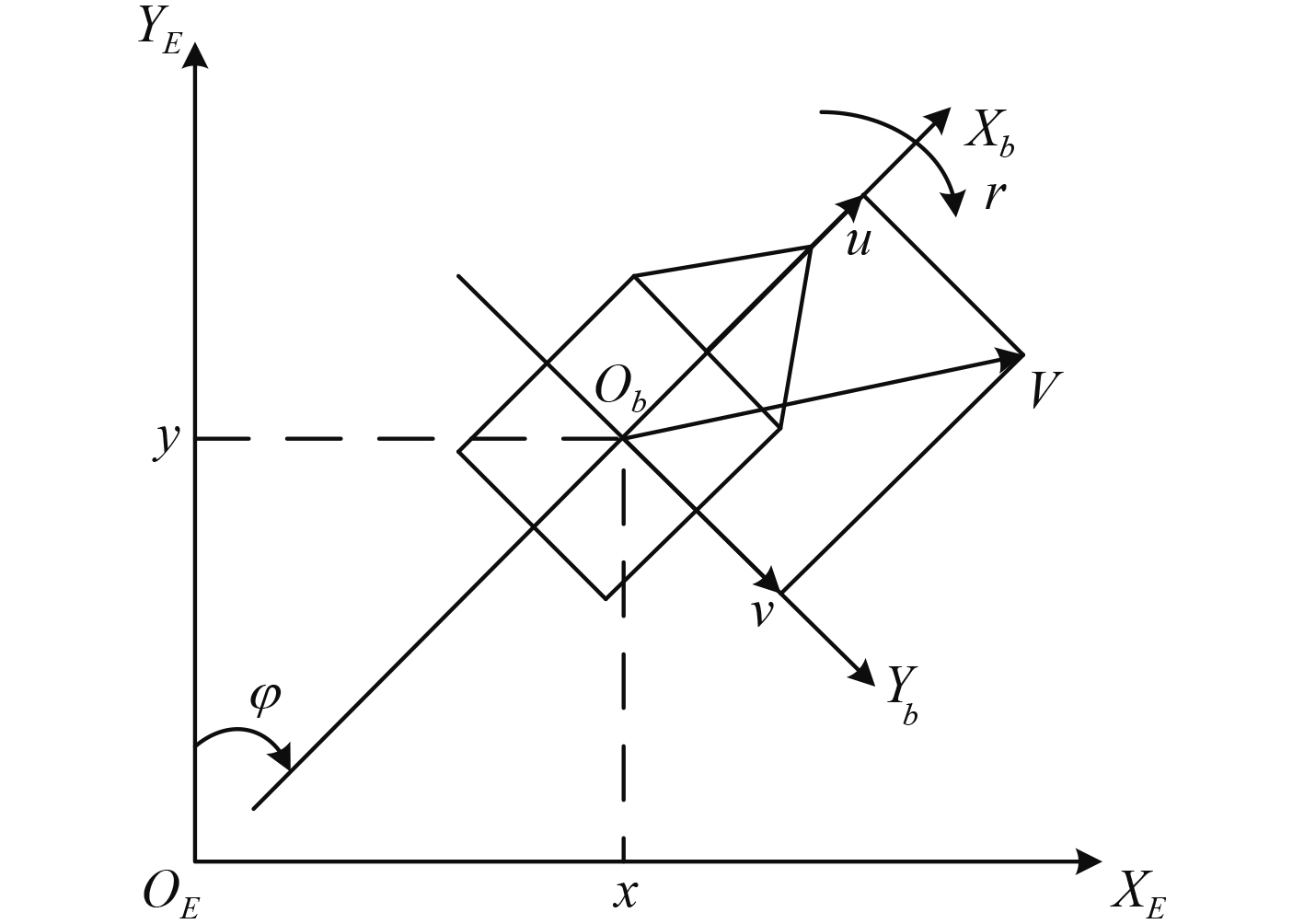
|
图 2 无人船模型示意图 Fig. 2 Schematic diagram of unmanned ship model |
对四旋翼无人机进行建模,图3为四旋翼无人机的结构示意图。
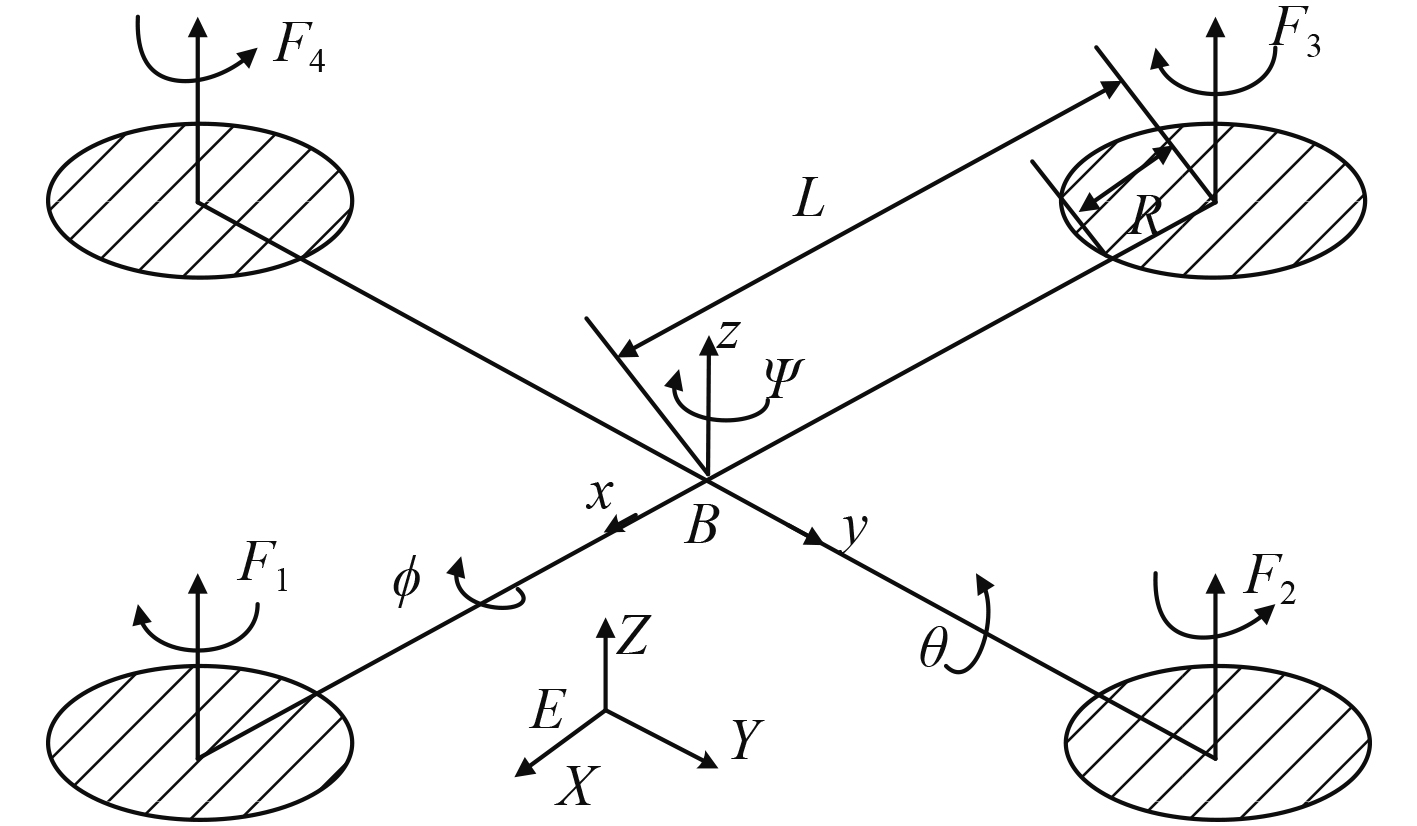
|
图 3 四旋翼无人机结构示意图 Fig. 3 Schematic diagram of the four-rotor UAV structure |
建模前需要首先引入大地坐标系
用欧拉角来表示大地坐标系与机体坐标系之间的夹角,包括滚转角(-roll)、俯仰角(-pitch)、偏航角(-yaw)这三个姿态角。机体的向量在机体坐标系与大地坐标系之间是可以通过旋转3次欧拉角来互相转换的,绕
| $ \begin{split}&{R}_{x}(\varphi )=\left[\begin{array}{ccc}1& 0& 0\\ 0& {C}_{\varphi }& -{S}_{\varphi }\\ 0& {S}_{\varphi }& {C}_{\varphi }\end{array}\right] ,\;\;{R}_{y}(\theta )=\left[\begin{array}{ccc}{C}_{\theta }& 0& {S}_{\theta }\\ 0& 1& 0\\ -{S}_{\theta }& 0& {C}_{\theta }\end{array}\right] ,\\ &{R}_{\textit{z}}(\psi )=\left[\begin{array}{ccc}{C}_{\psi }& -{S}_{\psi }& 0\\ {S}_{\psi }& {C}_{\psi }& 0\\ 0& 0& 1\end{array}\right] 。\\[-25pt]\end{split}$ | (2) |
坐标系旋转的结果可由基于固定坐标系旋转的组合获得,由机体坐标系首先绕
| $ {C}_{b}^{e}=\left[\begin{array}{ccc}{C}_{\theta }{C}_{\psi }& {S}_{\varphi }{S}_{\theta }{C}_{\psi }-{C}_{\varphi }{S}_{\psi }& {C}_{\varphi }{S}_{\theta }{C}_{\psi }+{S}_{\varphi }{S}_{\psi }\\ {C}_{\theta }{S}_{\psi }& {S}_{\varphi }{S}_{\theta }{S}_{\psi }+{C}_{\varphi }{C}_{\psi }& {C}_{\varphi }{S}_{\theta }{S}_{\psi }-{S}_{\varphi }{C}_{\psi }\\ -{S}_{\theta }& {S}_{\varphi }{C}_{\theta }& {C}_{\varphi }{C}_{\theta }\end{array}\right]。$ | (3) |
假设U1为无人机的垂直高度控制量,U2~U4分别代表无人机的滚转、俯仰和偏航输入控制量,F1~F4为无人机4个旋翼分别提供的拉力,则有
| $ \left\{\begin{aligned}&{U}_{1}={F}_{1}+{F}_{2}+{F}_{3}+{F}_{4},\\ &{U}_{2}={F}_{2}-{F}_{4},\\ &{U}_{3}={F}_{1}-{F}_{3},\\ &{U}_{4}={F}_{1}-{F}_{4}+{F}_{2}-{F}_{3}。\end{aligned}\right.$ | (4) |
基于上述做出的4个假设,若四旋翼无人机处于低速飞行状态且风速较小时,空气阻力对无人机的影响小到忽略不计。同时,假设无人机只在固定高度进行飞行,即俯仰角和滚转角及其变化率都很小,因此可以对无人机建立如下简化数学模型:
| $ \left\{\begin{aligned}&\ddot{\varphi }=\frac{L}{{I}_{x}}{U}_{2},\ddot{\theta }=\frac{L}{{I}_{y}}{U}_{3},\ddot{\psi }=\frac{1}{{I}_{\textit{z}}}{U}_{4},\\ &\ddot{x}=\frac{{U}_{1}}{m}\left({C}_{\varphi }{C}_{\psi }{S}_{\theta }+{S}_{\varphi }{S}_{\psi }\right),\\ &\ddot{y}=\frac{{U}_{1}}{m}\left({C}_{\varphi }{S}_{\psi }{S}_{\theta }-{S}_{\varphi }{C}_{\psi }\right),\\ &\ddot{\textit{z}}=\frac{{U}_{1}}{m}{C}_{\varphi }{C}_{\theta }-g。\end{aligned}\right. $ | (5) |
考虑
假设1 各智能体之间的通信图无向连接;
假设2 无人机的飞行高度保持不变,因此在编队控制时取无人机的二维平面坐标作为控制量,将该异构多智能体模型进行简化。
2 控制器设计 2.1 观测器设计考虑
| $ {\dot{\beta }}_{i}\left(t\right)={u}_{i}\left(t\right)。$ | (6) |
其中对于
设计的基于采样的分布式事件触发机制为:
| $ \underset{t\to \infty }{{\rm{lim}}}{\beta }_{i}\left(t\right)=\underset{t\to \infty }{{\rm{lim}}}{\beta }_{j}\left(t\right)=\frac{\displaystyle\sum _{i=1}^{n}{\beta }_{i}\left(0\right)}{n} 。$ | (7) |
观测器为:
| $ \left\{\begin{array}{c}{\dot{\beta }}_{i}\left(t\right)=-\displaystyle\sum _{j=1}^{n}{a}_{ij}\left({\widehat{\beta }}_{i}(t)-{\widehat{\beta }}_{j}(t)\right),\\ {\dot{\xi }}_{i}\left(t\right)=-\displaystyle\sum _{j=1}^{n}{a}_{ij}\left({\widehat{\xi }}_{i}(t)-{\widehat{\xi }}_{j}(t)\right)。\end{array}\right. $ | (8) |
其中对于
定义测量偏差变量为:
| $ {e}_{i}\left(t\right)={\widehat{\beta }}_{i}\left(t\right)-{\beta }_{i}\left(t\right) 。$ | (9) |
在算法中引入采样机制,
将式(7)的事件触发条件设计为:
| $ {d}_{i}{{e}_{i}}^{2}\left(kh\right)\geqslant \sigma {{\gamma }_{i}}^{2}\left(kh\right)。$ | (10) |
其中
为简化符号,定义
| $ \dot{\beta }\left(t\right)=-L\widehat{\beta }\left(t\right) 。$ | (11) |
假设模型(1)具有无向图和连通图,若参数满足以下条件,则在事件触发条件(10)下的机制(7)可达到一致性。
| $ \frac{1}{2}-h{\lambda }_{n}-2\sigma > 0 。$ | (12) |
其中
针对无人船数学模型(1)以及无人机模型(5),结合所设计的事件触发观测器(8)估计位置信息,进一步设计多智能体一致性控制器跟踪所估计的信息从而实现一致性控制。
2.2.1 虚拟控制律设计定义位置跟踪误差为:
| $ \left\{\begin{array}{c}{e}_{xi}={x}_{i}-{\beta }_{i},\\ {e}_{yi}={y}_{i}-{\xi }_{i}。\end{array}\right. $ | (13) |
对式(20)进行求导可得:
| $ \left[\begin{array}{c}{\dot{e}}_{x}\\ {\dot{e}}_{y}\end{array}\right]=\left[\begin{array}{cc}\rm{cos}\varphi & -\rm{sin}\varphi \\ \rm{sin}\varphi & \rm{cos}\varphi \end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]-\left[\begin{array}{c}\dot{\beta }\\ \dot{\xi }\end{array}\right] 。$ | (14) |
式中:
| $ \left[\begin{array}{c}{\alpha }_{u}\\ {\alpha }_{v}\end{array}\right]=\left[\begin{array}{cc}\rm{cos}\varphi & \rm{sin}\varphi \\ -\rm{sin}\varphi & \rm{cos}\varphi \end{array}\right]\left[\begin{array}{c}\dot{\beta }-k{e}_{x}\\ \dot{\xi }-k{e}_{y}\end{array}\right] 。$ | (15) |
其中
定义Lyapunov函数为:
| $ V=\frac{1}{2}{e}_{xi}^{2}+\frac{1}{2}{e}_{yi}^{2}。$ | (16) |
对式(23)进行求导可得:
| $ \left[\begin{array}{c}{\dot{e}}_{x}\\ {\dot{e}}_{y}\end{array}\right]=\left[\begin{array}{cc}\rm{cos}\varphi & -\rm{sin}\varphi \\ \rm{sin}\varphi & \rm{cos}\varphi \end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]-\left[\begin{array}{c}\dot{\beta }\\ \dot{\xi }\end{array}\right] 。$ | (17) |
令
| $ \dot{V}=-k{e}_{xi}^{2}-k{e}_{yi}^{2}\leqslant 0 $ | (18) |
则
| $ \left\{\begin{array}{c}{u}_{i}{{\rm{cos}}}{\phi }_{i}-{v}_{i}{{\rm{sin}}}{\phi }_{i}-{\dot{\beta }}_{i}=-ke_{xi},\\ {u}_{i}{{\rm{sin}}}{\phi }_{i}+{v}_{i}{{\rm{cos}}}{\phi }_{i}-{\dot{\xi }}_{i}=-ke_{yi}。\end{array}\right. $ | (19) |
矩阵形式为:
| $ \left[\begin{array}{cc}\rm{cos}\varphi & -\rm{sin}\varphi \\ \rm{sin}\varphi & \rm{cos}\varphi \end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{c}\dot{\beta }-kex\\ \dot{\xi }-k{e}_{y}\end{array}\right]。$ | (20) |
由此可得到虚拟控制律
定义纵向速度误差为:
| $ {e}_{ui}={u}_{i}-{\alpha }_{ui}。$ | (21) |
设计滑模面为:
| $ {s}_{1}={\mu }_{1}{e}_{ui} 。$ | (22) |
其中
对式(22)进行求导可得:
| $ \dot{{S}}_{1} ={\mu }_{1}{\dot{e}}_{ui} \\ ={\mu }_{1}\left({\dot{u}}_{i}-{\dot{\alpha }}_{ui}\right) \\ ={\mu }_{1}\left(\frac{{m}_{22}}{{m}_{11}}{v}_{i}{r}_{i}-\frac{{d}_{11}}{{m}_{11}}{u}_{i}+\frac{{\tau }_{ui}}{{m}_{11}}-{\dot{\alpha }}_{ui}\right) 。$ | (23) |
令
| $ {\dot{s}}_{1}=-{\varepsilon }_{1}{{\rm{sgn}}}({s}_{1})。$ | (24) |
其中
可得:
| $\begin{split} &{\mu }_{1}\left(\frac{{m}_{22}}{{m}_{11}}{v}_{i}{r}_{i}-\frac{{d}_{11}}{{m}_{11}}{u}_{i}+\frac{{\tau }_{ui}}{{m}_{11}}-{\dot{\alpha }}_{ui}\right)=-{\varepsilon }_{1}{\rm{sgn}}\left({s}_{1}\right),\\ &\frac{{m}_{22}}{{m}_{11}}{v}_{i}{r}_{i}-\frac{{d}_{11}}{{m}_{11}}{u}_{i}+\frac{{\tau }_{ui}}{{m}_{11}}-{\dot{\alpha }}_{ui}=-\frac{{\varepsilon }_{1}}{{\mu }_{1}}{\rm{sgn}}\left({s}_{1}\right),\\ &{m}_{22}{v}_{i}{r}_{i}-{d}_{11}{u}_{i}+{\tau }_{ui}-{m}_{11}{\dot{\alpha }}_{ui}=-\frac{{m}_{11}{\varepsilon }_{1}}{{\mu }_{1}}{\rm{sgn}}\left({s}_{1}\right) 。\\[-34pt] \end{split}$ | (25) |
综上可得纵向推进力控制律为:
| $ {\tau }_{ui}={m}_{11}{\dot{\alpha }}_{u}-\frac{{m}_{11}{\varepsilon }_{1}}{{\mu }_{1}}{\rm{sgn}}({s}_{1})-{m}_{22}{v}_{i}{r}_{i}+{d}_{11}{u}_{i}。$ | (26) |
定义Lyapunov函数为:
| $ {V}_{1}=\frac{1}{2}{s}_{1}^{2} 。$ | (27) |
对式(27)求导可得:
| $ \begin{split} {\dot{V}}_{1}=&{s}_{1}\cdot {\dot{s}}_{1} ={s}_{1}\cdot {\mu }_{1} \Biggr(\frac{{m}_{22}}{{m}_{11}}{v}_{i}{r}_{i}-\frac{{d}_{11}}{{m}_{11}}{u}_{i}+\\ &\dfrac{{m}_{11}{\dot{\alpha }}_{ui}-\dfrac{{m}_{11}{\varepsilon }_{1}}{{\mu }_{1}}{\rm{sgn}}\left({s}_{1}\right)-{m}_{22}{v}_{i}{r}_{i}+{d}_{11}{u}_{i}}{{m}_{11}}\Biggr)= \\ &-{s}_{1}{\varepsilon }_{1}{\rm{sgn}}\left({s}_{1}\right) -{\varepsilon }_{1}\left|{s}_{1}\right|\leqslant 0。\end{split} $ | (28) |
定义横向速度误差为:
| $ {e}_{vi}={v}_{i}-{\alpha }_{vi} 。$ | (29) |
设计滑模面为:
| $ {s}_{2}={\dot{e}}_{vi}+{\mu }_{2}{e}_{vi} 。$ | (30) |
对式(30)求导可得:
| $ {\dot{S}}_{2}={\ddot{e}}_{vi}+{\mu }_{2}{\dot{e}}_{vi} =\left({\ddot{v}}_{i}-{\ddot{e}}_{vi}\right)+{\mu }_{2}\left({\dot{v}}_{i}-{\dot{\alpha }}_{vi}\right) 。$ | (31) |
为方便后面的表示,令
| $ f=-\left[{\ddot{\beta }}_{i}-k{\dot{e}}_{xi}\right]{{\rm{sin}}}{\phi }_{i}+\left[{\ddot{\xi }}_{i}-k{\dot{e}}_{yi}\right]{{\rm{cos}}}{\phi }_{i}。$ | (32) |
则
| $ {\ddot{\alpha }}_{vi}=-{\dot{r}}_{i}{\alpha }_{ui}-{r}_{i}{\dot{\alpha }}_{ui}+\dot{f}。$ | (33) |
将式(33)代入到式(31)可得:
| $ {\dot{s}}_{2}={\ddot{v}}_{i}+{\dot{r}}_{i}{\alpha }_{ui}+{r}_{i}{\dot{\alpha }}_{ui}-\dot{f}+{\mu }_{2}({\dot{v}}_{i}-{\dot{\alpha }}_{vi}) 。$ | (34) |
令
| $ {\dot{s}}_{2}=-{\varepsilon }_{2}{\rm{sgn}}({s}_{2}) 。$ | (35) |
其中
可得:
| $ \begin{split}&{\ddot{v}}_{i}+\left(\frac{{m}_{11}-{m}_{22}}{{m}_{33}}{u}_{i}{v}_{i}-\frac{{d}_{33}}{{m}_{33}}{r}_{i}+\frac{{\tau }_{ri}}{{m}_{33}}\right){\alpha }_{ui}+{r}_{i}{\alpha }_{ui}-\dot{f}+{\mu }_{2}{\dot{e}}_{vi}=\\ &-{\varepsilon }_{2}{\rm{sgn}}({s}_{2})\left(\frac{{m}_{11}-{m}_{22}}{{m}_{33}}{u}_{i}{v}_{i}-\frac{{d}_{33}}{{m}_{33}}{r}_{i}+\frac{{\tau }_{ri}}{{m}_{33}}\right){\alpha }_{ui}= -{\ddot{v}}_{i}-\\ &{r}_{i}{\alpha }_{ui}+\dot{f}-{\mu }_{2}{\dot{e}}_{vi}-{\varepsilon }_{2}{\rm{sgn}}({s}_{2})({m}_{11}-{m}_{22}){u}_{i}{v}_{i}-{d}_{33}{r}_{i}+{\tau }_{ri}=\\ &-\frac{{m}_{33}}{{\alpha }_{ui}}({\ddot{v}}_{i}+{r}_{i}{\alpha }_{ui}-\dot{f}+{\mu }_{2}{\dot{e}}_{vi}+{\varepsilon }_{2}{\rm{sgn}}({s}_{2}))。\\[-18pt] \end{split}$ | (36) |
综上可得转向力矩控制律为:
| $ \begin{split}{\tau }_{ri}=&-({m}_{11}-{m}_{22}){u}_{i}{v}_{i}+{d}_{33}{r}_{i}-\\ &\frac{{m}_{33}}{{\alpha }_{ui}}({\ddot{v}}_{i}+{r}_{i}{\dot{\alpha }}_{ui}-\dot{f}+{\mu }_{2}{\dot{e}}_{vi}+{\varepsilon }_{2}\rm{sgn}({s}_{2}))。\end{split}$ | (37) |
定义Lyapunov函数为:
| $ {V}_{2}=\frac{1}{2}{{s}_{2}}^{2}。$ | (38) |
对式(38)求导可得:
| $ \begin{split}&{\dot{V}}_{2}={\dot{s}}_{2}{s}_{2} ={s}_{2}\cdot {\ddot{v}}_{i}+ \left(\frac{{m}_{11}-{m}_{22}}{{m}_{33}}{u}_{i}{v}_{i}-\frac{{d}_{33}}{{m}_{33}}{r}_{i} +\right. \\ &\frac{ - \left({m}_{11} - {m}_{22}\right){u}_{i}{v}_{i} + {d}_{33}{r}_{i} }{{{m}_{33}}}-\\ &\left. \frac{ \dfrac{{m}_{33}}{{\alpha }_{ui}}\left({\ddot{v}}_{i}+{r}_{i}{\alpha }_{ui}-\dot{f}+{\mu }_{2}{\dot{e}}_{vi}+{\varepsilon }_{2}{{\rm{sgn}}}({s}_{2})\right)}{{m}_{33}}\right),\\ &{\alpha }_{ui} +{r}_{i}{\dot{\alpha }}_{ui}-\dot{f}+{\mu }_{2}{\dot{e}}_{vi} ={s}_{2}\left({\ddot{v}}_{i}-{\ddot{v}}_{i}-{r}_{i}{\dot{\alpha }}_{ui}+\dot{f}-\right.\\ &\left.{\mu }_{2}{\dot{e}}_{vi}{-\varepsilon }_{2}{{\rm{sgn}}}({s}_{2})+{r}_{i}{\dot{\alpha }}_{ui}-\dot{f}+{\mu }_{2}{\dot{e}}_{vi}\right)=-{s}_{2}{\varepsilon }_{2}{{\rm{sgn}}}({s}_{2}) =\\ &-{\varepsilon }_{2}\left|{s}_{2}\right|\leqslant 0。\end{split}$ | (39) |
由式(27)和式(39)可知
通过数值仿真验证设计的基于事件触发的异构多智能体一致性控制律的有效性及稳定性,多智能体系统1架领航无人机和3艘跟随无人船组成。设置参数为:
无人船和无人机之间的通信拓扑结构如图4所示。4号智能体为领航无人机,其余为跟随无人船,在事件触发时,按照图4所示进行通信。
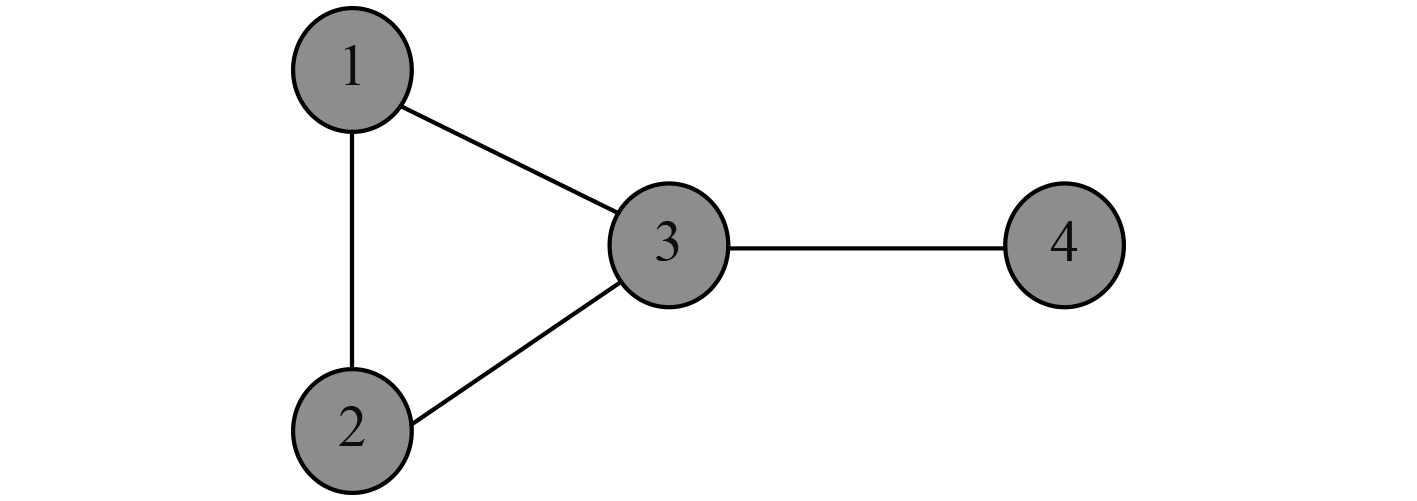
|
图 4 通信拓扑图 Fig. 4 Communication topology diagram |
根据通信拓扑结构,可得到Laplacian矩阵为:
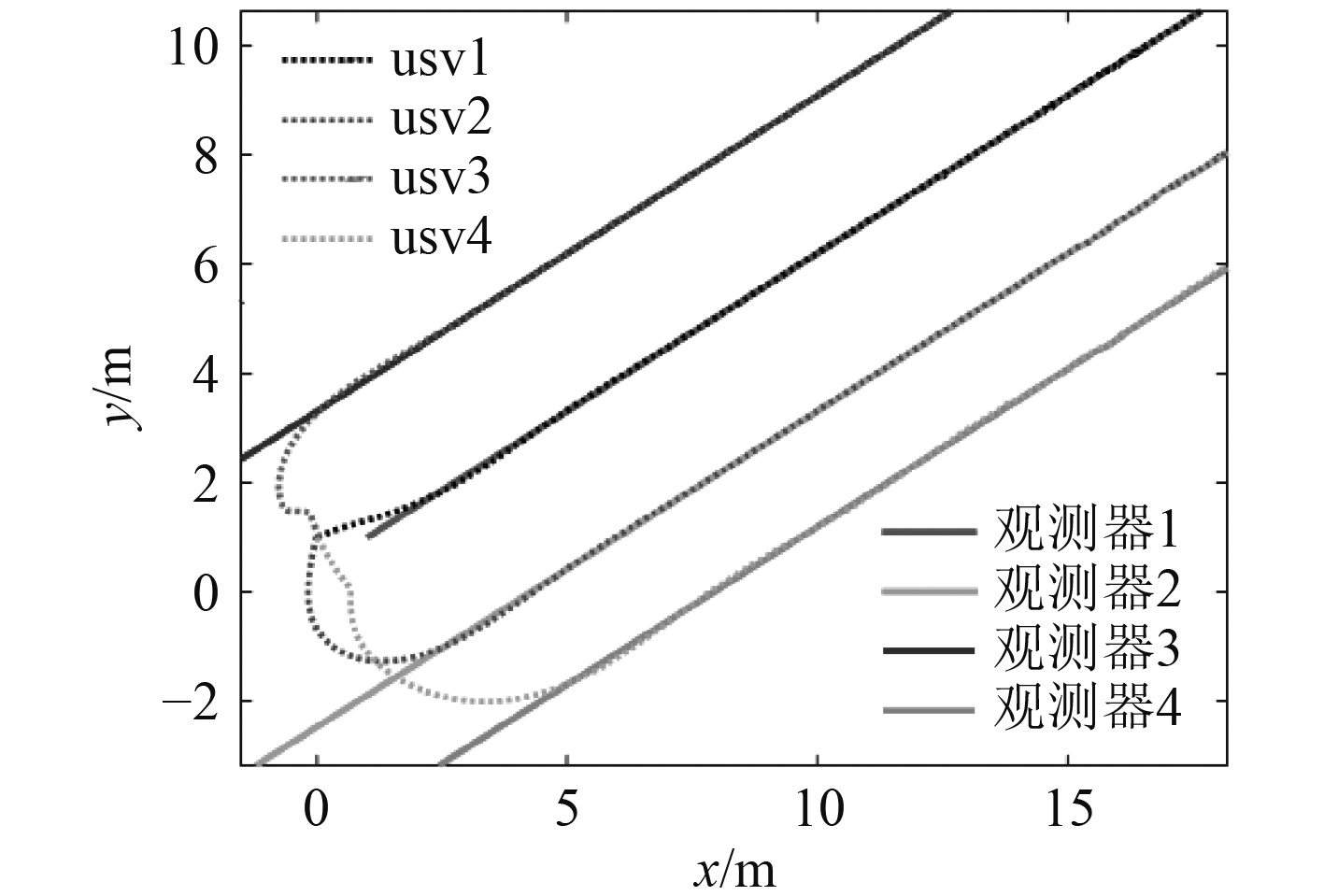
|
图 5 各智能体状态轨迹观测值 Fig. 5 Observed value of each agent state trajectory |
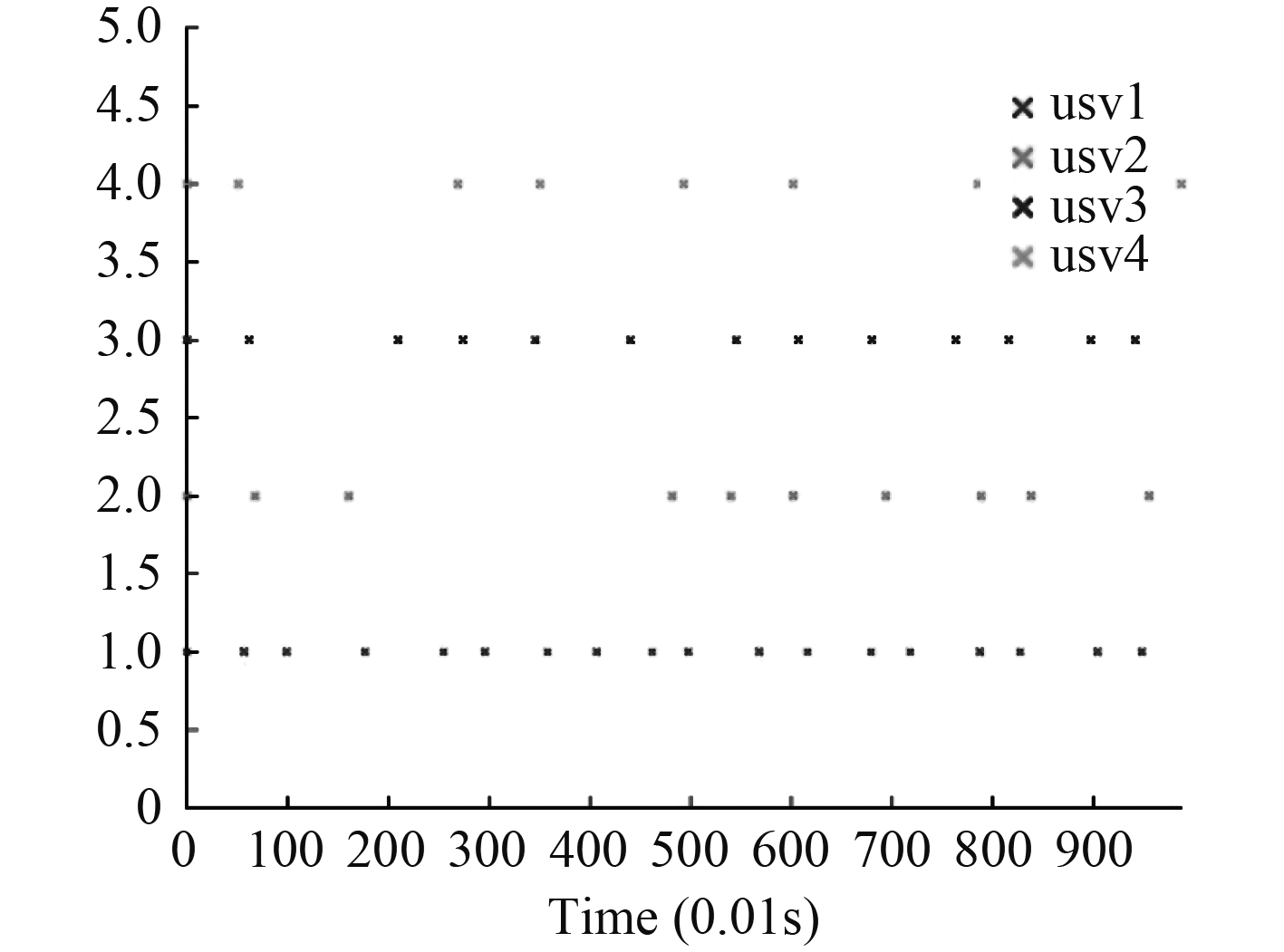
图6为每个智能体的事件,并且每个智能体的事件稀疏,事件只需在触发时刻触发,实现了节省资源的目的,在实际应用中,资源的节约对多智能体系统完成任务具有重要意义。
|
图 6 事件触发间隔 Fig. 6 Event trigger interval |
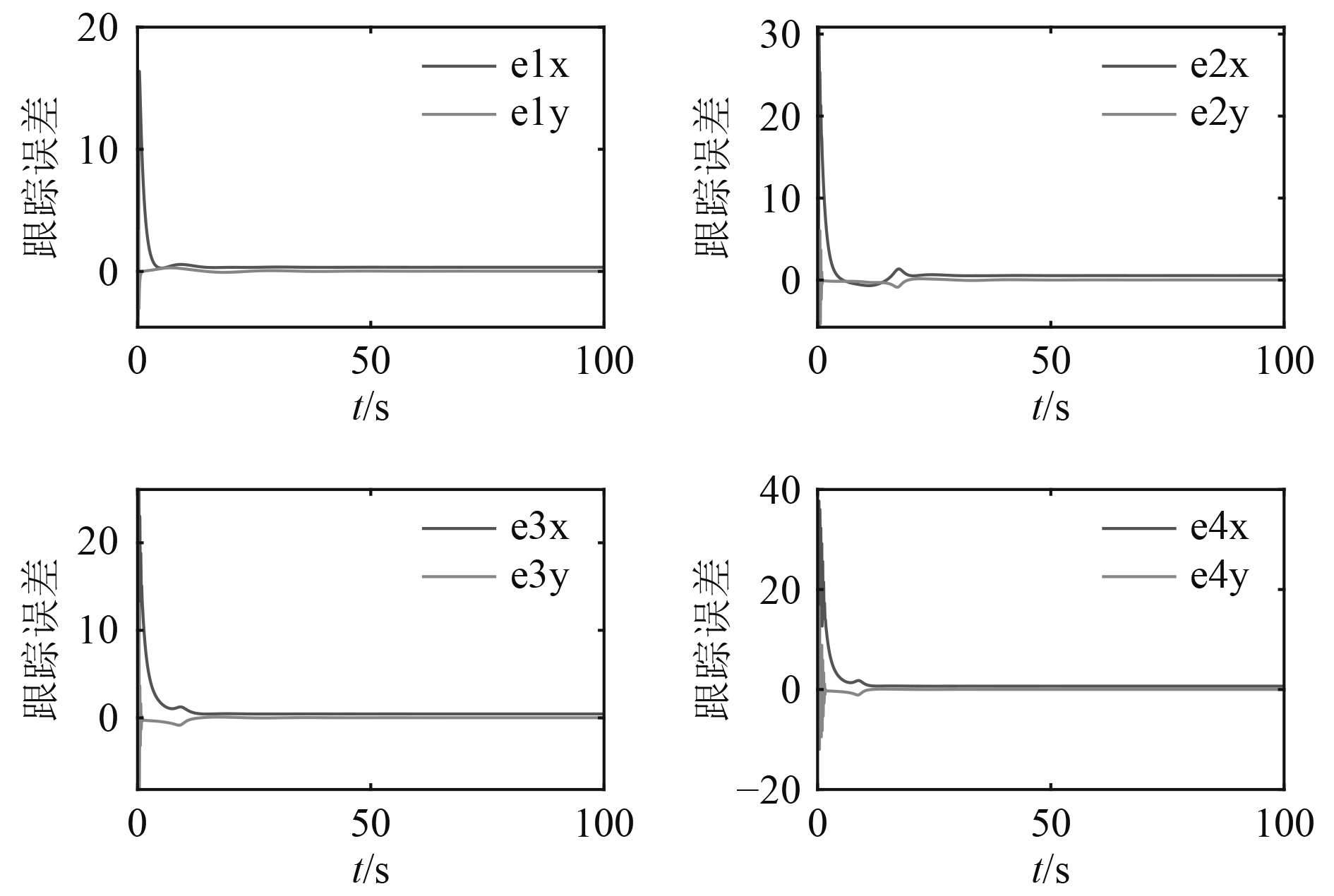
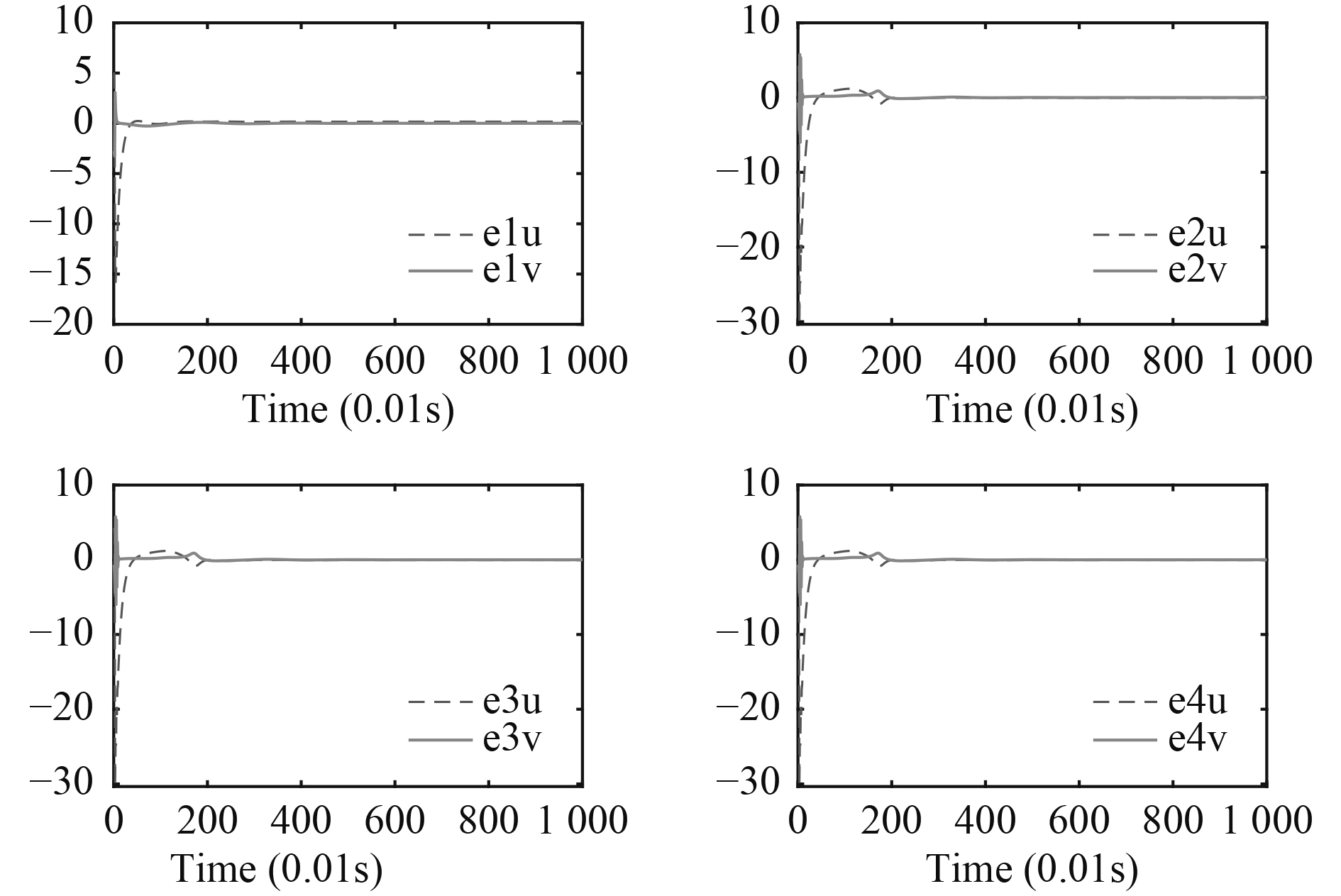
在控制器的作用下,按照图6所示的事件触发时刻进行通信,3艘无人船和1架无人机组成的异构系统可实现一致性,图7和图8为智能体的位置误差与速度误差。
|
图 7 位置误差 Fig. 7 Position error |
|
图 8 速度误差 Fig. 8 Speed error |
可以看出,位置和速度误差在很短的时间内趋于稳定,且系统的超调量较小,具有很强的鲁棒性。即由1架无人机和3艘无人船组成的异构编队能在很短的时间内形成稳定的编队,从而实现系统一致性。
4 结 语本文针对多智能体一致性控制问题,设计一种基于事件触发的异构多智能体一致性控制器,使得系统仅在事件触发时刻进行通信,在触发时间间隔之间休眠,大大节约了资源,减少连续通信对系统造成的负担。理论分析表明,系统可在该控制协议作用下达到一致。最后,通过仿真实验证明了理论分析的正确性。
| [1] |
LIU Z, ZHANG Y, YU X, et al. Unmanned surface vehicles: an overview of developments and challenges[J]. Annual Reviews in Control, 2016, 41: 71-93. DOI:10.1016/j.arcontrol.2016.04.018 |
| [2] |
MA Y, HU M, YAN X. Multi-objective path planning for unmanned surface vehicle with currents effects[J]. Isa Transactions, 2018, 75: 137-156. DOI:10.1016/j.isatra.2018.02.003 |
| [3] |
PENG Z, WANG J, WANG D, et al. An overview of recent advances in coordinated control of multiple autonomous surface vehicles[J]. IEEE Transactions on Industrial Informatics, 2020(99): 1-1. |
| [4] |
FU M Y, WANG D S, WANG C L. Formation control for water-jet USV based on bio-inspired method[J]. China Ocean Engineering, 2018, 32(01): 117-122. DOI:10.1007/s13344-018-0013-1 |
| [5] |
SUN X, WANG G, FAN Y, et al. A formation collision avoidance system for unmanned surface vehicles with Leader-Follower Structure[J]. IEEE Access, 2019, 1. |
| [6] |
欧阳子路, 王鸿东, 黄一, 等. 基于改进RRT算法的无人艇编队路径规划技术[J]. 中国舰船研究, 2020(3): 18-24. |
| [7] |
Zhou Y J, JIANG G P, XU F Y, et al. Distributed finite time consensus of second-order multi-agent systems via pinning control[J]. IEEE Access, 2018, 6: 45617-45624. DOI:10.1109/ACCESS.2018.2865479 |
| [8] |
LIU Z Q , WANG Y L , WANG T B . Incremental predictive control-based output consensus of networked unmanned surface vehicle formation systems[J]. Information Sciences, 2018.
|
| [9] |
DING L, HAN Q L, GE X, et al. An overview of recent advances in event-triggered consensus of multiagent systems[J]. IEEE Transactions on Cybernetics, 2018, 48(4): 1110-1123. DOI:10.1109/TCYB.2017.2771560 |
| [10] |
BIN C, ZHONGKUI L. Fully distributed event-triggered protocols for linear multi-agent networks[J]. IEEE Transactions on Automatic Control, 2018, 1-1. |
| [11] |
WANG, R POSTOYAN, D. Nešić, et al. Periodic event-triggered control for nonlinear networked control systems[J]. IEEE Transactions on Automatic Control, 2020, 65(2), 620–635 .
|
| [12] |
DIMAROGONAS D V, FRAZZOLI E, JOHANSSON K H. Distributed event-triggered control for multi-agent systems[J]. IEEE Transactions on Automatic Control, 2012, 57(5): 1291-1297. DOI:10.1109/TAC.2011.2174666 |
| [13] |
周绍磊, 赵学远, 王帅磊, 等. 基于事件触发的多智能体系统编队控制[J]. 兵器装备工程学报, 2019, 040(012): 85-89. |
| [14] |
YU Mei, wang Hangfei, XIE Guangming, et al. Event-triggered circle formation control for second-order-agent system[J]. Neurocomputing, 2018, 275: 462-469. DOI:10.1016/j.neucom.2017.08.061 |
| [15] |
YANG J, XIAO F, MA J. Model-based edge-event-triggered containment control under directed topologies[J]. IEEE Transactions on Cybernetics, 2018, 1-12. |
| [16] |
LIU S , FEI Q , WU C , et al. Finite-time event-triggered attitude consensus control for multiple unmanned surface vessels[C]// Proceedings of 2019 Chinese Intelligent Automation Conference, 2020.
|
 2022, Vol. 44
2022, Vol. 44
