针对当前水下维修机器人续航时间短、灵活性差、可携带负载较少等问题,设计一种水下机器人载体结构,用于搭载和输送水下机器人及辅助设备,实现船舶停留在水面上对水线以下船体和附体进行检测和应急维修。然而,复杂多样的海洋环境中常伴随着风、浪、流等联合作用,这对水下机器人载体结构的可靠性能提出了更高的要求[1]。
目前,线性波理论是处理波流与结构物相互作用方面应用较多的理论,但波流与结构物相互作用的本质却是非线性问题[2]。此外,实际的海洋环境十分复杂、变化多端,遇到的波浪同样大多是非线性问题。如果简单地线性化处理,则误差较大,因此须考虑运用非线性边界条件的有限振幅波理论对其进行分析[3-4]。
二阶stokes波具有质点漂移与质量前移的特点,同时相比较线性波精度更高且接近实际海浪[5-6],因此本文基于目前应用广泛的非线性stokes波浪理论,通过CFD法建立三维数值波浪水槽,实现二阶stokes波浪数值模拟,对波流作用下的载体结构进行分析。
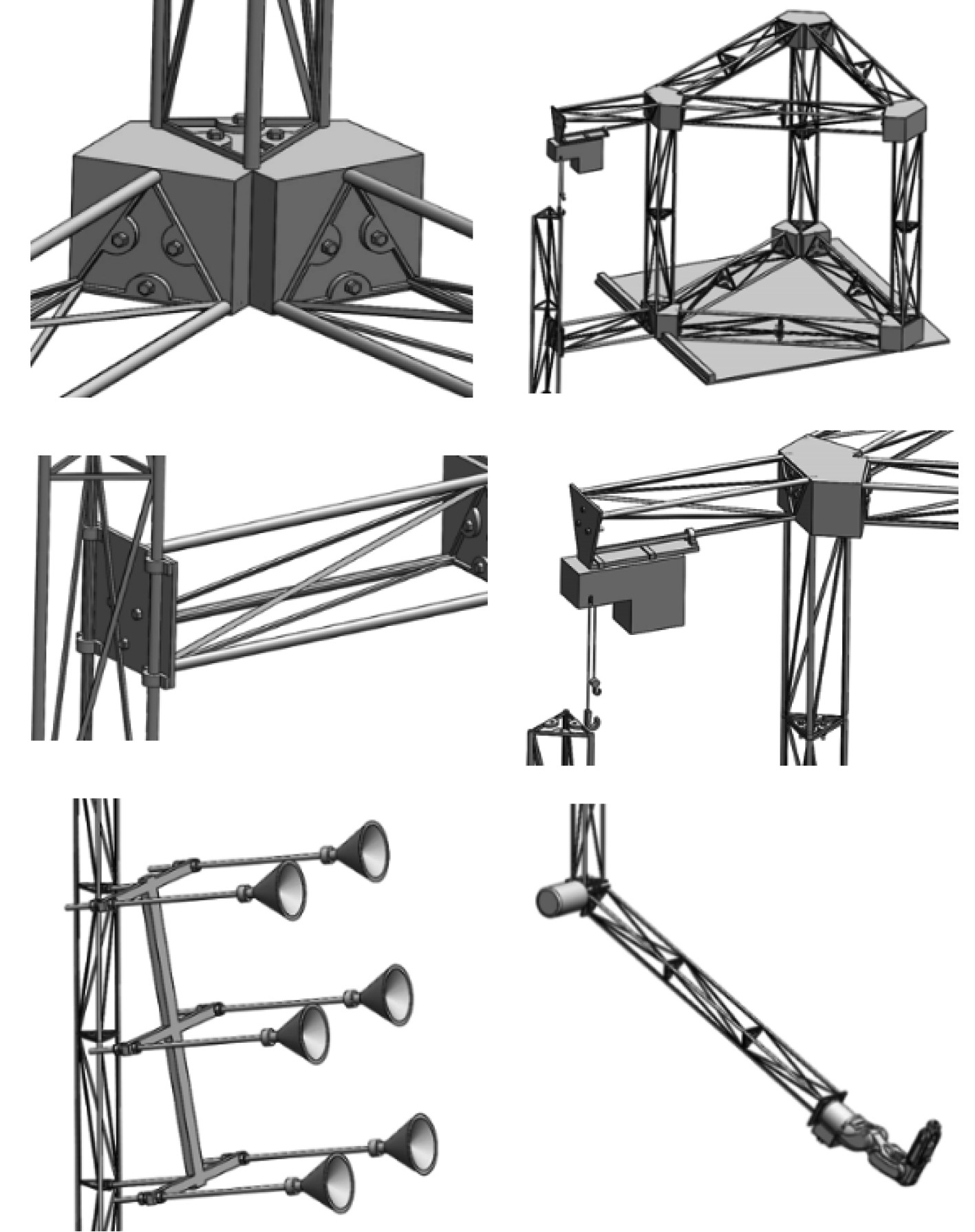
1 水下机器人载体结构设计基于模块化的设计思想,设计一种以桁架结构为主体并可搭载和输送水下机器人及辅助设备进行水下作业的载体结构,以代替传统的ROV作为水下维修机器人的输送载体。该结构特点在于简单、实用、轻便,需使用时能够快速组合安装,不用时能够迅速拆装分解并仅占较小船舶空间进行储藏。水下机器人载体结构总体结构以及分部件结构分别如图1和图2所示。

|
图 1 水下机器人载体总体结构图 Fig. 1 Overall structure of the platform |
|
图 2 水下机器人载体结构分部件图 Fig. 2 Overall structure of the platform |
在二维平面上,根据势流理论得到波浪的速度势函数为:
| $ \begin{split} \varphi \left( {x,y,t} \right) = &\frac{{H\omega }}{{2k}}\left[\frac{{\cosh k\left( {y + d} \right)}}{{\sinh kd}} \times \sin \left( {kx - \omega t} \right)+ \right.\\ &\left. \frac{3}{{16}}Hk\frac{{\cosh 2k\left( {y + d} \right)}}{{{{\sinh }^4}kd}} \times \sin \left( {2kd - 2\omega t} \right)\right] 。\end{split} $ | (1) |
式中:
对于二阶stokes波浪的自由表面流动问题,控制方程采用连续性方程[7]和以速度和压力为变量的不可压缩粘性流体的N-S方程[8],控制方程如下:
| $ \rho\left(\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}\right)=S_{m} 。$ | (2) |
N-S方程:
| $ \left\{ \begin{gathered} \rho \left( {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}}} \right) = - \frac{{\partial p}}{{\partial x}} + \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right) + {S_x} ,\\ \rho \left( {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}}} \right) = - \frac{{\partial p}}{{\partial y}} - \rho g + \mu \left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right) + {S_y} 。\\ \end{gathered} \right. $ | (3) |
式中:ρ为流体的密度;
参考《海岸动力学》中对波浪的调研报告,选取发生频率较高的二阶stokes波浪参数,按照波浪模型实验规程中重力相似原则,换算得到与载体结构水下部分尺寸匹配的波浪参数[9-10]。
|
|
表 1 二阶stokes波浪参数 Tab.1 Second-order stokes wave parameters |
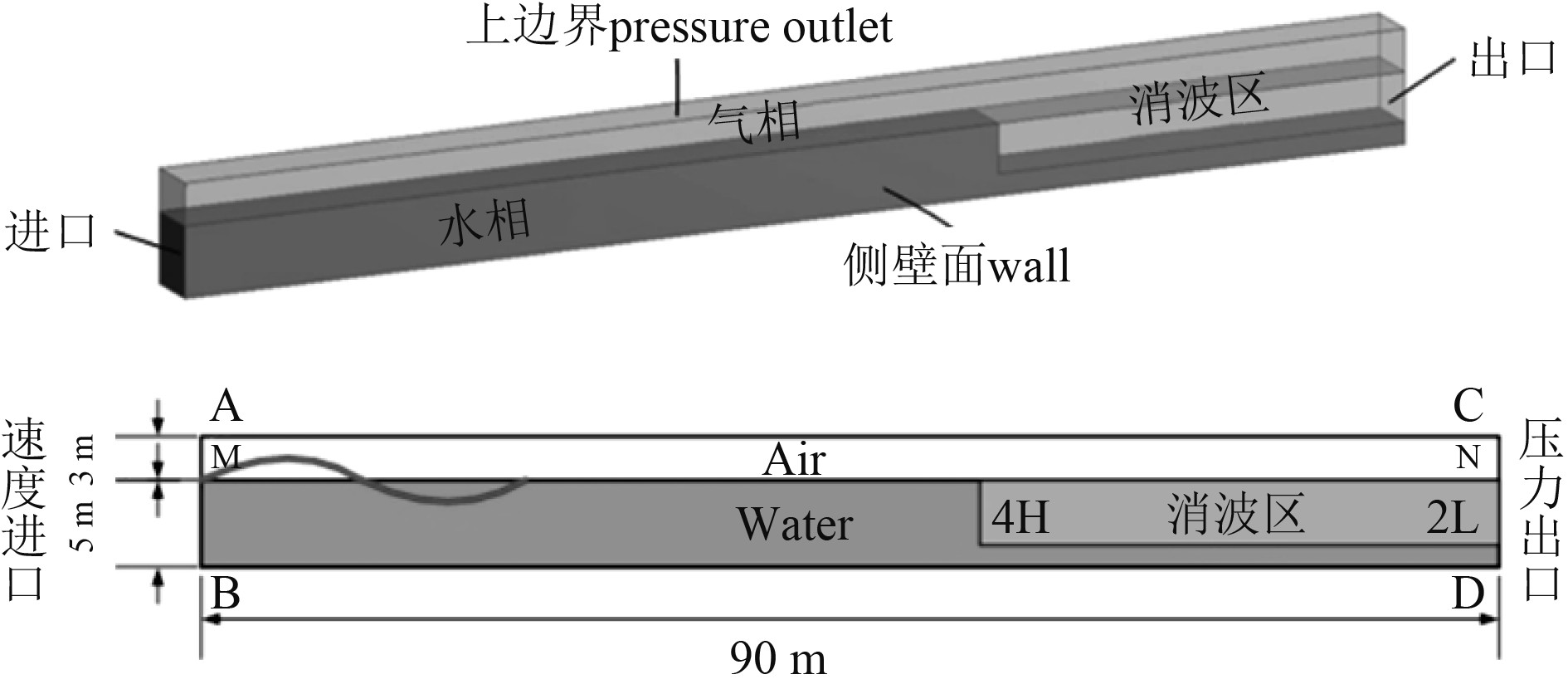
二阶stokes波浪水槽的建立包括选择波浪参数、进行网格划分、设置边界条件和应用消波技术等。本文采用边界造波的方法给定流体运动的速度和波高,结合VOF多相流模型界定波浪气液分界面上下的各相体积分数[11-12],在设置计算域和边界条件时,配合Fluent软件的编译系统UDF进行各项体积分数的编译,实现自由液面的追踪。在水槽尾端利用线性阻尼消波方法来削弱波浪的波动,求解器选用全局预测较好的
|
图 3 三维数值波浪水槽示意图 Fig. 3 Diagram of 3D numerical wave flume |

|
图 4 添加消波后波浪的历时演化过程 Fig. 4 The diachronic evolution of waves after wave elimination is added |
从40 s时的波浪形态直观上可以看出,波浪表现出波峰突尖、波谷平坦,波峰偏离静水位置的距离大于波谷偏离静水位置的距离,这与stokes波基本理论相符。
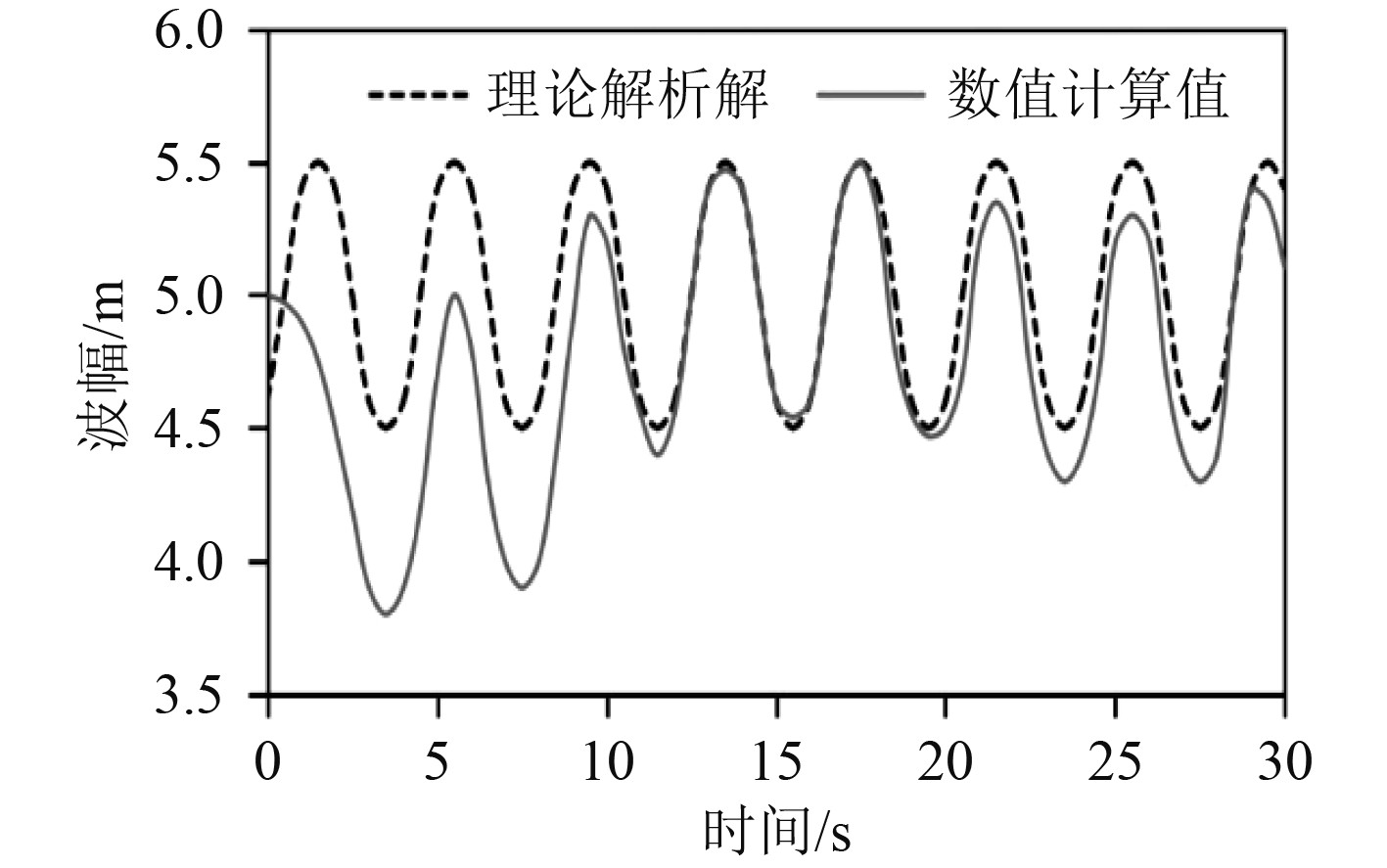
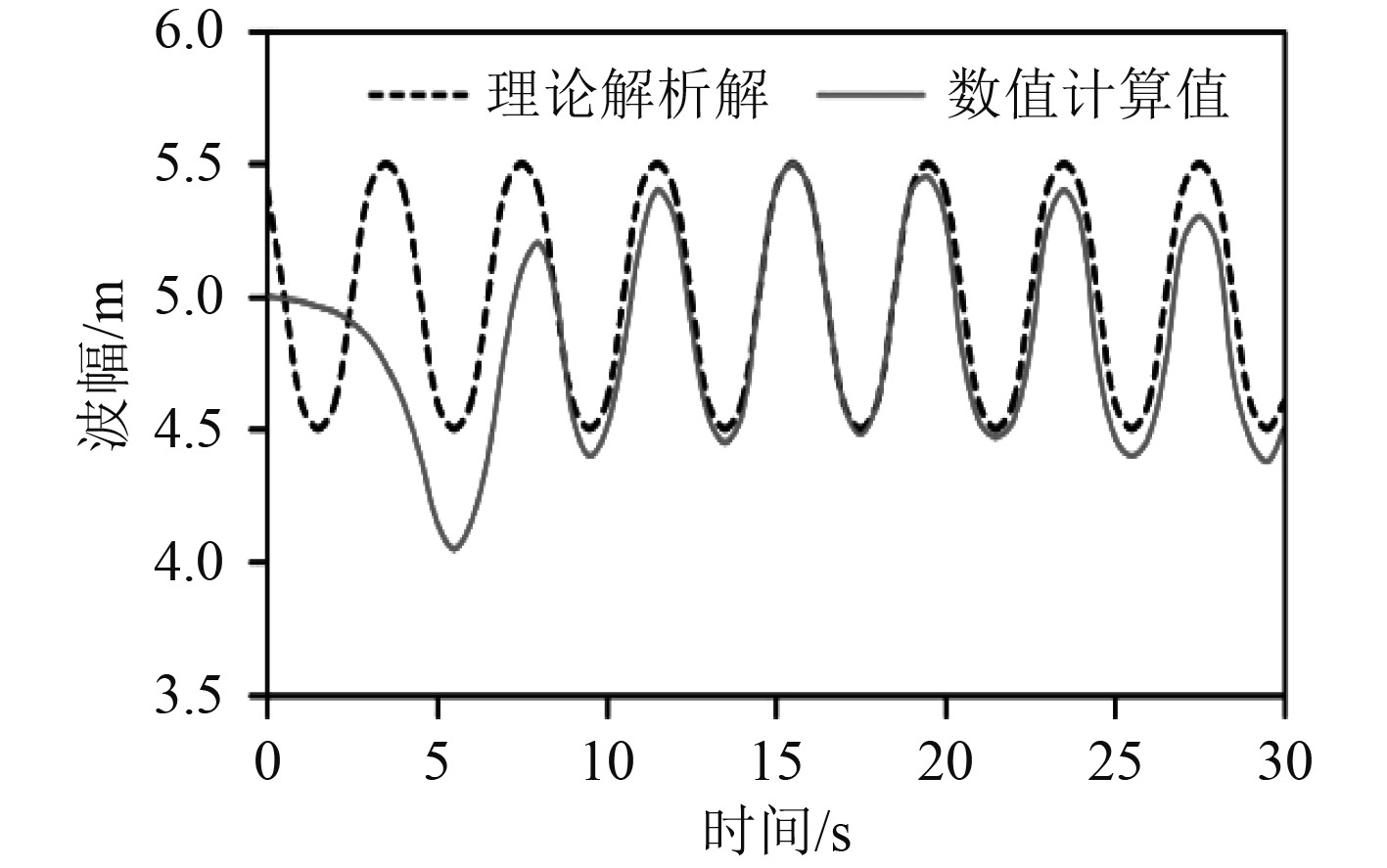
为进一步验证水槽的造波能力、波浪精度,将数值波浪和理论波浪进行对比分析。图5~图7分别为距离入口边界10 m,20 m,40 m处的波面时程曲线与理论时程曲线的对比。
|
图 5 距离入口边界10 m处波面时程曲线 Fig. 5 Time history curve of wave surface at 10 m away from the entrance boundary |
|
图 6 距离入口边界20 m处波面时程曲线 Fig. 6 Time history curve of wave surface at 20 m away from the entrance boundary |
|
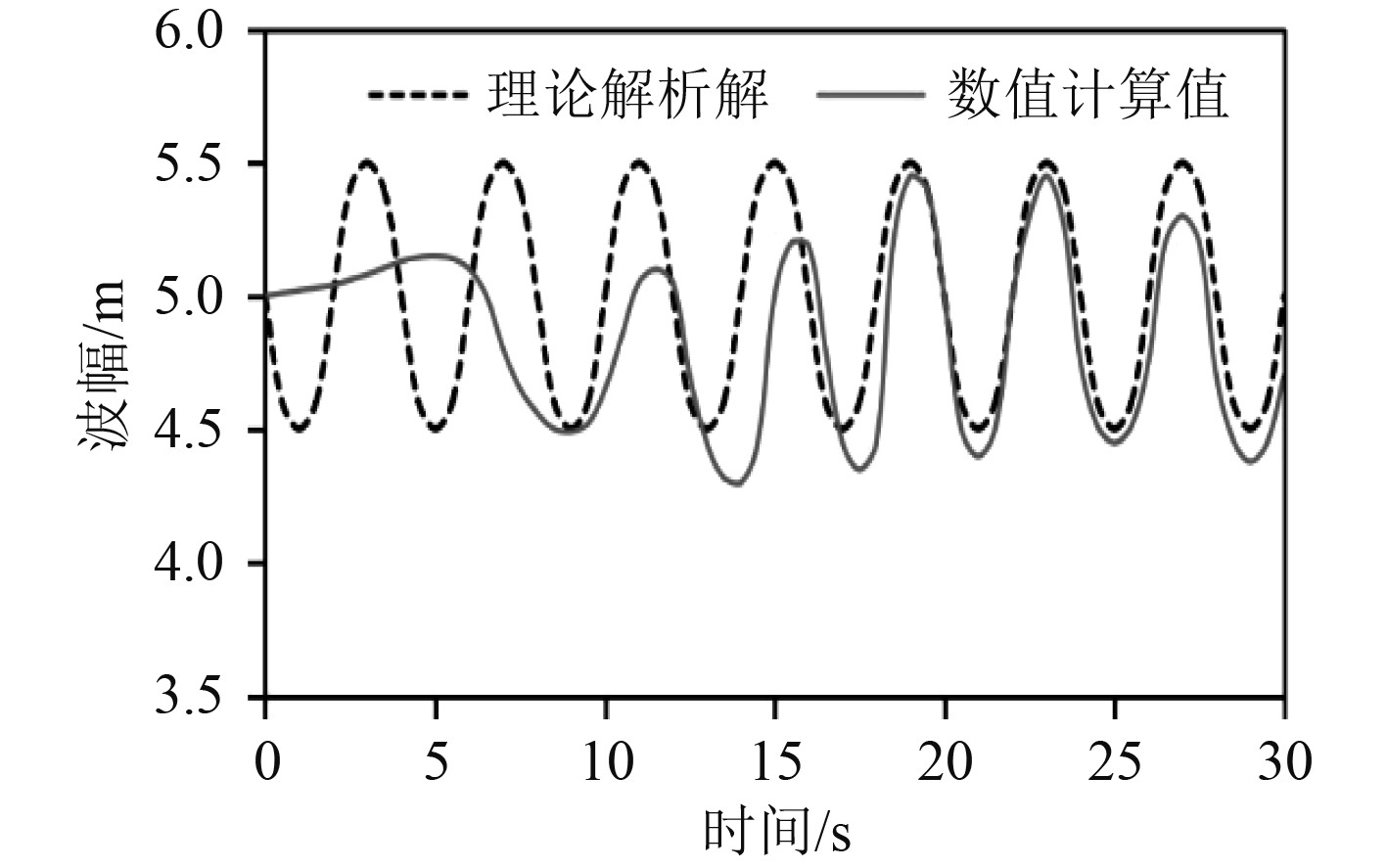
图 7 距离入口边界40 m处波面时程曲线 Fig. 7 Time history curve of wave surface at 40 m away from the entrance boundary |
对比发现,10 m位置的初始时刻波动最大,这是因为该位置靠近入口边界,容易受入口条件扰动。20 m位置波幅形态良好,这是因为该点占有位置优势,不受入口条件和消波作用的影响。40 m位置出现一定程度的相位偏差,这是因为位置偏离造波源,离入口边界越远,相位偏差越严重。在波高和波长2种参数误差中,波高误差偏大,这是由于波浪的粘性耗散和数值耗散作用造成波高衰减。随着观测位置偏离造波源,波幅出现不同程度的相位偏差,距离入口边界越远,相位偏差越严重。通过综合分析可知,边界造波方法结合阻尼消波技术是一种行之有效的波浪模拟方法。
3 载体结构波流力仿真计算考虑极限载荷状态(转动装置在来流垂直方向的投影面积最大)的条件,将转动装置所受波流载荷折算到加粗后的垂直桁架结构进行分析。垂直桁架结构水下部分长度2~4 m,取3 m进行波流力计算。
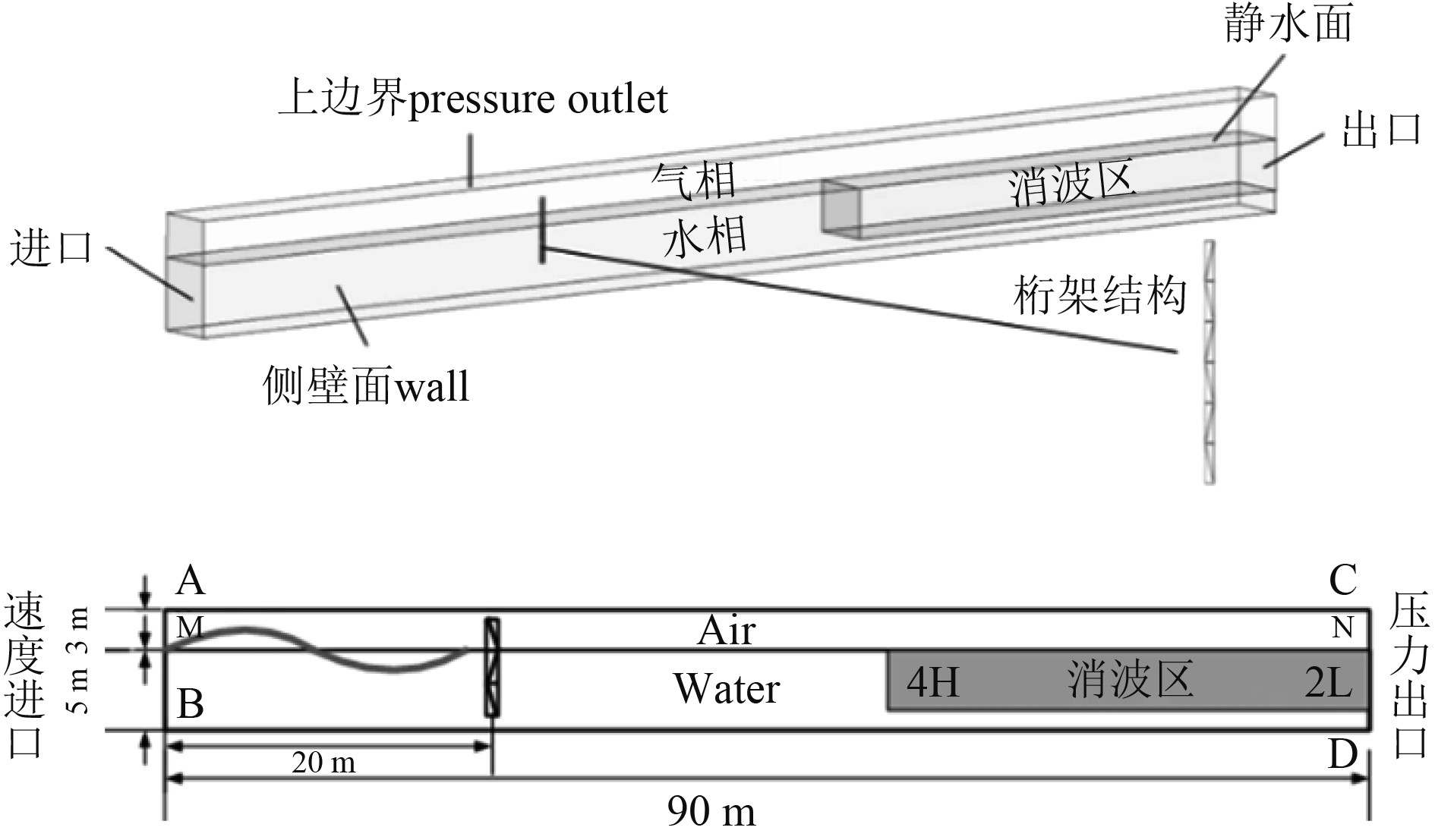
3.1 波浪力仿真计算三维水槽中添加垂直桁架结构,为准确反映波浪瞬时运动,在对桁架结构波浪数值模拟中需采用瞬态计算方法并基于单向流固耦合的方法进行波浪力的计算[16-18]。计算域模型如图8所示。
|
图 8 计算域模型 Fig. 8 Computational domain model |
桁架结构和靠近桁架结构周围的计算域采用非结构化网格划分并进行加密处理,其余部分采用结构化网格划分,时间步长设置为0.005 s,模拟总时长为40 s,收敛标准设置为最大残差小于
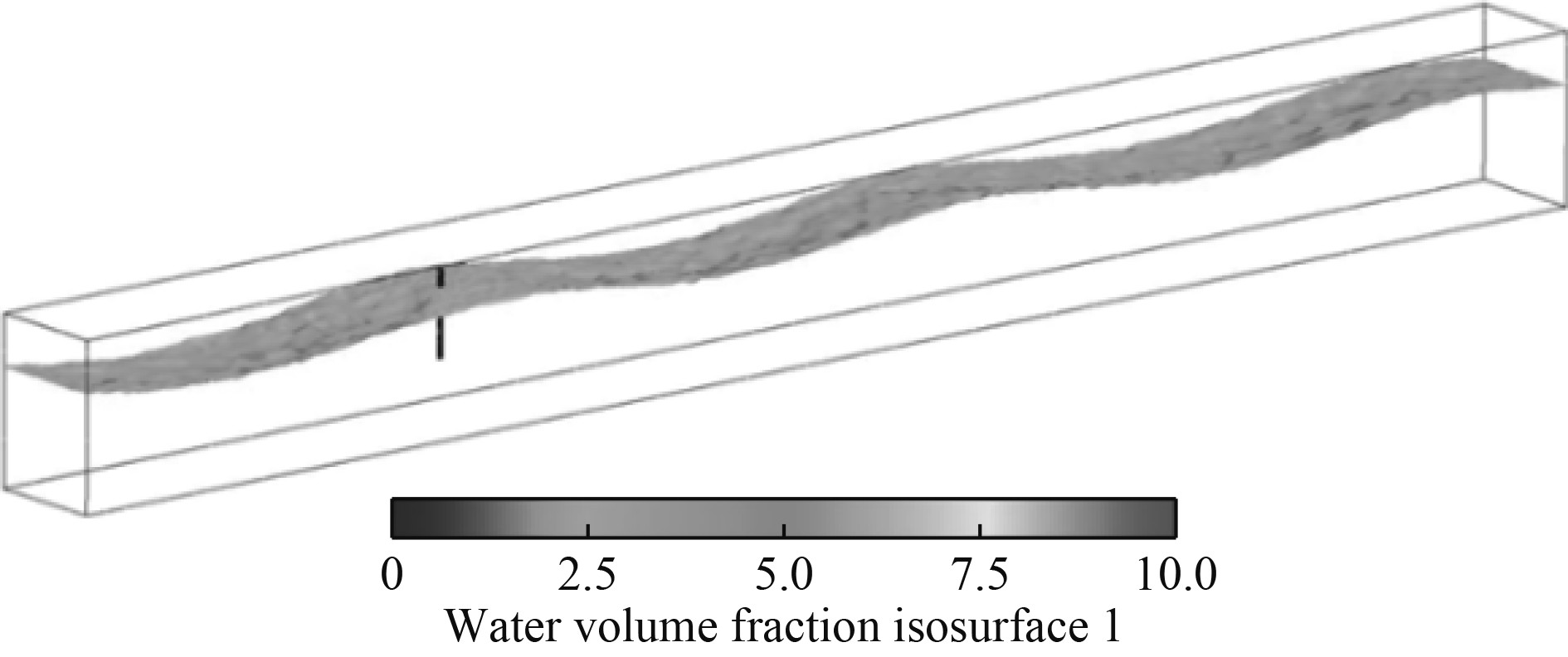
|
图 9 波浪作用下的液面图 Fig. 9 Liquid level diagram under wave action |
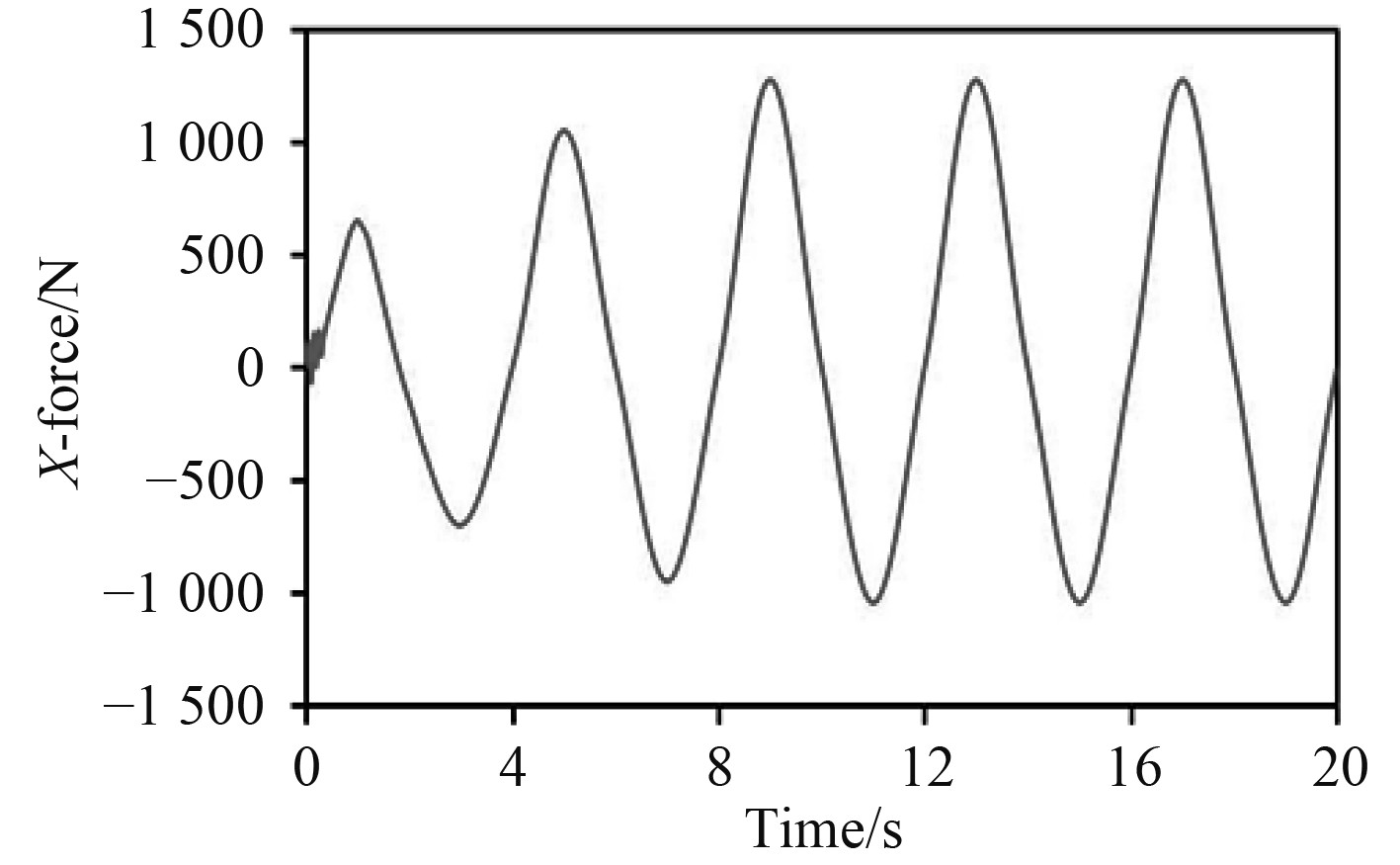
|
图 10 桁架结构水平波浪力时程曲线 Fig. 10 Time history curve of horizontal wave force of truss structure |
可知,桁架结构所受波浪作用在初始时并不稳定,这是由于波浪生成导致流场突然从静止状态变成运动状态。经过一个多周期后,波浪传播逐渐稳定,此时水平波浪力的值和方向呈现周期性变化,并基本维持稳定。通过观察可知,其变化周期约为4 s,与所设波浪周期一致。经过仿真计算可得,桁架结构所受最大水平波浪力约为1.277 kN。
3.2 水流力仿真计算对载体结构的水流力计算同样折算到加粗后的垂直桁架结构水下部分长度3 m进行计算。水域长度为90 m,宽度4 m,高度8 m,水深为5 m,并在水槽沿程 处放置桁架结构。采用
|
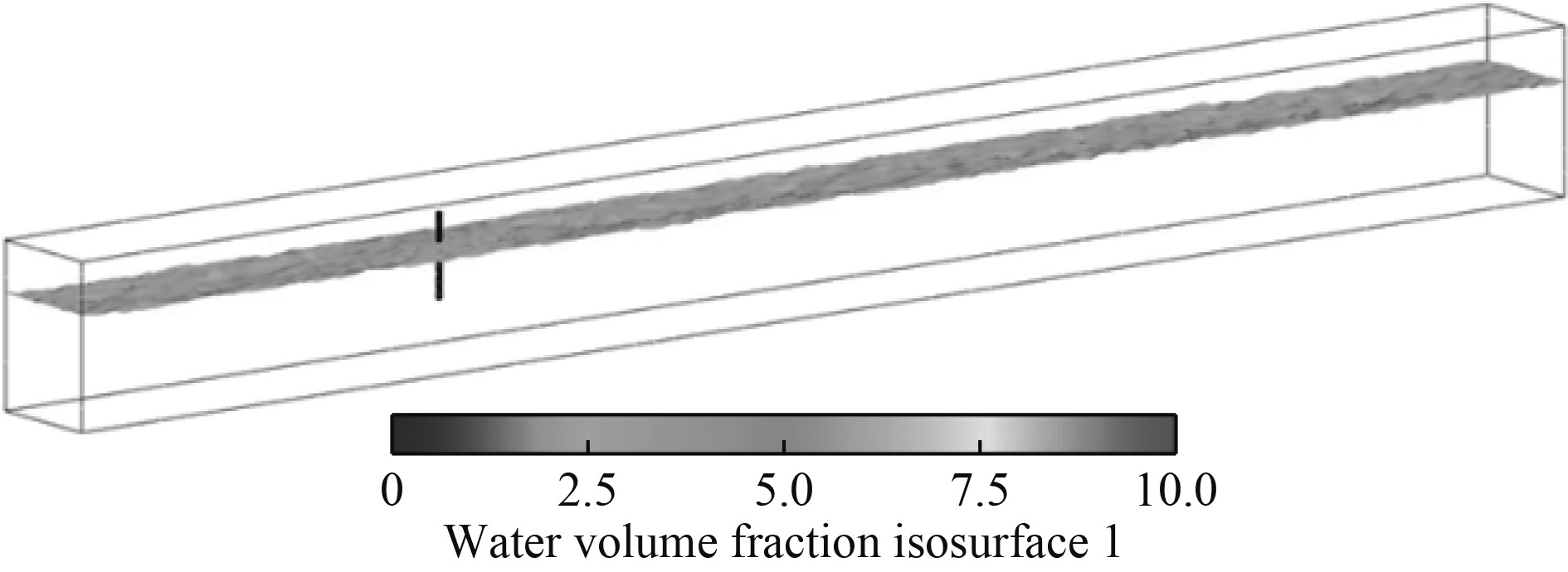
图 11 水流作用下的液面图 Fig. 11 Liquid level diagram under the action of water flow |
当雷诺数较高时,由旋涡脱落产生的横向水流力值远小于纵向水流力值,即纵向水流力应为载体结构主要考虑的作用力。提取该模型的纵向水流力时程曲线如图12所示。
|
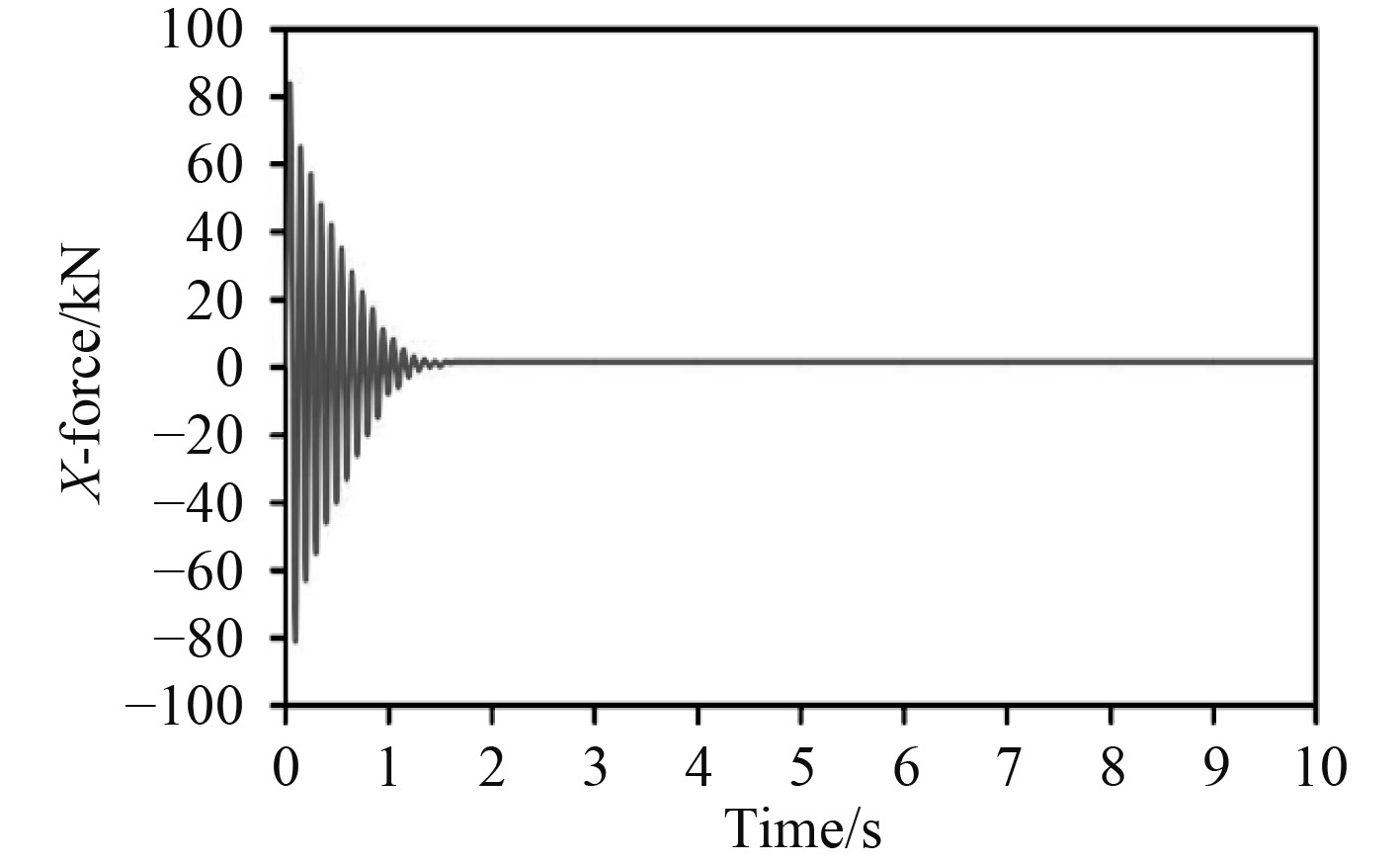
图 12 纵向水流力时程曲线 Fig. 12 Time history curve of longitudinal flow force |
在迭代初始水流力有往复振荡现象,1.5 s后达到平衡,形成稳定流场,此时所需水流力值的计算结果为1.486 kN。
4 波流作用下载体结构响应 4.1 载体结构模态分析Ansys的模态分析是线性分析,任何非线性特性即使定义了也将被忽略[20],因此利用Block Lanzcos法特征值求解器提取模态特征值,采用一组向量来实现Lanzcos递归的计算,实现对载体结构的模态分析,获得结构的振型并与波浪载荷的固有频率进行对比,分析结构发生共振的可能性。安装吸盘与未安装吸盘时一阶模态分析模型结果分别如图13和图14所示。
|
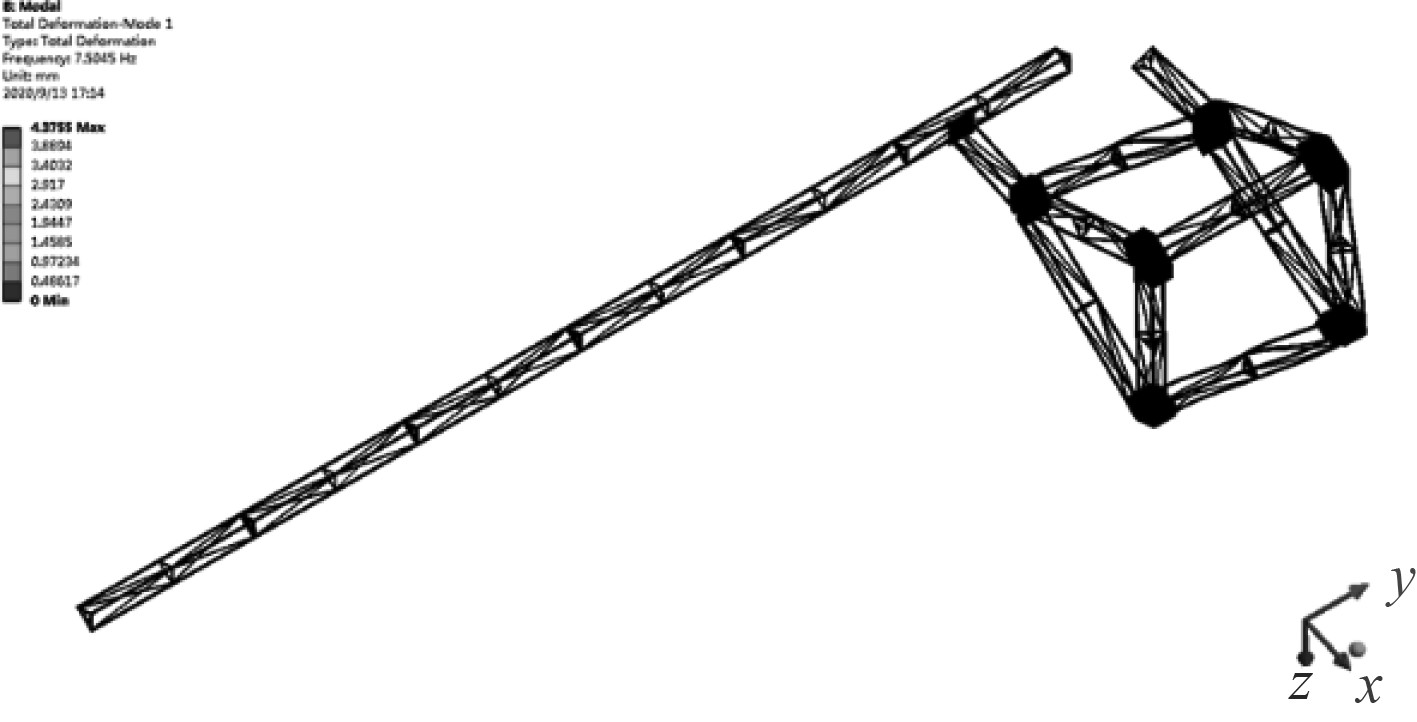
图 13 安装吸盘一阶振型 Fig. 13 Installation of suction cups Mode 1 |
|
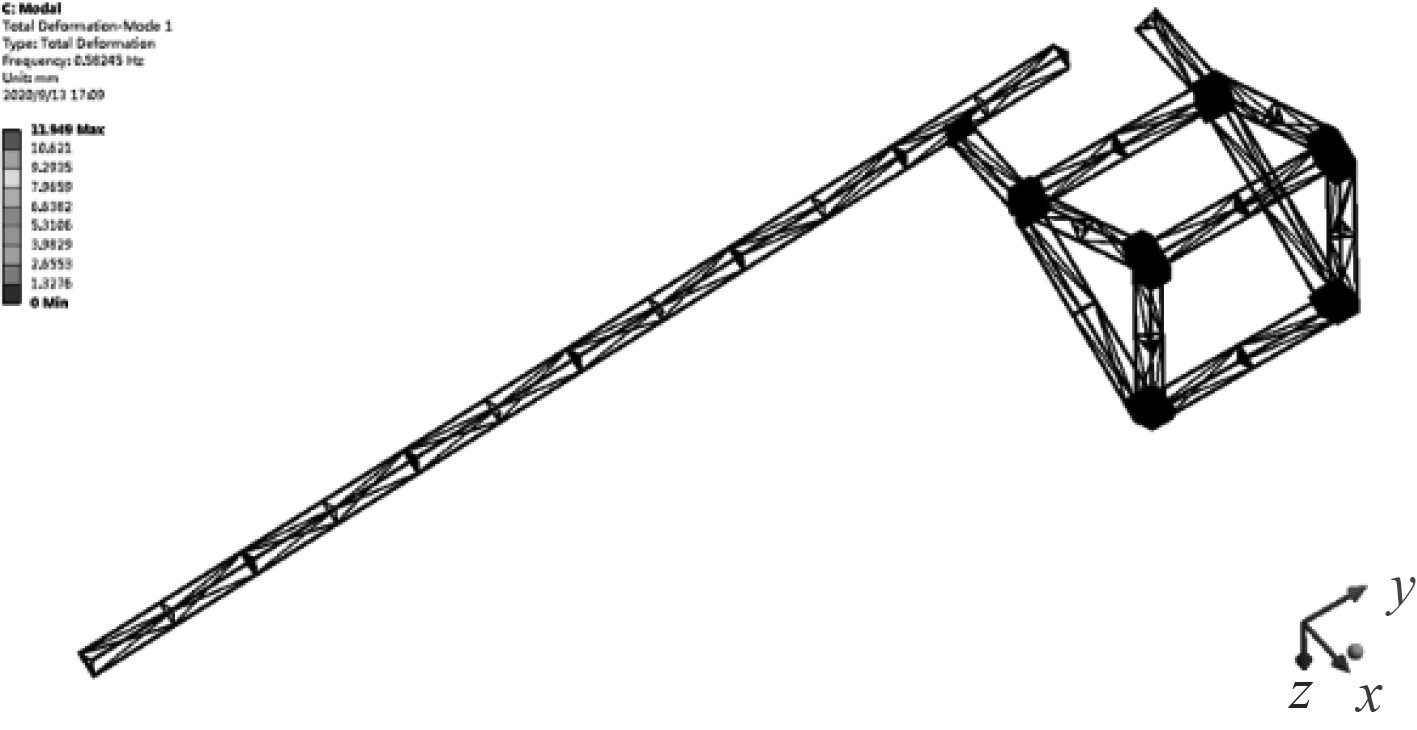
图 14 未安装吸盘一阶振型 Fig. 14 without suction cups installed Mode 1 |
对模态分析的结果进行统计,得到结构的前6阶固有频率、周期以及位移极值如表2所示。
|
|
表 2 各阶振型的固有频率、周期及位移极值 Tab.2 Natural frequency, period and displacement extreme value of each mode |
可知水下机器人载体结构第1阶振型的自振频率分别为7.5045 Hz和0.58245 Hz。而一般海浪的平均周期为0.5~25 s,即波浪载荷的频率范围主要在0.04~2 Hz,而本文模拟的stokes波是基于平均周期为4 s的海浪,对应频率为0.25 Hz。因此,安装吸盘时的固有频率不在0.04~2 Hz范围内,而未安装吸盘时载体结构的1阶和2阶频率在0.04~2 Hz这一范围内,即未安装吸盘时,载体结构可能与波浪载荷发生共振,安装吸盘时则理论上不会与波浪载荷发生共振。
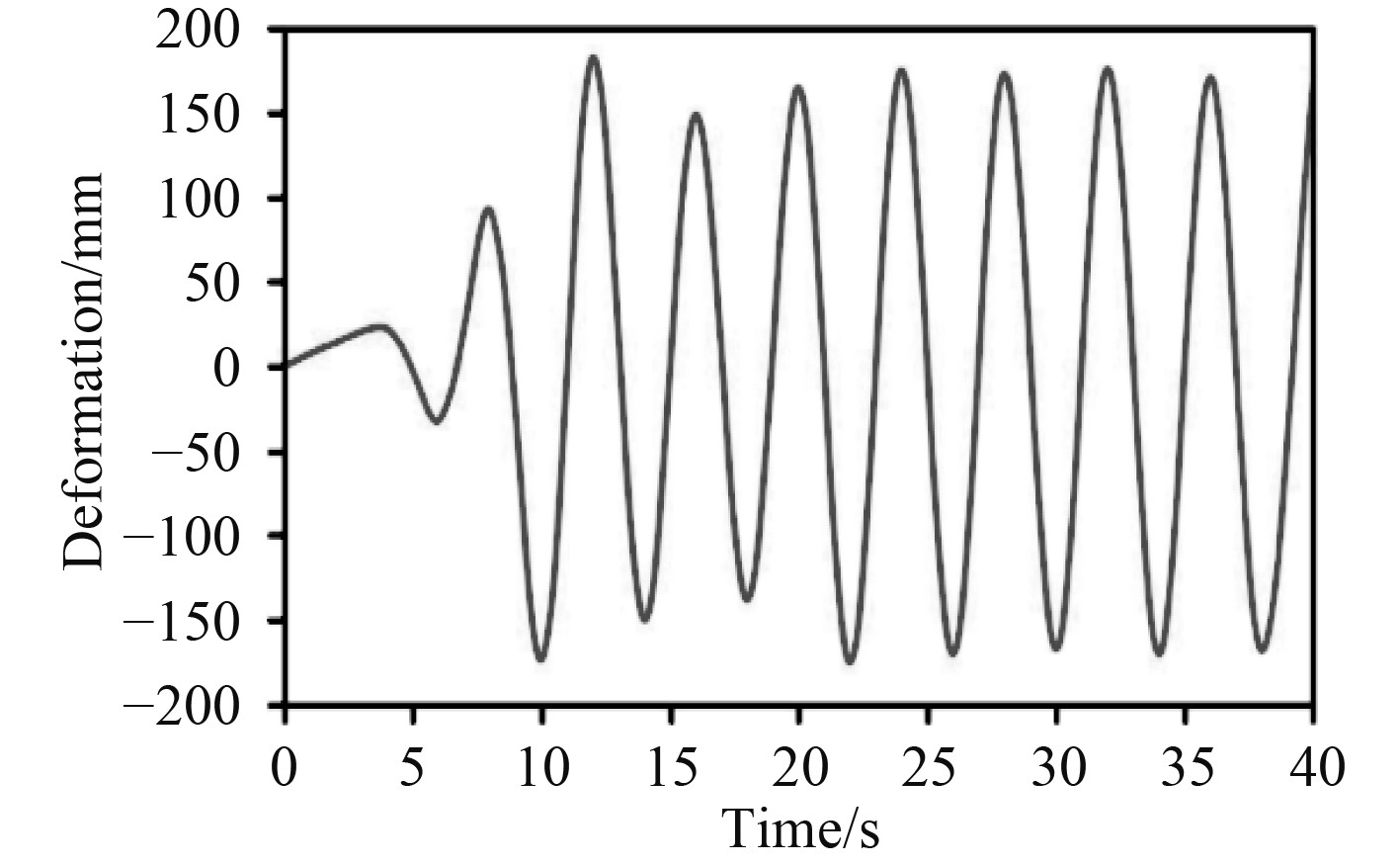
4.2 载体结构瞬态动力分析将Fluent求解得到的二阶stokes波波浪荷载导入动态结构分析Transient Structural模块中,仅考虑二阶stokes波作用,将其波浪力时程施加到载体结构上,进行瞬态动力分析得到未安装吸盘时载体结构底端总位移值和垂直桁架与水平桁架锁紧连接处等效应力值的历时曲线,如图15和图16所示,以及安装吸盘时载体结构底端总位移值和垂直桁架安装吸盘处等效应力值的历时曲线,如图17和图18所示。
|
图 15 未安装吸盘时载体结构底端总位移 Fig. 15 Total displacement of the bottom of the carrier structure without suction cup |
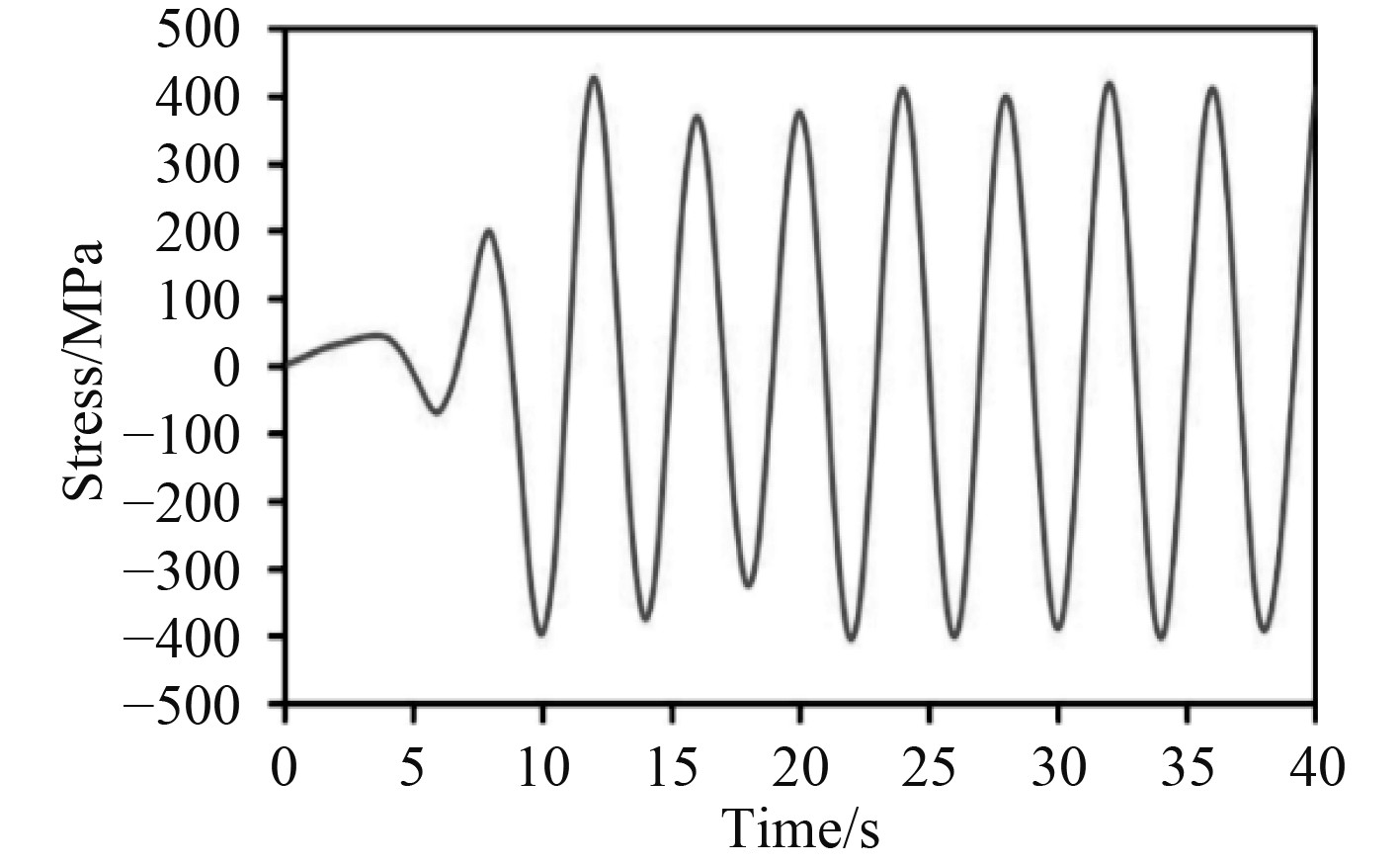
|
图 16 未安装吸盘时锁紧连接处等效应力 Fig. 16 Equivalent stress of locking joint without suction cup |
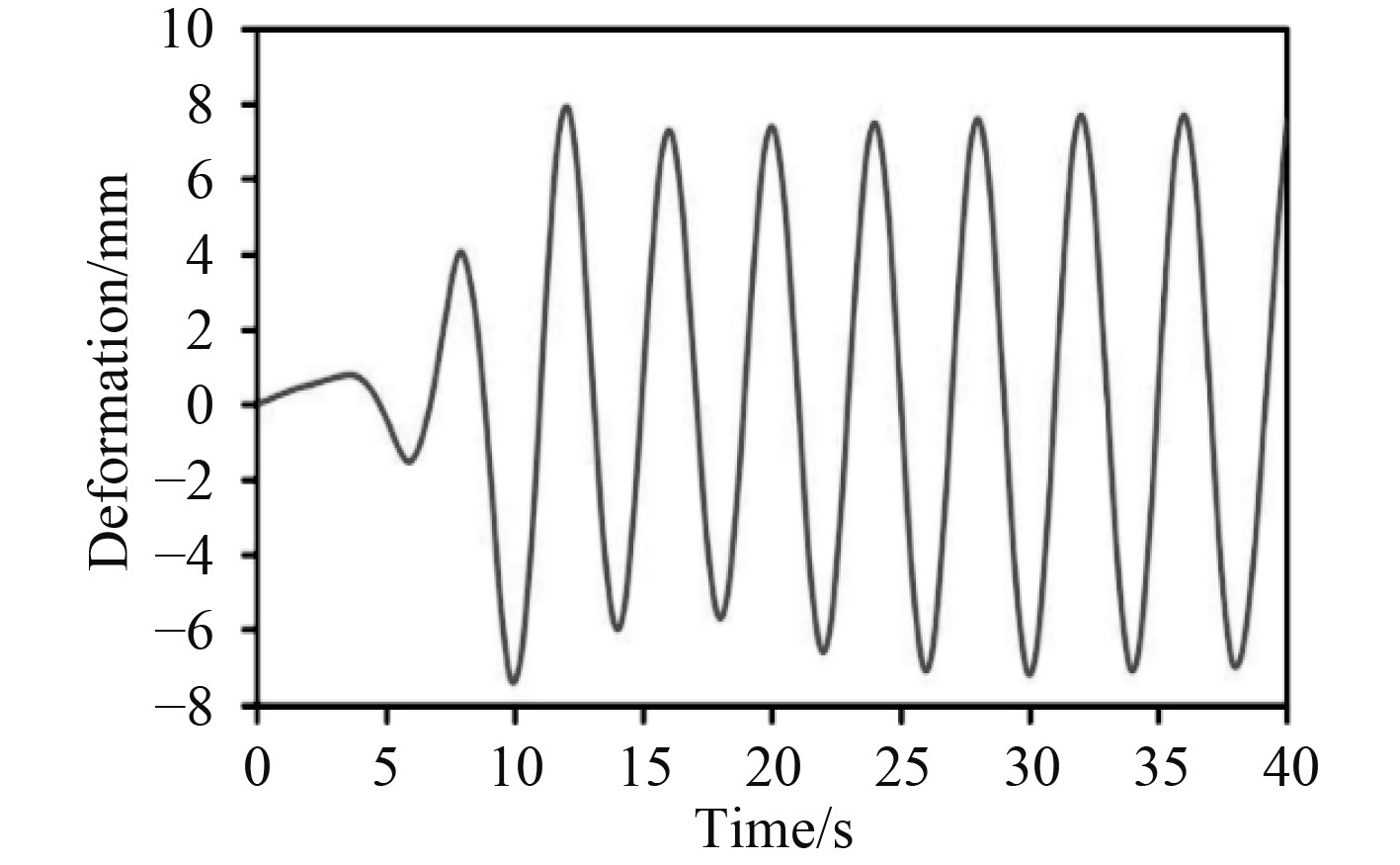
|
图 17 安装吸盘时载体结构底端总位移 Fig. 17 Total displacement of the bottom of the carrier structure when installing the suction cup |
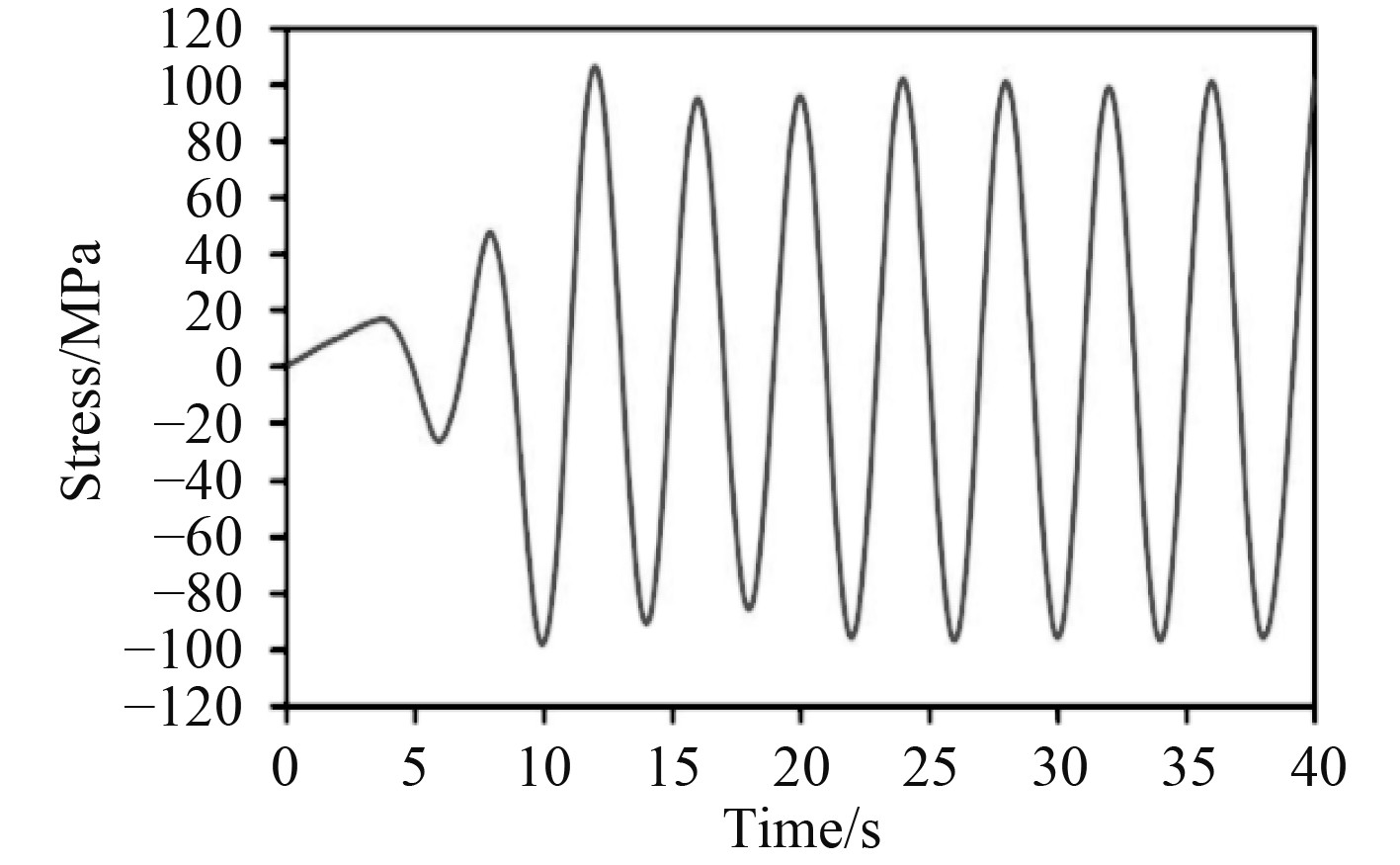
|
图 18 安装吸盘时垂直桁架安装吸盘处等效应力 Fig. 18 Equivalent stress of suction cup in vertical truss |
通过数值统计可以更直观地反映图像的一些关键信息,故从图像中提取载体结构的关键部位未安装吸盘与安装吸盘时的位移和应力极值,见表3。
|
|
表 3 载体结构关键部位位移和应力极值 Tab.3 Displacement and stress extremum of key parts of carrier structure |
由上述瞬态动力分析结果可知,在二阶stokes波作用下,水下机械臂载体结构关键部位的位移和应力,除了在加载初期相当短的时间内反应敏感,其余时间点均表现为周期性的振荡变化情况。
5 结 语基于Ansys软件,采用边界造波法和线性阻尼消波技术建立了三维二阶stokes波浪水槽,得到水下机器人载体结构在二阶stokes波作用下的浪力和水流力。采用Block Lanzcos法,对水下机械臂载体结构进行整体模态分析,分别求得结构安装吸盘与未安装吸盘时的前6阶振型。分析得到,未安装吸盘时,载体结构的一阶和二阶频率处于波浪频率范围内,而安装吸盘时的固有频率则不在波浪频率范围内,即安装吸盘能有效避免与波浪载荷发生共振,对整个结构的安全性和稳定性具有重要作用。
将波浪力时程施加到载体结构上进行瞬态动力分析,结构响应特性表现为:
1)无论是否安装吸盘,载体结构底端位移值在加载初期都表现出比较强烈的波动且在某一时刻达到最大,之后位移逐渐表现为稳定周期性变化。位移曲线和stokes波的波浪力时程曲线形状相似并且位移与波浪力的关系符合载体结构材料的线弹性特征。因此,水下机器人载体结构材料选择上要保证有足够的弹性性能。
2)载体结构关键部位的应力值在加载初期表现出比较强烈的波动,之后才逐渐稳定,而未安装吸盘时的应力极值远大于安装吸盘时的应力极值,即从另一方面说明安装吸盘能有效地抵抗类似stokes波等的冲击作用,对于整个结构的安全性和稳定性具有重要作用。
| [1] |
WALDEMAR K. Some considerations on an underwater robotic manipulator subjected to the environmental disturbances caused by water current. [J]. Acta Mechanica Et Automatica, 2016, 10(1): 43–49.
|
| [2] |
GE Jian-jiang, DU Zeng-ji. The solitary wave solutions of the nonlinear perturbed shallow water wave model[J]. Applied Mathematics Letters, 2020, 103.
|
| [3] |
景信信. 浪-流联合作用对垂直轴水轮机水力性能的影响[D]. 西安: 西安理工大学, 2019.
|
| [4] |
张可心. 基于二阶造波方法确定性波浪的实验室模拟[D]. 大连: 大连理工大学, 2019.
|
| [5] |
田宏升. 固定式海洋结构物载荷分析与研究 [D]. 大连: 大连理工大学, 2005.
|
| [6] |
封星, 吴宛青, 吴文锋, 等. 二维数值波浪水槽在FLUENT中的实现[J]. 大连海事大学学报, 2010, 36(3): 94-96+101. |
| [7] |
韦承勋. 风—浪—流联合作用场数值模拟及其对圆柱构件的作用研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
|
| [8] |
郭晓宇. 数值波浪水槽及其应用研究 [D]. 上海: 上海交通大学, 2011.
|
| [9] |
范会渠. 波浪中大尺度立柱的势流理论分析与应用研究[D]. 北京: 中国舰船研究院, 2017.
|
| [10] |
SIGNE S, HENRIK B, HARRY B B. The influence of fully nonlinear wave forces on aero-hydro-elastic calculations of monopile wind turbines[J]. Marine structure, 2016, 50: 162–188.
|
| [11] |
SUNNY KUMAR P, VENDHAN C P, KRISHNANKUTTY P. Study of water wave diffraction around cylinders using a finite-element model of fully nonlinear potential flow theory[J]. Ship and Offshore Structures, 2017, 12(2): 276–289.
|
| [12] |
任森. 波浪效应下深水桥梁群桩基础结构形式研究[D]. 成都: 西南交通大学, 2018.
|
| [13] |
丁俊杰. 考虑波流相互作用的数值水槽及循环水槽消波装置开发研究[D]. 上海: 上海交通大学, 2019.
|
| [14] |
MAGDALENA I, MARIAN P. ROQUE. Analytical and numerical solution for wave reflection from a porous wave absorber[C]// International Conference on Mathematics: Pure, Applied and Computation, 2018, 974(1).
|
| [15] |
SCOTT J B, BRYCE B, KUSH B, et al. Experimental and numerical comparisons of self-reacting point absorber wave energy converters in irregular waves[J]. Oceon Engineering, 2019, 173: 716–731.
|
| [16] |
JAN-TORE H H, JORGEN R K, JORGEN A. Hydro-elastic contributions to fatigue damage on a large monopile[J]. Energy Procedia, 2016, 94: 102–114.
|
| [17] |
ISAACSON M, CHEUNG K F. Wave-current interaction with a large structure[J]. Oceans, 2015, 3(1): 66-80. |
| [18] |
骆成. 海洋立管动态响应及动态可靠度分析[D]. 兰州: 兰州理工大学, 2014.
|
| [19] |
路宽, 齐连明, 王鑫, 等. 不同湍流模型在波浪水槽数值模拟中的应用与比较[J]. 海洋通报, 2013, 32(6): 695-699. |
| [20] |
韦承勋. 风—浪—流联合作用场数值模拟及其对圆柱构件的作用研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
|
 2022, Vol. 44
2022, Vol. 44

