为了减轻船员的工作强度,需要使用现代化的信息技术对船舶的状态进行监测。在信息化的升级过程中,船舶采用了自动识别系统,该系统是由陆地上的基站和船舶自身携带的设备2部分共同构成。船舶使用自身携带的电力电子设备通过甚高频频道将船舶的位置信息广播给附近的陆地基站以及附近的船舶,这样船舶和附近陆地的基站以及海面上附近的船舶之间就架起了沟通的桥梁[1-2]。当前对于船舶自动识别系统的应用还停留在比较浅的一个层面,如何基于现存的船舶自动识别的数据对船舶的航行轨线进行分析,形成船舶轨迹模型,对船舶在海面上航行过程中的轨迹进行实时的检测,并且给船舶在海面上的安全行驶提供指导,成为重要的研究方向[3]。卡尔曼滤波算法是一种基于最小方差的递推线性滤波算法,作为一种滤波以及预测技术得到了广泛使用,可以应用于实时在线预测估计[4]。
1 卡尔曼滤波预测技术 1.1 卡尔曼滤波算法的基本原理在船舶轨迹检测系统中,最终需要达到对海面上正在航行的船舶进行精确的定位以及跟踪,并实时地解算出目标船只的运行状态,例如速度、方向角等[5]。
卡尔曼滤波算法需要执行预测、实测、修正3个顺序递进的步骤,基于实际测量得到的可能含有噪声的数据信息,对数据信息中的随机噪声进行消除,并解算出整个船舶航行轨迹状态的最优估算数值[6]。卡尔曼滤波算法在对船舶航行轨迹进行跟踪解算的过程中不但使用了当前实际的测量数据,还使用了之前实际的测量数据,根据最小的线性方差的解算原理,对最优估计值进行解算[7]。
1.2 卡尔曼滤波算法数学模型卡尔曼滤波算法的基本原理是使用最小方差进行最优值的估算,因此卡尔曼滤波算法在解算过程中不断地接收最新的数据信息,并对相关计算参数进行更新,卡尔曼滤波算法的噪声处理算法能够降低外界的干扰,同时基于测量得到的实际数据信息对目标未来的运动状态进行预测,根据这种方法不断地对噪声进行迭代消除,最终获得精确的预测结果[8]。
由于卡尔曼滤波算法解算得到的预测结果是基于实时更新的数据,因此在不清楚系统受到的干扰源来自哪里的时候,通过该方法预测的结果具备一定的实时性以及准确性。卡尔曼滤波算法基于实时的数据信息对以前的系统状态进行预测并更新,这样可以获得很好的预测效果[9]。
为了能够描述卡尔曼滤波模型的预测流程,需要定义部分数学方程,第一步需要定义出该系统状态数学方程以及观察方程,公式如下:
| $ x\left( k \right) = Ax\left( {k - 1} \right) + Bu\left( k \right) + w\left( k \right)\text{,} $ | (1.1) |
| $ Z\left(k\right)=Hx\left(k\right)+v\left(k\right) \text{。} $ | (1.2) |
式(1)是卡尔曼滤波系统本身的状态更新模型;式(2)是卡尔曼滤波观测模型。式中:x(k)为k时刻的状态;u(k)为该滤波系统在k时刻的控制信息;A为该滤波系统的状态矩阵;B为该滤波系统的增益系数;w(k)为该滤波系统的过程噪声;Z(k)为该滤波系统在k时刻测量得到的数值;v(k)为该滤波系统测量得到的噪声,H为该滤波系统的系统常量,如果该系统是多测量系统,则H为一个矩阵。
接着则是对系统当前的最优预测进行解算,即基于系统当前的状态,对于未来时刻的系统状态进行预测。如果系统当前的状态用k表示,则基于系统前一刻的状态对当前状态的预测可以表示为:
| $ X\left( {k\left| {k - 1} \right.} \right) = AX\left( {k - 1\left| {k - 1} \right.} \right) + BU\left( k \right)\text{。} $ | (1.3) |
式中:X(k|k-1)为基于上一刻状态对当前状态的预测结果;X(k-1|k-1)为上一时刻的最优预测结果;U(k)为系统当前时刻的状态控制信息。根据式(3)不断地迭代计算,则预测结果也会不断地变化,接下来需要修正系统状态的协方差,公式为
| $ P\left( {k\left| {k - 1} \right.} \right) = AP\left( {k - 1\left| {k - 1} \right.} \right){A'} + Q\text{。} $ | (1.4) |
式中:P(k|k-1)为X(k|k-1)的协方差;P(k-1|k-1)为X(k-1|k-1)的协方差。当前时刻状态k的最优预测结果X(k|k),如下式:
| $ X\left(k|k\right)=X\left(k|k-1\right)+Kg\left(k\right)\left(Z\left(k\right)-HX\left(k|k-1\right)\right) \text{。} $ | (1.5) |
其中Kg(k)的求解方法,如下式:
| $ Kg\left( k \right) = p\left( {k\left| {k - 1} \right.} \right){H'}/\left( {HP\left( {k\left| {k - 1} \right.} \right){H'} + R} \right)\text{。} $ | (1.6) |
基于上述方程自身的不断迭代更新,则可以解算出最优的预测值X(k|k)。最后对当前时刻系统状态的协方差进行不断更新,则卡尔曼滤波算法也会不断地迭代更新,如下式:
| $ P\left( {k\left| k \right.} \right) = \left( {I - Kg\left( k \right)H} \right)P\left( {k\left| {k - 1} \right.} \right)\text{。} $ | (1.7) |
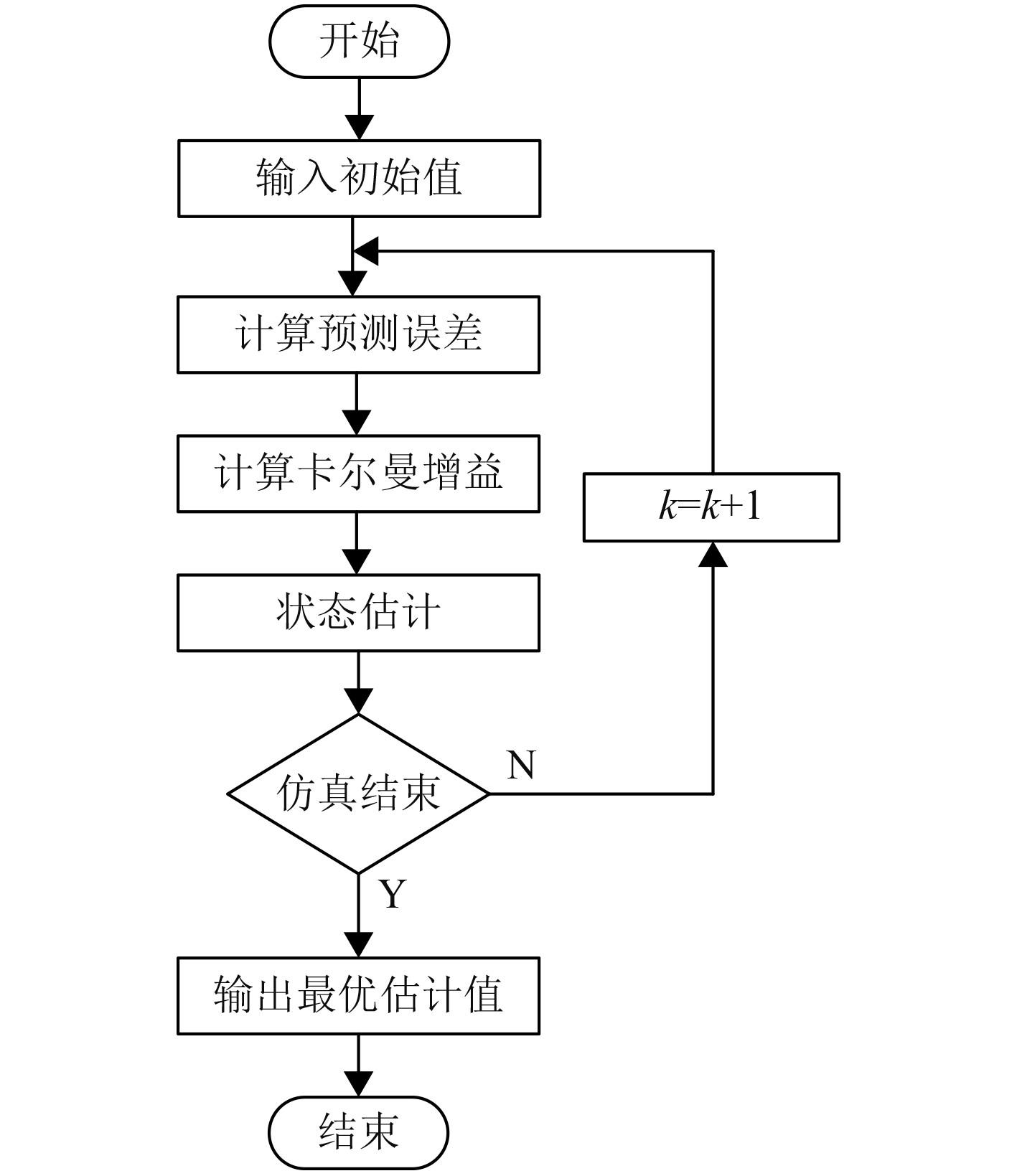
可以看出,卡尔曼滤波算法每次对状态进行估计之后,均会获得一个新的协方差。该协方差的初始值对卡尔曼滤波算法的收敛性存在一定的影响,因此在不一样的预测系统中,协方差的值也会存在一定的差异。卡尔曼滤波算法的解算流程如图1所示。
|
图 1 卡尔曼滤波算法的解算流程 Fig. 1 Solution flow of Kalman filter algorithm |
在大多数的工程应用中,系统的状态方程以及观测方程都为非线性函数,即使计算系统模型比较简单,也有可能是非线性的。此外,构建出和实际情况一样的数学模型相对而言比较困难,并且在实际情况下环境中都伴随着有色噪声,因此以卡尔曼滤波为基础的扩展卡尔曼滤波算法得到广泛的使用[10]。
扩展卡尔曼滤波算法本质上是实时线性化算法的一种,因此扩展卡尔曼滤波算法计算过程中,显示执行线性化转换,然后再使用卡尔曼滤波算法进行解算。
对系统状态进行提前预测,如下式:
| $ {\hat x_{k\left| {k - 1} \right.}} = f\left( {{{\hat x}_{k - 1\left| {k - 1} \right.}}} \right) \text{。} $ | (1.8) |
系统状态的协方差预测误差计算方法,如下式:
| $ {P}_{k|k-1}={f}_{k-1}^{x}{P}_{k-1|k-1}{\left({f}_{k-1}^{x}\right)}^{{\rm{T}}}+{Q}_{k-1} \text{。} $ | (1.9) |
提前对k时刻进行预测,如下式:
| $ {\hat z_{k\left| {k - 1} \right.}} = {h_k}\left( {{{\hat x}_{k\left| {k - 1} \right.}}} \right)\text{。} $ | (1.10) |
对滤波算法的测量误差协方差进行解算,如下式:
| $ {S_k} = h_k^x{P_{k\left| {k - 1} \right.}}{\left( {h_k^x} \right)^{\rm{T}}} + {R_k}\text{。} $ | (1.11) |
使用下式进行滤波增益解算:
| $ {K}_{k}={P}_{k|k-1}{\left({h}_{k}^{x}\right)}^{{\rm{T}}}{S}_{k}^{-1} \text{。} $ | (1.12) |
基于式(12)的滤波增益可以对系统状态进行迭代更新,公式为:
| $ {\hat x_k} = {\hat x_{k\left| {k - 1} \right.}} + {K_k}\left( {{z_k} - {h_k}\left( {{{\hat x}_{k\left| {k - 1} \right.}}} \right)} \right)\text{。} $ | (1.13) |
最后对系统预测误差协方差进行求解,如下式:
| $ {P_{k\left| k \right.}} = \left( {I - {K_k}h_k^x} \right){P_{k\left| {k - 1} \right.}}{\left( {I - {K_k}h_k^x} \right)^{\rm{T}}} - {K_k}{R_k}K_k^{\rm{T}}\text{。} $ | (1.14) |
式中,
| $ h_k^x = \frac{{\partial {h_k}\left( {{x_k}} \right)}}{{\partial {x_k}}}\left| {_{{x_k} = {{\hat x}_{k\left| {k - 1} \right.}}}} \right.\text{。} $ | (1.15) |
作为海面上交通运输的主体,船舶的异常轨迹行为在水面交通管理中主要包括船舶航向和航道的非正常偏离,同时船舶的这些异常航行轨迹通常与劫持、醉驾、碰撞以及走私等事件紧密相关。对船舶的异常航行轨迹的检测即是对船舶在海面上航行过程中的地理位置、船舶航行的方向、船舶航行的速度以及船舶的航迹等运动数据信息进行分析,根据这些数据信息的分析结果,进一步对船舶的运动状态进行判别,一旦识别到船舶存在异常的航行轨迹,则进行危险评估,并及时地发出警告。以船舶历史航行的数据模型为基础,同时利用轨迹聚类获得船舶在实验航道上的历史轨迹的聚类模型,并且将船舶的这些历史轨迹聚类模型看作船舶正常情况下的航行轨迹,然后以船舶的这些历史轨迹聚类模型为基础,设置一定的范围阈值,构建出船舶的轨迹异常检测机制,对在实验测试水域航行中的船舶进行异常检测实验,一旦检测出该船舶的航行轨迹越过了既定的航线阈值,则将该船舶的航行轨迹看作是异常的轨迹。
2.2 船舶轨迹异常评价指标船舶轨迹异常检测系统需要用最短的时间以及最快的速度检测出航迹异常的船舶,这样才能够最大概率地避免由于船舶的航迹异常而导致的危险事故。本文采用检测率、时效性和误警率3个标准对船舶异常轨迹检测算法进行评估。
时效性是为了评价船舶异常轨迹检测算法系统的执行时间。任取某一时间段内船舶异常检测系统完成异常轨迹检测的时刻ti和船舶轨迹采样点到达时刻tci之间的差值的均值,并将该均值作为轨迹异常检测系统的时效性评价标准,为了达到检测过程中的时效性,本文设置时间为1 s,即每隔1 s计算一次船舶轨迹异常检测算法系统的失效性,计算方法如下式:
| $ T = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{t_i} - {t_{ci}}} \right)} \text{。} $ | (2.1) |
式中:n为某段具体的时间段内处理的船舶轨迹点的数量;ti为每个船舶轨迹点处理完成的时刻;tci为船舶异常轨迹检测系统接收到轨迹点的时刻。
在某段时间内对船舶异常轨迹进行检测的时候,通过异常轨迹检测系统检测出的船舶异常轨迹和船舶实际异常轨迹之间的比值作为检测率,公式如下:
| $ DR = \frac{N}{M} \times 100 \text{% 。} $ | (2.2) |
式中:M为通过系统检测得到的船舶异常轨迹点的个数;N为实际的船舶轨迹异常的个数。
在某段时间内对船舶异常轨迹进行检测的时候,船舶的正常航行轨迹被误检为异常轨迹的比例作为误报率,公式如下:
| $ FR = \frac{{{N_f}}}{{{M_t}}} \times 100 \text{% 。} $ | (2.3) |
式中:
在船舶异常轨迹检测系统的3个评价指标中,时效性表示了检测系统的实时性,检测率表示了检测系统的准确性,误警率表示了检测系统的误差大小。在最理想的情况下,船舶异常轨迹检测系统应该能够在最短的时间里,检测出任意一个异常轨迹,同时不包含正常的船舶轨迹。
2.3 船舶异常轨迹检测结果分析在对船舶异常轨迹检测过程中,首先需要确定航向-航速距离CSD和相关距离RD的阈值大小。本文认为船舶自动航行的数据模型中,正常的船舶轨迹点占船舶所有航行轨迹点的95%,因此在对CSD和RD进行阈值选择的时候,可以以船舶正常轨迹占船舶总航行轨迹的95%为基础,进行阈值的选择。本次实验中,RD的阈值定为5.738,同时CSD的阈值定为0.495,这样根据采样得到的RD以及CSD的值和相应的阈值相比较,则可以进行船舶异常轨迹的判断。
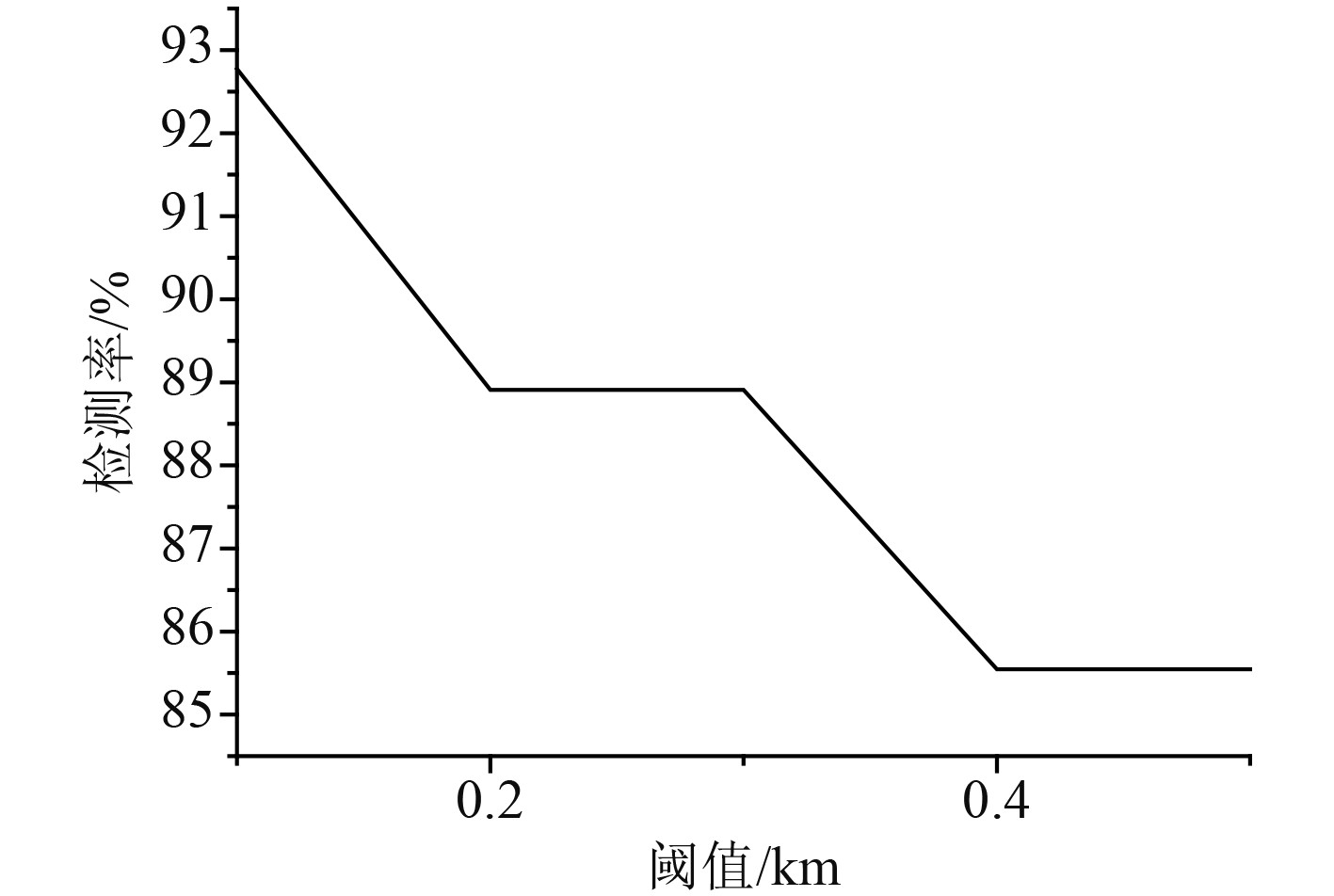
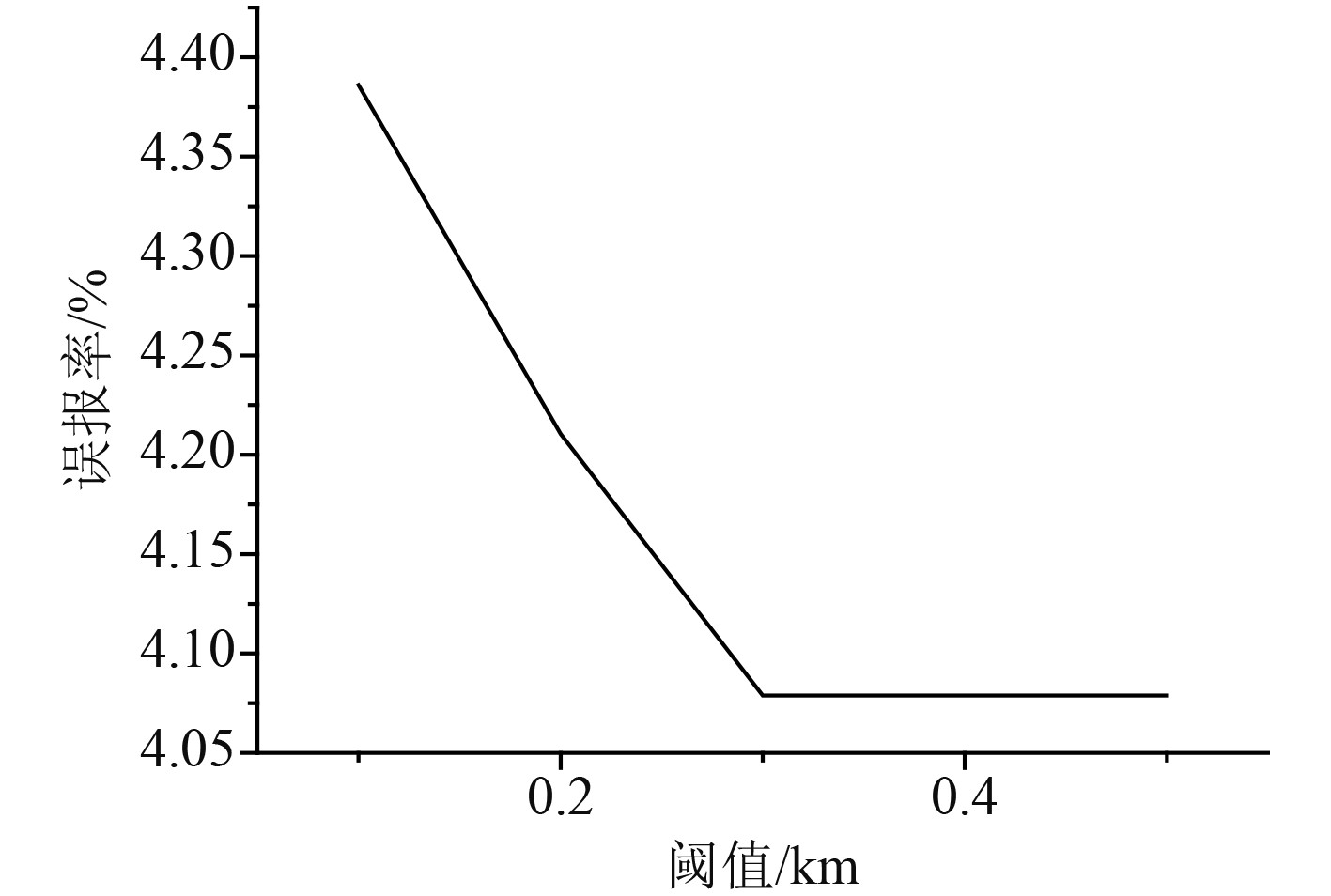
分别采用不同的阈值对船舶异常轨迹的检测结果进行量化分析,用于实验测试的阈值定为0.1,0.2,0.3,0.4,0.5。在不同的实验测试阈值下,基于卡尔曼滤波预测算法对船舶的异常轨迹进行检测,同时将基于卡尔曼滤波算法的测量结果和原始的测量结果数据进行比较,其中检测率和误报率分别如图2和图3所示。
|
图 2 不同阈值情况下的检测率 Fig. 2 Detection rate at different thresholds |
|
图 3 不同阈值情况下的误报率 Fig. 3 False positive rate under different threshold conditions |
从图2可以看出,当阈值大于0.3时,检测率在降低。从图3可以看出,当阈值大于0.3时,误报率并没有降低,因此本次实验中阈值可以使用0.3。基于卡尔曼滤波预测的船舶异常轨迹检测中的RD以及CSD的阈值是利用统计方法得出的,在选择这2个阈值的时候,需要使得船舶正常的航行轨迹处于正常的范围。从图3还可以看出,当阈值选择0.3的时候,误报率为3.96%即可以保证96.04%的正常轨迹可以正常识别,这个结果和实验一开始的设想一致。从图2也可以看出,当阈值设置成0.3的时候,船舶轨迹的检测率能够达到88.89%。通过上述分析可以看出,结合船舶的位置、速度以及航行方向等数据信息,以聚类得到船舶正常航行的轨迹,同时构建出船舶的正常轨迹模型,然后再通过距离阈值的方法进行船舶异常轨迹的检测,这种技术可行。
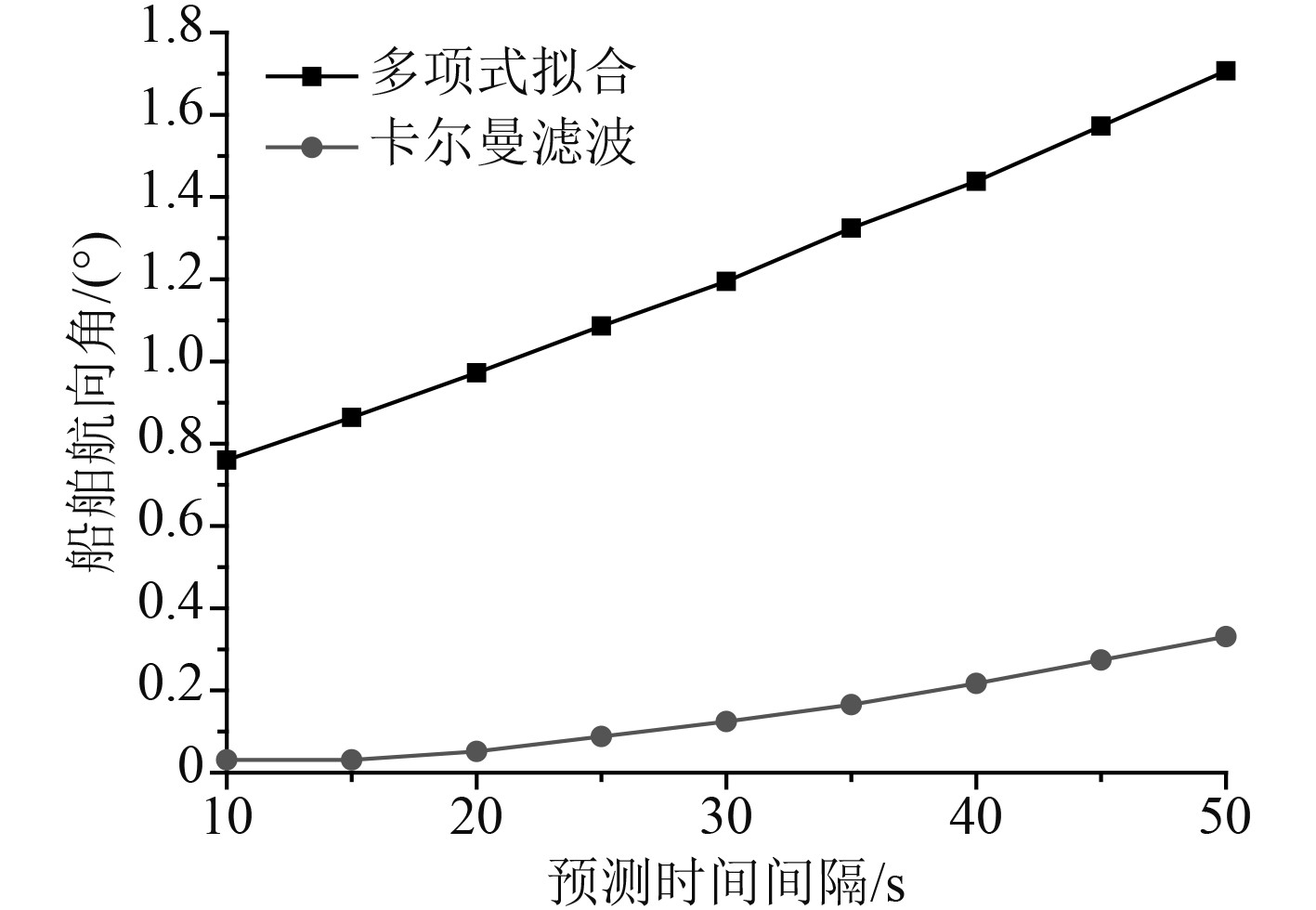
从图4可以看出,基于卡尔曼滤波预测算法的精度明显优于多项式拟合算法。这是因为卡尔曼滤波算法可以根据相关数据信息的历史值,不断地对相关参数进行识别和线性评估,并根据评估的结果实时地对参数进行调整,最终达到降低模型误差、提升模型预测精度的效果。
|
图 4 不同算法下航向角的预测精度比较 Fig. 4 Comparison of heading angle prediction accuracy under different algorithms |
船舶的航行轨迹描述了船舶在海面上的运动情况,基于船舶的航行轨迹可以对船舶的海况进行判断,同时根据船舶的航迹信息,排查安全隐患,最终确保船舶在海面上的安全性。
| [1] |
杨紫煜, 焦朋朋, 云旭, 等. 基于相空间重构的卡尔曼滤波短时交通流预测模型[J]. 北京建筑大学学报, 2021, 37(4): 43-50. |
| [2] |
陈明强, 傅嘉赟. 基于无迹卡尔曼滤波的飞行航迹预测方法研究[J]. 计算机仿真, 2021, 38(6): 27-30. DOI:10.3969/j.issn.1006-9348.2021.06.006 |
| [3] |
于继宇, 李宪, 杨明业. 基于YOLOv3与卡尔曼滤波的行人短时社交冲突预测[J]. 传感器与微系统, 2021, 40(6): 133-137. |
| [4] |
周晓, 唐宇舟, 刘强. 基于卡尔曼滤波的道路平均速度预测模型研究[J]. 浙江工业大学学报, 2020, 48(4): 392-396. |
| [5] |
姜佰辰, 关键, 周伟, 等. 基于多项式卡尔曼滤波的船舶轨迹预测算法[J]. 信号处理, 2019, 35(5): 741-746. DOI:10.16798/j.issn.1003-0530.2019.05.002 |
| [6] |
冯安琪, 钱丽萍, 黄玉蘋, 等. RFID环境下基于自适应卡尔曼滤波的高速移动车辆速度预测[J]. 计算机科学, 2019, 46(4): 100-105. DOI:10.11896/j.issn.1002-137X.2019.04.016 |
| [7] |
包磊. 基于聚类距离计算的船舶轨迹异常检测方法[J]. 舰船电子工程, 2020, 40(9): 56-61. DOI:10.3969/j.issn.1672-9730.2020.09.014 |
| [8] |
张春玮, 马杰, 牛元淼, 等. 基于行为特征相似度的船舶轨迹聚类方法[J]. 武汉理工大学学报, 2019, 43(3): 517-521. |
| [9] |
刘志方. 大数据网络下船舶轨迹异常故障检测技术优化[J]. 舰船科学技术, 2019, 41(10): 34-36. |
| [10] |
马力. 卡尔曼滤波算法在船舶航行轨迹异常行为检测中的应用[J]. 舰船科学技术, 2017, 39(12): 144-146. |
 2022, Vol. 44
2022, Vol. 44
