2. 西南交通大学,四川 成都 611756
2. Southwest Jiaotong University, Chengdu 611756, China
海上避碰规则要求船舶规避碰撞风险,以此来提高航行安全性。为实现这一目标,在构建自动避碰系统的过程中,可以运用模糊控制技术,通过模糊控制器,提高避碰系统的整体性能,降低碰撞风险,使船舶能够安全航行。本文对船舶避碰路径模糊控制系统展开分析。
1 船舶避碰原理 1.1 碰撞原因相关调查统计结果显示,在船舶碰撞事故的原因中,不遵守避碰规则的占比最高,接近50%,未做出及时有效瞭望次之,约为35%,其余15%为其他因素。导致碰撞的原因有的是单独出现,有的则是多因素并存。为避免船舶航行时发生碰撞事故,要采取有效的方法和措施加以预防。比较常用的避碰预防措施有改善航行环境、提高操纵性能、优化航行技术等。
1.2 船舶避碰过程处于航行状态的船舶如果相遇,需要采取避让行动,此时的决策过程分为信息采集与分析和最终决策等阶段。驾驶员经过观察发现来船后,要对来船的运动信息进行收集,并对这些信息分析处理,根据信息分析结果,结合驾驶经验,判断两船是否能够安全驶过,有无碰撞风险。如果可以安全驶过,则不需要采取任何行动,只要按照既定航线和航速前进即可,若是无法安全驶过,驾驶员则应当按照避碰规则,确定两船处于何种会遇格局,以此作为主要依据,对避让责任加以明确。本船为让路船时,要采取避让措施,避免与来船发生碰撞,避让操作后,待来船安全驶过,本船恢复正常航行,这样一次避让便顺利完成。
1.3 碰撞危险碰撞危险(risk of collision,ROC),船舶航行时,按照当前环境,使用各种技术手段,判断是否存在碰撞危险,如有怀疑,则认为存在ROC,这是避碰规则明确规定。而在实际中,避碰规则却并未给出确切的定义,这个术语具有非常大的弹性,可以指某个海域内发生碰撞事故的可能性大小,具体可以用会遇率和碰撞率表示。船舶的会遇态势指会遇局面或能见度不良时的态势,对该态势的判断,是确定避让责任和应采取行动的重要依据。碰撞态势可分为对遇局面、右舷交叉相遇、左舷交叉相遇、追越局面和被追越局面等。判断会遇双方是否存在碰撞危险及确定碰撞危险度时,可以运用DCPA(最近会遇距离)和TCPA(会遇时间)。因部分船舶装载的雷达系统仅能提供目标船的方位与距离信息。所以要建立相应的数学模型,以此来实现智能避碰决策与控制。对本船与目标船的航向和航速作出假设,分别用

|
图 1 两艘相对运动舰船的基本参数示意图 Fig. 1 Schematic diagram of basic parameters of two relatively moving ships |
当本船与目标船之间的碰撞危险度超过规定要求时,本船便需要采取行动,避免与目标船发生碰撞,这个过程即避让决策。首先要在避让决策中,合理确定避让时机,通过对会遇格局进行分析后发现,海上的避让规则是指将碰撞危险、紧迫局面和紧迫危险这3个局面的出现,作为避让行动的起始时机。也就是说,可以将上述3个局面作为确定避让时机的主要因素。同时避让规则还给出一些基本原则,可以归纳为早、大、宽、清四点。具体如下:要及早做出避让行动,避免形成碰撞危险,防止产生紧迫的局面;为避免碰撞,应在环境许可的情况下,做出大幅度行动,大到足以使目标船用雷达可以察觉到;两船避让过程中,要保持宽裕的距离,以此来确保避让安全;采取避让行动,要驶过让清,不存在任何碰撞风险。
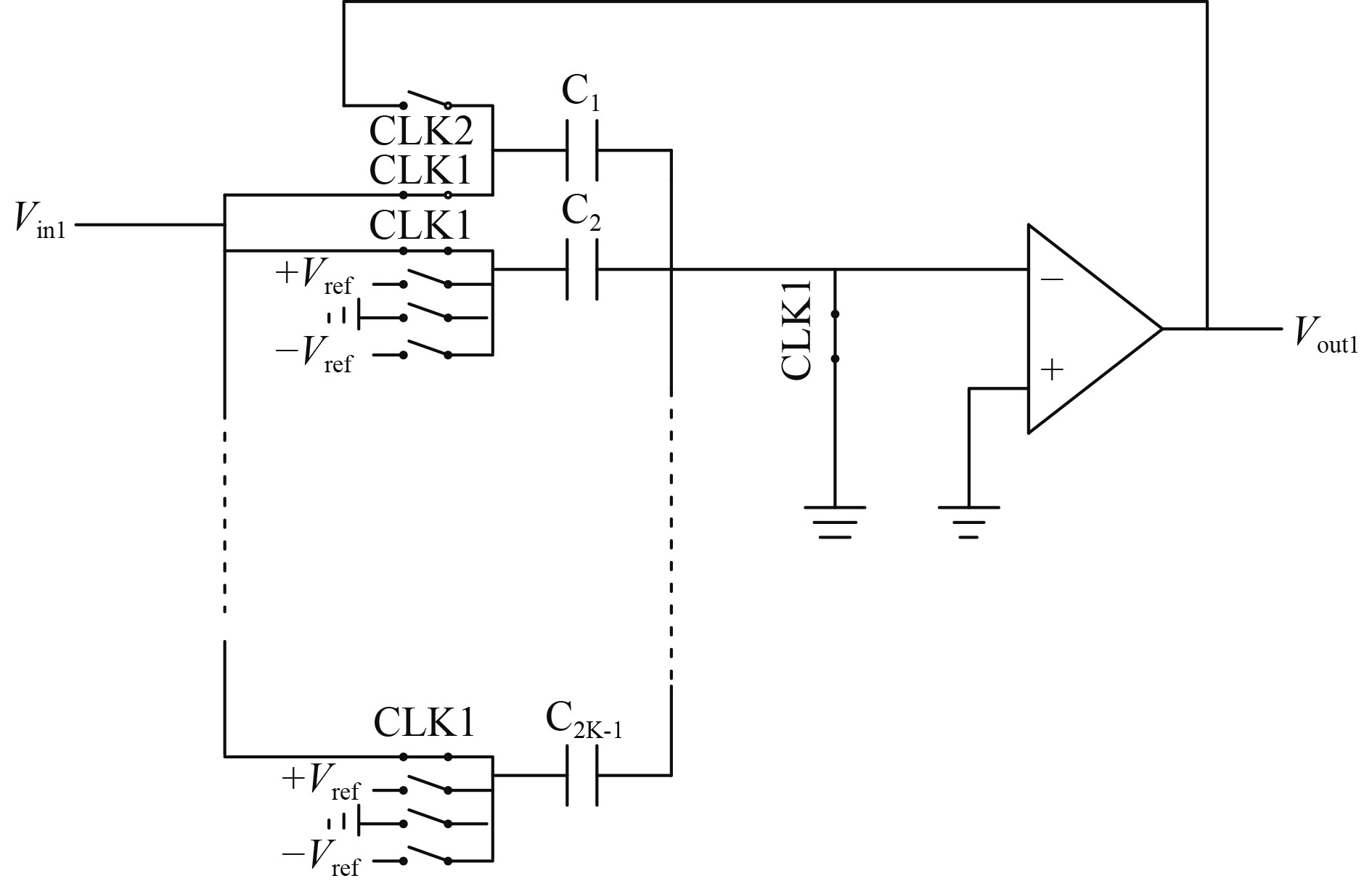
2 船舶避碰路径模糊控制系统 2.1 模糊控制系统构建对于模糊系统而言,模糊控制器是核心部分,由4个模块组成,分别为Fuzzifcation(模糊化模块)、Knowledge Base(知识库模块)、Inference(模糊推理模块)以及Defuzzification(解模糊模块)。经过简化的模糊控制系统结构如图2所示。
|
图 2 简化后的船舶避碰路径模糊控制系统结构示意图 Fig. 2 Structure diagram of simplified fuzzy control system for ship traffic collision avoidance path |
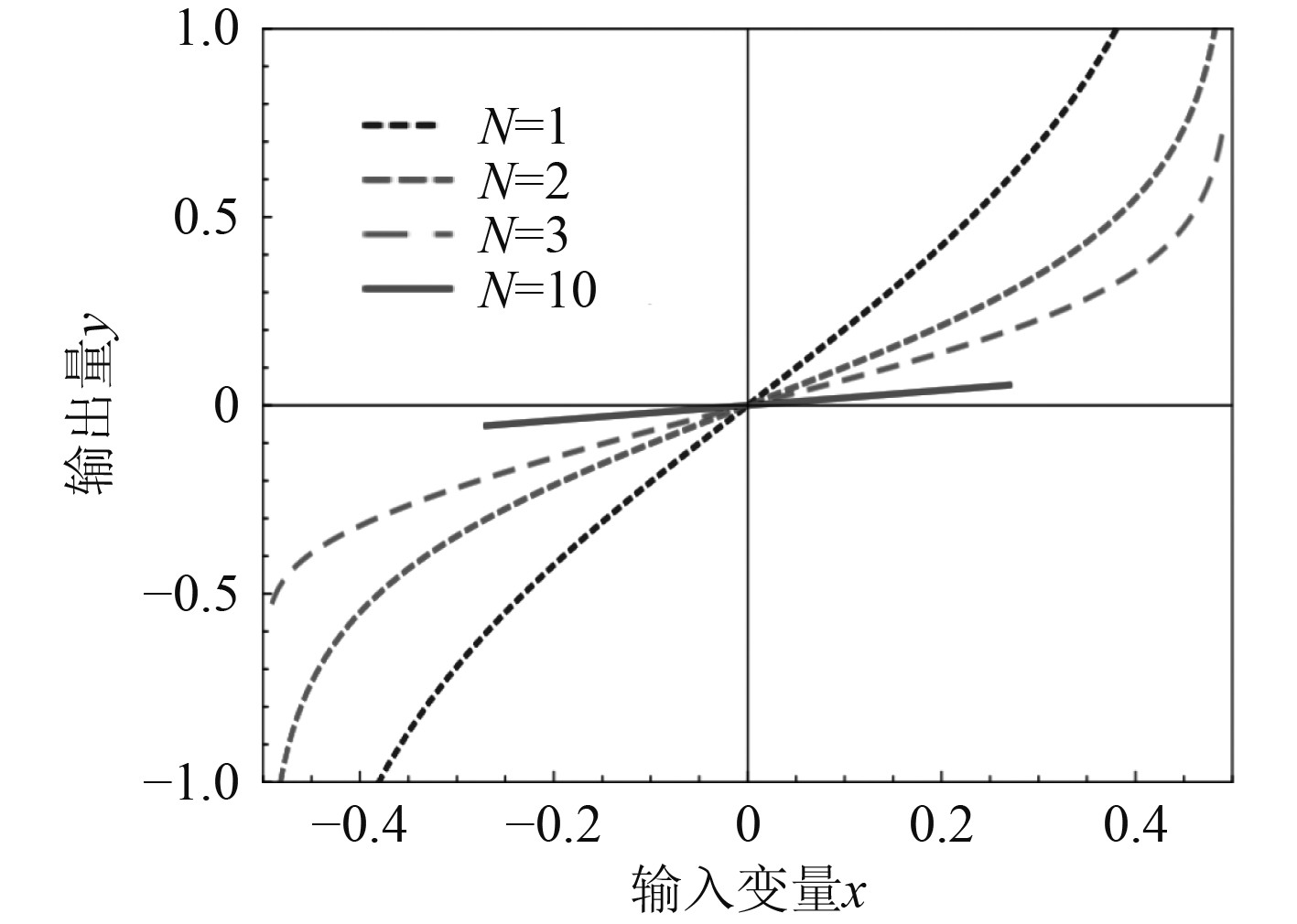
模糊控制系统的简化步骤如下:对包含输入量和输出量在内的模糊子集及其论域加以确定,随后确定输入与输出隶属度函数,最后确定模糊控制规则表。不同误差变化N下的输入量误差与输出量的关系曲线如图3所示。
|
图 3 不同误差变化N下的输入量误差与输出量的关系曲线 Fig. 3 The relationship curve between input error and output under different error changes N |
当模糊控制系统只对误差和误差变化进行分析判断,但却不能对误差累积估算时,这个系统的原理与PD控制相类似,它只有微分控制功能,无法将余差彻底消除。向系统中加入积分,能够使缺陷得到弥补。由于偏差的变化量对系统的控制稳定性影响不大,不对其做具体讨论。
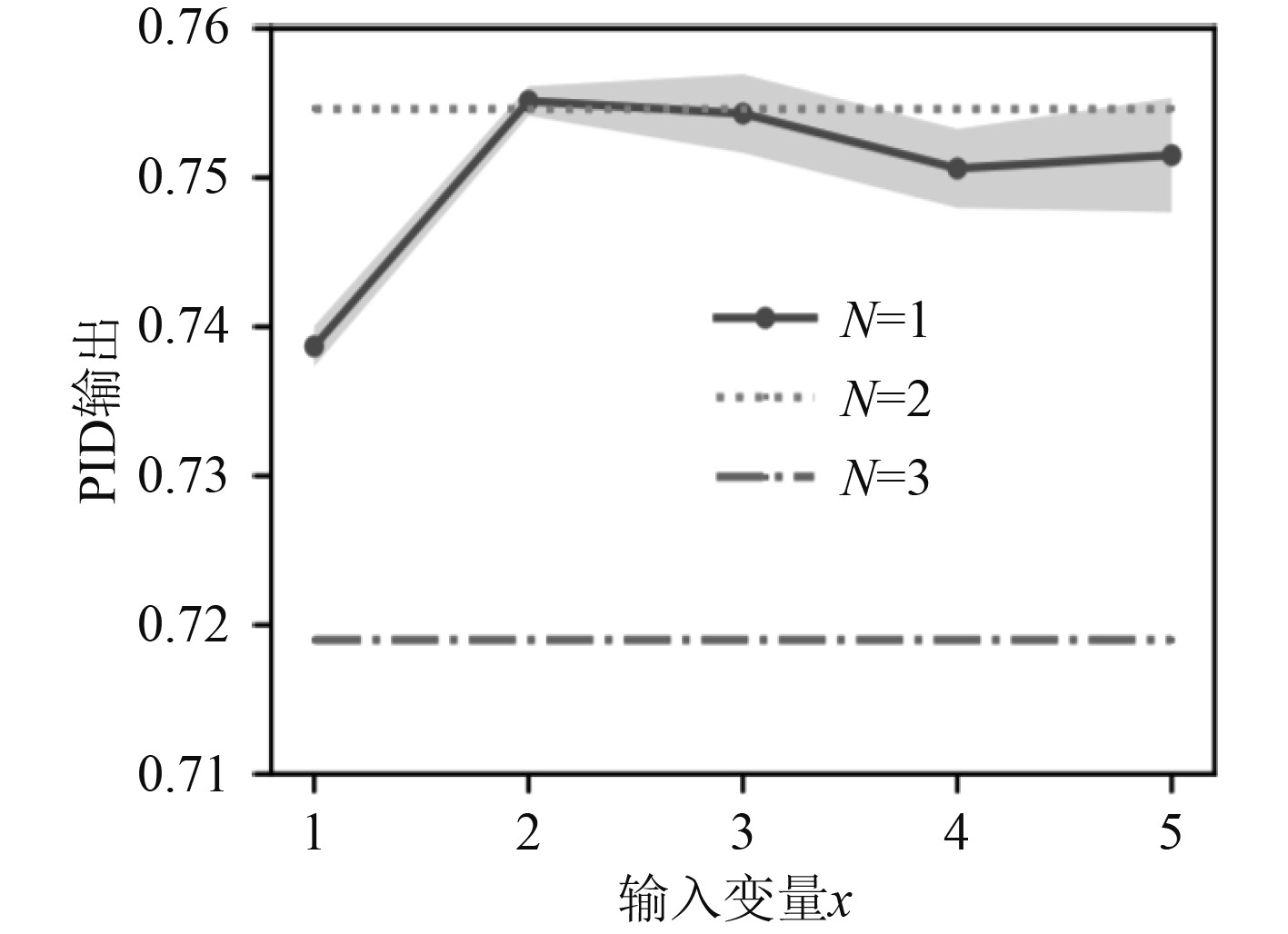
2.2 仿真分析构建模糊控制系统时,要将所有误差及变化率从精确输入转变为模糊输入,这个过程即模糊化过程。通过模糊计算后,最终要转变为精确输出,为具体执行提供条件。可知,精确输出与模糊化呈现为相反的情况,可以将这种情况称为模糊判决。按照实际情况,借助模糊集和模糊控制方法,可以在实现模糊化的基础上,完成解模糊化,进而获得精确的输出。船舶运动PID控制模型采用了阶跃函数及微分方程,控制过程可以借助闭环模糊控制系统来完成。基于二阶传递函数的船舶运动PID模糊控制仿真结果如图4所示。
|
图 4 基于二阶传递函数的船舶运动PID模糊控制仿真结果 Fig. 4 Simulation results of ship motion PID fuzzy control based on second order transfer function |
可以看出,船舶运动二阶受控模型经过简化处理后,运用PID模糊控制方式,能够使得船舶的的动态性能在原本的基础上进一步完善。
2.3 训练结果为使神经网络的收敛速度在原本的基础上进一步加快,通过快速收敛找到全局最优解,进而获得最小点,对现有的BP算法优化改进,在原算法中增加惯性项,使惯性校正量随着学习进程向有利于收敛的方向变化。仿真实验的误差曲线如图5所示。通过多次反复计算后,得到神经网络的权值(
|
图 5 神经网络仿真试验网络训练误差曲线示意图 Fig. 5 Diagram of network training error curve of neural network simulation test |
以随机的方式选取1组与训练值不同的样本对结果进行检验,采用模糊系统和神经网络分别计算。由计算结果可知,二者最终所得的结果极为接近。由此可见,用神经网络代替模糊推理系统,不但能够提高系统的运算速度,而且还能使计算结果的精确度满足使用要求。
通过增加惯性项的方法对BP算法优化改进后,使神经网络的收敛速度得到显著提升,网络能够尽快收敛达到全局最小点,算法优化达到一定的效果。由非线性的相关理论可知,最速梯度下降法仅适用于局部优化,如果是全局优化,则不一定是最速下降的方向。由该方法的计算过程可知,它在逼近极小点时的运行路径为锯齿形,收敛速度会在靠近极小点的过程中不断减慢,距离极小点越近,收敛速度减慢的程度越大,简单来说,就是与极小点的距离越近,收敛速度就越慢。BP算法的学习速度为确定值,若是将该值定的比较大,虽然能够使学习速度显著加快,但却会引起学习过程震荡,这样一来,全局误差很难达到期望值。为使权值误差极小化,学习时,确定值不宜过大,这样能够使全局误差达到期望值,但学习过程比较慢。将附加动量项算法和自适应学习速率算法有机结合到一起,使两者共同作用于权值的调整。利用前者可以使训练时间显著缩短,具体做法是设定初始步长,然后检查权值修正结果,看误差函数是否降低,如果降低,表明学习速度低,此时要增加学习速度,若是未降低,表明调节过度,要减小学习速度。经过优化改进后的BP算法迭代次数减少,收敛速度进一步加快,精度得到提升。不仅如此,还弥补了原算法容易陷入局部极小值的缺陷。基于此,可将结合后的2种算法,运用到船舶避碰路径模糊控制系统中。
采用动量自适应学习速率算法计算得出的网络训练误差结果如图6所示。经优化改进后的算法,不但收敛速度加快,而且精度大幅度提高,性能较之未优化前得到进一步改善。
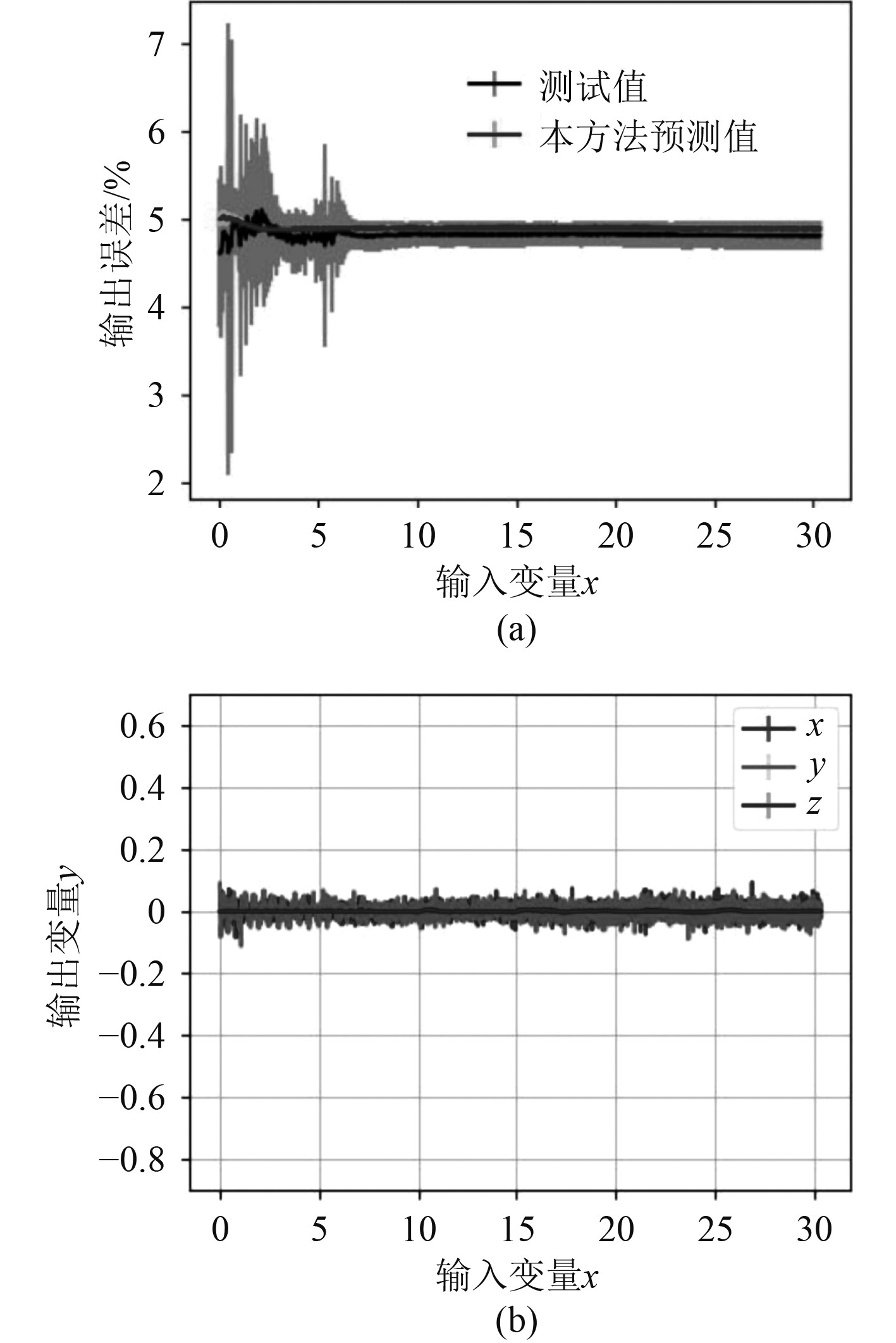
|
图 6 采用动量自适应学习速率算法计算得出的网络训练误差结果 Fig. 6 Network training error results calculated by momentum adaptive learning rate algorithm |
神经网络与模糊逻辑控制各具特点,为使二者的优势得到最大限度的发挥,将其融合到一起,这样便可适用于各种学习方式。在模糊隶属函数中,船舶领域可以用Do表示,而船舶动态则可用Dm表示,由驾驶员依据诸多因素结合经验决定。这里的因素包括:能见度、操纵性、目标船方位舷角等。通常情况下,在某个特定的水域内,当能见度降低后,船舶的有效领域范围会变大,而当能见度降至一定程度时,便不会对船舶领域产生影响。
船舶动态避碰控制系统的传输函数为:
| $ {V}_{out1}={2}^{K-1}\cdot {V}_{i{n}_{1}}-{V}_{DA{C}_{1}} \text{,} $ |
式中,
| $ {V}_{DA{C}_{1}}={V}_{ref}\cdot {D}_{1} \text{,} $ |
式中:
| $ {D_1} \in \left\{ {0, \pm \frac{{{C_2}}}{{{C_1}}}, \pm \frac{{{C_2} + {C_3}}}{{{C_1}}}, \cdots , \pm \sum\limits_{i = 2}^{{2^{K - 1}}} {\frac{{{C_i}}}{{{C_1}}}} } \right\} 。$ |
在存在较大的环境误差情况下,为了进一步提高精度,减小误差,可以采用如下函数进行补偿:
| $ \frac{{{C_2}}}{{{C_1}}} = 1 + {\Delta _{{C_2}}},\frac{{{C_2} + {C_3}}}{{{C_1}}} = 2 + {\Delta _{{C_2}}} + {\Delta _{{C_3}}},\cdots 。$ |
其中,每个
船舶航行中不同距离下的能见度关系曲线如图7所示。在导航系统好、操纵灵活性强的船舶控制系统中d1和d2的值差异比较小,而导航系统性能差、操纵不灵活的船舶中d1和d2的值差异比较大。船舶的操纵性会对安全域产生一定程度的影响,虽然船长、船宽等几何参数与安全域之间存在未知的关系,但却可以利用神经网络学习到它们之间的非线性映射关系。当目标船接近本船时,受驾驶员心理因素的影响,使船舶前方的安全区域要大于船后。
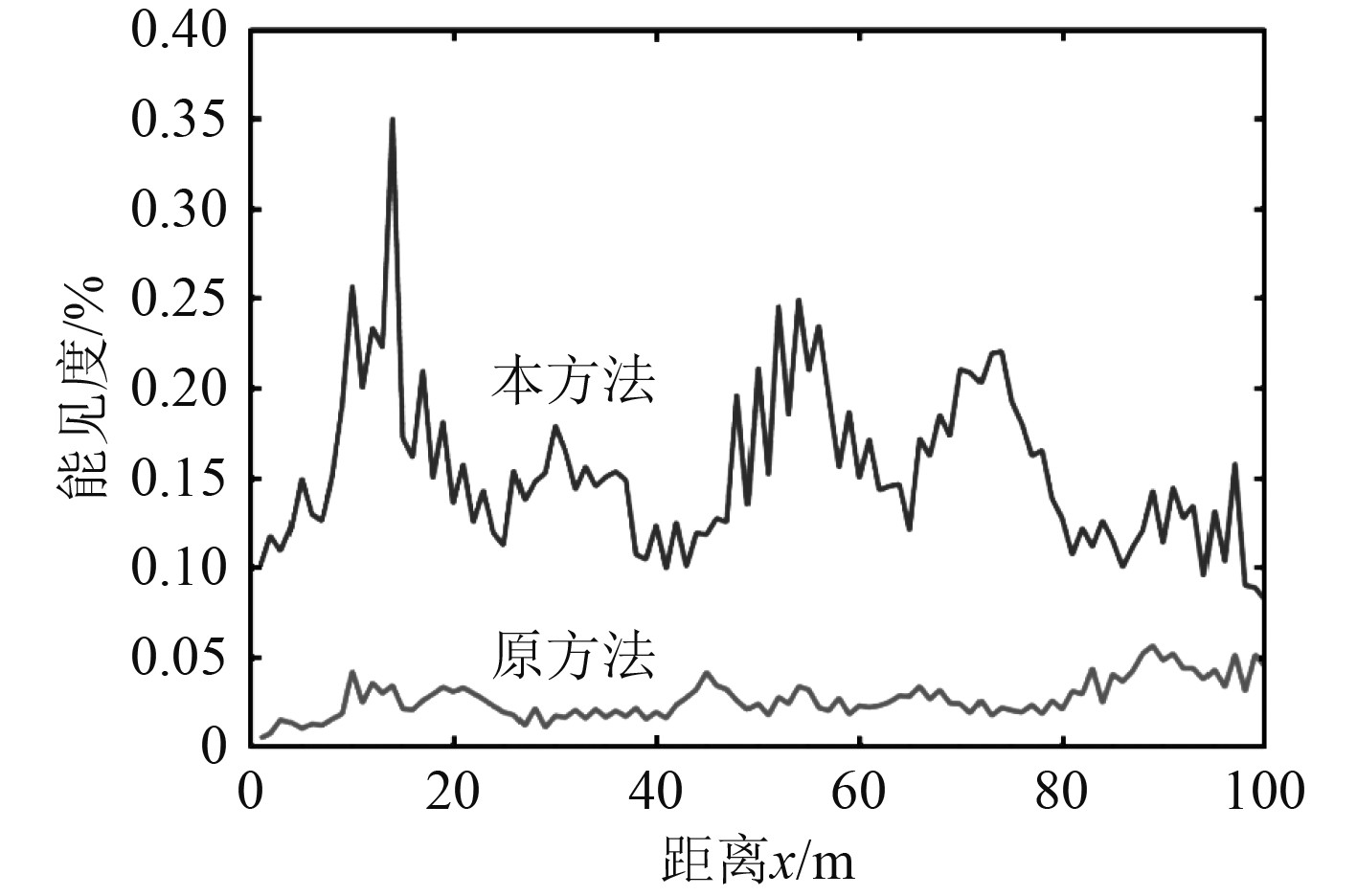
|
图 7 船舶航行中不同距离下的能见度关系曲线 Fig. 7 Visibility relationship curves at different distances during ship navigation |
借助神经网络学习104个专家样本,以此来记忆船舶领域和船舶动态,得到的信息源权值矩阵如下:
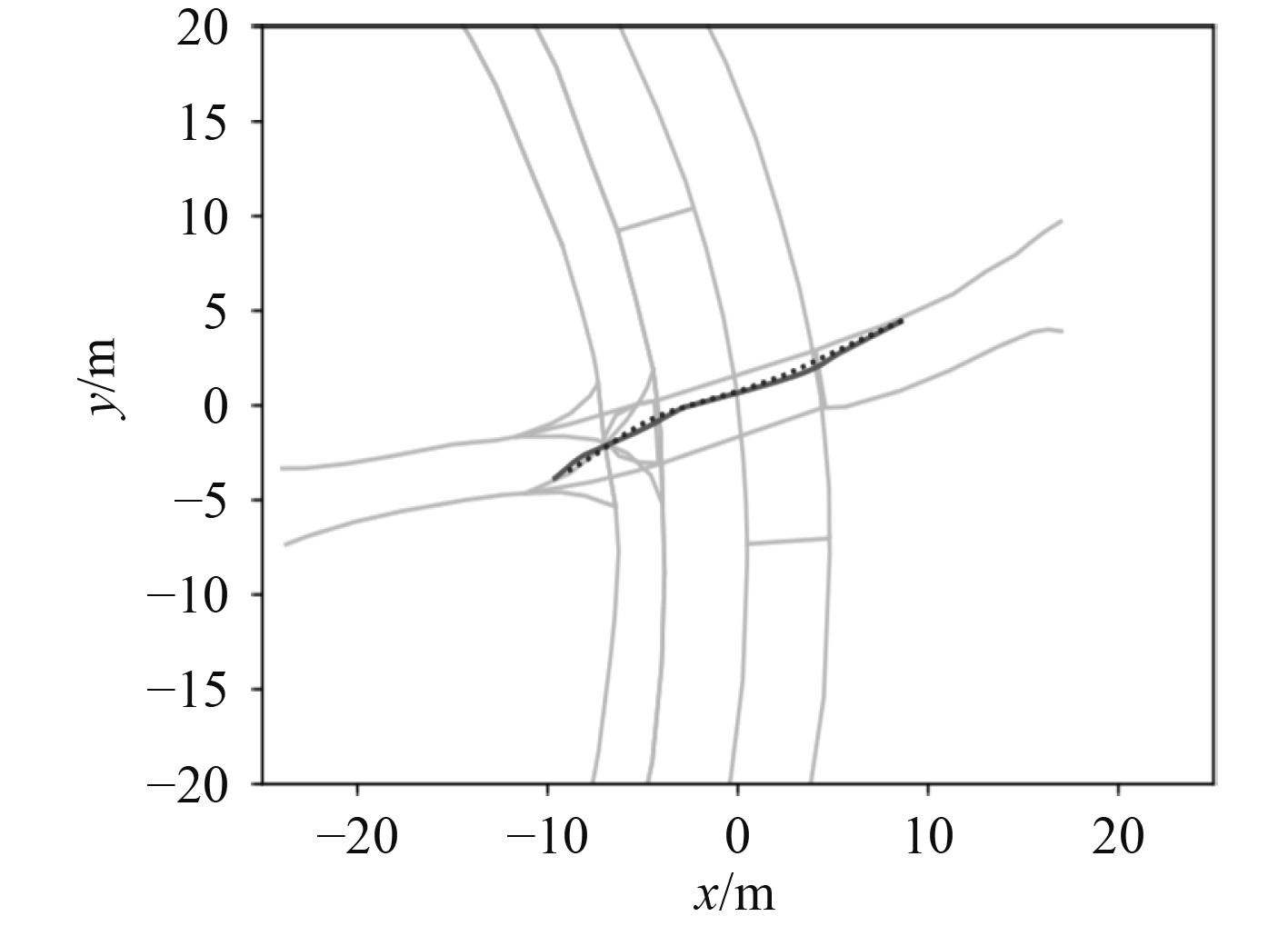
在航区内的能见距离为4 n mile,假定在未来的10 min内,本船与目标船的航行状态全都保持不变,通过计算得出DCPA和TCPA,并确定不同时刻的碰撞危险度,根据计算结果,模糊控制系统会自动避碰。由此可见,本文开发的模糊控制系统在船舶避碰路径中具有良好的适用性。
3 结 语船舶避碰是保证航行安全性的关键,必须予以高度重视。在构建自动避碰系统时,应用模糊控制技术提高控制效果,达到有效避碰的目标。
| [1] |
唐晓暄, 熊波, 杨芳贵, 等. 基于内河航标的船舶智能识别和避碰预警系统的研究与实现[J]. 珠江水运, 2022(5): 64-68. DOI:10.14125/j.cnki.zjsy.2022.05.004 |
| [2] |
周凤杰. 船舶避碰的粒子群-遗传(PSO-GA)的混合优化算法研究[J]. 船舶力学, 2021, 25(7): 909-916. DOI:10.3969/j.issn.1007-7294.2021.07.008 |
| [3] |
左川. 从一起海上船舶碰撞事故论协议避让在船舶避碰行动中的运用条件[J]. 中国海事, 2020(12): 30-32. DOI:10.16831/j.cnki.issn1673-2278.2020.12.011 |
| [4] |
马杰, 苏钰栋, 熊勇, 等. 基于速度障碍和人工势场的受限水域船舶避碰决策方法[J]. 中国安全科学学报, 2020, 30(11): 60-66. DOI:10.16265/j.cnki.issn1003-3033.2020.11.009 |
| [5] |
聂鸿博. 对基于人工智能和软计算的船舶自动避碰决策算法分析[J]. 中国信息化, 2020(2): 80-82. |
| [6] |
时庆涛, 朱兴宇. 基于大数据与人工智能的舰船避碰路径优化调度算法[J]. 舰船科学技术, 2020, 42(2): 55-57. DOI:10.3404/j.issn.1672-7649.2020.02.010 |
| [7] |
叶璇. 基于嵌入式的红外探测桥式起重机防撞系统设计[J]. 起重运输机械, 2010(02): 23-25. DOI:10.3969/j.issn.1001-0785.2010.02.007 |
 2022, Vol. 44
2022, Vol. 44
