0 引　言

受到海上恶劣环境的影响，船舶在行驶过程中会遇到较多的意外^[1-3]，因此合理规划行驶航迹，并对船舶行驶路线进行规划，可以避免船舶行驶过程中发生意外事故^[4-6]。有学者对船舶航迹控制进行了研究，祝亢等^[7]基于深度强化学习的智能船舶航迹跟踪控制，虽然该方法通过不断迭代优化获取了最短航行轨迹，但该方法得到的轨迹无法以最短的时间到达目的地。祁林等^[8]基于RBF神经网络的水面船舶轨迹跟踪控制，该方法可以利用跟踪船舶行驶实现轨迹规划，但规划得到的航迹安全性不高。为此，本文研究基于关联规则的船舶航迹分布式控制方法，获取最合理的船舶行驶轨迹，并对船舶进行精确的控制。

1 船舶航迹分布式控制设计 1.1 基于关联规则A*改进算法的船舶最佳航迹搜索 1.1.1 基于关联规则A*改进算法

A*算法是一种较早应用在数据挖掘领域的关联规则算法，利用基于关联规则的A*改进算法，搜索最佳船舶航迹，为航迹分布式控制提供可靠基础。最佳航迹搜索时考虑多约束的A*算法代价函数模型，即

$ f\left( n \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{w_{ij}}{x_{ij}}} } 。$

(1)

式中：f(n)表示代价函数；w_ij为综合权值系数^[9]。

通过这一形式的计算，虽然可以有效搜索得到最短距离，但在计算过程中更依靠专业知识与使用者的行业经验，导致算法存在一定随机性。本文针对传统A*算法中的不足，通过关联规则对其进行改进。在改进过程中，主要利用关联规则挖掘计算过程中除距离外的其他全部最佳航迹因素，并对此进行关联分析，获取每个最佳航迹因素的支持度。通过设置航迹支持度阈值挑选出引入代价函数分析的频繁因素，以此降低需计算的最佳航迹因素数量。分析每个频繁因素之间的置信度，并对其权值系数进行设定。在计算时，仅需给定其中一个权值系数，即可自动获取最佳航迹多因素的权值系数，从而降低每个最佳航迹因素权值的不确定性，提升计算效率。

1.1.2 算法搜索船舶最佳航迹流程

步骤1　 针对包含船舶航迹最短路径的m个因素集合 $ E = \left[ {{e_1},{e_2},{e_3},\cdots ,{e_m}} \right] $ 进行关联计算。分析每个航迹因素的支持度，并设定支持度阈值 $ \min \_\sup $ ，将该阈值设定在合理范围内，获取航迹的频繁因素。将获取到的频繁因素设定为代价函数的考虑范围，以此获取航迹的代价函数约束集合E_k。

步骤2　设定航迹集合E_k中因素e_i的权值，分析集合E_k中其他因素与e_i之间的置信度，即分析条件概率 $ p\left( {{e_j}\left| {{e_i}} \right.} \right) $ ，同时 $ {e_j} \in {E_k} $ ， $ i \ne j $ 。

步骤3　设定航迹起始位置S与目标位置D，同时向Open表内存放起始位置S。

步骤4　分析Open表是否为空，若为空则说明最佳航迹搜索失败，停止计算；若不为空则将Open表内的首个节点设定为当前节点n，开始下一步。

步骤5　将节点n作为基点，探测周围的8个基点，并分析目前的代价函数，与航迹代价函数相关联的因素以及因素系数已通过步骤1和步骤2给定；挑选代价函数最低的节点，存入Open表内，并返回步骤4再次进行循环分析，完成最佳航迹搜索。

1.2 船舶航迹分布式控制数学模型

当通过关联规则获取最佳船舶航行轨迹后，构建船舶航迹分布式控制数学模型，对该模型进行航迹控制。在航迹控制过程中，针对船舶主要控制2个部分，分别为航向与船位，图1为航迹控制坐标。在图1的固定坐标系XOY下，x和y为船舶重心的坐标，U为其行驶速度。

假设通过上述计算步骤得到的最佳航迹与X轴重合，则首偏角与航向角 $ \phi $ 相等，因此，建立船舶航迹分布式控制的非线性数学模型，在实际船舶行驶过程中，通常存在不稳定性与临界状态，导致船舶未按照控制形式行驶。为此，本文考虑船舶模型的非线性情况，通过构建控制器，实现船舶航迹的分布式控制。

1.3 船舶航迹分布式反推控制器设计 1.3.1 输入-状态反馈线性化

将船舶航迹分布式控制非线性船舶模型进行抽象化处理，抽象形式为：

$ \dot x = f\left( x \right) + g\left( x \right)u 。$

(2)

式中： $ \dot x $ 为抽象处理后的航迹分布式控制坐标x；f为局部Lipschitz连续函数；g为实际速度。

若存在一个微分同胚映射 $ W:D \to {R^n} $ ，可以使式(1)中航迹分布式控制的平衡点存在于D_z=W(D)，此时可利用坐标变换z=W(x)，将公式(1)调整为如下形式：

$ \dot z = Az + B\vartheta \left( x \right)v。$

(3)

式中： $ \dot z $ 表示变换后的航迹分布式控制坐标； $ \vartheta $ 表示跟踪控制律；(A,B)表示能控矩阵；v表示横漂速度；v(t)控制输入。

通过在船舶中装置速度、角速度传感器以及导航装置，可以测定模型中航迹分布式控制的状态变量，因此可对这些可测变量进行线性化处理。本文利用反推控制技术，使每一参数能够整定，即设计航迹分布式控制控制器，通过控制器使变量逐渐稳定，保障船舶能够按照关联规则挖掘得到的最佳航迹行驶。

1.3.2 反推船舶航迹分布式控制器

此时，可得到Lyapunov函数的导数，用Barbalat定理，状态变量z₁逐渐趋近于0。此时，式(10)的控制输入可以保证航迹分布式控制模型式(2)渐近稳定，以此完成航迹分布式控制控制器的设计，实现船舶航迹的有效控制。

$ {\dot V_1} = {z_1}{z_2} = - {\vartheta _1}z_1^2 + {z_1}{\tilde z_2} 。$

(4)

$ {\dot V_1} $ 为微分后的Lyapunov函数 $ {V_1} $ ，可将式(3)中的前2个状态方程调整为：

$ \left\{ \begin{gathered} {{\dot z}_1} = - {\vartheta _1}{z_1} + {{\tilde z}_2}，\\ \dot {\tilde z} = - \vartheta _1^2{z_1} + {\vartheta _1}{{\tilde z}_2} + {z_3}。\\ \end{gathered} \right. $

(5)

式中，z₃为航迹分布式控制控制器的虚拟输入。

为保障式(4)可以实现，将z₃的期望值设为：

$ {z_{3d}} = \left( {\vartheta _1^2 - 1} \right){z_1} - \left( {{\vartheta _1} - {\vartheta _2}} \right){\tilde z_2} 。$

(6)

选取Lyapunov函数V₂，并表示为：

$ {V_2} = {V_1} + \frac{1}{2}\tilde z_2^2 。$

(7)

此时，可得到Lyapunov函数的导数，用Barbalat定理，状态变量z₁逐渐趋近于0。此时，式(10)的控制输入可以保证航迹分布式控制模型式(2)渐近稳定，以此完成航迹分布式控制控制器的设计，实现船舶航迹的有效控制。

$ {z_{3d}} = - {h_1}{z_1} - {h_2}{z_2}。$

(8)

式中，h为前进控制力。通过该公式，可以使航迹分布式控制模型中的以下部分渐近稳定：

$ \left\{ \begin{gathered} {{\dot z}_1} = {z_2} ，\\ {{\dot z}_2} = {z_3} 。\\ \end{gathered} \right. $

(9)

设 $ {\tilde z_3} = {z_3} - {z_{3d}} $ ，此时可将航迹分布式控制模型式(2)变换为以下形式：

$ \left\{ \begin{gathered} {{\dot {\tilde z}}_1} = {z_2}，\\ {{\dot {\tilde z}}_2} = {{\tilde z}_3} + {z_{3d}}，\\ {{\dot {\tilde z}}_3} = {h_1}{z_2} + {h_2}{z_{3d}} + {h_2}{{\tilde z}_3} + v\left( t \right)。\\ \end{gathered} \right. $

(10)

为式(9)挑选Lyapunov函数，使 $ {V_3} = {V_2} + \frac{1}{2}\tilde z_3^2 $ ，此时，控制输入为：

$ v\left( t \right) = - {\vartheta _3}{\tilde z_3} - {h_2}{\tilde z_3} - \left( {{\vartheta _1} - {h_1}{h_2}} \right){z_1} - \left( {1 + {h_1} - h_2^2} \right){z_2} 。$

(11)

此时，可得到Lyapunov函数的导数，用Barbalat定理，状态变量z₁逐渐趋近于0。此时，式(10)的控制输入可以保证航迹分布式控制模型式(2)渐近稳定，以此完成航迹分布式控制控制器的设计，实现船舶航迹的有效控制。

2 实验结果分析

此时，可得到Lyapunov函数的导数，用Barbalat定理，状态变量z₁逐渐趋近于0。此时，式(10)的控制输入可以保证航迹分布式控制模型式(2)渐近稳定，以此完成航迹分布式控制控制器的设计，实现船舶航迹的有效控制。

分析应用本文方法前后，船舶在前往10个目的地所需航程以及时间，分析结果如表1所示。可知，利用本文方法得到的航行轨迹不仅能够有效避开暗礁等影响，还可以在最大程度下实现最短里程行驶，船舶航行所需时间下降，得到的航行轨迹为最佳轨迹。

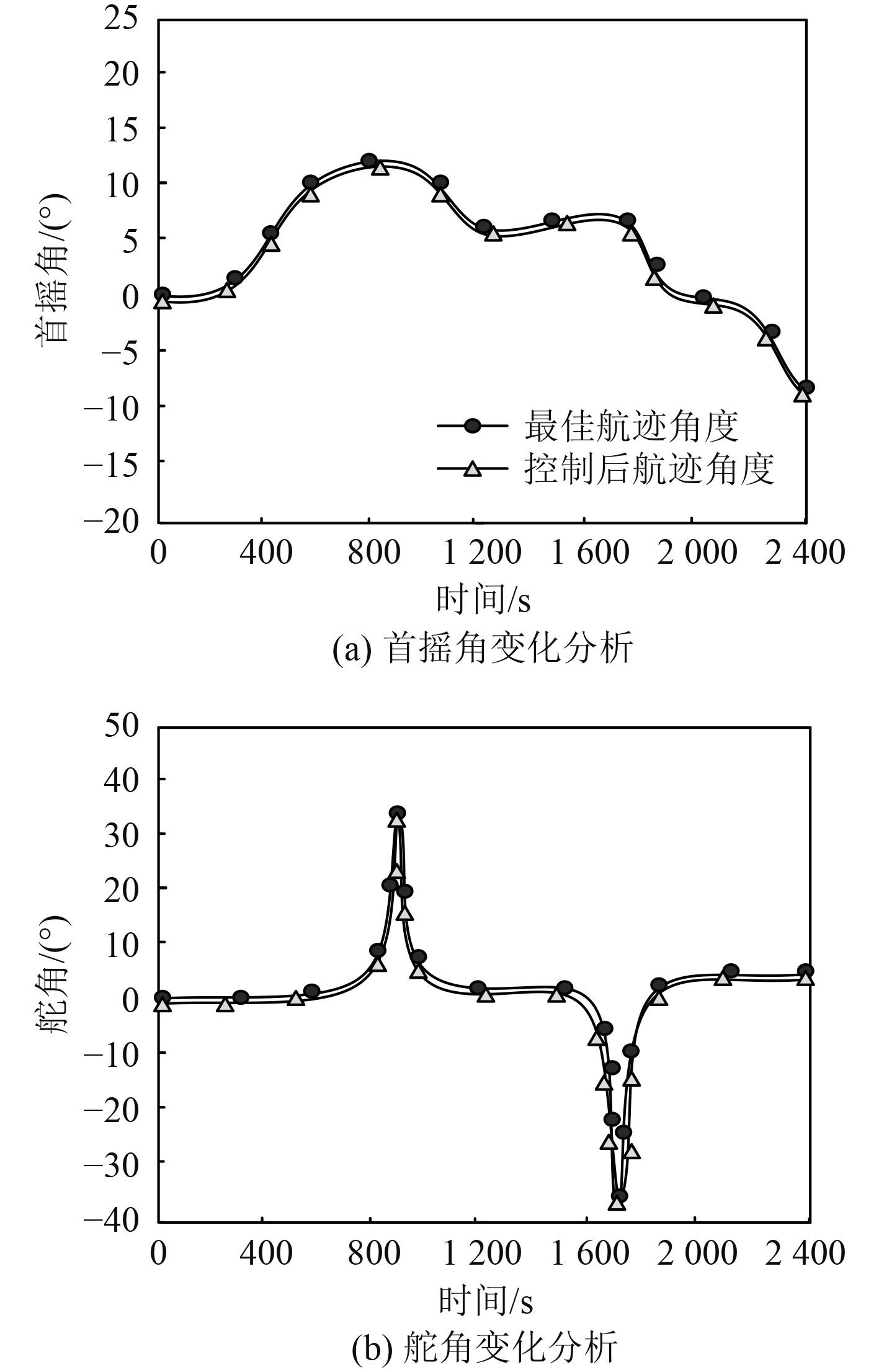
最佳航迹行驶分析结果如图2所示。可知，本文方法可以实现船舶航行过程中的首摇角、舵角控制，使船舶角度更符合最佳角度，以实现最完美行驶角度。

分析船舶从起始位置到目的位置的航迹控制效果，结果如图3所示。可知，应用本文方法后，在坐标轴上船舶从起始位置行驶的航迹能够以最短里程达到目的位置，且在航行过程中遇到的障碍点能够精确躲避，实现安全、合理的航迹形式。

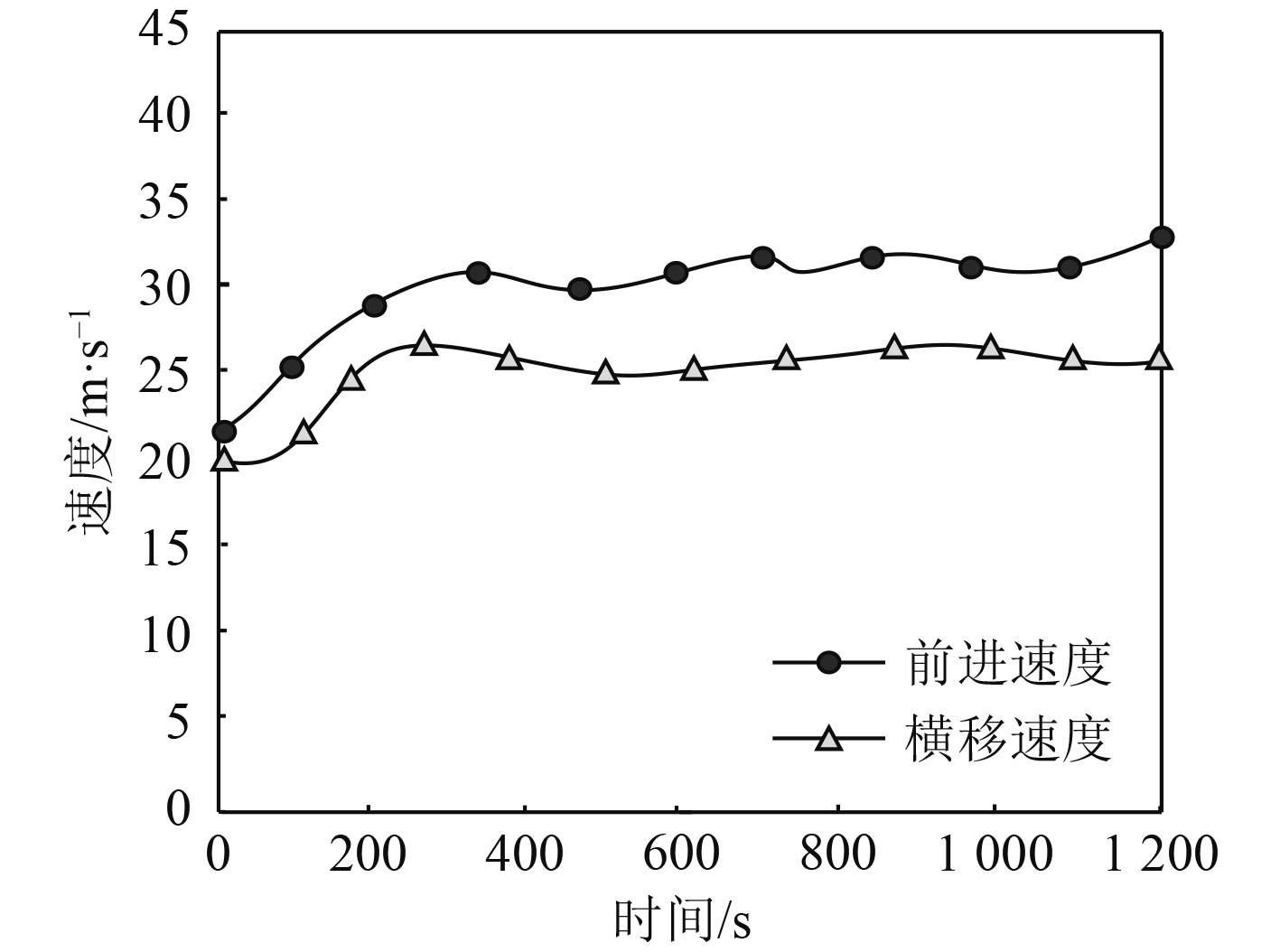
分析应用本文方法控制船舶航行时，在行驶过程中的前进速度与横移速度变化情况，结果如图4所示。可知，随着时间的增加，控制后的船舶前进速度与横移速度出现一定幅度的上升，在之后的行驶过程中，速度始终保持在20 m/s以上，而前进速度要略高于横移速度，这说明船舶在前进过程中更容易被控制，横移速度也始终保持在较高水平，说明经本文方法控制后，船舶的行驶速度始终较快。

3 结　语

本文研究基于关联规则的船舶航迹分布式控制方法，通过实验，验证了船舶航行时的控制效果，能够实现更精准的航迹控制，为船舶行驶提供安全保障。