0 引　言

船舶路径规划指针对船舶航行的起始点以及目的地设计一条安全航行的路线^[1-3]，规划的船舶航行路径应满足船舶碰撞规则需求，同时需要考虑船舶路径规划的经济性以及实时性。船舶从起始点到达目的地的时间应尽量短^[4-6]。由于船舶航行时具有时滞性强以及惯性大的特点，因此船舶航行时的运动状态无法实现大幅度更改。

目前针对船舶路径规划的研究较多，向金林等^[7]将双向RRT方法应用于无人艇局部路径规划中，该方法可以实现无人艇航行过程中局部路径规划，但是不具备全局路径规划性能，应用性能较差；童帮裕等^[8]将改进的蚁群算法应用于船舶航行过程中的冰区路径规划中，但该方法仅适用于冰区船舶航行路径规划，对于其他包含较多障碍物的船舶航行区域，规划性能较差。

针对以上2种方法对船舶航行路径规划时存在的缺陷，研究基于改进神经网络的船舶航行路径规划方法。

1 船舶航行路径规划 1.1 构建船舶航行路径规划模型

用 $ S $ 表示船舶，设船舶属于二维空间中存在航行运动的刚体，通过小波滤波处理后，获取的船舶质心坐标表示为(x_e,y_e)，船舶航行区域表示为 $ {\Omega _f} $ ，由船舶航行区域组成的水域表示为 $ {\Omega _0} $ 。设水域中存在危险区域数量为 $ n $ ，为了满足船舶航行路径规划过程中不存在障碍物的条件，船舶航行路径规划时，路径 $ L $ 中的全部节点与障碍物不存在交集。将船舶航行路径规划问题描述为：寻找一个二元函数f(x,y)=0于二维坐标系中，依据船舶航行路径与障碍物间的距离要求，建立船舶航行路径规划模型表达式如下^[9]：

$ y=d\left( {{X_S}} \right) = \mathop {\min }\limits_{{X_0} \in {\Omega _0}} \left\| {{X_S} - {X_0}} \right\|。$

(1)

船舶航行路径规划问题描述为：搜寻一个二元函数(x,y)=0，满足船舶航行起点、船舶航行终点以及船舶航行路径中均不存在障碍物的条件下，令公式(1)为尽量最大化。

1.2 改进神经网络的船舶航行规划模型求解

BP神经网络是由输入层、隐含层、输出层构成的多层前馈网络。输出层与隐含层的权重增量求解公式如下：

$ \Delta {w_{jk}} = \left( {{d_0}\left( n \right) - {y_0}\left( n \right)} \right){\delta _j}\eta {y_j}f{\left( {ne{t_k}} \right)^\prime } 。$

(2)

输入层与隐含层的权重增量求解公式如下：

$ \Delta {w_{ij}} = \left( {\sum\limits_{k = 1}^L {{\delta _k}\eta {w_{jk}}} } \right){x_i}\eta f{\left( {ne{t_j}} \right)^\prime } 。$

(3)

式中：x_i与y_i分别表示节点 $ i $ 的输入以及输出。δ_k与δ_j分别表示输出层至输入层的误差反向传播信号，η表示学习率， $ f{\left( {ne{t_k}} \right)^\prime } $ 与 $ f{\left( {ne{t_j}} \right)^\prime } $ 分别表示输出层与隐含层传递函数的导数；d_o(n)与y_o(n)分别表示神经网络的期望输出值以及实际输出值。

神经网络输出节点的误差函数表达式为：

$ E = \frac{1}{2}\sum\limits_{o = 1}^q {\eta {{\left( {{d_o}\left( n \right) - {y_o}\left( n \right)} \right)}^2}} 。$

(4)

为了提升神经网络的运算性能，选取修正线性单元ReLU函数替代原神经网络的激活函数。该激活函数可以保证输入数据在大于0时，输入数据与输出数据相同。ReLU函数定义如下：

$ f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {x,x > 0} ，\\ {\lambda x,x \leqslant 0} 。\end{array}} \right. $

(5)

式中， $ \lambda $ 表示调节参数。

为了实现神经网络的快速收敛，选取梯度下降法更新神经网络权重表达式如下：

$ {w_{i + 1}} = {w_i} - \alpha \eta \frac{{\partial C}}{{\partial {w_i}}} 。$

(6)

式中： $ C $ 表示成本函数； $ \alpha $ 与 $ {w_i} $ 分别表示学习率以及节点 $ i $ 的权重。

选取均方根反向传播算法优化神经网络，将神经网络过去时间段各周期获取的梯度平方均值利用变量 $ M\left( {w,{t_0}} \right) $ 存储，实现神经网络求解船舶航行路径规划模型时，学习率的自适应调整。均方根反向传播算法优化神经网络的表达式如下：

$ M\left( {w,{t_0}} \right) = 0.8M\left( {w,{t_0} - 1} \right) + 0.2{\left( {\eta \frac{{\partial E}}{{\partial {w^{{t_0}}}}}} \right)^2}。$

(7)

式中，t₀与 $\dfrac{{\partial E}}{{\partial {w^{{t_0}}}}}$ 分别表示神经网络的训练步骤以及t₀中 $ w $ 的梯度。

通过利用改进神经网络获取船舶航行路径规划模型的最优解，即船舶航行路径规划结果。

1.3 船舶航行路径碰撞检测

碰撞检测中设船舶行驶区域中包含差异形状的动态障碍物以及静态障碍物，利用船舶航行起点至终点的点集组成船舶航行路径，利用线性不等式表示船舶航行过程中的障碍物。当船舶航行路径规划结果中包含约束条件中的路径点坐标时，表示路径规划中存在障碍物；规划结果中不包括约束条件中的路径点坐标时，表示路径规划结果中不存在障碍物。选取改进神经网络进一步实现障碍物的碰撞检测。利用二维有限的笛卡尔坐标系表示船舶航行路径规划范围，设船舶航行区域中包括多个圆形或矩形的障碍物。利用船舶航行区域中矩形障碍物的4个顶点作为船舶航行路径规划的约束条件，利用神经网络建立船舶航行路径规划的矩形障碍物模型。神经网络中矩形障碍物输入与输出之间关系的表达式如下：

$ C_R^t = f\left( {T_R^t} \right) 。$

(8)

将式(8)输出结果作为神经网络中间层的输入数据，通过激活函数获取中间层的输出如下：

$ T_R^t = \sum\limits_{m = 1}^{{G_R}} {O_m^t + {\theta _{TR}}}。$

(9)

神经网络中间层全部节点输出结果与阈值相加，作为神经网络的顶层输入的表达式如下：

$ O_m^t = f\left( {I_m^t} \right)。$

(10)

通过激活函数处理神经网络的顶层输入，获取船舶航行路径规划的路径点与障碍物碰撞结果如下：

$ I_m^t = {w_{xm}}x + {w_{ym}}y\left( {v_{Rx}^t + v_{Ry}^t} \right) + \theta _m^t 。$

(11)

式中： $ C_R^t $ 与 $ T_R^t $ 分别表示时间为 $ t $ 时，神经网络顶层节点的输出与输入； $ O_m^t $ 与 $ {G_R} $ 分别表示中间层节点 $ m $ 的输出以及中间层的节点数量； $ \theta _m^t $ 与 $ I_m^t $ 分别表示输入层第 $ m $ 个节点的阈值与输出； $ {w_{xm}} $ ， $ {w_{ym}} $ 与 $ v_{Rx}^t $ ， $ v_{Ry}^t $ 分别表示输入层节点坐标至中间层的权值以及矩形障碍物速度矢量在x轴以及在y轴中的分量。

障碍物为圆形障碍物时，将约束条件由4个顶点转化为障碍物半径，将神经网络中间层节点的阈值转变为圆形坐标 $ \left( {{\theta _a},{\theta _b}} \right) $ 。 $ C_R^t $ 表示船舶航行路径规划模型中，检测的路径点与障碍物碰撞的神经网络输出。输出值为1时，表示船舶航行路径规划结果中的路径点存在于障碍物中，此时需要返回重新实现船舶航行路径规划；神经网络输出值为0时，表示船舶航行路径规划的路径点并未与障碍物存在碰撞情况。设船舶航行区域存在障碍物数量为 $ Q $ 个，船舶航行路径规划时，需要对全部的障碍物进行碰撞检测，碰撞检测表达式如下：

$ E = \sum\limits_{k = 1}^Q {\sum\limits_{j = 1}^Q {{C_{{R_{kj}}}}} }。$

(12)

式中， $ {C_{{R_{kj}}}} $ 表示船舶航行路径点 $ k $ 与障碍物 $ j $ 碰撞检测时，神经网络的输出结果。

当式(12)输出的碰撞检测结果为0时，表示该路径点为可行状态，船舶航行路径中并未存在障碍物。当式(12)输出的碰撞检测结果大于0时，表示船舶航行路径规划结果中存在障碍物，船舶航行时，可能存在碰撞情况。利用神经网络所建立的船舶航行路径碰撞检测模型可以监测船舶航行路径规划结果是否存在碰撞情况。

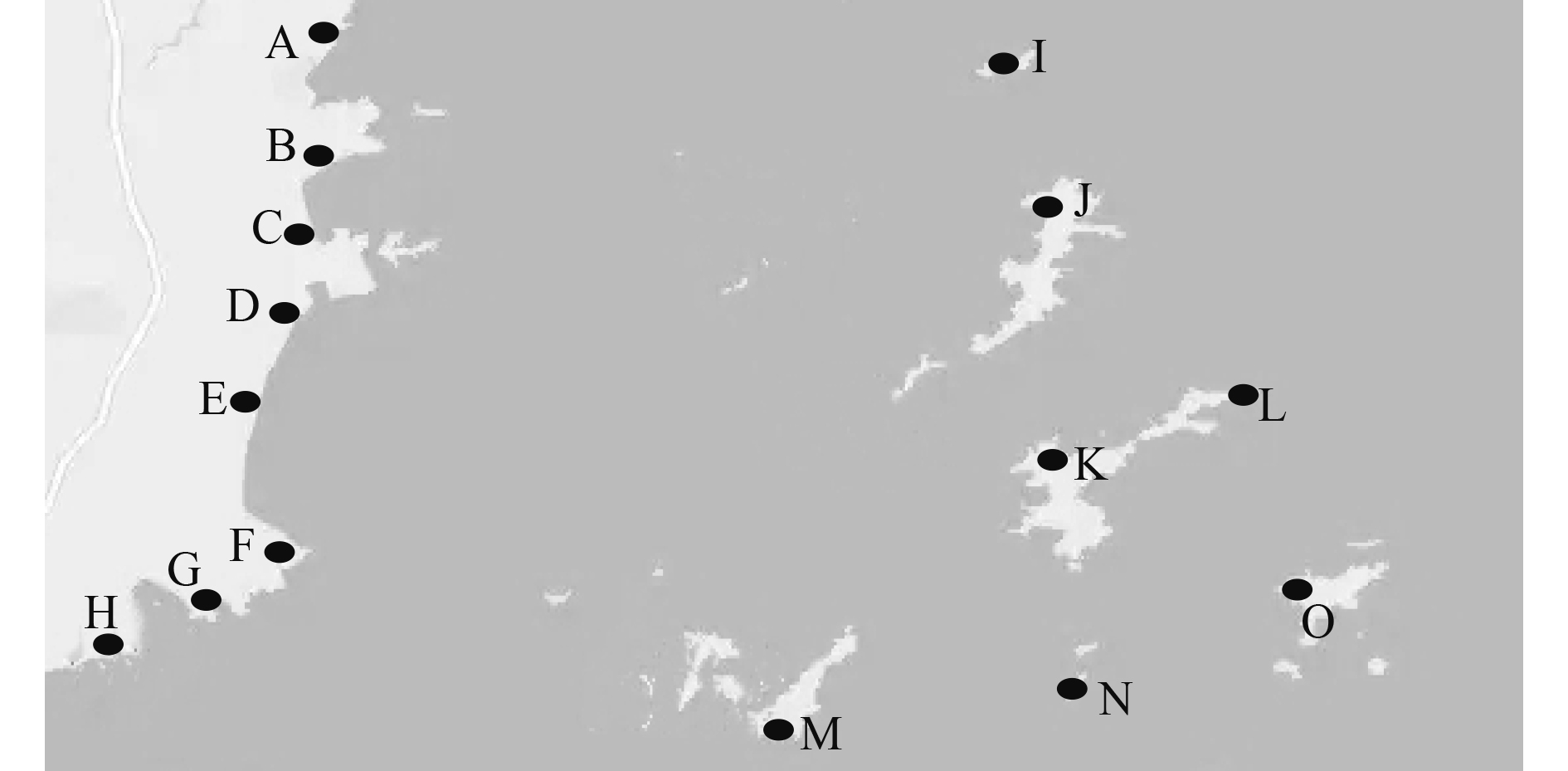
2 实验结果与分析

将该方法应用于某海域的船舶航行路径规划中，利用Matlab软件模拟该海域环境状况，将该海域划分为200个路径节点。设置不同形状的障碍物，船舶航行路径规划海域地形图如图1所示。

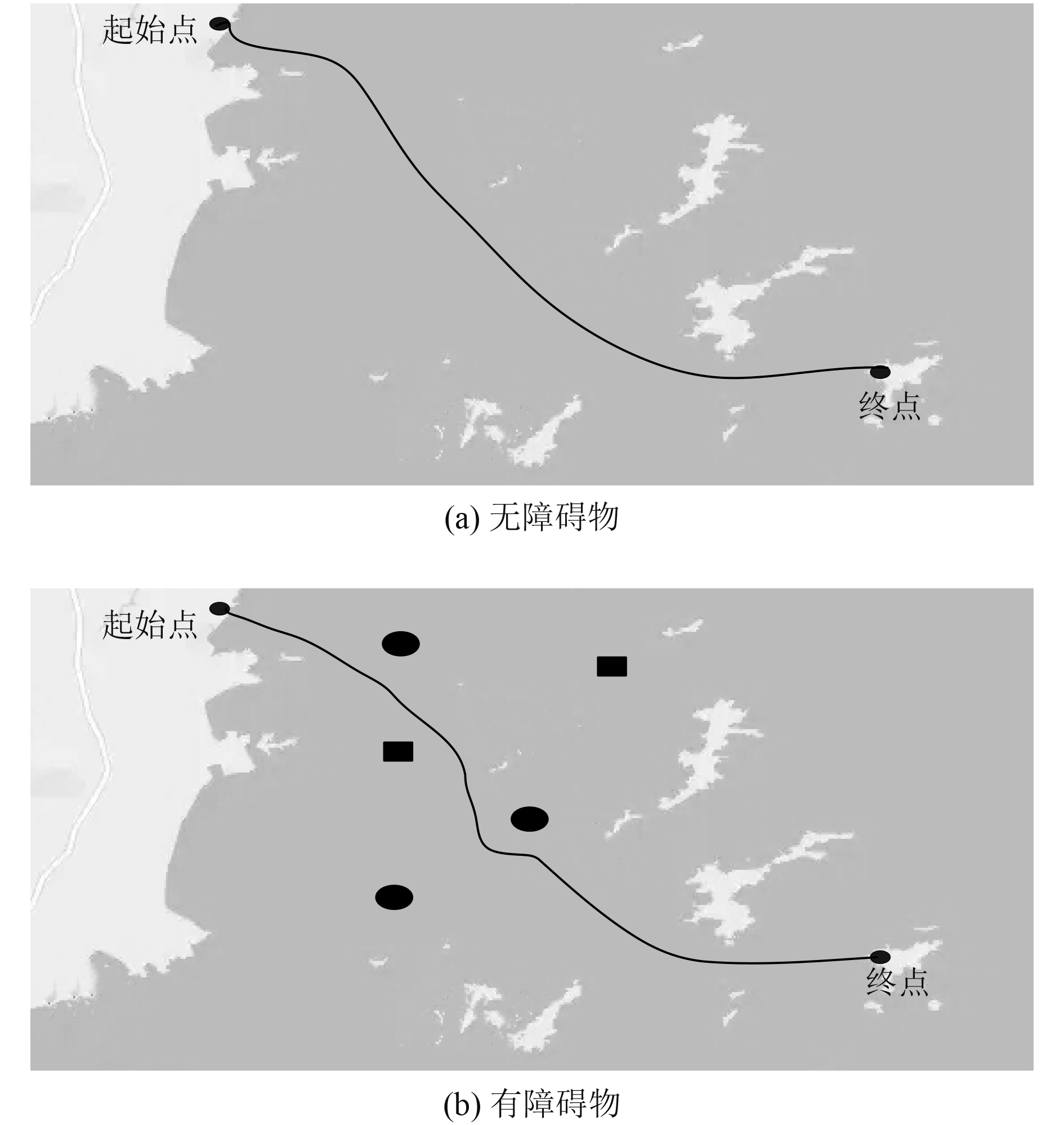
采用本文方法针对图1的船舶路径规划海域进行船舶航行路径规划，无障碍物以及增设障碍物时，船舶航行路径规划结果如图2所示。可以看出，采用本文方法可以实现船舶航行路径的有效规划。本文方法在有障碍物以及无障碍物时，均可以有效规划船舶航行路径。有障碍物时，船舶航行路径规划结果与障碍物存在一定距离，可以保证船舶航行安全性。

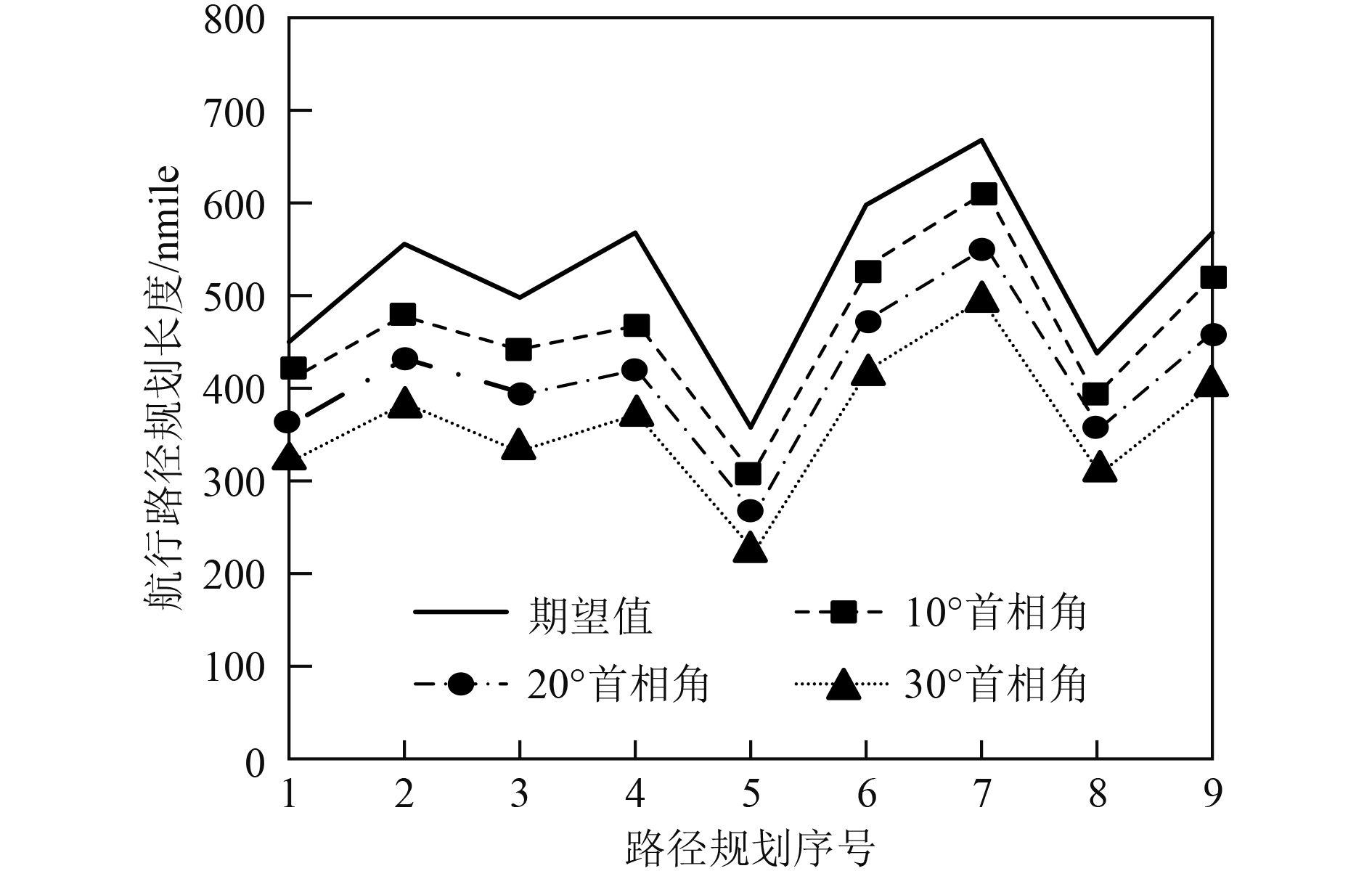
统计采用本文方法规划船舶航行路径，船舶不同首相角时，不同航行路径规划结果中的路径长度变化，统计结果如图3所示。可知，船舶首相角对船舶航行路径的长度存在一定的影响。船舶在不同首相角时，采用本文方法规划的船舶航行路径结果均满足期望值的要求。

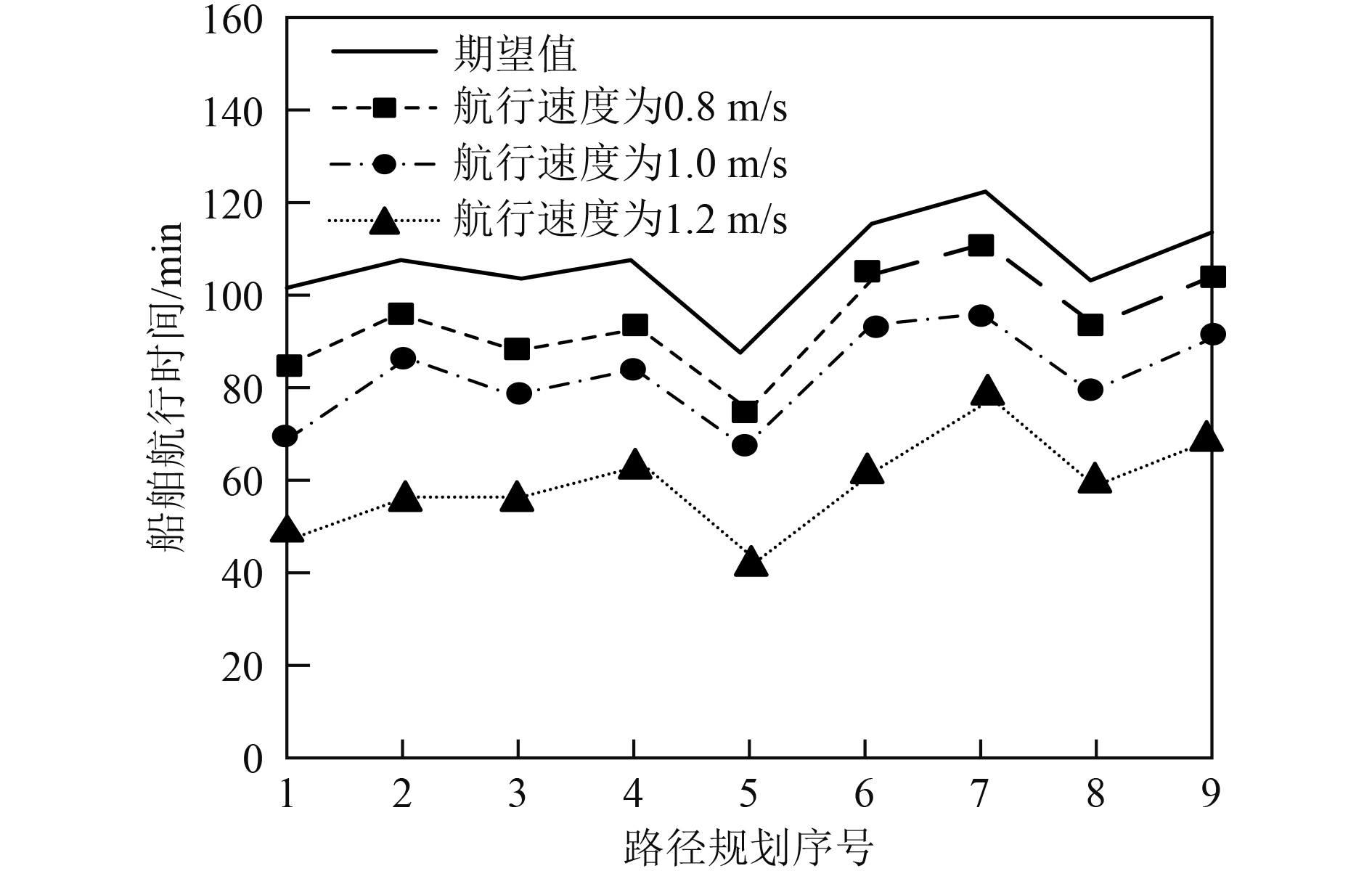
统计采用本文方法规划船舶航行路径，船舶不同航行速度时，船舶依据规划的航行路径，从起始点航行至终点，船舶航行时间统计结果如图4所示。可知，采用本文方法规划船舶航行路径，船舶不同航行速度时，船舶航行时间均低于期望值。验证了采用本文方法规划船舶航行路径，可以保证船舶航行时效性，为船舶安全可靠航行提供理论基础。

3 结　语

利用改进神经网络实现船舶航行路径规划，建立船舶航行路径规划模型，通过改进神经网络求解所建立的船舶航行路径规划模型。获取船舶航行路径规划结果后，利用改进神经网络方法进一步实现船舶航行路径规划的碰撞检测，实现船舶航行路径的有效规划。结果表明实验将该方法应用于船舶航行路径规划中，具有可行性以及有效性。采用该方法规划的船舶航行路径长度可以满足期望需求，未发生障碍物碰撞情况。