2. 中国船舶及海洋工程设计研究院,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
船舶在海上机动航行过程中,在快速回转时,会出现较大横倾,导致航行舒适度的降低,严重时会妨碍船上作业的正常开展。在恶劣海况航行时,由于风浪干扰的影响,船舶横摇剧烈,剧烈的横摇会严重阻碍船上作业,激烈横摇甚至会导致船舶海损及倾覆沉没。
剧烈的横摇除了影响船舶的安全性外,对船舶的适航性、船上设备的正常工作、货物的固定及船员的舒适性也都有很大的影响。对于军舰来说,剧烈的横摇会影响舰载飞机的正常起降,还会使火炮无法精确命中目标, 以至于在战争中处于被动地位。因此,船舶减摇控制成为船舶运动控制技术的一个重要研究方向[1]。
舵鳍联合操纵是20世纪70年代在舵减摇和鳍减摇的基础上兴起的一种综合减摇操纵方式。1972年, Carley 和Duberley首次提出舵鳍联合控制的设想。1981年,Kallstrom[2] 提出采用多变量线性二次型控制理论对舵鳍实施综合控制, 能够在控制航向和减摇两方面同时取得优异的性能, 并且考虑了在横浪作用下的舵/鳍联合控制的调节器设计问题。1990 年开始,Roberts等[3]对船舶舵鳍联合减摇控制展开研究,给出了分离型舵鳍联合减摇系统的数学模型,并用经典的频域分析法设计了舵鳍联合线性控制器。1994年和1995年,一艘装备了舵鳍联合控制器的英国皇家海军护卫舰进行了2次海上试验,Sharif等[4]总结了海试结果,对舵机没进行任何的改造,利用舵辅助鳍减摇,同样可以提高减摇效果[4]。1999年,Sgobbo 和Parsons 联合报道了美海岸警卫队WMEC 901 级舰发展舵鳍联合减摇系统的情况[5]。Tristan Perez等[6]开展了基于模型预测控制的舵鳍联合控制技术研究,在算法中考虑了舵机和鳍机的偏转角度和运转速度物理约束。
金鸿章[7]设计了一种具有积分器的舵鳍联合最优控制器,仿真结果表明该方法可提高自动舵和减摇鳍的性能。于萍[8]将非线性船舶舵鳍联合控制设计问题转化为干扰抑制的H∝线性系统设计问题,设计了状态反馈H∝舵鳍联合控制算法,仿真结果取得了较好的控制效果。田军[9]采用多目标优化理论对二次型线性最优控制器的控制参数进行优化,仿真结果表明舵鳍联合减摇可有效在保证良好航向精度的前提下,取得更好的减横摇效果。
2008年以来,王新屏[10-11]利用MMG建模思想,建模仿真了舵鳍联合非线性数学模型,开展了舵鳍联合简捷非线性鲁棒控制技术研究。2017年,郭亦平等[12-13]等在总结分析文献基础上,开展了舵鳍联合非线性数学模型基础上的舵鳍联合最优控制和模型预测控制算法研究,仿真结果表明提出的舵鳍联合控制具有较强的环境适应性,减摇控制效果良好。
本文在前人研究基础上,利用自航船模,开展恶劣海况下的舵鳍联合控制技术研究和试验验证。试验结果表明,设计的基于动态校正的舵鳍联合最优控制算法,在保证航向控制性能的同时,可提高恶劣海况下减横摇效果。
1 基于动态校正的舵鳍联合最优控制算法设计船舶舵鳍联合的动力学方程可描述为:
| $ \left\{ \begin{gathered} m(\dot u - vr) = X ,\\ m(\dot v + ur) = Y ,\\ {I_{xx}}\dot p = K ,\\ {I_{zz}}\dot r = N 。\\ \end{gathered} \right. $ | (1) |
运动方程为:
| $ \left\{ \begin{gathered} {{\dot x}_0} = u\cos \phi - v\cos \varphi \sin \phi,\\ {{\dot y}_0} = u\sin \phi + v\cos \varphi \cos \phi ,\\ \dot \varphi = p ,\\ \dot \phi = r\cos \varphi 。\\ \end{gathered} \right. $ | (2) |
从式(1)和式(2)抽取出横荡、横摇和首摇方程并线性化后,可得航向控制线性化模型如下:
| $ \left\{ \begin{gathered} \dot v = {a_{11}}v + {a_{12}}r + {a_{14}}p + {a_{15}}\phi + {b_{11}}{\delta _r} + {b_{12}}{\delta _f} ,\\ \dot r = {a_{21}}v + {a_{22}}r + {b_{21}}{\delta _r} ,\\ \dot \varphi = r,\\ \dot p = {a_{41}}v + {a_{42}}r + {a_{44}}p + {a_{45}}\phi + {b_{41}}{\delta _r} + {b_{42}}{\delta _f},\\ \dot \phi = p\; 。\\ \end{gathered} \right. $ | (3) |
由此可构建航向横摇耦合运动控制状态方程为:
| $ \begin{gathered} \dot x = Ax + B\delta ,\\ y = Cx。\\ \end{gathered} $ | (4) |
对船舶运动进行控制时,为了使船舶能够取得满意的控制品质的同时,减少打舵次数,减小出舵角,使舵机平稳运行,故在设计控制器时,必须考虑舵机的影响。同理,也需考虑鳍机的平稳运行要求。因此,在设计控制器时,可考虑将舵机和鳍机的传动方程补充到式(3)中,舵机和鳍机的简化传动模型为:
| $ \left\{ \begin{gathered} {{\dot \delta }_r} = {u_r} ,\\ {{\dot \delta }_f} = {u_f} 。\\ \end{gathered} \right. $ | (5) |
式中:
设置性能指标函数为:
| $ J(u) = \int_0^\infty {({{\boldsymbol {x}}^{\rm{T}}}Qx + {u^{\rm{T}}}Ru){\rm{d}}t}。$ | (6) |
式中,
则有最优状态反馈增益矩阵
得到反馈控制律为:
| $ \begin{split} &{u_r} = - {k_{11}}v - {k_{12}}p - {k_{13}}r - {k_{14}}\phi - {k_{15}}(\varphi - {\varphi _z}) - {k_{16}}{\delta _r} - {k_{17}}{\delta _f} ,\\ &{u_f} = - {k_{21}}v - {k_{22}}p - {k_{23}}r - {k_{24}}\phi - {k_{25}}(\varphi - {\varphi _z}) - {k_{26}}{\delta _r} - {k_{27}}{\delta _f},\\ &K = \left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}&{{k_{14}}}&{{k_{15}}}&{{k_{16}}}&{{k_{17}}} \\ &{{k_{21}}}&{{k_{22}}}&{{k_{23}}}&{{k_{24}}}&{{k_{25}}}&{{k_{26}}}&{{k_{27}}} \end{array}} \right]。\\[-15pt] \end{split} $ | (7) |
由理论分析知,该控制律不能保证航向控制的无静差性,可以通过数学变换将该状态反馈控制律转化为状态变量的变化率的无静差反馈控制律如下:
| $ \begin{gathered} {u_r} = {\mu _{11}}\dot v + {\mu _{12}}\dot p + {\mu _{13}}\dot r + {\mu _{14}}p + {u_{15}}r + {\nu _{11}}(\varphi - {\varphi _z}) + {\nu _{12}}\phi ,\\ {u_f} = {\mu _{21}}\dot v + {\mu _{22}}\dot p + {\mu _{23}}\dot r + {\mu _{24}}p + {u_{25}}r + {\nu _{21}}(\varphi - {\varphi _z}) + {\nu _{22}}\phi 。\\ \end{gathered} $ | (8) |
简记为:
| $ {\boldsymbol{\mu}} = \left[ {\begin{array}{*{20}{c}} {{\mu _{11}}}&{{\mu _{12}}}&{{\mu _{13}}}&{{\mu _{14}}}&{{\mu _{15}}} \\ {{\mu _{21}}}&{{\mu _{22}}}&{{\mu _{23}}}&{{\mu _{24}}}&{{\mu _{25}}} \end{array}} \right] \text{,} {\boldsymbol{\nu}} = \left[ {\begin{array}{*{20}{c}} {{\nu _{11}}}&{{\nu _{12}}} \\ {{\nu _{21}}}&{{\nu _{22}}} \end{array}} \right] 。$ |
由于状态反馈控制律中需要用到
由状态观测器和状态反馈控制律式(8)可得:
| $ \left\{ \begin{gathered} \dot z = Az + B\delta + L(y - Cz),\\ \dot \delta = Kz + {K_0}\delta + {\nu _0}y。\\ \end{gathered} \right. $ | (9) |
式中:
| $ K = \mu (A - LC) \text{,} $ |
| $ {K_0} = \mu B \text{,} $ |
| $ {\nu _0} = \mu L + \nu 。$ |
设动态校正器方程为:
| $ \left\{ \begin{gathered} \dot p = {\alpha _ * }p + {\beta _ * }\zeta ,\\ \xi = \gamma p 。\\ \end{gathered} \right. $ | (10) |
式中:
由式(10)可导出动态校正器中的传递函数矩阵为:
| $ {\boldsymbol{F}}(s) = {\boldsymbol{\gamma}} {(Is - {\alpha _ * })^{ - 1}}{{\boldsymbol{\beta}} _ * } 。$ | (11) |
式中:
| $ \begin{split}{{\boldsymbol{\alpha} _ * }} = \left[ {\begin{array}{*{20}{c}} {{a_1}_ * }&0 \\ 0&{{a_2}_ * } \end{array}} \right] \text{,} {{\boldsymbol{\beta} _ * }} = \left[ {\begin{array}{*{20}{c}} {{\beta _{11}}}&{{\beta _{12}}} \\ {{\beta _{12}}}&{{\beta _{12}}} \end{array}} \right],\\ {{\boldsymbol{\beta _{ij}}}} = {\left[ {\begin{array}{*{20}{c}} 0&{{\beta _1}}&{{\beta _2}}&{{\beta _3}}&{{\beta _4}}&{{\beta _5}}&{{\beta _6}} \end{array}} \right]^{\rm{T}}},\end{split} $ |
| $ {\boldsymbol{\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\gamma _{11}}}&0 \\ 0&{{\gamma _{22}}} \end{array}} \right],{\gamma _{ii}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0&0 \end{array}} \right]。$ |
综合上述状态观测器、最优控制器和动态校正器,可以建立图1所示闭环系统。
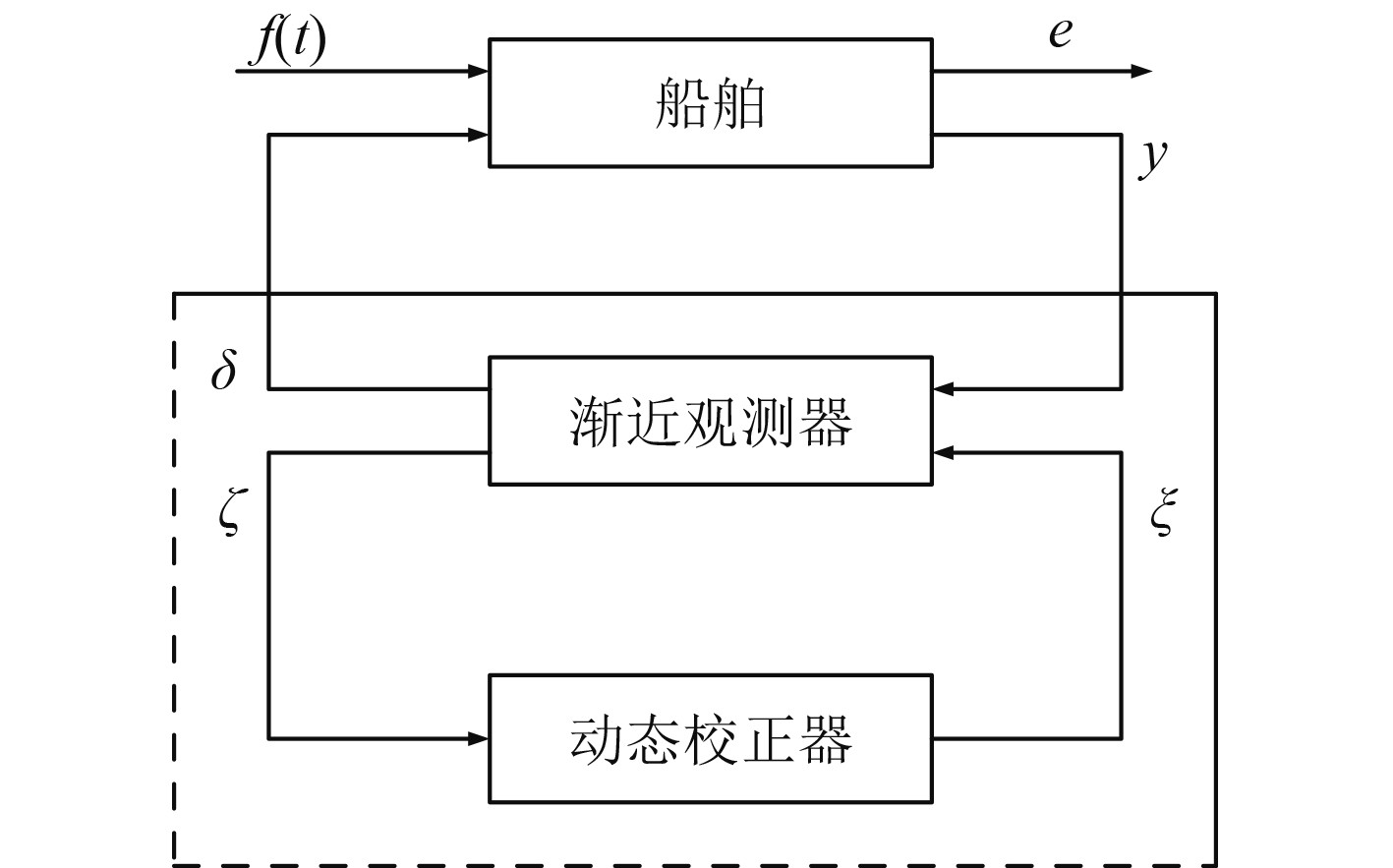
|
图 1 船舶舵鳍联合控制闭环控制方框图 Fig. 1 Close loop control block diagram of rudder/fin joint control of ship |
由线性渐近观测器、控制器和动态校正器方程可组合成一个闭环控制系统如图1虚线框中所示,该系统的状态方程为式(12),量测方程为式(13)。
| $ \left[ {\begin{array}{*{20}{c}} {\dot z} \\ {\dot \delta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {A - LC}&B \\ K&{{K_0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} z \\ \delta \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} L&{{0_{3 \times 1}}} \\ {{\nu _0}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \psi \\ \xi \end{array}} \right],$ | (12) |
| $ \left[ {\begin{array}{*{20}{c}} \delta \\ \zeta \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{0_{1 \times 3}}}&1 \\ { - C}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} z \\ \delta \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&0 \\ 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \psi \\ \xi \end{array}} \right]。$ | (13) |
该闭环系统的传递函数矩阵为:
| $ \left[ {\begin{array}{*{20}{c}} \delta \\ \zeta \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{T_{11}}(s)}&{{T_{12}}(s)} \\ {{T_{21}}(s)}&{{T_{22}}(s)} \end{array}} \right]\left[ \begin{gathered} \psi \\ \xi \\ \end{gathered} \right]。$ | (14) |
记动态校正器的输入-输出关系为:
| $ \xi = F(s)\zeta。$ | (15) |
由式(14)和式(15)可得:
| $ {F_{\psi \delta }}(s) = {T_{11}}(s) + {T_{12}}(s)F(s){\left[ {1 - {T_{22}}(s)F(s)} \right]^{ - 1}}{T_{21}}(s)。$ | (16) |
可得输入-输出传递函数矩阵方程为:
| $ \delta = {F_{\psi \delta }}(s)\psi。$ | (17) |
可以找到一个校正器传递矩阵
| $ {{{{\boldsymbol{F}}}}_{_{\psi \delta }}}(j{\omega _0},{\boldsymbol{F}}) = {\boldsymbol{R}}。$ | (18) |
式中:
舵−航向控制算法和鳍−横摇控制算法的设计类似该舵鳍联合控制算法。
2 自航船模验证试验及结果分析为验证舵鳍联合控制算法的控制性能和品质,在中国船舶及海洋工程设计研究院的试验水池中开展了5级和6级海况下的舵鳍联合控制与舵鳍分别控制对比测试试验。
1) 规则波对比试验
在5级海况下,自航模航速分别为2.846 kn,3.637 kn,进行了规则波横浪、首斜浪自航模航向保持、舵鳍分别控制和舵鳍联合控制的对比试验。
图2和图3为2.846 kn航速、5级海况、横浪航行环境下,舵鳍分别控制试验和舵鳍联合控制试验的相关试验数据曲线。
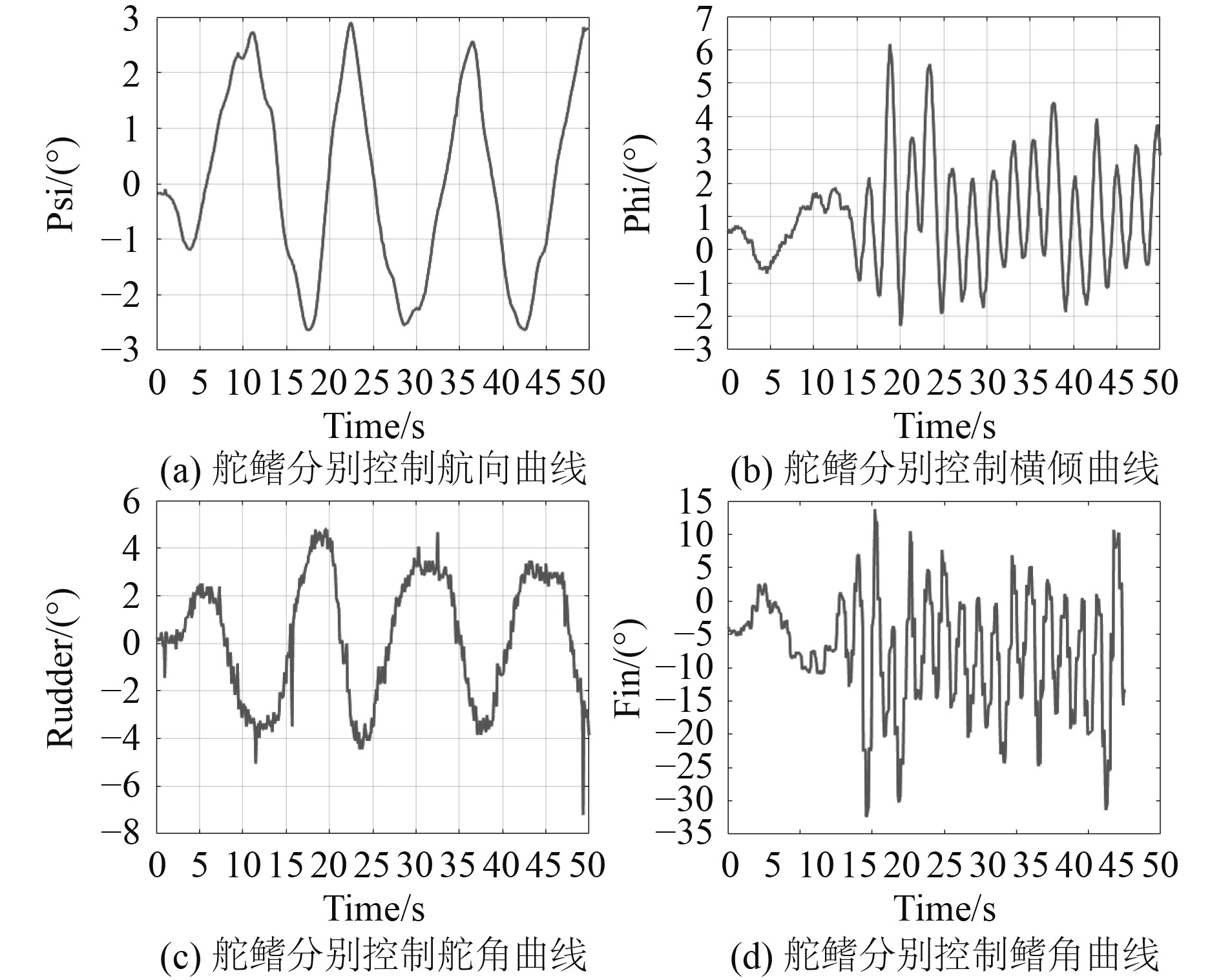
|
图 2 规则波下舵鳍分别控制试验曲线 Fig. 2 Trial curve controlled by rudder or fin alone under regular wave |
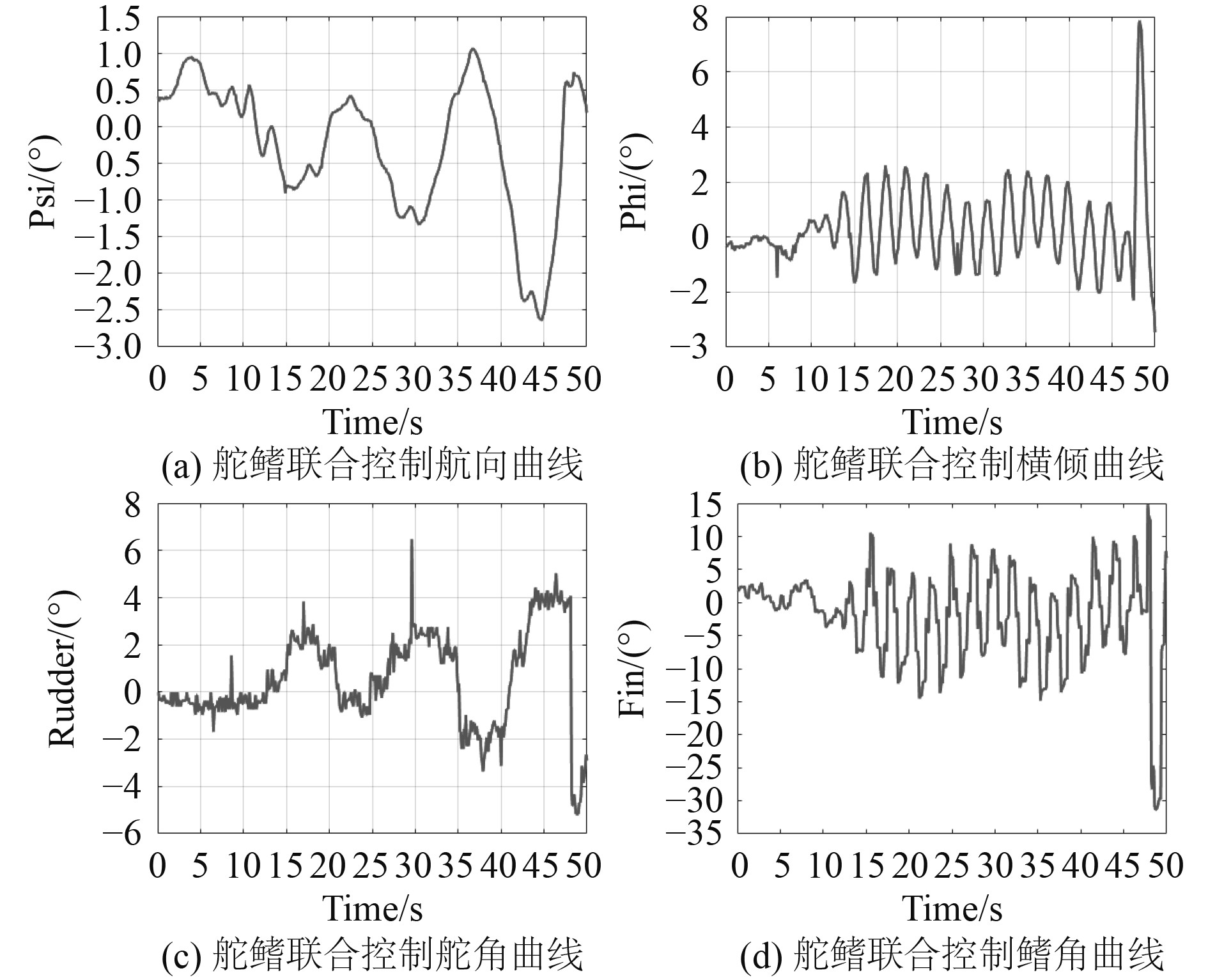
|
图 3 舵鳍联合控制试验曲线 Fig. 3 Trial curve of rudder/fin joint control |
试验统计结果如表1所示。
|
|
表 1 5级海况规则波对比试验统计表 Tab.1 Comparative test statistical table of regular wave at level 5 sea state |
2) 不规则波对比试验
在6级海况下,进行了2.846 kn和3.637 kn航速下横浪、不规则波自航模航向保持、舵鳍分别控制和舵鳍联合控制对比试验。
3.637 kn航速下的航向保持、舵鳍分别控制和舵鳍联合控制对比曲线如图4~图6所示。
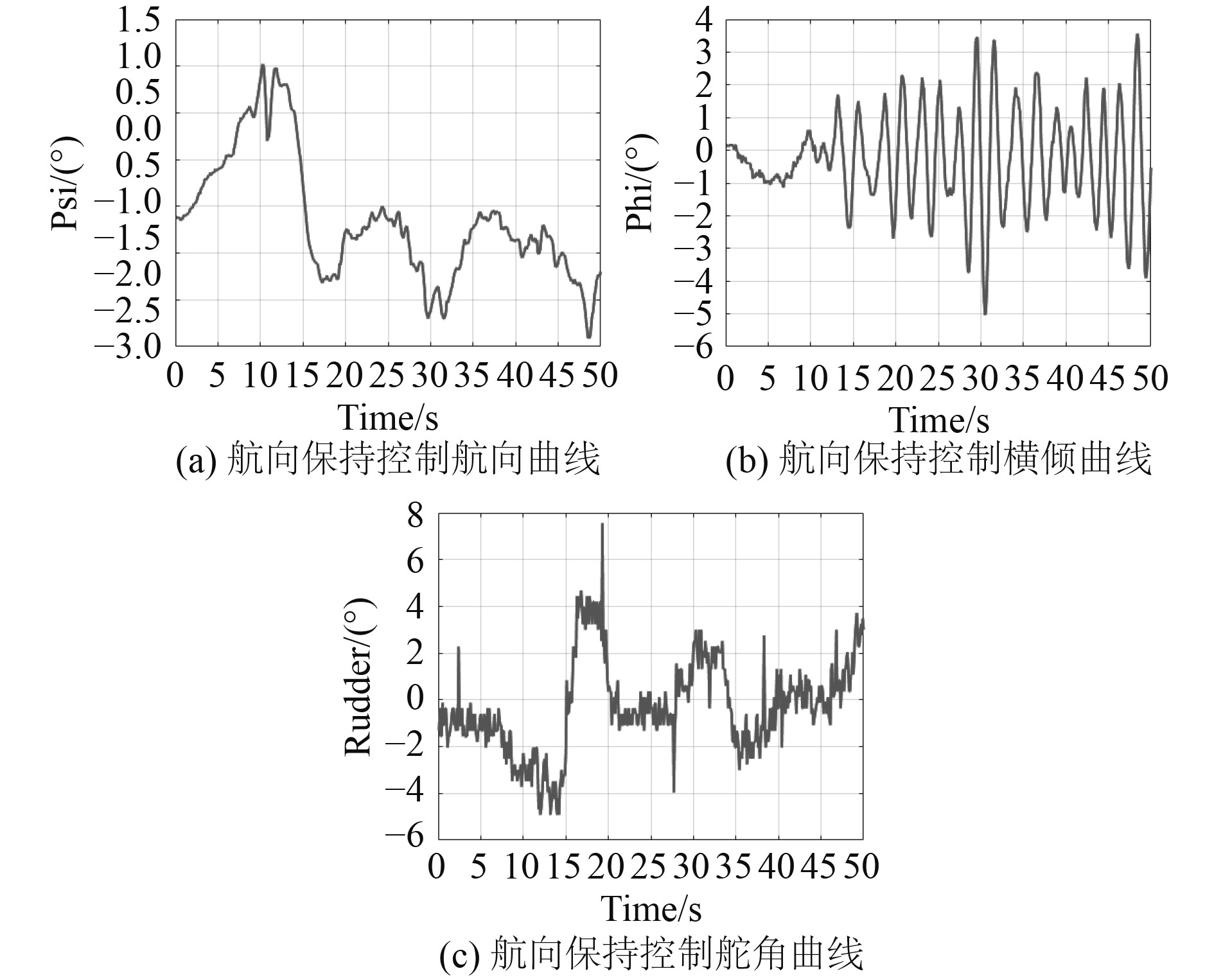
|
图 4 不规则波下航向保持控制试验曲线 Fig. 4 Control test curve of heading keeping under irregular wave |
|
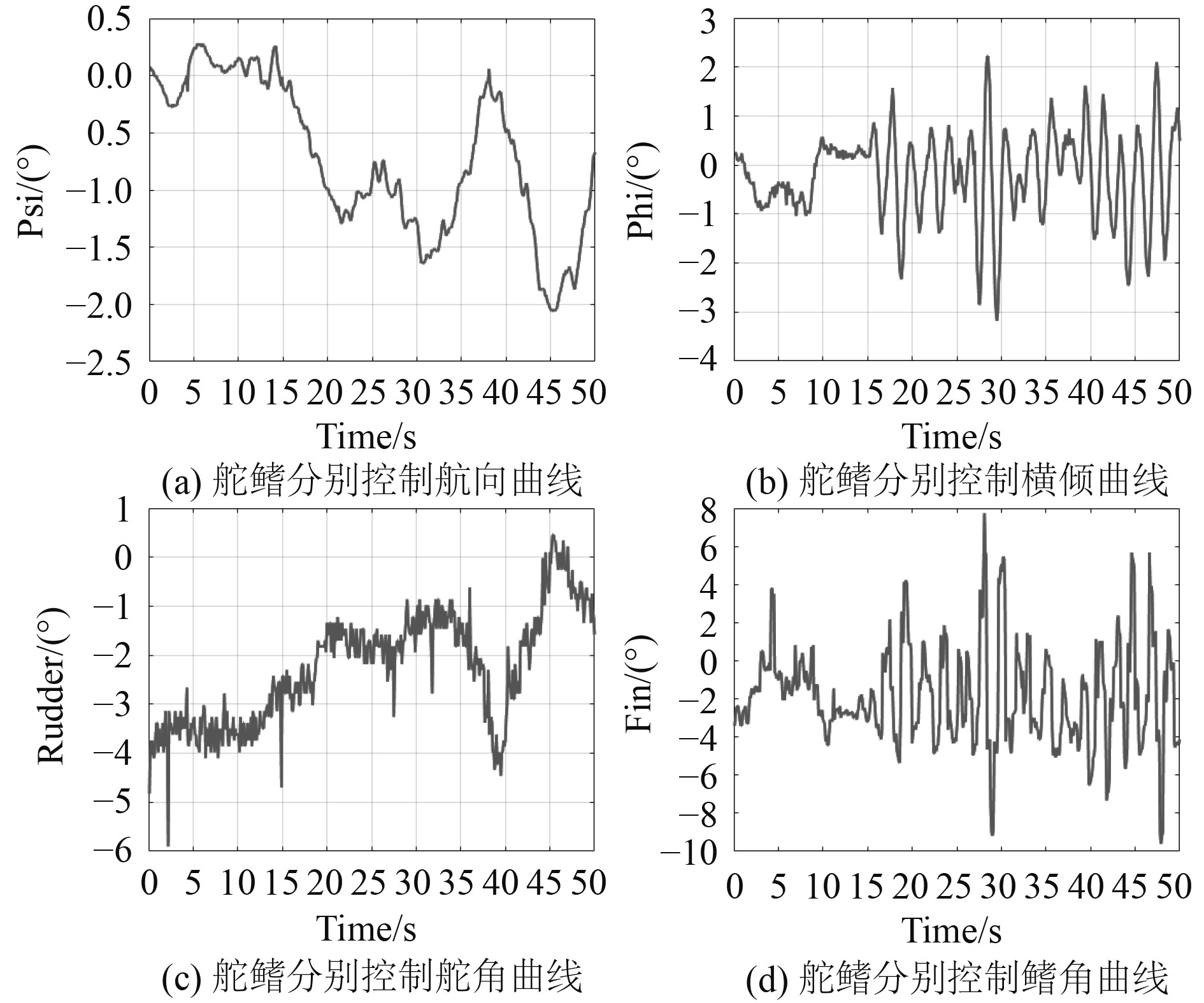
图 5 不规则波下舵鳍分别控制试验曲线 Fig. 5 Test curve controlled by rudder or fin alone under irregular wave |
|
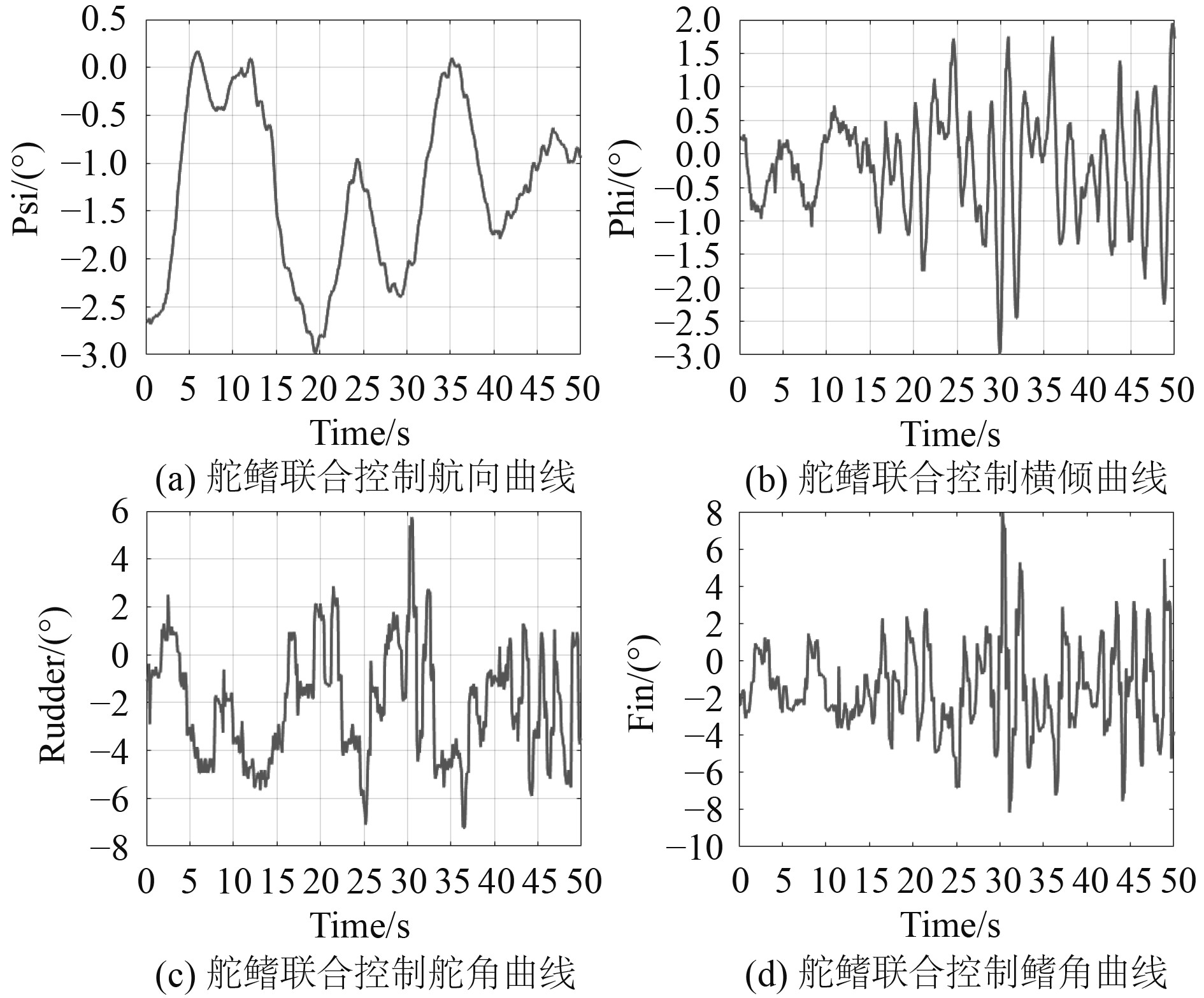
图 6 不规则波下舵鳍联合控制试验曲线 Fig. 6 Test curve of rudder/fin joint control under irregular wave |
由试验性能指标对比表可以看出:
1)舵鳍分别控制方式的航向稳定精度与不减摇时相差不大,说明鳍对航向保持性能的影响极小;
2)舵鳍联合控制方式的减摇率最高、减摇效果最好、比舵鳍分别控制方式的减摇率高5%以上。
3)舵鳍联合减摇控制方式中最大舵角值比不减摇时大,说明该控制方式下鳍减摇起主要作用,舵主要负责航向保持,辅助减摇。
3 结 语本文利用最优控制理论、渐近观测器理论和动态校正理论,提出一种基于动态校正的船舶航向横摇联合控制的最优控制算法,以自航船模为控制对象,开展了5级海况规则波首斜浪、横浪和6级海况不规则波横浪航行环境下的航向保持、舵鳍分别控制和舵鳍联合控制的水池对比试验验证。试验结果表明,与舵鳍分别控制相比,本文提出的舵鳍联合控制方法具有良好的航向保持控制性能和更高的减横摇控制效果。
| [1] |
王新屏, 张显库, 关巍. 船舶舵鳍联合控制的综述[J]. 中国航海 2009(6) 20−25.
|
| [2] |
KALLSTROM C G. Control of yaw and roll by a rudder /fin stabilization system [C]// 6th Ship Control System Symposium, Proc. Vol. 2, Canada, 1981.
|
| [3] |
ROBERTS G N, BRAHAM S W. The control of warship rolling motion using the rudder and the stabilizing fins[J]. Computing and Control Engineering Journal, 1991(2): 49-56. |
| [4] |
SHARIF M T, ROBERTS G N, SUTTON R. Sea- trial experimental results of fin/ rudder roll stabilization[J]. Control Engineering Practice, 1995, 3(5): 703-708. DOI:10.1016/0967-0661(95)00047-X |
| [5] |
SGOBBO J N, PARSONS M G. Rudder/ fin roll stabilization of the USCG WMEC 901 class vessel[J]. Marine Technology, 1999, 36(3): 157-170. |
| [6] |
TRISTAN P. Ship motion control [M]. London: Springe, 2005.
|
| [7] |
金鸿章, 李国斌. 船舶特种装置控制系统[M]. 北京: 国防工业出版社, 1995.
|
| [8] |
于萍. 舵鳍联合鲁棒控制系统研究[D] . 哈尔滨: 哈尔滨工程大学, 2001.
|
| [9] |
田军. 舵鳍联合控制参数优化及仿真[J]. 自动化技术与应用, 2015, 34(7): 9−13
|
| [10] |
王新屏, 张显库, 关巍. 舵鳍联合非线性数学模型的建立及仿真[J]. 中国航海, 2009(12): 58−64.
|
| [11] |
王新屏. 舵鳍联合系统的简捷非线性鲁棒控制[D]. 大连: 大连海事大学, 2009.
|
| [12] |
林超, 郭亦平, 林莉. 舵鳍联合操纵运动数学模型研究[C]// 2017年数字化造船学术交流会议论文集, 2017: 12−19.
|
| [13] |
郭亦平, 林超, 林莉, 等 基于MPC的舵鳍联合操纵控制算法研究[C]// 2017年数字化造船学术交流会议论文集, 2017: 269−273.
|
| [14] |
Katsuhiko Ogata. 现代控制工程(第四版)[M]. 电子工业出版社, 2003.
|
 2022, Vol. 44
2022, Vol. 44
