船舶是精密的机电液一体化设备,在航行时,振动问题的发生会使轴段以及连接附件断裂,对于船舶的安全航行造成不利影响。为提高船舶海上航行的安全性,要对推进轴的扭转振动问题全面分析,对超出安全范围的要进行减振避振处理。本文对船舶海上航行推进轴瞬态扭转振动响应展开研究。
1 船舶推进轴扭转振动有限元分析本文利用有限元法对船舶推进轴的扭转振动进行分析。依托有限元分析软件,构建弹簧与质量模型,确定约束条件,模拟多自由度振动系统,其中质量单元选用MASS21,弹簧单元选用的是COMBIN14,推进轴扭转振动的前6阶频率依次为40.663 Hz,70.429 Hz,87.711 Hz,202.30 Hz,224.20 Hz,311.96 Hz。对有限元分析结果进行换算,并以Holzer法进行比较,结果显示误差在1%以内。在自振频率的计算中,Holzer是比较成熟的一种方法,因此,采用有限元软件计算自振频率具有可行性。与Holzer法相比,有限元软件不会出现漏根的情况,计算结果的精确度得到显著提升,不仅如此,有限元软件的计算速度要比Holzer法快很多,计算效率随之提高。利用有限元分析软件中相关命令LIST,可对各个节点的扭转角及力矩情况进行查看,第一阶频率为40.663 Hz时的扭转角为0.37620,0.13145,0.12747和0.11649,与扭转角相对应的惯性力矩为–0.14685E+06,–9267.1,–8653.7,–22150;第二阶频率为70.429 Hz时的扭转角为–0.10330,0.98305E-01,0.10086,0.10617,与扭转角对应的惯性力矩为0.12096E+06,–20790,–20540,–60560。经过有限元分析软件处理后,能够清楚地看到各阶频率上,不同节点位置处的扭转角对应的惯性力矩,计算结果的误差在1%以内。由此说明,利用有限元分析软件,计算轴系振动特性具有良好的可行性。
2 船舶海上航行推进轴瞬态扭转振动响应 2.1 选择实体模型在轴系自由振动的计算中,可以对有限元分析软件加以利用,与Holzer法相比,有限元分析软件的效果更好。然而,有限元分析软件的建模过于简单,其中能够反映的信息量并不是很多,这对于结果分析造成一定的影响。为获得更多与轴系应力分布有关的信息,要根据船舶推进轴系的特点,选择一个实体模型。为使轴系实体模型满足应用需要,通过BEAM188单元建模,之所以选择该单元主要是因为它有6个自由度,能够满足不同的振动要求,利用不同的截面形状,可对直径的轴系结构加以模拟。船舶柴油发动机的轴系支撑为橡胶轴承,其突出的特点是硬度适中,能有效降低船舶航行过程中的轴系振动,试验阶段可用各种不同的材料改变轴系的特征参数。本文选择的船用柴油机轴系为CW6200ZC,分别设置船尾轴系前后轴承,并在有限元分析软件中,借助COMBIN14单元对轴承进行模拟。由于船舶的齿轮箱与轴系间存在弹性支撑,据此可以通过设置弹簧对曲轴输出法兰进行减震。船尾轴系中的联轴器的刚度及惯量,可采用加粗梁单元直径的方法进行模拟,因船舶螺旋桨本身的形状具有复杂性的特点,为便于研究,对螺旋桨外形予以简化,只按照叶片的数量、直径和材质构建实体模型,据此模拟螺旋桨的变形情况。具体的建模参数如下:曲轴选用的材料为CT45,弹性模量为2.06E+11 Pa,密度为7.90E+03 kg/m3,泊松比为0.30;中间轴的材质选用的是钢35#焊接件,弹性模量为2.12+11 Pa,密度为7.87E+03 kg/m3,泊松比为0.291;飞轮选用的材料为HT200,弹性模量为1.48E+11 Pa,密度为7.20E+03 kg/m3,泊松比为0.31;螺旋桨选用的材料为CU4,弹性模量为2.06E+11 Pa,密度为7.50E+03 kg/m3,泊松比为0.34;联轴器选用的材料为ZG35#,弹性模量为2.12E+11 Pa,密度为7.87E+03 kg/m3,泊松比为0.291。结构阻尼的取值均为0.05,试验过程中,仅保留轴线的ROTX自由度,共计建立499个节点,截面形式选用8种,弹簧单元为10个。实体建模情况如图1所示。

|
图 1 船舶推进轴系整体建模与轴承建模及约束条件有限元实体模型 Fig. 1 Integral modeling and bearing modeling of marine propulsion shafting and finite element solid model of constraints |
船舶推进轴的振动情况与外界激振力矩的大小有极为密切的关联,此外,还与自身特性有关。激振与固有频率相同,会引起共振,在这个状态下,对船舶推进轴的危害性最大。因此,在对船舶推进轴扭转振动研究的过程中,主要是对轴系共振时的振动特性进行研究,通过模态分析,可以得到推进轴的自振频率,由此能够为共振特性的分析提供参考依据。本文选用的船舶轴系为CW6200ZC实体模型,在对它的扭转振动进行模态分析时,将精度确定为0.1,取前6阶频率。由于第一个频率为刚体振动频率,它的值为0,所以不需要考虑。其余各阶的频率值取前3阶,对转角及应力加以分析,3阶的频率依次为20.842 Hz,46.896 Hz和62.164 Hz。当频率为20.842 Hz时,曲轴自由端瞬时针最大转角为0.117 298 rad,该角度出现在一二缸主轴颈与曲柄臂交界的位置处。而逆时针的最大转角为0.027 493 rad,出现在螺旋桨的桨叶位置处。从分析中能够看出,转角呈现出减小的态势,这与一阶振动振幅的特点完全相符。在螺旋桨的桨叶位置处出现了最大应力,一缸曲柄臂处出现最小应力,中间轴承受的应力比较大。当频率为46.896 Hz时,顺时针最大转角出现在一二缸主轴颈与二缸曲柄臂处,转角为0.136 rad,逆时针最大转角出现在飞轮处,转角为0.101 855 rad。由分析结果可知,扭转角的方向发生2次变动,为二阶振动,出现最大应力的部位为转角为0的点。当频率为62.164 Hz时,振动类型有3种,最大振幅出现在螺旋桨叶片的端部,但螺旋桨的变形情况有所差别,振型却相同,由此说明同频率下,不同的振型具有一定的相似性。3种振型的最大应力全部出现在桨毂处,只是应力的大小有所区别,但彼此之间相差并不是很大。通过对前3阶频率进行扭转振动分析后得出如下结果:主轴颈与曲柄臂连接位置处的应力较大,为减小该部位的应力,可用倒角或是圆角过度。同时,为减小轴系振幅,可在自由段增设减振器。
在对船体的推进轴震动进行分析时,需要借助ADC对传感信号进行采样。在ADC采样系统中通过信噪比的大小来定义传感信号的保真度。因此可以通过传感器对震动信号的幅度进行采集,然后由ADC转换获得数字信号,再由计算机进行高效的分析。常见的ADC采样输出表达式为:
| $ SNR = 10\log \frac{{{P_s}}}{{{P_n}}} 。$ |
因此,在传感器端可以获得输入信号为VFS,其信噪比公式为:
| $ SNR = 10\log \frac{{{P_s}}}{{{P_n}}} = {2^N}\sqrt {\frac{3}{2}} \approx \left( {6.02 \cdot N + 1.76} \right){\rm{dB}} 。$ |
在信号采集过程中,可以采用过采样的方式进行信号处理,即当采样速度足够快,那么传感器就可以获得更高的信噪比信号,其表达式为:
| $ SNR = {2^N}\sqrt {\frac{3}{2}} \cdot \sqrt {OSR} 。$ |
实践表明,通过稳态分析能够对轴系的振动特性进行分析,由此得出的结果与外界激励无任何关联。但是推进轴作为船舶动力装置的重要组成部分之一,它的振动主要是在内燃机周期性激振力及力矩的作用下发生。为对船舶推进轴的强迫振动特性做系统研究,要分析推进轴的谐响应。谐响应分析的特点有:可分析周期性激励下的轴系振动;分析过程为稳态响应,能够为轴系抗疲劳及损坏强度的判断提供依据。借助有限元分析软件,开展振动谐响应分析时,可按已知频率的谐波载荷计算出响应情况,依据多种荷载分析结果,以此为基础,分析推进轴的谐响应。具体做法如下:
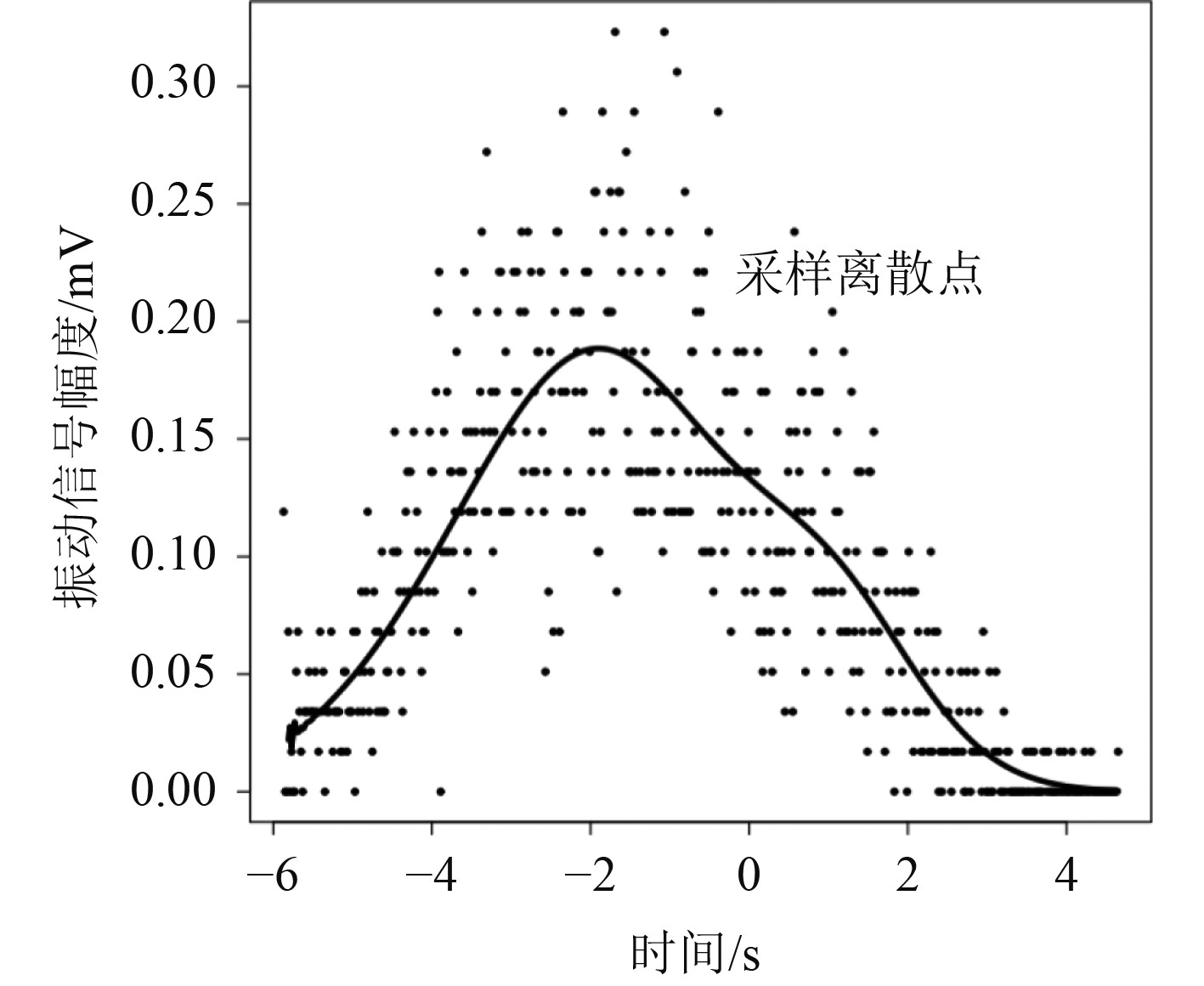
船舶内燃机处于正常运行时,气缸会按发火顺序做功,本次研究中的船舶柴油机为6缸设备,它在做功的过程中,会按照一定的顺序,如1-5-3-6-2-4。每个缸做功时,都会对振幅产生一定程度的影响。缸的最大扭矩为1000 N·m,振动频率从0~200 Hz不等,频率的变化方式为Ramped。船舶推进轴系中螺旋桨振幅随时间变化曲线如图2所示。
|
图 2 船舶推进轴系中螺旋桨振幅随时间变化曲线示意图 Fig. 2 Schematic diagram of the variation curve of propeller amplitude with time in ship propulsion shafting |
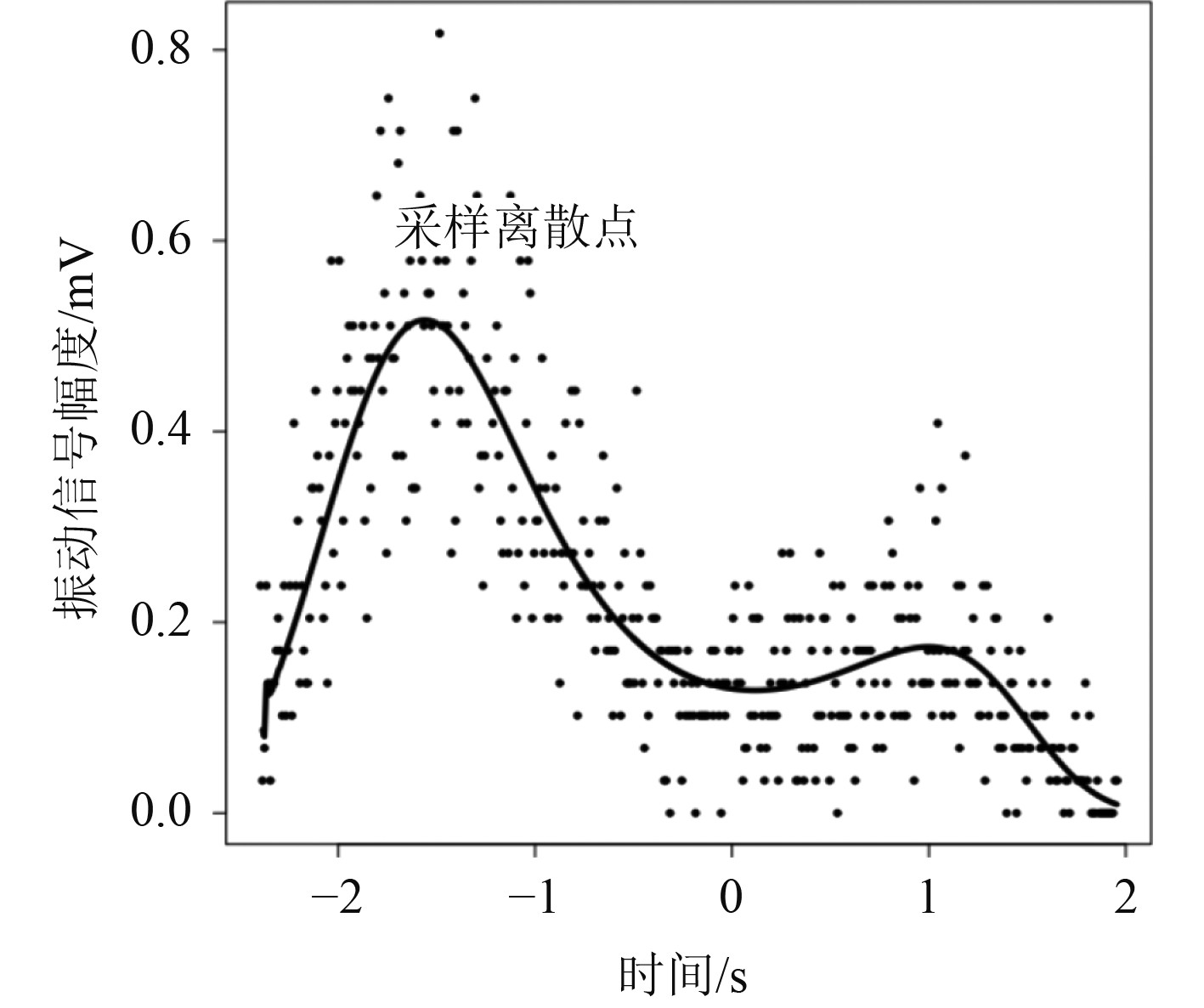
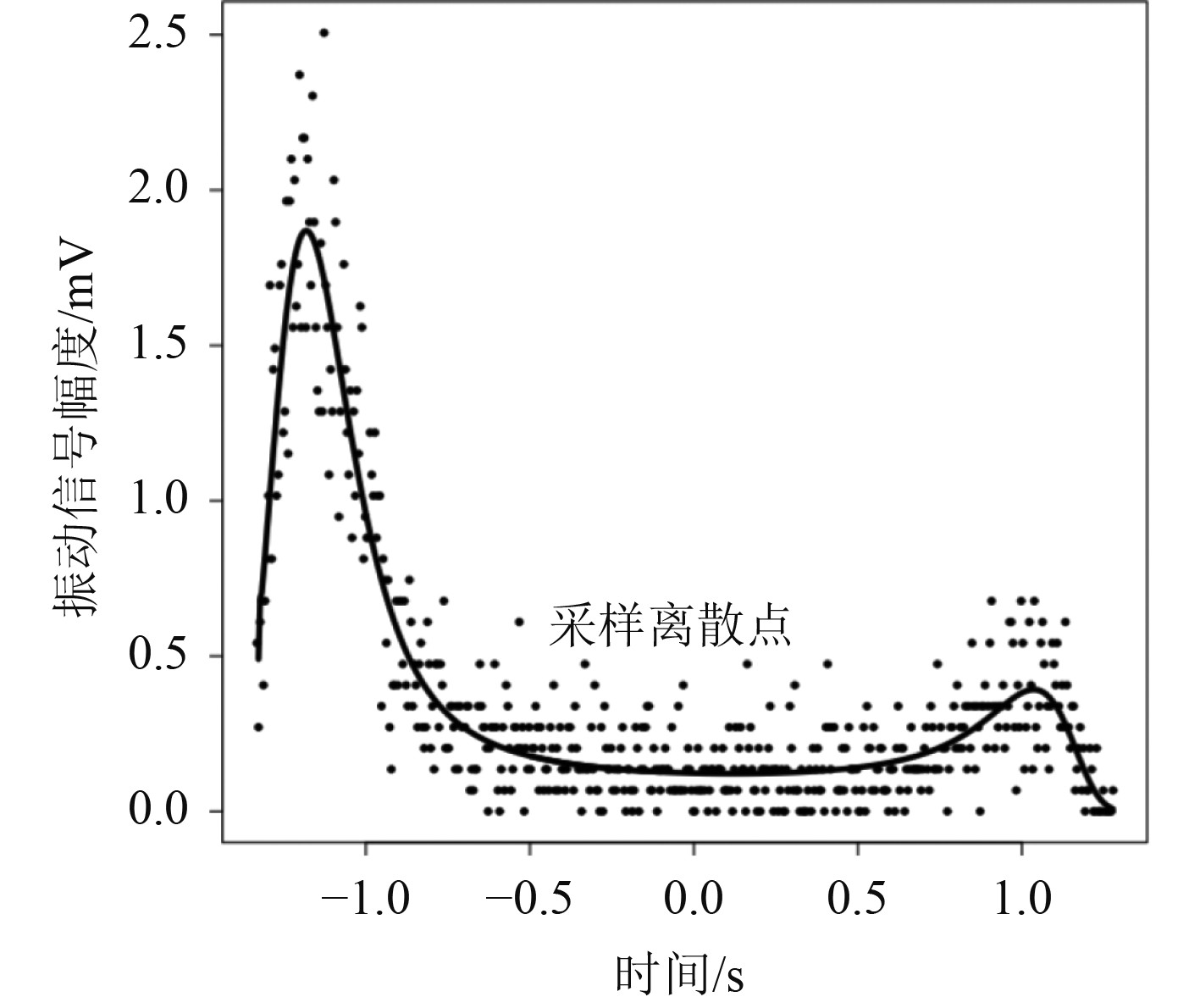
对于船舶内燃机而言,各气缸的激励情况并不完全相同,在误差允许范围,可以存在激励不均匀的现象。因激励不均匀会导致扭振特性发生恶化,所以二冲程柴油机各缸激振力矩的差能够达到5%左右,而四冲程柴油机的误差则会达到10%左右。以船舶柴油机的曲轴轴系作为研究对象,对不同气缸激振力矩作用进行调整,分析发火不均匀对扭振振幅的影响,振幅变化以曲线的形式表现,推进轴阻尼比为0.05时第一质量振动变化曲线如图3所示,船舶柴油机曲轴轴系发火不均匀时各气缸的振幅值如图4所示。
|
图 3 推进轴阻尼比为0.05时第一质量振动变化曲线示意图 Fig. 3 Schematic diagram of the first mass vibration change curve when the propulsion shaft damping ratio is 0.05 |
|
图 4 船舶柴油机曲轴轴系发火不均匀时各气缸的振幅值 Fig. 4 Amplitude value of each cylinder in case of uneven ignition of crankshaft shafting of marine diesel engine |
所以交替变化产生的影响,要比连续变化产生的影响小很多。不仅如此,交替变化时,各个气缸的激振相差越多,后面气缸的振动幅度影响就越大。
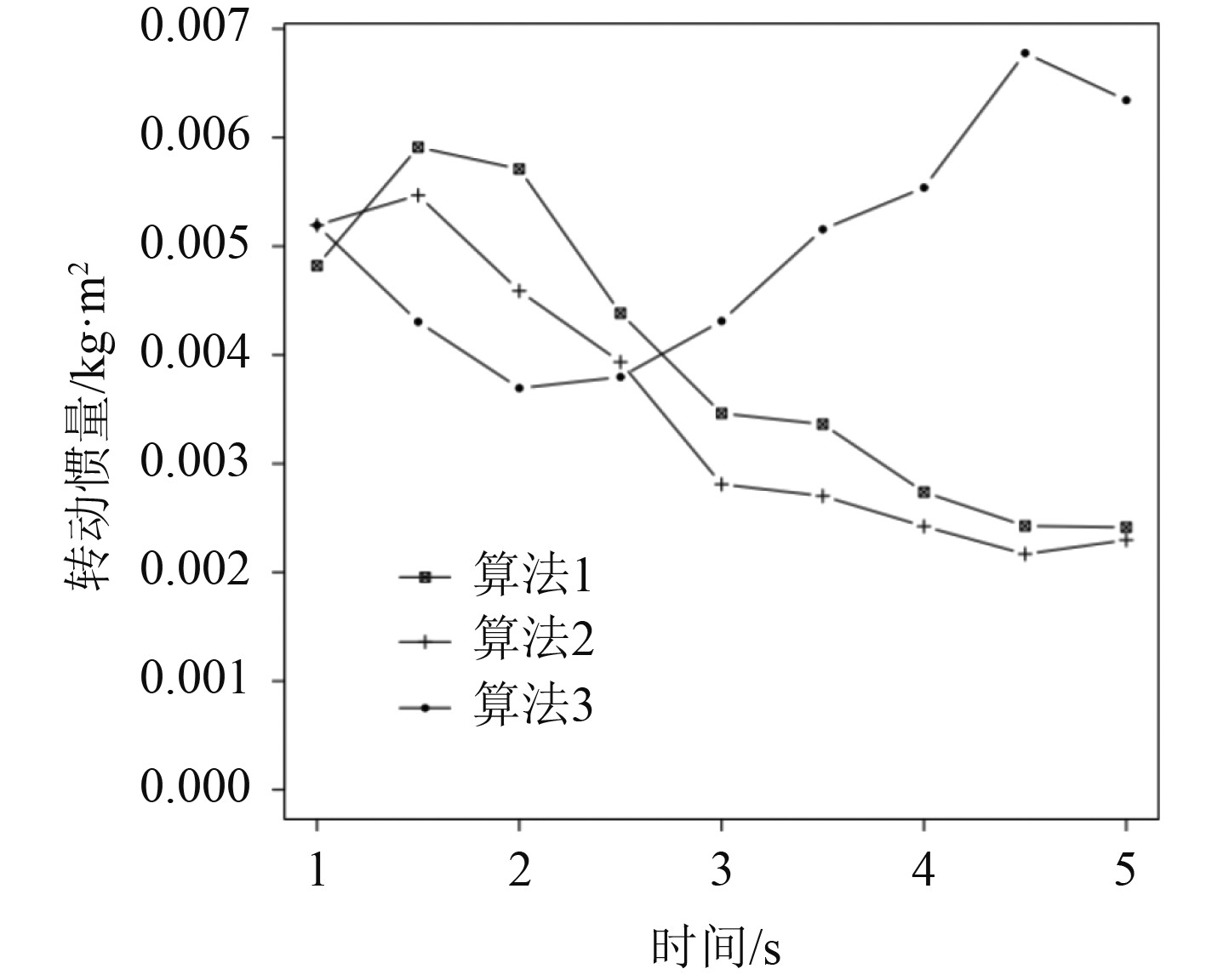
本次研究中选用的船舶柴油机为CW6200ZC,以其曲轴作为研究对象,通过分析后得出单杠转动惯量,通过Matlab软件绘制出变化曲线,柴油机曲轴不同算法下的转动惯量曲线如图5所示。
在不同的算法下,转动惯量的结果有所差别,当转角为230°时转动惯量达到最大值,二者的差约为3。随着误差的累计,使扭振特性发生改变,基于此,以瞬时动能计算所得的结果准确性更高。
|
图 5 柴油机曲轴不同算法下的转动惯量曲线示意图 Fig. 5 Schematic diagram of moment of inertia curve of diesel engine crankshaft under different algorithms |
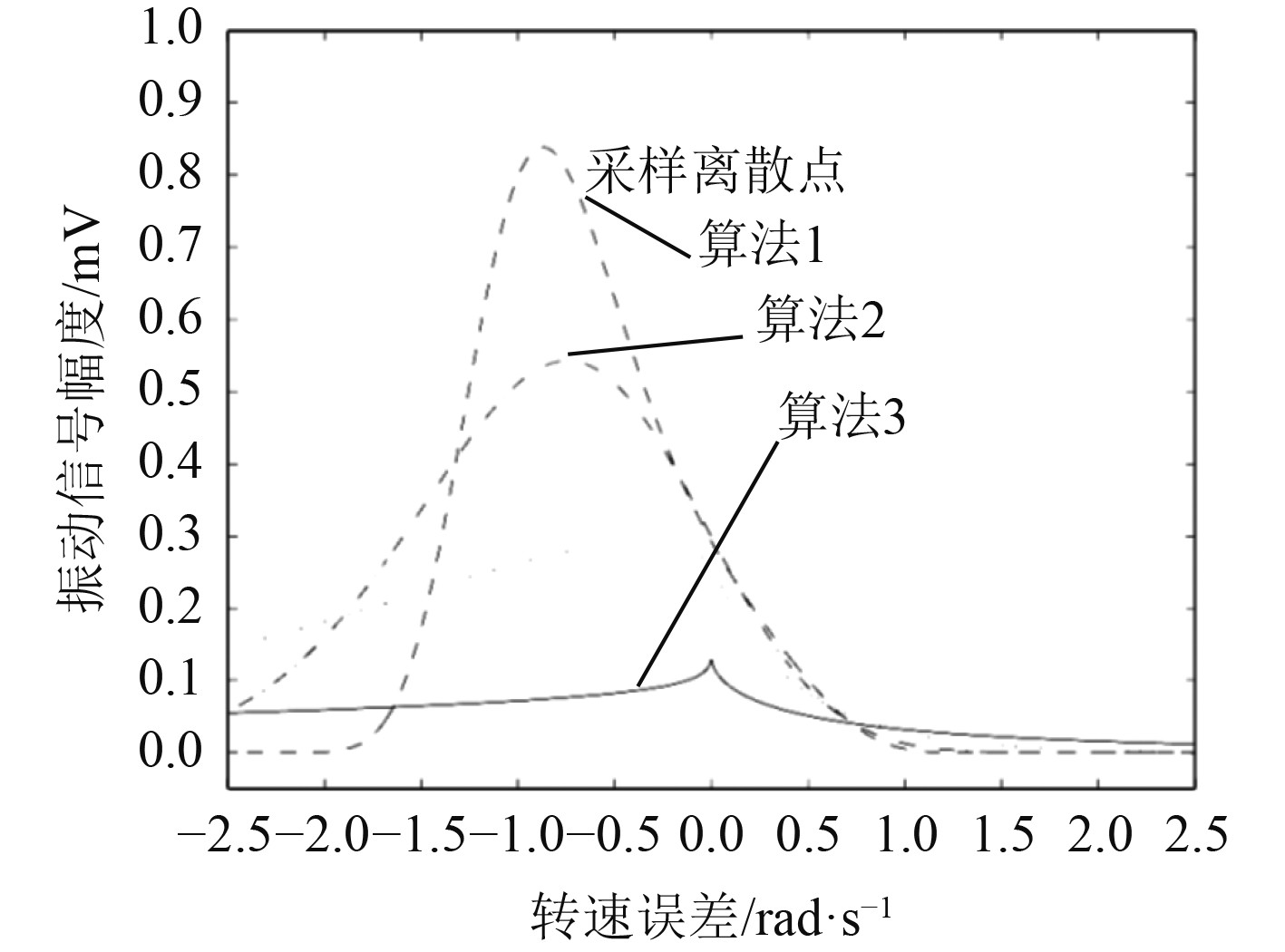
船舶拖轮轴系的螺旋桨螺距具有可变的特点,本次研究中的柴油机功率为1100 kW,调距桨第一质量下振幅与转速曲线如图6所示。
|
图 6 调距桨第一质量下振幅与转速曲线示意图 Fig. 6 Schematic diagram of amplitude and speed curve of controllable pitch propeller under the first mass |
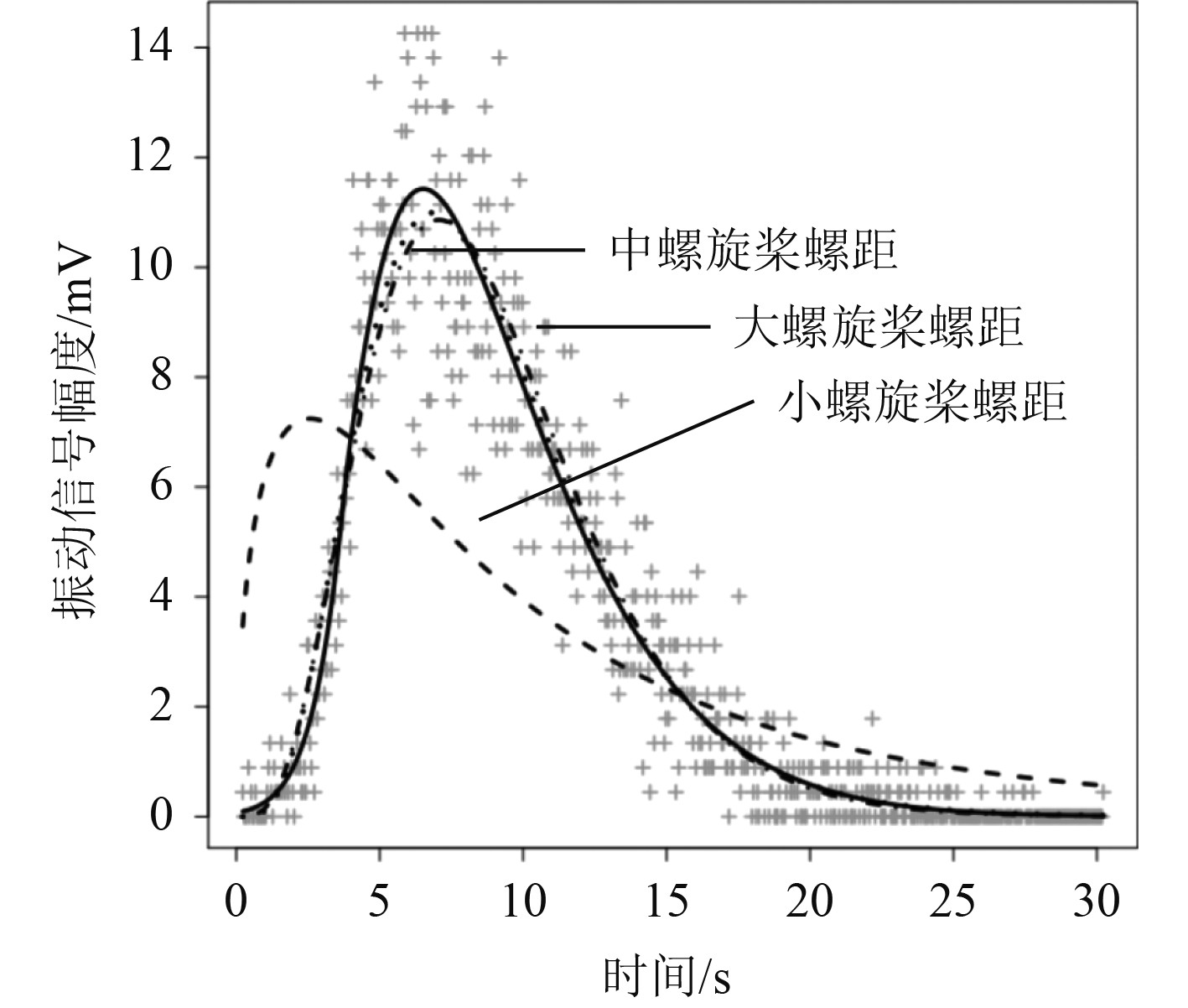
由于螺距与第一质量振幅存在密切的关联,即前者越大,后者越小,螺距为0时,振幅最大,较之额定螺距振幅大28.6%,超过最大螺距振幅50%。船舶拖轮轴系螺旋桨螺距1 阶 4 谐次共振转速曲线如图7所示。
|
图 7 船舶拖轮轴系螺旋桨螺距1 阶 4 谐次共振转速曲线 Fig. 7 1st order 4th harmonic resonance speed curve of propeller pitch of ship tug shafting |
由于单阶4谐次共振转速会随着螺旋桨螺距的增大而减小,当桨距为额定时,共振转速要比螺距为0时的共振转速降低4.3%左右。可见,螺旋状转动惯量所占的比重与其螺距大小有关。
3 结 语船舶在海上航行时,安全性尤为重要,若是推进轴发生瞬态的扭转振动现象,则会导致安全性下降。对此可以运用有限元分析软件,对瞬态扭转振动的影响因素加以分析,从而为减振避振处理提供依据。
| [1] |
温小飞, 蔡保刚, 王杏娣. 周期性载荷作用下船舶推进轴系运行状态的数值仿真[J]. 中国航海, 2021, 44(3): 13-19. DOI:10.3969/j.issn.1000-4653.2021.03.003 |
| [2] |
周凌波, 段勇, 孙玉东, 等. 船体纵横倾对推进轴系支撑轴承润滑动特性的影响[J]. 舰船科学技术, 2021, 43(1): 23-27. |
| [3] |
赵含, 杨志荣, 塔娜, 等. 基于准零刚度隔振器的船舶推进轴系纵向减振研究[J]. 振动与冲击, 2020, 39(23): 90-95. |
| [4] |
张赣波, 席敬波. 基于连续-离散混合模型的船舶推进轴系纵向振动动力吸振分析[J]. 船舶工程, 2020, 42(7): 9-14. |
| [5] |
肖能齐, 陈保家, 徐翔, 等. 基于冰载荷动态激励的船舶推进轴系瞬态振动计算研究[J]. 船舶力学, 2020, 24(3): 390-399. |
| [6] |
张涵, 万振刚. 基于压缩感知与VMD的船舶推进轴系轴承振动故障分析[J]. 舰船电子工程, 2020, 40(1): 157-161. DOI:10.3969/j.issn.1672-9730.2020.01.037 |
| [7] |
李小军, 朱汉华, 范世东, 等. 船舶艉轴承刚度和螺旋桨陀螺效应对轴系回旋振动特性影响的分析[J]. 船舶力学, 2019(7): 851-858. DOI:10.3969/j.issn.1007-7294.2019.07.011 |
 2022, Vol. 44
2022, Vol. 44
