0 引　言

船舶水动力性能包括船体阻力、动力系统特性、耐波特性等，为了提高船舶的操纵运动，实现船体快速、准确的运动控制，必须要充分分析船舶的水动力特性，从船舶-船舵-螺旋桨等系统的维度提升船舶操纵运动质量。

近年来，CFD技术及CFD计算仿真软件获得了快速的发展，为船舶水动力性能分析提供了有力的工具支持。基于CFD技术的船体水动力特性分析具有计算精度高^[1]、仿真周期短、成本低等优点，目前已经成为船舶领域广泛使用的工具。此外，计算流体力学还具有普通试验方法不具有的优势，比如在CFD仿真软件中能够设置试验情况下很难实现的边界条件，例如修改液体的粘性系数等，可以通过不断的迭代计算，获取某一边界条件参数对于整个系统的敏感性。

本文采用计算流体力学技术对船舶的操纵运动进行仿真分析，采用的计算流体力学软件平台为Ansys-Fluent平台，分别对计算流体力学的原理、船舶流体动力学模型、船舵及螺旋桨推力流体动力学模型等进行建模，展示了CFD方法在船舶操纵性能预报和优化上的应用优势。

1 计算流体力学原理

使用计算流体力学对船舶的操纵运动进行仿真分析的关键步骤包括：

1）计算域的定义和模型搭建；

2）控制方程构建；

3）有限元离散和仿真；

4）数值求解。

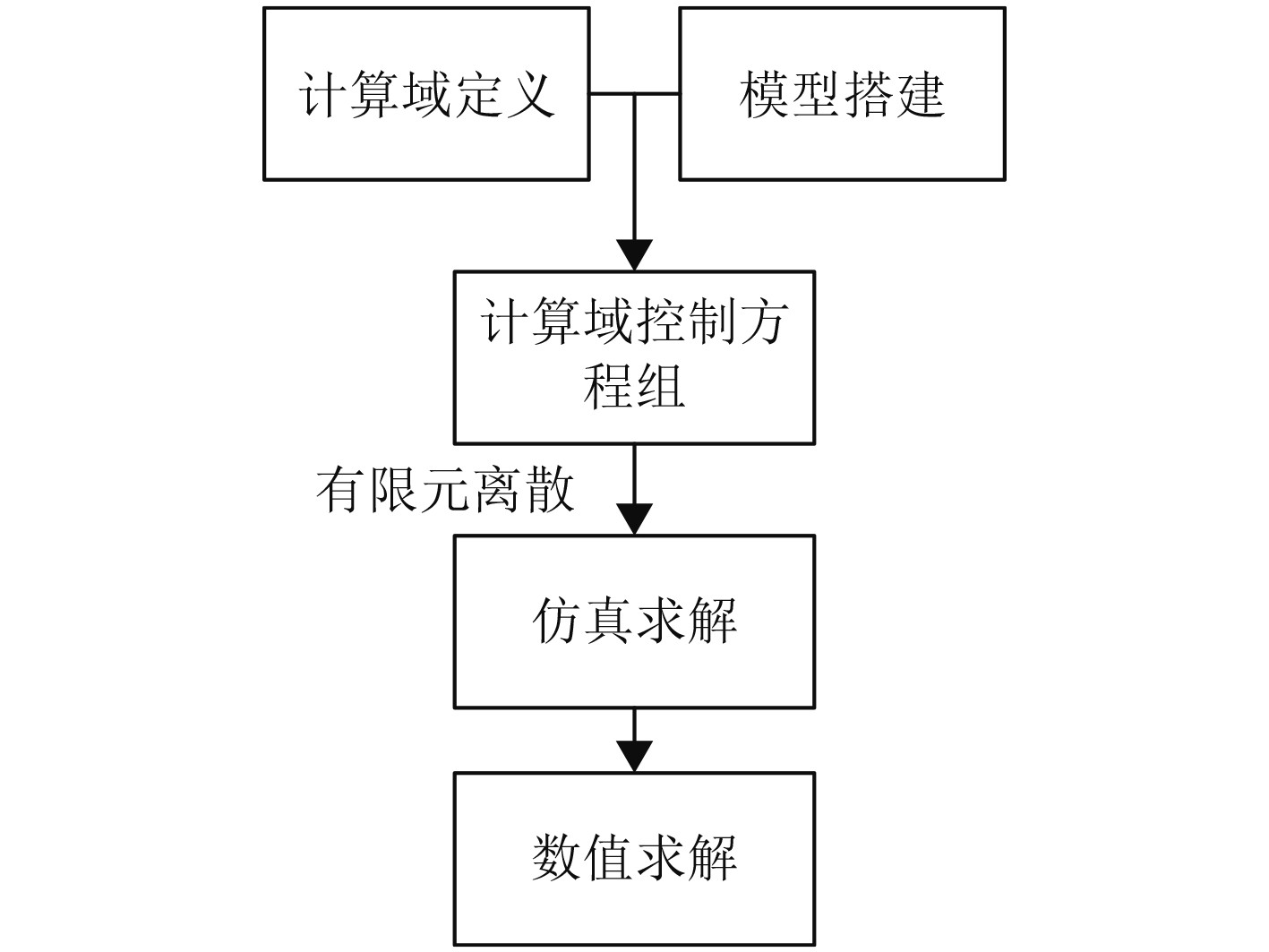
图1为基于计算流体力学的船舶操纵运动仿真流程图。

计算流体力学的基本方程包括湍流方程、质量守恒方程和连续性方程，分别如下：

1）海水湍流方程

本文使用标准的 $ k - \varepsilon $ 模型^[2]来描述船舶操纵运动过程中海水的湍流，建立湍流方程如下式：

$ \begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} = \frac{\partial }{{\partial {x_i}}}\left\{ {\left( {{\mu _t} + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{{\text{δ}} k}}{{{\text{δ}} {x_i}}}} \right\} + {G_k} - \rho \varepsilon ，\\ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} = \frac{\partial }{{\partial {x_j}}}\left\{ {\left( {{\mu _t} + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{{\text{δ}} \varepsilon }}{{{\text{δ}} {x_j}}}} \right\} + {G_k} - \rho \frac{{{\varepsilon ^2}}}{k}。\\ \end{gathered} $

式中： $ {\rho _{}} $ 为海水的密度， $ k 和 \varepsilon $ 均为基本参数， $ {\mu _t} $ 为湍流的粘度， $ {\sigma _k} $ 为湍流的普朗特系数， $ {G_k} $ 为海水产生的湍流动能， $ {x_i} $ 和 $ {x_j} $ 均为方向分量， $ \varepsilon $ 为耗散系数，湍流粘度 $ {\mu _t} $ 计算公式为：

$ {\mu _t} = {C_0}\frac{\varepsilon }{\rho }\left( {\frac{{{k^2}}}{\varepsilon }} \right) 。$

2）海水连续性方程

假定海水为连续性流体，得到连续性方程为：

$ \frac{\partial }{{\partial t}}\iiint\limits_V {}{\rm{d}}x{\rm{d}}y{\rm{d}}z + \oint {\rho {V_t}{n_t}{\rm{d}}A} = 0 。$

其矢量形式为：

$ \frac{{{\text{δ}} \vec Vt}}{{{\text{δ}}\rho }} + {\rm{div}}\left( {\sum\limits_{i = 1}^n {{A_i}} } \right) = 0 。$

式中： $ {V_t} $ 为流体速度， $ {A_i} $ 为流体控制面， $ {n_t} $ 为流体控制面的矢量。

2 计算流体力学的有限体积法

有限体积法是计算流体力学的一种关键等效思路，在有限流域内对一个控制方程进行离散，产生离散的方程。

有限体积等效公式如下式：

$ \frac{{\rm{d}}}{{{\rm{d}}t}}\int_V \rho \phi {\rm{d}}s + \int_A \rho {\mathbf{v}}\phi \cdot {\rm{d}}s = \int_A {} \nabla \phi {\rm{d}}s + \int_V {{S_\phi }} {\rm{d}}s \text{，} $

式中， $ \nabla $ 为哈密尔顿算子，计算方法如下：

$ \nabla = \left( {\frac{\partial }{{\partial x}},\frac{\partial }{{\partial y}},\frac{\partial }{{\partial z}}} \right) 。$

式中： $ \phi $ 为表面势能； $ {S_\phi } $ 为有限域^[3]。

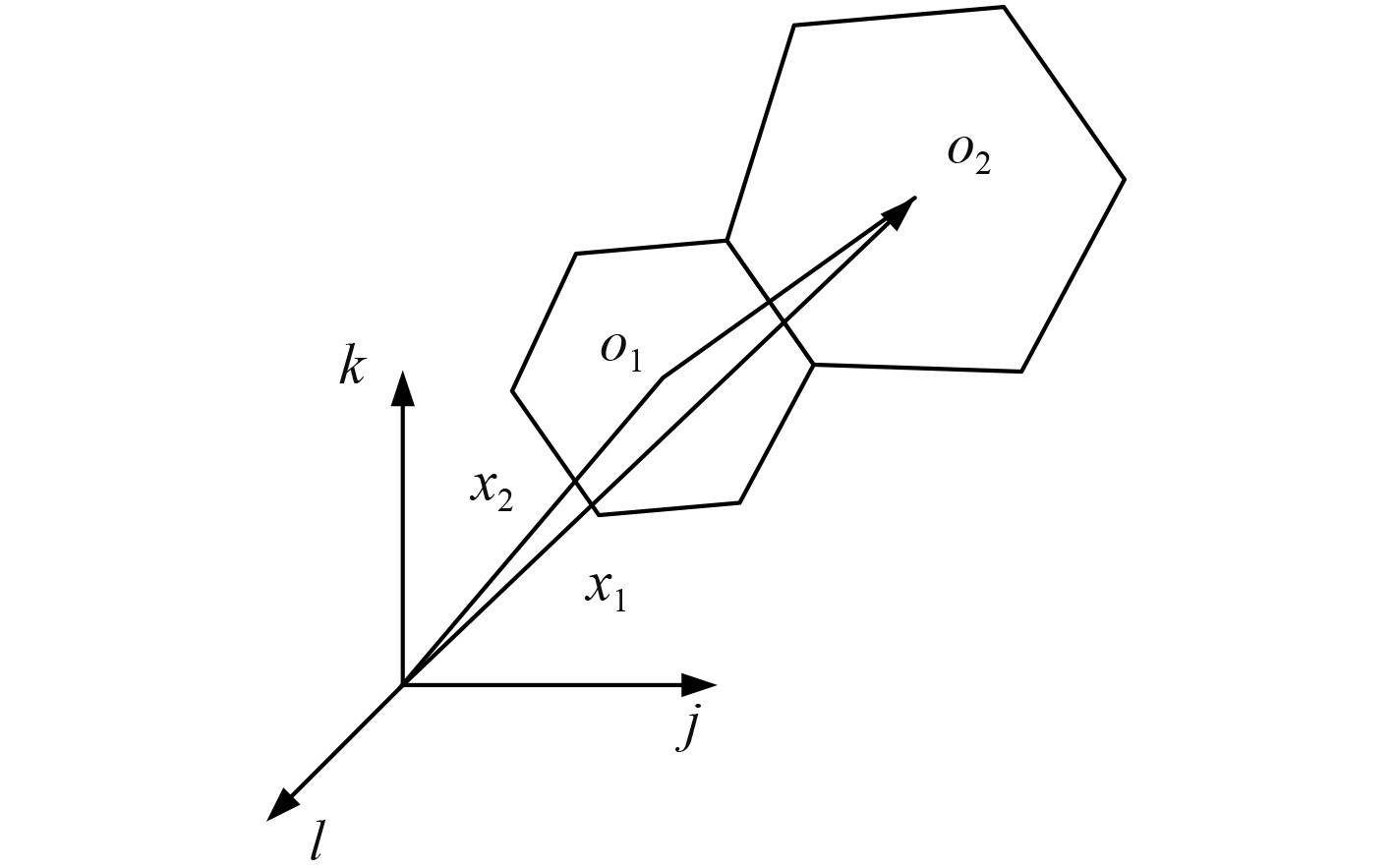
有限体积离散的方法是将某一局域坐标位置的流域离散为多个多面体网格，示意图如图2所示。

3 基于计算流体力学的船舶操纵运动仿真 3.1 船舶运动系统建模

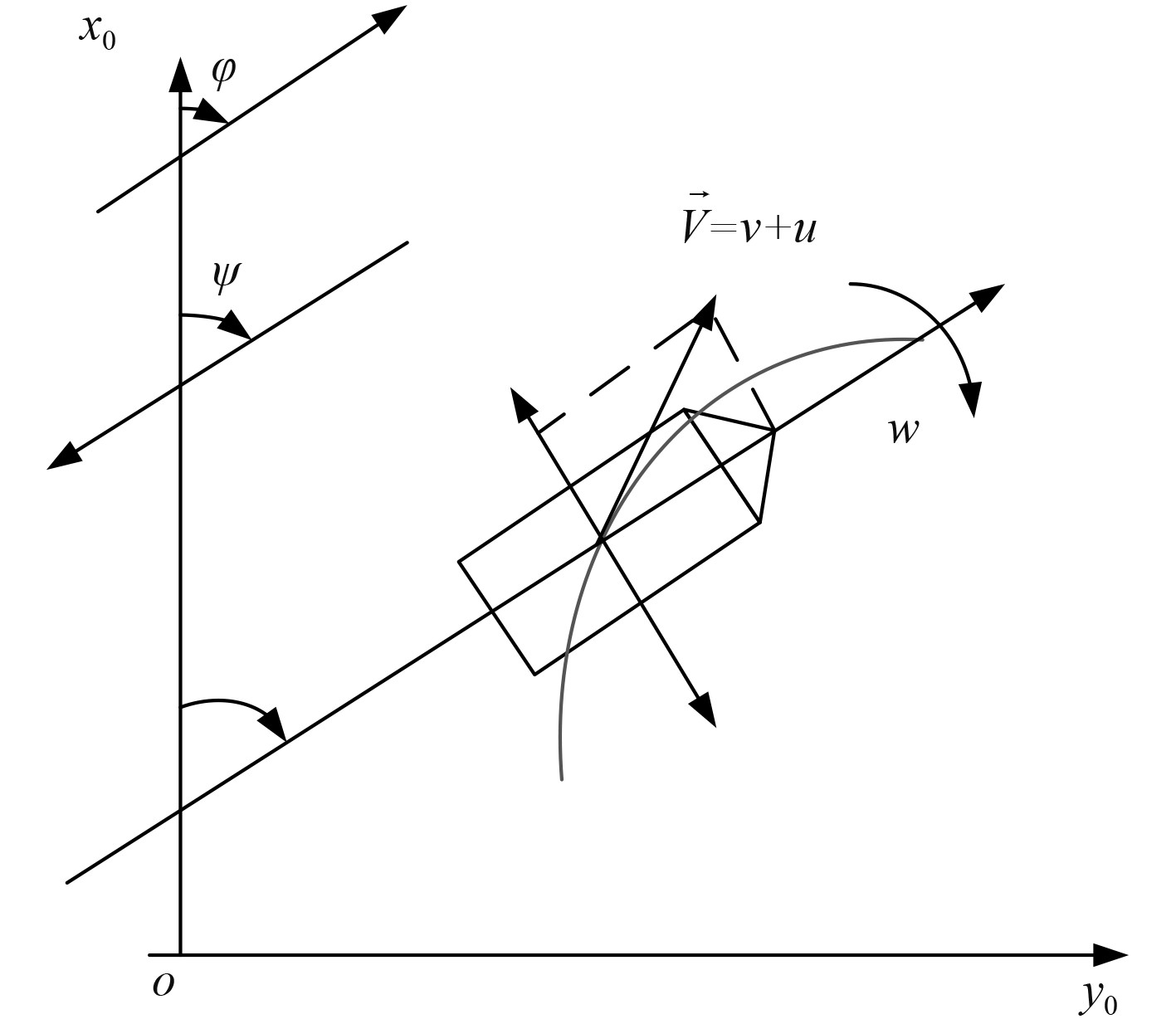
建立船舶运动坐标系如图3所示。

结合坐标系的轨迹模型如下：

$ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\rm{d}}}{{{\rm{d}}t}}{x_0} = u\cos \psi - v\cos \phi \sin \psi } ，\\ {\dfrac{{\rm{d}}}{{{\rm{d}}t}}{y_0} = u\sin \psi + v\cos \phi \cos \psi } ，\\ {\dot \psi = r\cos \phi }，\\ {\dot \phi = w} 。\end{array}} \right. $

式中： $ \phi $ 为横摇角度； $ \psi $ 为船舶航向角； $ r $ 为船首位置转动角速度； $ w $ 为横摇运动的角速度；船舶速度为：

$ \vec V = v + u 。$

基于牛顿第二定律，建立船舶的自由度方程为：

$ \left\{ {\begin{array}{*{20}{l}} {\left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)vr = {X_H} + {X_P} + {X_R} + {X_w}}，\\ {\left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ur = {Y_H} + {Y_P} + {Y_R} + {Y_{{\text{wind }}}}}，\\ {\left( {{I_z} + {J_z}} \right)\dot r = {N_H} + {N_P} + {N_R} + {N_{{\text{wind }}}} + {N_{{\text{wave }}}}}，\\ {\left( {{I_x} + {J_x}} \right)\dot w = {L_H} + {L_P} + {L_R} + {L_{{\text{wind }}}} + {L_{{\text{wave }}}}} 。\end{array}} \right. $

式中： $ m $ 为船舶重量； $ {m_x} $ ， $ {m_y} $ 为重量在2个坐标轴上的附加重量； $ {I_z} $ 为船舶绕z轴的转矩； $ {I_x} $ 为船舶绕x轴的转矩； $ {J_z} $ 为船舶沿z轴的转动惯量^[4]； $ {J_x} $ 为船舶沿x轴的转动惯量； $ {X}_{H}，{X}_{P}，{X}_{R}，{X}_{w} $ 分别为作用于x轴上的船舶水动力、螺旋桨推力、螺旋桨力矩、船体横摇力矩； $ {Y}_{H}，{Y}_{P}，{Y}_{R}；{Y}_{\text{wind }} $ 分别为在y轴上的船舶水动力、螺旋桨推力、螺旋桨力矩、海风作用力； $ {N}_{H}，{N}_{P}，{N}_{R}，{N}_{\text{wind }}，{N}_{\text{wave }} $ 分别为绕x轴转动方向的船舶水动力、螺旋桨动力、螺旋桨力矩、海风作用力和海浪作用力； $ {L}_{H}，{L}_{P}，{L}_{R}，{L}_{\text{wind }}，{L}_{\text{wave }} $ 分别为绕y轴转动方向的船舶水动力、螺旋桨推力、螺旋桨力矩、海风作用力和海浪作用力。

3.2 船体附加质量及附加惯性矩

船体的附加惯性矩^[5]用下式计算：

$ M = \left| {\begin{array}{*{20}{c}} {{m_x}}&0&0 \\ 0&{{m_y}}&{{m_y}{\alpha _x}} \\ 0&{{m_y}{\alpha _x}}&{{J_z}} \end{array}} \right| 。$

式中， $ {\alpha _x} $ 为附加质量 $ {m_y} $ 相对于坐标中心的坐标，船舶的附加动量及动量矩用下式计算：

$ \left\{ {\begin{array}{*{20}{l}} {{K_x} = {m_x}u} ，\\ {{K_y} = {m_y}v + {m_y}{\alpha _x}r} ，\\ {{I_z} = {m_y}{\alpha _x}v + {J_z}r} 。\end{array}} \right. $

将船体简化为一个椭圆体，长轴a为 $ L/2 $ ，短轴为d，计算船体的附加质量及惯性矩如下：

$ \left\{ {\begin{array}{*{20}{l}} {{m_x} = {k_x}\frac{{4\text{π} }}{3}\rho L{b^2}}，\\ {{m_y} = {k_y}\frac{{4\text{π} }}{3}\rho L{d^2}} ，\\ {{J_z} = {k_z}\frac{{4\text{π} }}{{15}}\rho L{d^2}\left( {{L^2} + {d^2}} \right)} 。\end{array}} \right. $

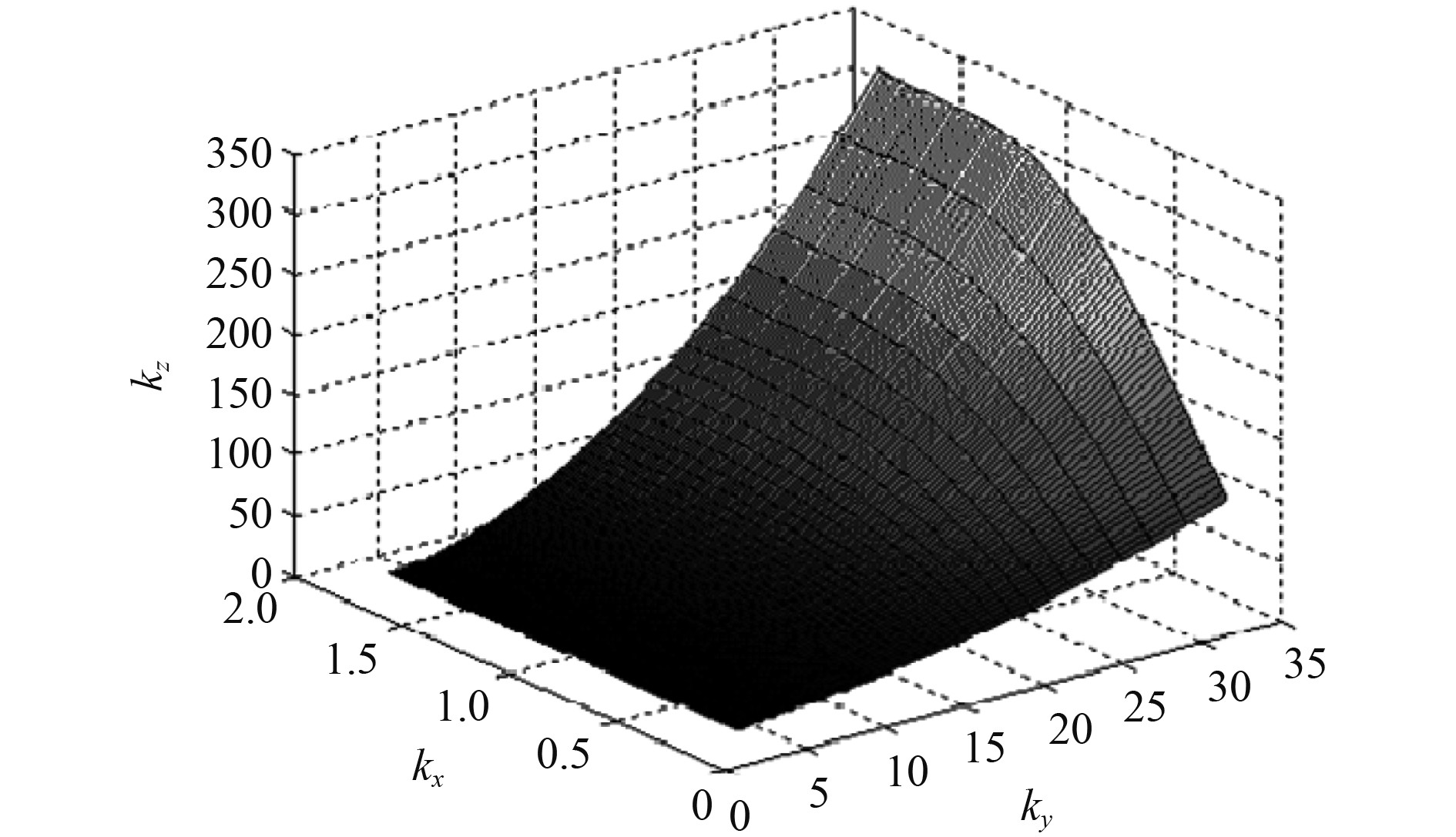
式中： $ {k_x} $ ， $ {k_y} $ ， $ {k_z} $ 分别为惯性矩系数^[5]，本文通过大量计算统计，得到3种系数的关系如图4所示。

3.3 基于计算流体力学的船舶螺旋桨推力数学模型

船舶操纵运动过程中，动力系统螺旋桨起到主要的推力作用，螺旋桨的流体动力学建模同样也是船体操纵运动分析的重要环节。

建立螺旋桨的推力模型如下：

$ \left\{ {\begin{array}{*{20}{l}} {T = {t_p}\rho \left[ {{V_A} + {{(0.7\text{π} nD)}^2}} \right]\dfrac{\text{π} }{4}{D^2}{M_T}C_T^{}(\beta )} ，\\ {\beta = {{\tan }^{ - 1}}\dfrac{{\left( {1 - {\omega _p}} \right)}}{{0.7 \text{π} nD}}} 。\end{array}} \right. $

式中： $ {t_p} $ 为螺旋桨的推力衰减系数； $ {V_A} $ 为船舶前进的速度； $ D $ 为螺旋桨的直径； $ n $ 为螺旋桨的转速； $ {M_T} $ 为扭矩系数； $ C_T^{} $ 为推力系数； $ \beta $ 为螺旋桨的螺距角^[6]； $ {\omega _p} $ 为螺旋桨的角速度。

图5给出了不同螺旋桨转速下的扭矩系数与推力系数的关系曲线，A，B，C，D分别表示螺旋桨转速为500 r/min，600 r/min，700 r/min，800 r/min。

4 基于计算流体力学的船舶操纵运动仿真

基于计算流体力学软件平台Ansys-Fluent进行船舶操纵运动的仿真^[7]，仿真采用的螺旋桨参数如表1所示。

仿真过程如下：

1）建立船体和螺旋桨的有限元模型

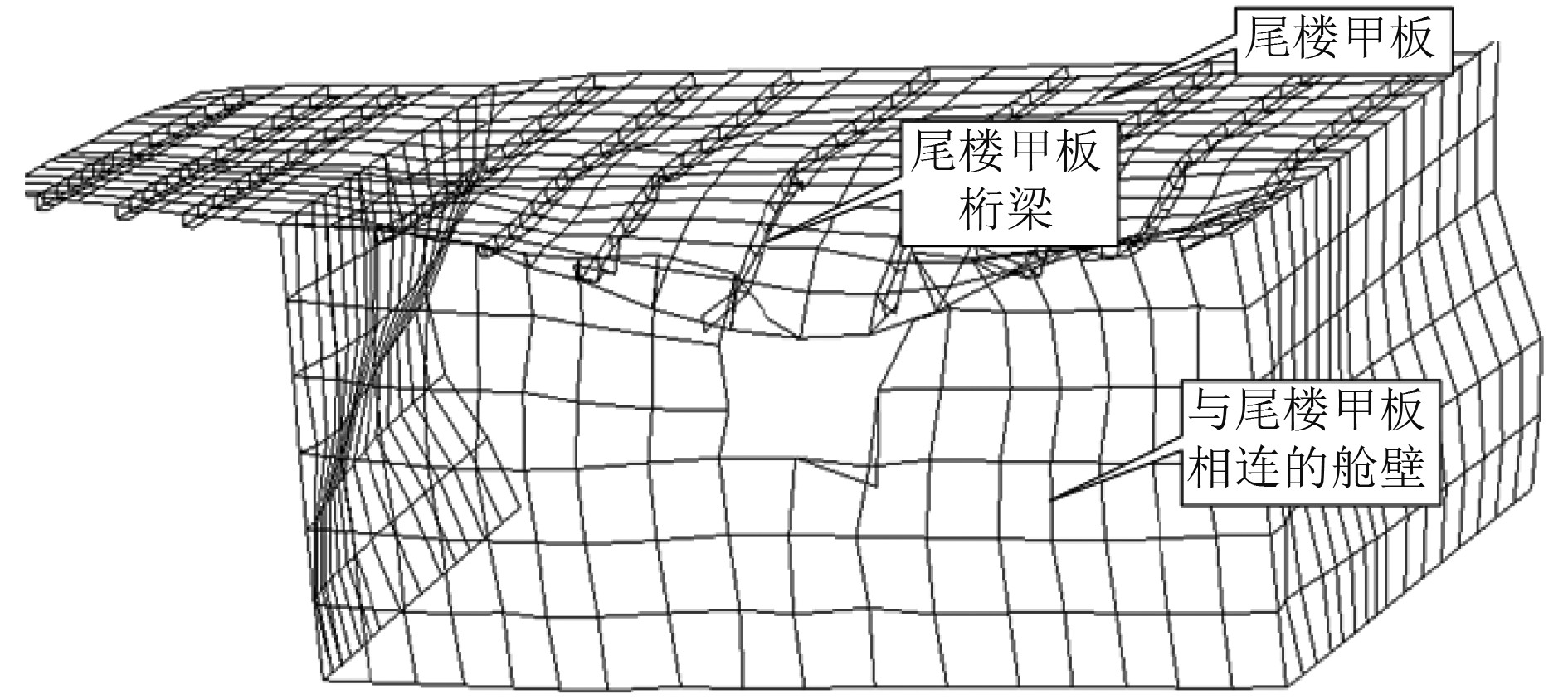
根据螺旋桨参数和船舶的主体尺寸，在仿真软件中建立船体有限元模型，图6为船尾位置有限元模型示意图。

2）模型解算

将所建的船舶运动流体力学模型、流体的边界条件、螺旋桨流体力学模型输入Ansys-Fluent软件，进行计算和求解。

3）仿真数据显示与输出

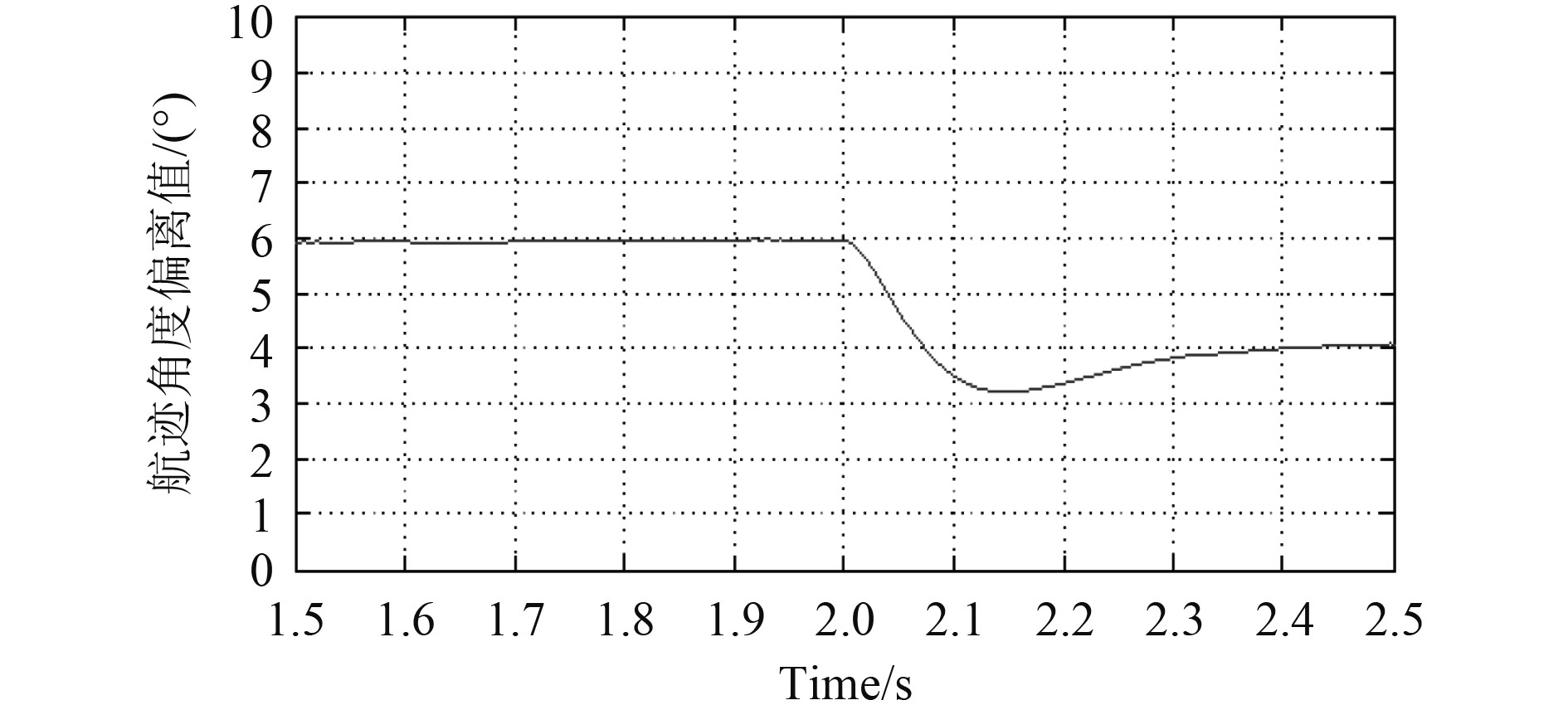
设定船舶航迹角度为6°，得到一段时间内的船舶航迹角度的仿真曲线如图7所示。

5 结　语

船舶在复杂海况下的航向保持性、动力特性、抗风浪干扰能力等决定了船舶的安全和效能，本文基于计算流体力学理论对船舶的操纵运动进行仿真，建立船体、螺旋桨的流体力学模型，并基于计算流体力学仿真软件Ansys-Fluent进行了船体航向保持性的仿真。