2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligence Equipment, Zhengzhou 450015, China
水下航行体的出水姿态是保证其航行精度的重要指标[1]。筒体不仅是水下航行体的储存结构,也对水下航行体的运动起到导向作用[2]。在水下航行体出筒过程中,筒体不仅受到支撑机构带来的非对称周向载荷,也受到航行器尾部对称的均布压力载荷[3]。筒体在这些载荷作用下的动态响应会对水下航行体的运动轨迹产生影响,进一步影响到水下航行体的出筒姿态[4]。因此,深入研究水下航行体出筒过程动力学特性,预测筒体变形是水下发射技术的重要课题之一。对于大型结构而言,开展试验研究需要大量的人力物力资源,试验成本过高。在这种情况下,针对水下航行体出筒过程的动力学特性进行数值仿真显得愈发重要。现阶段针对出筒动力学特性的研究方向主要是将筒体简化为二维模型,这种方法忽略了筒体圆周方向的对称压力载荷,也无法描述筒体的局部变形。
本文针对水下航行器出筒过程,以薄壁圆柱壳体结构作为研究对象,基于Ansys仿真软件提出二维与三维2种出筒过程动力学特性仿真计算方法,通过对圆柱壳体在非对称周向载荷下的变形情况进行分析,对比不同仿真方法的差异,为后续水下航行体的出筒导向研究提供理论支撑及仿真依据。
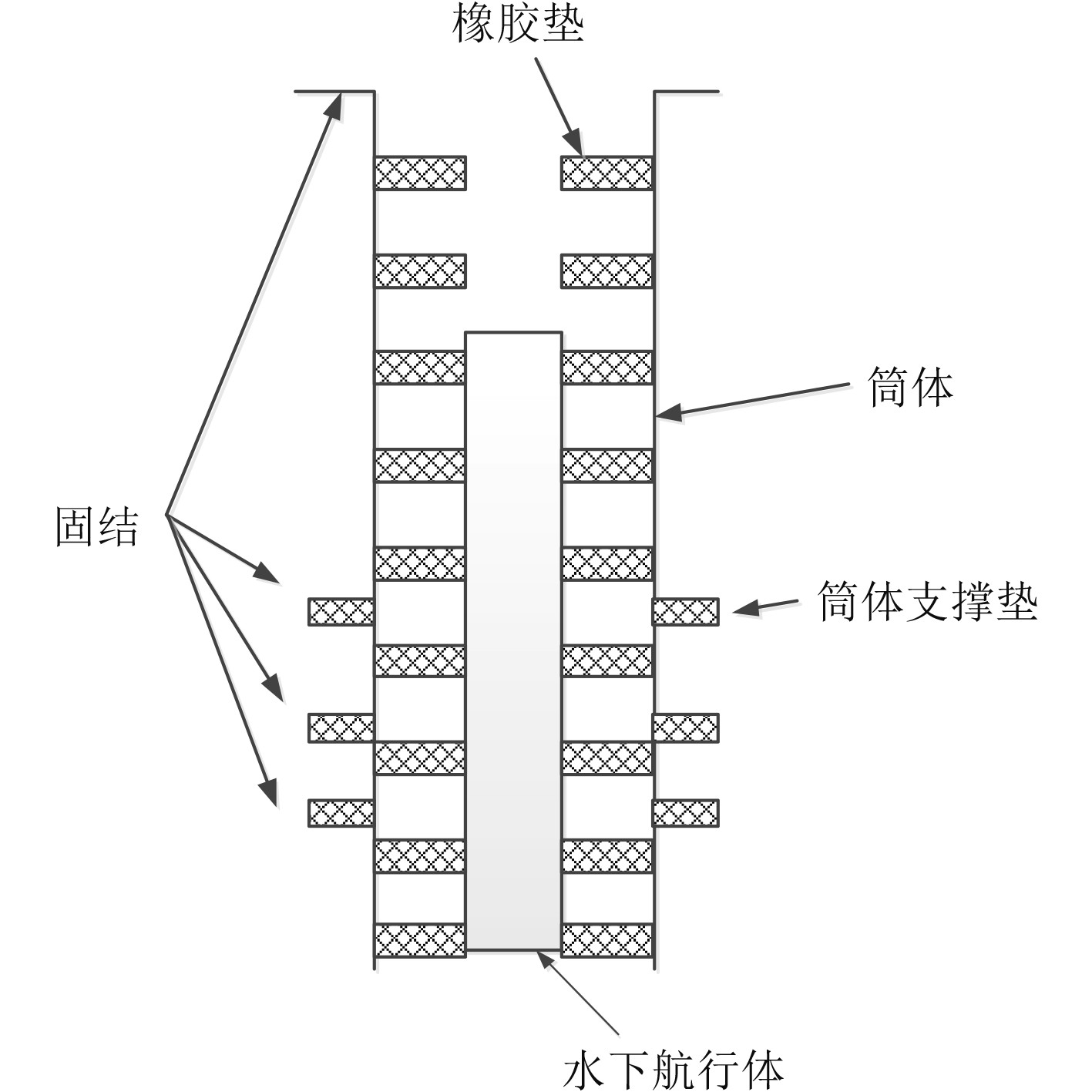
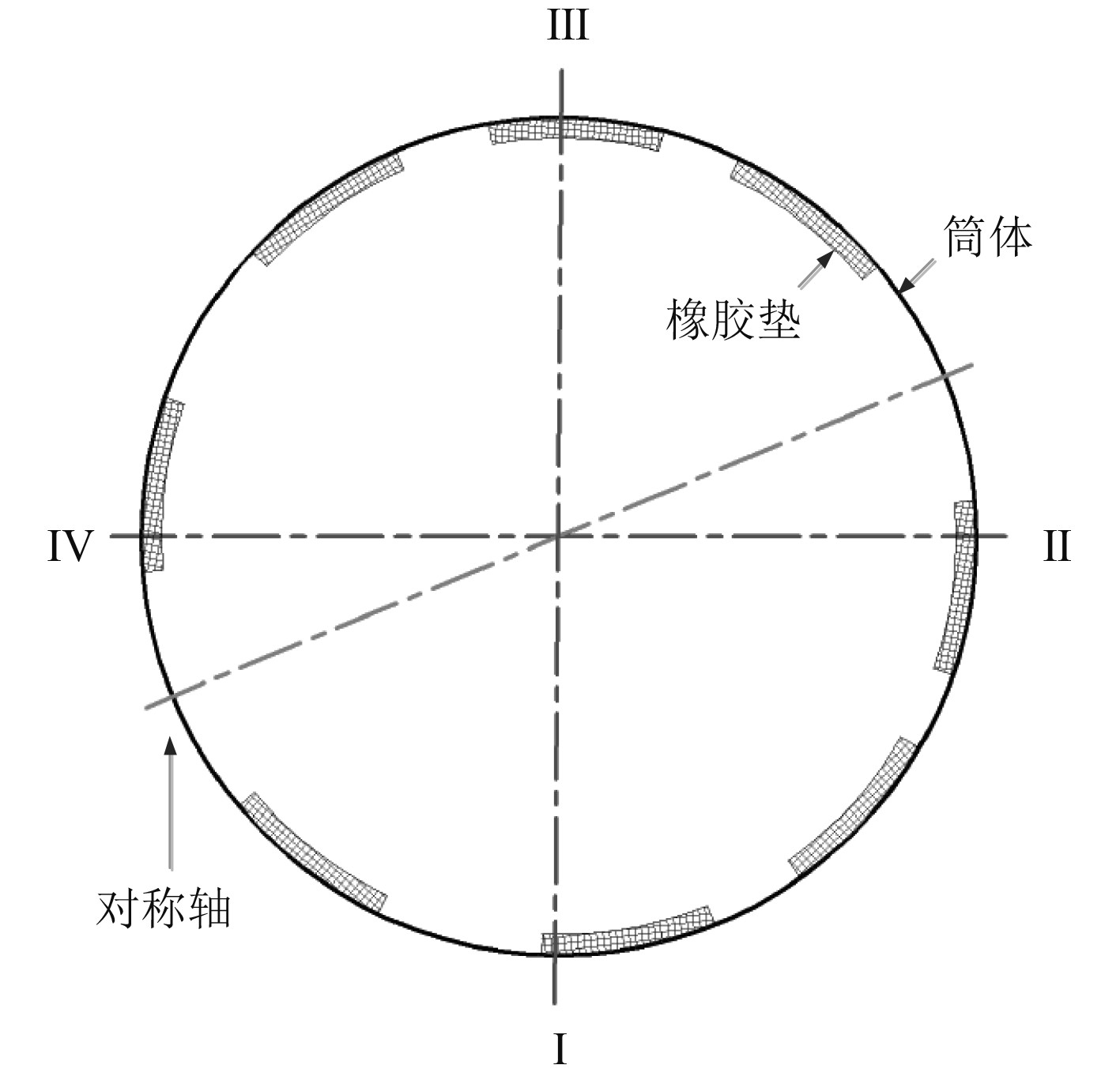
1 动力学计算方法 1.1 结构模型本文研究对象如图1所示。筒体为薄壁圆柱壳体结构,外部安装3圈支撑垫。水下航行体位于筒体内部,与筒体之间的空隙内填充九圈橡胶垫,为水下航行体提供支撑与导向作用。每圈共有8块橡胶垫,沿顺时针方向分为4个区域,其关于第1块与第8块对称分布,如图2所示。水下航行体的运动方向为II、IV象限。
|
图 1 水下航行体整体结构图 Fig. 1 The overall structure of the underwater vehicle |
|
图 2 结构剖面图 Fig. 2 Structure section view |
由于水下航行体的出筒过程涉及到多个结构的参与,对完整结构进行分析具有一定难度。因此,采用解耦方式,计算水下航行体出筒过程中筒体的变形。首先由出筒动力学课题假设筒体为刚性,计算求解水下航行体出筒过程中橡胶垫的压缩量,进而获得橡胶垫的受力情况。假设水下航行体出筒过程筒体安装橡胶垫的位置的受力与橡胶垫受力相同,并将橡胶垫受力作为动载荷施加到筒体模型上,通过瞬态动力学方法求解筒体变形。
1.3 动力学理论二阶结构系统一般的运动方程可以反映瞬态力学特征,表达式为:
| $ {\boldsymbol{M}}\ddot {\boldsymbol{X}} + {\boldsymbol{C}}\ddot {\boldsymbol{X}} + {\boldsymbol{K}}{\boldsymbol{X}} = {\boldsymbol{F}}\left( t \right)。$ | (1) |
式中:M为结构质量矩阵;C为结构阻尼矩阵;K为结构刚度矩阵;X为节点位移向量;F为外载荷向量[5]。可以看出,结构的响应与质量、刚度、阻尼息息相关[6]。
二维仿真方法中的筒体支撑垫刚度与阻尼通过弹簧单元进行定义。
三维仿真方法中筒体支撑垫的三维模型无法直接定义刚度与阻尼。对于刚度设置,首先通过Ansys对筒体支撑垫进行静力学计算,得到筒体支撑垫处的位移-载荷曲线,则仿真模型中的支撑垫刚度为位移-载荷曲线的斜率。在此基础上,通过调试材料属性等参数,使三维仿真模型中的刚度与理论值相一致。
在三维模型中添加阻尼过程比较复杂。一般通过材料的瑞利阻尼施加。瑞利阻尼表达式为:
| $ {\boldsymbol{C}} = \alpha {\boldsymbol{M}} + \beta {\boldsymbol{K}}。$ | (2) |
在实际应用中,只需要输入阻尼常数
| $ {\omega _i} = 2 \text{π} {f_i} ,$ | (3) |
| $ {\xi _i} = \frac{\alpha }{{2{\omega _i}}} + \frac{{\beta {\omega _i}}}{2}。$ | (4) |
在Ansys中一个载荷步只能输入一个
| $ \beta = 2{\xi _i}/{\omega _i}。$ | (5) |
根据模态试验结果及有关文献资料,本次计算瑞利阻尼
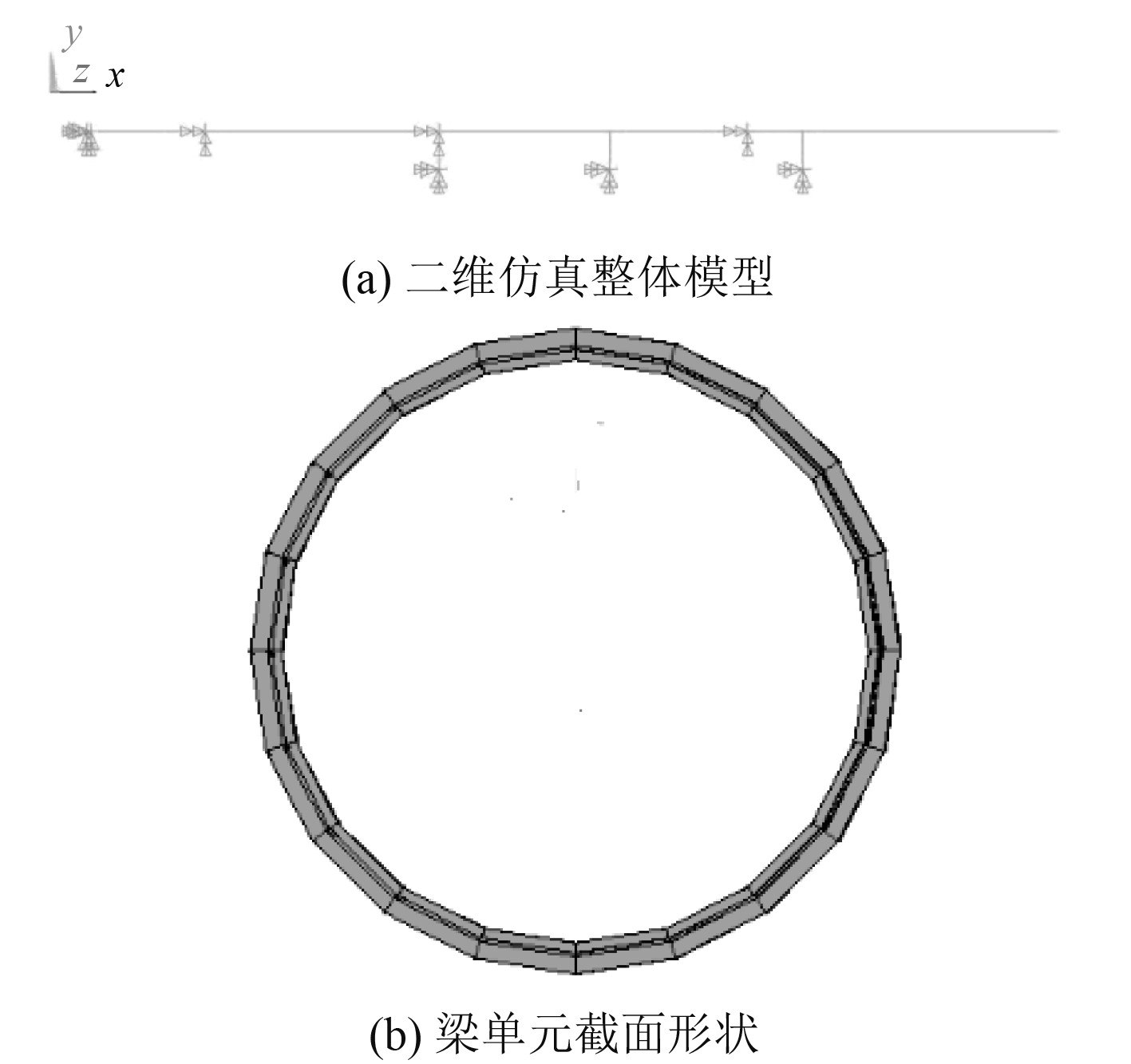
薄壁圆柱壳体结构细长比(GAL2/EI≈69)>30,故可采用Ansys中的BEAM188梁单元建立其有限元模型,梁单元截面为管状,如图3所示。筒体支撑垫的刚度与阻尼采用Ansys中的COMBIN39非线性弹簧单元来模拟,弹簧一端与筒体梁单元节点相连,另一端设置为固定约束[7]。筒体顶部与基座连接,计算中认为连接部分没有位移,因而筒体梁模型顶部节点设置为固定约束。
|
图 3 二维仿真模型 Fig. 3 Two-dimension simulation model |
水下航行体发射过程中基座变形可以忽略不计,不建立具体模型,仅定义固定约束点模拟基座对筒体支撑垫和筒体的位移限制作用。水下航行体出筒时所产生的倾角主要来自于水流的作用,因此,对二维模型的载荷简化为迎流背流方向的合力,即二维仿真中的Y方向(与轴向相垂直)。
2.2 二维仿真结果依据水下航行体出筒动力学仿真二维模型以及出筒动力学所提供的各圈橡胶垫处载荷,采用瞬态计算方法对水下航行体出筒过程中薄壁圆柱筒体横向位移进行求解计算。
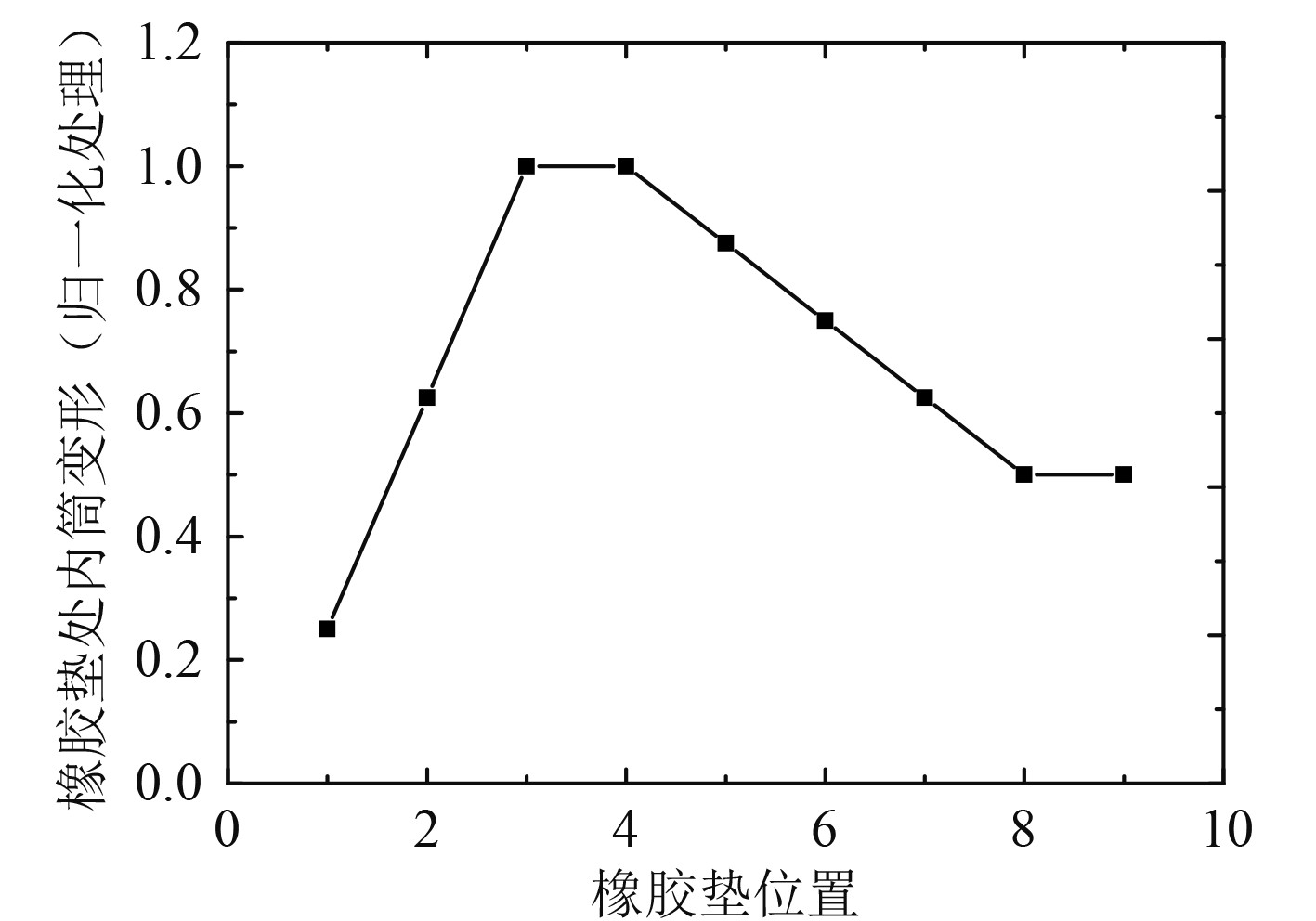
提取各圈橡胶垫位置处筒体最大横向位移(迎流背流方向),以其中最大变形为参考(第3圈),对各圈橡胶垫处筒体位移进行归一化处理,结果如图4所示。第1块橡胶垫靠近筒口,第9块圈橡胶垫位于筒底附近。
|
图 4 二维仿真各圈橡胶垫处筒体最大位移 Fig. 4 Two-dimensional simulation of the maximum displacement of the cylinder at each ring rubber mat |
可以发现,筒体最大横向位移从筒底到筒口先逐渐增大后逐渐减小,在第3圈~第4圈位置处筒体横向位移出现最大值。
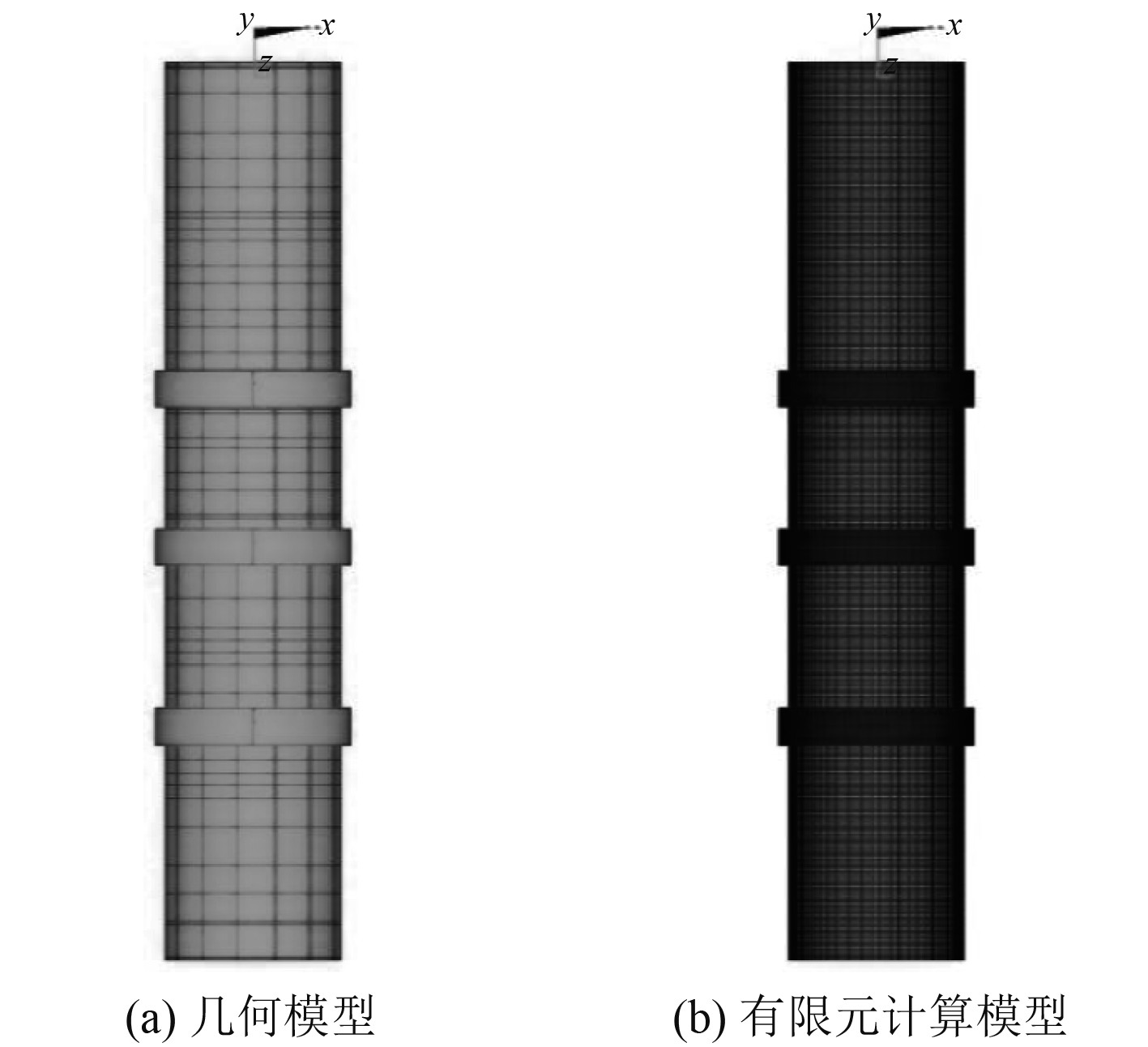
3 三维模型仿真计算 3.1 三维计算模型筒体与筒体支撑垫的模型如图5所示。筒体支撑垫外径即筒体支撑垫与基座接触部分设为固定约束,筒体上法兰部分也设为固定约束。其中,筒体用Shell181壳单元,筒体支撑垫用Solid185实体单元,筒体与筒体支撑垫用接触对来模拟(接触单元用Conta174,目标单元用Targe170)。
|
图 5 三维仿真模型 Fig. 5 Three-dimension simulation model |
假设水下航行体与筒体均为刚体。初始时刻水下航行体位于筒体中心。当水下航行体开始出筒运动时,依照几何关系,计算得到水下航行体出筒过程各圈各块橡胶垫的压缩量。根据橡胶垫刚度特性,可以计算出筒过程中每圈中每块橡胶垫压力随时间变化历程。由于橡胶垫在迎流背流方向非对称分布,因此得到的等效压力载荷属于非对称周向载荷。在出筒过程中,动力系统产生的压力载荷在筒内对称分布。其对筒体轴向应力有影响,但对挠度变形影响可以忽略不计。因此,在二维仿真计算中,出筒过程中筒内压力载荷被忽略。但在三维仿真中由于需考虑每处橡胶垫位置的局部变形,显然出筒过程中筒内压力作用不可忽略不计。将水下航行体运动产生的非对称周向载荷与动力系统产生的均布周向压力施加在筒体对应位置,作为出筒动力学的载荷输入。
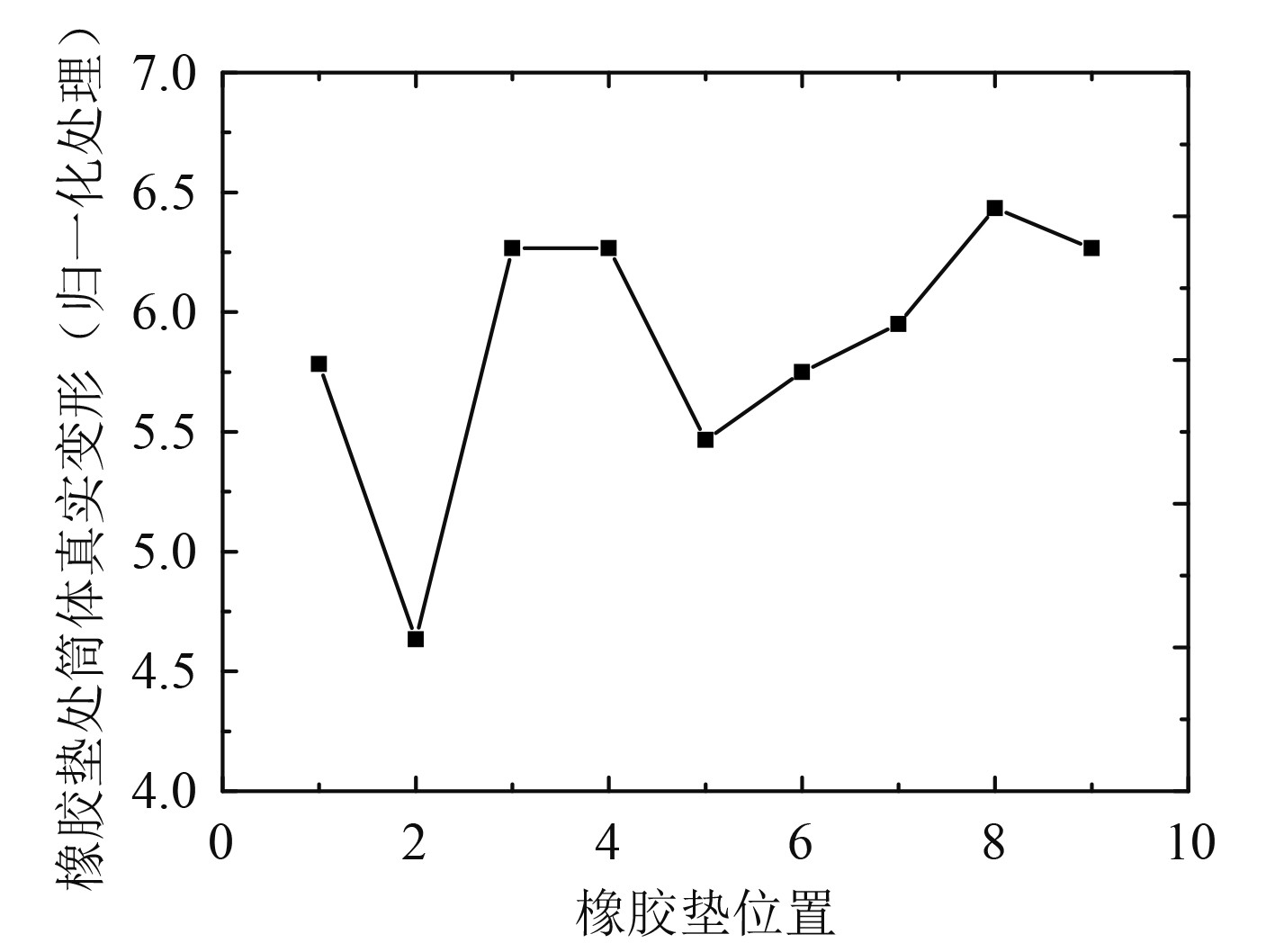
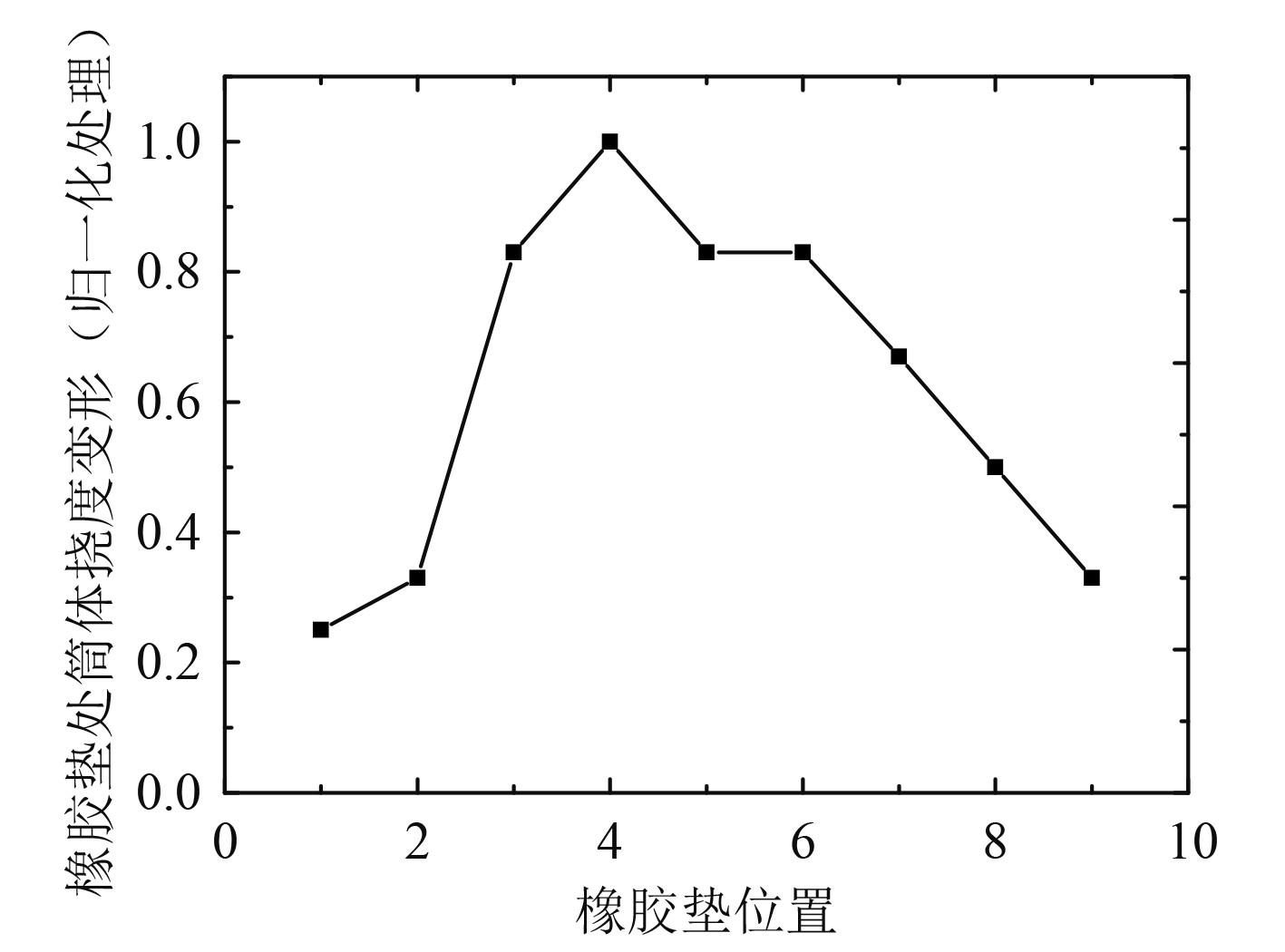
3.2 三维仿真结果三维模型中筒体变形分为挠度变形与考虑筒体周向椭圆度变化的真实变形。挠度变形反应筒体形心的变形趋势,定义为每圈橡胶垫处筒体形心在迎流背流方向的位移。真实变形数值上等于软件中提取的结果变形,由筒体的局部变形与筒体的椭圆度变化一起组成。仿真中X方向为筒体的迎流背流方向,因此提取每圈橡胶垫处筒体在X方向的挠度变形与该位置处筒体最大真实变形。以筒体最大挠度变形为参考,对真实变形与挠度变形进行归一化处理,结果分别如图6和图7所示。
|
图 6 筒体真实变形图 Fig. 6 Real deformation diagram of the cylinder |
|
图 7 筒体挠度变形图 Fig. 7 Deflection diagram of cylinder |
有结果图可知,筒体真实变形在第8圈橡胶垫处出现最大值,挠度变形在第4圈橡胶垫出现最大值,两者出现的位置并不一致。由图6可知,筒体的最大真实变形是挠度变形的6.5倍。这是由于挠度变形为筒体在圆周方向所有节点真实变形的均值,尽管筒体在局部某一节点的真实变形很大,但圆周方向所有节点的真实变形相互叠加抵消之后使其均值减小。
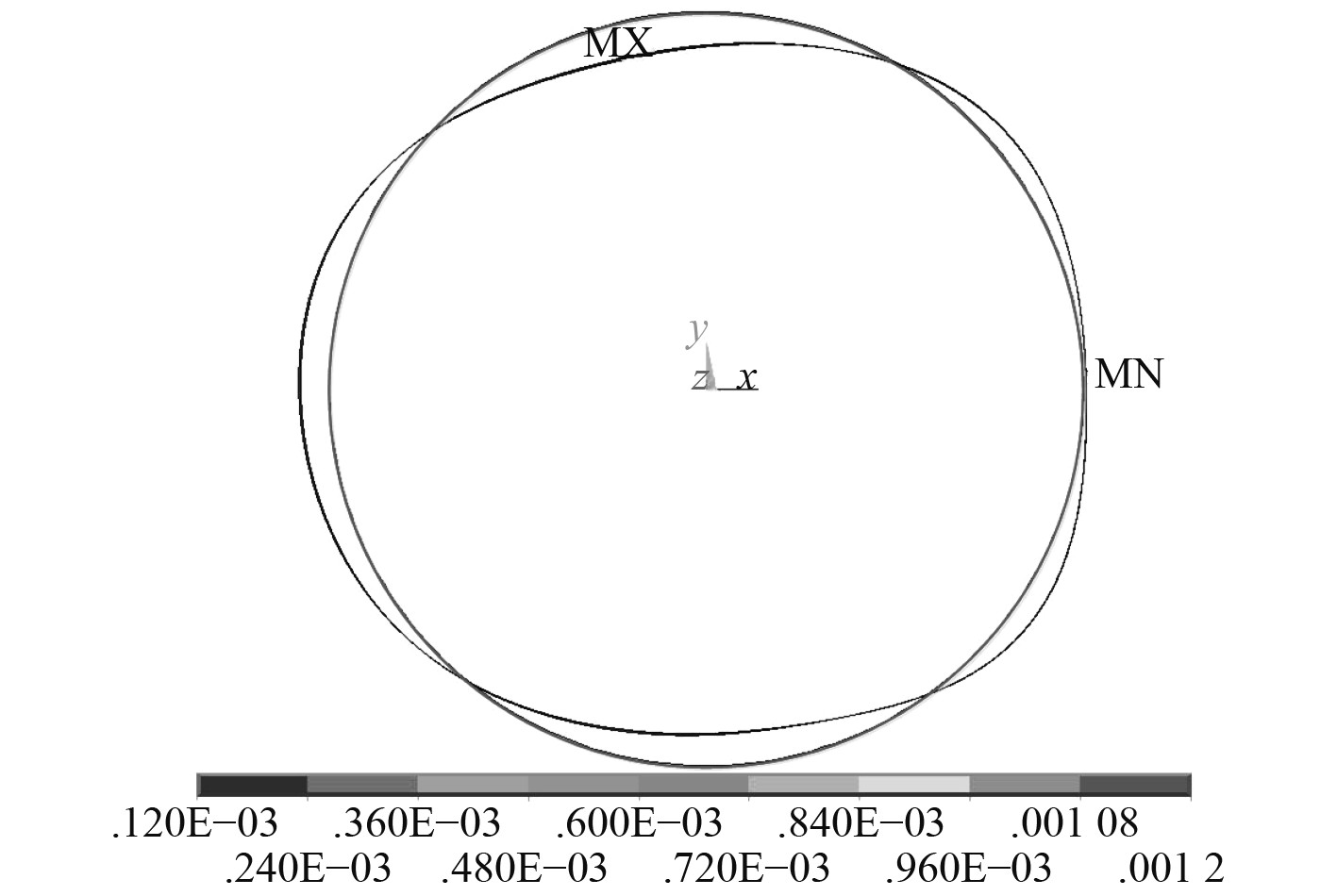
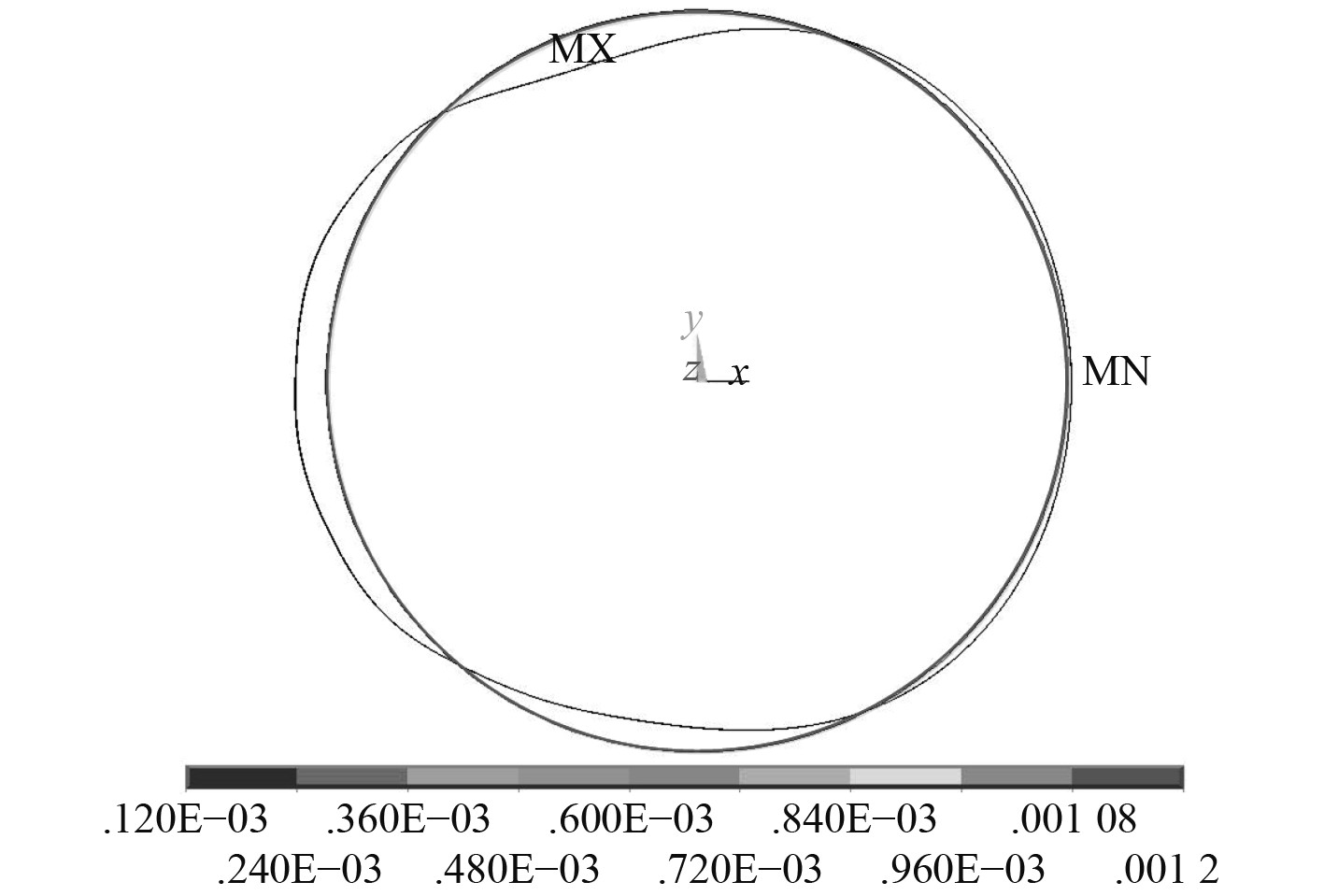
分别提取该时刻各圈橡胶垫处筒体变形轮廓,以第2圈和第3圈橡胶垫处筒体变形为例(见图8和图9)。图中圆形为筒体变形前剖面形状,不规则曲线为变形后剖面形状。经分析可知,各圈橡胶垫处筒体在II、IV 象限(X方向)拉伸,在I、III象限压缩。
|
图 8 第2圈橡胶垫处筒体变形轮廓 Fig. 8 Deformation contour of cylinder at the second ring of rubber mat |
|
图 9 第3圈橡胶垫处筒体变形轮廓 Fig. 9 Deformation contour of cylinder at the third ring of rubber mat |
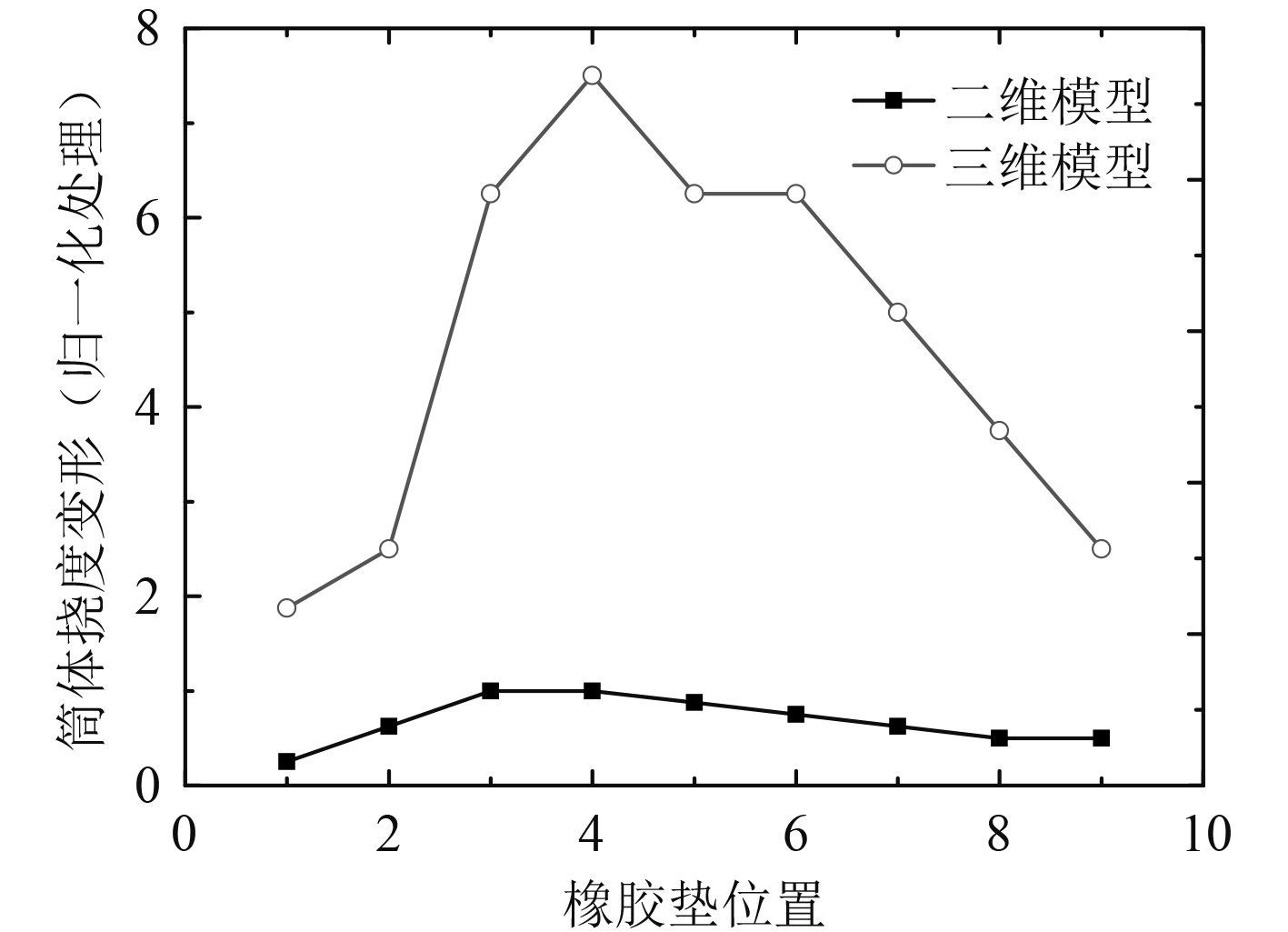
以二维挠度变形最大值为参考,将二维与三维仿真计算中的筒体挠度变形归一化处理,结果如图10所示。可以发现,虽然三维仿真的筒体挠度变形较二维仿真大,但2种仿真方法中筒体挠度变形在同一量级上,2种计算结果相当,并且,2种方法的挠度变形最大值沿橡胶垫位置分布规律一致。从筒口逐渐增大,在第4圈橡胶垫位置处出现最大值,随后沿筒底方向逐渐减小。这也可以证明,二维仿真方法仅仅描述筒体的挠度变形。
|
图 10 筒体挠度变形对比 Fig. 10 Comparison in deflection of cylinder |
图11分别给出了二维与三维模型筒体挠度变形最大时刻各自对应的应力云图。可以看出,二维模型此时的最大应力出现在筒口附近,为0.19 MPa;三维模型此时的最大应力出现在筒底附近,为85 MPa。这是由于三维模型添加了发射过程筒内压力载荷,因此三维模型分析得出的内筒变形及VonMises应力大于二维模型分析结果。2种计算模型中内筒最大VonMises应力均小于筒体材料的屈服极限。

|
图 11 筒体应力云图 Fig. 11 Stress diagram of cylinder |
可以发现,二维仿真方法仅仅描述筒体的挠度变形。三维模型不仅可以考虑水下航行体运动产生的非对称周向载荷,也可以考虑动力系统产生的均布周向压力,计算结果更加准确,可以精确地描述筒体局部变形与应力分布情况。但与之对应,三维仿真计算所需的计算资源远大于二维仿真方法。
5 结 语以出筒动力学课题所提供的数据,假设水下航行体与筒体为刚体,依据几何关系,求解得出各圈中每块橡胶垫处动载荷。采用二维仿真与三维仿真2种计算方法,解决不同仿真方法中阻尼、刚度等材料参数的等效设置问题,对薄壁圆柱壳体结构在非对称周向载荷下响应进行计算分析。对比分析2种动力学仿真模型的差异,可以得出以下结论:
1)由于水下航行体出筒过程中筒体变形是一个典型动态变形过程,阻尼对结果影响很大;二维采用线性弹簧加上阻尼进行描述,三维通过材料的瑞利阻尼进行描述,两者存在差异。
2)二维仿真方法仅考虑了橡胶垫产生的非对称周向载荷,而三维仿真方法添加了筒内的均布周向压力载荷,因此三维模型分析得出的内筒变形及VonMises应力大于二维模型分析结果。
3)用三维模型橡胶垫处横截面的变形量平均值,作为挠度描述筒体的变形,三维挠度变形和二维挠度变形计算结果相当。
4)二维仿真模型可以描述筒体形心挠度变形,三维模型可以具体描述出筒体局部的变形模式。与之对应,三维仿真所需的计算资源远大于二维仿真。
5)在工程设计中,可以通过二维仿真方法对筒体的变形程度进行初步评估,再通过三维仿真模型进行具体的工况分析。
| [1] |
MORROCCO J D. Second Trident 2 test failure points to vehicle design flaw[J]. Aviation Week, 1989(8): 21-26. |
| [2] |
JEANS TL, BAKER CR, HOLLOWAY AGL, et al. A critical review of classical force estimation methods for streamlined underwater vehicles using experimental and CFD data[J]. Proceedings of the ASME Fluids Engineering Division Summer Conference, 2005(1): 139-148. |
| [3] |
乐光明. 潜射导弹出水姿态与载荷特性分析[D]. 哈尔滨: 哈尔滨工业大学, 2011.
|
| [4] |
尚书聪, 张宇文, 袁绪龙. 导弹水下动机座垂直发射过程的水动力计算[J]. 舰船科学技术, 2009, 31(9): 56-60. DOI:10.3404/j.issn.1672-7649.2009.09.008 |
| [5] |
姜百川. 水下航行体发射过程动力学特性及载荷分析[D]. 哈尔滨: 哈尔滨工业大学, 2012.
|
| [6] |
李代金, 张宇文, 党建军, 等. 潜艇垂射导弹出筒姿态的研究[J]. 弹箭与制导学报, 2009, 29(4): 171-173+178. DOI:10.3969/j.issn.1673-9728.2009.04.049 |
| [7] |
王英华. 轴向载荷对潜射导弹横向振动特性影响分析[J]. 导弹与航天运载技术, 2002(6): 9-15. DOI:10.3969/j.issn.1004-7182.2002.06.003 |
 2022, Vol. 44
2022, Vol. 44
