2. 海军研究院,北京 100071
2. Naval Academy, Beijing 100071, China
潜艇流水孔是指布置在潜艇非水密上层建筑上,用于潜艇下潜或上浮时非水密上层建筑内水自由进出的孔口。潜艇上层建筑设置流水孔,是为了能够在潜艇上浮出水过程中及时排出上层建筑内的水,确保潜艇上浮的安全性。同时,艇体表面开孔的形状、结构形式以及尺寸大小直接影响潜艇的快速性及中高航速下的隐身性能。
孟生等[1-2]采用CFD数值计算,研究了不同流水孔的形状、尺寸以及数量对潜艇航行阻力的影响,同时对不同偏角下的阻力还展开分析,探索了流水孔对阻力的影响规律。张航等[3]采用大涡(LES)模拟方法,以Suboff标模建立二维模型,研究了4种开孔分布对空腔流动阻力、频谱特性及内外流交换的影响。张楠等[4-5]基于RANS方程,采用PISO算法和
大多数学者对流水孔的研究仅局限于流水孔的相关参数对航行体阻力的影响,目前还未有关于开展流水孔参数研究,且关于流水孔的尺度效应、流量系数等重要特性参数尚未详细说明,显然无法满足实艇中流水孔方案设计、面积优化等问题的探索研究,现代潜艇带有的大容积非水密上层建筑进一步增大了应急出水问题的复杂程度,在缩比模型上,上层建筑流水孔较小,有必要开展上层建筑流水孔流量系数等特性参数的分析和研究。本文基于CFD软件平台,采用滑移网格和内外域交互的计算方法,研究了不同缩比的圆形流水孔在不同吃水下上层建筑余水容积、余水高度以及流水孔流量系数等特征参数的变化规律,可为实艇的流水孔设计提供一定的理论指导。
1 计算方法 1.1 控制方程应用粘流CFD方法开展数值计算的基础是Navia-Stokes(N-S)方程,然而受限于计算能力,当前还不能通过直接求解N-S方程获得潜艇周围复杂的粘性流场。将N-S方程中的湍流脉动项进行时均化处理可以极大地减小计算量,所得雷诺平均方程(RANS)如式(1)所示。然而,N-S方程在时均化的过程中增加了含未知量时均的雷诺应力项,通过引入湍流模型,可使方程封闭,该方法已在舰艇流体力学理论研究及工程实践中得到广泛应用。
| $ \left\{ \begin{gathered} \frac{{\partial {{\bar u}_i}}}{{\partial t}} + {{\bar u}_j}\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{1}{\rho }\frac{\partial }{{\partial {x_j}}}\left(\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} - \rho \overline {{{u'}_i}{{u'}_j}} \right) + {f_i},\\ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0 。\\ \end{gathered} \right. $ | (1) |
式中:
开展计算时,控制方程离散均采用二阶迎风格式,并应用分离式解法(segregated flow)对离散后的方程组进行求解。压力速度耦合迭代采用Simple算法,涉及非稳态计算时,设定计算过程中的时间步长为
| $ \frac{{{\rm{d}}\chi }}{{{\rm{d}}t}} = \frac{{3 \times \left[ {\chi (n + 1) - \chi (n)} \right] - \left[ {\chi (n) - \chi (n - 1)} \right]}}{{2 \times \Delta t}}。$ | (2) |
式中:
通过编译程序,可对上层建筑内余水的容积、流水孔的流量及内部液面高度差分别进行实时积分及均化,得到不同时刻上层建筑的溢流参数,其具体表达式如下:
| $ \left\{ \begin{gathered} {V_{{\rm{water}}}} = \int {a{\rm{d}}V},\\ {Q_{{\rm{mass}}}} = \int {Q{\rm{d}}S/} {S_0},\\ {H_{{\rm{average}}}} = \int H {\rm{d}}S/{S_{iso}}。\\ \end{gathered} \right. $ | (3) |
式中:
流水孔实时平均流量
| $ \mu = \frac{{{Q_{{\rm{mass}}}}}}{{\rho {S_0}\sqrt {2g{H_{{\rm{average}}}}} }},$ | (4) |
| $ H' = {H_{{\rm{average}}}}/D。$ | (5) |
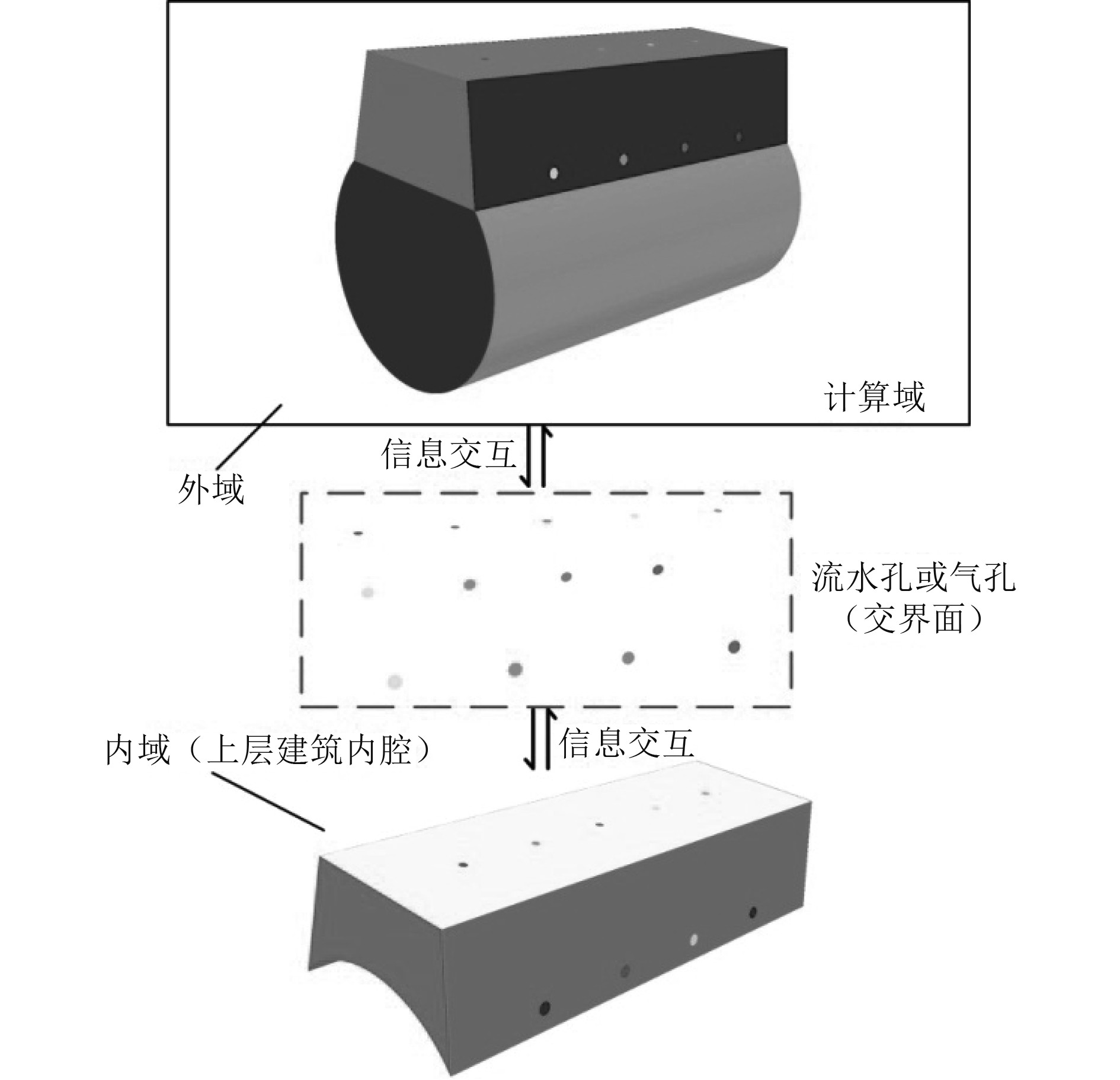
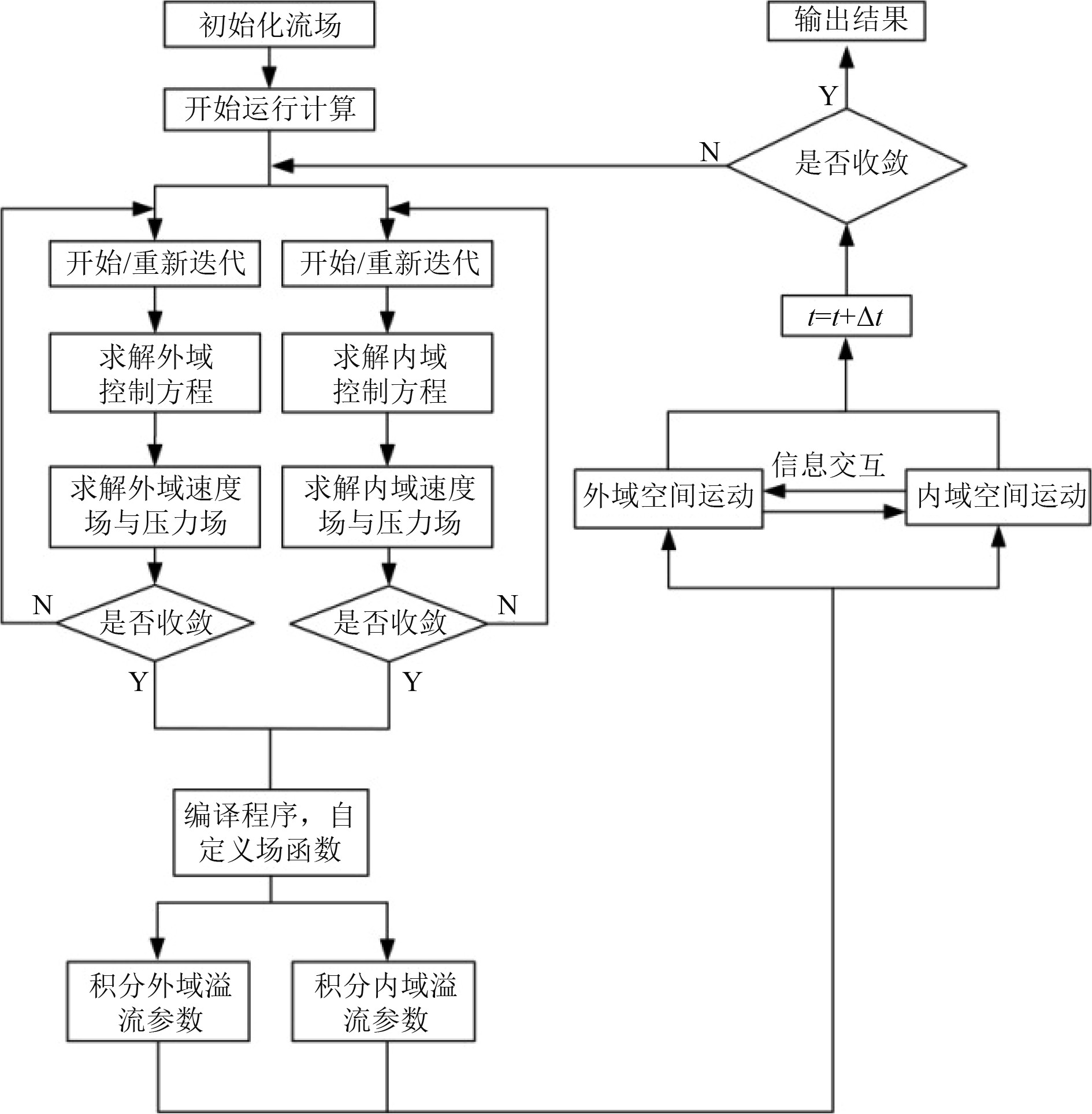
为了更好捕捉上层建筑内余水的容积、余水的高度、流水孔的流量以及内外域流通量等参数的时历变化,可将整个艇体外表面(含上层建筑以及流水孔的外表面)和计算域设定为外域,将上层建筑内腔设定为内域,将圆形流水孔和气孔设定为交界面(interface)作为内域和外域信息交互的媒介,内域和外域是同步运动的,内域与外域交互的示意图如图1所示,含内外域交互的计算方法的流程如图2所示。
|
图 1 内域与外域交互的示意图 Fig. 1 Schematic diagram of the interaction between inner and outer domains |
|
图 2 内域与外域交互计算方法的流程图 Fig. 2 Flowchart of computation methods for the interaction between inner and outer domains |
为了研究圆形流水孔的尺度效应问题以及对其流量系数展开探索研究,本文以某型潜艇的艇体中段且包含简易的上层建筑模型作为研究对象,对其开展多个不同大小的圆形流水孔自由出流的计算,模型由主艇体的平行体中段、梯形上层建筑、5个等距布置的通气孔及左右对称的多个圆形流水孔组成,模型三维图如图3所示,模型的主尺度参数如表1所示。
|
|
表 1 模型主尺度参数 Tab.1 Main scale parameters of the model |

|
图 3 含上建流水孔的艇中局部模型 Fig. 3 A partial model of the middle part of submarine |
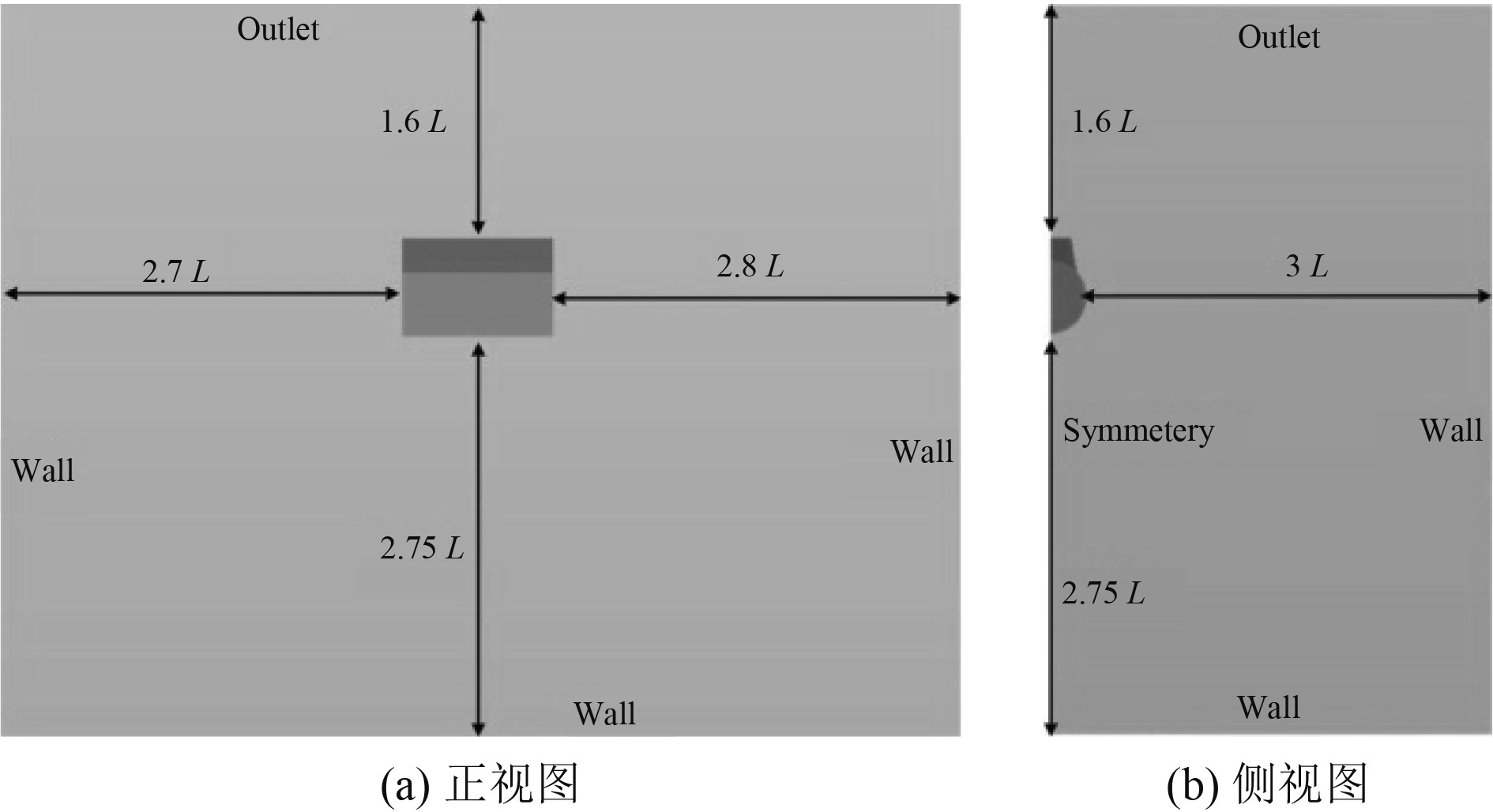
计算域采用方形计算域,艇体的首部、尾部、上部、底部以及中部距计算域的前端、后端、顶端、底端及侧面边界的距离分别为2.8 L,2.7 L,1.6 L,2.75 L,3 L,其中L=1 m。为了减少计算量,采用一半的计算域和一半的艇体进行计算,计算域右侧、前后端以及底部均设定为无滑移壁面(wall),上侧为压力出口(outlet),计算域左侧为对称面(symmetery),具体计算域及边界条件的划分如图4所示。
|
图 4 计算域及边界类型 Fig. 4 Calculate the domain and boundary conditions |
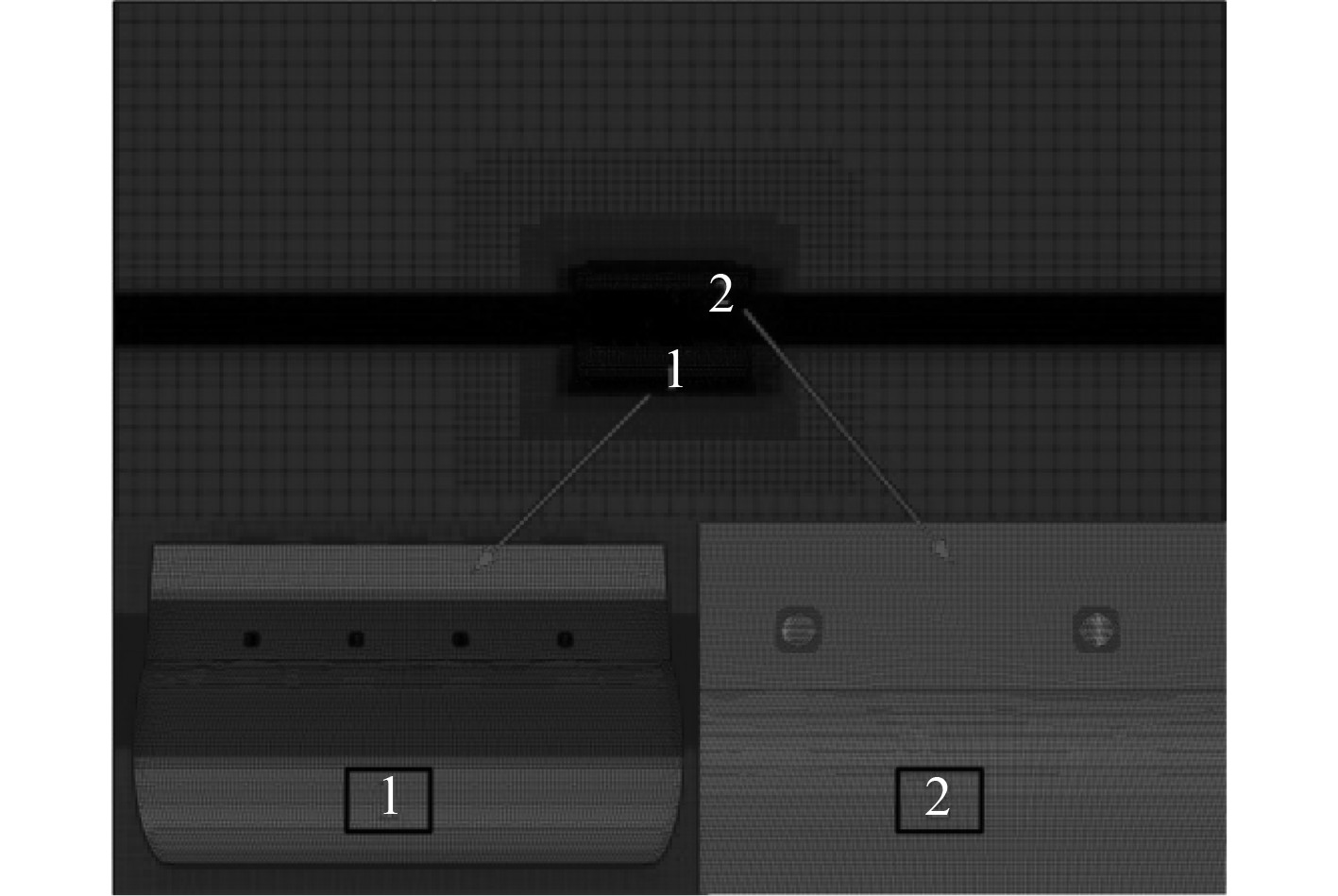
采用切割体网格对计算域和艇中模型进行网格离散,为确保近艇体湍流的准确求解以及流水孔流量、非水密上层建筑内部液舱高度的捕捉,需对艇体、流水孔以及非水密上层建筑的网格进行加密。为了清晰捕捉流水孔出水运动情况,采用内域和外域2种计算域相互交互的方式进行数值模拟计算,其中以流水孔和气孔为interface对内域和外域进行信息的交互,内域及外域网格划分如图5和图6所示。
|
图 5 外域网格 Fig. 5 Outland grid |

|
图 6 内域网格 Fig. 6 Domain grid |
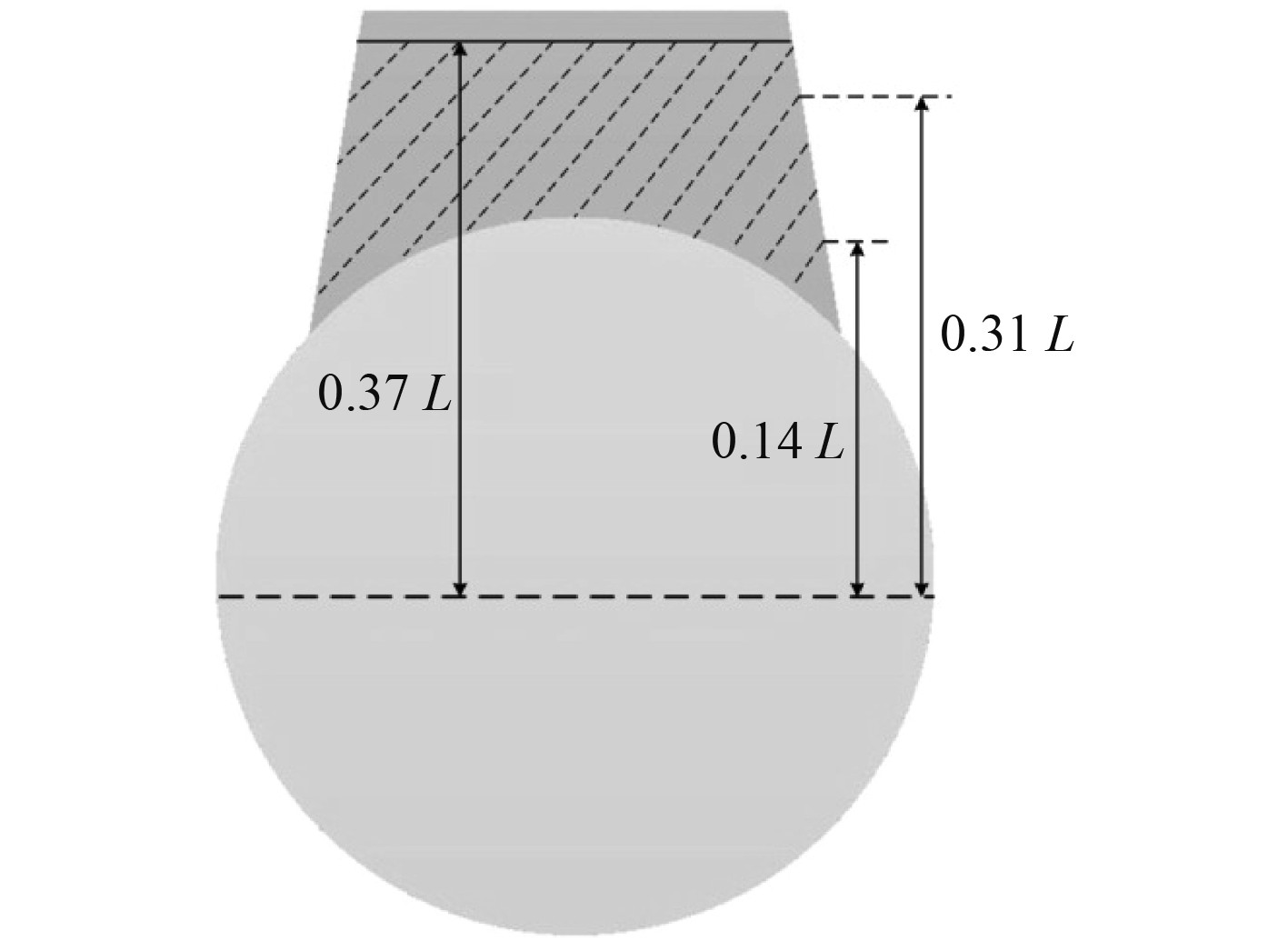
根据实艇的平行中体段流水孔的总面积,依据缩比将流水孔总面积等效成模型的流水孔总面积,为了研究不同尺寸大小流水孔对潜艇上层建筑背水的影响,分别选取缩比1∶25,1∶16.67以及1∶12.5三种不同尺寸的流水孔,参考实艇在水面状态的排水量以及其应急上浮出水后艇体的状态,根据缩比设计了2种模型的吃水,分别为0.14 L和0.31 L,非水密上层建筑内部液体的初始高度为0.37 L,模型的吃水如图7所示,流水孔的具体形式、尺寸大小及数量如表2所示。
|
|
表 2 流水孔的形式及尺寸大小 Tab.2 Form and size of water hole |
|
图 7 模型的吃水示意图 Fig. 7 The draft diagram of the model |

|
图 9 缩比为1∶16.67圆形流水孔的溢流情况 Fig. 9 The overflow condition of circle water hole with scale is 1∶16.67 |
图8~图10分别给出了不同缩比的圆形流水孔在吃水T=0.14 m时不同时刻孔口溢流以及上层建筑内的余水容积变化情况。对于缩比为1∶25的圆形流水孔,在t=20 s时上层建筑内还有少部分余水;对于缩比为1∶16.67的圆形流水孔,在t=12 s时上层建筑内还少部分余水;对于缩比为1∶12.5的圆形流水孔,在t=8 s时上层建筑内余水已经很少,在t=12 s时上层建筑内几乎没有余水。由此可知,流水孔的尺寸越大,在相同的时间内,流出的水越多,上层建筑内的余水越少。

|
图 8 缩比为1∶25圆形流水孔的溢流情况 Fig. 8 The overflow condition of circle water hole with scale is 1∶25 |

|
图 10 缩比为1∶12.5圆形流水孔的溢流情况 Fig. 10 The overflow condition of circle water hole with scale is 1∶12.5 |
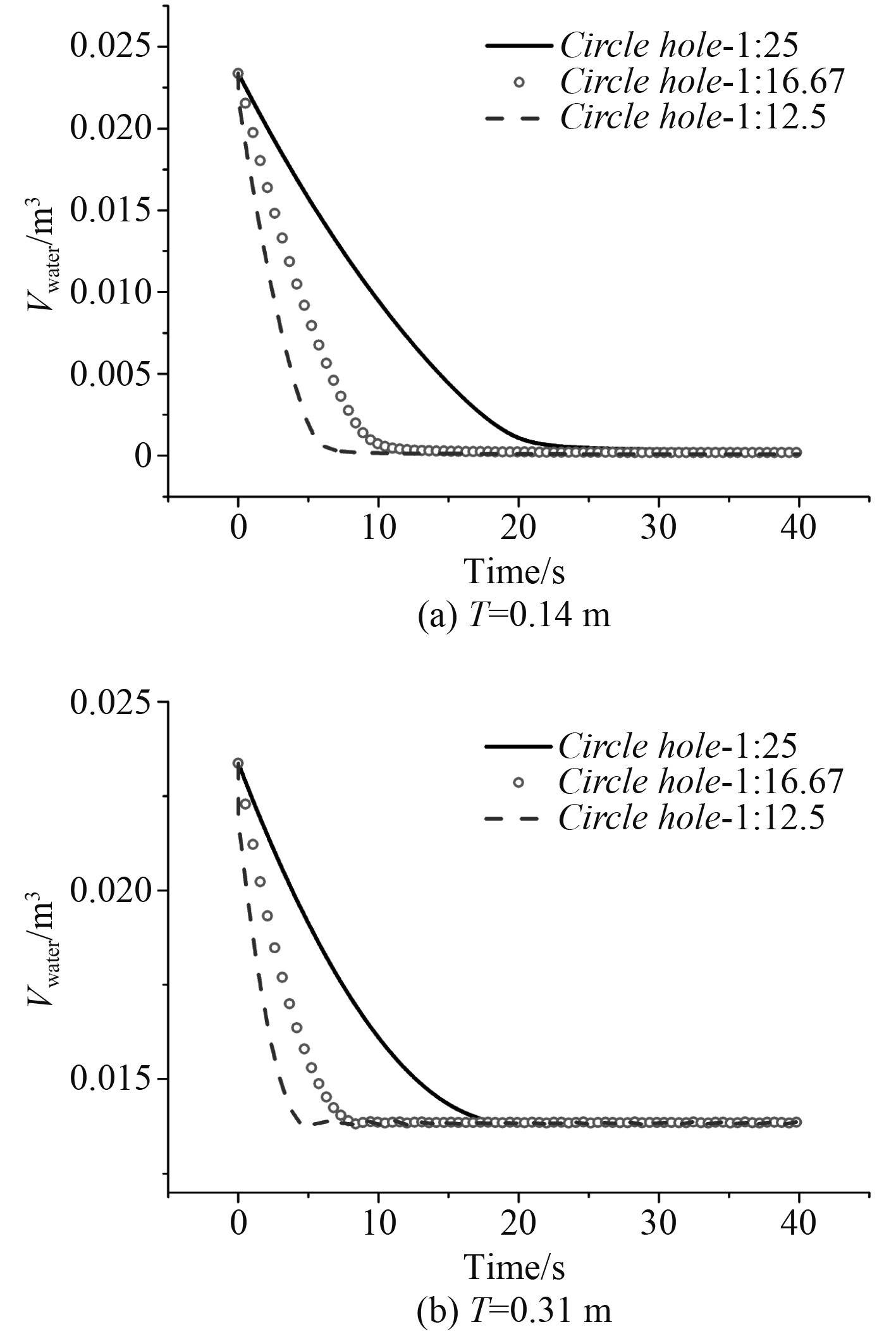
根据式(2),通过自定义场函数,对圆形流水孔上层建筑内余水容积、流水孔的流量、以及余水的高度等展开计算,图11~图13分别给出了不同缩比圆形流水孔在不同吃水下非水密上层建筑内余水的容积
|
图 11 不同圆形流水孔的上层建筑余水容积的时历曲线 Fig. 11 Time series of residual water volume of superstructure with different circle water holes |
|
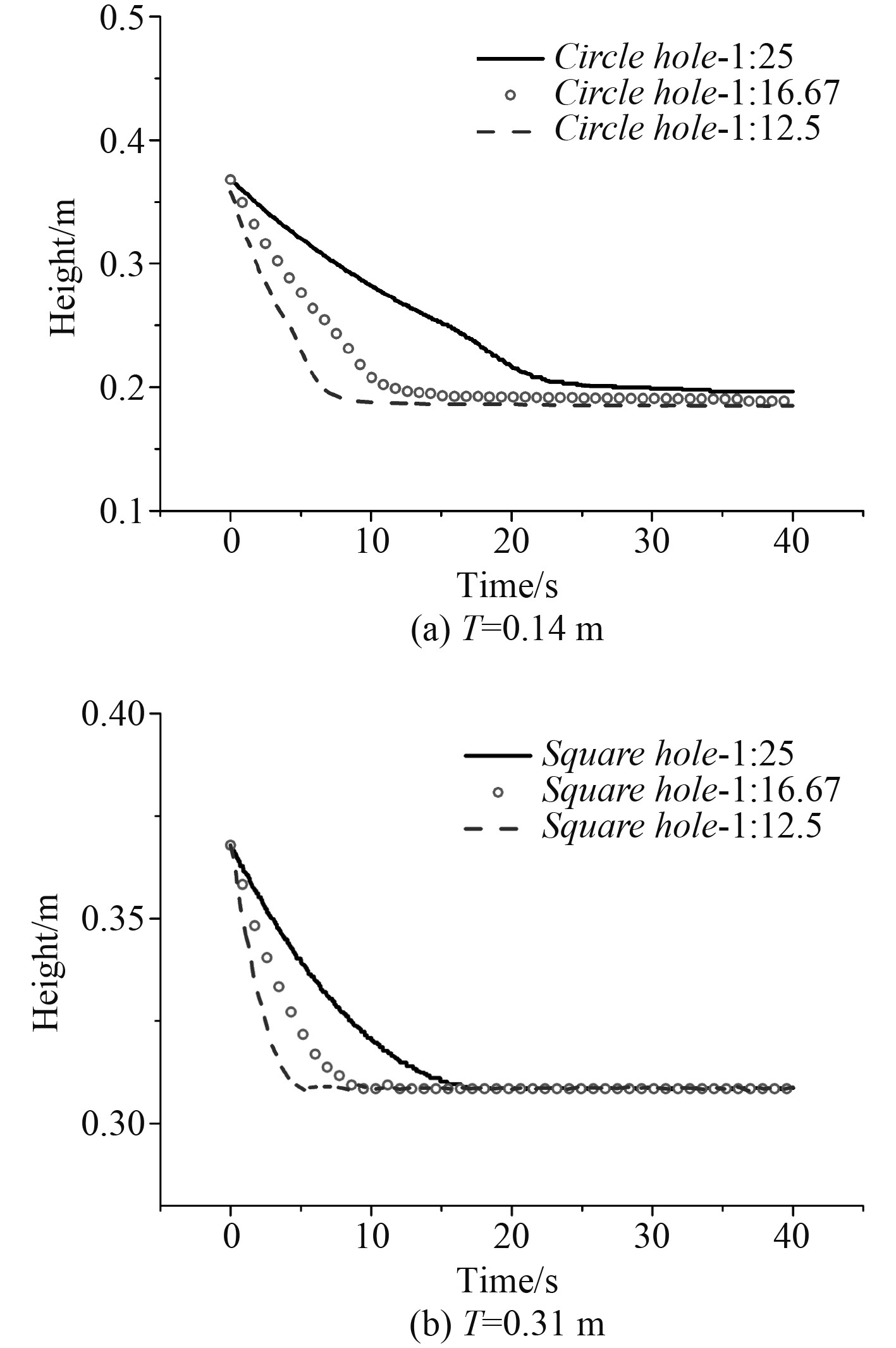
图 13 不同圆形流水孔上层建筑余水的高度的时历曲线 Fig. 13 Time series of residual water height of superstructure with different circle water holes |
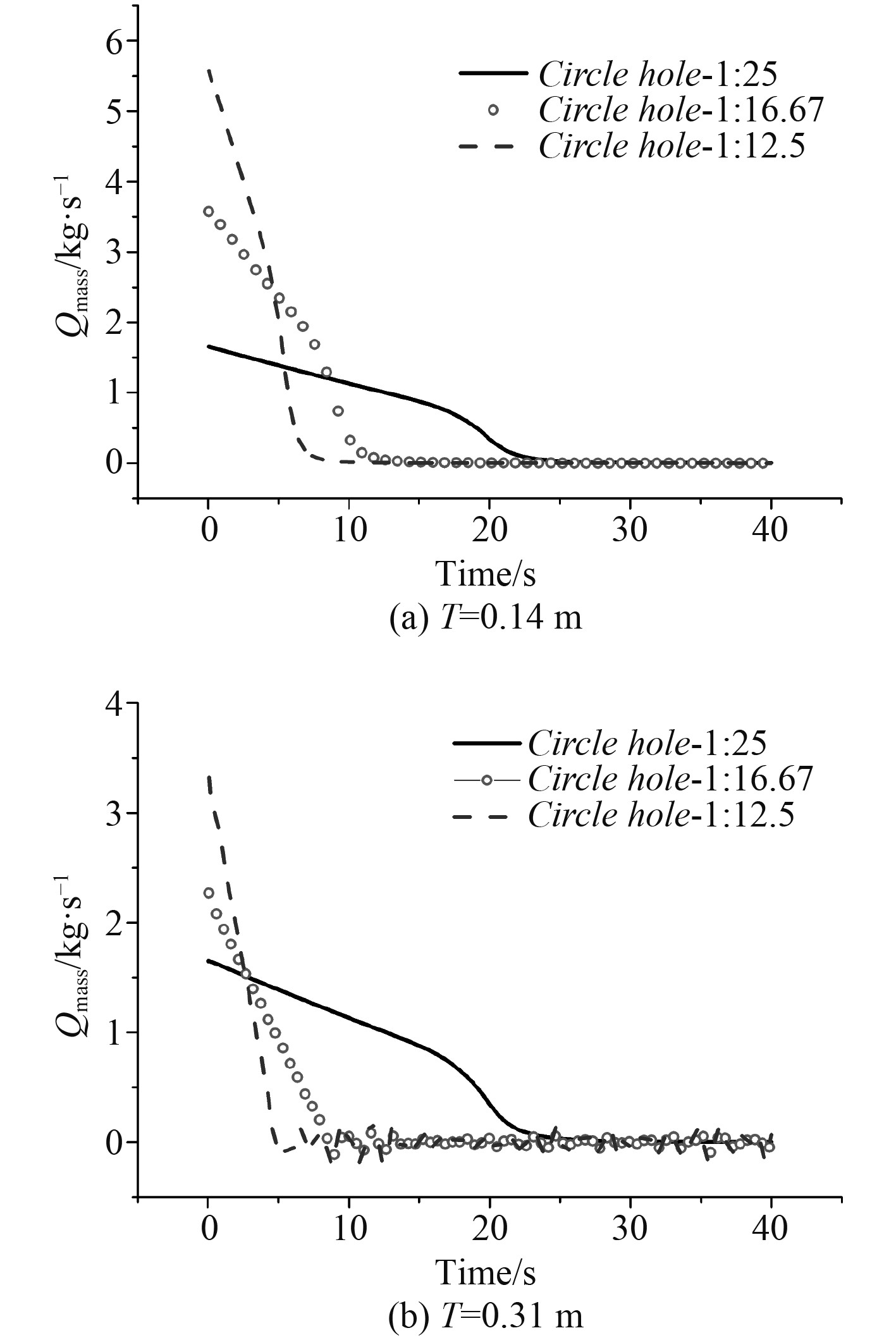
从图11~图13亦可知,当吃水T=0.14 m时,由于流水孔的位置高度大于吃水的高度,非水密上层建筑内的水经过一定时间流动,无论是哪种缩比的圆形流水孔,最终上层建筑的余水几乎为0;当吃水T=0.31 m时,即非水密上层建筑外的吃水高度大于流水孔开孔的高度时,非水密上层建筑内余水容积以及流水孔流量稳定后的值都存在一定的波动。这是由于当发生水流的流动时,容易造成非水密上层建筑内存在回流的现象;无论吃水是0.14 m还是0.31 m,圆形流水孔面积越大,余水高度值就越小。
|
图 12 不同圆形流水孔的流量时历曲线 Fig. 12 Time series of the rate of flow with different circle water holes |
同理根据流水孔孔口质量流量
|
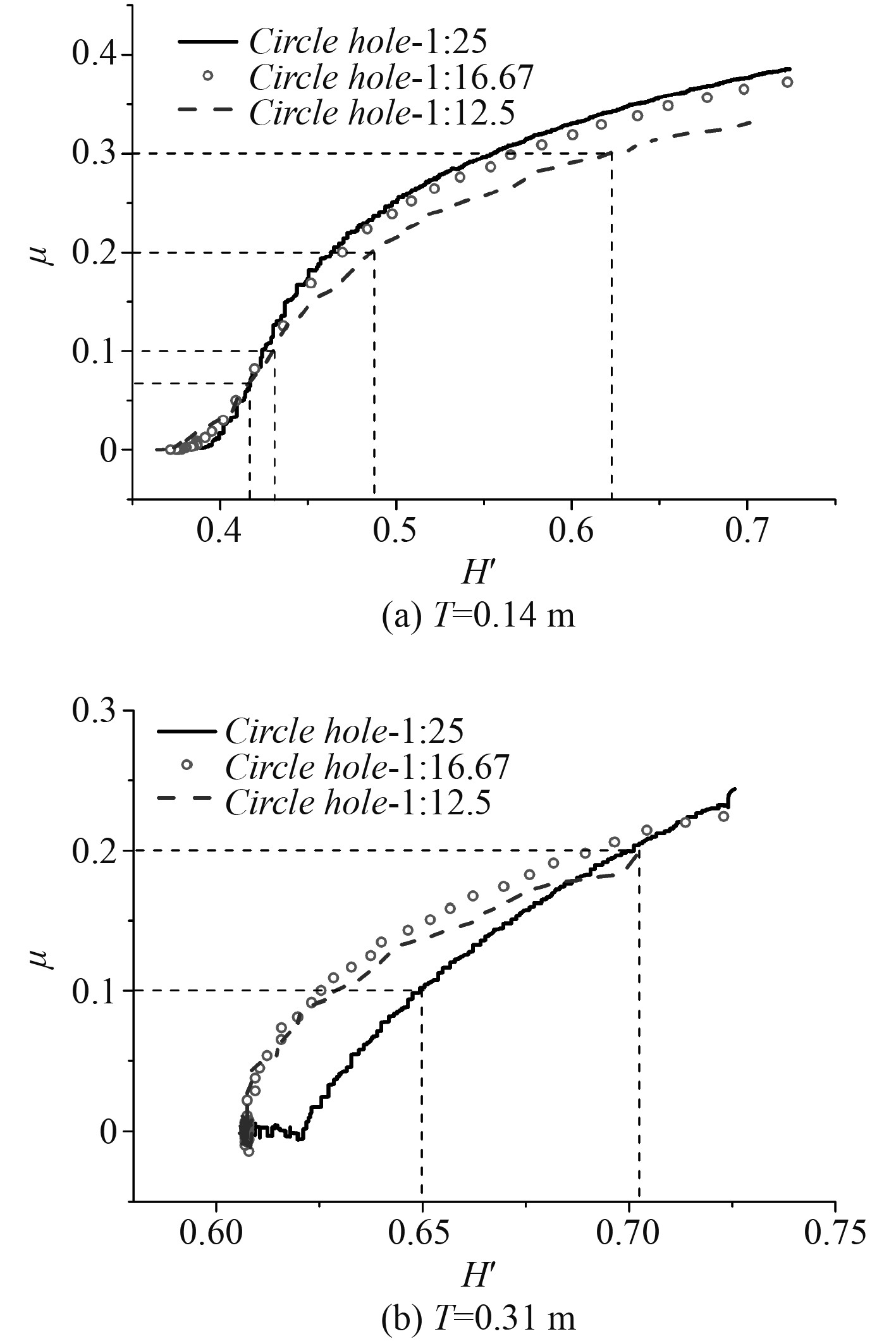
图 14 不同圆形流水孔的流量系数 Fig. 14 Flow coefficient of different square water holes |
对于吃水T=0.14 m,无因次高度差
从图14可知,对于吃水T=0.14 m,圆形流水孔面积越大,其流水孔流量系数就越大。圆形流水孔缩比为1∶25时,流量系数最大,圆形流水孔缩比为1∶16.67时,流量系数次之,圆形流水孔缩比为1∶12.5时,流量系数最小。对于吃水T=0.31 m,圆形流水孔缩比为1∶16.67时,流量系数最大,圆形流水孔缩比为1∶12.5时,流量系数次之,圆形流水孔缩比为1∶25时,流量系数最小。综合2种吃水的对比分析,缩比为1∶16.67的流水孔尺寸为最优。
4 结 语1)基于滑移网格,采用内外域交互的计算方法,对潜艇的局部含上层建筑模型在不同吃水下不同尺寸大小流水孔的流量系数开展数值计算,该方法可为流水孔的特性分析和实艇的流水孔方案设计提供一定的借鉴。
2)通过对比分析不同缩比的圆形流水孔在不同吃水下流量系数随无因次高度差的变化,研究发现流水孔的尺寸越大,其非水密上层建筑内余水的容积和余水的高度变化值越快,流水孔的流量越大;综合对比分析,圆形流水孔缩比为1∶16.67的流量系数最优,因此,实艇流水孔尺寸大小及总面积的优化设计中,根据换算可参考此缩比的流水孔尺寸进行优化设计。
| [1] |
孟生, 张宇文, 裴環. 潜艇流水孔阻力特性分析[J]. 计算机测量与控制, 2011, 19(5): 1098-1011. |
| [2] |
孟生, 张宇文, 李林杰. 潜艇流水孔偏角特性研究[J]. 计算机仿真, 2011, 28(5): 17-25. DOI:10.3969/j.issn.1006-9348.2011.05.005 |
| [3] |
张航, 冯大奎, 蔡潇, 等. 开孔分布对空腔流动特性的分析[J]. 舰船科学技术, 2017, 39(6): 48-52. DOI:10.3404/j.issn.1672-7619.2017.06.010 |
| [4] |
张楠, 沈泓萃, 姚惠之. 带流水孔潜体流场数值模拟[J]. 船舶力学, 2004, 8(1): 1-11. DOI:10.3969/j.issn.1007-7294.2004.01.001 |
| [5] |
张楠, 沈泓萃, 姚惠之. 潜艇流水孔阻力数值计算与回归分析研究[J]. 船舶力学, 2004, 8(4): 5-15. DOI:10.3969/j.issn.1007-7294.2004.04.002 |
| [6] |
张言才, 宋建荣. 船舶压载水舱流水孔选型的模糊综合评判[J]. 江苏船舶, 2014, 31(3): 4-7. DOI:10.3969/j.issn.1001-5388.2014.03.002 |
| [7] |
张允. 开孔潜体流场与声场的数值模拟[D]. 上海: 上海交通大学, 2011.
|
| [8] |
熊鳌魁, 仲夏, 包胜平. 二维潜艇流水孔空腔减阻数值研究[J]. 武汉理工大学学报(交通科学与工程版), 2014, 38(2): 280-284. |
| [9] |
李维嘉, 江涛, 蔡斌. 基于ADAMS优化设计的某潜艇用流水孔启闭装置[J]. 中国舰船研究, 2014, 9(4): 113-119. DOI:10.3969/j.issn.1673-3185.2014.04.019 |
 2022, Vol. 44
2022, Vol. 44
