随着海洋工程与海上交通运输事业的快速发展,国际、国内航行船舶与日俱增,运力得到大幅提升,海上安全问题越来越受到重视。不管是海上补给还是海上作业,船与船间的水动力干扰问题不容忽视。一方面,由于船舶本身受到风、浪、流等环境外力的影响,会产生6个自由度的运动响应,从而严重影响海上补给或作业的顺利实施;另一方面,两船在有限间距范围内同速、同向航行时,两船对其内侧的流场将产生干扰,因此即使是在风浪较小的低海况下,两船并行作业时也可能产生剧烈的运动响应。所以,近年来有关两船间的水动力干扰问题受到许多学者的关注。
Inoue等[1]使用三维源汇法,计算了浮式生产储油设备(floating production storage and offloading,FPSO) 与液化天然气(liquefied natural gas,LNG)船在旁靠状态下的一阶波浪力、附加质量和阻尼系数,并与模型试验结果进行对比验证。Fang等[2]对两船波浪中的相对运动及波面抬高进行了数值计算和模型试验。Hong等[3]对一艘FPSO与LNG终端船的旁靠系统在不规则波浪下进行时域分析,并与模型试验进行对比。郑平宇等[4]对补给过程中并行两船的耐波性进行时域分析,并总结出两船在补给过程中的耐波性特点。何学军等[5]采用势流理论对横向补给的两船在波浪中的运动响应进行频域和时域分析。周广礼等[6]基于求解RANS方程的方法,对静水中单船与两船并行航行时的水动力差异进行讨论。
目前,研究两船间水动力干扰的研究主要是基于势流理论来开展。近年来,随着计算机技术的发展,采用基于RANS方程的粘流理论来求解船舶在波浪中的运动得以实现,因此采用粘流理论求解波浪中船舶的水动力特性逐渐受到学者们的青睐。本文采用商业软件STAR-CCM+中基于求解RANS方程的方法,对波浪中两船的水动力特性进行数值模拟。首先,通过数值造波和消波技术模拟规则波,对波浪中并靠两船的水动力相互作用进行分析;然后,通过与试验结果的对比,验证数值方法的可行性。最后在此基础上,进一步分析并行两船在不同波长和不同间距下的运动响应以及波浪力的变化规律。
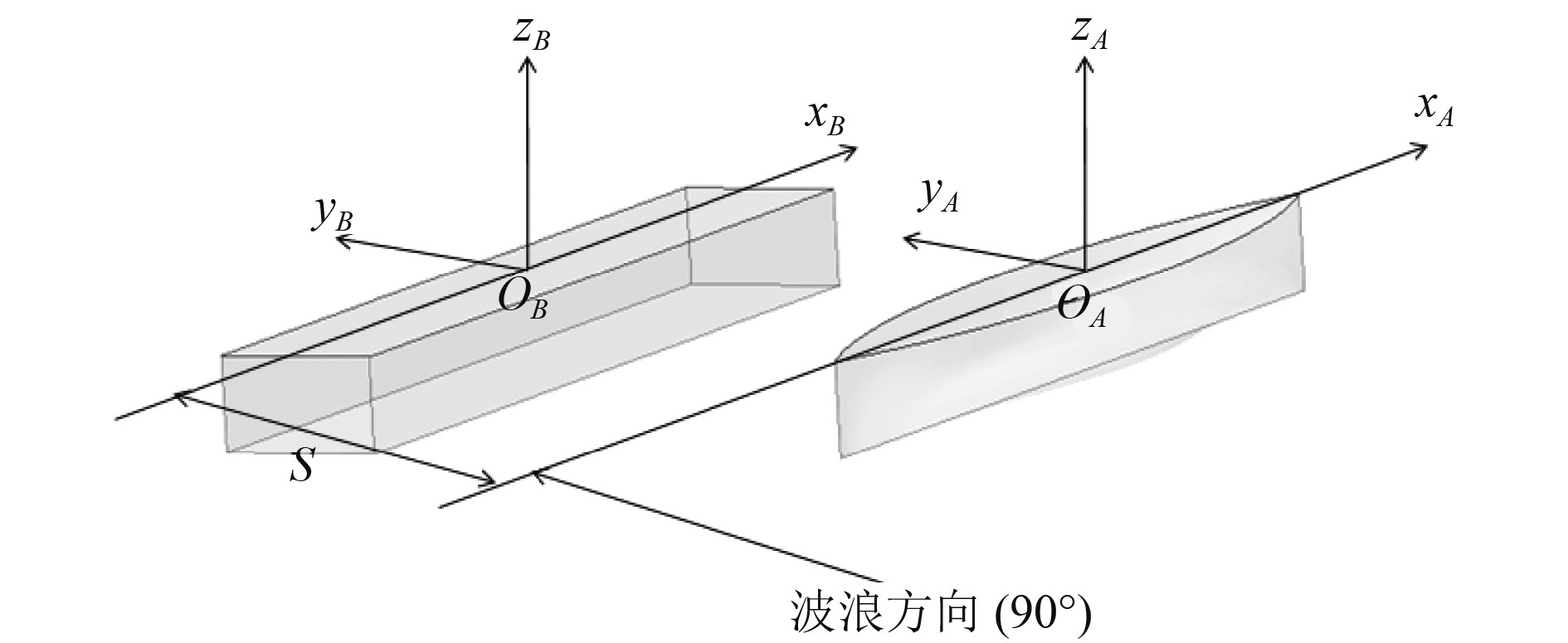
1 数值方法 1.1 坐标系及结果表达形式本文采用的坐标系如图1所示。图中,x轴的正方向指向船首,y轴的正方向指向船的右舷,坐标原点为船舶中线面、中站面与水线面的交点,S为两船中纵剖线的相对位置(两船横向间距)。本文主要研究两船在横浪(90°)中的水动力特性。
|
图 1 两船的随船坐标系 Fig. 1 Coordinate systems of ships |
采用雷诺平均方法对两船的水动力特性进行求解。在空间固定坐标系下,控制方程如下:
| $ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0 \text{,} i=\mathrm{1,2},3 ;$ | (1) |
| $ \mathrm{\rho }\frac{\partial {u}_{i}}{\partial t}+\mathrm{\rho }{u}_{j}\frac{\partial {u}_{i}}{\partial {x}_{j}}=-\frac{\partial p}{\partial {x}_{i}}+\mu \frac{\partial }{\partial {x}_{j}}\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}-\rho \overline{{u}_{i}'{u}_{j}'}\right)。$ | (2) |
式中:
计算选用RNG
| $ \frac{\partial (\rho k)}{\partial t}+\frac{\partial (\rho k{u}_{i})}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left[\left(\mu +\frac{{u}_{t}}{{\sigma }_{k}}\right)\frac{{\partial }_{k}}{\partial {x}_{j}}\right]+{P}_{k}-\rho \varepsilon,$ | (3) |
| $ \begin{split} \frac{\partial (\rho \mathrm{\varepsilon })}{\partial t}+\frac{\partial (\rho \mathrm{\varepsilon }{u}_{i})}{\partial {x}_{i}}=&\frac{\partial }{\partial {x}_{j}}\left[\left(\mu +\frac{{u}_{t}}{{\sigma }_{\mathrm{\varepsilon }}}\right)\frac{{\partial }_{k}}{\partial {x}_{j}}\right]+ \\ &{C}_{\mathrm{\varepsilon }1}{\frac{\mathrm{\varepsilon }}{k}P}_{k}+{C}_{\mathrm{\varepsilon }2}\rho \frac{{\mathrm{\varepsilon }}^{2}}{k}-{R}_{\varepsilon }。\end{split} $ | (4) |
式中:
采用重叠网格实现船体在计算域中的运动。重叠网格方法是将复杂的流动区域分成几何边界比较简单的子区域,各子区域各自生成独立的计算网格,子区域与背景区域之间存在着重叠、嵌套或覆盖的关系,它们之间的流场信息通过在重叠域边界进行插值来传递。在处理动态问题上,重叠网格技术可以解除物体与网格之间在拓扑结构上的约束关系,能够让结构物在计算域内自由的运动而不受背景区域网格结构的影响。因此,重叠网格技术能够用来模拟船舶在波浪中的运动响应问题。
1.4 自由液面的模拟现阶段在使用RANS方程求解流场的粘性流动时,自由面的模拟主要有界面追踪法和界面捕捉法2种。作为界面捕捉法中的一种,在处理多相流问题方面,流体体积(volume of fluid,VOF)方法的应用比较广泛。本文所研究的两船干扰水动力特性问题属于气、液两相流问题,因此,采用VOF方法对自由液面进行捕捉。
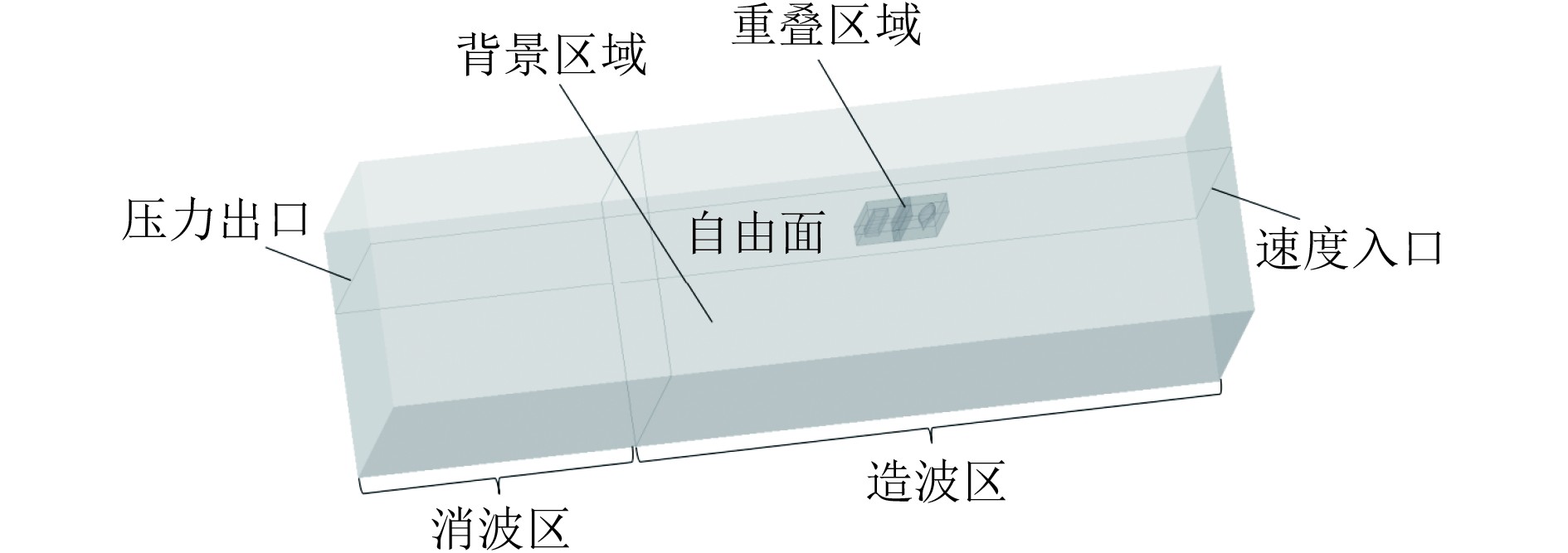
2 计算模型及网格划分 2.1 计算模型及边界条件选取Wigley船型(船a)和方形驳船(船b)作为计算对象来开展两船间水动力干扰的数值计算,其主尺度及船型参数如表1所示,计算区域及边界条件的设置如图2所示。计算域为长方体,尺寸为18 m×6 m×6 m,水深4 m,远大于1/2的波长。计算域的边界条件为:造波入口设为速度入口,计算域尾端设为压力出口,流域左、右两侧设为对称面,流域顶部和底部设为速度入口。另外,在背景域尾端设置6 m长的消波区域,在造波入口进行造波,并通过水池尾端的消波区进行消波。
|
|
表 1 模型主尺度 Tab.1 Main dimensions of models |
|
图 2 计算域及边界条件 Fig. 2 Computational domain and boundary conditions |
在CFD数值仿真中提高计算精度的方法之一,就是选择合理的网格划分方案。为了能够准确计算船舶在波浪中的运动,在划分网格时,需保证一个波长内至少有60个网格,一个波高内至少有10个网格。数值水池采用重叠网格进行模拟,分为背景和重叠2个区域。整个计算域设为背景区域,两船附近区域则设置为重叠区域,重叠区域和背景区域的交界面设置为Interface overset,2个区域通过此交界面进行流场数据的传递。建立3个不同网格数量的计算模型,3种计算模型的总网格数分别为320万(粗网格M1)、400万(中网格M2)和540万(细网格M2)。表2给出了不同网格数模型的计算结果与试验值的对比,其中,船舶所受的波浪力峰值按
|
|
表 2 不同网格数条件下的计算结果对比 Tab.2 Comparison of calculation results with different grids |

|
图 3 整个计算域网格 Fig. 3 Grid of whole computational domain |

|
图 4 重叠网格区域局部网格 Fig. 4 Overset grids |
相比于传统的物理试验水池,数值波浪水池具有更高效、更快捷的水动力预报功能,同时还可对多种流动参数进行选择。国内外研究人员在数值造波方面进行了大量研究。王永学[8]基于造波机理论,采用VOF方法建立了二维数值水池模型。邹志利等[9]应用仿物理造波原理,通过设定造波板边界的运动模拟出了规则波。刘加海[10]基于仿物理造波原理,通过设定造波板边界的运动,在Fluent软件建立了二维数值波浪水池。之后,Park等[11]建立了三维随机波浪数值水池。为了较好地模拟船舶在波浪中的运动响应,首先建立数值波浪水池并验证其造波的正确性和可行性。根据两船的主尺度,选取水池主尺度为18 m×6 m×6 m进行造波。为了获得较为准确的造波结果,在网格加密形式上进行了大量探索,最后采用3层控制体网格加密形式,其中第1层控制体波浪传播方向的网格尺寸为5 cm,波高方向的网格尺寸为0.5 cm,也就是在一个波长范围内设置80个网格,一个波高范围内设置10个网格。在本文的造波算例中(波长为4 m,波高为0.025 m),网格总数约为100万。
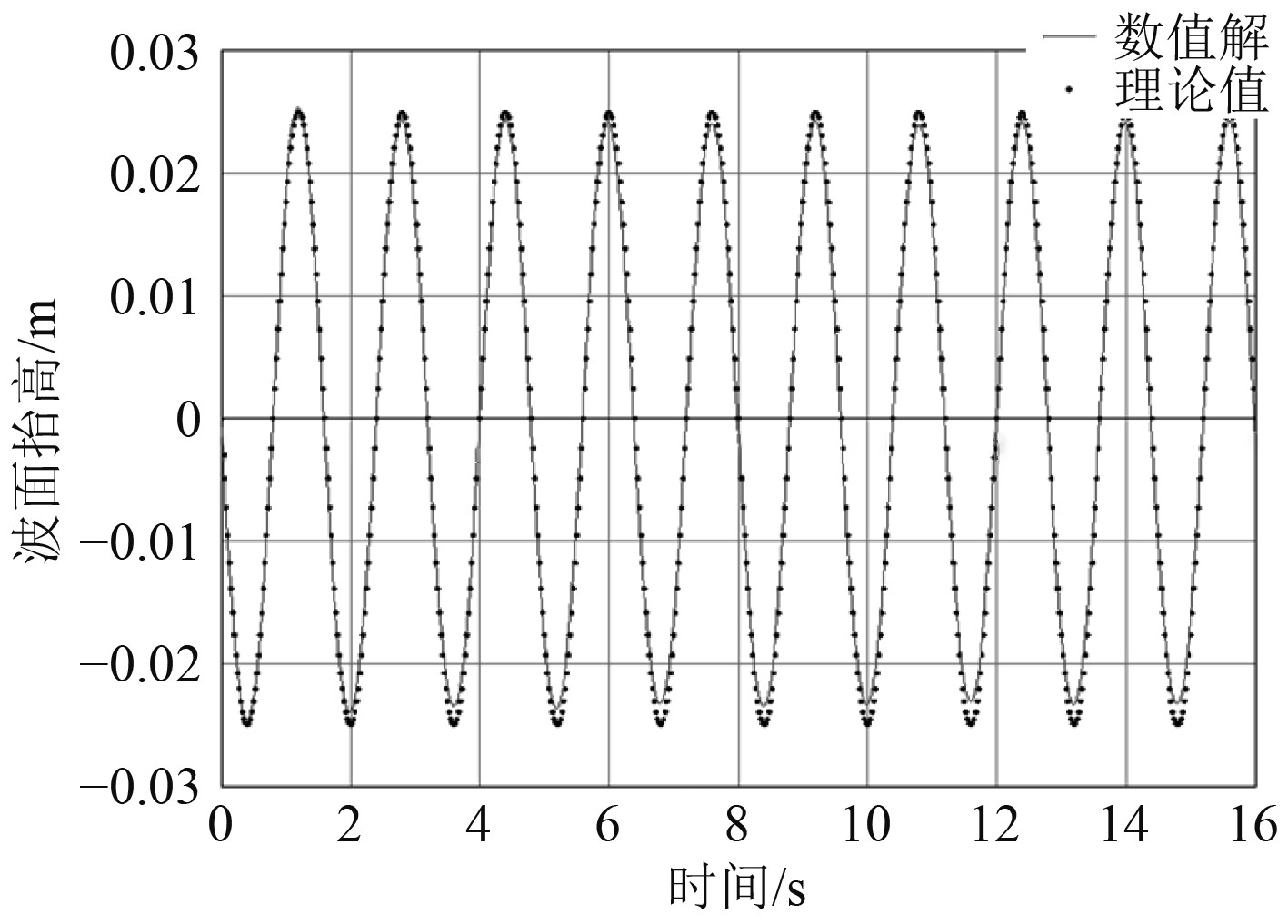
图5为水池内10个波浪周期后的波形情况,图6为y=6 m(

|
图 5 10个周期后的波面图 Fig. 5 Distribution of calculated wave pattern |
|
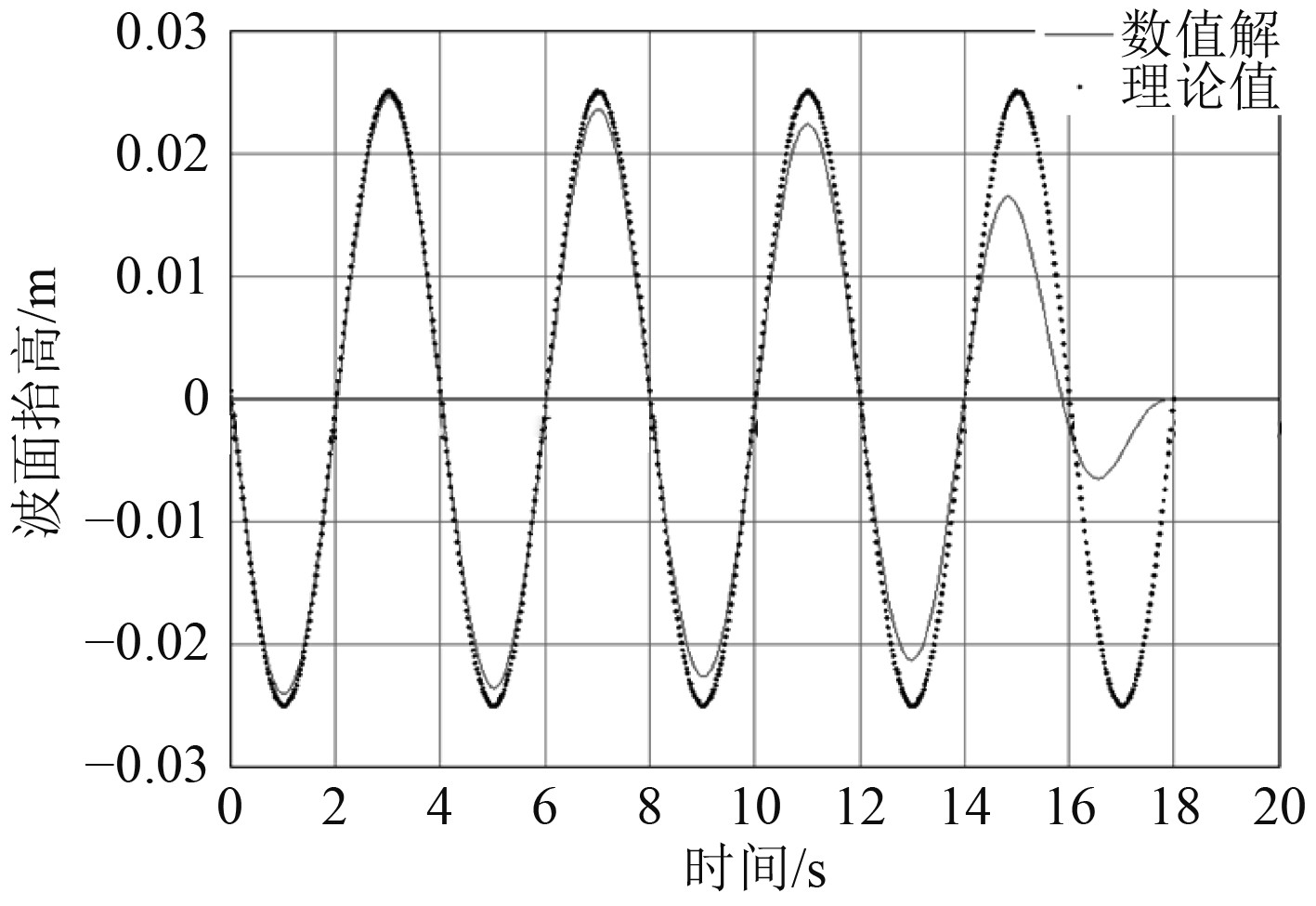
图 6
|
|
图 7 规则波10个周期后波形与理论值的对比 Fig. 7 Comparison of calculated wave pattern and theoretical values |
为了获得两船在不同波长条件下所受横荡力和垂荡力的变化规律,计算两船在
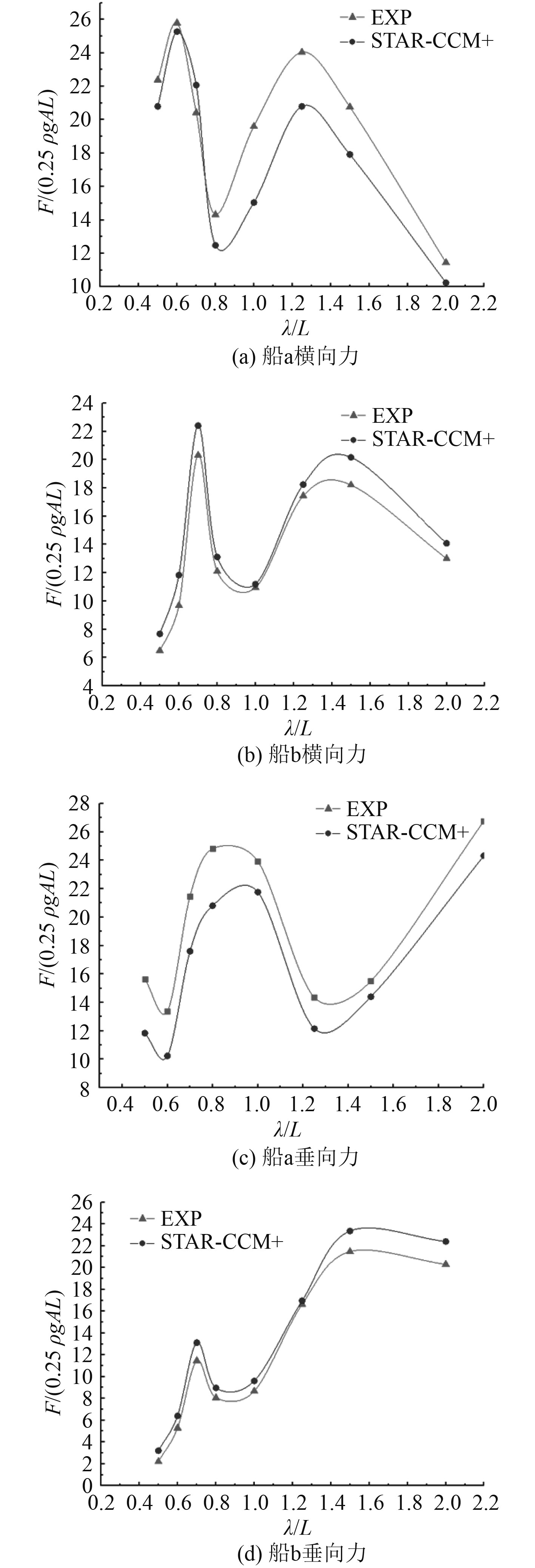
|
图 8 试验值与数值计算值的对比 Fig. 8 Comparison of numerical results and experimental data |
由前述讨论可知,当波长
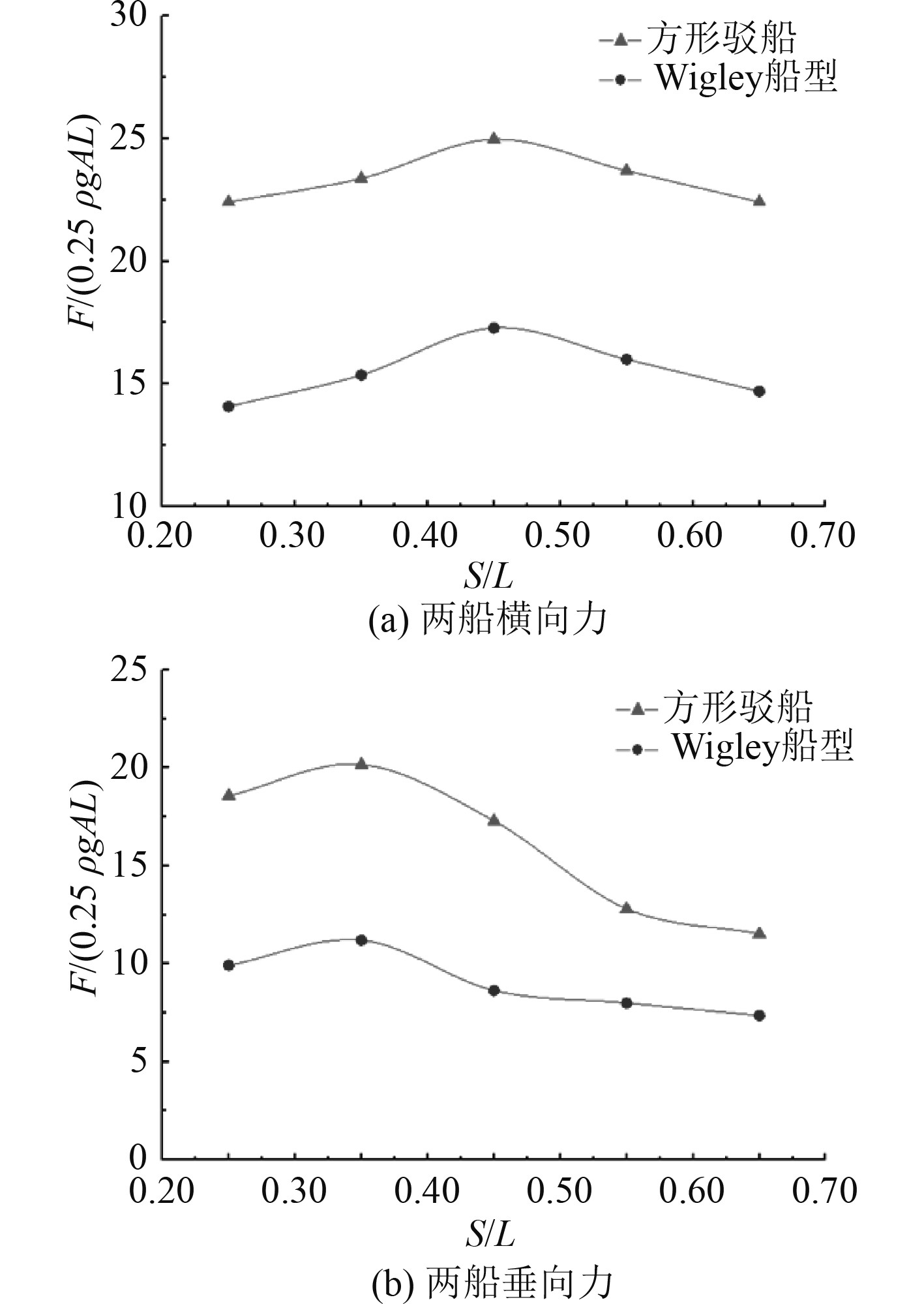
|
图 9 不同间距下两船所受横向力和垂向力的变化规律 Fig. 9 Lateral force and vertical force of two ships with different distances |
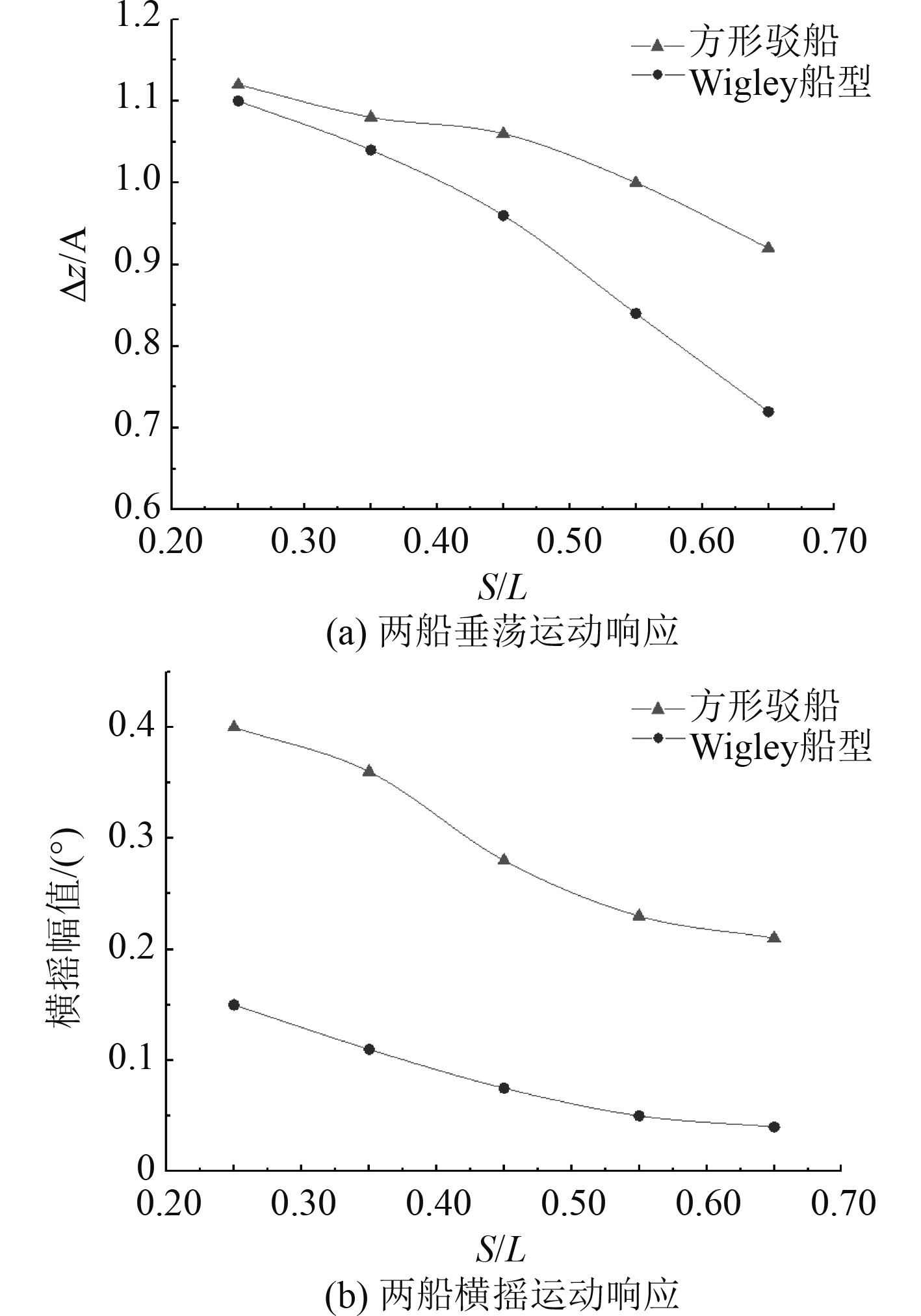
|
图 10 不同间距下两船运动响应的变化规律 Fig. 10 Responses of two ships with different distances |
图11为间距S/L=0.35时一个波浪周期内两船间的波面情况。可以看出,两船间隔内的波面抬高峰值基本为入射波波幅的2倍,且波面抬高峰值主要出现在间隔内的中部区域,这说明能量在间隔中部区域较为集中。这是因为在此间距条件下,入射波从船首和船尾进入两船间隔内后,在两船侧不断地反射与叠加作用下,致使间距内出现了比较明显的波面放大。

|
图 11 一个周期内两船间波面的升高变化 Fig. 11 Distribution of wave heights between two ships |
本文采用重叠网格技术对波浪中两船间的水动力特性进行数值模拟,并将计算结果与试验结果进行比较分析。同时,讨论了波长和两船间距对两船受力的影响,主要得到以下结论:
1)在采用基于重叠网格的数值方法计算两船间的水动力特性时,得到了稳定、收敛的计算结果,说明本文采用的方法可行、稳定。
2)计算了在一定横向间距条件下,不同入射波波长对两船横向力和垂向力的影响,发现计算结果与试验结果吻合较好,能够较准确地捕捉到波长变化时两船受力特性的变化规律。
3)在入射波波长一定时,随着两船间距的增加,两船的横向力和垂向力呈现出先增大后减小的趋势,两船的横向力和垂向力分别在
综上所述,本文采用的基于重叠网格的数值方法预报波浪中两船间的水动力特性可行而有效。
| [1] |
INOUE Y, ISLAM M. Relative motions of multiple floating offshore structures[C]//Proceedings of the18th Offshore Mechanics and Arctic Engineering Conference, Canada, OMAE, 1999.
|
| [2] |
FANG M C, CHEN G R. On three-dimensional solutions of drift forces and moments between two ships in waves[J]. Journal of Ship Research, 2002, 46(4): 280-288. DOI:10.5957/jsr.2002.46.4.280 |
| [3] |
HONG S Y, KIM J H, CHO S K, et al. Numerical and experimental study on hydrodynamic interaction of side-by-side moored multiple vessels[J]. Ocean Engineering, 2005, 32(7): 783-801. DOI:10.1016/j.oceaneng.2004.10.003 |
| [4] |
KASHIWAGI M, ENDO K, YAMAGUCHI H. Wave drift forces and moments on two ships arranged side in waves[J]. Ocean Engineering, 2005, 32(5/6): 529-555. |
| [5] |
郑平宇, 李鹏, 刘敬喜, 等. 两船并行补给过程中耐波性的分析[J]. 中国舰船研究, 2017, 12(2): 30-40,48. ZHENG Peng-yu, LI Peng, LIU Jing-xi, et al. Seakeeping analysis of two ships advancing parallel for underway replenishment[J]. Chinese Journal of Ship Research, 2017, 12(2): 30-40,48. DOI:10.3969/j.issn.1673-3185.2017.02.004 |
| [6] |
何学军, 谭智尤, 余鹏. 横向补给状态下两船的摇荡运动特性[J]. 舰船科学技术, 2014, 36(10): 23-26. HE Xue-jun, TAN Zhi-you, YU Peng. Analysis of ship swaying motions of alongside replenishment[J]. Ship Science and Technology, 2014, 36(10): 23-26. DOI:10.3404/j.issn.1672-7649.2014.10.006 |
| [7] |
周广礼, 董文才, 肖汶斌. 静水中并行两船水动力干扰数值研究[J]. 船舶力学, 2015, 19(3): 237-248. ZHOU Guang-li, DONG Wen-cai, XIAO Wen-bin. Numerical study on the hydrodynamic interaction of ship-ship models in calm water[J]. Journal of Ship Mechanics, 2015, 19(3): 237-248. DOI:10.3969/j.issn.1007-7294.2015.03.002 |
| [8] |
王永学. 无反射造波数值波浪水槽[J]. 水动力学研究与进展(A辑), 1994, 9(2): 205-214. WANG Yong-xue. Numerical wave channel with absorbing wave-maker[J]. Journal of Hydrodynamics(Ser. A), 1994, 9(2): 205-214. |
| [9] |
邹志利, 邱大洪, 王永学. VOF方法模拟波浪槽中二维非线性波[J]. 水动力学研究与进展(A辑), 1996, 11(1): 93-103. |
| [10] |
刘加海. 二维水槽数值造波分析研究[J]. 黑龙江水利科技, 2006, 34(2): 39-41. DOI:10.3969/j.issn.1007-7596.2006.02.013 |
| [11] |
PARK J C, UNO Y, SATO T, et al. Numerical reproduction of fully nonlinear multi-directional waves by a viscous 3D numerical wave tank[J]. Ocean Engineering, 2006, 31(11/12): 1549-1565. |
 2022, Vol. 44
2022, Vol. 44

