0 引　言

一旦船舶发生故障，不仅会影响既定作业的顺利完成，还会威胁船上人员的生命安全。船舶在运行过程中，会产生海量的运行数据，其中因外部环境干扰、船舶本身故障以及不合理参数设置等产生的船舶故障数据^[1-3]，是反映船舶运行状态的重要依据，因此从海量船舶运行数据中挖掘出船舶故障数据，对船舶故障诊断和维修发挥着巨大价值^[4]。

相关专家对海量船舶故障数据挖掘方法展开了深入研究，黄文秀等^[5]和常文兵等^[6]，分别利用改进的k最邻近算法以及文本分析方法，实现海量船舶故障数据挖掘。这2种方法能有效避免空洞数据集对挖掘结果的干扰，且挖掘效率较高，但所得挖掘结果存在较多冗余，同时易受类间小扰动的影响。模糊运算聚类算法可依据分类对象特征，通过模糊数学方法将具有较大相似性的对象样本划分到同一类，对于大规模、不确定的数据具有极好的聚类能力，已被广泛应用于商业和地理等领域的数据挖掘中，因此本文分析海量船舶故障数据挖掘中的模糊运算聚类算法。

1 海量船舶故障数据挖掘研究 1.1 海量船舶故障征兆变量提取

船舶运行过程中生成的全部数据均保存在SCADA系统历史数据库内，为从海量船舶运行数据中提取船舶故障征兆变量，引入局部切空间排列算法，海量船舶故障征兆变量提取的具体过程：

1）通过相空间对海量船舶运行数据表示，时间序列为x₁,x₂,…,x_N，维数为m，相空间向量为X_i=[x_i,x_i+τ,…,x_{i+(m-1) τ}，时延步长为τ。

2）相空间内的船舶运行数据点为x_i，利用欧式距离测度函数获取数量为k的邻近点，局部邻域为 ${X_j} = \left[ {{x_{{i_1}}},{x_{{i_2}}},...,{x_{{i_k}}}} \right] 。$ .

3）从x_i邻域中选取的正交基向量Q_i，邻域中各点至W的正交投影为 $\theta _j^{\left( i \right)} = Q_i^{\rm{T}}\left( {{x_{{i_j}}} - {{\bar x}_i}} \right)$ ，局部邻域内某点为 $ {x_{{i_j}}} $ ；邻域数据的平均值为 $ {\bar x_i} $ 。 $ {\Theta _i} $ 表示各正交投影组成的局部向量坐标，反映x_i邻域中的几何结构信息。

4）依据 $ {\Theta _i} $ 获得的x_i的全局向量坐标。

5）相空间向量内的低维全局坐标矩阵O，由矩阵B内第2~ $ d + 1 $ 个最小特征值所匹配的特征向量构成。在特征空间中，原始船舶运行数据前几个维度的坐标一致或十分接近，是因为X_i中的船舶运行数据点间的相似度很高^[8]，因此提取的船舶故障征兆变量对应于全局坐标矩阵O的第一维。

1.2 海量船舶故障征兆变量离散化

使用基于可辨识矩阵的离散化算法，对提取的海量船舶故障征兆变量进行离散化处理，以降低所提取数据的维度，从而提升后续海量船舶故障数据挖掘质量。设船舶故障征兆变量决策表系统为Y=(U,R,M,f)，其中R满足 $ R = P \cup D $ ，P和D分别表示条件属性集、决策属性集，分别表示为P={a_i|i=1,2,..,n}、D={d_i}，D中包含n个类，第l个类即为d_l，船舶故障征兆变量样本集为U={u₁,u₂,…,u_N}，船舶故障征兆变量u_j位于属性a_i上的取值为a_i(u_j)，则可以得到可辨识矩阵。

在可辨识矩阵中，如果2个船舶故障征兆变量具有同样的决策属性取值，则两者的可辨识矩阵元素的取值等于0；如果2个船舶故障征兆变量的决策属性取值不一致，且能利用p个条件属性取值进行辨别，则两者的可辨识矩阵元素的取值为p个条件属性集合；如果2个船舶故障征兆变量具有同样的条件属性取值，但决策属性取值不一致，则两者的可辨识矩阵元素的取值为空集。

若想对相邻初始区间的决策属性分布结构进行辨别，设初始区间为I_r和I_s。在2个区间的类别一致的条件下，可辨识矩阵对应位置的标号等于0；在两个区间的类别不一致的条件下，可辨识矩阵对应位置的标号等于 $ \phi $ 。

可辨识矩阵实现海量船舶故障征兆变量离散化过程为：

1）初始区间的创建，需要离散化的条件属性为a_k，对应值域为{a_k,min,a_k,max}，以升序形式排列a_k的全部不同观测值，得到{a_k1,a_k2,…,a_kn}，初始区间可通过选取排列结果中每2个值的中点完成创建。求解初始区间的频数，使用I₁,I₂,…,I_n对初始区间进行编码，以获得列联表。

2）获取可辨识矩阵后，其内空集区间为I_q，I₁逐一将矩阵首行中I₂及其之后位置标号等于0的区间进行合并，停止条件为遇到I_q；将矩阵q行作为起点，I_q逐一与I_q+1及其之后位置标号等于0的区间进行合并，停止条件为遇到第一个空集的相应区间；重复执行以上操作，若遇到最后一个区间，则停止，并使用 $ I_1^{'},I_2^{'},... $ 重新完成合并后区间的编码。

3）设船舶故障征兆变量样本集实例数为N，给定阈值用 $ Z = \sqrt N $ 描述，针对步骤2获得的合并区间内实例数不超过阈值的区间，其并入相邻区间的位置可以通过平均互信息量来确定。

4）循环执行步骤2和步骤3，停止条件为各区间的决策属性分布结构存在差异，同时全部区间实例数超过给定阈值。

1.3 模糊运算聚类算法的海量船舶故障数据挖掘

1）船舶运行数据集为Y¹,Y²,..,Y^E，其中数据点个数为E，某类船舶故障征兆变量为Y^E+1，将两者排成一列，选取某月船舶故障征兆变量离散化结果当作数据样本，并排列各数据点的取值。

2）为过滤船舶运行数据集中的冗余数据点，将列视作对象完成数据点的聚类。设定g代表数据点次序，r¹代表依据数据样本特点选取的半径，利用Y¹构造第一个聚类中心点，可得到船舶故障数据集。

3）g=g+1，针对次序为g的数据点Y^g，假设此时聚类个数为M，聚类中心为C¹,C²,…,C^M，利用|Y^g-C^l|分别计算Y^g和各聚类中心的距离，若最小距离用 $ \left| {{Y^g} - {C^{{l_g}}}} \right| $ 描述，则Y^g的最近邻聚类即为 $ {C^{{l_g}}} $ 。

①在 $ \left| {{Y^g} - {C^{{l_g}}}} \right| $ 小于等于半径 $ {r_1} $ 的条件下，Y^g的所属类别为 $ {C^{{l_g}}} $ ；若l=l_g，则船舶故障数据集为 ${F^{{l_g}}}\left( g \right) = {F^{{l_g}}}\left( {g - 1} \right) + {Y^g}$ ，不然船舶故障数据集为F^l(g)=F^l(k-1)。

②在 $ \left| {{Y^g} - {C^{{l_g}}}} \right| $ 的值大于半径 $ {r_1} $ 的条件下，Y^g即为新聚类中心，表示为C^M+1=Y^g，此时船舶故障数据集为F^M+1(g)=Y^g；若l的值与M+1的值不相等，则船舶故障数据集为F^l(g)=F^l(k−1)。

4）重复执行步骤3，停止条件为船舶运行数据集内的N个数据点均完成处理，此时所得M个聚类的聚类中心即为挖掘出的船舶故障数据。

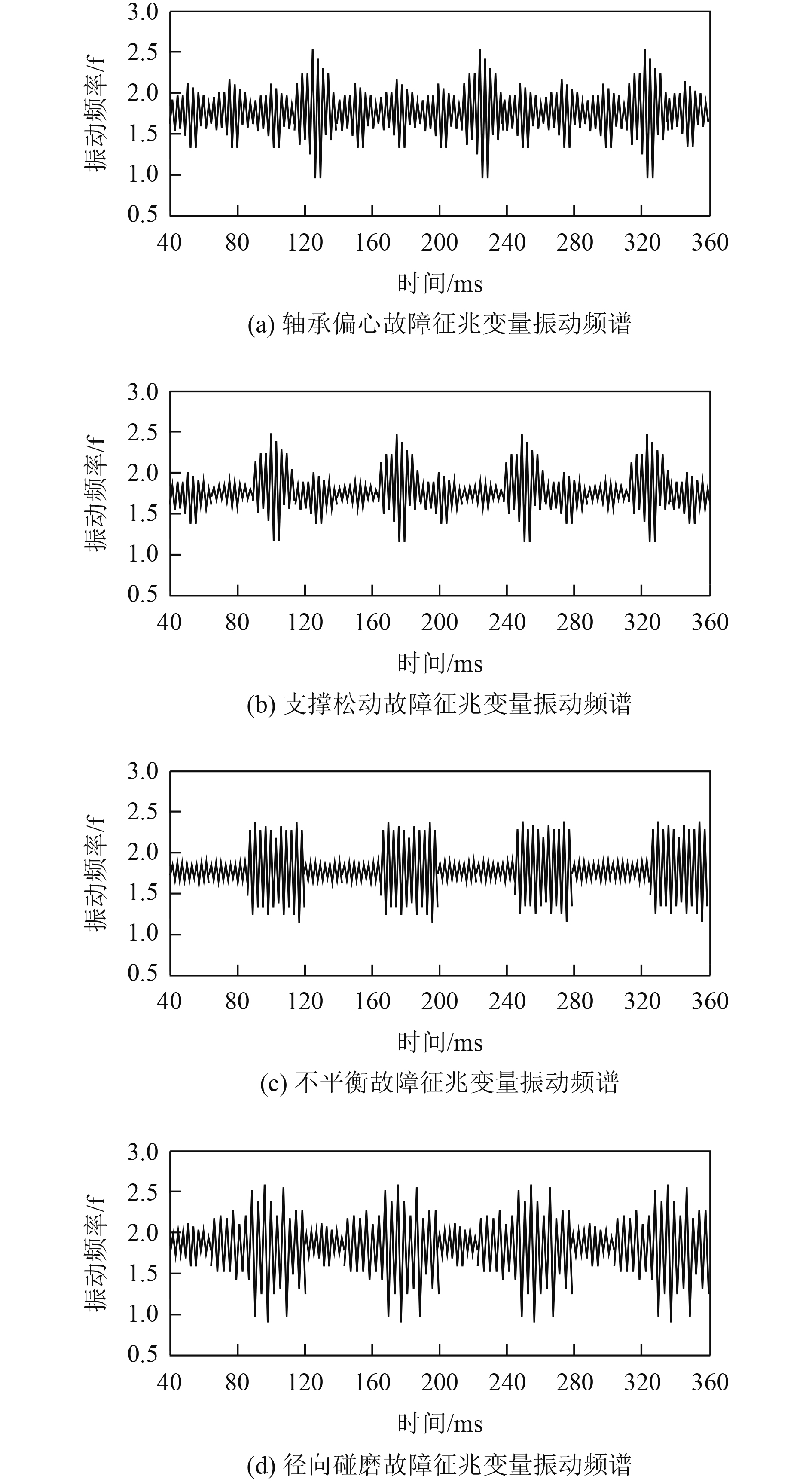
2 结果分析

选取某船舶作为实验对象，其SCADA系统历史数据库内，航行一个月的运行数据作为待挖掘数据集，共计154873个数据点，使用本文方法从中挖掘船舶故障数据，包括不平衡、径向碰磨以及油膜振荡等8种类型。针对轴承偏心、支撑松动、不平衡和径向碰磨4种船舶故障数据类型，使用本文方法提取的故障征兆变量的振动频谱图，用图1描述。从图1可以发现，不同船舶故障征兆变量均呈现出不同的振动频谱特征，其中轴承偏心和支撑松动2种故障征兆变量的振动频谱较为接近，但仍能区分开来，因此表明本文方法提取的船舶故障征兆变量具有较强的代表性，可以作为海量船舶故障数据挖掘的依据。

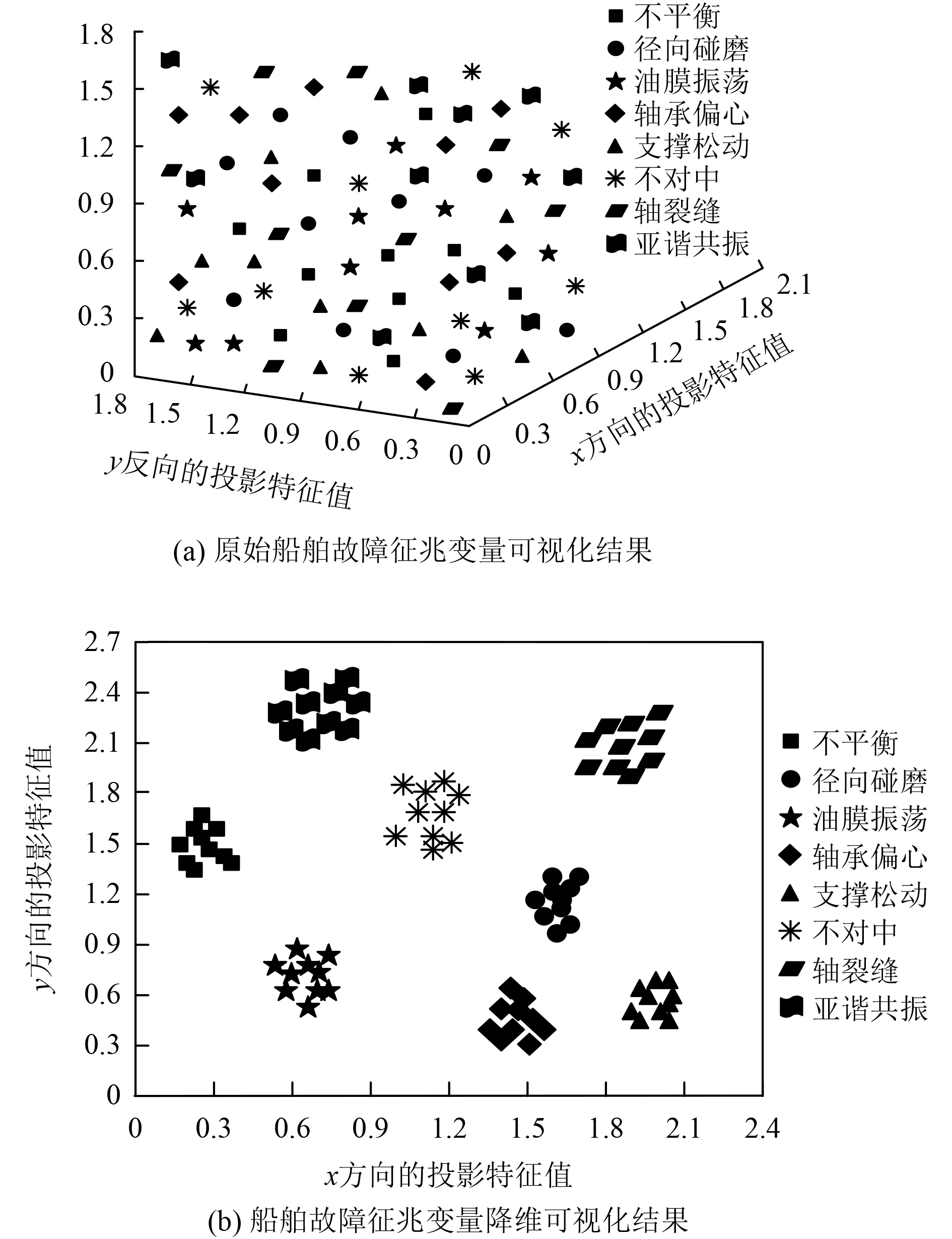
以随机形式从提取的船舶故障征兆变量中选取100个样本进行降维测试，每种类型各包含10个样本，并可视化展示降维结果，具体用图2描述。分析图2可以发现，原始船舶故障征兆变量呈混合分布，无法区分其类型，经过本文方法的降维处理后，相同类型的船舶故障征兆变量均被划分到同一区域，且各区域的间隔较大。因此表明本文方法具有较优良的船舶故障征兆变量降维效果。

引入调整兰德系数衡量本文方法的海量船舶故障数据挖掘性能，该系数的值域为[0,1]，其值越大，表明方法的挖掘结果与船舶故障征兆变量所代表的故障数据类型的吻合度越高。不同待挖掘数据集规模下，各类型船舶故障数据挖掘的调整兰德系数结果，用表1描述。使用字母A～H代表图2中各故障数据类型。分析表1可以看出，随着待挖掘数据集规模增加，不同类型的船舶故障数据挖掘调整兰德系数呈小幅度递减趋势，但始终高于0.90，受待挖掘数据集规模的影响极小。因此表明本文方法获得了理想的海量船舶故障数据挖掘结果。

3 结　语

随着船舶规模和结构复杂性的增加，船舶运行数据呈快速上升趋势，其中故障数据可以直接反映船舶的运行状态，因此本文分析海量船舶故障数据挖掘中的模糊运算聚类算法。本文方法引入局部切空间排列算法提取船舶故障征兆变量，所提取结果具有较强的代表性，并且通过可辨识矩阵的离散化处理，能够有效降低船舶故障征兆变量的维度。此外该方法在待挖掘数据集规模较大的情况下，仍能表现出较好的海量船舶故障数据挖掘效果。