0 引　言

船舶海上无线通信技术不同于陆地通信，面临多种挑战，比如船舶的移动、海上恶劣气象条件对无线通信信号的干扰作用、缺少信号中心基站等。随着船舶工业和海上航运业的迅速发展，海上无线数据传输的需求越来越高，无线通信网络传递的数据也越来越大，因此，解决当前海上无线通信网络的信息传输具有非常重要的意义。

在通信网络中，通信节点之间的信息交互是普遍存在的，由于通信节点的功能属性不同，通常进行信息交互的2个节点之间需要中继节点的存在，中继节点的作用是进行信息的转发。由于海上船舶无线通信网络的复杂性，节点直接信息传输的效率往往与节点协作的方法、中继节点的特性等相关^[1]。

本文介绍一种基于编码技术的复杂船舶无线通信网络的信息传输方式，从编码技术的原理和信息传输的特性方面进行阐述。

1 复杂船舶通信网络的无线协作系统

一个基础的船舶无线通信网络由3种节点构成，分别为源节点、中继节点和目的节点。其中，中继节点作为协助节点，它的工作模式和信息接收、发送的效率对于整个通信网络具有重要的作用，这也是本文研究的重点。

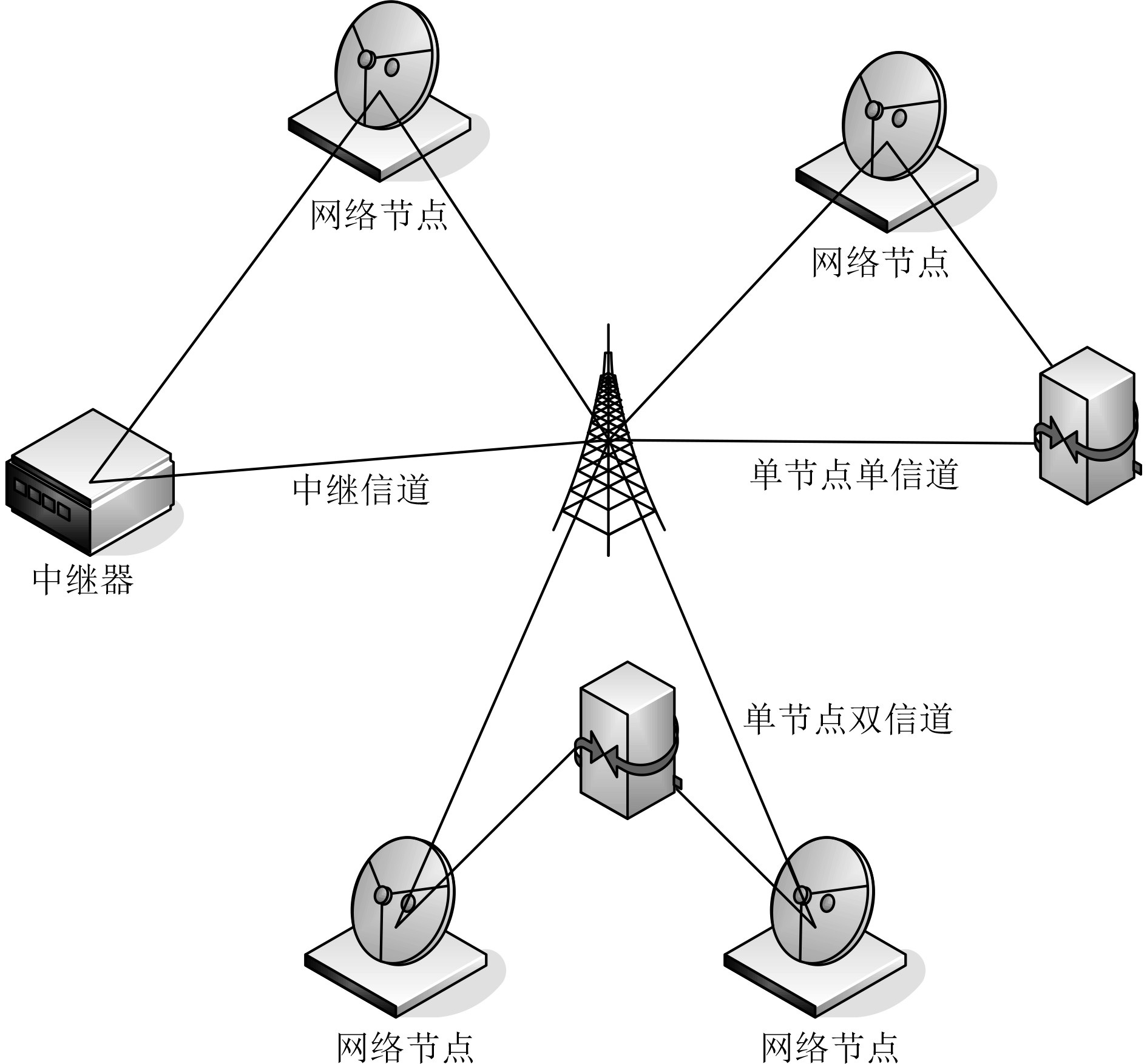
本文针对复杂船舶无线通信网络的协作通信技术进行研究，将协作通信网络模型划分为中继信道网络、单协作节点单信道网络和单协作节点双信道网络3种，协作通信网络模型如图1所示。

1）中继信道网络

中继信道网络模型中包括1个源节点，1个中继器和1个目的节点，网络简单可靠，经常用在蜂窝系统的上行链路中。

2）单协作节点单信道网络

网络模型中包括1个源节点，1个协作节点和1个目的节点，常用在2个船舶通信网络中的下行链路中。

3）单协作节点双信道网络

网络模型中包括2个源节点，1个协作节点和1个目的节点，网络结构相对复杂，但可并行传输的数据量增大。

协作通信技术的特点归纳如下：

1)协作通信技术的节点之间可以通过正交信道发送信息，尽管会降低低频域段的信道利用率，但通过频域分解和编码的方法能够提高通信效率^[2]；

2)当一个通信网络中存在多个协作节点，且每个协作节点已知当前的信道状态，那么多个协作节点之间可以采用波束成型技术，实现多协作节点信息的时间和空间配准。这种波束成型技术能够降低通信网络中的噪声干扰，实现通信网络中的信噪比最大化。

3)协作节点在获取信道状态信息时，可通过反馈信道获取幅度和相位等信息，但不可避免的，信道的相位信息有一定的时间滞后。

2 基于网络编码技术的复杂船舶网络节点信息交换技术 2.1 网络编码技术原理

网络编码技术由Ahlswede等针对有线网络的容量等性能提出，大量的仿真和实验测试数据表明，相对于普通的协作通信模式，协作通信若采用编码方式可以大幅度提升通信网络的数据容量。

网络编码技术的关键是进行信息的编码，允许通信网络中的节点对接收到的信息进行编码，然后将信息发送至下一节点，目前，网络编码技术常用的方法包括线性编码技术和非线性编码技术2种，其基本原理和拓扑结构特性分别如下：

1）线性编码技术

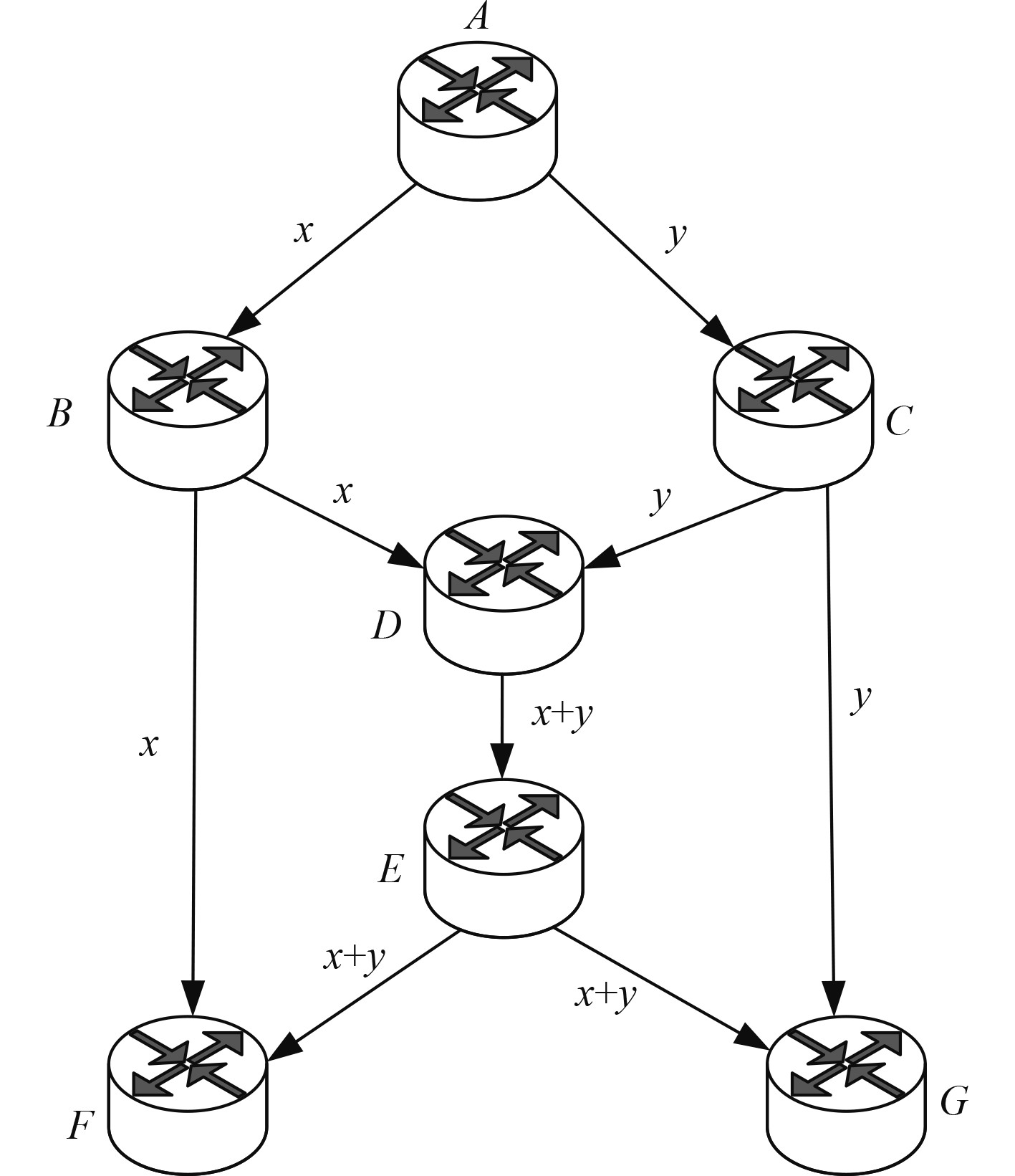
线性编码技术的网络拓扑结构如图2所示。

假设基于线性编码技术的网络为 $ G = \left( {P,L} \right) $ ， $ P $ 为网络节点的集合， $ L $ 为链路的集合，如图2所示。源节点A到目标节点F和G的链路有多条，假定源节点A中的数据个数为 $ N $ ，定义 $ {x_i} $ 为A节点产生的第i条数据， $ M $ 为中间节点接收到的数据个数，当数据个数大于2时，中间节点为每条数据构造线性编码 $ p_{{\text{out }}}^{(v,u)} $ 如下式：

$ p_{{\text{out }}}^{(v,u)} = \sum\limits_{i = 1}^{{M^{}}} {c_i^{(v,u)}} p_i^{[v]} \text{。} $

式中： $ c_i^{(v,u)} $ 为数据的编码向量； $ p_i^{[v]} $ 为输出数据。将编码数据发送至输出链路 $ (v,u) $ ，可将编码数据表示为：

$ p_{{\text{out }}}^{(v,u)} = \sum\limits_{j = 1}^N {c_j^{(v,u)}} {x_j},\quad c_j^{(v,t)} \in G 。$

线性编码网络拓扑中的目标节点接收的数据形成一个线性方程组，定义 $ X $ 为目标节点的原始数据向量， $ Y $ 为接收的编码数据向量， ${\boldsymbol{C }}$ 为编码转换矩阵，分别如下：

$ X = \left( {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ \vdots \\ {{x_N}} \end{array}} \right),\quad Y = \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ \vdots \\ {{y_{M - 1}}} \end{array}} \right),\quad {\boldsymbol{C}} = \left( {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \\ \vdots \\ {{c_M}} \end{array}} \right) \text{，} $

可得： $Y = {\boldsymbol{C}}X$ ，即

$ \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ \vdots \\ {{y_{M - 1}}} \end{array}} \right) = \left\{ {\begin{array}{*{20}{c}} {{c_{1,1}}}&{{c_{1,2}}}&{}&{{c_{1,N}}} \\ {{c_{1,2}}}&{{c_{2,2}}}&{}&{} \\ {...}&{...}&{...}&{...} \\ {{c_{1,M}}}&{{c_{2,M}}}&{}&{{c_{M,N}}} \end{array}} \right\}\left( {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ \vdots \\ {{x_N}} \end{array}} \right) \text{。} $

2）非线性编码技术

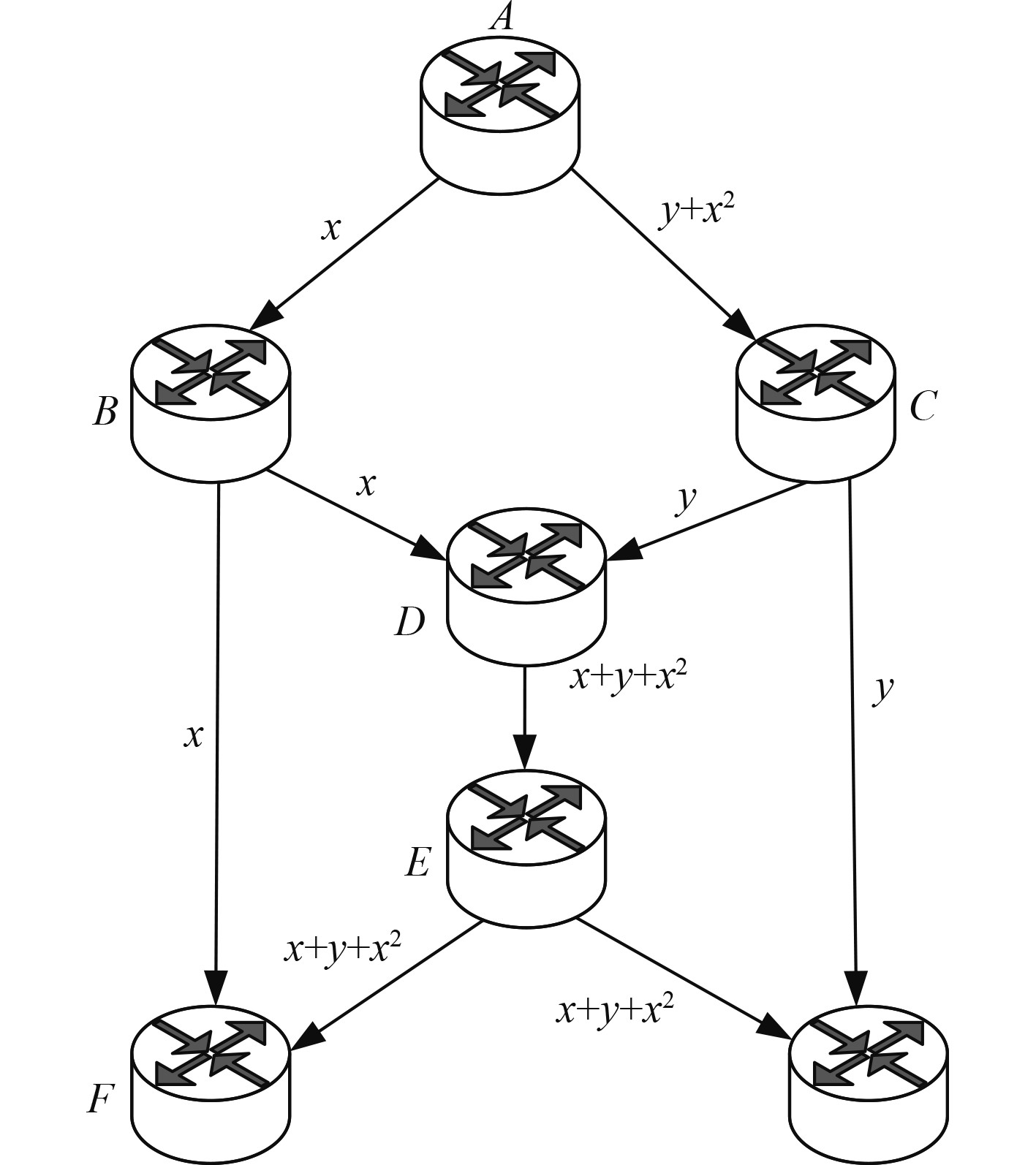
线性编码技术存在一定局限性^[3]，比如当通信网络中的数据量特别大时，协作节点的数据处理能力达到限值，此时网络的通信能力会明显下降。非线性编码技术能够避免这一问题，图3为非线性编码技术的拓扑结构。

不同于线性网络拓扑，非线性编码技术的数据传输链路 $ (v,u) $ 中存在二次或多次方程组，无法用简单的线性方程表示，可将编码数据表示为：

$ p_{{\text{out }}}^{(v,u)} = f\left( t \right)\sum\limits_{j = 1}^N {c_j^{(v,u)}} {x_j},\quad c_j^{(v,t)} \in G \text{，} $

编码数据变换矩阵定义为 $ Y = F{\boldsymbol{C}}X $ ，即

$ \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ \vdots \\ {{y_{M - 1}}} \end{array}} \right) = \left\{ \begin{gathered} {f_a} \\ {f_b} \\ ... \\ {f_M} \\ \end{gathered} \right\}\left\{ {\begin{array}{*{20}{c}} {{c_{1,1}}}&{{c_{1,2}}}&{}&{{c_{1,N}}} \\ {{c_{1,2}}}&{{c_{2,2}}}&{}&{} \\ {...}&{...}&{...}&{...} \\ {{c_{1,M}}}&{{c_{2,M}}}&{}&{{c_{M,N}}} \end{array}} \right\}\left( {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ \vdots \\ {{x_N}} \end{array}} \right) 。$

2.2 基于网络编码的单向中继节点网络信息交换

中继节点的功能是进行数据转发，而编码技术能够将接收的信息先进行编码，然后转发给其他节点。

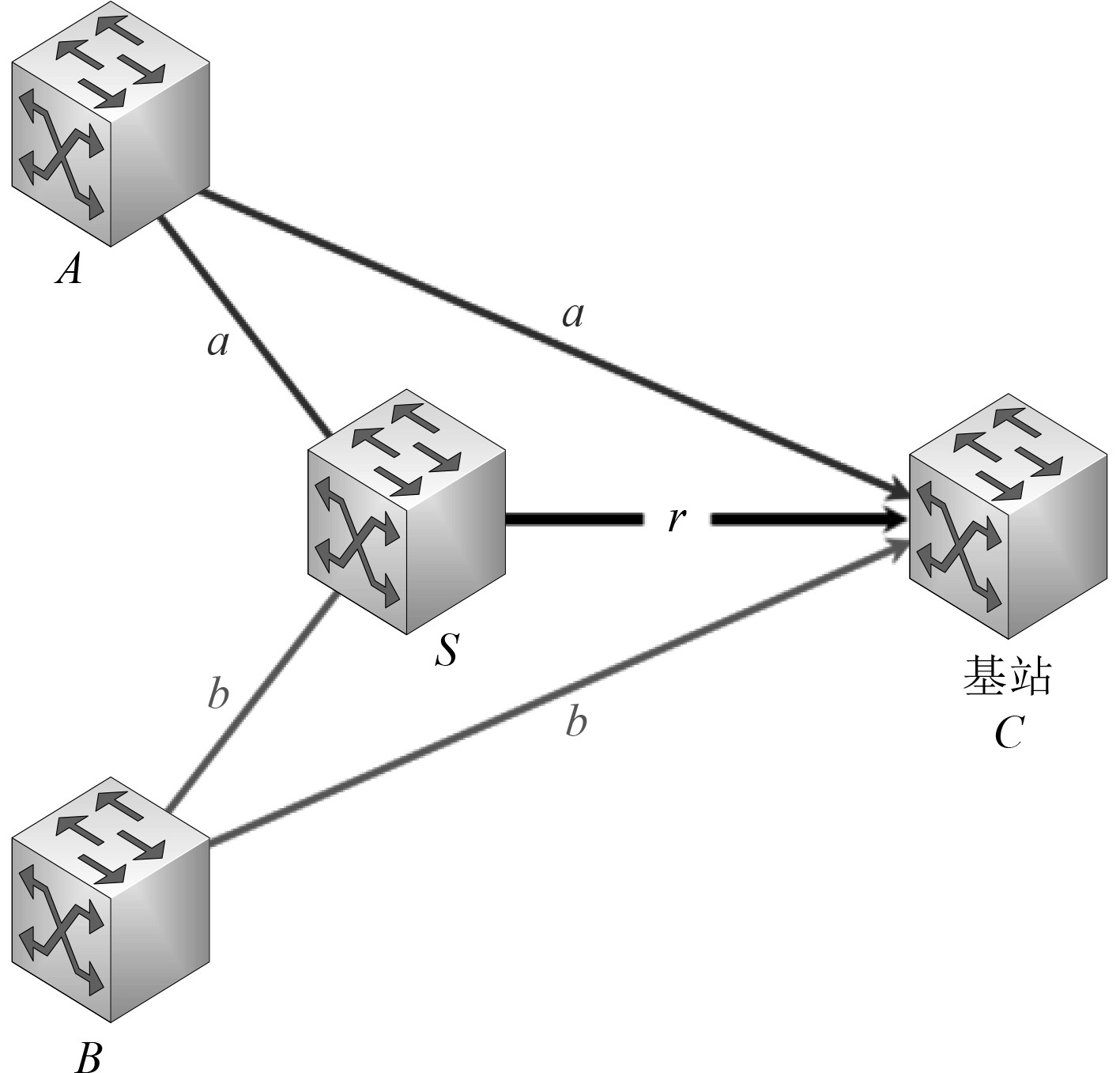
为了提高通信网络的信号强度^[4]，降低信道中的信号衰落，中继节点会将信号转发给基站，这种方式能够提高信号增益。同时，这种方式也存在一定的问题，当每个用户节点配置中继节点时，网络的效能会明显不足，因此，必须要考虑多个用户节点共用中继节点。网络结构如图4所示。

如图，用户节点A与B共用中继节点S，用户节点的数据通过中继节点转发至基站C。

在该网络模型中，当用户节点A与B已发送数据信号，而基站C没有收到信号，则说明网络系统中发生了信号中断，系统发生该事件的概率称为中断概率，假定网络中的信道相互独立，定义 $ {P_{xy}} $ 为节点X到Y的信号中断概率，可得：

基站C无法获取节点A信号的概率为

$ {P^a} = {P_{ad}}\left( {{P_{ar}} + {P_{rd}} - {P_{ar}}{P_{rd}}} \right) \text{，} $

基站C可以获取节点A信号的概率为

$ {P^b} = {P_{bd}}\left( {{P_{br}} + {P_{rd}} - {P_{br}}{P_{rd}}} \right) \text{，} $

同时无法获取节点A和节点B信号的概率为

$ {P^{ab}} = {P^a} \cdot {P^b} \text{。} $

定义节点的信号发射功率为 $ E $ ^[5]，信道的增益服从高斯分布，可得用户节点到基站的比特出错概率BER为：

$ p = E\left[ {Q\left( {\sqrt {2|h{|^2}{\gamma _{{\text{ud}}}}} } \right)} \right] = \frac{1}{2}\left( {1 - \sqrt {\frac{{{\gamma _{{\text{ud}}}}}}{{1 + {\gamma _{{\text{ud}}}}}}} } \right) \text{。} $

其中： $ h $ 为信号增益； $ {\gamma _{{\text{ud}}}} $ 为信噪比； $ Q $ 为接收功率。

当 $ {\gamma _{{\text{ud}}}} > 1 $ 时，可近似计算为：

$ p \approx \frac{1}{{4{\gamma _{{\text{ud}}}}}} 。$

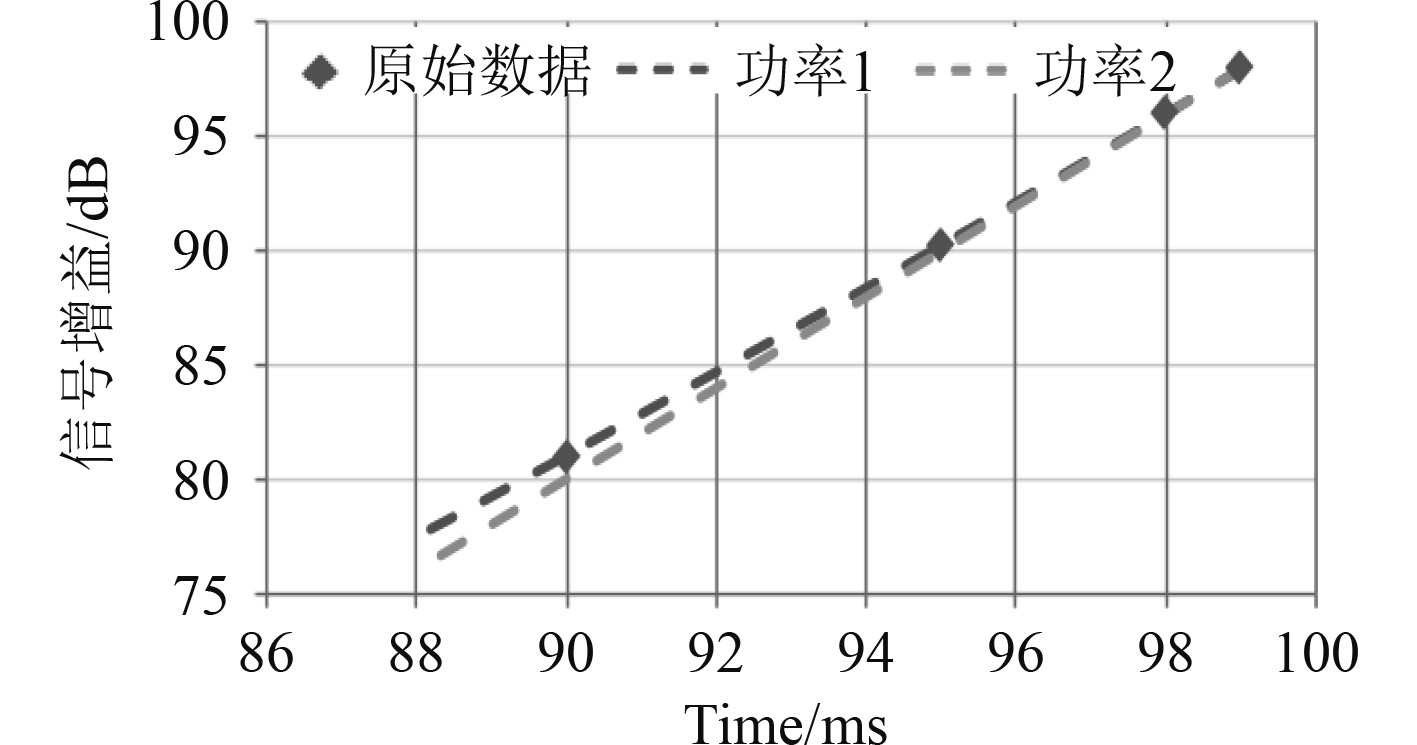
图5为不同发射功率下的信号增益曲线。

信噪比 $ {\gamma _{{\text{ud}}}} $ 的计算公式为：

$ {\gamma _{{\text{ud}}}} = {\left( {\frac{{{d_{{\text{ud}}}}}}{{{d_{{\text{ur}}}}}}} \right)^n} \text{。} $

式中： $ {d_{{\text{ud}}}} $ 为信号当量； $ {d_{{\text{ur}}}} $ 为噪声当量；n为增益。

2.3 基于网络编码的双向中继节点信息交换

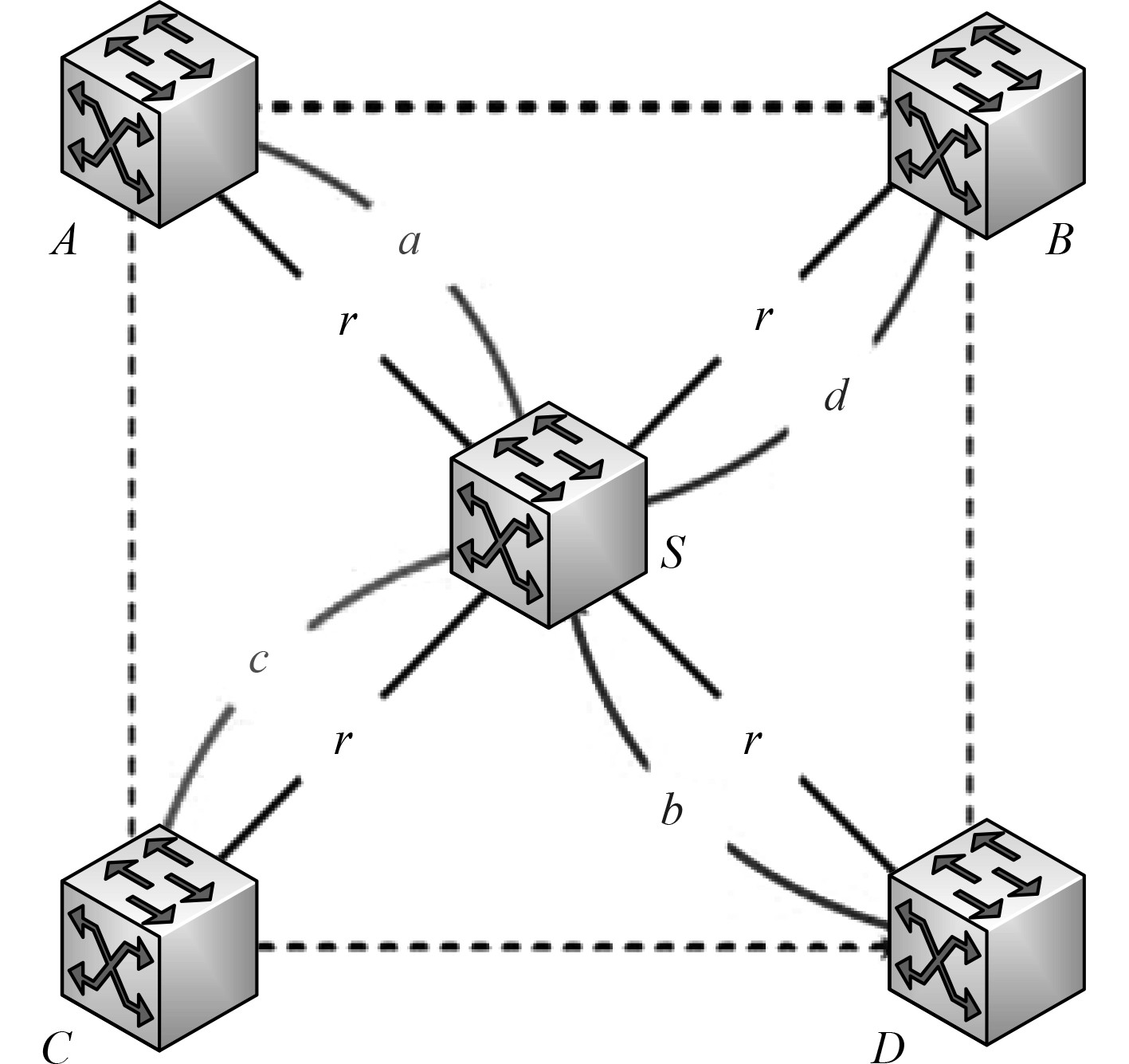
双向中继通信网络原理是2个单向中继网络的复合形态，其结构如图6所示。

双向中继通信网络中节点(A, B)和节点(C, D)通过一个公共的中继节点S进行数据交换，这种情况在船舶无线网络中经常遇到，为了避免网络中信号传输的冲突问题，在实际通信时采用分时复用的模式，将信号传输的一个时隙划分为5份，每个节点对应一个时隙。

在双向中继通信网络中，信号的时延和功耗要更加明显，由于采用了分时复用的方法，信号时延会在数据传输过程中不断积累，因此中继节点的缓冲区中可能存储大量的数据，从而导致后续的数据无法实现编码和转发。

双向中继通信网络的信号时隙满足高斯分布^[6]，定义传输时延为：

$ T\left( n \right) = {T_0}\prod\limits_{j = 0}^i {\left( {\frac{{{p_{j,j + 1}}}}{{{p_{j + 1,j}}}}} \right)} ,i = 1,2,...,M \text{。} $

式中， $ {T_0} $ 为初始时隙。

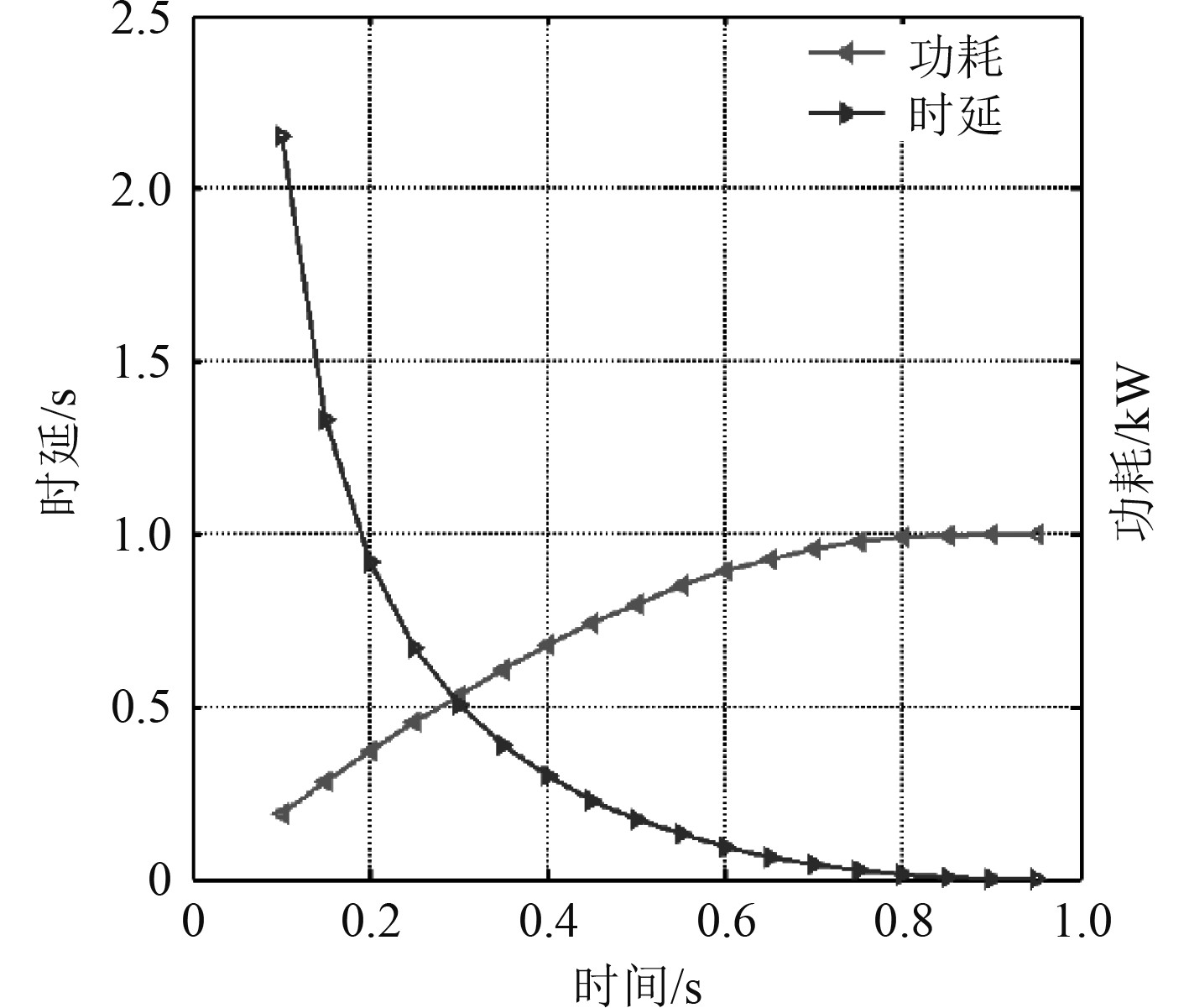
采集双向中继通信网络的信号时延与功耗的关系，如图7所示。

3 结　语

本文的研究目标是提高复杂船舶网络的节点信息交互能力，分别从无线协作网络的原理、基于编码技术的节点通信技术出发，分析了单向中继通信网络和双向中继通信网络的特性，对通信网络的信号增益、信噪比、时延等问题进行了研究。