目标跟踪技术作为计算机视觉技术中的一种,其目的是对预定的目标进行监控,并确保在后续的监控中均能包含该目标,一直能够定位出该目标的位置,并且保证跟踪目标的外形、光照强度以及尺寸的变化相对比较稳定,可以将目标有效锁定,同时将该目标的位置信息发送到计算机[3]。利用计算机视觉技术进行目标跟踪,不需要在目标上安装任何的传感器,同时该目标跟踪技术的硬件成本低并且测量范围宽[1]。为了实现无人艇在海面上自主地完成任务,进行目标物体的跟踪定位,提升无人艇的鲁棒性,本文基于可见光视觉技术,研究无人艇的目标跟踪系统的设计方法,有助于无人艇技术的发展。
1 无人艇系统设计 1.1 无人艇海面坐标系统的构建为了可以精确地定位出无人艇在海面上的位置,需要以无人艇所在水域为基础,构建出合适的坐标系,这样可以将跟踪目标所在的位置和无人艇本身所在的位置进行对比[2]。通常情况下,使用惯性坐标系和船体坐标系对海面上的船舶的航行位置进行描述。惯性坐标系一般用来表示船舶在海面上的绝对位置,但是在有些情况下,单纯地知道船舶在海面上的绝对位置不够,还需要知道船舶纵向、垂直以及转向等运动,这时候则需要使用船体坐标系。在对无人艇进行建模和分析的过程中,为了简化研究,一般假设无人艇是一个刚体,质量恒定不变,并且不考虑气压以及重力加速度对无人艇的影响[3]。
本文采用随动坐标系对船舶系统进行建模。与惯性坐标系不同的是,随动坐标系使用船体上的某一点作为自身坐标系的原点。为了使得构建出的模型更加便于运动学分析,通常使用无人艇的重心作为随动坐标系的原点O;无人艇的船头方向为x轴正方向;向地心方向为z轴正方向,同时和海平面垂直[4]。无人艇在海面上航行过程中,通常存在6个自由度。但是对无人艇的6个自由度进行运动模型的构建是十分复杂的,这样极大地增加了计算机的运算成本,因此在实际应用中很难实现[5]。本文对无人艇的运行模型进行了部分简化,为了简化模型,只考虑其中3个自由度。海面上无人艇的速度在2个坐标系之间的转换方法如下式:
| $ \left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta \sin \phi }&{\sin \phi \cos \phi } \\ 0&{\cos \phi }&{ - \sin \phi } \\ {\sin \theta }&{ - \cos \theta \sin \theta }&{ - \cos \theta \cos \phi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} U \\ V \\ W \end{array}} \right]\text{。} $ | (1.1) |
海面上无人艇的角速度在随动坐标系以及惯性坐标系之间的转换公式,如下式:
| $ \left[ {\begin{array}{*{20}{c}} p \\ q \\ r \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\sin \phi \tan \theta }&{\cos \theta \tan \theta } \\ 0&{\cos \phi }&{ - \sin \phi } \\ {\sin \theta }&{\dfrac{{\sin \phi }}{{\cos \theta }}}&{\dfrac{{ - \cos \phi }}{{\cos \theta }}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} P \\ Q \\ R \end{array}} \right]\text{。} $ | (1.2) |
无人艇在海面上对目标进行跟踪,其重点在于对无人艇自身以及跟踪目标的航向以及位置信息的获取,为简化分析,本文将无人艇看作是一个刚体,并且只考虑3个自由度,即横荡自由度、纵荡自由度以及首摇自由度,如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)vr = {X_P} + {X_H} + {X_W}} ,\\ {\left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ur = {Y_P} + {Y_H} + {Y_W}},\\ {\left( {{I_{ZZ}} + {J_{ZZ}}} \right)\dot r = {N_P} + {N_H} + {N_W}} 。\end{array}} \right. $ | (1.3) |
式中:m为重量;X,Y,N分别为无人艇在X,Y,Z三个方向上受到的合力,这些力包括无人艇上螺旋桨的推力、水流的动力以及海面上的风力。
作为一个闭环系统,无人艇在海面上进行目标跟踪过程中,由于漂流角在平衡点附件比较小,因此可以将海水部分看作是线性的,则式(3)可以简化成下式:
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {m + {m_x}} \right)\Delta \dot u = {X_u}\Delta u} ,\\ {\left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ur = {Y_v}v + {Y_r}r + {Y_\delta }\delta },\\ {\left( {{I_{ZZ}} + {J_{ZZ}}} \right)\dot r = {N_v}v + {N_r}r + {N_\delta }\delta } 。\end{array}} \right. $ | (1.4) |
式中:δ为无人艇的舵机转角。假设无人艇在海面上航行的速度恒定不变,则式(4)可以继续简化成下式:
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {m + {m_y}} \right)\dot v = {Y_v}v + \left( {{Y_r} - \left( {m + {m_x}} \right){u_0}} \right)r + {Y_\delta }\delta } ,\\ {\left( {{I_{ZZ}} + {J_{ZZ}}} \right)\dot r = {N_v}v + {N_r}r + {N_\delta }\delta } 。\end{array}} \right. $ | (1.5) |
通过拉普拉斯变换,可以从式(5)中推导出首向角和舵机角之间的函数关系式为:
| $ H\left( s \right) = \frac{{\psi \left( s \right)}}{{\delta \left( s \right)}} = \frac{{K\left( {1 + {T_3}s} \right)}}{{s\left( {1 + {T_1}s} \right)\left( {1 + {T_2}s} \right)}}。$ | (1.6) |
考虑到无人艇在海面上具备较大的惯性,因此无人艇的首摇角的速度相对较慢,在高频扰动的影响下,无人艇的首摇角的变化也很小,因此只需要对海面上的无人艇进行低频运动分析,式(6)可以简化为:
| $ H\left( s \right) = \frac{{\psi \left( s \right)}}{{\delta \left( s \right)}} \approx \frac{K}{{s\left( {1 + Ts} \right)}}\text{。} $ | (1.7) |
时域中的公式如下式:
| $ T\ddot \psi + \dot \psi = K\delta \text{。} $ | (1.8) |
式中:δ为舵机的转角;ψ为首向角;K为旋回参数;T为跟踪参数,该参数越小,则无人艇的首向转动则越快。这使得无人艇变换舵角之后,首向角的加速度越大,由于r=ψ,因此式(8)可以简化成下式:
| $ T\dot r + r = K\delta \text{。} $ | (1.9) |
经过上述一系列的简化之后,无人艇的运动数学模型可能存在一定的失真现象,例如无人艇在海面上受到风浪流的影响,为了提高模型的精度,本文引入了非线性干扰因素d(t),如下式:
| $ T\dot r + \dot r = K\delta + d\left( t \right)\text{。} $ | (1.10) |
在不同运算迭代次数的情况下的无人艇的速度变化如图1所示。

|
图 1 海面上无人艇航速变化 Fig. 1 Speed variation of unmanned craft on the sea surface |
大海中的天气等环境十分复杂,因此需要对从海面上采集到的可见光图像进行预处理,这样可以降低图像中的噪声、提高图像的信噪比和质量,有利于无人艇的目标跟踪系统执行目标检测以及跟踪任务。本文在对可见光图像预处理过程中,第1步是降低可见光图像的噪声;第2步是提升可见光图像的质量;第3步是使用灰度投影法改善图像抖动现象[6]。
降低可见光图像噪声的方法,通常使用均值滤波法。该算法基于模板对可见光图像的像素灰度均值进行求解,同时将该像素均值赋值给其他的像素点[7]。即对于一个特定的可见光图像的像素点(x,y),在该像素点附近选取一定数量的其他像素点,这些像素点的集合就构成了模板,均值滤波算法则求解模板内像素灰度均值,则当前的像素点(x,y)的值采用模板内的所有像素点的像素灰度均值代替,公式如下:
| $ g\left( {x,y} \right) = \frac{1}{N}\sum\limits_{\left( {i,j} \right) \in S} {f\left( {i,j} \right)} \text{。} $ | (2.1) |
本文采用灰度变换的方法来增强可见光图像。灰度变换方法通过扩展可见光图像来增加该图像的清晰度。对于任意可见光图像f(x,y),假设该可见光图像的灰度值取值范围为[a,b],则可以得到下式:
| $ g\left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} c,&{0 \leqslant f\left( {x,y} \right) \leqslant a},\\ {\dfrac{{d - c}}{{b - a}}},&{a \leqslant f\left( {x,y} \right) \leqslant b} ,\\ d,&{b \leqslant f\left( {x,y} \right) \leqslant \max f} 。\end{array}} \right. $ | (2.2) |
当光照强度较弱的时候,可见光图像的灰度值比较小,这就导致图像变得不清晰。通过式(12)的线性变换,可以对可见光图像中的像素灰度进行拉伸,原始可见光图像得到了增强。
海面上海波不断,因此无人艇在跟踪目标的过程中,采集得到的可见光图像会抖动,这会增加辨认图像中跟踪目标的难度,有可能会导致目标跟踪失败,因此需要使用视频稳像技术[8]。视频稳像技术是指使用算法,对采集得到的可见光图像进行处理,以达到去抖动的作用。采用稳像技术的过程中,运动估计是十分重要的一个环节,本文使用灰度投影来实现运动估计。首先对可见光图像的灰度值的行和列分别进行投影,如式(13)和式(14)所示,然后再计算当前图像帧和参考图像帧之间的投影关系,该方法的执行效率高。灰度投影算法在计算的时候需要图像的全局灰度值,并且整个过程中只需要计算一次,就可以获得运动矢量,计算时间和精度都很好。
| $ {R_x}\left( w \right) = \sum\limits_{j = 1}^M {{{\left[ {Co{l_{cur}}\left( {y + w - 1} \right) - Co{l_{ref}}\left( {m + y} \right)} \right]}^2}} \text{,} $ | (2.3) |
| $ {R_y}\left( v \right) = \sum\limits_{i = 1}^N {{{\left[ {Co{l_{cur}}\left( {x + v - 1} \right) - Co{l_{ref}}\left( {n + x} \right)} \right]}^2}} \text{。} $ | (2.4) |
本文采用的无人艇航向角度的测量方法虽然存在一定的偏差,但是经过目标跟踪系统处理之后,无人艇的航向会和跟踪目标的航向一致,这样就可以获得精确的判断,因此该系统那个会收敛与跟踪目标的航向上[9]。本文设计的无人艇目标跟踪系统采用PID算法进行控制,PID算法利用3个相互独立的分量对偏差进行控制,这样可以快速地降低误差、减少调节次数,同时PID算法可以持续地进行迭代运算,不断地减小误差[10],其基本公式如下:
| $ U\left( t \right) = kp\left( {err\left( t \right) + \frac{1}{{{T_I}}}\int {err\left( t \right)dt + \frac{{{T_D}derr\left( t \right)}}{{dt}}} } \right)\text{。} $ | (2.5) |
在实际使用过程中使用的是增量式PID算法,该算法通过不断地计算需要增加的偏差来降低误差,其计算方法如下式:
| $ \Delta u\left[ n \right] = u\left[ n \right] - u\left[ {n - 1} \right]\text{。} $ | (2.6) |
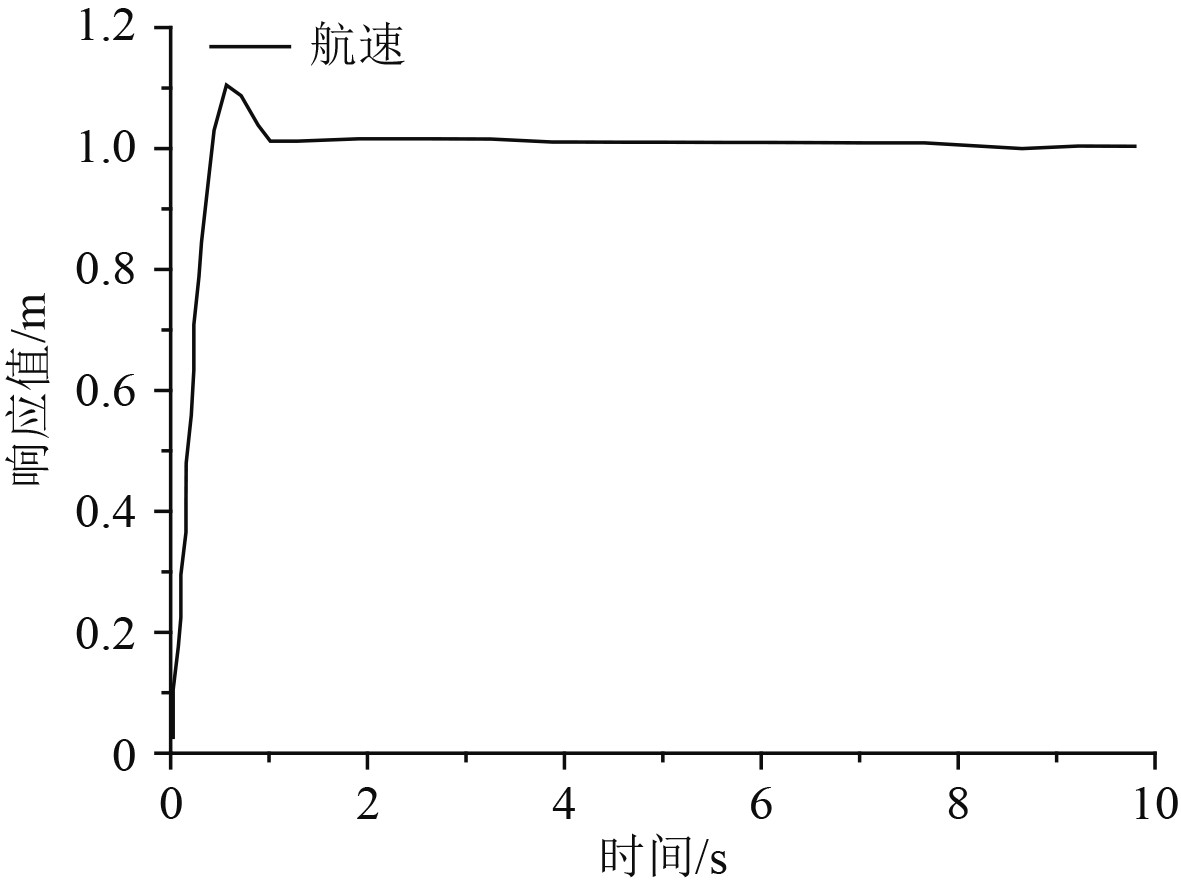
本文在仿真过程中,使用的无人艇速度为0.3 m/s,K为0.64;T为0.17。利用Maltab对无人艇的航向角进行控制,结果如图2所示。
|
图 2 PID控制算法的单位阶跃响应 Fig. 2 Unit step response of PID control algorithm |
根据上述分析可知,获得无人艇和跟踪目标的位置以及航向之后,可以实现对目标的实时跟踪。无人艇利用自身携带的摄像头采集图像,选择图像中的跟踪目标,启动目标跟踪系统,根据采集到的图像中的畸变内容,计算出无人艇和跟踪目标的航速以及航向,根据两者的航速和航向,计算出航向偏差,最后基于航迹跟踪算法,计算出无人艇舵机的偏转角度,实现目标跟踪。
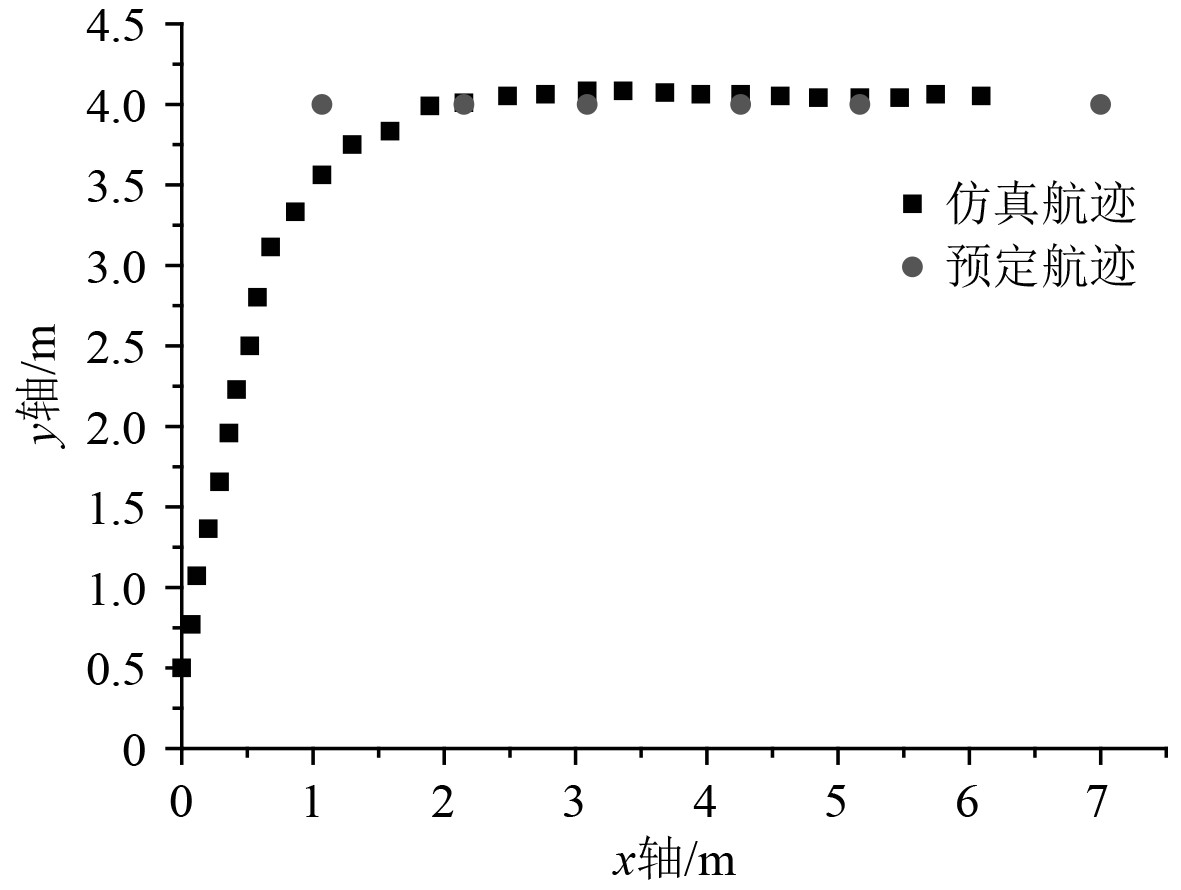
2.3 无人艇的目标跟踪系统仿真测试获得无人艇的相关参数之后,可以对目标跟踪系统的有效性进行仿真测试。在本文的仿真中假定无人艇的航线已知,并且在航线上每隔一段设置一个航迹点,航迹点之间的距离并不一定相等,在不同的仿真条件下得到仿真结果如图3~图5所示。
|
图 3 直线航迹仿真 Fig. 3 Straight track simulation |
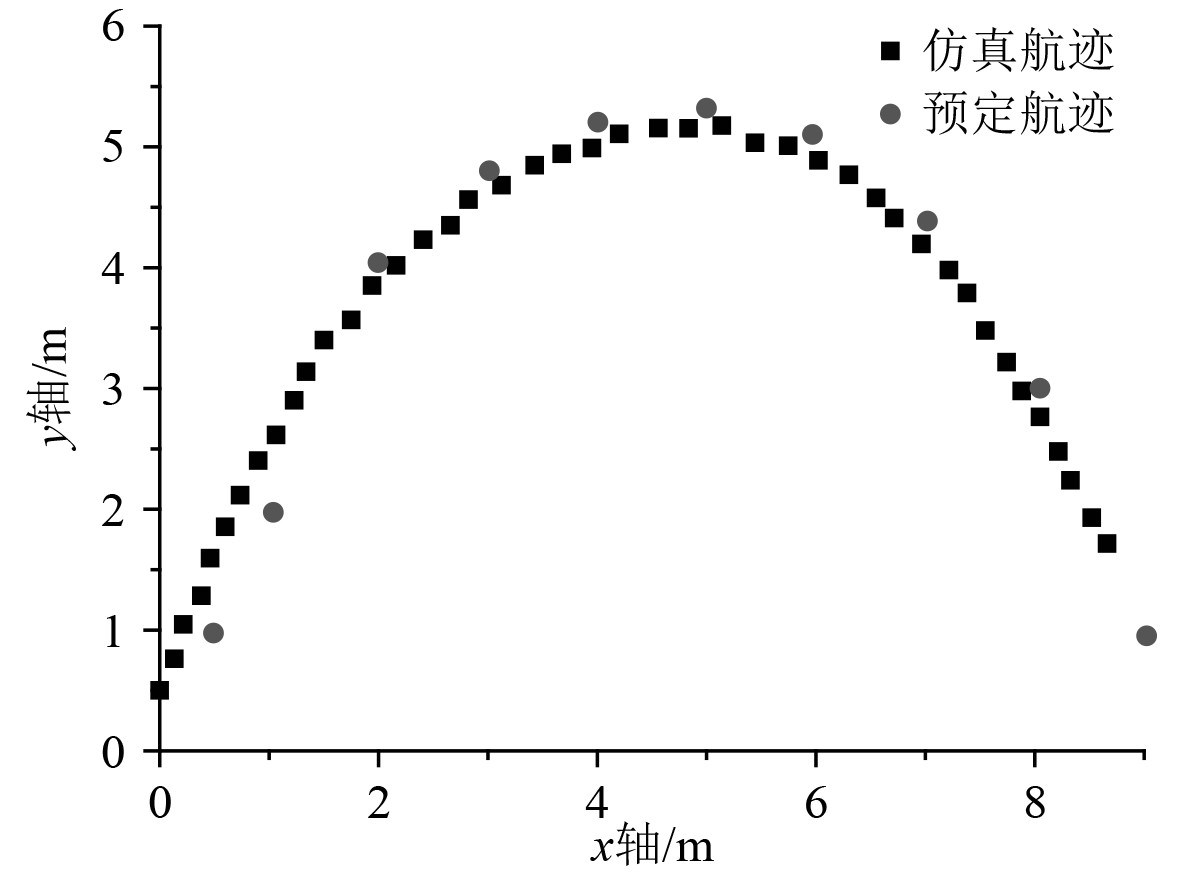
|
图 5 曲线航迹仿真 Fig. 5 Curve track simulation |
图3中设定了一条直线航迹。无人艇从原点(0,0)出发,并且无人艇初始航向和x轴之间的角度为90°,从图3可以发现,无人艇在航行4 s之前,其航行方向为朝着第1个航迹点,在4~9 s之间,航行方向为第2个航迹点,同时在对最终目标的行进过程中始终保持对目标航向的不断调整,调整的幅度在可控范围内,因此无人艇的目标跟踪航迹收敛。
图4设定了一条直角航迹。无人艇从原点(0,0)出发,并且无人艇初始航向和x轴之间的角度为90°,从图4可以发现,无人艇的航线快速进入y轴平行直线航道,在1~2 s时开始偏向x轴平行航道,无人艇的航迹跟踪是收敛的。

|
图 4 直角航迹仿真 Fig. 4 Right angle track simulation |
图5给出了一条正弦型的无人艇曲线航迹,无人艇航行的初始点为(0,0),并且无人艇初始航向和X轴的夹角为90°。从图5可以发现,无人艇的航迹在预定轨迹的正弦波峰处,一直沿着预定轨迹的内侧航行,没有越过预定轨迹航线,因此无人艇的目标跟踪航迹收敛。
3 结 语作为一种能够自主地在海面上进行航行的智能系统,无人艇的优点在于速度快、隐身效果好、体积小等,同时以相对较低的成本实现相关的考察以及工程任务,而且可以在一些人员无法到达的水域开展相关的预定任务,例如浅海、海况恶劣的水域等。无人艇在复杂的海面上能够精确地跟踪目标物体,有利于实现无人艇的目标探测、障碍物自主避让等功能。本文对无人艇目标跟踪系统的研究,有利于无人艇技术的发展。
| [1] |
刘小虎, 桂凡. 基于激光雷达和机器视觉融合的无人艇目标检测[J]. 海军工程大学学报, 2021(33): 91-96. DOI:10.7495/j.issn.1009-3486.2021.02.015 |
| [2] |
徐凯凯, 宋利飞, 史晓骞, 等. 基于雷达数字孪生的水上多目标跟踪方法研究[J]. 无人系统技术, 2022(5): 60-68. |
| [3] |
程亮, 杨渊, 张云飞, 等. 面向无人艇智能感知的水上目标识别算法研究[J]. 电子测量与仪器学报, 2021(35): 99-104. DOI:10.13382/j.jemi.B2003637 |
| [4] |
董慧颖, 赵鹏. 水面无人艇动态障碍目标视觉跟踪方法[J]. 沈阳理工大学学报, 2016(35): 77-81+87. DOI:10.3969/j.issn.1003-1251.2016.06.015 |
| [5] |
唐平鹏, 刘德丽, 洪昌建, 等. 水面无人艇全局航迹多目标规划算法[J]. 华中科技大学学报, 2015(43): 290-293. |
| [6] |
董慧颖, 徐鹏. 水面无人艇运动目标检测技术研究[J]. 沈阳理工大学学报, 2016(35): 33-38. DOI:10.3969/j.issn.1003-1251.2016.05.007 |
| [7] |
周志杰, 徐海祥. 水面无人听自主跟踪系统设计[J]. 江苏船舶, 2017(34): 1-5. |
| [8] |
秦世洋, 张腾, 武绍宽, 等. 水上无人艇目标跟踪控制方法研究[J]. 中北大学学报, 2020(41): 148-153+160. |
| [9] |
张恒, 宋佳, 林鹏. 一种适用于无人艇平台的慢速小目标检测方法[J]. 舰船电子对抗, 2020(43): 75-78+85. DOI:10.16426/j.cnki.jcdzdk.2020.02.016 |
| [10] |
王玉龙, 马勇. 一种用于群无人艇避碰的动态分组策略[J]. 中国航海, 2019(42): 87-92_103. DOI:10.3969/j.issn.1000-4653.2019.01.018 |
 2022, Vol. 44
2022, Vol. 44
