0 引　言

目标运动分析(target motion analysis，TMA)是利用带噪测量数据来估计目标的运动状态。复杂的海战环境下，观测平台的机动不被允许，目标的方位几乎是唯一可靠的信息，本文利用双阵的方位数据来估计目标的运动状态。

纯方位目标运动分析^[1-3]（bearings-only target motion analysis, BO-TMA）是典型的非线性滤波问题，几十年来该领域发展迅速。经典的方法有卡尔曼滤波类算法如扩展卡尔曼滤波算法、无迹卡尔曼滤波算法、容积卡尔曼滤波算法等。近年来，基于变分贝叶斯技术的方法逐渐引起人们的关注。然而，大部分方法都忽略了目标状态约束信息，实际上，目标的速度、距离以及航向都是在一定范围之内的。

考虑到这一先验信息，本文利用一种不等式约束条件下的容积卡尔曼滤波器来估计目标运动状态，并进行了仿真和试验数据处理，验证了算法的有效性。

1 问题阐述

图1为基阵和目标的几何关系，考虑二维平面情形，目标和基阵均进行匀速直线运动。D为双阵间距， $ \ \beta_1 $ ， $\ \beta _2 $ 分别代表左边基阵和右边基阵观测到的目标方位， ${X_k} = {[{r_{xk}},{v_{xk}},{r_{yk}},{v_{yk}}]^{{{\rm{T}}}}}$ ，代表目标在k时刻的相对参考基阵(左边基阵)的运动状态。其中， $ {r_{xk}} $ ， $ {r_{yk}} $ 分别代表目标相对参考基阵的x，y方向的距离， $ {v_{xk}} $ ， $ {v_{yk}} $ 分别代表目标相对参考基阵的x，y方向的速度。

状态方程和测量方程分别如下：

$ {X_k} = F{X_{k - 1}} + {w_{k - 1}} ，$

(1)

$ Z_{k} =h\left(X_{k}\right)+v_{k} =\left[\begin{array}{l} a \tan \left(r_{x k} / r_{y k}\right) \\ a \tan \left(\left(r_{x k}-D\right) / r_{y k}\right) \end{array}\right]+v_{k} $

(2)

式中： $ {w_{k - 1}} $ 是非零均值的高斯噪声； $ {Z_k} $ 为k时刻的双阵对目标的观测方位； $ {v_k} $ 为测量噪声，服从正态分布， $ {v_k}\sim N(0,{R_k}) $ ；转换矩阵F如下：

$ {\boldsymbol{F}} = \left[ \begin{array}{*{20}{c}} 1& T& 0& 0 \\ 0& 1& 0& 0 \\ 0& 0& 1& T \\ 0& 0& 0& 1 \\ \end{array} \right]。$

(3)

实际中，可以得到目标速度和航向的不等式约束条件如下：

$ lower1 \leqslant {r_{x2k}} + {r_{y2k}} \leqslant upper1 ，$

(4)

$ lower2 \leqslant a\tan ({v_{xk}}/{v_{yk}}) \leqslant upper2。$

(5)

本文所考虑的约束条件BO-TMA问题就是在式(4)和式(5)约束条件下进行目标运动状态的估计。

2 方法原理

纯方位目标运动分析是一个典型的非线性滤波问题，扩展卡尔曼滤波方法经常被用来解决这类问题，但它的线性化能力较弱，因此本文采用容积卡尔曼滤波算法来估计目标运动状态，然后用非线性约束滤波器进行进一步的约束滤波处理。

2.1 容积卡尔曼滤波器

${\hat{{\boldsymbol{X}}}}_{k|k-1}，{{\boldsymbol{P}}}_{k-1|k-1}$ 分别代表k−1时刻估计的目标状态和状态误差协方差矩阵，k时刻的目标运动状态和状态误差协方差矩阵预测如下：

$ {\hat {\boldsymbol{X}}_{k\left| {k - 1} \right.}} = {\boldsymbol{F}}{\hat {\boldsymbol{X}}_{k - 1\left| {k - 1} \right.}}，$

(6)

$ {P_{k\left| {k - 1} \right.}} = F{P_{k - 1\left| {k - 1} \right.}}{F^{{{\rm{T}}}}} 。$

(7)

容积卡尔曼滤波器的预测阶段需要用到容积点，预测容积点如下：

$ \chi _{k\left| {k - 1} \right.}^i = \sqrt {{P_{k\left| {k - 1} \right.}}} {\xi _i} + {\hat X_{k\left| {k - 1} \right.}}，i = 1,2 \cdots 8。$

(8)

式中： $ {\xi _i} $ 为矩阵2[ $ {I_4} - {I_4} $ ]的第i列，预测的测量值对应的容积点为 $ {z}_{k|k-1}^{i}=h({\chi }_{k|k-1}^{i}) $ ，则可得观测值的预测值为：

$ {\hat Z_{k\left| {k - 1} \right.}} = \frac{1}{8}\sum\limits_{i = 1}^8 {z_{k\left| {k - 1} \right.}^i}。$

(9)

目标状态的更新步骤如下：

$ {P_{zz}} = \frac{1}{8}{\sum\limits_{i = 1}^8 {(z_{k\left| {k - 1} \right.}^i - {{\hat Z}_{k\left| {k - 1} \right.}})} ^2} + {R_k} ，$

(10)

$ {P_{xz}} = \frac{1}{8}\sum\limits_{i = 1}^8 {(\chi _{k\left| {k - 1} \right.}^i - {{\hat X}_{k\left| {k - 1} \right.}})} (z_{k\left| {k - 1} \right.}^i - {\hat Z_{k\left| {k - 1} \right.}})，$

(11)

$ K={P}_{xz}{({P}_{zz})}^{-1}，$

(12)

$ {\hat{X}}_{k|k}={\hat{X}}_{k|k-1}+K({Z}_{k}-{\hat{Z}}_{k|k-1})，$

(13)

$ {P_{k\left| k \right.}} = {P_{k\left| {k - 1} \right.}} - K{P_{{\text{zz}}}}{K^{{{\rm{T}}}}}。$

(14)

2.2 不等式约束滤波器

利用容积卡尔曼滤波估计出的目标运动状态 $ {\hat X_{k\left| k \right.}} $ 后，需要在给定的约束不等式条件下对该结果进行进一步滤波，约束不等式的形式如下：

$ \varphi _{\text{i}}^{{{\rm{T}}}}a({\hat X_{k\left| k \right.}}) \geqslant {\partial _i}，i = 1,2, \cdots L。$

(15)

考虑式(4)和式(5)描述的距离和航向约束条件，采用Tully提出的不等式约束滤波器[4]进行滤波。该方法首先将目标的状态映射到约束空间中，即 $ {s_k} = a\left( {{X_k}} \right) $ ，此时，非线性不等式约束问题就转换为了线性不等式约束问题。采用线性不等式约束滤波器估计出 $ {s_k} $ ，然后再把约束空间返回到状态空间，则估计出非线性不等式约束条件下的目标状态。

${\hat{s}}_{k}，{C}_{k}$ 代表 $ {s_k} $ 在k时刻的状态和误差协方差矩阵的估计值，进行如下转换：

$ {y}_{k}=V{W}^{-1/2}{T}^{{{{\rm{T}}}}}\left({s}_{k}-{\hat{s}}_{k-1}\right) ，$

(16)

其中 $ V，W，T $ 分别为：

$ {C_{k - 1}} = TW{T^{{{\rm{T}}}}}，$

(17)

$ V{W^{1/2}}{T^{{{\rm{T}}}}}{\phi _{\text{i}}} = \left[{\left( {\phi _i^{{{\rm{T}}}}{C_{k - 1}}{\phi _{\text{i}}}} \right)^{1/2}}\;0\; \cdots 0\right] ，$

(18)

则非线性不等式约束式可转换为如下线性不等式约束式：

$ \left[ {1\;0 \cdots 0} \right]{y_k} \geqslant {\beta _i} ，$

(19)

$ {\beta _i} = \frac{{{\alpha _{\text{i}}} - \phi _i^{\rm{T}}{{\hat s}_{k - 1}}}}{{{{\left( {\phi _i^{\rm{T}}{C_{k - 1}}{\phi _{\text{i}}}} \right)}^{1/2}}}}。$

(20)

$ {y_k} $ 服从截断的高斯分布，它的均值和协方差矩阵如下：

$ {\hat y_k} = {[\mu ,0, \cdots 0]^{{{\rm{T}}}}}，$

(21)

$ {\sum _k} = {\rm{diag}}({\sigma ^2},1, \cdots 1)，$

(22)

$ \mu = \frac{1}{{\sqrt {2\text{π} } }}{e^{\frac{{\beta _i^2}}{2}}} + \frac{{{\beta ^i}}}{2}\left[ {1 + Erf\left(\frac{{{\beta ^i}}}{{\sqrt 2 }}\right)} \right] ，$

(23)

$ \begin{gathered} {\sigma ^2} = \frac{1}{{4\text{π} }}\Bigg[ - 2{e^{ - \beta _i^2}} + (2 + \beta _i^2)\text{π} + \\ \;\;\;\;\;\;\;\; ( - 2{\text{π}} - 2\beta _i^{}{e^{\frac{{\beta _i^2}}{2}}}\sqrt {2\text{π} } )Erf\left( { - \frac{{\beta _i^{}}}{{\sqrt 2 }}} \right) - \beta _i^2{\text{π}} Erf{\left( { - \frac{{\beta _i^{}}}{{\sqrt 2 }}} \right)^2}\Bigg] , \\ \end{gathered} $

(24)

此时， $ {s_k} $ 值被估计出，然后将约束空间返回到状态空间， $ {A_k} $ 表示 $ a\left( {{{\hat X}_{k\left| k \right.}}} \right) $ 的雅可比矩阵， $ {X}_{k|k}^{+}，{P}_{k|k}^{+} $ 表示估计的均值和协方差矩阵。 $ {X_k} $ 的状态估计如下：

$ {X}_{k|k}^+={X}_{k|k}^{}+K（{A}_{k}K{）}^{-1}\left({\hat{s}}_{k}-{X}_{k|k}^{}\right)，$

(25)

$ K = {P_{k\left| k \right.}}A_k^{\rm{T}}(P_{k\left| k \right.}^{ - 1} - P_{k\left| k \right.}^{ - 1}{C_k}P_{k\left| k \right.}^{ - 1}) ，$

(26)

$ {P}_{k|k}^+={P}_{k|k}-{P}_{k|k}{A}_{k}^{{{T}}}({P}_{k|k}^{-1}-{P}_{k|k}^{-1}{C}_{k}{P}_{k|k}^{-1})（{P}_{k|k}{A}_{k}^{{{{\rm{T}}}}}{）}^{{{{\rm{T}}}}}。$

(27)

3 仿真和试验数据处理结果

为了验证算法的性能，本文对该算法和忽略约束先验信息的容积卡尔曼滤波方法进行了比较，并通过仿真和试验数据处理验证了该方法的性能

3.1 仿真结果

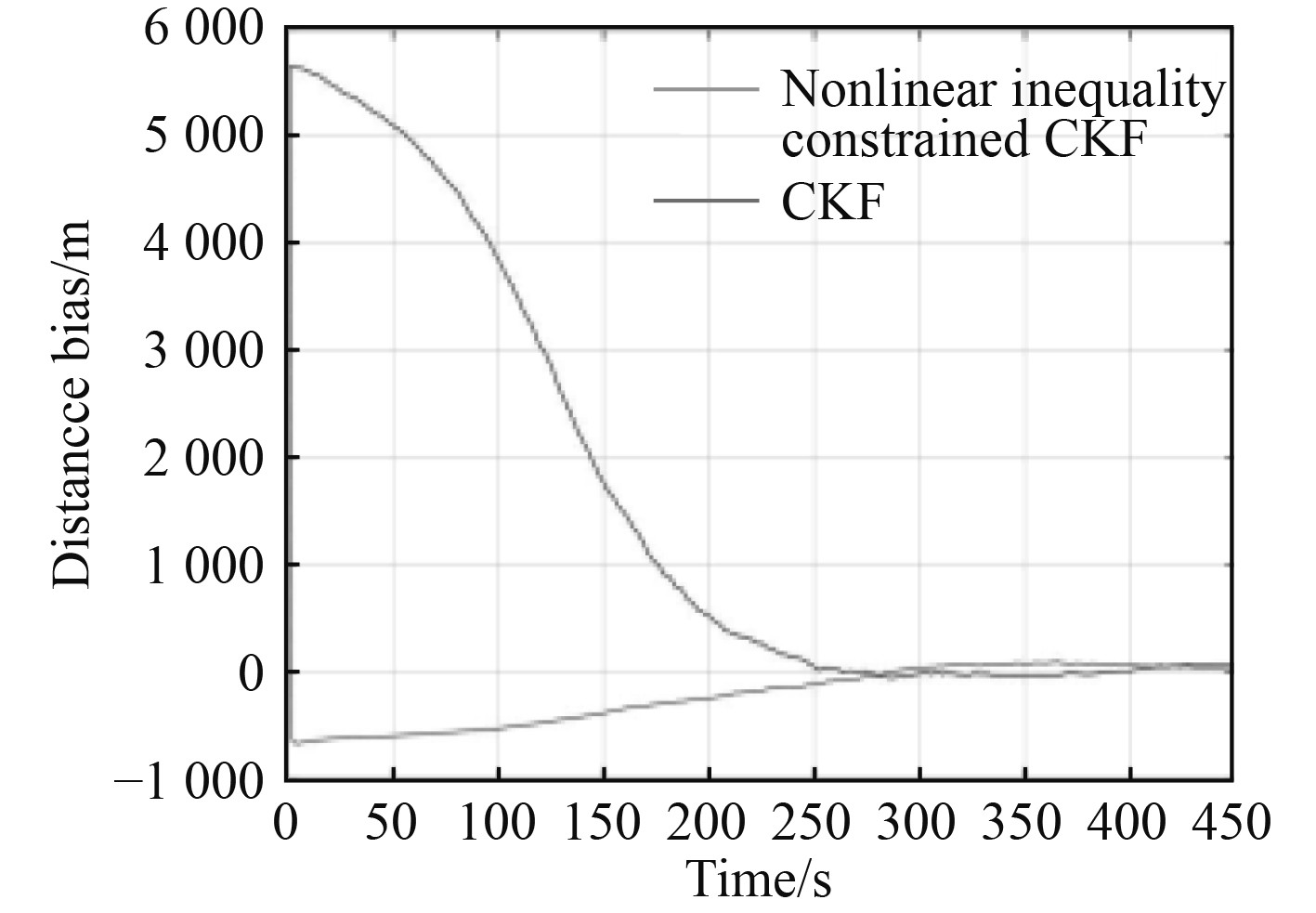
考虑图1所示的场景，双阵间距400 m，双阵均朝x正方向匀速直线运动，速度均为3m/s，目标速度为10 m/s，航向130°。初始时刻，参考基阵位于坐标原点，目标位于(−6000, 6000)处，测量噪声均服从正态分布，标准差均为1.5°，考虑式（4）和式(5)的约束条件，假定lower1，lower2，upper1和upper2分别为1000，0，8000和 $ {\text{π}} $ 。图2和图3为upper1为8000时的目标距离和速度的估计偏差。

由图可知，两者性能差异很大，考虑了约束信息之后，算法的收敛速度和精度都有明显的提升。

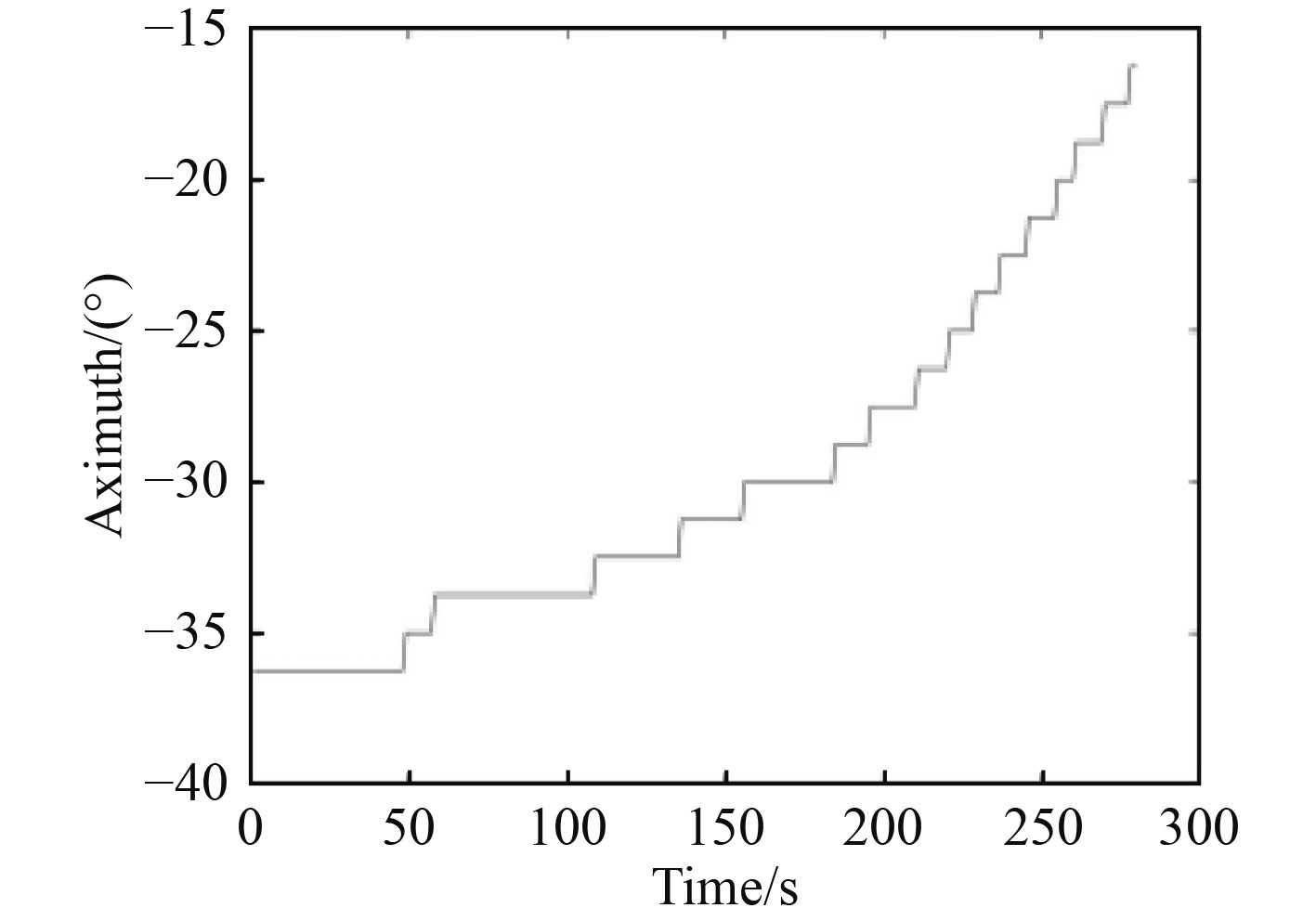
3.2 试验数据处理

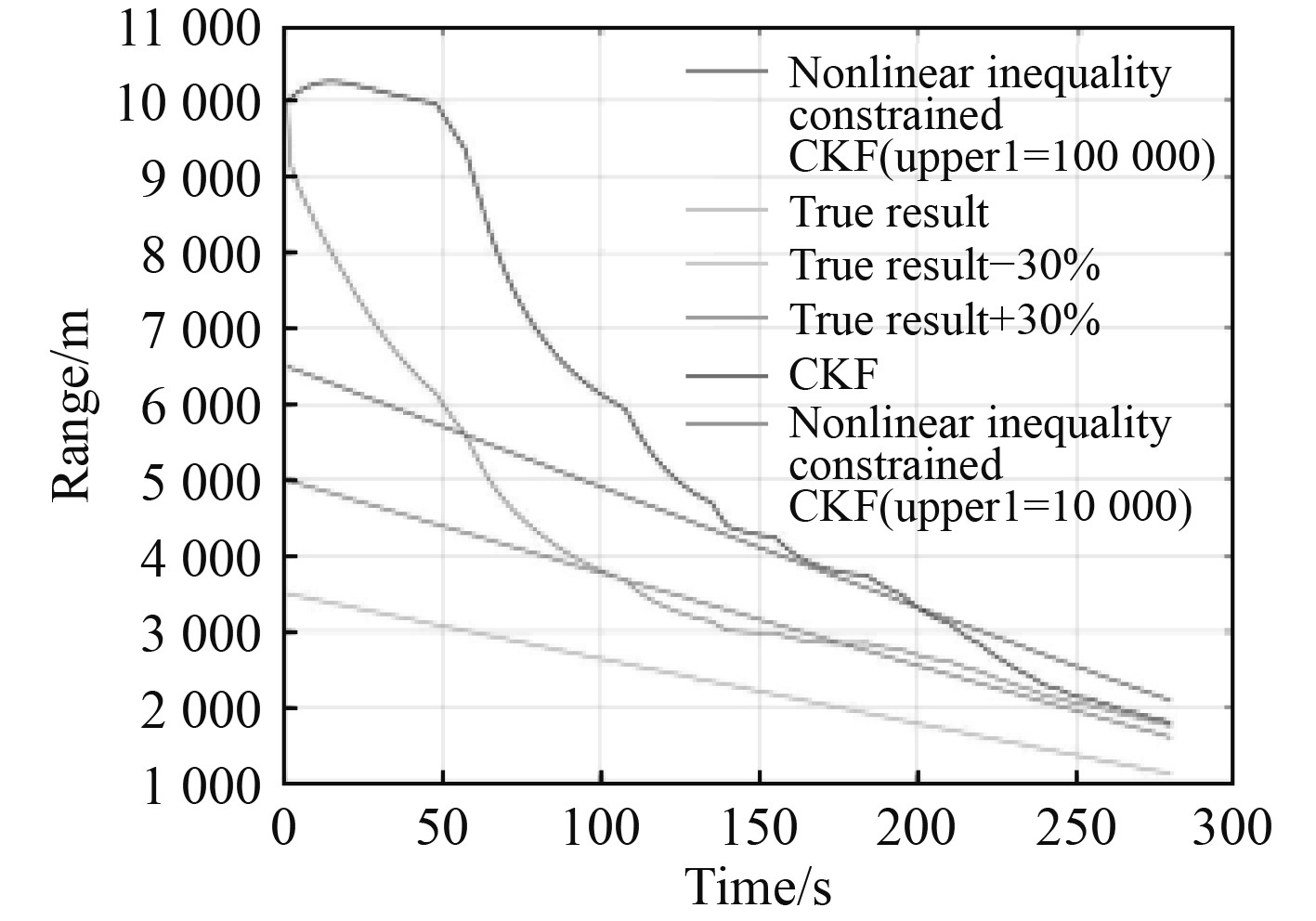
图4和图5为2个观测平台测量的目标方位，同样考虑距离和航向的不等式约束，这里lower1，lower2，upper1和upper2分别取为2 000，0，10000和 ${\text{π}}$ 。图6为距离估计结果。

由图6可知，试验数据处理结果和仿真结果一致，相比未考虑约束信息的容积卡尔曼滤波方法，考虑约束信息后，算法的收敛速度和精度均得到明显的提升。

4 结　语

本文研究非线性不等式约束条件下的纯方位目标运动分析问题，考虑目标速度和航向的约束，将非线性不等式约束滤波器和容积卡尔曼滤波结合起来对目标运动状态进行估计，并通过仿真和试验数据处理验证了该方法的性能，和未考虑约束信息相比，该方法的收敛速度和精度均有明显提升。