2. 天津职业大学 电子信息工程学院,天津 300410;
3. 天津航海仪器研究所,天津 300131;
4. 中国船舶集团航海保障技术实验室,天津 300131
2. School of Electronic Information Engineering, Tianjin Vocational Institute, Tianjin 300410, China;
3. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China;
4. Laboratory of Science and Technology on Marine Navigation and Control, CSSC, Tianjin 300131, China
舰船导航系统一般包括惯性导航设备、卫星导航设备、天文导航设备、计程仪等导航传感器设备,这些导航传感器都有各自的优点和适用特性,同时也都具有一定的不足,并且在运行过程中可能发生故障[1-2]。为了获得高精度、高可靠、高稳定的导航信息,导航系统必须向综合化、容错化发展[3-5]。目前导航系统中设计了专用设备对系统内所有导航传感器信息进行融合处理,即以惯性导航设备为基础,对导航系统内其他传感器信息进行综合和容错。对于容错组合导航系统而言,其内部含有多个子系统,一旦某个子系统发生故障,而没有好的故障检测措施,让故障信息进入主系统,经过信息融合和反馈后,每个子系统都有可能被污染,导致最终输出的导航与定位信息不准确,甚至不能使用[6-9]。因此,为了提高容错导航系统的可靠性和准确性,需要进行故障检测与诊断。常用的故障检测方法有广义似然比检测法、神经网络法和
本文针对残差
导航系统中参与信息融合的传感器主要有惯性导航设备(惯导)、卫星导航设备(卫导)、天文导航设备(天导)、多普勒计程仪,这些传感器通过联邦滤波实现信息的融合,其融合算法架构如图1所示。

|
图 1 导航系统信息融合算法架构 Fig. 1 Information fusion algorithm architecture of navigation system |
如图1所示,导航信息融合处理设备接收惯导过来的原始观测量信息,通过各个惯导解算单元完成惯性导航的递推,与其他导航传感器信息通过联邦滤波结构进行信息融合,采用残差
选取捷联惯导系统的误差向量作为信息融合算法的状态向量,在建模时假设陀螺角速率随机漂移由随机常值漂移和白噪声组成,加速度计的随机漂移由随机常值漂移和白噪声组成,公式为:
| $ {{X}}_{{\rm{INS}}}=[\begin{array}{ccccc}{\delta \varphi}^{{n}}& {\delta{{V}}}^{{n}}& {\delta{{P}}}^{{n}}& \in_{\text{b}}^{\text{b}}& {\nabla }_{\text{b}}^{\text{b}}\end{array}]。$ | (1) |
式中:
信息融合算法的状态方程为:
| $ {{\dot X}_{{\text{INS}}}} = {{{F}}_{{\text{INS}}}}{{{X}}_{{\text{INS}}}} + {{{W}}_{{\text{INS}}}} 。$ | (2) |
其中:
影响卫导定位精度的因素有电离层和对流层对电磁波产生的附加延时,卫星运动引起的相对论效应,地球运动的不均匀性及太阳和月亮引力场的作用。这些误差对卫导定位的影响不是太大,故将其视为白噪声。SINS/GNSS的量测方程为:
| $ {{{Z}}_{{\text{GNSS}}}} = \left[ {\begin{array}{*{20}{c}} {{\text{δ }}{{{V}}_{{\text{GNSS}}}}} \\ {{\text{δ }}{{{P}}_{{\text{GNSS}}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{{V}}_{{\text{wGNSS}}}}} \\ {{{{P}}_{{\text{wGNSS}}}}} \end{array}} \right] 。$ | (3) |
式中:
多普勒计程仪是利用声波传播的多普勒效应测量传播速度,其量测方程为:
| $ {{{Z}}_{{\text{DVL}}}} = {\text{δ }}{{{V}}_{{\text{DVL}}}} + {{{V}}_{{\text{wDVL}}}}。$ | (4) |
其中:
天文导航利用对星体的观测数据来确定航行体的位置,可以同时测量一颗星的方位角
| $ {{{Z}}_{CNS}} = {\text{δ }}{{{P}}_{{\text{CNS}}}} + {{{P}}_{{\text{wCNS}}}} 。$ | (5) |
式中:
导航系统信息融合对各子滤波器运行状态进行故障检测,当检测到子滤波器状态异常时,在联邦滤波器中将其隔离,使用正常的子系统继续进行组合,即保证组合导航的精度,又保证主滤波器输出不受故障子系统的干扰。当子滤波器发生故障时,量测中包含了故障信息,因此状态估计和残差都会发生偏离,通过构造残差
由于子滤波器均为卡尔曼滤波器,其残差为:
| ${{r}}_{k}={{Z}}_{k}-{{H}}_{k}{\hat{{X}}}_{k/k-1}。$ | (6) |
故
根据数理统计中假设检验的理论,构造统计量
以往残差
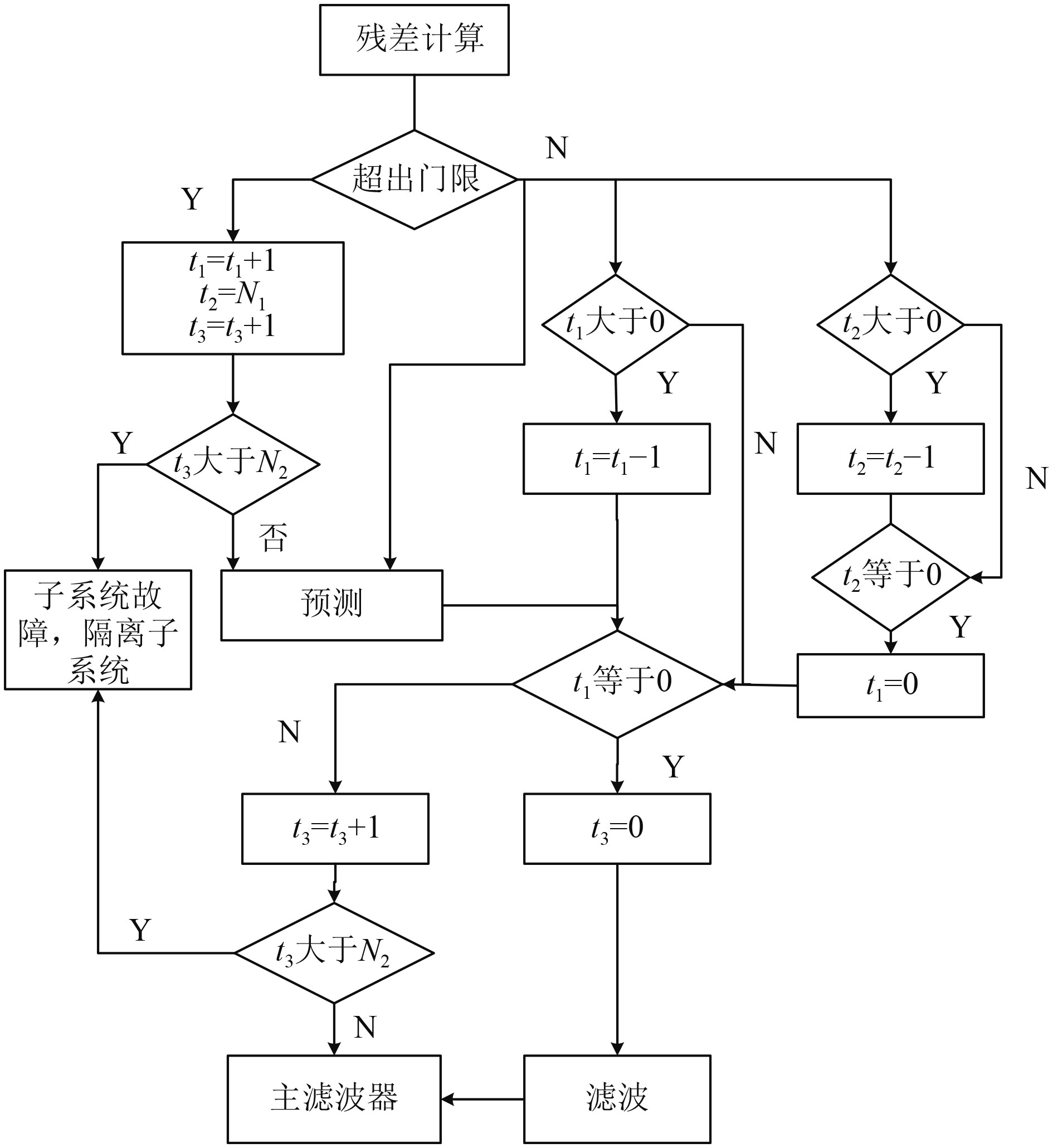
|
图 2 故障检测流程图 Fig. 2 Fault detection flow chart |
以INS/GNSS子系统存在故障为例,说明本文故障检测算法相比传统算法的效果。仿真中惯导初始姿态误差为
假设卫导在1 080 s时,位置发生突变故障,纬度和经度都突变0.02′,持续时间2 min,在1 800 s,速度发生突变故障,东向、北向速度突变0.4 m/s。故障检测门限分别设置为13和20。
传统算法和改进算法的速度误差如图3和图4所示,位置误差如图5和图6所示。为了便于观察,将4种情况下的残差
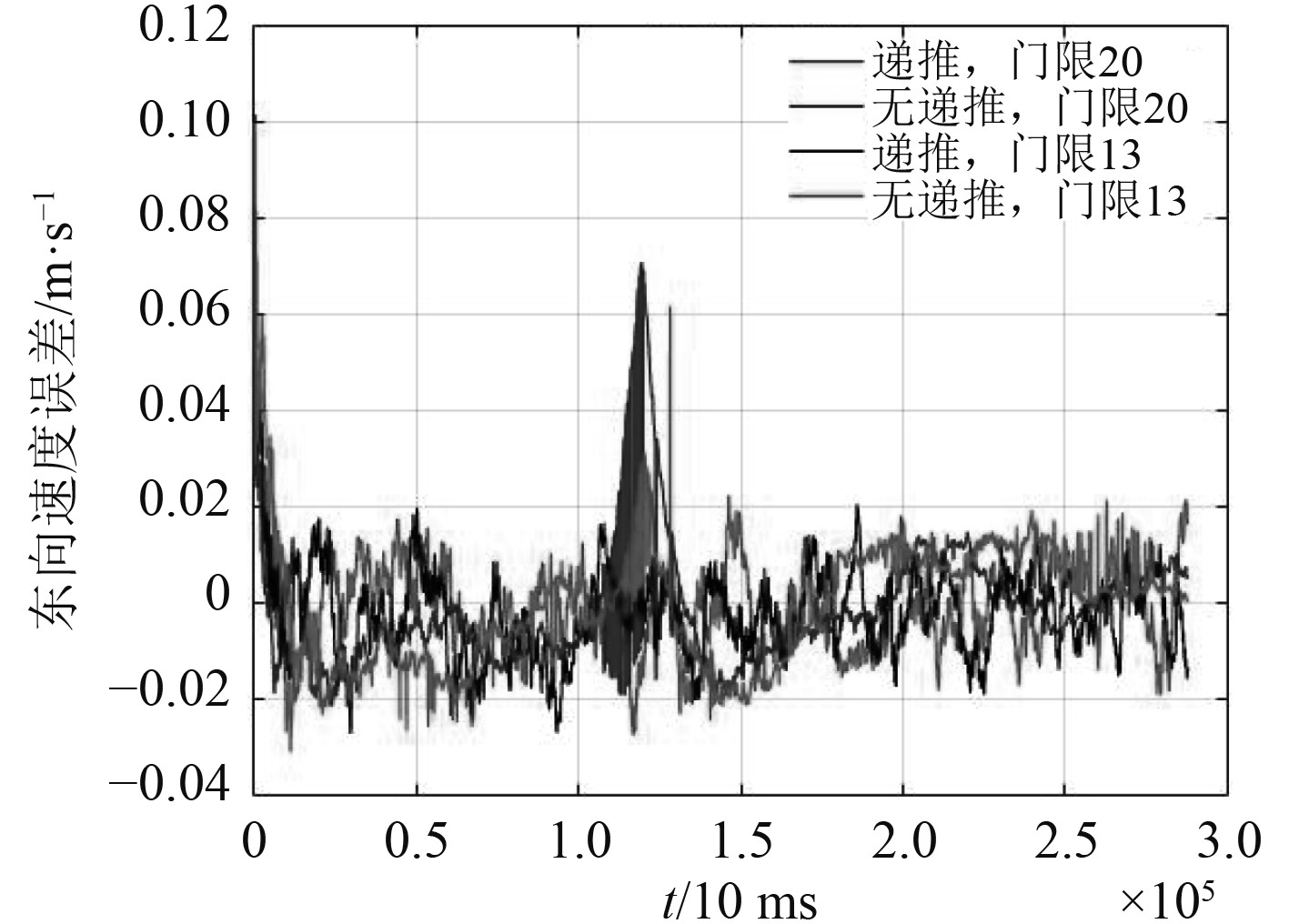
|
图 3 东向速度误差 Fig. 3 Eastward velocity error |
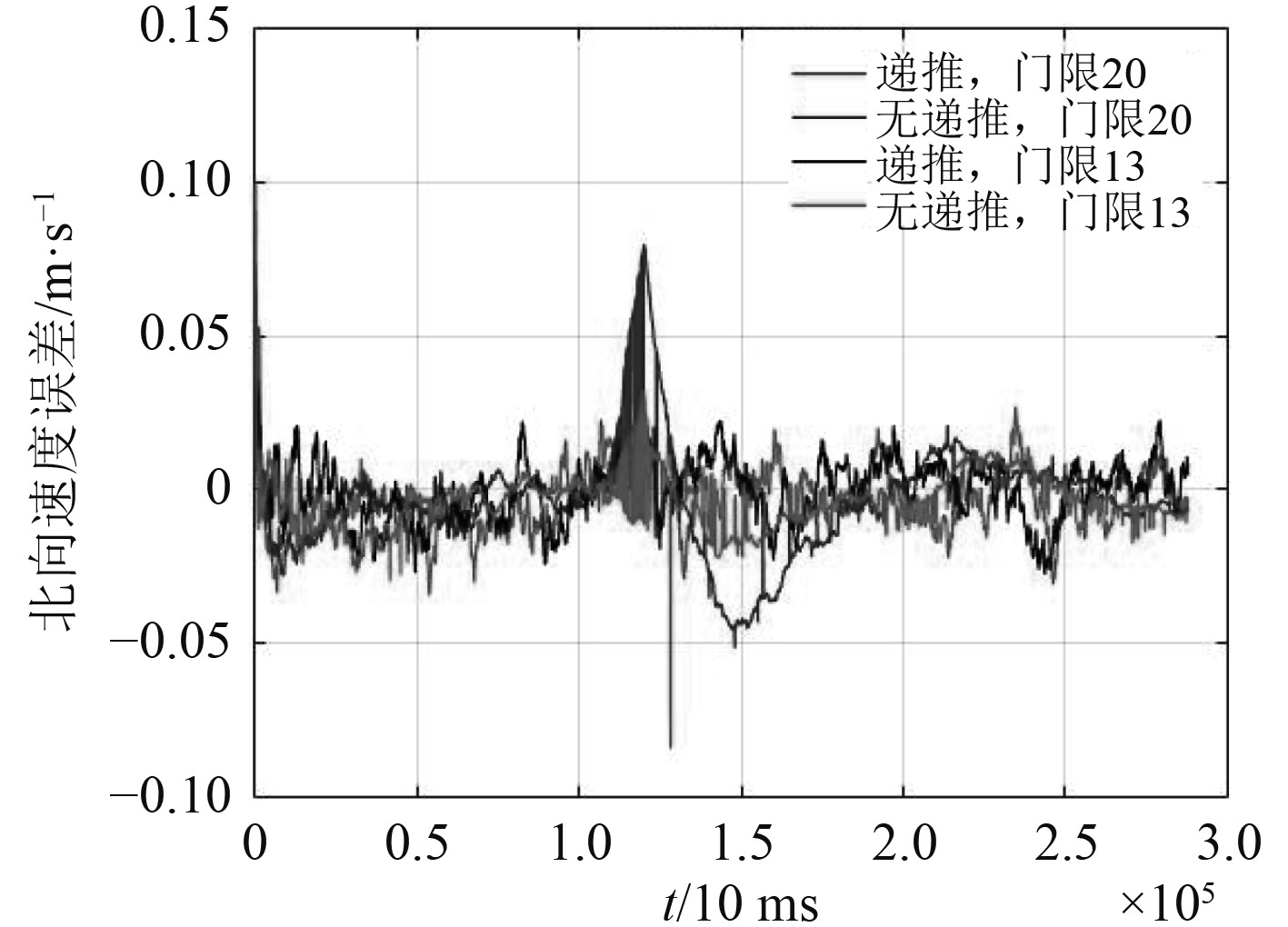
|
图 4 北向速度误差 Fig. 4 Northward velocity error |
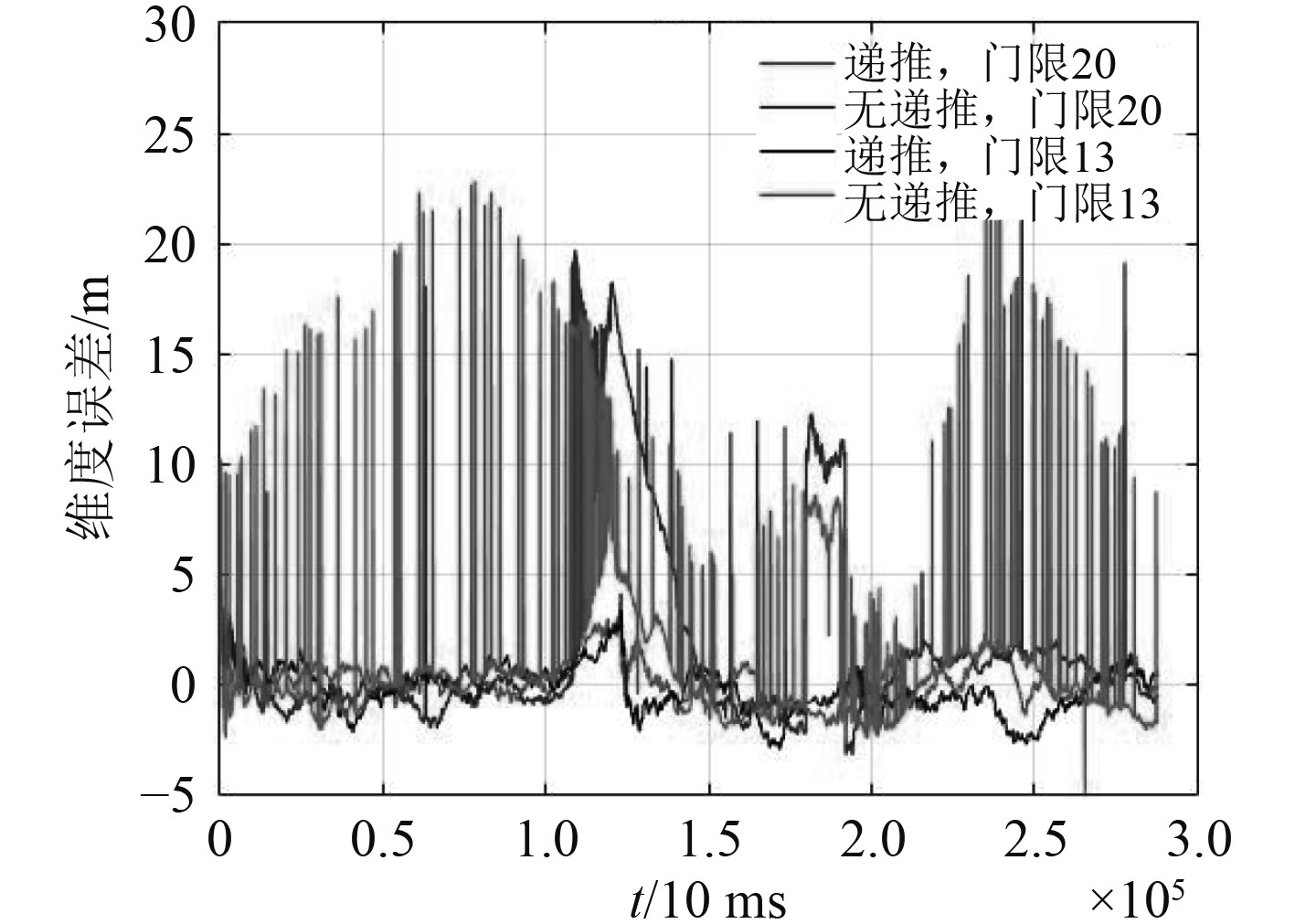
|
图 5 纬度误差 Fig. 5 Latitude error |

|
图 6 经度误差 Fig. 6 Longitude error |
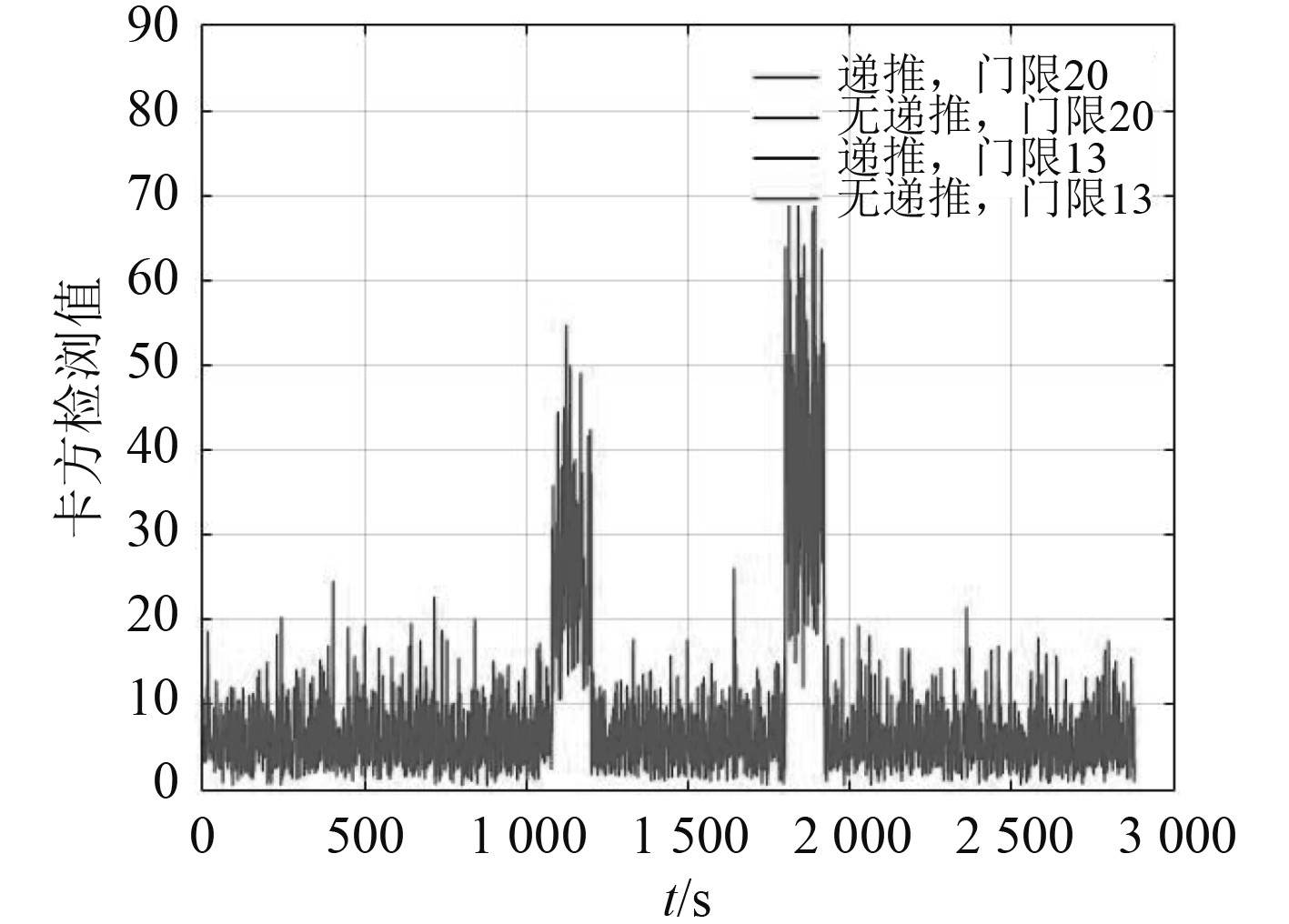
|
图 7
改进算法门限20残差
|
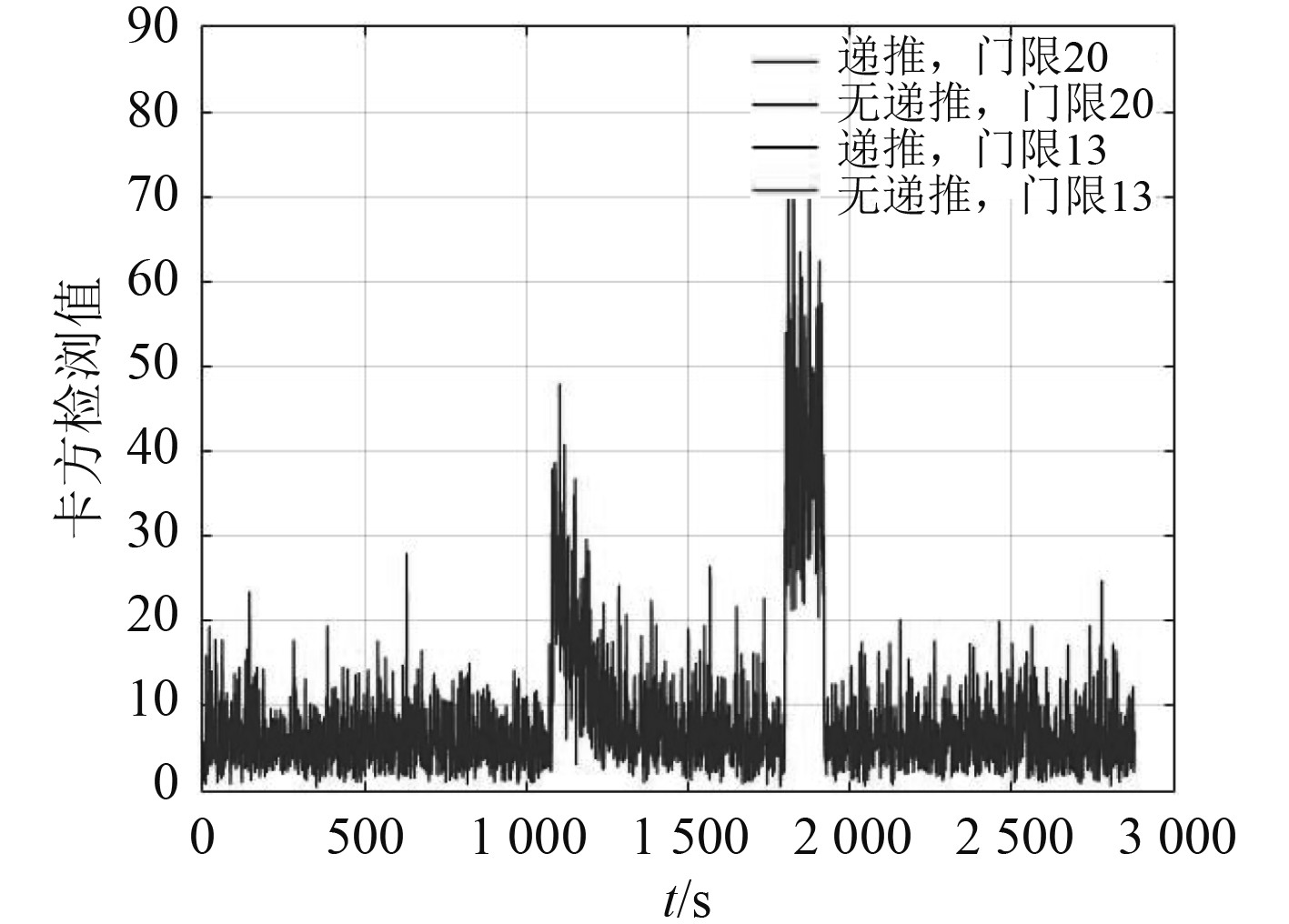
|
图 8
传统算法门限20残差
|
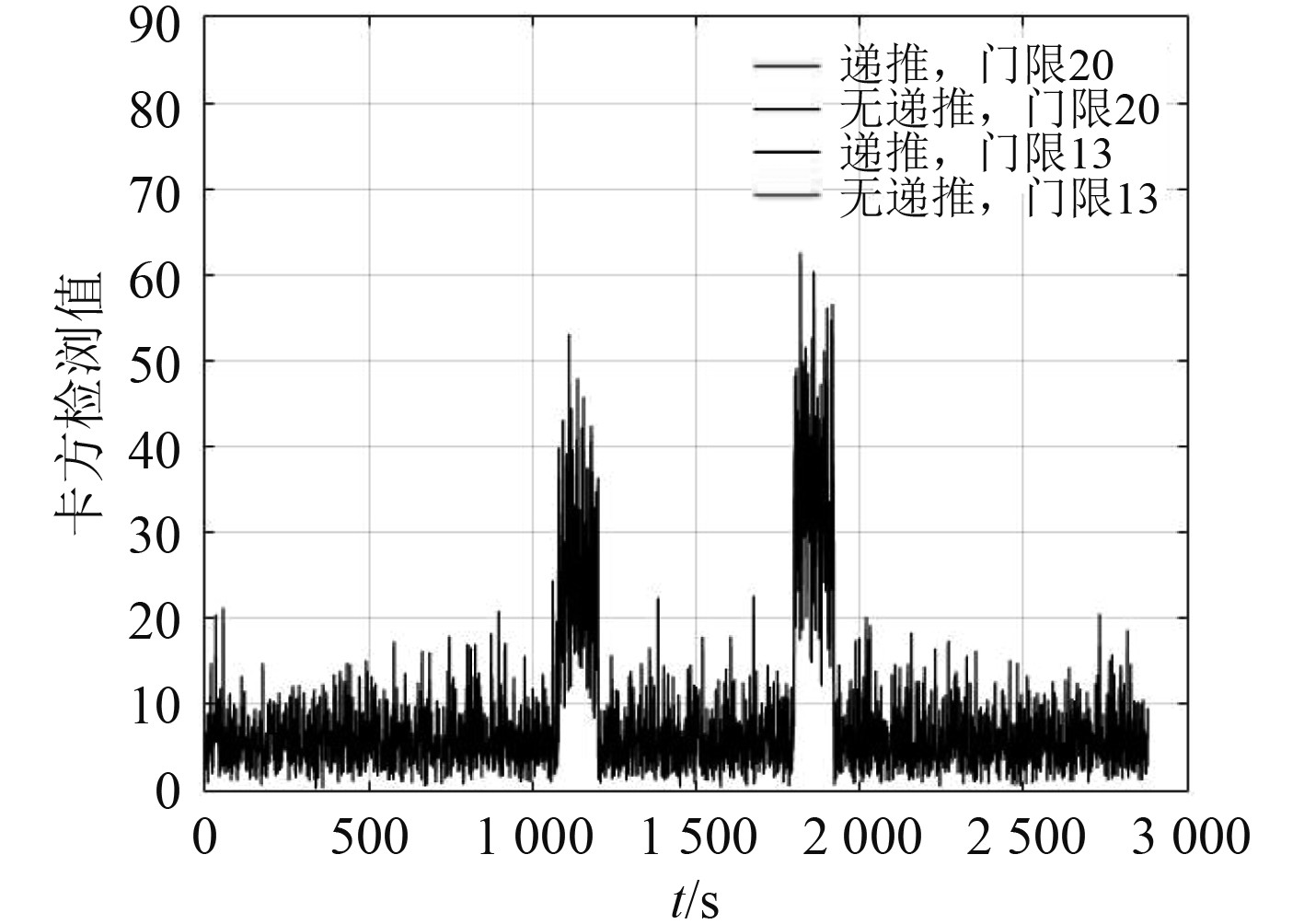
|
图 9
改进算法门限13残差
|
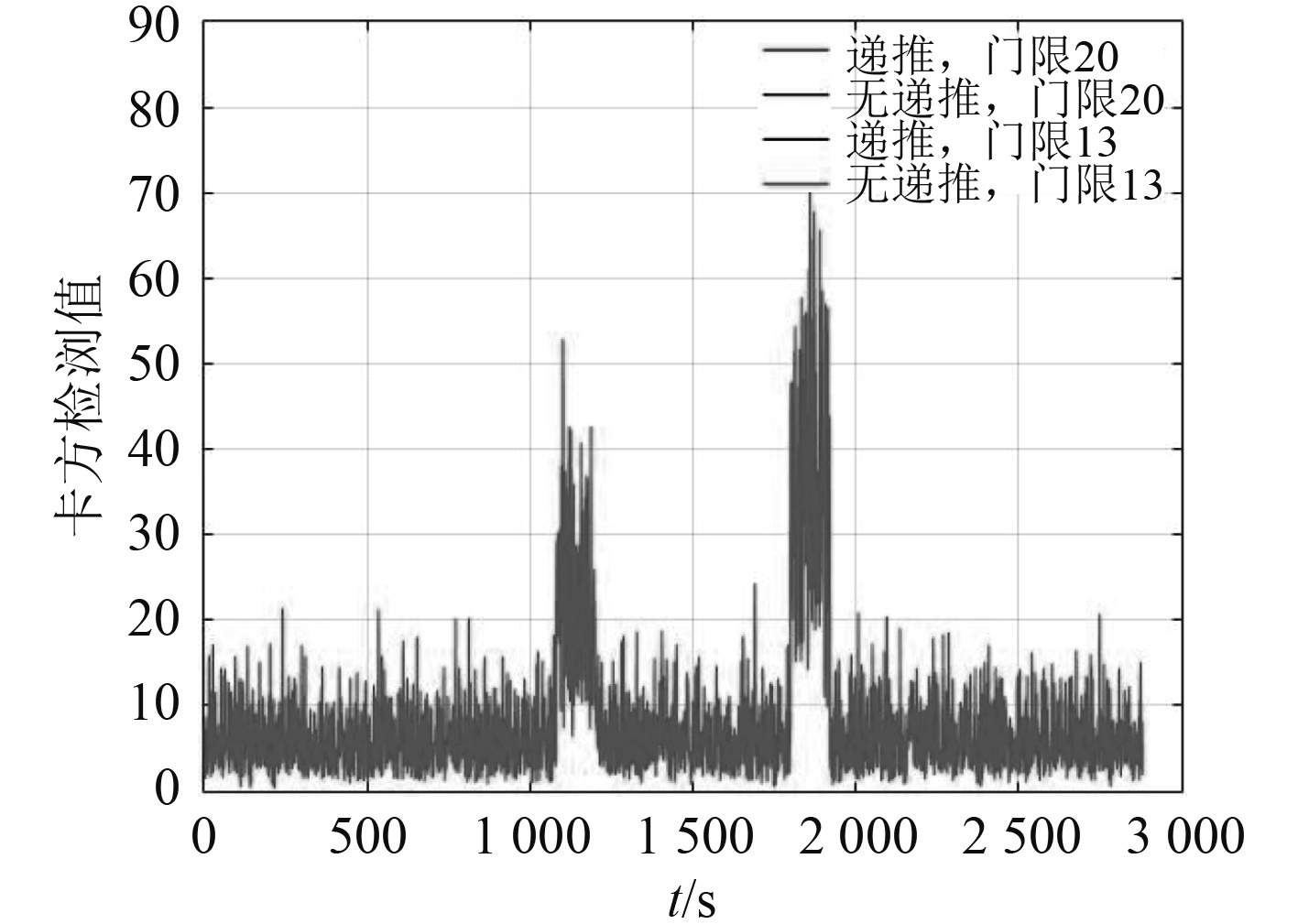
|
图 10
传统算法门限13残差
|
对比图7~图10可知,当检测门限设置较高时,传统残差
表1~表3统计了上述4种状态下,系统的精度、稳定度和最大值。
|
|
表 1 四种状态下,系统精度统计 Tab.1 Four precision statistics |
|
|
表 2 四种状态下,系统稳定度统计 Tab.2 Four stability statistics |
|
|
表 3 四种状态下,系统最大值统计 Tab.3 System maximum statistics |
表1~表3的统计结果进一步验证了上述结论。从表1可知,改进算法的速度误差较传统算法有所改善,位置误差较传统算法有明显改善,如当门限为20时,改进算法的纬度误差将为传统算法的18%。从表2可知,改进算法的速度误差和位置误差波动更小,如当门限为20时,传统算法纬度误差波动为4.15 m,而改进算法纬度误差波动为0.57 m,大约降为原来的14%。从表3可知,改进算法的最大位置误差在5 m以内,而传统算法最小位置误差为16.36 m,可知改进算法能够有效降低位置误差。
综上所述,改进算法在均方误差、稳定度和最大误差等3个方面都优于传统算法,具有较大的实用价值。
4 结 语本文针对舰船导航系统信息融合中的故障检测问题,提出了一种改进的故障检测算法。该算法充分利用误差模型特性,设置多个计数器,在有故障的时候利用误差模型进行递推,仿真结果表明,该算法能够有效改善信息融合的速度和位置指标,提高导航系统的稳定性和精度。
| [1] |
赵万龙, 孟维晓, 韩帅. 多源融合导航技术综述[J]. 遥测遥控, 2016(6): 54-60. DOI:10.3969/j.issn.2095-1000.2016.06.006 |
| [2] |
张靖, 陈鸿跃, 陈雨, 等. 一种基于联邦卡尔曼滤波器的多源信息融合定位算法[J]. 导弹与航天运载技术, 2018(2): 90-98. DOI:10.7654/j.issn.1004-7182.20180219 |
| [3] |
WANG R, XIONG Z, LIU J, et al. Chi-square and SPRT combined fault detection for multisensor navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1352-1365. DOI:10.1109/TAES.2016.140860 |
| [4] |
XU J, XIONG Z, LIU J, et al. A dynamic vector-formed information sharing algorithm based on two-state chi square detection in an adaptive federated filter[J]. The Journal of Navigation, 2019, 72(1): 101-120. DOI:10.1017/S0373463318000565 |
| [5] |
杨镜, 华冰, 熊智. 多源导航系统软、硬故障检测新方法研究[J]. 压电与声光, 2013, 35(5): 647-652. DOI:10.3969/j.issn.1004-2474.2013.05.009 |
| [6] |
张闯, 赵修斌, 庞春雷, 等. LS-SVM 辅助的小幅值及缓变故障检测与容错方法[J]. 中国惯性技术学报, 2019, 27(3): 415-420. |
| [7] |
CHENG J, SUN X, LIU P, et a1. An improved residual Chi-square test fault isolation approach in four-gyro SINS[J]. IEEE Access, 2019, PP(99): l-1. |
| [8] |
郭慧娟, 刘慧英, 石静, 等. 基于自适应分类容错滤波的SINS/GNSS组合导航方法[J]. 中国惯性技术学报, 2018, 26(1): 39-44. |
| [9] |
李振威, 程咏梅, 刘刚, 等. INS/ADS/GPS组合导航高灵敏故障检测和识别方法[J]. 中国惯性技术学报, 2020, 28(5): 694-700. |
| [10] |
周朋进, 吕志伟, 丛佃伟, 等. 基于双状态χ2检测和快速强跟踪AUKF 的组合导航算法
[J]. 中国惯性技术学报, 2019, 27(6): 771-777. |
 2022, Vol. 44
2022, Vol. 44
