当舰船海上航行时,螺旋桨旋转调制腐蚀或防腐电流会产生轴频电场信号,其基频与螺旋桨的转动频率一致,该信号具有明显的线谱特征,适合用于舰船目标的探测[1]。为了提高探测的机动性,基于运动平台进行电场探测得到广泛关注[2]。但是由于轴频电场信号随着探测距离的增大而快速衰减,为了提高在运动平台下对轴频电场的远程探测能力,需要深入研究轴频电场的信号处理方法以提高信噪比。
对轴频电场的检测方法一直都是舰船目标探测方向上的重要研究内容。文献[3]提出一种基于负熵的舰船轴频电场信号检测方法,该方法根据目标信号与背景噪声在高斯性上的显著差异可以将信号检测出来,但该方法受限于背景噪声为高斯噪声。文献[4]提出一种基于高阶累量的船舶轴频电场信号自适应增强方法,可以有效抑制背景噪声。文献[5] 在分析轴频信号和环境噪声物理特征上的差异的基础上,提出一种功率谱能量峰值熵比特征的检测算法,用于提取微弱轴频电场信号。文献[6]提出了基于尺度-小波能量谱的舰船轴频电场检测算法,该算法在低信噪比下也有较好的性能。但上述轴频电场检测方法主要针对沉底测量平台,由于沉底测量平台下海洋环境电场具有良好的高斯性,因此大多将其作为高斯背景进行处理。然而在实际的运动或者晃动平台下观测所得的海洋环境电场,往往存在非高斯统计特性[7],可能使得上述在高斯背景下的信号处理方法性能下降甚至失效,例如经典的最小均方(least mean square,LMS)算法在高斯环境下有较好性能,但在非高斯环境下会出现性能退化[8]。而最小平均p-范数(least mean p-norm,LMP)算法在非高斯环境下能够有较好的性能[9],为了提高在运动平台下对轴频电场信号检测距离和抑制背景噪声能力,本文将LMP算法应用在轴频电场信号处理中,通过理论仿真和实测数据分析验证该方法能够使用于运动平台下的轴频电场探测。
1 LMP自适应算法基本原理自适应算法能够将滤波器的输入、输出及原参量值,按照一定准则修改滤波参量,最终使滤波器达到有效跟踪外部环境变化的效果。
最简单的经典自适应算法是最小均方算法,该算法基于最小均方误差(minimum mean square error,MMSE)准则,在该准则下LMS算法以平方误差为代价函数,但是由于非高斯
图1为M阶FIR自适应滤波器结构,给定输入序列{x(n)},根据最小分散系数准则选择合适的权值w(n),使得滤波器的输出y(n)尽可能接近期望的响应d(n),Z−1表示一个采样间隔的延迟。
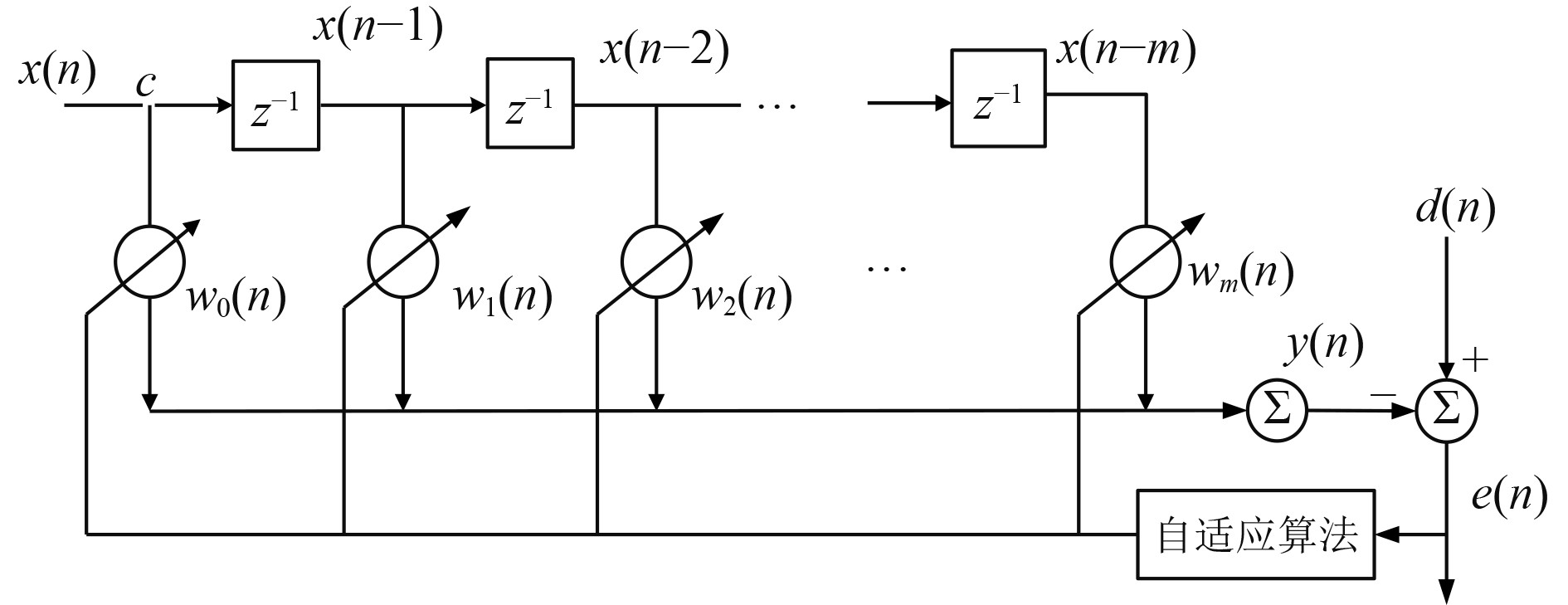
|
图 1 自适应滤波器结构 Fig. 1 Adaptive filter structure |
假定:
在非高斯
| $ J\left[ {w(n)} \right] = E[{\left| {e(n)} \right|^p}] = E[{\left| {d(n) - X_{}^{\rm{T}}(n){\text{w}}(n)} \right|^p}],$ | (1) |
利用最速梯度下降法,并以误差的瞬时值代替其统计平均,则瞬时梯度估计为:
| $ \begin{split}\mathop g\limits^ \wedge (n)= &\frac{{\partial J}}{{\partial W(n)}}= pe(n)[ - x(n)] = \\ & p|e(n){|^{p - 1}}{\rm{sign}}(e(n))[ - x(n)] ,\end{split}$ | (2) |
利用梯度估计,可以导出LMP的权系数调整公式:
| $ W(n + 1) = W(n) - \mu p{X_N}(n){\left| {e(n)} \right|^{p - 1}}{{\rm{sgn}}} (e(n)) ,$ | (3) |
其中
μ为算法的步长因子,用于控制算法的收敛速度和稳态误差,为了保证算法的收敛,μ的取值必须足够小。在保证算法收敛的条件下,μ越大则算法收敛速度越快,同时步长因子也决定算法的失调,μ越大则失调越大。所以为了达到较好的效果,应根据实际的应用场合需求,合理选择收敛因子。
p为算法的阶数,可以调整权值更新,对算法的性能有很大影响,正是由于p阶矩对脉冲型数据具有很强的抑制能力[13],所以LMP算法理论上比LMS算法更适用于非高斯信号处理。
2 仿真分析为了验证LMP算法在非高斯环境下的有效性,并比较LMS算法和LMP算法的效果,采用仿真模拟轴频电场信号,该信号是由基频为2 Hz及其倍频(2倍频及3倍频)的正弦信号加以非高斯噪声,形成信噪比SNR分别为−6 dB和−12 dB的2组信号。正弦信号可表示为:
非高斯噪声模型采用拉普拉斯噪声,在许多实际应用环境中,具有和实际噪声相似的特性,可表示为:
产生一个信噪比为−6 dB的信号,频谱图如图2所示。可以看出,轴频电场线谱信号强度与环境电场噪声强度相当,2 Hz位置的线谱已经被环境噪声掩盖,线谱特征不明显。

|
图 2 SNR=−6 dB 时仿真信号频谱图 Fig. 2 Spectrum diagram of simulated signal at SNR=−6 dB |
分别采用LMP算法和LMS算法对上述仿真信号进行处理,2种算法选取的参数为:步长μ=0.0001,滤波器阶数M = 100,LMP算法的阶数p=1.2。处理后的信号频谱图如图3所示。
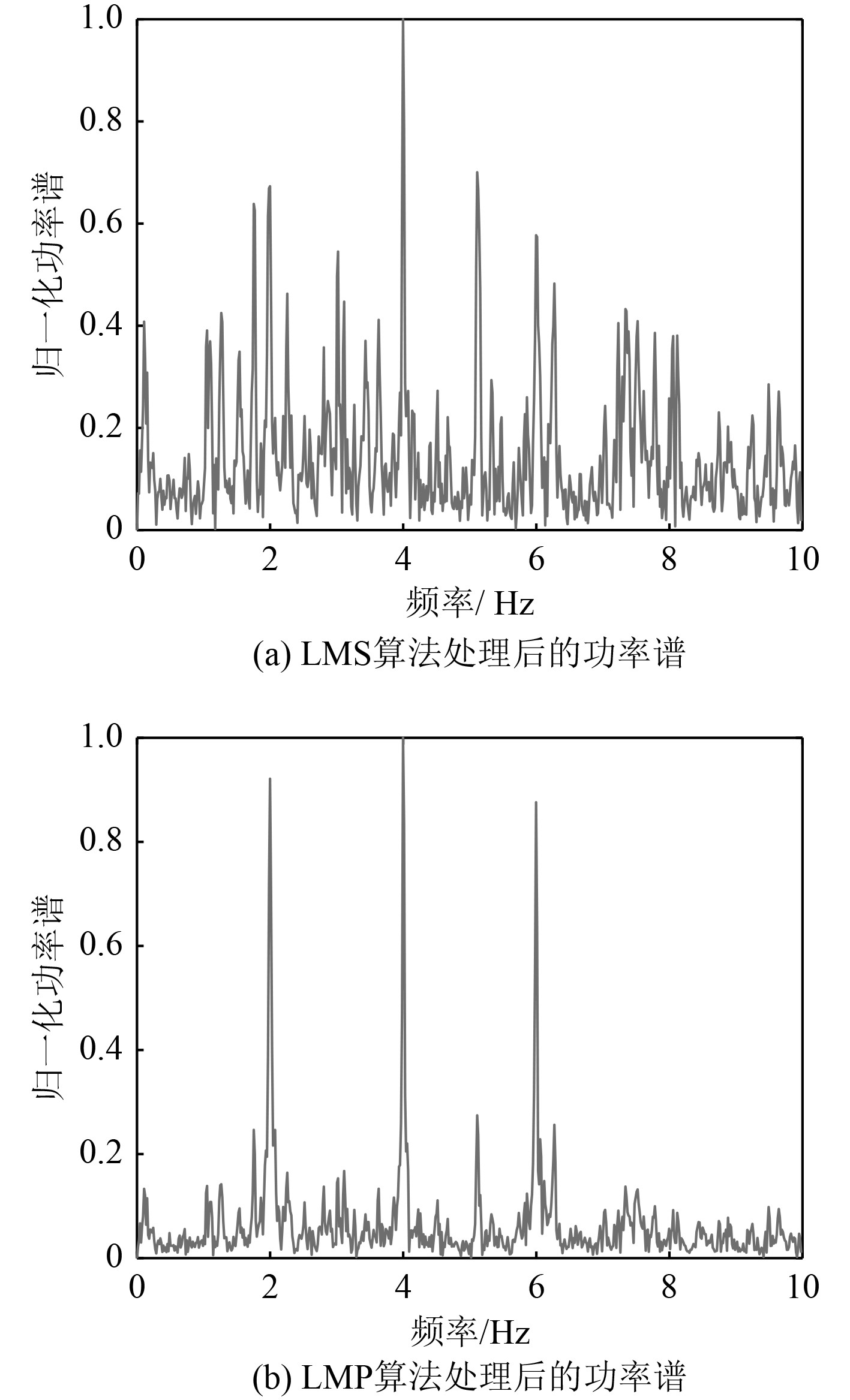
|
图 3 SNR=−6 dB时2种算法对仿真信号处理后的频谱图 Fig. 3 Spectrum diagram of simulation signal processed by the two algorithms at SNR=−6 dB |
可知,当信噪比为−6 dB时,经典的LMS未能有效得压制其他频率的背景噪声信号。而LMP算法可以明显检测出轴频电场的基频(2 Hz)及其倍频(4 Hz和6 Hz),信噪比得到了较大提高。
当信噪比为−12 dB时,信号的频谱图如图4所示。
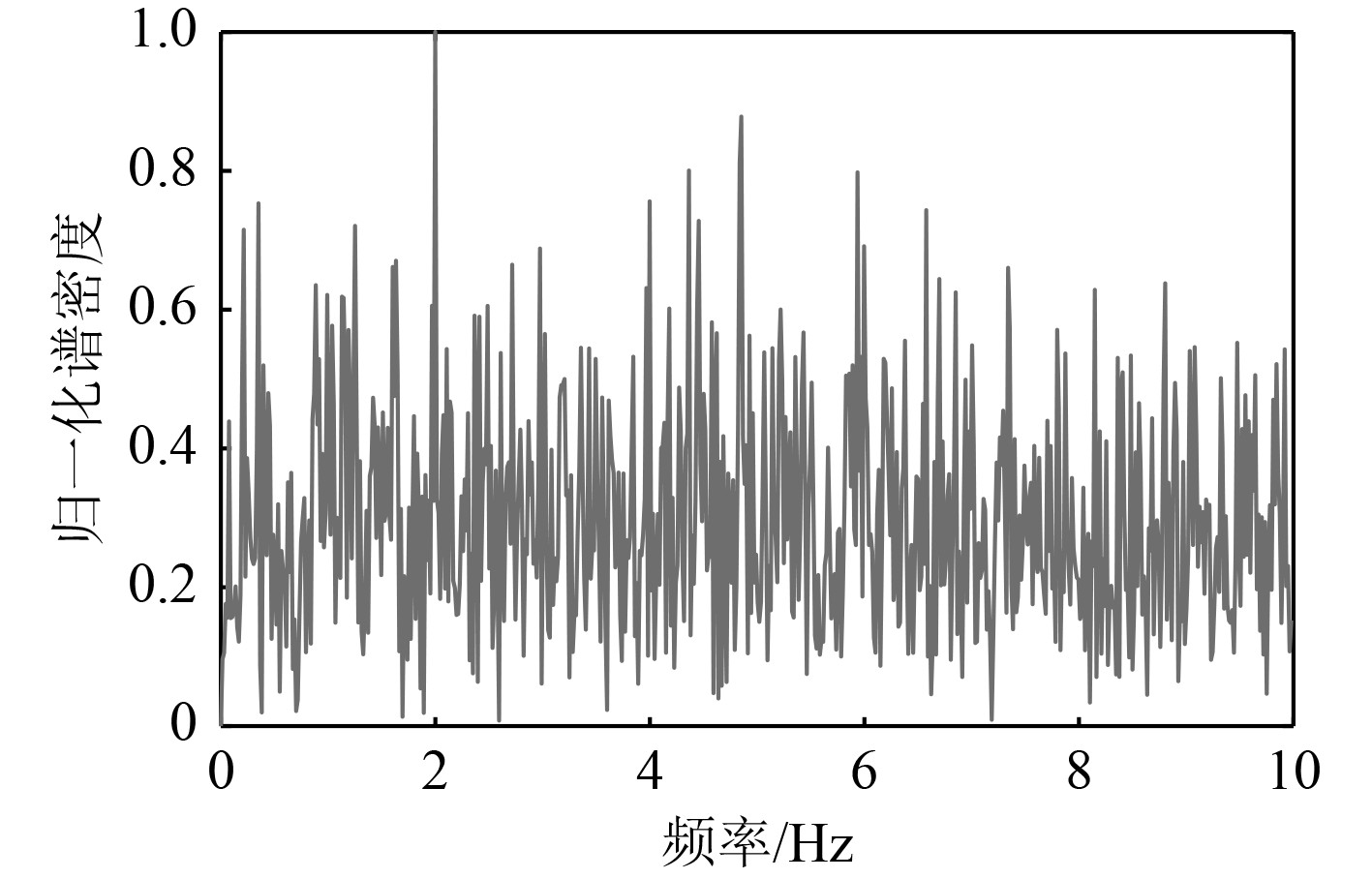
|
图 4 SNR=−12 dB时仿真信号频谱图 Fig. 4 Spectrum diagram of simulation signal at SNR=−12 dB |
由图4可知,当信噪比降为−12 dB时,轴频电场信号已经完全被背景噪声所淹没,并不能看出轴频电场的基频(2 Hz)及其倍频(4 Hz和6 Hz)。
分别采用LMP算法和LMS算法对上述仿真信号进行处理,处理后的信号频谱图如图5所示。
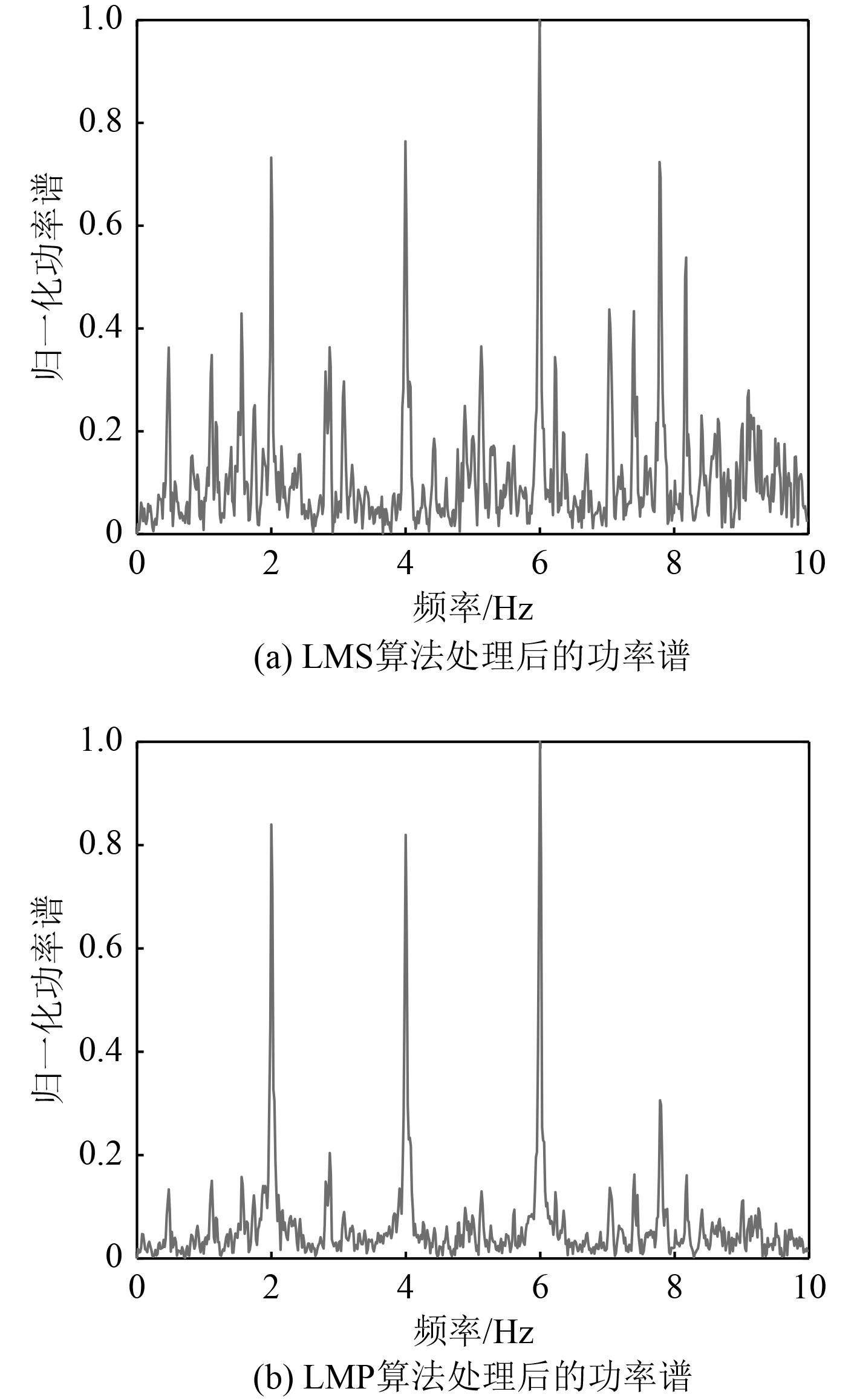
|
图 5 SNR=−12 dB时2种算法对仿真信号处理后的频谱图 Fig. 5 Spectrum diagram of simulation signal processed by the two algorithms at SNR=−12 dB |
由图5(a)可知,经过LMS算法处理后,轴频电场的基频和倍频已经被背景噪声所掩盖,无法提取出轴频电场的特征信息。
由图5(b)可知,经过LMP算法的处理后,背景噪声被有效地抑制,能够有效地提取出有用的轴频电场信号(2 Hz)和其谐波(4 Hz和6 Hz),在低信噪比下也能有效地提取到信号。
3 试验验证为了进一步检验LMP算法对舰船轴频电场的检测效果,利用海上运动平台试验对其进行检验。
试验海况2级,试验时将电场传感器安装在船体底部(船材料为玻璃钢),用于测量水中的电场信号。
将一电场模拟源固定在浮标附近,该模拟源可用于模拟轴频电场信号。试验场景示意图如图6所示,电场测量船在不同方向分别以一定的速度驶向或者驶离模拟源信号。

|
图 6 试验场景示意图 Fig. 6 Schematic diagram of test scene |
利用正态分布概率图(Q-Q图)对实测环境电场数据进行高斯性检验。Q-Q图是一种标准正态分布的分位数为横坐标、样本值为纵坐标的散点图,通过看Q-Q图上的点是否可以拟合在一条直线上,可以大致判断样本数据是否服从于高斯分布[15]。
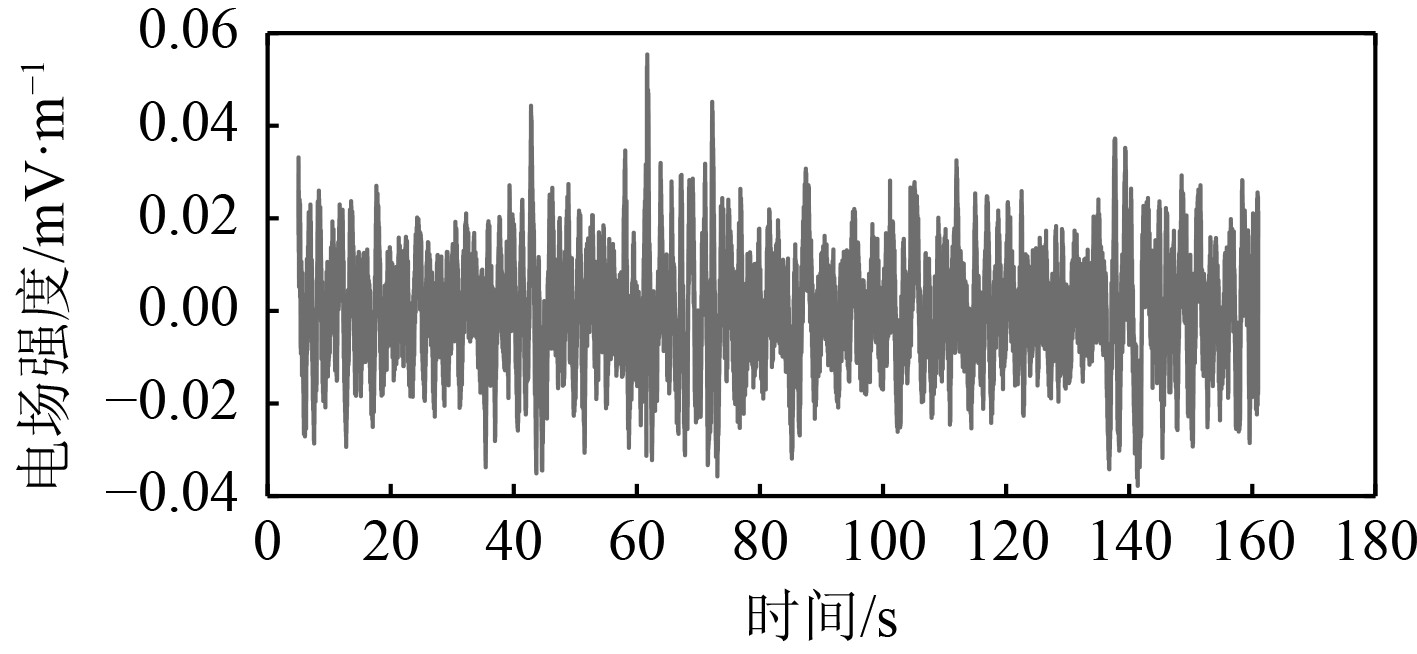
当电场测量船速为20 kn时,选取一个航次,采集到的海洋环境电场信号时域图如图7所示。
|
图 7 船速20 kn时海洋环境电场时域图 Fig. 7 Time domain diagram of Marine environmental electric field at ship speed of 20 kn |
抽取40 s为起点,分别选取3段时间长度(T=5 s,10 s,20 s)的噪声数据,再对这3段数据进行正态概率图分析。如图8为对图7噪声数据进行高斯性分析的结果,可以看出,输入样本分布的分位数跟标准正态分位数的线性度较差,说明船速为20 kn时环境电场噪声的高斯性较弱,非高斯性较强。

|
图 8 海洋环境电场信号在选取时间段的正态概率图 Fig. 8 Normal probability diagram of marine environmental electric field signals in selected time periods |
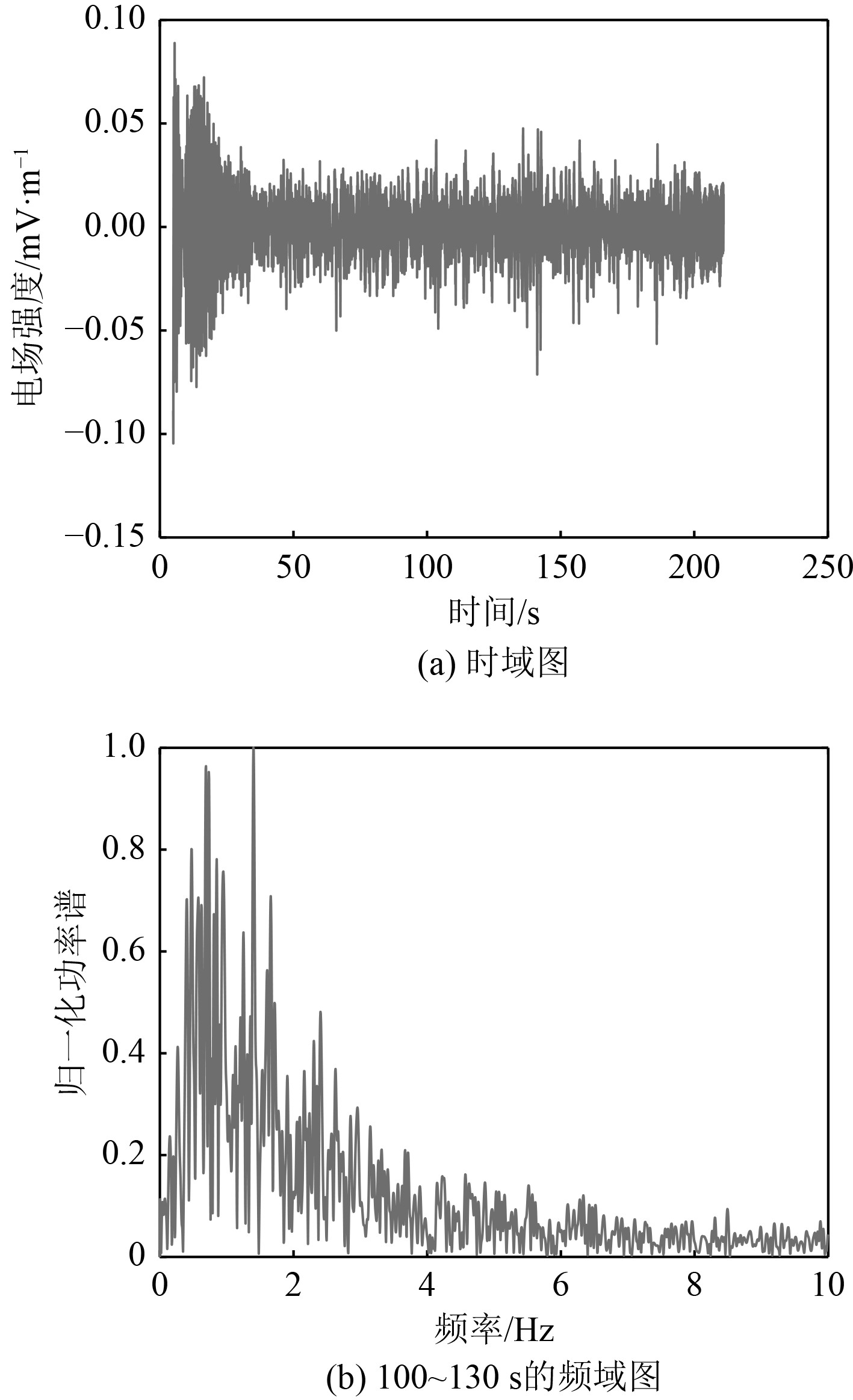
电场测量船从模拟源信号附近以20 kn的速度驶离模拟源,此时模拟源信号为3 Hz的正弦信号,图9(a)为采集到的原信号的时域图,图9(b)为选取图9(a)内100~130 s的数据进行频谱分析后得到的频域图。由图9(b)可见3 Hz的信号已被环境噪声所淹没,信噪比很低。
|
图 9 信号源为3 Hz时的时域频域图 Fig. 9 Time-domain and frequency-domain diagram when the signal source is 3 Hz. |
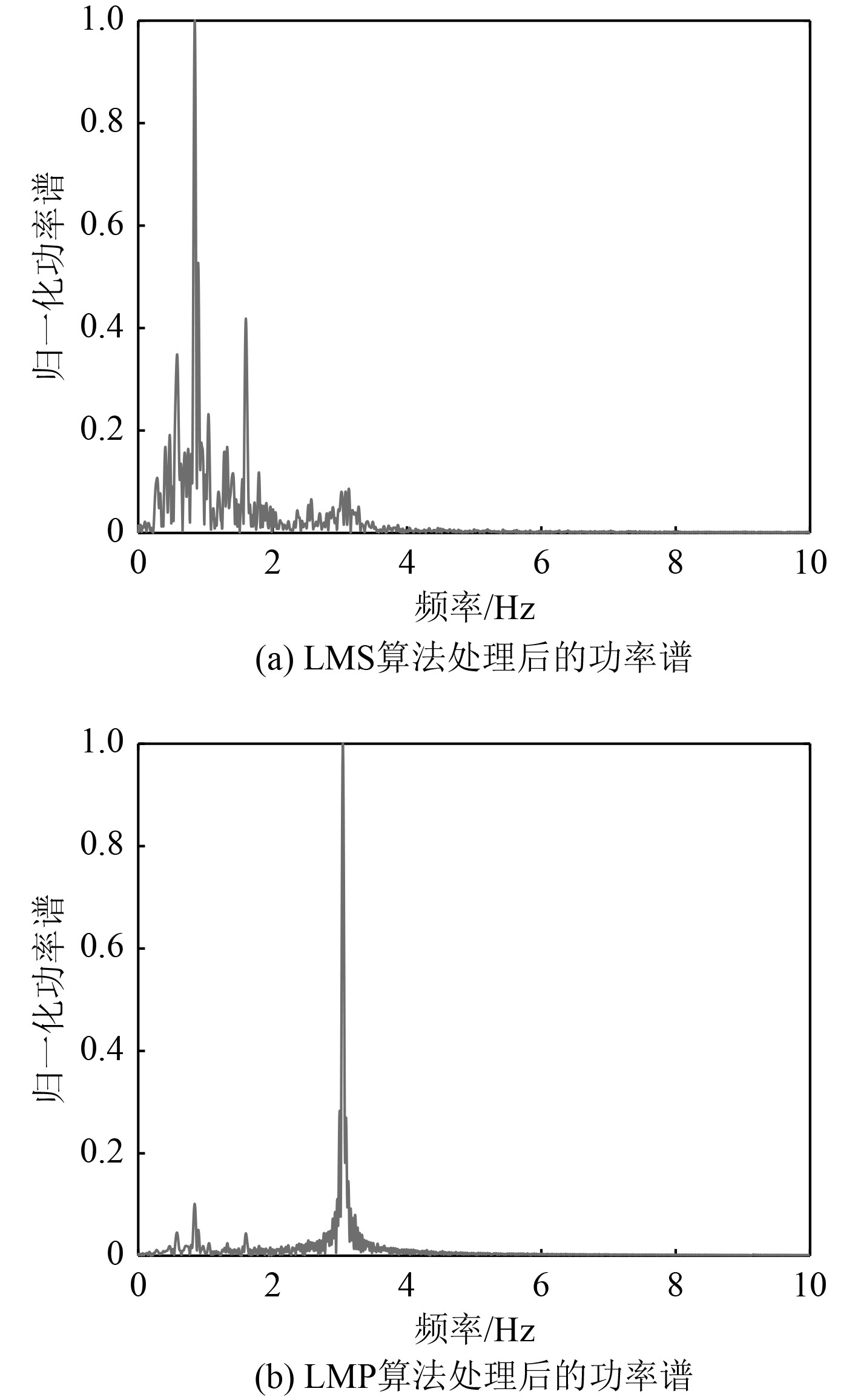
分别采用LMS算法和LMP算法对170~200 s的信号进行处理,2种算法的主要参数均为:步长μ=0.0001,滤波器阶数M = 60,LMP算法的阶数p=1.5。处理后的频谱图如图10所示。
|
图 10 两种算法的处理结果 Fig. 10 Processing results of the two algorithms |
由图10(a)可得,LMS算法能检测出3 Hz的模拟源信号,但未能有效压制噪声。
由图10(b)可得,经过LMP算法处理后,较好压制了背景噪声,且增强了3 Hz的信号,信噪比得到较大提高。
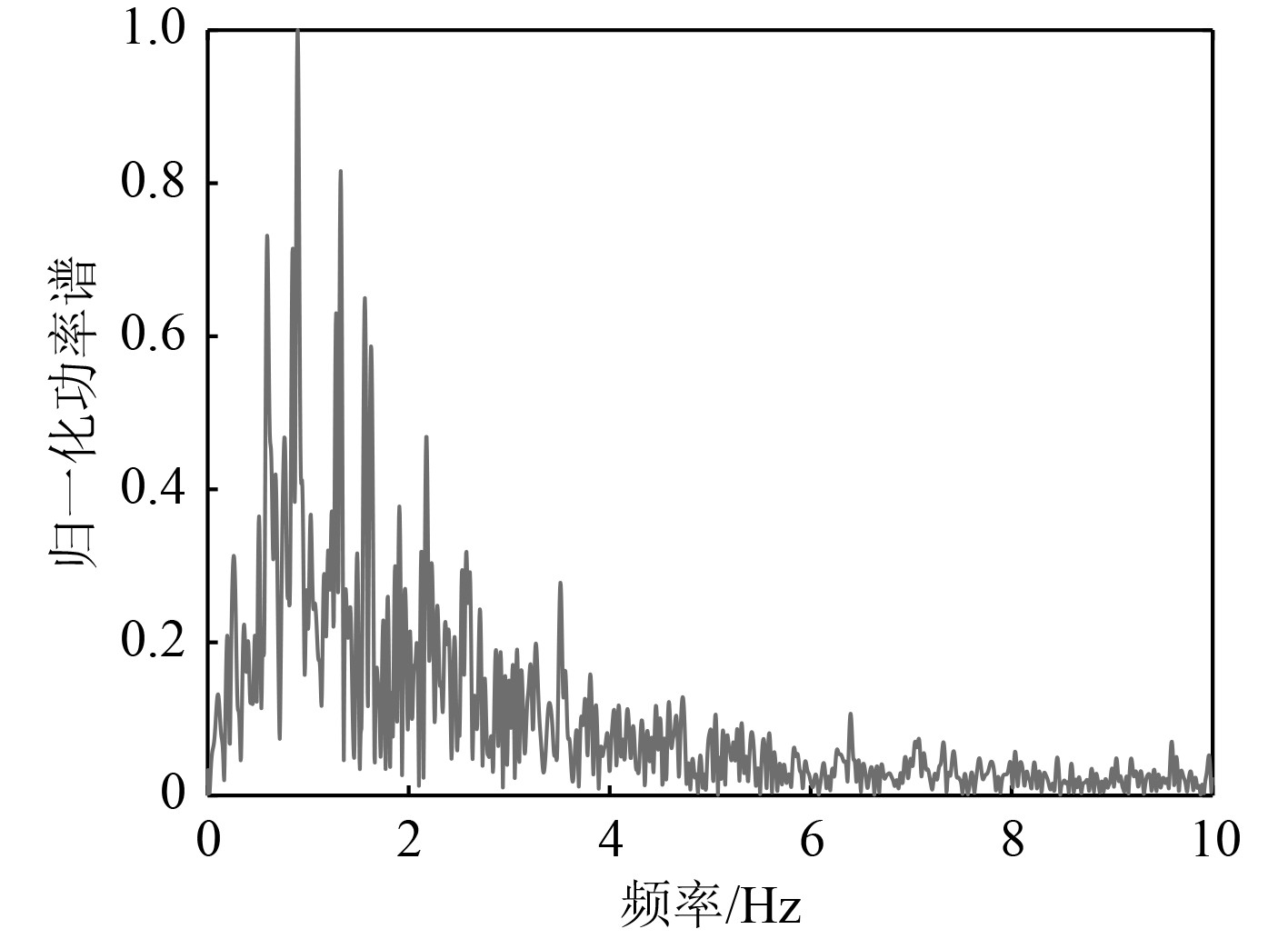
为了研究算法在远距离探测的性能,对图9(a)中150~180 s数据进行频谱分析得到频谱图,如图12所示。
|
图 11 150~180 s的频谱图 Fig. 11 Spectrum diagram of 150~180 s |

|
图 12 两种算法的处理结果 Fig. 12 Processing results of the two algorithms |
分别采用LMS算法和LMP算法对150~180 s的信号进行处理,2种算法的主要参数均为:步长μ=0.0001,滤波器阶数M = 60,LMP算法的阶数p=1.5。处理后的频谱图如图12所示。
由图12(a)可知,LMS算法不能检测出3 Hz的模拟源信号,对比图10(a)可得,当探测距离增大时,LMS算法不能有效得检测出轴频电场。
由图12(b)可知,经过LMP算法处理后,能较好检测出3 Hz的模拟源信号。对比图10(b)可得,当探测距离增大时,LMP算法仍能有效检测到轴频电场。对比图12(a)可得,当探测距离增大时,LMP算法相比于LMS算法有更好的检测效果。
4 结 语本文针对传统的LMS算法在非高斯背景下轴频电场信号检测中性能退化的问题,比较了LMP算法和LMS算法在轴频电场检测中的效果。仿真结果表明,在非高斯背景下,LMS算法性能有所下降,而LMP算法仍具有较好的检测效果。海上模拟源试验表明,在运动平台下的环境电场噪声具有非高斯特性,且在非高斯背景下,LMP算法与经典的LMS算法相比,能够更有效提高轴频电场信号的信噪比,从而可以进一步提升探测距离。
| [1] |
林春生, 龚沈光. 舰船物理场(第2版)[M]. 北京: 兵器工业出版社, 2007
|
| [2] |
程锦房, 张伽伟, 姜润翔, 等. 水下电磁探测技术的发展现状[J]. 数字海洋与水下攻防, 2019, 2(4): 45-49. |
| [3] |
包中华, 龚沈光, 李俊, 等. 一种基于负熵的舰船轴频电场信号检测方法[J]. 仪器仪表学报, 2010, 31(10): 2210-2215. |
| [4] |
费志刚, 蔡旭东, 包中华. 基于高阶累量的船舶轴频电场信号自适应增强[J]. 舰船科学技术, 2014, 36(5): 120-124. DOI:10.3404/j.issn.1672-7649.2014.05.025 |
| [5] |
程锐, 陈聪, 张伽伟. 基于EEMD和改进功率谱熵的船舶轴频电场检测[J]. 华中科技大学学报(自然科学版), 2017, 45(05): 11-16. |
| [6] |
李越, 张伽伟, 程锦房, 等. 基于尺度-小波能量谱的舰船轴频电场检测算法[J]. 舰船电子工程, 2020, 40(5): 152-156. DOI:10.3969/j.issn.1672-9730.2020.05.036 |
| [7] |
喻鹏, 程锦房, 张伽伟, 等. 基于Rao检测器的舰船轴频电场滑动门限检测方法[J]. 兵工学报, 2021, 42(4): 827−834.
|
| [8] |
陈泽军. 非高斯噪声环境下的最小误差熵自适应滤波算法研究[D]. 成都: 西南交通大学, 2020.
|
| [9] |
石颖. 非高斯噪声环境下的比例自适应滤波算法研究[D]. 成都: 电子科技大学, 2019.
|
| [10] |
SHAO M, NIKIAS C L. Signal processing with factional lower order moments: stable processes and them applications. Proceedings of the IEEE, 1993, 81(7): 986−1010.
|
| [11] |
KUMAR P A, MOULI B C, GANESH S, et al. Extraction of target parameters using underwater electric field analysis[C]// International Conference on Communication & Electronics Systems. Coimbatore, India: IEEE, 2016.
|
| [12] |
赵知劲, 金明明. α稳定分布噪声下的核最小平均P范数算法[J]. 计算机应用研究, 2017, 34(11): 3308-3310+3315. DOI:10.3969/j.issn.1001-3695.2017.11.024 |
| [13] |
沈锋, 姜利, 单志明. 非高斯噪声环境下的信号检测与自适应滤波方法[M]. 北京: 国防工业出版社, 2014.
|
| [14] |
StevenM. Kay, 罗鹏飞. 统计信号处理基础[M]. 北京: 电子工业出版社, 2014.
|
| [15] |
梁小筠. 正态性检验[M]. 北京: 中国统计出版社, 1997.
|
 2022, Vol. 44
2022, Vol. 44

