2. 工业和信息化部,海洋信息获取与安全工信部重点实验室(哈尔滨工程大学),黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security (Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
声呐探测作为现代反潜、反舰中的一项重要手段,准确掌握探潜、探舰时声呐的作用距离,将大大提高对目标的探测效率[1]。声呐的作用距离与具体的水文、地形等条件下的水下声传播现象密切相关。同样一部声呐,在特定的工作环境中,针对不同目标的探测其作用距离往往大相径庭[2]。因此,研究在不同海洋环境中的声传播规律以及如何根据实际作战环境与探测工作需求进行合理的使用声呐,一直以来均是研究的热点[3]。
海水中最重要的声学参数是声传播速度,它是影响声波在海水中传播的最基本物理量。文献[4-5]针对声速剖面的变化对声呐在不同水文环境中探测性能进行分析比较,文献[6]利用WOA13数据采用Bellhop对大西洋海区的声传播进行仿真,分析季节因素对大西洋声传播的影响分析。文献[7]针对分类的声速剖面结构进行声呐作用距离研究,揭示了声速剖面凹凸结构对声传播影响的规律,这些规律对于声呐的使用有良好的指导作用。海底地形作为影响水下声场结构的重要环境要素,同样一直是海洋学家的研究重点。早在1968年,Northrop等[8]通过在美国加利福尼亚海域斜坡上布置声源进行实验测量发现,与平坦海底相比,由于斜坡的存在深海声道轴接收的声能量会增多,因此这种现象被称作“斜坡增强效应”,这种斜坡可以是大陆坡,也可以是岛礁斜坡。国内众多学者[9-11]针对海底斜坡环境下的声传播进行了多次实验与仿真研究,表明斜坡地形对水体中声能量的分布,以及实现声能的远距离传播均存在影响。文献[12]从实际作战出发,重点针对浅海的上坡海底以及下坡海底对声呐探测影响的研究,采用抛物方程RAM仿真得出下坡海底方向为声呐探测的有利方向。其中抛物近似方程RAM是一种基于抛物近似的水声传播模型,主要用于解决与距离相关环境下的远距离低频声传播问题。当海底起伏比较大时,抛物方程方法可以精确计算全场解,对于低频问题的计算速度也很快,通常被认作为标准解[13]。
本文以环礁斜坡为研究区域,基于抛物近似计算仿真模型RAM对岛礁斜坡区域目标辐射噪声仿真,计算在特定水文环境下,不同位置声源在斜坡地形的声传播损失,以声呐优质因子为门限,得到进行有效探测的最大作用距离,对比分析影响声呐作用距离的具体因素,总结出岛礁斜坡区声呐探测的使用规律。
1 声呐作用距离计算 1.1 理论计算作用距离是指声呐在一定条件下能有效地发现目标,并发现、测量其数据的最大距离。这些条件包括发射声源级、传播衰减、环境噪声、目标强度等。目标信号强度以及接受机灵敏度指标是声呐的重要技术指标之一,它直接影响到声呐的作用距离[14]。利用抛物方程近似声场模型RAM对水平变化的斜坡环境进行声场计算[15-16],远场环境中声压
| $ \frac{{{{\partial}} {p^2}}}{{\partial {r^2}}} + \rho \frac{\partial }{{\partial z}}\left( {\frac{1}{\rho }\frac{{\partial p}}{{\partial z}}} \right) + {k^2}p = 0。$ | (1) |
式中:
| $ \left( {\frac{\partial }{{\partial r}} + {{i}}{k_0}{{\left( {1 + X} \right)}^{1/2}}} \right)\left( {\frac{\partial }{{\partial r}} - {\text{i}}{k_0}{{\left( {1 + X} \right)}^{1/2}}} \right)p = 0 ,$ | (2) |
| $ X{\text{ = }}{k_0}^{ - 2}\left( {\rho \frac{\partial }{{\partial z}}(\frac{1}{\rho }\frac{\partial }{{\partial z}}) + {k^2} - k_0^2} \right),$ | (3) |
假定忽略后向散射波[17],则前向输出波动方程为:
| $ \frac{{\partial p}}{{\partial r}} = {{i}}{k_0}{(1 + X)^{1/2}}p ,$ | (4) |
解式(4)可得:
| $ p(r + \Delta r,z) = {\rm{exp}}\left( {i{k_0}\Delta r{{(1 + X)}^{1/2}}} \right)p(r,z),$ | (5) |
式中,Δr为距离步长。RAM模型采用声压P的分裂步Pade近似解为:
| $ p(r+\Delta r,z)={\rm{exp}}(i{k}_{0}\Delta r)\left(1+{\displaystyle \sum _{j=1}^{n}\frac{1+{\alpha }_{j,n}X}{1+{\beta }_{j,n}X}}\right)p(r,z) ,$ | (6) |
其中
| $ I\left( {r,z} \right) = \left( {\frac{{{p^2}\left( {r,z} \right)}}{{{Z_\omega }}}} \right) 。$ | (7) |
对于以海洋环境噪声为主要背景干扰的被动声呐方程,
对于被动声呐,定义信号余量SE为优质因子(FOM)与传播损失的差值:
| $ SE = FOM - TL = SL - TL - (NL - DI),$ | (8) |
声呐的最大作用距离
| $ TL\left( {r,z} \right) = - 10{\log _{10}}\frac{{I\left( {r,z} \right)}}{{I\left( {r = 1} \right)}}。$ | (9) |
假定当
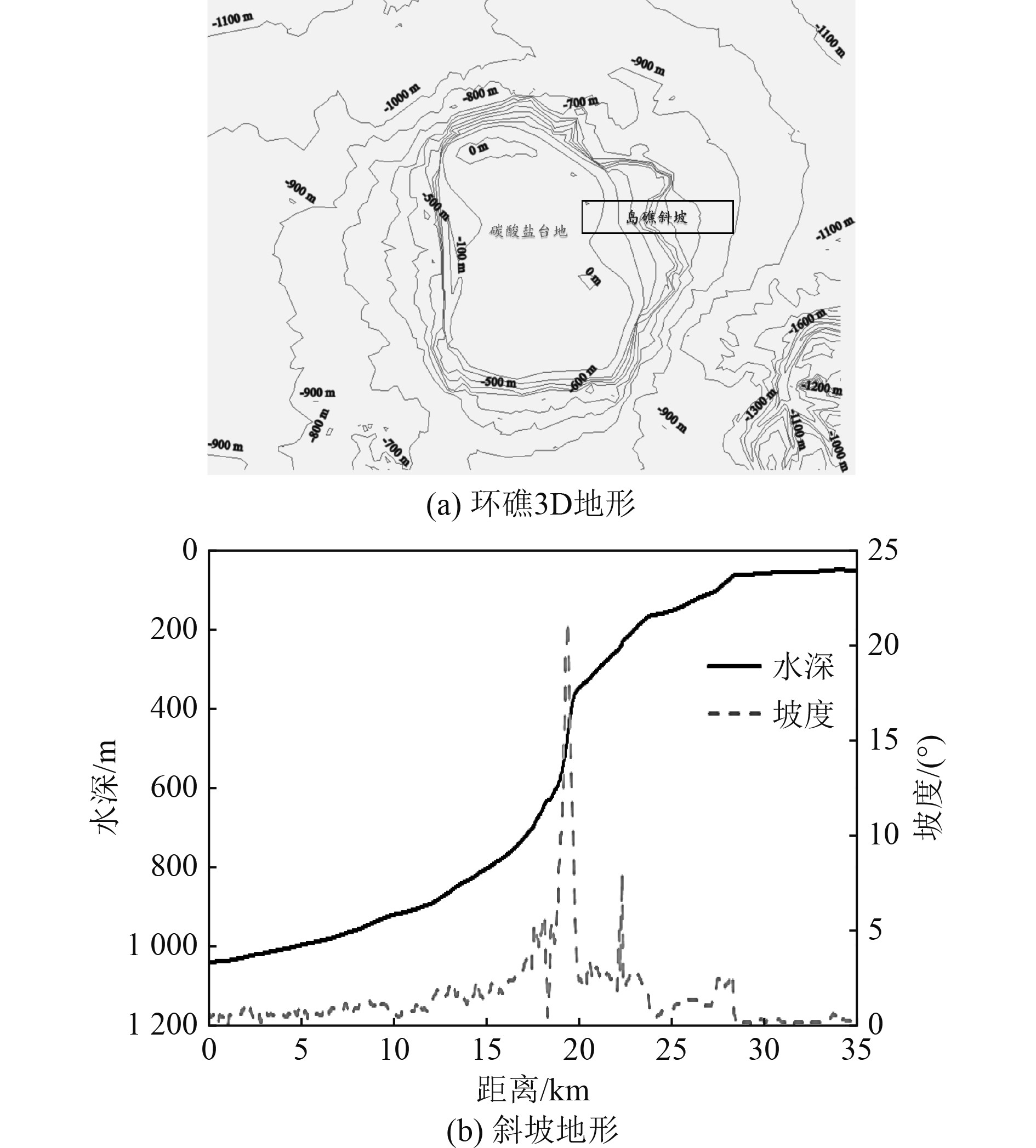
图1的岛礁斜坡地形,水平距离36 km,斜坡上端为50 m水深浅海海域,斜坡底部为1100 m水深的深海海域,坡面最大坡度20°。声波在该区域传播存在2种形式:一种是从斜坡底部向岛礁台地传播(上坡地形),与之对应的是从岛礁台地向斜坡底部的传播(下坡地形)。这2种传播方式在岛礁声学研究中都是十分重要的问题,岛礁海区目标探测、声隐身与反潜等均围绕着斜坡地形展开。
|
图 1 仿真地形 Fig. 1 Simulated terrain |
文献[20]对岛礁区海底珊瑚沉积物进行的采样调查结果显示,与常见砂泥沉积物相比,岛礁区独特的珊瑚砂沉积物具有较高的孔隙度和孔隙比、较大的含水量,以及较小的湿密度。岛礁浅海区域由于海浪、海流等水动力因素的存在,使得细粒沉积物难以在停留,而以块状、片状和粗短枝状的珊瑚为主。表1给出了岛礁区域海底珊瑚类沉积物物性参数。
|
|
表 1 海洋底质沉积物参数 Tab.1 Marine sediment parameters |
依据文献[20]中沉积物声速
| $ c = 1\;365.26 - 510.022\;6d + 17\;606.45{d^2} ,$ | (10) |
根据经验公式[20],沉积物中声衰减系数
| $ \alpha = 0.3{f^{0.8}} 。$ | (11) |
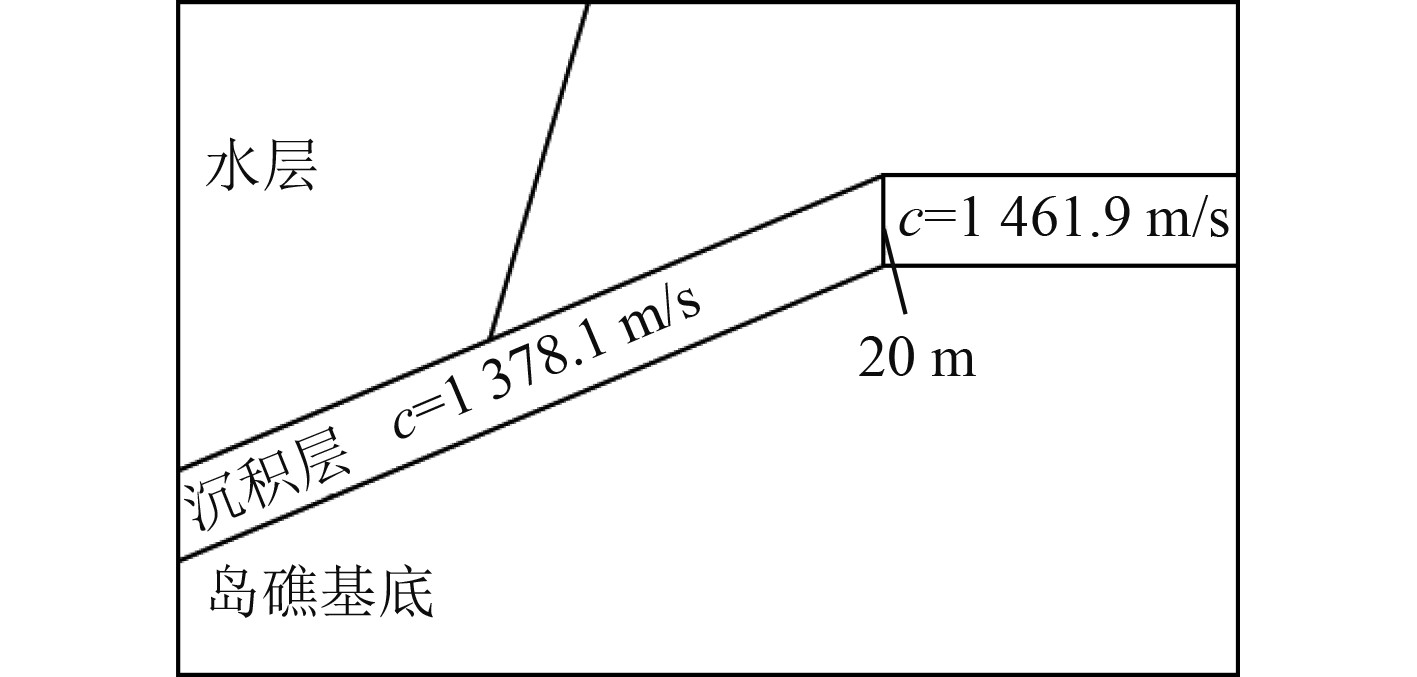
|
图 2 岛礁斜坡声场模型 Fig. 2 Slope terrain in the model |
仿真中声源频率1.5 kHz,选取沉积物密度1.80 g/cm 3,吸收系数0.35
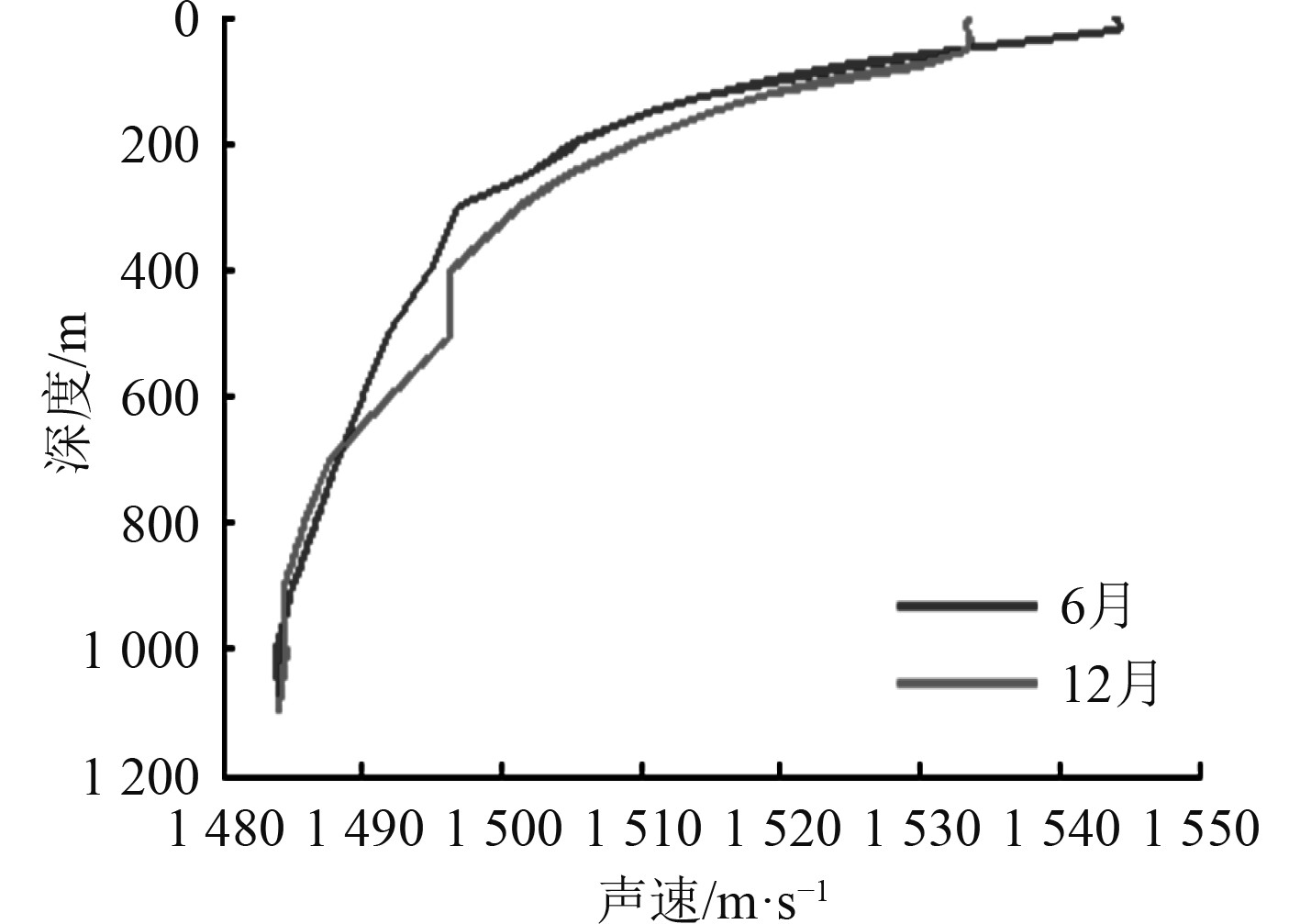
图3给出了通过研究区水下1100 m的实测温度剖面计算得到的夏季、冬季声速剖面。环礁海区夏、冬季节声速分布均属于深海典型声速剖面。在夏季的海洋表面,因受日照影响,水温较高,高于冬季表面声速约11.5 m/s,随着深度增加,形成表面声速负梯度层;秋冬季节海面风浪较大,在风浪的搅拌作用下,冬季海面会行成一定厚度表面混合层,层内平均声速1 533.5 m/s,形成了良好的表面声道。跃变层,声速变化过渡区,层内声速随深度地而逐渐降低,声速梯度为负值。在水深1 100 m的海底,夏、冬季节最小声速值相异不大。
|
图 3 环礁海域6月、12月声速剖面 Fig. 3 Sound speed profiles in June and December in Xuande Atoll |
岛礁斜坡地形中,斜坡上端为浅海区域,水深0~50 m,斜坡外缘为深海区域,水深0~1050 m。下坡地形中,声源位于斜坡上端的7 m和45 m水深,模拟岛礁浅海区域靠近海面与海底的目标噪声;上坡地形中,声源位于岛礁外缘7 m,350 m,750 m,1 000 m水深分别用于模拟岛礁深水区域海面、浅海、深海以及海底的目标噪声[21]。
3.1 下坡地形采用RAM模型计算声传播损失。图4中,6月的传播损失场图,其声传播形式以岛礁斜坡顶端浅海区域的会聚波导为主,大部分声能在浅海区发生海底和海面反射,衰减速度很快;12月时,由于表面波导的存在,声能可以在表面波导内以更少的传播损失抵达至远处。声能在传递过程中,部分声能从表面波导中向深海泄漏,因此表面波导以外的声场的声传播损失明显低于6月。同时处于表面声道上部的海面目标,其大部分掠射角小的声能以表面波导内传播为主,小部分掠射角较大声能在海底和海面边界发生反射,因此海面目标的声传播损失低于海底目标。

|
图 4 下坡地形声场仿真 Fig. 4 Sound field simulation of downhill terrain |
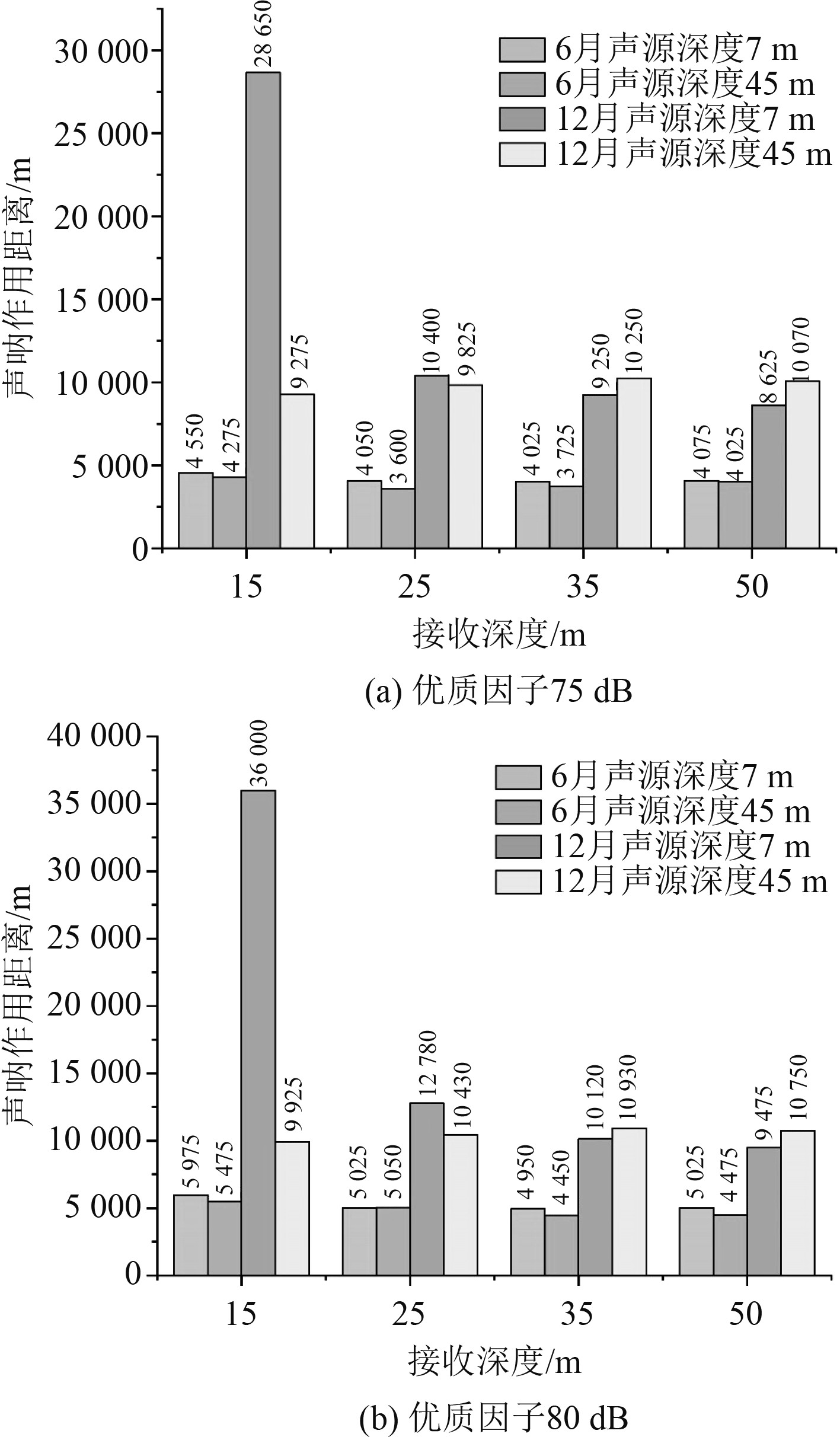
依据声传播损失大小与声呐优质因子,图5给出声呐作用距离,下坡地形的声呐作用距离结果显示,12月时针对海面目标的探测,声呐作用距离最远,并且12月时的声呐作用距离普遍高于6月,因此季节变化引起的声速剖面结构的差异是影响在该地形下的声呐作用距离的主要因素。在针对海面、海底不同目标探测中,6月时不同的接收深度下针对海面目标时的声呐作用距离略高于海底目标;12月时接收深度在15~25 m范围内,针对海面目标时的声呐作用距离明显高于海底目标,随着接收深度增加,针对海底目标探测的声呐作用距离开始高于海面目标。优质因子的增加,虽然声呐作用距离增大,但是估计的误差也在增加。
|
图 5 下坡地形的声呐作用距离计算结果 Fig. 5 Calculation results of sonar range on downhill terrain |
在图6中可以看出,在上坡地形中,夏季声速环境下的声能会聚区多数集中在斜坡外部的声源周围以及深海区域,而冬季声速环境下的浅海声能分布更均匀,能量数值更大。其中当声源处于水深 7 m 时,夏季环境时的海面目标的会聚区集中在从声源至与海底发生第一次接触位置的三角区域内,经过一次发射,声传播损失增加明显。然后在 10 km 距离位置附近经过一次海面与海底反射,会聚区逐渐消失;相比于夏季环境,冬季环境时,海面声源位于表面声道内,其发射的声能可以远程传播至斜坡顶部,同时经过一次海底反射后的声传播损失均能维持在 100 dB 以下。图6(c)和图6(d)中,声源位于750 m水深时,三角会聚区面积增加,是由于部分掠射角较小的声能在经过一次海底反射后与海面未发生反射,传播损失得以减小,因此在400 m深度以下会聚区普遍存在。

|
图 6 上坡地形声场仿真 Fig. 6 Sound field simulation of uphill terrain |
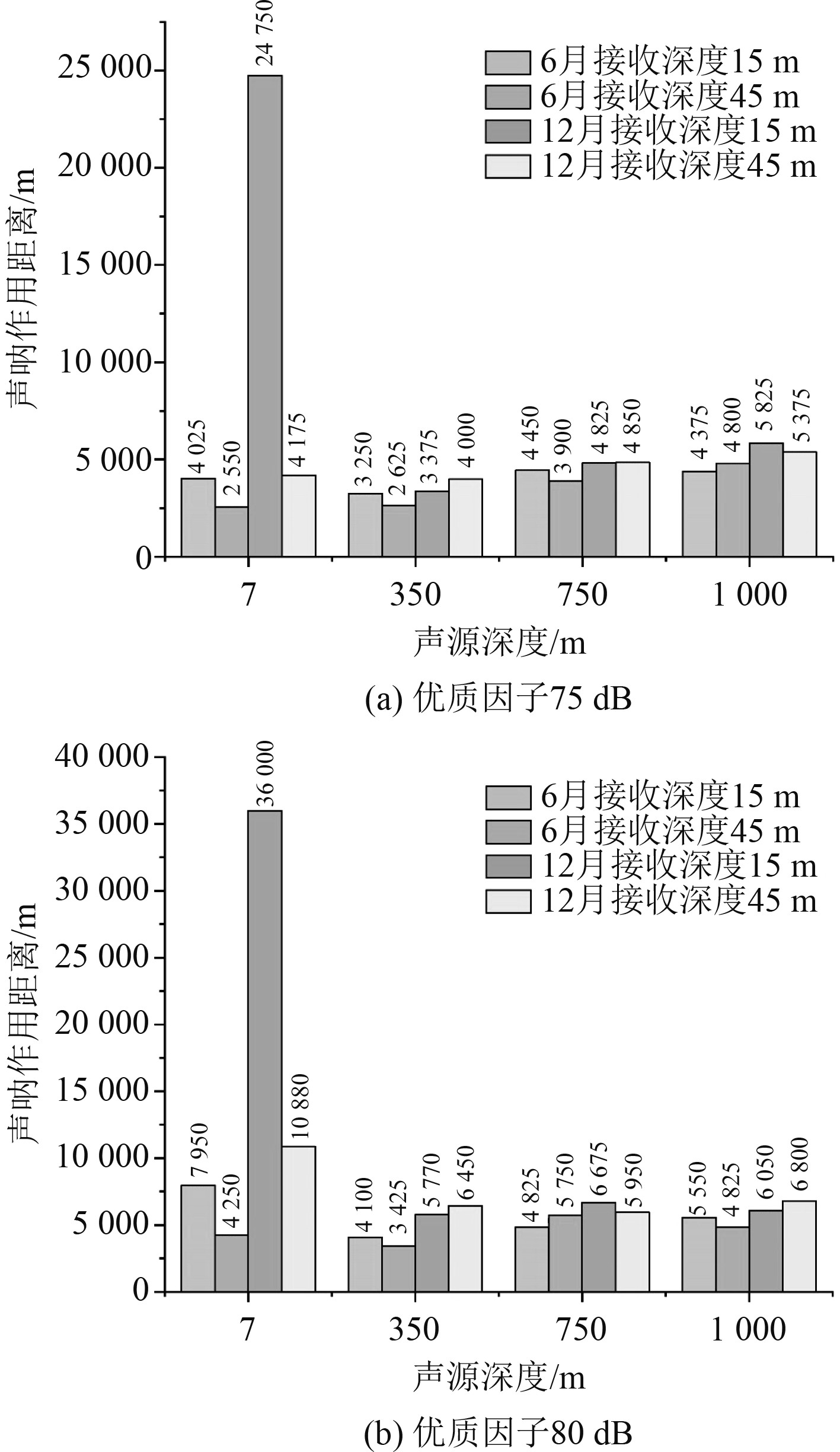
图7给出在上坡地形中声源深度分别为 7 m、350 m、750 m、1 000 m时声呐作业距离计算结果,可以看出季节的变化对声呐作用距离的影响,主要集中在针对海面目标的探测时,在探测深水目标时差距并不明显。在冬季时,声呐对海面目标探测的作用距离最远,探测范围更大,而6月时声呐作用距离峰值出现在针对海底目标的探测时。除去海面目标的其他情况下,随着被探测目标深度越深,声呐作用距离起伏增加。
|
图 7 上坡地形的声呐作用距离计算结果 Fig. 7 Calculation results of sonar range on uphill terrain |
综上,适宜的水文条件能够有效提高声呐的作用距离,在针对海面目标探测时,作用距离可增加2~6倍。相比于夏季,冬季更有利于声传播,声呐作用距离最高可增加188%。在夏季时的下坡地形中,针对斜坡顶端目标的探测中,声呐探测海面目标时的作用距离比海底目标增加约325 m,同时位于15 m水深的声呐比50 m水深时,声呐作用距离增加约668 m。优质因子提高5 dB,声呐作用距离平均提高约500 m;在上坡地形中,针对水深350~1 000 m的目标,声呐作用距离随着目标深度增加而缓慢增加。声呐探测深海目标比浅海目标作用距离增加约1 200 m,探测海底目标比深海目标时的作用距离增加约500 m。对于浅海目标的探测,选取声呐深度越浅,作用距离越大,长度提升约9%,对于深海区域以及海底目标,声呐的深度对于探测作用距离的影响相对较小。优质因子提高5 dB,声呐作用距离平均提高约1200 m。在上坡地形中,海水的深度由1000 m变化到50 m,斜坡坡度达到20°,属于高陡斜坡地形,十分不利于声波的传播,因此声呐作用距离普遍低于下坡地形。
4 表面波导内的声呐作用距离考虑到实际作战中,被动声呐在目标探测中通常是宽带工作的,因此单个频率下声呐作用距离的适用场景存在限制。利用RAM程序对200~2 000 Hz频带下的7 m水深声源在表面波导内的声传播进行计算,得到宽带声传播损失数据,采用最小二乘法进行数据拟合后依据优质因子(75 dB)得到表面波导内的被动声呐作用距离,并分析其形成机理。
图8为15 m接收深度下不同频率的传播损失场图。可以看出,表面波导内的声传播损失与声波频率相关。图8(a)和图8(c)中1800~2000 Hz频带内的声传播损失较小,并随距离缓慢增加;在200~1 800 Hz频率范围内,影区面积较大,十分不利于声传播。图8(b)和图8(d)中影区面积明显减小,300~800 Hz范围内声传播损失随距离增加速度减缓,在1 000~2 000 Hz范围内声传播损失数值较小,有利于目标探测。其原因在于不同模态的声波在表面波导内传播时,受表面波导厚度影响,不同模态声波的截至频率存在差异,由于夏季混合层厚度小,因此各模态的截至频率较大,当声波频率高于某模态的截至频率时,声能在表面波导内衰减缓慢。由表面波导不同模态的经典截至频率公式可知m阶模态时的经典截止频率

|
图 8 不同频率下的声传播损失结果 Fig. 8 Sound propagation loss results at different frequencies |
| $ {f_{c,m}} = 1.5(m - 0.25)g{\left[ {1 - {{\left(\frac{{{c_0}}}{{{c_0} + gh}}\right)}^2}} \right]^{ - 1.5}} $ | (12) |
式中:g为表面波导声速梯度;
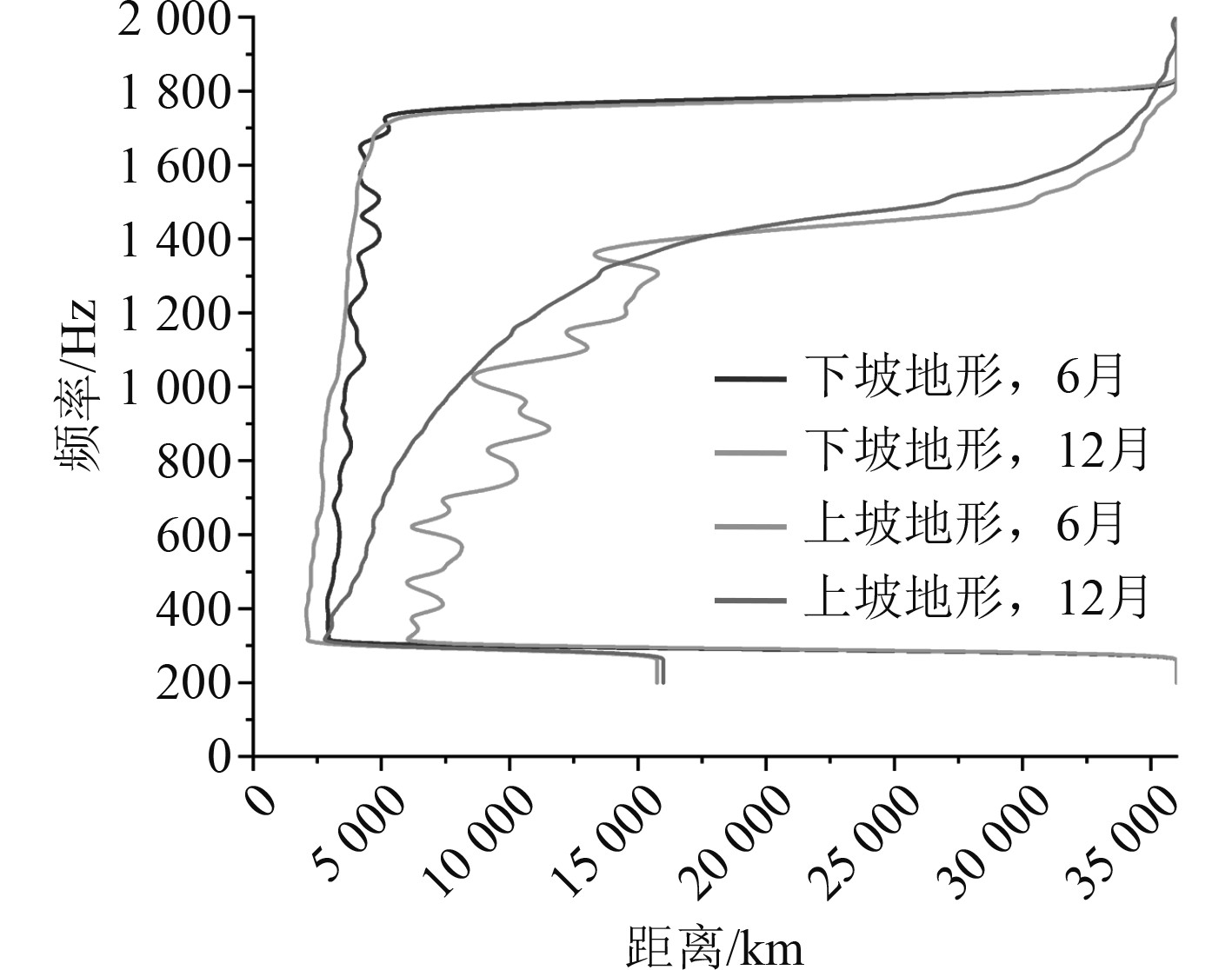
从图9可以看出在300~1 800 Hz频率范围内,声呐作用距离受季节、地形以及噪声频率影响严重,其声源频率的增加,声呐作用距离持续增大。同时,12月时声呐作用距离增加速度明显高于6月时。在200~300 Hz范围内,下坡地形声呐作用距离为36 km,而此时上坡地形的声呐作用距离为16 km。当声源频率在1.8~2 kHz范围内,声呐作用距离均达到36 km。同时,地形对声呐作用距离的影响还体现在上坡地形时声呐作用距离随频率单调增长,而下坡地形时声呐作用距离波动上升。
|
图 9 不同频率下的作用距离结果 Fig. 9 Action distance results at different frequencies |
本文根据在岛礁海区目标探测应用中声呐作用距离估计的需求,结合宣德岛礁区域的6月、12月不同季节时的水文环境,针对岛礁斜坡区域声呐探测中的目标可能存在位置,利用抛物近似方程RAM进行声传播仿真计算。结合被动声呐方程,引入优质因子对声呐作用能力进行描述,得到特定优质因子下,声呐能够有效探测目标的作用距离,总结被动声呐在岛礁斜坡区域进行有效探测的几点规律:
1)声呐作用距离与水文条件密切相关,存在表面波导的特定季节时,被动声呐可利用独特的水文条件提高作用距离,特别是,当目标处于海面附近时,能够大幅度提高声呐探测效果。当表面声道不存在或影响较小时,在对斜坡顶部的目标进行探测中,此时声呐作用距离较短,声呐位置不应脱离岛礁浅水区。
2)在上坡地形中,目标位于岛礁外侧深海区域,由于此时被动声呐作用距离均较短,因此布放于岛礁附近的声呐无法及时发现目标。同时针对处于深海或位于斜坡下端海底的目标,声呐探测效果更好,声呐作用距离越远。
3)声呐在表面波导内的进行探测时,选取合适的工作频率范围可使声呐的作用距离更远。
| [1] |
郁红波, 鞠建波, 魏帅, 等. 浅海海底地形对吊放声呐探测距离的影响[J]. 声学技术, 2021, 40(1): 49-56. YU Hong-bo, JU Jianbo, WEI Shuai. Effects of shallow seabed topography on the detection range of hanging sonar[J]. Technical Acoustics, 2021, 40(1): 49-56. |
| [2] |
杨日杰, 何友, 田宝国. 双基地航空声呐搜潜距离误差估计[J]. 兵工学报, 2004(5): 540-543. DOI:10.3321/j.issn:1000-1093.2004.05.008 |
| [3] |
杨秀庭, 赵晓哲. 远程鱼雷目标主动声纳探测性能分析[J]. 兵工学报, 2012, 33(4): 503-507. |
| [4] |
张纪铃, 胡鹏涛. 浅海声速剖面对声呐作用距离的影响研究[J]. 电声技术, 2014, 38(10): 36-38. DOI:10.3969/j.issn.1002-8684.2014.10.009 |
| [5] |
苏林, 马力, 宋文华, 等. 声速剖面对不同深度声源定位的影响[J]. 物理学报, 2015, 64(2): 272-279. DOI:10.3969/j.issn.1672-7940.2015.02.024 |
| [6] |
曹震卿, 张永刚, 李庆红, 等. 季节因素对大西洋声传播的影响分析[J]. 应用海洋学学报, 2018, 37(4): 514-524. DOI:10.3969/J.ISSN.2095-4972.2018.04.007 |
| [7] |
赵建昕, 过武宏. 浅海声速剖面结构变化对声呐作用距离的影响[J]. 海洋技术学报, 2020, 39(4): 22-28. |
| [8] |
NORTHROP J, LOUGBRID M S, WERNER E W. Effects of near-source bottom conditions on long range sound propagation in the deep ocean[J]. Geophys, 1968, 73: 3905-3908. |
| [9] |
秦继兴, 张仁和, 骆文于, 等. 大陆坡海域二维声传播研究[J]. 声学学报, 2014, 39(2): 145-153. |
| [10] |
张乾初, 郭新毅, 马力. 岛礁区域斜坡地形对深海环境噪声级深度分布的影响[J]. 声学学报, 2019, 44(3): 329-336. |
| [11] |
胡治国, 李整林, 张仁和, 等. 深海海底斜坡环境下的声传播[J]. 物理学报, 2016, 65(1): 229-237. |
| [12] |
付留芳, 许林周, 李文哲. 浅海倾斜海底对声呐探测影响研究[J]. 舰船电子工程, 2020, 40(7): 172-177. |
| [13] |
COLLINS MD. A split‐step Padé solution for the parabolic equation method[J]. The Journal of the Acoustical Society of America, 1998, 93(93): 1736-1742. |
| [14] |
杨一. 工作平台深度对被动声呐探测性能的影响[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [15] |
COLLINS MD. Generalization of the split-step Padé solution[J]. The Journal of the Acoustical Society of America, 1994, 96(1).
|
| [16] |
COLLINS MD, CEDERBERG R J, KING D B, et al. Comparison of algorithms for solving parabolic wave equations[J]. The Journal of the Acoustical Society of America, 1996, 100(1): 178-182. DOI:10.1121/1.415921 |
| [17] |
CEDERBERG R J, MD COLLINS. Application of an improved self-starter to geoacoustic inversion[J]. IEEE Journal of Oceanic Engineering, 1997, 22(1): 102-109. DOI:10.1109/48.557544 |
| [18] |
COLLINS MD, WESTWOOD E K. A higher-order energy-conserving parabolic equqation for range-dependent ocean depth, sound speed, and density[J]. Journal of the Acoustical Society of America, 1991, 89(3): 1068-1075. DOI:10.1121/1.400526 |
| [19] |
李凡, 郭圣明, 王鲁军, 等. 一种新的声纳作用距离指标评估方法[J]. 声学技术, 2009, 28(3): 235-239. DOI:10.3969/j.issn1000-3630.2009.03.008 |
| [20] |
李赶先, 龙建军. 南海南部海域岛礁区海底珊瑚砂声速影响因素的初步研究[J]. 海洋学报(中文版), 2014, 36(5): 152-160. |
| [21] |
李琳. 深海环境中水面目标和水下目标深度分类方法研究[D]. 西安: 西北工业大学, 2015.
|
| [22] |
Labianca F M. Normal modes, virtual modes and alternative representations in theory of surface-duct sound propagation[J]. The Journal of the Acoustical Society of America, 1973, 53(2): 1137-47. |
 2022, Vol. 44
2022, Vol. 44

