0 引　言

汽轮发电机组将锅炉或蒸汽发生器产生的蒸汽热能转换为电能，不仅为船舶提供全船电力需求，还可为船舶提供主动力。汽轮机调速系统是汽轮发电机组的控制大脑，具有非常重要的作用，其调节品质和响应特性直接影响机组运行经济性、机动性、安全性和可靠性^[1]，进而直接影响船舶安全经济航行。不同于陆上电站汽轮机，船舶汽轮机组常处于变负荷运行，尤其是承担主动力的汽轮发电机组的负荷变化幅度大、外界影响因素复杂，对汽轮发电机组的控制精度和可靠性提出了更高的要求。

船用汽轮发电机组电液调节系统（digital electric hydraulic，DEH）由多个组件构成，调节组件的高精度参数辨识是调节系统进行性能预测^[2]，实现汽轮机组动态仿真分析，以及PID控制器参数优化的基础。目前，有关汽轮机调速系统参数辨识的方法主要有经典法和智能法，经典法包括最小二乘法^[3]、极大似然法、直接辨识法^[4]等方法，此类方法一般只适用于低阶传递函数，应用于高阶时参数辨识精度低，鲁棒性较差；智能法有遗传算法^[5]、粒子群算法^[6]、引力搜索算法^[7]、差分进化算法^[8]，以及它们的混合算法等，上述智能算法普遍存在耗时长、随机大、容易陷入“局部最优”，辨识结果可重复性较差等问题。船用汽轮发电机组DEH系统中PID参数整定作为改善调节系统特性的重要手段，其高精度、高性能、快速性一直是学者们追求的目标，为此智能算法在PID参数整定中得到广泛研究。智能PID参数整定方法主要有遗传算法、神经网络、模糊控制、粒子群算法、人群搜索算法等，此类算法虽然能够减少整定时间，改善系统的控制效果，但是也存在初始参数设置对结果影响较大、目标函数难建立和整定后系统鲁棒性不足等问题。

为此，本文结合遗传算法局部搜索能力强和粒子群算法收敛速度较快，容易实现、学习能力强等优点，提出一种融合遗传算法改进的粒子群优化算法，同时实现汽轮发电机组DEH核心组件参数辨识和复杂工况PID参数智能自整定，提升船用汽轮发电机组变工况运行特性。

1 船用汽轮机DEH建模

船用汽轮机调节系统主要由PID控制器、伺服放大器、电液转换器、油动机、汽轮机、发电机和反馈机构等组件构成，实现汽轮发电机组的转速调节等功能。调节系统转速调节的基本流程为：转速偏差（给定转速与转子输出转速的差值）作为伺服放大器的输入信号，油动机输出信号作为阀位反馈信号，以PID控制器输出信号与阀位反馈信号的偏差作为电液转换器的输入信号，输出油动机阀位信号，通过调节油动机阀位调整主汽阀的阀门开度，通过改变蒸汽进汽量来控制转速。考虑以下假设：1）针对小偏差进行线性化处理；2）运动部件的质量不计；3）液态摩擦力不计。采用模块化建模法建立每个调节组件的传递函数数学模型。

PID控制器： $ W(S) = {K_{\text{p}}}(1 + \dfrac{1}{{{T_i}s}} + \dfrac{{{T_d}s}}{{{T_d}s + 1}}) $ ； $ {K_{\text{p}}} $ 为比例系数， $ {T_{{i}}} $ 为积分时间常数， $ {T_{{d}}} $ 为微分时间常数。

伺服放大器： $ W(S) = \dfrac{1}{\delta } $ 。 $ \delta $ 为汽轮机调节系统的转速不等率。

电液转换器： $ W(S) = \dfrac{{\text{1}}}{{{T_{\text{e}}}s + 1}} $ 。 $ {T_e} $ 为电液转换器时间常数。

油动机： $ W(S) = \dfrac{1}{{{T_s}{\text{s}} + {\text{1}}}} $ 。 $ {T_{\text{s}}} $ 为油动机时间常数。

蒸汽容积： $ W(S) = \dfrac{1}{{{T_{HP}}s + 1}} $ 。 $ {T_{HP}} $ 为蒸汽容积时间常数。

汽轮机转子： $ W(S) = \dfrac{{\text{1}}}{{{T_a}s + B}} $ 。 $ {T_{\text{a}}} $ 为转子时间常数，B为自平衡系数，单机运行时为0，并网运行时为1。

测速反馈： $ W(S) = \dfrac{1}{{{T_v}s + 1}} $ 。因测速装置时间常数 $ {T_v} $ 很小，通常视为比例环节， $ W(S) = 1 $ 。

考虑执行机构摩擦、间隙、滞环等因素的存在，引进非线性环节，在DEH仿真模型中引入死区和限幅等非线性模块。此外，机组正常运行时，经常受到内扰蒸汽压力扰动和外扰负荷的变化，影响机组的动态响应，需在DEH仿真模型中引入负荷变化、蒸汽压力波动等扰动信号对调节系统进行修正，使其能够准确反映船用汽轮发电机组的运行特性和转速调节性能。根据各环节的数学模型、传递关系和反馈理论，耦合后得如图1所示船用汽轮机DEH系统的Simulink模型。

2 融合遗传算法的改进粒子群算法 2.1 融合遗传算法的改进粒子群算法改进原理

粒子群优化算法（particle swarm optimization，PSO)是Eberhart和Kennedy博士在对鸟类习性研究基础上提出来的，模拟鸟类随机搜寻食物的捕食行为^[9]。优化问题的潜在解当成搜索空间的一只鸟，称为“粒子”，以每只鸟离食物的距离当作适应度，评价解的品质，粒子通过比较自身最优位置与追随当前最优粒子不断迭代，得到优化问题的最优解。然而，传统粒子群算法没有跳出局部最优的举措，在迭代后期容易出现“早熟”现象，导致收敛精度不足问题。针对上述问题，提出一种融合遗传算法的改进粒子群算法，主要策略如下：

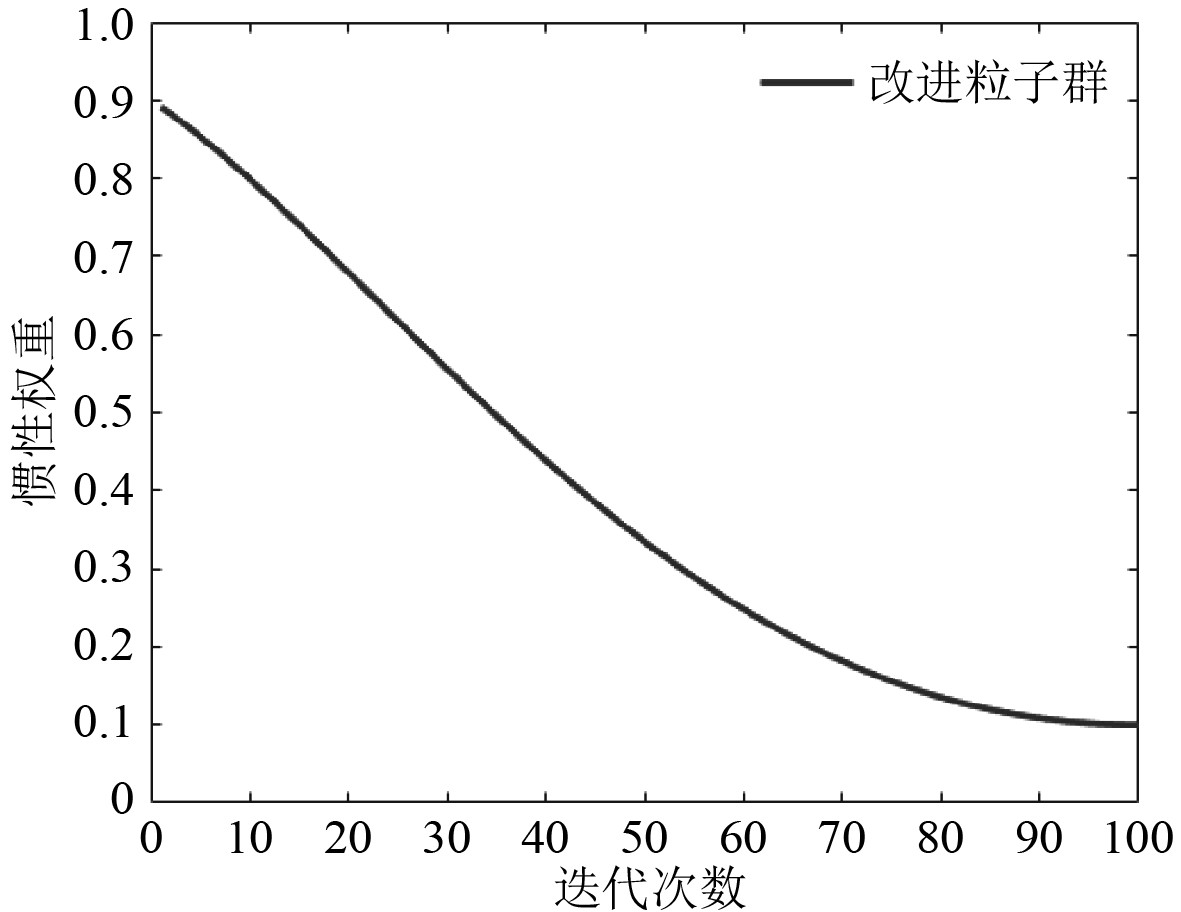
1）惯性权重是PSO中重要的参数，增大其值可以提高算法的全局搜索能力，减小其值可以提高其局部寻优能力。在迭代初期，为了增强全局搜索能力，应选择较大的惯性权重，快速跳出当前较差粒子的位置区域；在迭代中后期，粒子一般已趋于较优位置，容易在全局最优解附近产生震荡现象，此时应选择较小的惯性权重，增强其局部寻优能力。为此，本文引入自适应递减权重法，在线性递减的基础上加入随迭代次数T自适应的幂，使其在中后期惯性权重保持较小值，其公式为：

$ \omega = {\omega _{\max }} - ({\omega _{\max }} - {\omega _{\min }}) \times {(\frac{T}{{{T_{\max }}}})^{(1 - \frac{T}{{{T_{\max }}}})}}。$

(1)

其中： $ {\omega _{{\text{max}}}} $ 和 $ {\omega _{{\text{min}}}} $ 分别表示惯性权重最大值和最小值； $ {T_{{\text{max}}}} $ 表示最大迭代次数。

图2为改进后的惯性权重变化曲线，可以看出，随着迭代次数的增加，惯性权重前期数值较大，但其数值下降的幅度越来越小，中后期下降幅度开始趋于平稳，基本维持在最低权重的位置，有利于提高中后期的局部开发能力。

2）在粒子群繁殖操作基础上引入类似遗传算法的选择、杂交和变异等操作，使搜索过程具有更好的灵活性，有利于产生更多新的优良个体，提高粒子的多样性，使算法跳出局部最优。

选择、杂交过程：首先，初始化参数和N个粒子的速度与位置，更新粒子的速度、位置和适应度，依据适应度高低对粒子进行排序，选择种群中M（偶数）个亲和度最高的粒子。然后依照概率 $ {P_{\text{c}}} $ 对选出的个体进行随机两两杂交，产生相同数目的子代粒子，并用子代粒子替换父代粒子。子代粒子位置与速度公式如下：

$ {{z_x}} = rand \times m_x(1) + (1 - rand) \times m_x(2)。$

(2)

其中：m_x表示父代粒子的位置；zx表示子代粒子的位置，rand是0~1的随机数。

$ {{z_v}} = \frac{{m_v(1) + m_v(2)}}{{\left| {m_v(1) + m_v(2)} \right|}}\left| {m_v} \right|。$

(3)

其中：m_v表示父代粒子的速度；z_v表示子代粒子的速度。

变异操作：用杂交完的M个个体替换杂交前粒子群N中M个亲和度最低的个体，得到新的粒子群N'，以概率 $ {P_m} $ 对全部个体执行下面的变异操作：

$ z_x=left\Big\{ \begin{array}{*{20}{l}} m_x +b，& {\rm{if}} fitness(m_x+b)<fitness(m_x)，\\ m_x，& {\rm{otherwise}} 。\end{array} $

(4)

$ {{z_v}} = m_v 。$

(5)

其中：b为区间 $[x_{{\rm{min}}}-{m_x}，{{{{x}}}_{{{{\rm{max}}}}}}-{m_x}]$ 上均匀分布的随机数； $x_{\text{max}}$ 和 $x_{\text{min}}$ 为搜索空间粒子位置的上下限；fitness()为适应度函数。

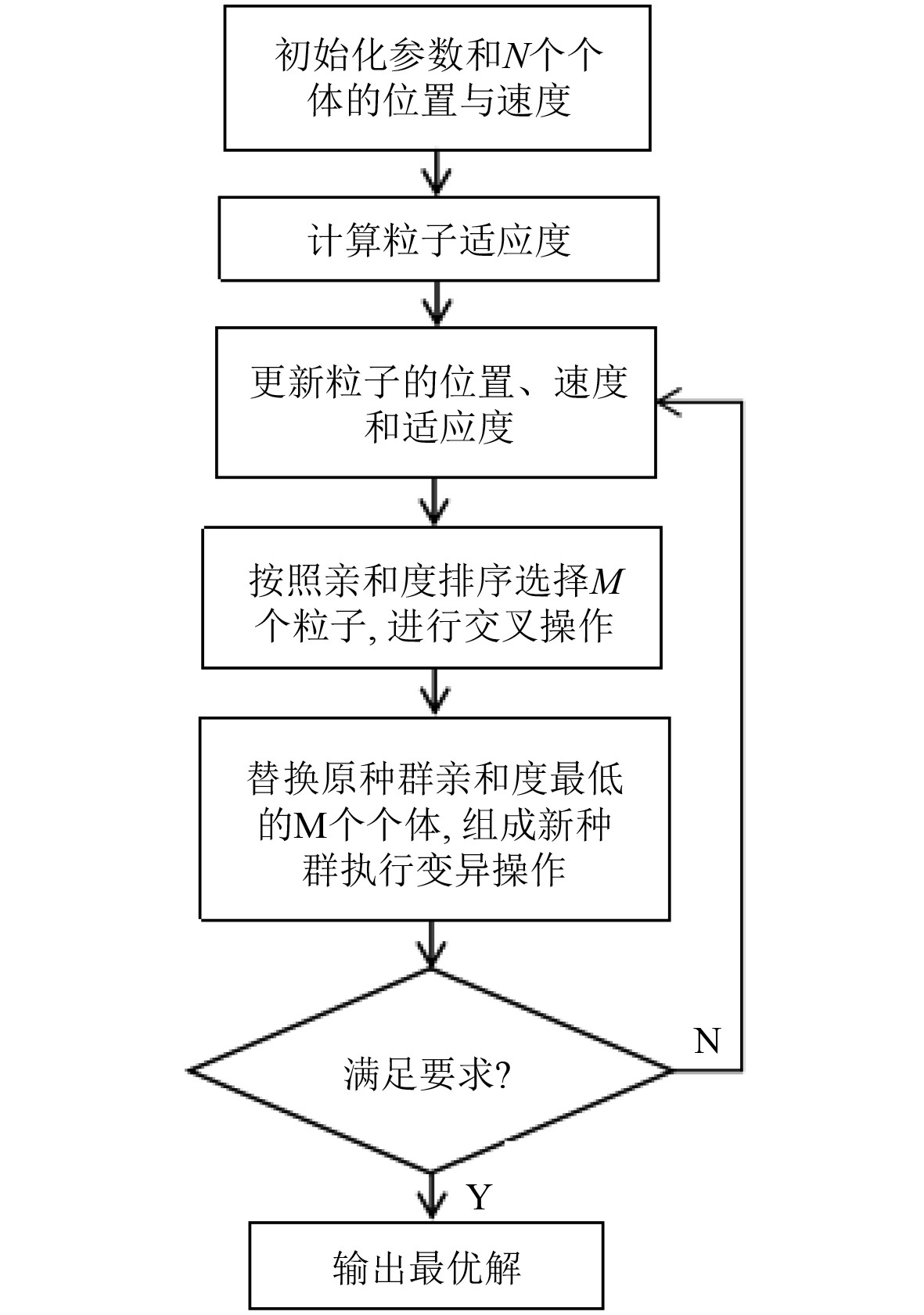
融合遗传算法的改进粒子群算法运行流程图如图3所示。

2.2 融合遗传算法的改进粒子群算法性能分析

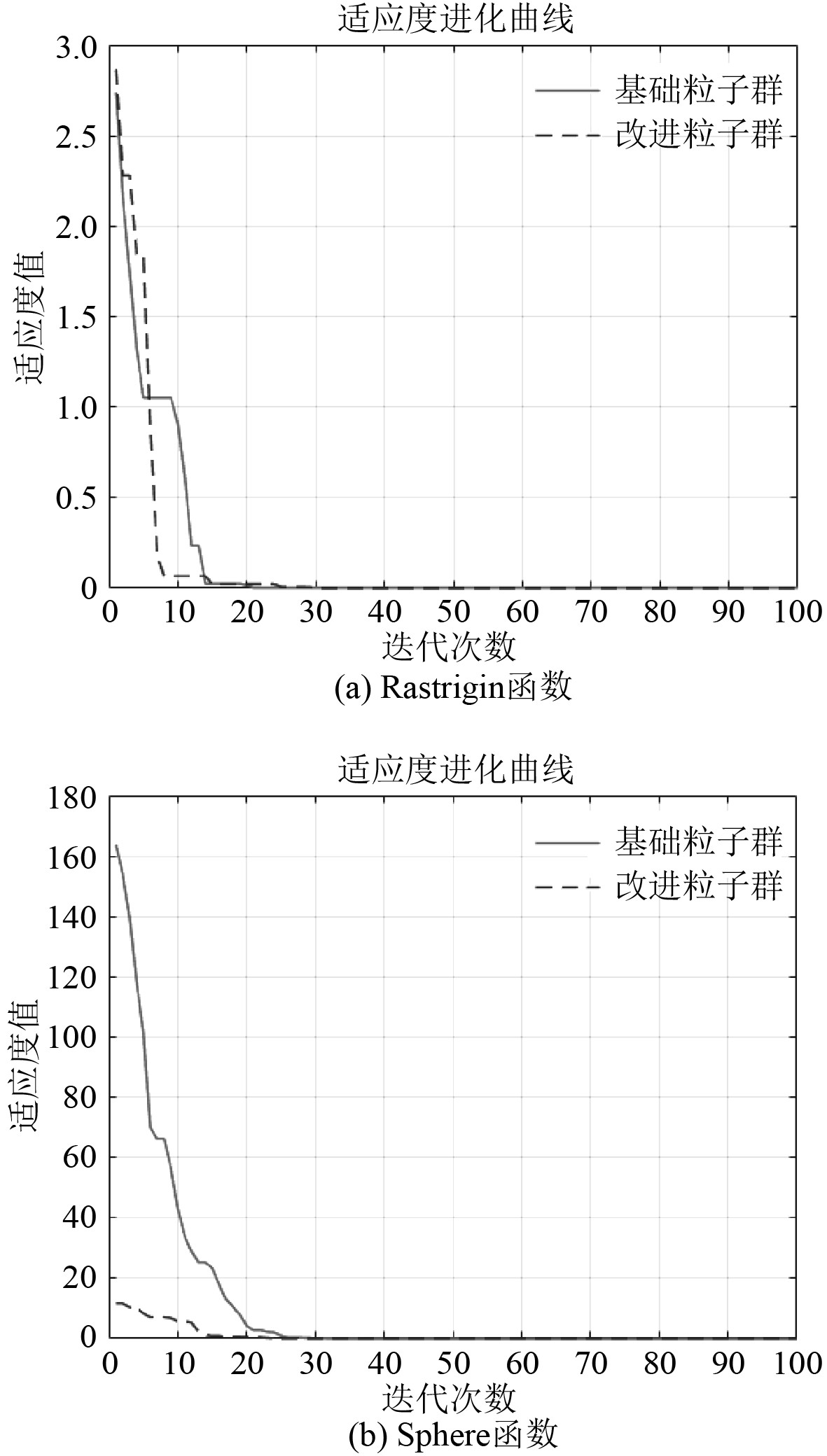
从收敛速度和收敛精度2个方面来分析改进粒子群算法的性能，选取Rastrigin和Sphere 两个标准测试函数进行试验，图4为粒子群算法改进前后的Rastrigin函数和Sphere函数适应度进化曲线。

由图4可知，Rastrigin标准测试函数下，适应度曲线进化的起点基本一致，经过简单迭代后，融合遗传算法的改进粒子群算法的的适应度曲线下降更显著，较早处于基础粒子群曲线的下方；Sphere标准测试函数下，融合遗传算法的改进粒子群算法起点更低，并且在更少的迭代次数下达到最低适应度处。说明改进后的粒子群算法能够更早接近最优解，具有更好的收敛性能。

表1列出了10组Rastrigin函数和Sphere 函数下粒子群算法改进前后的适应度均值以及完成迭代100次所需要的时间均值。

由表1可知，在2个标准测试函数下，融合遗传算法的改进粒子群算法的平均适应度不仅比基础粒子群算法的平均适应度小很多个数量级，而且完成相同迭代次数所需要的时间更短，充分说明融合遗传算法的改进粒子群算法比基础粒子群算法具有更快的收敛速度和更高的收敛精度。

3 船用汽轮机DEH重要组件参数的智能辨识

以船用汽轮机组为对象，对DEH系统线性环节参数进行辨识。其中伺服放大器中的 $ \delta $ 值与不等率对应，转子时间常数一般可由转速飞升曲线得到^[10]，所以需要辨识的参数主要有电液转换器、油动机和汽轮机蒸汽容积时间常数。辨识的主要步骤：1）以执行机构阀位指令阶跃信号为输入，油动机调门开度为输出，辨识电液转换器、油动机时间常数；2）以油动机调门的阶跃变化为输入，汽轮机的功率为输出，辨识汽轮机蒸汽容积时间常数。利用融合遗传算法的改进粒子群算法与基础粒子群算法、遗传算法、人群搜素算法，进行DEH重要组件参数辨识精度的比较。

3.1 参数智能辨识基本输入

各调节组件参数的理论值设置为： $ \delta = 0.04 $ ， $ {T_e} = 0.01 $ ， $ {T_s} = 0.2 $ ， $ {T_{{\text{ch}}}} = 0.25 $ ， $ {T_{\text{a}}} = 8 $ 。遗传算法参数设置为： $ {P_c} $ =0.8， $ {P_{\text{m}}} $ =0.1；人群搜索算法参数设置为： $ {U_{\max }} $ =0.95， ${U_{{\rm{m}}{\text{in}}}}$ =0.0111， $ {W_{\max }} $ =0.9， ${W_{{\rm{m}}{\text{in}}}}$ =0.1；粒子群算法参数设置为：c₁=1.3，c₂=1.7，W=1， $ {V_{\max }} $ =1， $ {V_{\min }} $ =-1；融合遗传算法的改进粒子群算法参数设置为 $ {W_{\max }} $ =0.9， ${W_{{\rm{m}}{\text{in}}}}$ =0.1，c₁=1.3，c₂=1.7， $ {V_{\max }} $ =1， $ {V_{\min }} $ =-1， $ {P_c} $ =0.85， $ {P_{\text{m}}} $ =0.01；种群规模和迭代次数统一设置为Size=200和T=100。

3.2 参数辨识结果分析

采用一组含随机噪声干扰的阶跃信号为输入，以系统实际输出与辨识后仿真输出的误差值作为辨识的适应度函数，采样周期为0.01 s，采样点数为1000，采用遗传算法（GA）、人群搜索算法（SOA）、基础粒子群算法（PSO）和融合遗传算法的改进粒子群算法（IPSO）开展参数辨识仿真，辨识10次的结果如表2所示。

由表2可知，辨识结果相对误差从小到大依次是融合遗传算法的改进粒子群算法、基础粒子群算法、人群搜索算法与遗传算法，其中基础粒子群与人群搜索算法辨识的相对误差相差较小，而融合遗传算法的改进粒子群算法比基础粒子群算法和人群搜索算法辨识的相对误差小了1个数量级，比遗传算法辨识的相对误差小了2个数量级，能够证明融合遗传算法的改进粒子群算法较本文提出的智能算法应用于参数辨识的准确性更高，辨识效果更显著。

4 船用汽轮机DEH的PID参数智能优化及运行特性

根据上述调节组件的参数辨识结果，得到开环系统的近似线性传递函数为：

$ {G_{\text{k}}}(s) = \frac{{25\;000}}{{4{s^4} + 436{s^3} + 5\;680{s^2} + 16\;000s}}。$

(6)

由于汽轮机DEH系统含有电液转换器和油动机等非线性元件，常规的PID参数整定方法难以获得很好的整定效果，且船用汽轮机在实际运行中，为应对复杂环境变化，汽轮发电机组经常会发生大幅度变负荷，以及更容易受到锅炉或蒸发器运行参数不稳定导致的压力扰动的影响。考虑非线性环节，以使DEH系统在大幅度变负荷和压力扰动下实现最佳的响应特性为优化目标，利用融合遗传算法的改进粒子群算法、基础粒子群算法、遗传算法和人群搜素算法优化PID控制器参数，提升机组的控制性能。

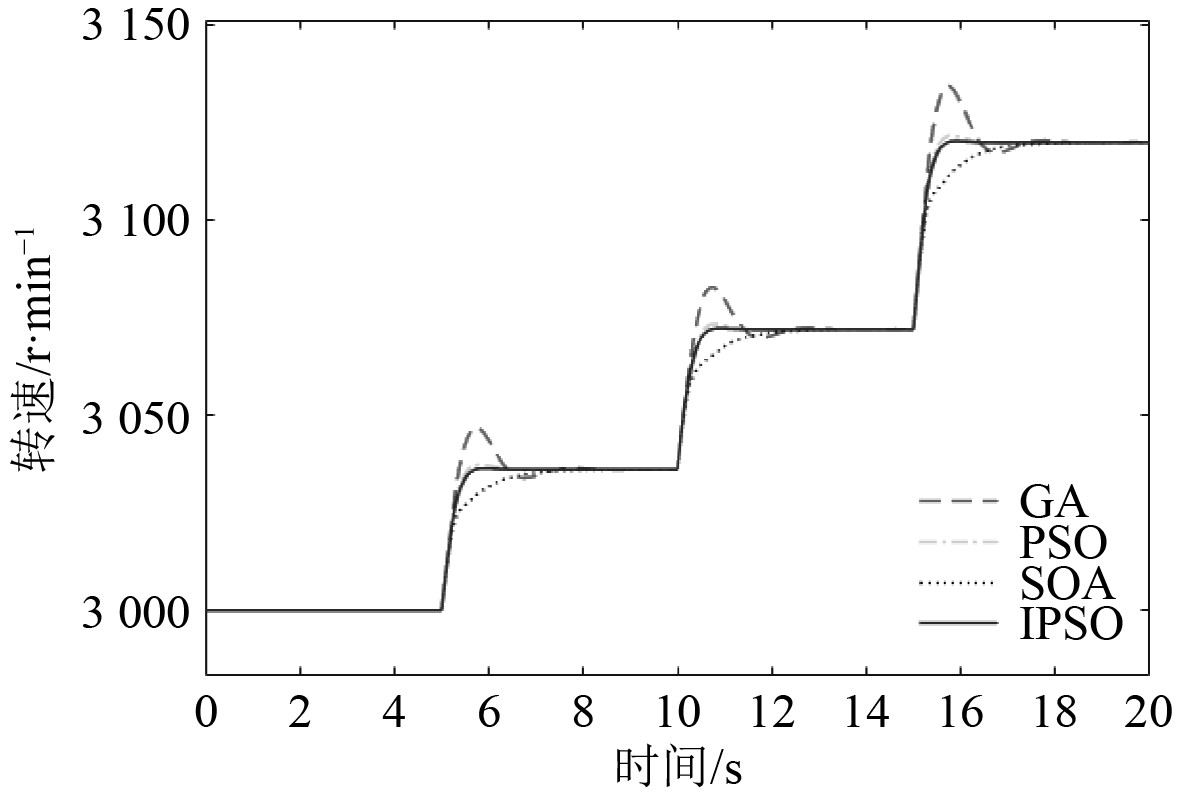
4.1 甩负荷工况

为优化汽轮机甩负荷后转速上升的动态响应，模拟汽轮机在额定负荷运行5 s后，负荷阶跃下降至60%额定负荷，持续运行5 s，然后负荷阶跃下降至30%额定负荷，继续运行5 s，负荷阶跃变为0的线性甩负荷动态过程。额定转速为3 000 r/min，仿真时间为20 s，融合遗传算法的改进粒子群算法、基础粒子群算法、遗传算法和人群搜索算法优化PID控制器后系统甩负荷的转速响应曲线如图5所示。

由图5可知，当负荷阶跃减小时，转子转速会迅速增加，负荷阶跃减少越多，转速上升幅度越大，甩100%阶跃负荷时，转速达到最大值3120 r/min，与前面所设置的转速不等率为0.04完全符合。融合遗传算法的改进粒子群算法优化PID控制器在负荷阶跃减少后系统动态超调量为0%，调整时间为1.23 s，在最小化超调百分比和调整时间方面均优于基础粒子群算法、遗传算法和人群搜索算法，且甩负荷后动态响应特性不随甩负荷阶跃的大小而变化，始终保持稳定。可见，融合遗传算法的改进粒子群算法优化PID控制器提供了减少汽轮机甩负荷过程的转速超调百分比和调整时间的优点，并且具有很好的鲁棒性。

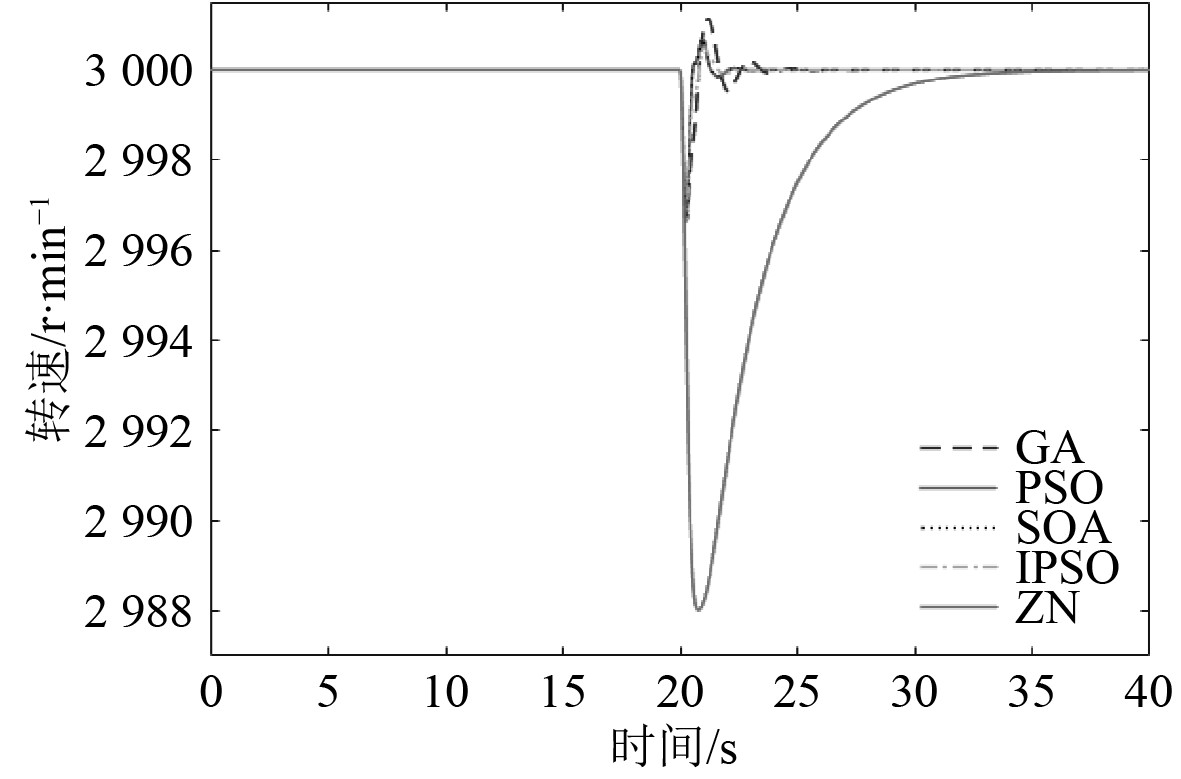
4.2 蒸汽压力扰动

为优化蒸汽压力波动对汽轮机组转速输出的影响，模拟汽轮机在额定功率运行20 s后，加入20%的蒸汽压力扰动系统转速调整的动态过程。仿真时间为40 s，融合遗传算法的改进粒子群算法、基础粒子群算法、遗传算法、人群搜索算法优化的PID控制器和Ziegler-Nichols方法^[11]整定PID控制器下系统蒸汽压力变化的转速响应曲线如图6所示。

由图6可以看出，当蒸汽压力变化时，汽轮机负载会随之变化，转速因为负载的变化会产生一定的波动。总的来说，与Ziegler-Nichols方法整定的PID控制器相比，上述4种智能算法优化的PID控制器都只有轻微的转速微调现象，并且转速调整时间较小，达到了良好的控制效果。其中基础粒子群算法与人群搜索算法优化的PID控制器系统控制性能基本一致，而基于改进粒子群算法的PID控制器在扰动发生后转速响应的快速性和稳定性等综合性能依次优于基础粒子群算法和遗传算法，且转速微调为0.12%，调整时间约为2.1 s，说明改进粒子群算法优化的PID控制器抗扰动能力强，稳定性好。

5 结　语

1）综合考虑DEH系统伺服机构的死区、摩擦等非线性和外界负荷变化、内部蒸汽压力扰动的影响，建立了引入限幅、死区模块和负荷与气压阶跃扰动模块的DEH系统模型，能够准确反映船舶汽轮机实际变工况运行特性。

2）融合遗传算法的改进粒子群算法改善了传统粒子群算法易陷入局部最优的缺点，其计算精度和速度均优于传统粒子群算法。该算法同时实现了DEH重要组件的参数辨识和PID控制器参数的智能自整定，且辨识精度与整定效果均优于其它三种智能算法。可见，基于融合遗传算法的改进粒子群算法DEH智能优化控制，能够实现船用汽轮发电机组大幅度变工况和外界复杂因素扰动下的稳定运行。