遥控无人潜水器(ROV)由于具有携带方便,操作简单的特点,被广泛应用于水下资源勘探与开采。保持ROV的深度不受干扰是保证ROV观察与作业的关键。传统的非线性自抗扰控制器(ADRC)存在待整定参数过多的问题,不利于工程实践[1-4]。线性自抗扰控制(LADRC)保留了ADRC的状态扩张观测器(ESO),减少了待整定参数[5]。本文构建ROV定深运动的数学模型,结合LADRC控制方法的优点,提出了基于粒子群算法(PSO)优化的LADRC控制方法,提高参数整定效率和系统响应性。
1 ROV定深运动数学模型本文以八推进器水下机器人(ROV)为研究对象,主要考虑水下机器人的重力与浮力,ROV三维模型如图1所示。

|
图 1 ROV三维模型 Fig. 1 ROV model |
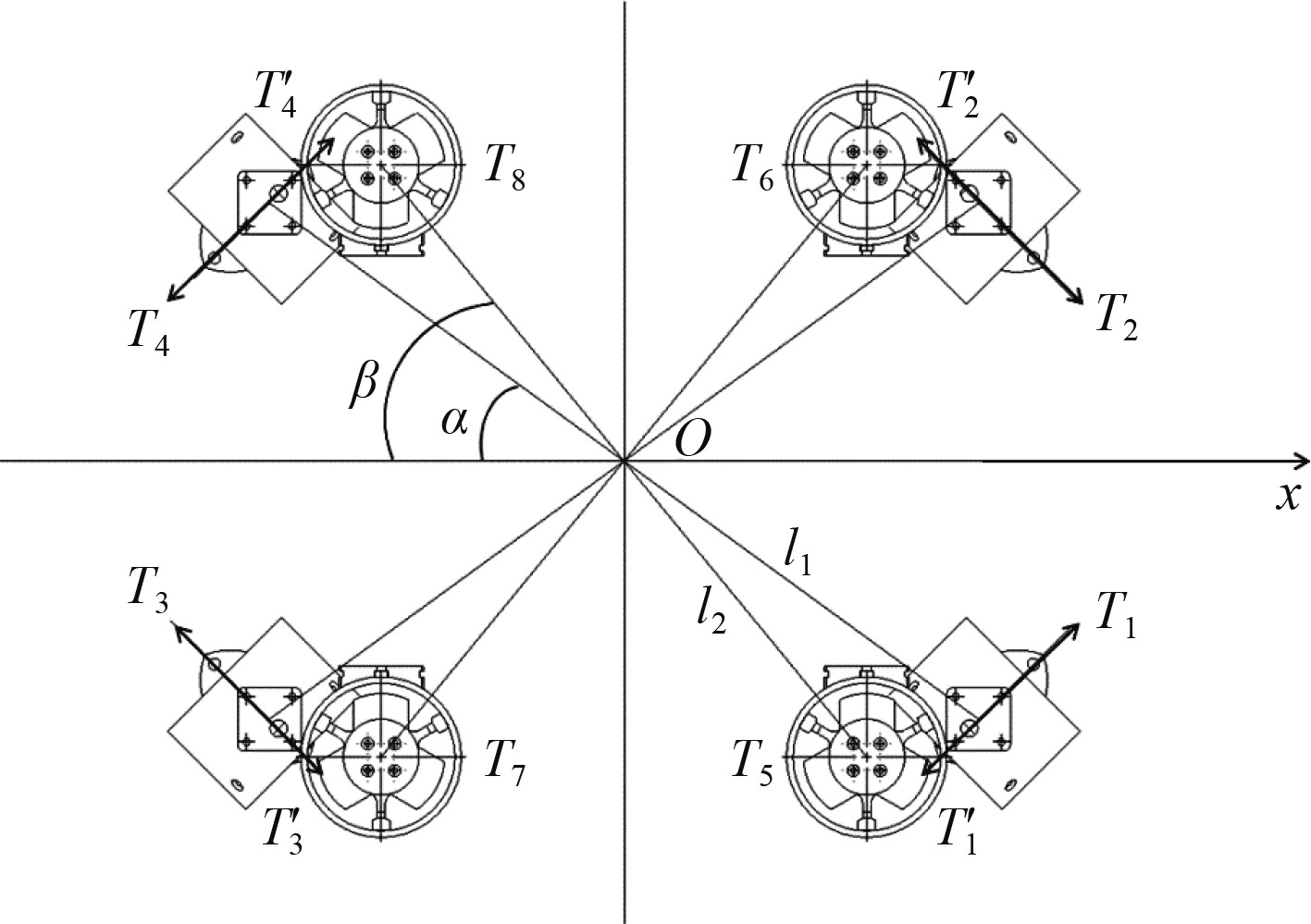
ROV的水平面推进器分布如图2所示。
|
图 2 ROV推进器分配图 Fig. 2 ROV thruster allocation diagram |
每个推进器可以产生2种推力,分别对应推进器的正转和反转,为坐标原点到推进器的距离,设ROV定深时不做其他运动,可得ROV定深时受到力矩作用为:
| $ \left\{\begin{array}{l} X_{T}=T_{1}^{\prime} \cos \alpha+T_{2}^{\prime} \cos \alpha+T_{3} \cos \alpha +T_{4} \cos \alpha,\\ Y_{T}=T_{1} \cos \alpha+T_{2}^{\prime} \cos \alpha+T_{3} \cos \alpha+T_{4}^{\prime} \cos \alpha,\\ Z_{T}=T_{5}+T_{6}+T_{7}+T_{8},\\ K_{T}=T_{5}^{\prime} l_{2}+T_{6}^{\prime} l_{2}+T_{7} l_{2}+T_{8} l_{2},\\ M_{T}=T_{5}^{\prime} l_{2}+T_{7}^{\prime} l_{2}+T_{6} l_{2}+T_{8} l_{2},\\ N_{T}=T_{1} l_{1}+T_{2}^{\prime} l_{1}+T_{3}^{\prime} l_{1}+T_{4} l_{1}。\end{array}\right. $ | (1) |
推进器的推力与水密度
| $ \left\{\begin{array}{l} T_{i}=\rho n^{2} D^{4} K_T,\\ T^{\prime}_i=\rho n^{2} D^{4} K^{\prime}_T。\end{array}\right. $ | (2) |
式中:
当水下机器人运动时,会与周围的水相互影响,受到一个由水流带来的反作用力,称为水动力[6-7]。水动力受很多因素的影响,比如水下机器人的形状,运动状态以及流体的性质等,但对于本文的水下机器人,速度不高,速度的变化也不快,故主要考虑粘性水动力与惯性水动力,其他水动力忽略不计[8],其函数表现形式为:
| $ F_{F}=f( u, v, w, \dot{u}, \dot{v}, \dot{w},p,q,r, \dot{p}, \dot{q}, \dot{r})。$ | (3) |
粘性水动力是低速状态下水下机器人受到的主要阻尼力,主要为克服水流粘性受到的阻力与阻力矩[9],由于形式复杂,不便表述,一般使用多元函数的泰勒展开法计算。由于水下机器人速度较低,高阶项影响较小,故保留到二次项,其垂直面的表达式如下:
| $ \left\{\begin{array}{l} X_{V}=X_{\dot{u}} \dot{u}+X_{u u} u^{2}+X_{\text {ww }} w^{2}+X_{q q} q^{2}+X_{\text {wq }} wq,\\ Z_{V}=Z_{w} \dot{w}+Z_{\dot{q}} \dot{q}+Z_{w} w+Z_{|w|}|w|+Z_{q} q+Z_{w|w|} w|w|+ \\ \quad\quad Z_{w^{2}} w^{2}+Z_{w|q|} w|q|+Z_{q|q|} q|q|,\\ M_{V}=M_{w} \dot{w}+M_{\dot{q}} \dot{q}+M_{w} w+M_{|w|}|w|+M_{q} q+ M_{q}q +\\ \quad\quad M_{w|w|} w|w|+ M_{w^{2}} w^{2} +M_{w|q|} w|q|+M_{q|q|} q|q|。\end{array}\right. $ | (4) |
式中:
惯性水动力是水下机器人在航行时克服流体惯性所产生的力,其大小与加速度、角加速度有关,二者的比例系数也称为附加质量,运用矩阵表示六自由度水下机器人空间运动中36个附加质量如下:
| $ \lambda_{i, j}=\left| \begin{array}{llllll} \lambda_{11} & \lambda_{12} & \lambda_{13} & \lambda_{14} & \lambda_{15}& \lambda_{16} \\ \lambda_{21} & \lambda_{22} & \lambda_{23} & \lambda_{24} & \lambda_{25}& \lambda_{26} \\ \lambda_{31} & \lambda_{32} & \lambda_{33} & \lambda_{34} & \lambda_{35}& \lambda_{36} \\ \lambda_{41} & \lambda_{42} & \lambda_{43} & \lambda_{44} & \lambda_{45}& \lambda_{46} \\ \lambda_{51} & \lambda_{52} & \lambda_{53} & \lambda_{54} & \lambda_{55} & \lambda_{56}\\ \lambda_{61} & \lambda_{62} & \lambda_{63} & \lambda_{64} & \lambda_{65}& \lambda_{66} \end{array} \right|。$ | (5) |
式中:
综合式(1)和式(4),假设当ROV进行定深运动时不进行其他运动,可得推力对ROV深度的传递函数:
| $\begin{split}& \left(T_{5}+T_{6}+T_{7}+T_{8}\right) l_{2}-\lambda_{33} \dot{w}+Z_{w} w+Z_{|w|}|w|+\\ &\qquad Z_{ w|w|} w|w|+Z_{|ww|}w^2+(G-P)\cos \theta=m\dot{w},\end{split} $ | (6) |
令
| $ G_{D}(s)=\frac{1}{\left(m+\lambda_{33}\right) s^{2}-Z_ws}。$ | (7) |
式(7)为下潜状态时的传递函数,由于上浮和下潜时,推进器转动方向相反,故传递函数略有不同,上浮过程的传递函数如下:
| $ G_{P}(s)=\frac{1}{\left(m+\lambda_\mathrm{33}^{\prime}\right) s^{2}-Z_w^{\prime}s}, $ | (8) |
将式(2)进行泰勒展开并略去高阶项,然后进行拉氏变换得:
| $ \left\{\begin{array}{l} G_{T}(s)=\dfrac{T(s)}{n(s)}=2 K_T\rho D^4,\\ G_{T}^{\prime}(s)=\dfrac{T(s)}{n(s)}=2 K_T^{\prime}\rho D^4。\end{array}\right. $ | (9) |
将推进器与电子调速器组成的单元近似为典型一阶惯性环节处理,其传递函数为:
| $ G_{M}(s) \frac{K_{E}}{1+T_Es}。$ | (10) |
式中:TE为电机的时间长常数;KE为放大系数。
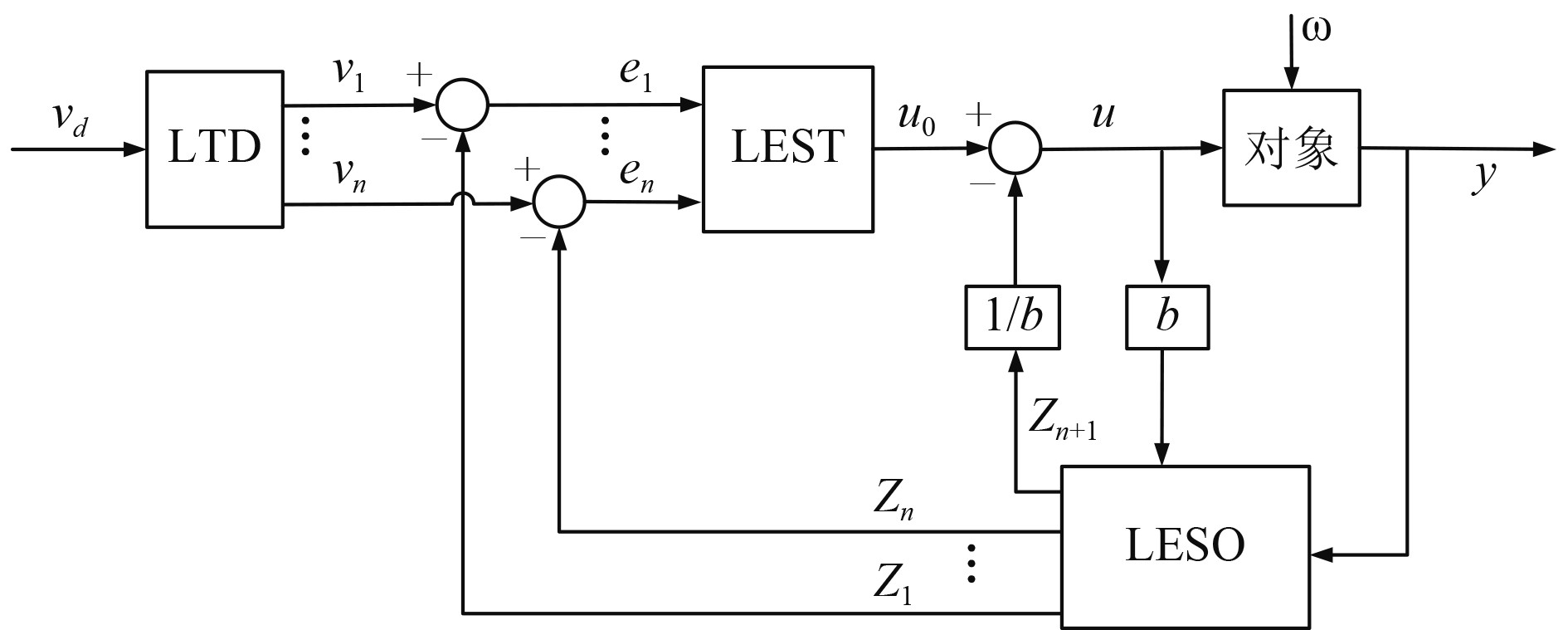
2 PSO优化的LADRC水下机器人深度控制系统 2.1 LADRC控制器LADRC控制器在ADRC的基础上保留了ESO,减少了可调参数,其组成为线性状态误差反馈率(LSEF)、状态扩张观测器(LESO)和线性跟踪微分器(LTD)。如图3所示,其中LTD的目的是安排过渡过程、消除超调量与控制快速性的矛盾并获取微分信号[11],为避免高频次震荡,取消LTD,LESO的目的是跟踪可能存在的各种扰动,也是LADRC的核心,其阶数比被控制对象的阶数高一阶。一般地,n阶被控对象的ESO形式如下:
| $ \left\{\begin{array}{l} e=z_{1}-r ,\\ \dot{z}_{1}=z_{2}-\beta_{1} e ,\\ \dot{z}_{2}=z_{3}-\beta_{2} e ,\\ \vdots \\ \dot{z}_{n}=z_{n+1}-\beta_{n} e,\\ \dot{z}_{n+1}=-\beta_{n+1} e。\end{array}\right. $ | (11) |
式中:β为LESO中需要调节的参数。
|
图 3 LADRC结构图 Fig. 3 LADRC structure diagram |
LSEF将LTD的输出与系统状态估计值之间的误差通过线性组合构成初始的控制量,再加入对LESO估计出的总扰动进行补偿,得到最终的控制量[12]。n阶被控对象的LSEF形式如下:
| $ \left\{\begin{array}{l} e_{1}=v_{1}-z_{1} ,\\ e_{2}=z_{2} ,\\ \vdots \\ e_{n}=z_{n} ,\\ e_{n+1}=z_{n+1},\\ u_0=\alpha_1 e_1+\alpha_2 e_2+\cdot\cdot\cdot+\alpha_{n+1} e_{n+1}。\end{array}\right. $ | (12) |
式中:v1为LTD的输出,α为LSEF需调参数。
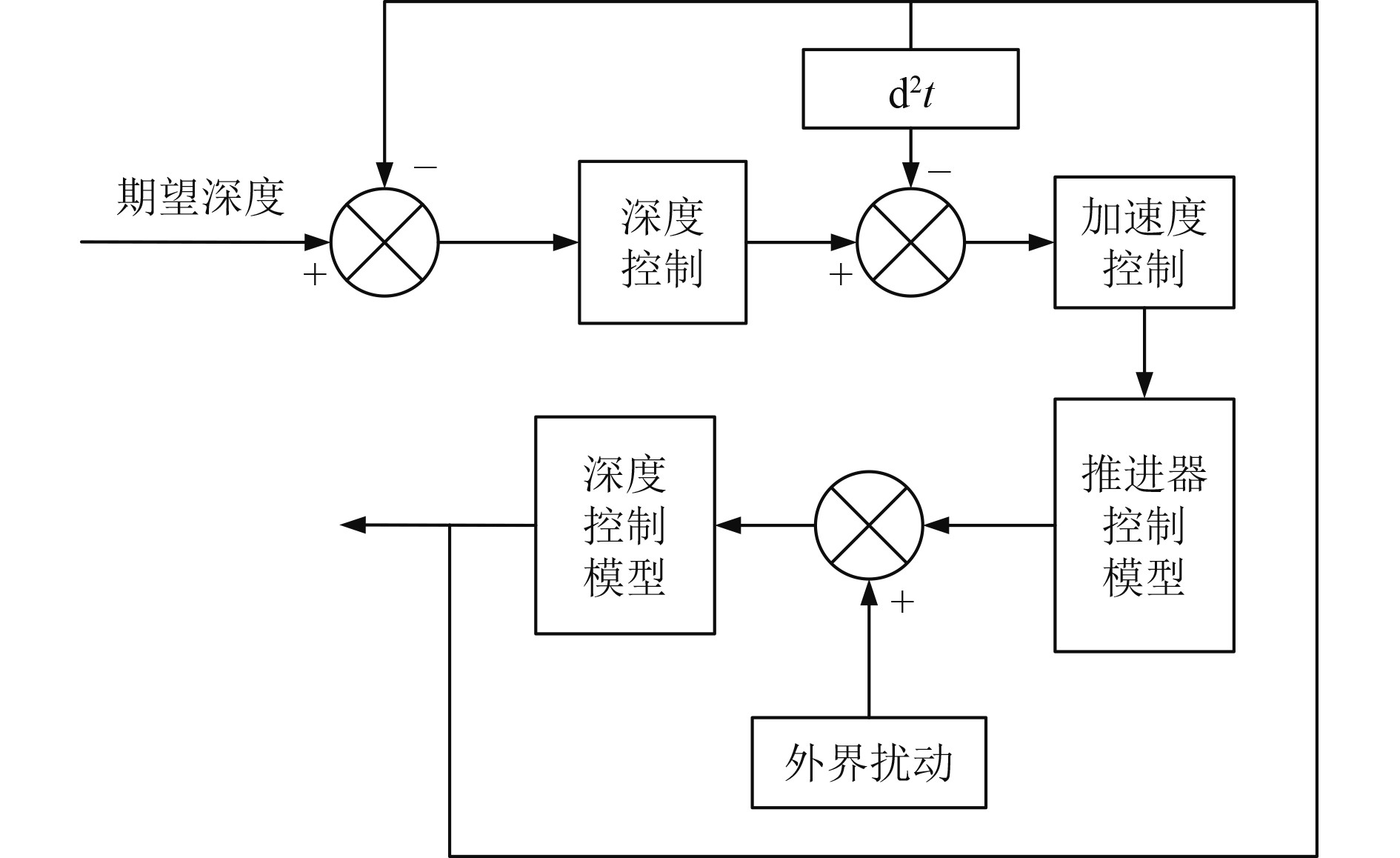
ROV深度控制器采用串级控制方式,根据数学模型分析,可以将ROV的深度控制过程的位移控制为串级系统的外环,加速度控制为串级系统的内环,ROV首向串级控制回路先进行外环位移控制,后进行内环加速度控制,其控制回路如图4所示。
|
图 4 ROV深度控制回路框图 Fig. 4 ROV depth control circuit diagram |
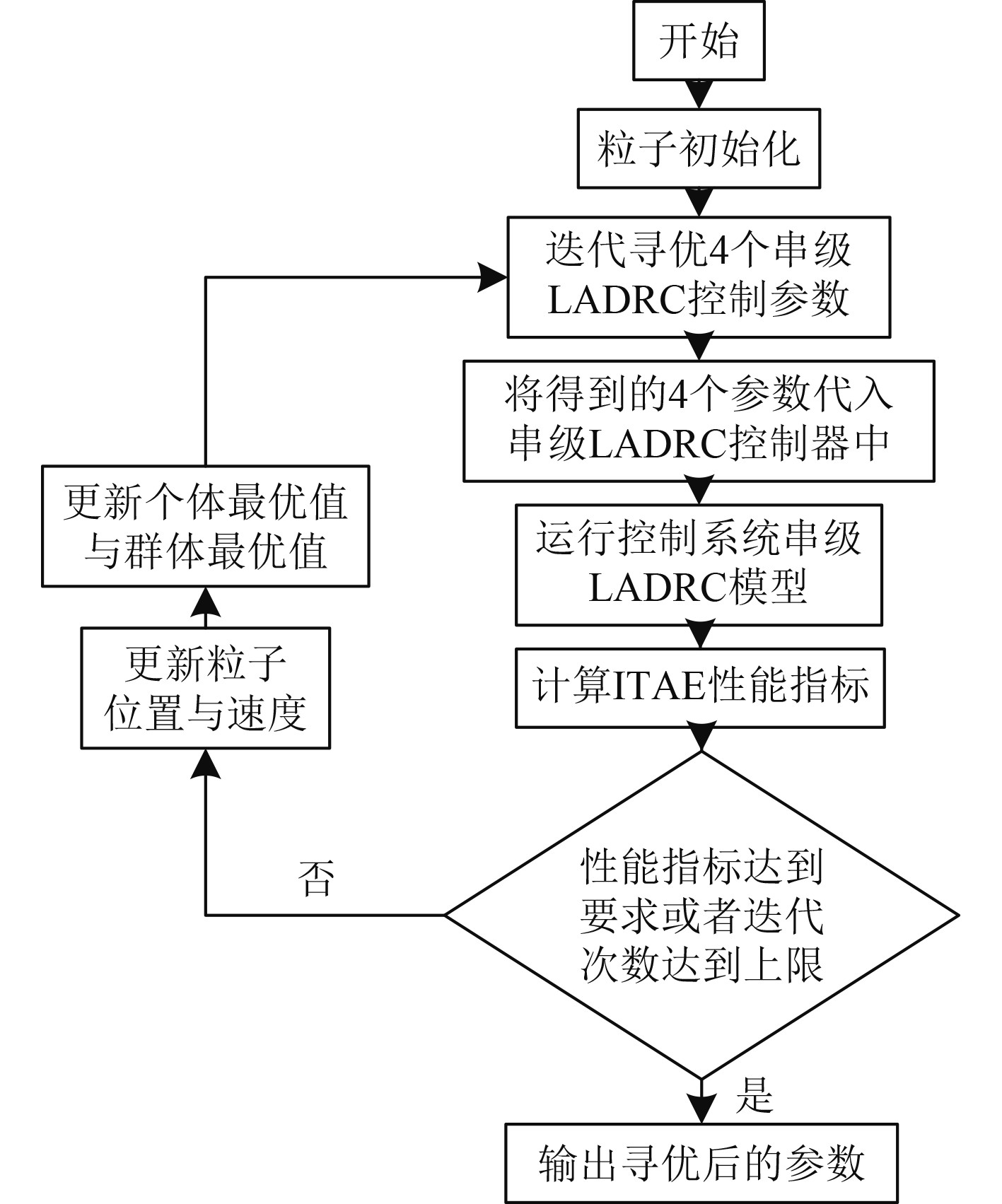
粒子群算法是模拟鸟类觅食的一种智能算法,粒子在寻找最优目标的过程中,不断改变位置,直到寻找到最优目标[13],该算法结构简单,收敛速度快,精确度较高[14],因此将其引入LADRC控制器的参数整定中,其控制流程图如图5所示。
|
图 5 PSO-LADRC流程图 Fig. 5 PSO-LADRC flow chart |
选取时间乘绝对误差积分准则(ITAE)为控制效果评价指标[15],其具体表现形式为:
| $ \int_{0}^{\infty} t \mid e(t)\mid {\rm{d}}t。$ | (13) |
在ROV深度控制器中加入ITAE评价指标与PSO,其控制流程图如图6所示。

|
图 6 PSO-LADRC深度仿真模型 Fig. 6 PSO-LADRC deep simulation model |
基于粒子群算法调参的串级LADRC控制方法,主要步骤为:1)设置并初始化粒子群需要的各个参数。2)将各个个体粒子的初始适应度值作为个体粒子对应的局部最优解,将各个个体粒子的适应值所对应的位置作为局部最优解所在的位置。3)将最佳的初始适应度值作为全局最优解,将最佳的初始适应值对应的位置作为全局最优解所在的位置。4)计算各个粒子对应的串级LADRC的4个参数。5)将各个粒子对应的串级LADRC的4个参数代入到串级LADRC控制器中,运行控制器,并计算对应的ITAE指标数值。6)判断ITAE指标是否达到预定最小值或者迭代次数达到上限。若达到要求,则将寻优得到的粒子对应的串级LADRC的4个参数输出,结束循环,若没有达到要求进入下一步。7)选出当前粒子中ITAE指标最佳的粒子,将其适应值作为新的全局最佳适应值。8)设置粒子飞行速度的上限,更新每个个体粒子的速度与位置。9)用新的个体最佳适应值和新的全局最佳适应值代替历史个体最佳适应值与历史全局最佳适应值,并返回步骤4进行循环。
3 仿真与实验 3.1 仿真验证由于升沉运动传递函数相差较小,为了方便进行仿真,上浮与下潜统一使用下潜运动的传递函数,根据所设计的控制器,在Simulink中搭建ROV深度运动仿真模型,如图6所示。
针对小型水下机器人的实际工作情况,对其外环限幅−0.5~0.5 m/s,对其内环限幅−100~100 μs。仿真时将期望深度设置在3m,仿真步长设置为0.01,在仿真时间20 s的时候加入一个大小为−10的阶跃信号模拟突然的外部干扰,搭建串级PID与串级LADRC,将PSO-LADRC、串级LADRC以及串级PID在相同条件下进行仿真对比实验。ROV的相关参数通过查阅文献与CFD仿真得到[10],如表1所示。
|
|
表 1 载体参数表 Tab.1 Carrier parameter table |
推进器的相关参数记录如表2所示。
|
|
表 2 推进器参数表 Tab.2 Propeller parameter table |
通过试凑法整定的串级LADRC参数如表3所示。
|
|
表 3 LADRC深度控制参数表 Tab.3 LADRC depth control parameter table |
串级PID使用Simulink的PID Tune工具箱进行参数整定,整定后的参数如表4所示。
|
|
表 4 深度控制PID参数表 Tab.4 PID parameter table of depth control |
|
|
表 5 水动力参数表 Tab.5 Hydrodynamic parameters table |
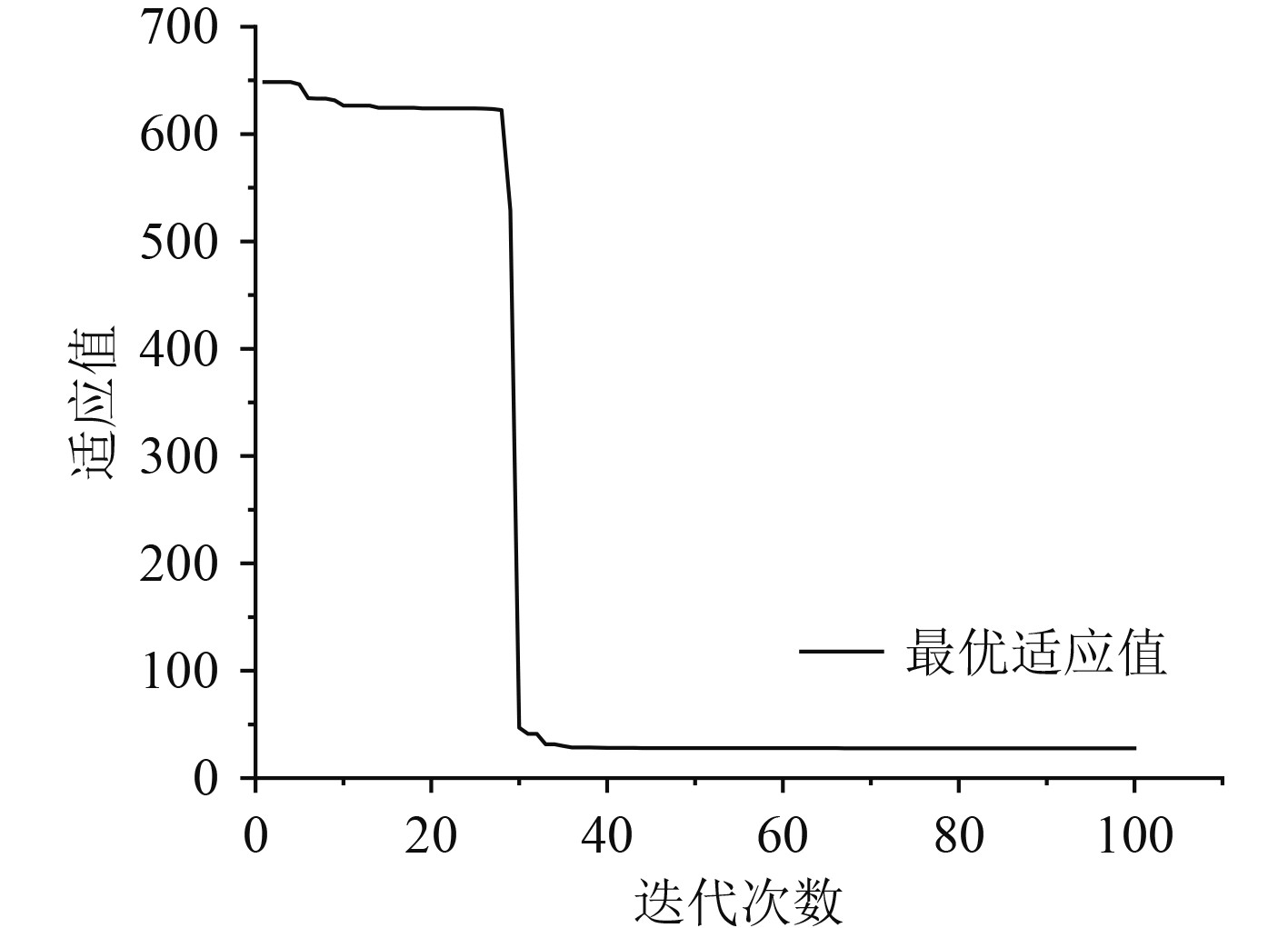
使用PSO对LADRC进行参数整定,在Matlab中运行PSO相关代码,运行代码10次,得到10个最优个体适应值,选取10次中最佳适应值最小的一次作为优化结果,其迭代的最优个体适应值曲线图如图7所示。
|
图 7 PSO-LADRC深度控制最优个体适应值 Fig. 7 Optimal individual fitness for PSO-LADRC depth control |
其寻优后LADRC的参数如表6所示。
|
|
表 6 PSO-LADRC深度参数表 Tab.6 PSO-LADRC Depth Parameter Table PSO-LADRC Depth Parameter Table |
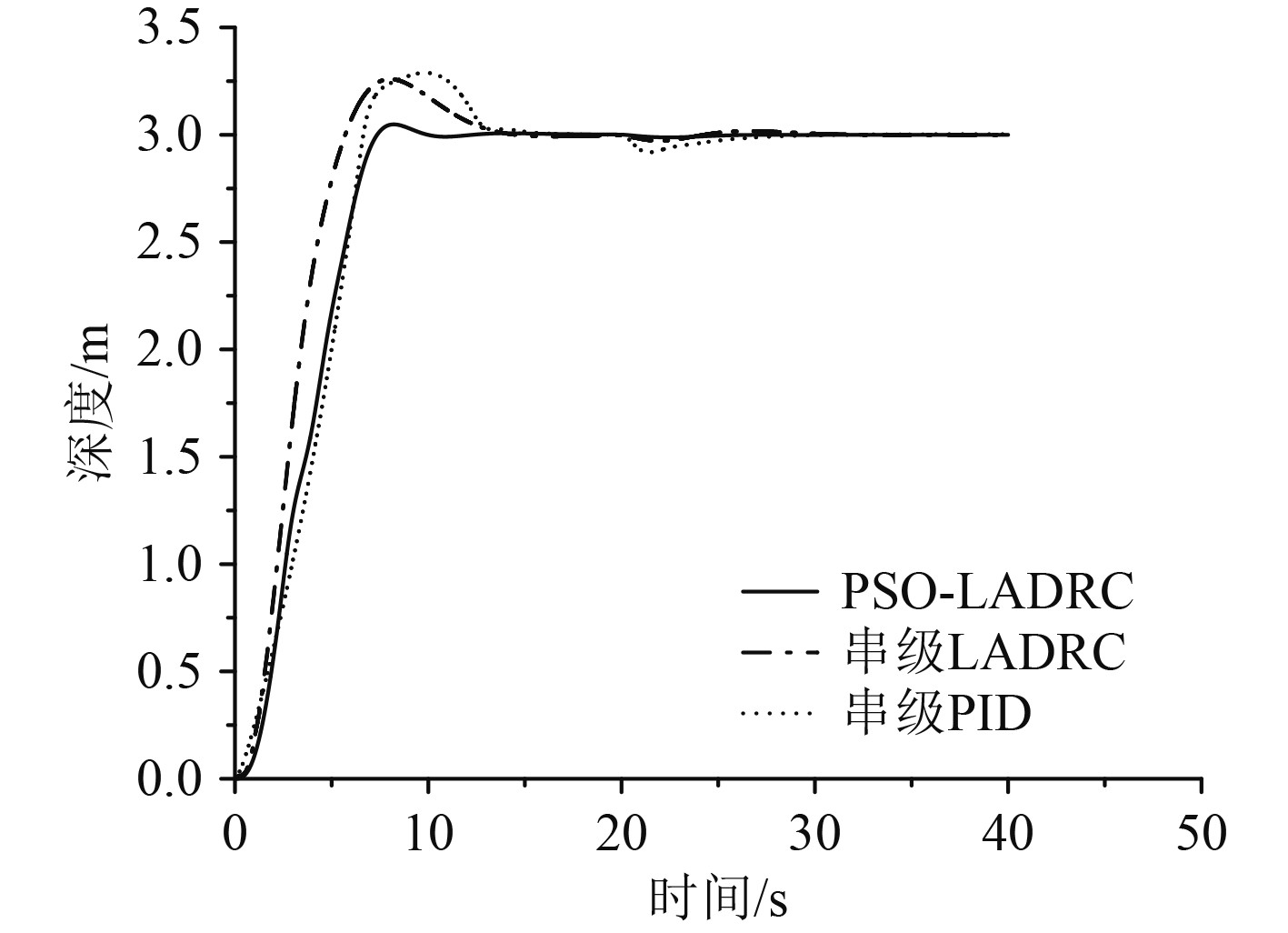
3种方法的控制效果的仿真对比,如图8所示。
|
图 8 串级PID与串级LADRC仿真对比 Fig. 8 Comparison of cascade PID and cascade ladrc simulation |
由图8可以看出,在3 m的深度控制中,串级LADRC的调节时间为15 s,超调量为0.25 m,产生了约8.3%的超调量,相较于串级PID超调量减少了37%,调节时间减少了6.25%。在受到与串级PID控制相同的干扰的情况,仅产生了较小的抖动,而串级PID受到了0.15 m左右的抖动,需要9 s的时间才能恢复稳定。在加入粒子群算法进行参数调节以后,调节时间仍为15 s,但是超调量为0.1 m,相较于根据试凑法调参的串级LADRC,超调量减少了60%,在时间为20 s受到相同干扰的情况下,两者受到的影响都很小,仅产生了少量的抖动。
3.2 实验验证为了验证所设计控制器的有效性,搭建实验测试平台。
所搭建的实验测试平台搭载8个推进器,采用Pixhawk开源飞控,其主处理器为STM32F427,集成有MPU6000陀螺仪和MEASMS5611气压深度计,采用海思Hi3516作为摄像头数据处理芯片,使用手柄实现对水下机器人的控制。由于是测试平台,采用外载浮力块的形式来平衡水下机器人的重力与浮力。
为了实现对水下机器人的数据采集,使用mission planner地面站实现对水下机器人航行数据的读取。地面站能读取MAVLink通信协议下的水下机器人数据传输,在水下机器人航行结束时,能够下载Pixhawk飞控中生成的航行日志,在航行日志中,能够提取水下机器人在这次航行中的姿态、速度和深度等各种信息。
分别在定深模式下读取串级PID控制方法和串级LADRC控制方法的航行日志,读取航行数据中的深度数据。
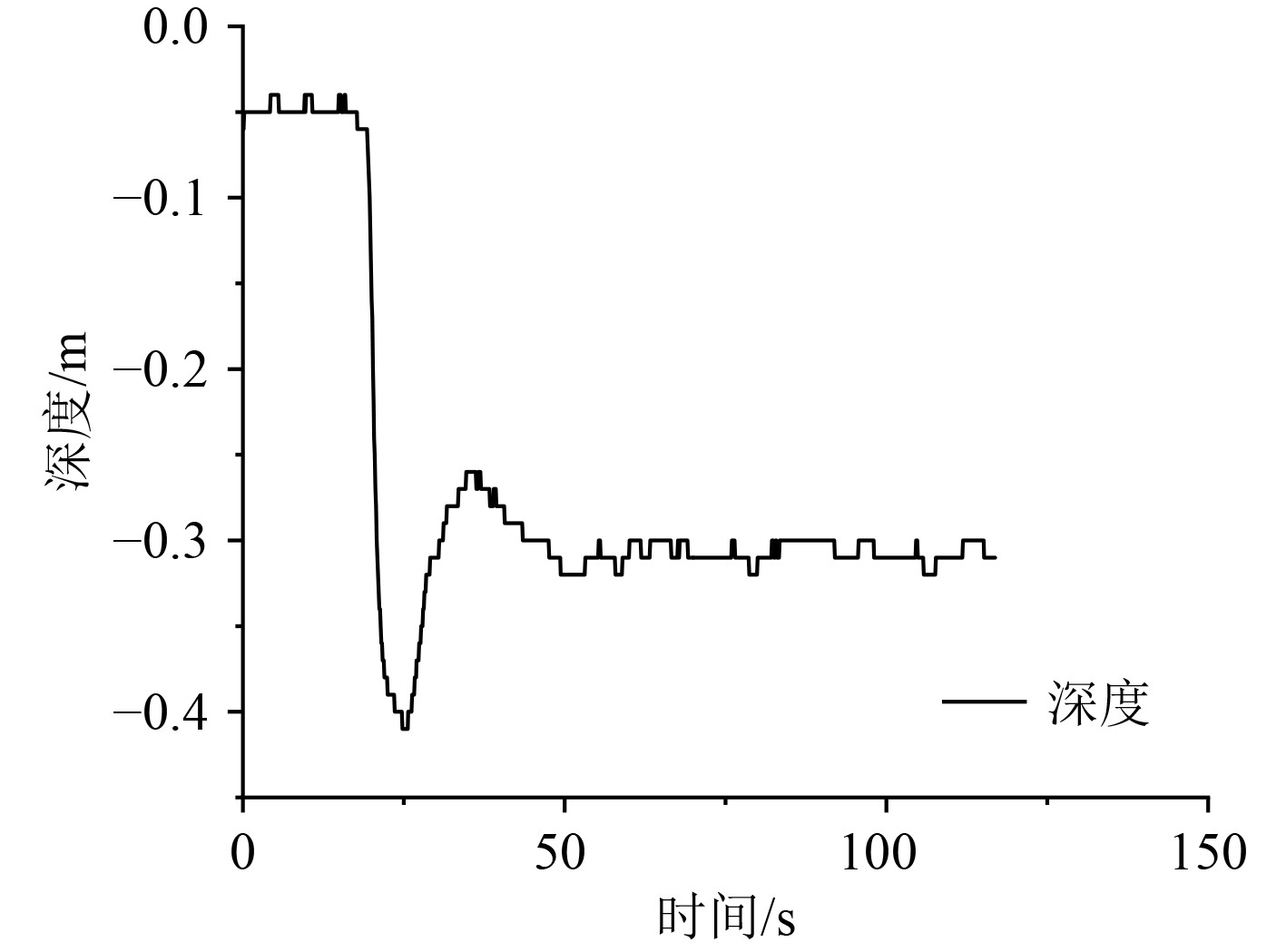
使用串级PID控制方法读取的数据如图9所示。
|
图 9 串级PID深度控制测试 Fig. 9 cascade PID depth control test |
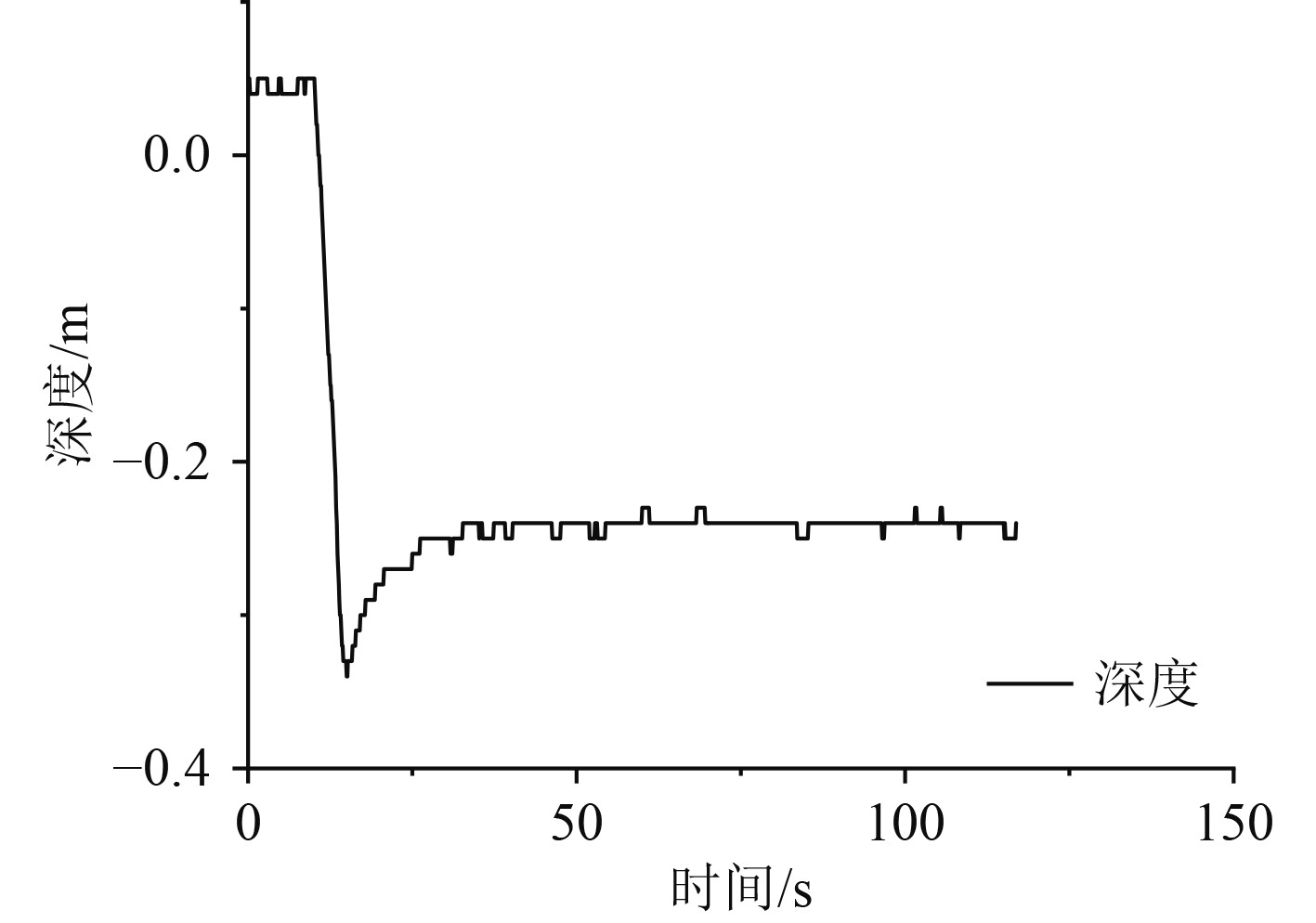
使用串级LADRC控制读取的定深控制曲线如图10所示。
|
图 10 串级LADRC深度测试 Fig. 10 Serial LADRC depth test |
由图9和图10可知,使用串级PID的水下机器人定深控制产生的抖动较多,下潜控制时产生的超调量也比较大;使用串级LADRC的水下机器人定深控制产生的抖动较少,下潜控制时产生的超调量也比较小。
4 结 语本文建立八推进器ROV的数学模型,对水下机器人进行了运动学与动力学分析。针对在传统串级PID控制下,ROV定深控制不稳定的问题,提出使用PSO算法自动调参的串级LADRC控制器用于ROV的定深控制,仿真结果表明:
1) 与串级PID相比,串级LADRC能够明显减少系统的超调量和调节时间。而使用PSO算法调参的LADRC能够进一步提高系统响应速度,减少超调量和调节时间
2) 使用PSO算法自动调参的串级LADRC控制器用于ROV定深控制,能够提高参数整定效率减少超调量和系统响应时间。
| [1] |
Luis GovindaGarcía-Valdovinos, Fonseca-Navarro F, Aizpuru-Zinkunegi J, et al. Neuro-sliding control for underwater ROV's subject to unknown disturbances[J]. Sensors, 2019, 19(13): 2943. DOI:10.3390/s19132943 |
| [2] |
申雨轩. 基于自抗扰控制器的水下机器人控制[D]. 大庆: 东北石油大学, 2015.
|
| [3] |
邵克勇, 申雨轩. 小波神经网络自抗扰控制器在水下机器人深度控制中的应用[J]. 计算机与现代化, 2015(6): 23-26. DOI:10.3969/j.issn.1006-2475.2015.06.005 |
| [4] |
GAO Z. Scaling and bandwidth-parameterization based controller tuning[C]//IEEE, 2003.
|
| [5] |
陈东军, 吴家鸣. 带缆水下机器人控制仿真模拟与水动力分析[J]. 船舶力学, 2020, 24(2): 170-178. |
| [6] |
漆小舟, 缪爱琴, 万德成. 水下潜器航行水动力导数CFD计算[J]. 水动力学研究与进展(A辑), 2018, 33(3): 297-304. |
| [7] |
高婷, 庞永杰, 王亚兴, 等. 水下航行器水动力系数计算方法[J]. 哈尔滨工程大学学报, 2019.
|
| [8] |
HU Jin hui, HU Da bin, XIAO Jian bo. Research on the method of numerical calculation for hydrodynamic parameters of underwater vehicle[J]. Applied Mechanics and Materials, 2014, 2983: 121-126. |
| [9] |
李杰, 齐晓慧, 万慧, 等. 自抗扰控制: 研究成果总结与展望[J]. 控制理论与应用, 2017, 34(3): 281-295. |
| [10] |
王震. 缆控水下机器人水动力建模与运动控制研究[D]. 济南: 山东大学, 2019.
|
| [11] |
韩京清. 自抗扰控制技术[J]. 前沿科学, 2007(1): 24-31. DOI:10.3969/j.issn.1673-8128.2007.01.004 |
| [12] |
Esperanza García-Gonzalo, Juan Luis Fernández-Martínez. Particle swarm optimization and inverse problems[M]// Combining Soft Computing and Statistical Methods in Data Analysis. 2010.
|
| [13] |
EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]// Mhs95 Sixth International Symposium on Micro Machine & Human Science. IEEE, 2002.
|
| [14] |
SHI Y . A modified particle swarm optimizer[C]// Proc of IEEE Icec Conference. 1998.
|
| [15] |
尹晖, 熊治国, 高翔, 等. 基于PSO的自抗扰飞行控制律参数优化方法[J]. 空军工程大学学报(自然科学版), 2013, 14(3): 19-22+32. DOI:10.3969/j.issn.1009-3516.2013.03.005 |
 2022, Vol. 44
2022, Vol. 44
