0 引　言

无人水下航行器（UUV）作为一种水下无人智能移动平台，在海洋资源探索、海洋科学考察和军事等领域有着广阔的应用前景和巨大的潜在价值。然而，现有的无人水下航行器采用的桨式推进器存在效率低、结构尺寸大、运动性能差等问题，严重制约了无人水下航行器的性能。通过模仿海龟、企鹅等海洋生物的鳍状肢及其运动方式而发展起来的仿生扑翼推进装置及无人水下航行器具有更高的推进效率和机动性，具有更广阔的应用前景^[1]。

国内外对仿生扑翼水下推进开展了许多研究。Traintafyllou等^[2]研制了扑翼推进装置并开展了实验测试，研究了影响扑翼水下推进性能的相关因素；杨璞^[3]通过数值计算对仿生扑翼的推进机理进行了相关研究；丁浩等^[4]基于二自由度水下扑翼运行开展了其推进效率的评估；宋保维等^[5]研究了摆动频率和摆动幅值对扑翼性能的影响；曹永辉等^[6]以多种基准翼型组合成的混合翼型作为扑翼的翼型，并对采用该翼型的二自由度扑翼的推进性能进行了研究；杜晓旭等^[7]研究了二自由水下扑翼的4种扑动方式对其推进性能的影响。

由上述研究可知，现有研究工作主要围绕运动参数、翼型等对其性能的影响展开，且扑翼的运动自由度多为二自由度，缺乏对不同自由度扑翼推进装置的性能对比研究。为了进一步探索水下扑翼推进相关机理，本文采用计算流体力学的方法，以水下刚性扑翼为研究对象，利用动网格技术对单自由度、二自由度和三自由度扑翼的性能进行对比研究，为无人水下航行器仿生扑翼推进装置的设计提供参考。

1 运动模型 1.1 运动的分解和简化

根据对海龟的观测，其前肢的划水动作可分解为3个基本动作^[8]，如图1所示。绕前肢关节处的转动，即绕图中所示X轴的转动，称为翻转运动，垂直于前肢翼面的挥动，即绕图中所示Y轴的转动，称为拍水运动；沿前进方向的划动，即绕图中所示Z轴的转动，称为划水运动。

对于单自由度扑翼则只考虑翻转运动，对于二自由度扑翼则同时考虑翻转运动和拍水运动，对于三自由度扑翼需同时考虑3个运动。

为简化计算，将扑翼视为刚性体，不考虑其在流体作用下产生的弹性形变。定义扑翼的3个基本运动均为简谐运动，则各运动的角位移表达式为：

$ \left\{ \begin{gathered} \alpha (t) = {\alpha _0}\sin (2\text{π} {f_\alpha }t + {\alpha _1})，\\ \beta (t) = {\beta _0}\sin (2\text{π} {f_\beta }t + {\beta _1})，\\ \gamma (t) = {\gamma _0}\sin (2\text{π} {f_\gamma }t + {\gamma _1}) 。\\ \end{gathered} \right. $

(1)

式中： $ \alpha $ ， $ \beta $ ， $ \gamma $ 分别为翻转运动角位移、拍水运动角位移和划水运动角位移； $ {\alpha _0} $ ， $ {\beta _0} $ ， $ {\gamma _0} $ 分别为各运动的幅值； $ {f_\alpha } $ ， $ {f_\beta } $ ， $ {f_\gamma } $ 为各分运动的运动频率； $ {\alpha _1} $ ， $ {\beta _1} $ ， $ {\gamma _1} $ 为各分运动的起始相位角，通过该值可以改变扑翼产生推力和升力的方向，具有改变水下航行器运行姿态的作用。

由上述角位移表达式可获得计算分析所需的各分运动的角速度表达式为：

$ \left\{ \begin{gathered} {\omega _\alpha }(t) = 2\text{π} {f_\alpha }{\alpha _0}\cos (2\text{π} {f_\alpha }t + {\alpha _1})，\\ {\omega _\beta }(t) = 2\text{π} {f_\beta }{\beta _0}\cos (2\text{π} {f_\beta }t + {\beta _1})，\\ {\omega _\gamma }(t) = 2\text{π} {f_\gamma }{\gamma _0}\cos (2\text{π} {f_\gamma }t + {\gamma _1})。\\ \end{gathered} \right. $

(2)

1.2 运动参数

仅对正常状态下扑翼的运行性能进行研究，不涉及特殊状态下（如急转弯、快速上浮等），因此扑翼的角速度表达式中的各参数经简化后设置如下：不考虑初始相位角的影响，则 $ {\alpha _1} $ ， $ {\beta _1} $ ， $ {\gamma _1} $ 取值均为0；各分运动的频率 $ {f_\alpha } $ ， $ {f_\beta } $ ， $ {f_\gamma } $ 均相同，取值为0，2，4，6，8，10；扑翼的翻转幅值 $ {\alpha _0} $ =±30°，拍水幅值 $ {\beta _0} $ =±10°，划水幅值 $ {\gamma _0} $ =±10°。

1.3 无量纲处理

为了便于比较和研究，对计算获得的升力及推力进行无量纲化处理。

推力系数：

$ {C_T} = \frac{{{F_T}}}{{1/2\rho {v^2}S}}，$

(3)

升力系数：

$ {C_L} = \frac{{{F_L}}}{{1/2\rho {v^2}S}}。$

(4)

式中： $ {F_T} $ 和 $ {F_L} $ 分别为推力和升力； $\ \rho $ 为流体密度； $ v $ 为来流速度； $ S $ 为扑翼的表面积。

2 数值计算 2.1 控制方程

二维不可压缩流动湍流问题的运动控制方程如下：

$ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0，$

(5)

$ \frac{{\partial {u_i}}}{{\partial {x_i}}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\gamma + {\gamma _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right]。$

(6)

式中： $ {u_i} $ 为流体运动速度； $ {x_i} $ 空间坐标； $ p $ 为流体压强； $ t $ 为时间； $ \gamma $ 为运动黏度； $ {\gamma _t} $ 为湍流黏度； $k$ 为湍流动能； $\varepsilon $ 为湍动能耗散率。

2.2 湍流模型

由于海龟的水下运动原理与与鸟类和昆虫等的飞行原理相似，因而推断模仿海龟运动的扑翼在运动过程中可能存在涡的生成和脱落。为了更好地捕捉这一特征，选择Realizable $k - \varepsilon $ 湍流模型，其相应的方程如下：

湍流动能 $k$ 方程。

$ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} + \rho \varepsilon，$

(7)

耗散率 $\varepsilon $ 方程

$ \begin{split}\rho \frac{{{\rm{D}}\varepsilon }}{{{\rm{D}}t}} = \frac{\partial }{{\partial {x_j}}} & \left[ {\left( {\mu + \frac{{\mu t}}{{\sigma \varepsilon }}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {c_1}S\varepsilon - \rho {c_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + \\ & \qquad \quad {c_{1\varepsilon }}\frac{\varepsilon }{k}{c_{3\varepsilon }}{G_b}。\end{split}$

(8)

2.3 计算域及网格

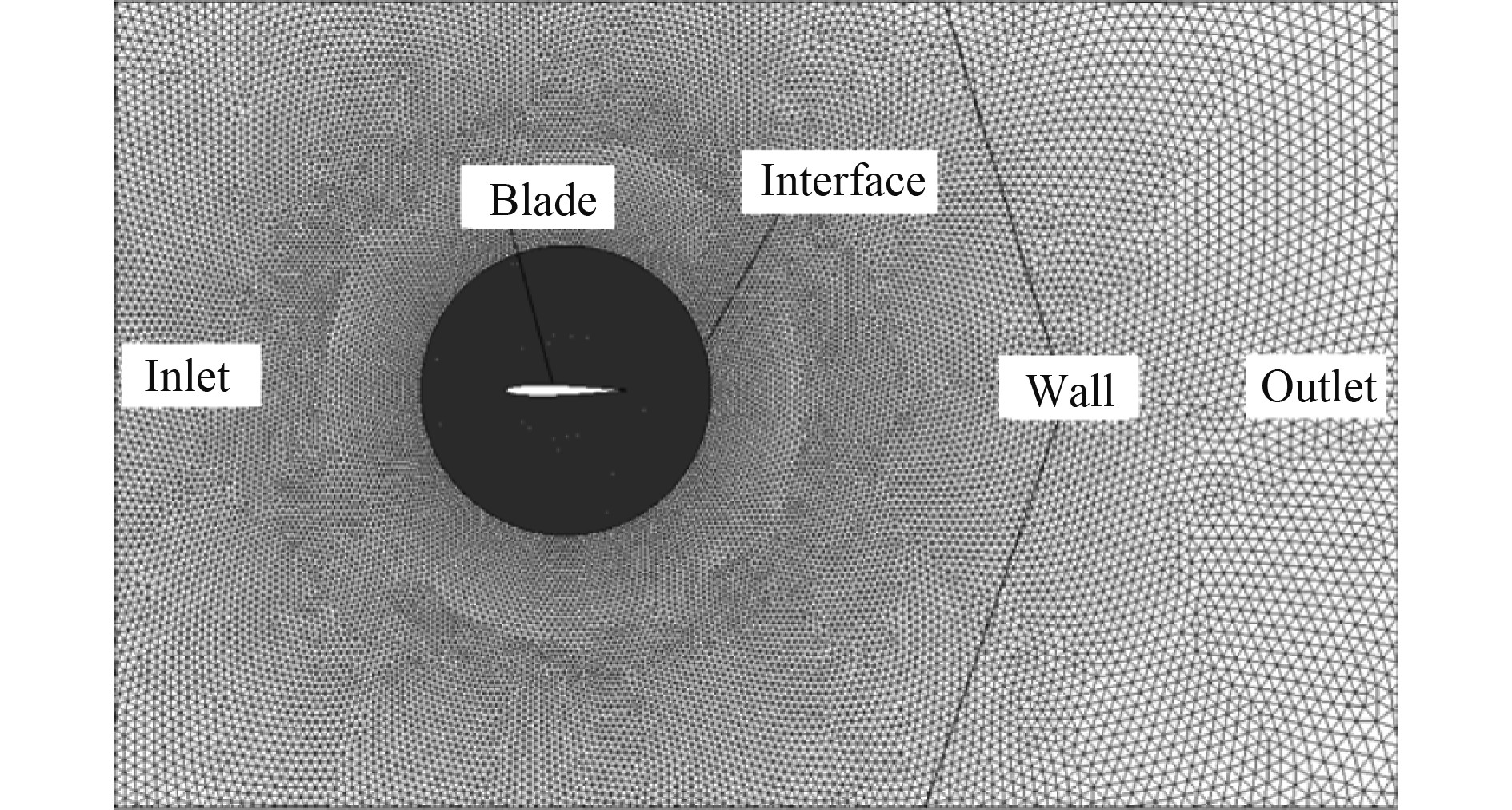
计算域尺寸为1 500 mm×800 mm；入口边界（Inlet）设置为velocity inlet；出口边界（Outlet）设置：outflow；其余壁面（Wall）设置：wall。

计算域网格采用非结构化的三角形网格，对扑翼近壁面网格进行细化处理。设置交界面（Interface）以区分不同流场域，同时采用弹簧光顺法和局部重划法对变形后的网格进行处理，以控制动网格的更新质量^[9]。其中，对于弹簧光顺，设定弹性系数（spring constant factor）为0.2，边界点松弛因子（boundary node relaxation）为0.5；对于局部重划，开启Size Function和Must Improve Skewness，根据初始网格的大小合理设置变形网格重划分的标准。计算域网格及边界条件设置如图2所示。

2.4 计算参数设置

采用单精度基于压力的分离式求解器进行计算，压力与速度修正方法采用SIMPLE方法，参数的离散化采用二阶迎风差分格式。来流速度为0.5 m/s，流体介质为水，密度为998.2 kg/m³，动力粘性系数为0.01 003 Pa·s。

3 计算结果分析

本文扑翼为平直刚性翼，截面为标准翼型NACA0010，弦长100 mm，展长200 mm，扑翼翻转运动中心点距离翼前缘距离为20 mm。

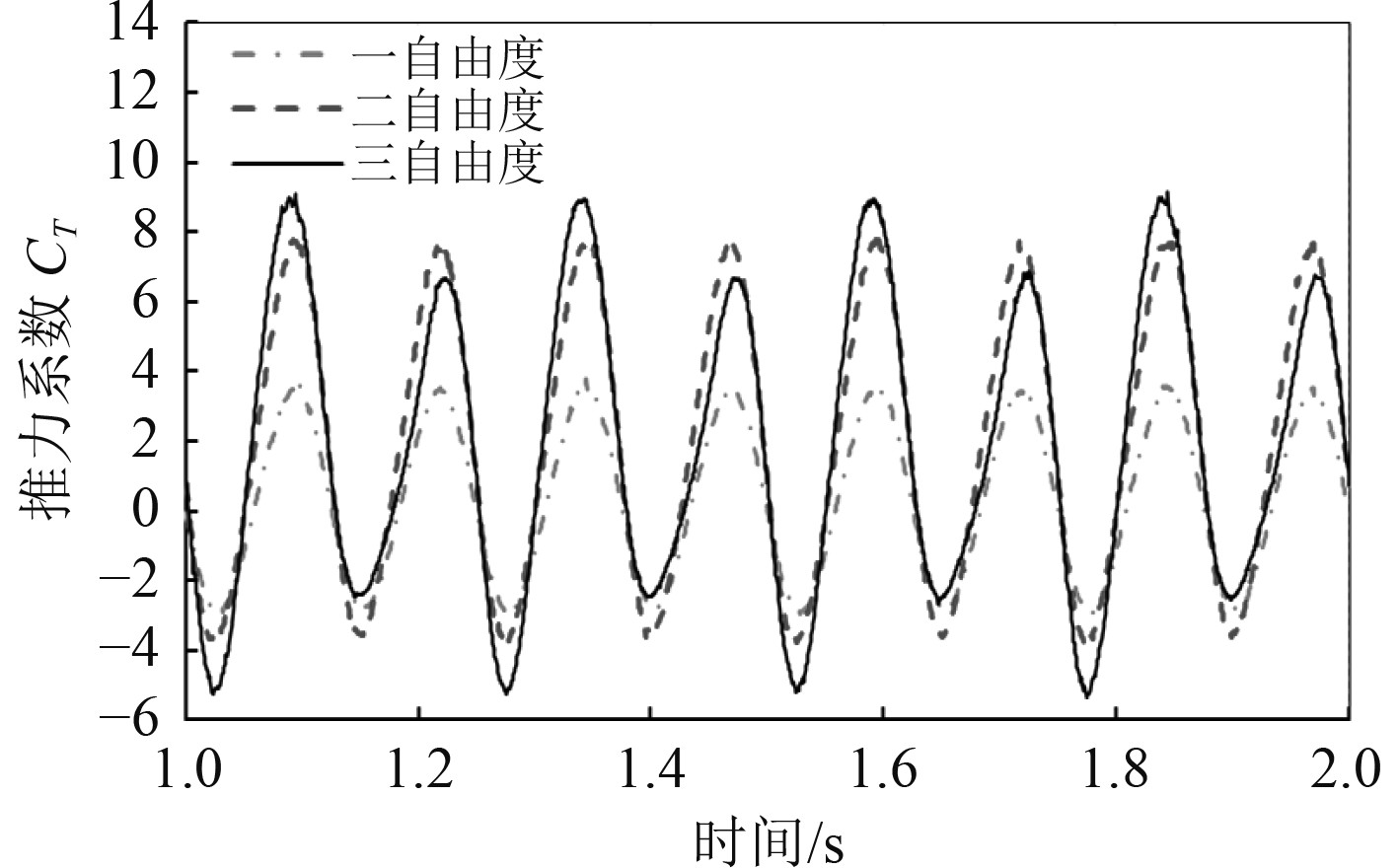
3.1 运动自由度对推力的影响

计算得到运动频率为4 Hz的采用不同自由度运动的扑翼产生推力变化如图3所示。

计算得到不同自由度扑翼在不同运动频率下单个运动周期的峰值推力和平均推力，如表1所示。

由计算结果和推力系数变化可知：

1）对于采用简谐运动的扑翼，其产生推力的变化也呈现简谐波动，且推力的变化频率是运动频率的2倍；

2）与单自由度和二自由度扑翼相比，三自由度扑翼在单个运动周期内产生的推力的幅值存在明显的不一致；

3）二自由度扑翼和三自由度扑翼产生的推力对运动频率更加敏感，表现推力随频率显著增大，故多自由度扑翼推进装置更适宜在恶劣海况和需要较高机动性的场合使用；

4）在相同运动频率下，增加扑翼的运动自由度，可以提高扑翼的峰值推力和平均推力。增加拍水运动后的二自由度扑翼所产生的推力显著增加（峰值推力增幅约为1.2倍，平均推力增幅约为1.6倍），而增加划水运动后的三自由度扑翼所产生的推力与二自由度扑翼相比并不显著（峰值推力增幅约为18%，平均推力增幅约为5%）。

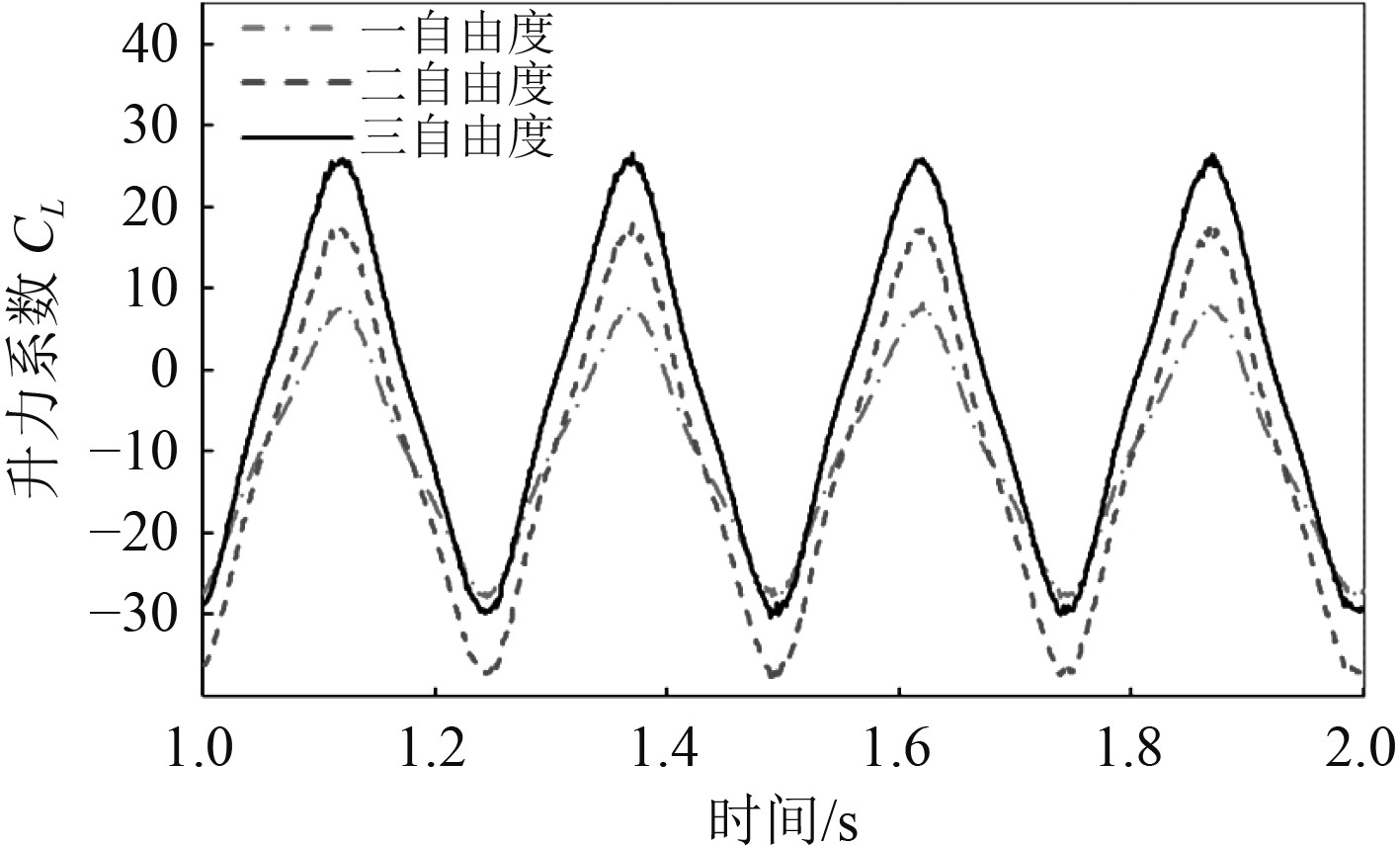
3.2 运动自由度对升力的影响

计算得到运动频率为4 Hz的采用不同自由度运动的扑翼产生升力变化如图4所示。

计算得到不同自由度扑翼在不同运动频率下单个运动周期的峰值升力和平均升力，如表2所示。

由计算结果和升力系数变化可知：

1）对于采用简谐运动的扑翼，其产生升力的变化也呈现简谐波动，且升力的变化频率与运动频率的相同。

2）二自由度和三自由度扑翼所产生的升力对运动频率的变化更加敏感，表现为升力的峰值随频率升高得到显著提升。

3）单自由度扑翼和二自由度扑翼在一个运动周期产生几乎不产生升力。三自由度扑翼虽然升力峰值较二自由度扑翼略微减小，但其升力系数曲线呈非对称分布，使得在单个周期内的平均升力显著提高了。

3）在相同频率下，二自由度扑翼运动产生的峰值升力最大，其次是三自由度扑翼，单自由度扑翼的峰值升力最小。

3.3 运动自由度对流场的影响

通过对不同自由度扑翼运动过程中的流场进行分析，可以增强对扑翼运动机理的认识。通过计算获得扑翼在一个运动周期结束时的流场矢量图如图5所示。

由速度矢量图可知：

1）不同自由度扑翼在运动过程中均产生了相似的尾涡和前沿涡；

2）二自由度扑翼运动时翼面的流动速度较单自由度扑翼显著提高，且其前沿涡和尾涡的影响范围更广，因而二自由度扑翼的性能较单自由度扑翼显著提高；

3）三自由度扑翼由于增加了与流动方向相同的划水运动，使得翼面附近的流体流速反而比二自由度扑翼略有降低，表现为推力和升力的峰值略微下降；但其尾涡的在纵平面内的影响范围更广，这可能是导致其平均升力显著提高的原因。

4 结　语

通过对海龟鳍状前肢的运动进行分析，建立了基于简谐运动的扑翼运动模型，利用动网格技术和CFD技术开展了不同运动自由度水下刚性扑翼性能的对比研究。研究结果表明：

1）随着运动自由度的增加，扑翼的性能均得到一定程度的增强，但二自由度扑翼是最经济的推进运动方式。表现为：其产生的推力和峰值推力较单自由度扑翼显著增加，与三自由度扑翼相差不大，且其机构的复杂程度适中，而计算中出现升力不足的问题可通过调节运动参数得到有效处理，故应为仿生扑翼水下航行器首选；

2）单自由度扑翼产生的推力虽稍小于二自由度扑翼，但其驱动结构简单，可通过提高运动频率的方式来弥补推力的不足，故在不要求高机动性的场合亦可采用；

3）扑翼运动过程中产生的前沿涡和尾涡随着运动自由度的增加，其影响范围显著增大。涡的存在，改变了扑翼附近的流场分布，从而对扑翼的性能产生了显著影响。