2. 自然资源部北海局,山东 青岛 266061
2. North China Sea Branch, Ministry of Natural Resources, Qingdao 266061, China
随着科技发展及海洋资源开发,水下机器人被广泛运用于水下勘探、作业及海上救援。部分水下机器人装载超过其自由度的推进器数量以保证其高效的运动及作业效率[1-2],由于推进器数量超过自由度数量,当控制器给出目标推力与力矩时,推力分配算法需要给出合适的每个推进器的推力值大小。目标推力与力矩较小时,运用推力分配算法能够实现各个推进器合成的实际推力与力矩和目标值相等;目标推力与力矩较大,运用推力分配算法后,部分推进的推力会超出限制范围,这类问题称为饱和问题。
推力分配算法可以分为直接法和伪逆法[3]。直接法[4-5]在水平面和垂直面能够分别实现控制,按照空间结构,分别从水平面和垂直面目标推力与力矩反推推进器推力大小,算法简洁易用,但是需要在水下机器人设计时考虑推进器的空间布局,联合控制较为复杂,且不能解决饱和问题。伪逆法[6]计算推力转换矩阵的伪逆,通过目标控制推力和力矩伪逆矩阵计算各个推进器的推力,需要通过放缩或削峰的方法解决饱和问题,这样将会导致各个推进器合成的实际推力与力矩和目标值差距较大。
本文利用可行方向法解决推力分配的饱和问题。首先,利用水下机器人推进器的空间布置建立了通用的ROV推力转换矩阵。然后,通过最小化目标推力与力矩将推力分配问题转化为二次规划问题并利用可行方向法求解该二次规划问题。最后,利用仿真实验比较了伪逆法和可行方向法输出的推力和力矩及其合成后和目标值相比较的结果。
1 水下机器人推进系统数学建模 1.1 坐标系与水下机器人推进器空间布置扁平式的水下机器人综合了遥控作业型潜水器(ROV)与无人自主潜水器(AUV)的特点,具有高效的响应速度和稳定性[7]。本文以扁平式尾主推多螺旋桨的水下机器人为实验对象。
如图1所示,建立全局坐标系
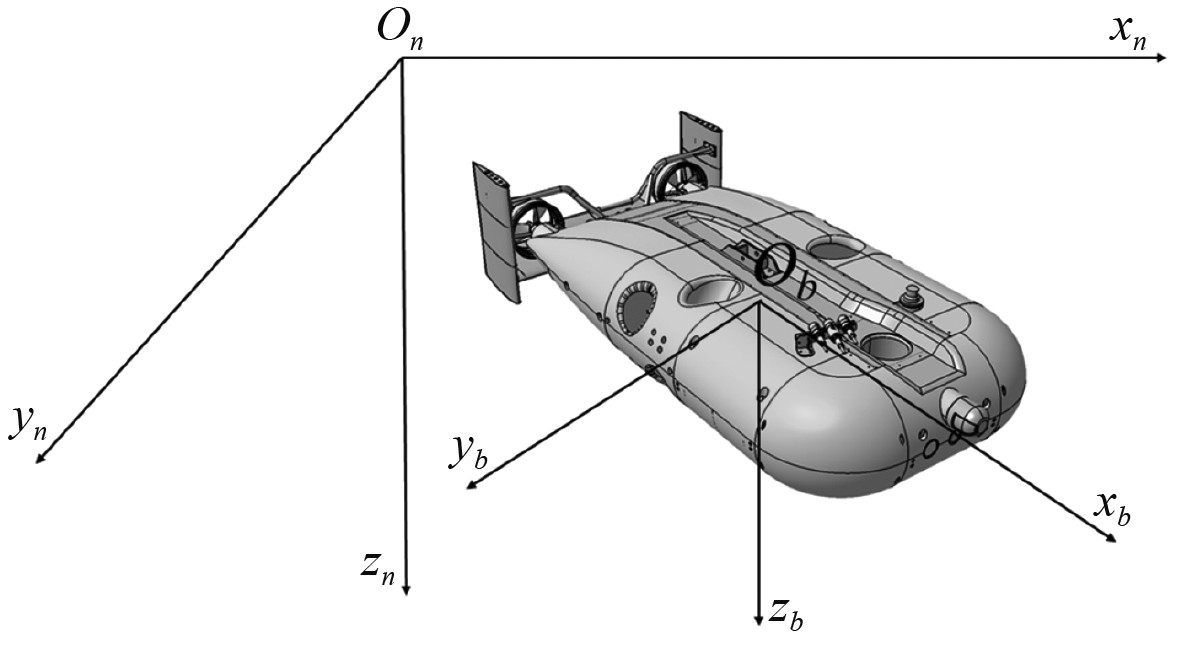
|
图 1 全局坐标系和随体坐标系 Fig. 1 North-East-Down coordinate system and body coordinate system |
图2为水下机器人推进器8个推进器的空间布置。水下机器人的推进器与重心的相对位置、推力方向和推力最值如表1所示,其中推进器1、推进器2和推进器3是主推进器。
|
|
表 1 推进器空间布置 Tab.1 The spatial arrangement of thrusters |
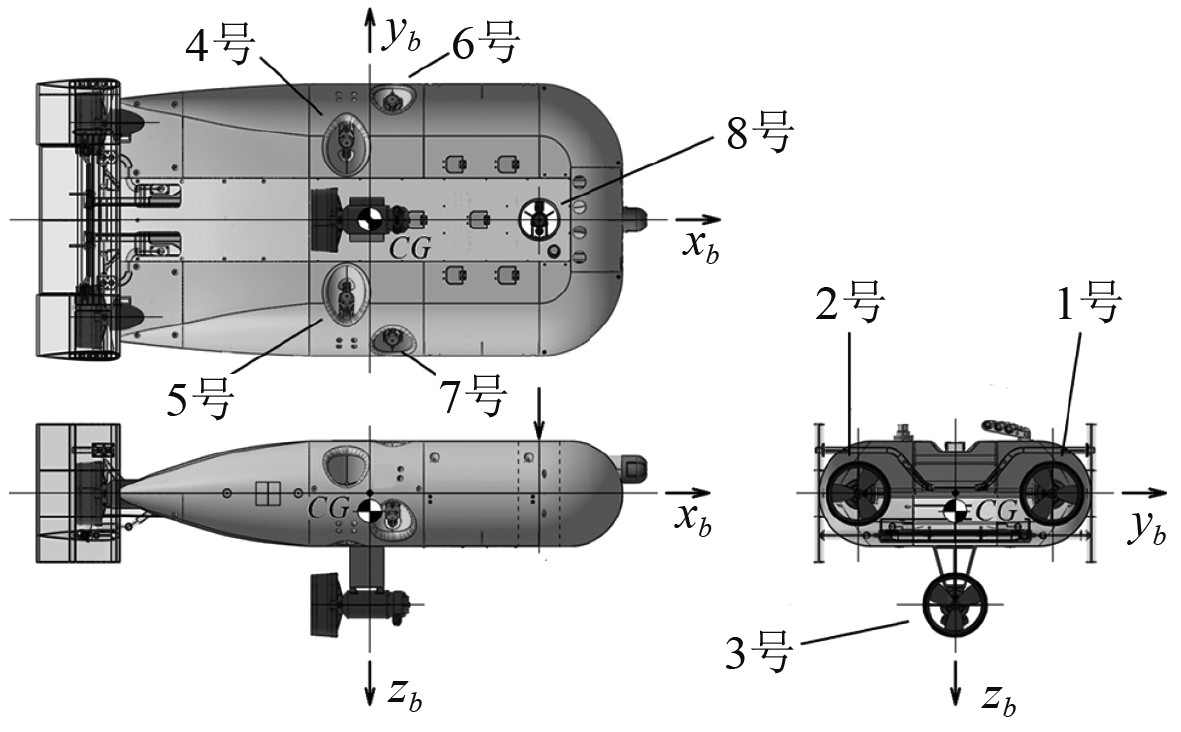
|
图 2 推进器空间布置 Fig. 2 The spatial arrangement of thrusters |
水下机器人的动力学方程[9]为:
| $ {{{\boldsymbol{M}}{\boldsymbol{\nu}} + {\boldsymbol{C}}}}{\text{(}}{{{\boldsymbol{\nu}} }}{\text{)}}{{{\boldsymbol{\nu}} + {\boldsymbol{D}}}}{\text{(}}{{{\boldsymbol{\nu }}}}{\text{)}}{{{\boldsymbol{\nu}} + {\boldsymbol{g}}}}{\text{(}}{{{\boldsymbol{\eta}} }}{\text{)}}{{ + }}{{{\boldsymbol{{g}}}}_0}{{ = {\boldsymbol{\tau}} + {\boldsymbol{w}}}}。$ | (1) |
式中:
| $ {{{\boldsymbol{\tau}} }} =[\,X \,\,\,Y \,\,\,Z\,\,\, K\,\,\,M\,\,\, N ]^{\text{T}}。$ | (2) |
式中:
当控制器在控制过程中,在每个控制时刻产生一个目标推力与力矩:
| $ {{{\boldsymbol{\bar \tau}} }} = [{\bar X}\,\,\,{\bar Y}\,\,\, {\bar Z}\,\,\, {\bar K} \,\,\,{\bar M} \,\,\,{\bar N} ]^{\text{T}}。$ | (3) |
式中:
然而水下机器人安装的主动控制器无法直接给出推力与力矩
水下推进系统数学模型主要与水下机器人的构造有关,设水下机器人主动控制器有n个推进器。
如图3所示,设第k个推进器中心的位置为
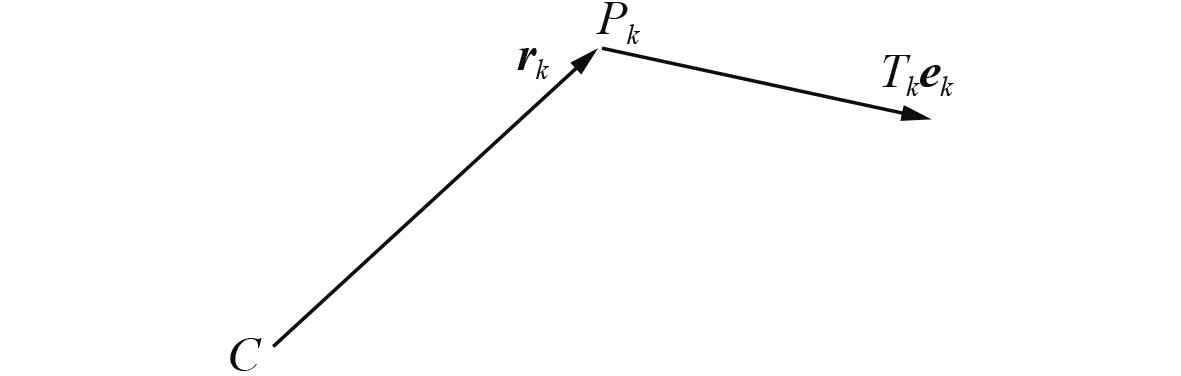
|
图 3 推进器位置及推力方向 Fig. 3 The position and direction of thruster |
| $ {{\boldsymbol{M}}_k} = {T_k}{{\boldsymbol{r}}_k} \times {{\boldsymbol{e}}_k}。$ | (4) |
将每个推力和力矩合成,可以用推力矢量和力矩矢量相加得到。主动控制力可用下式表示:
| $ [X\,\,\,Y \,\,\,Z]^{\text{T}} = \sum\limits_{k = 1}^n {{T_k}{{\boldsymbol{e}}_k}} , $ | (5) |
主动控制力矩可用下式表示:
| $ [K\,\,\,M \,\,\,N]^{\text{T}} = \sum\limits_{k = 1}^n {{T_k}{{\boldsymbol{r}}_k} \times {{\boldsymbol{e}}_k}} 。$ | (6) |
用
| $ {\boldsymbol{\tau }} = {\boldsymbol{B}} \cdot {\boldsymbol{T}}。$ | (7) |
式中:
| $ {\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_1}}& \cdots &{{{\boldsymbol{e}}_n}} \\ {{{\boldsymbol{r}}_1} \times {{\boldsymbol{e}}_1}}& \cdots &{{{\boldsymbol{r}}_n} \times {{\boldsymbol{e}}_n}} \end{array}} \right]_{n \times 6}}。$ | (8) |
在控制过程中,推力与力矩
| $ \begin{gathered} \min \qquad f({[{{\boldsymbol{T}}^{\text{T}}}\;{{\boldsymbol{s}}^{\text{T}}}]^{\text{T}}}) = \frac{1}{2}{{\boldsymbol{s}}^{\text{T}}}{\boldsymbol{Hs}},\\ {\text{s}}{\text{. t}}{\text{.}}\qquad {\boldsymbol{T}} \geqslant {{\boldsymbol{T}}_{\min }}, \\ \qquad \quad - {\boldsymbol{T}} \geqslant - {{\boldsymbol{T}}_{\max }}, \\ \qquad \quad {\boldsymbol{BT}} + {\boldsymbol{s}} = \overline {\boldsymbol{\tau }} 。\\ \end{gathered} $ | (9) |
式中:
将式 (9) 约束条件中的2个不等式合并,改写为:
| $ \begin{gathered} \min \qquad f({\boldsymbol{x}}) = \frac{1}{2}{{\boldsymbol{s}}^{\text{T}}}{\boldsymbol{Hs}},\\ {\text{s}}{\text{. t}}{\text{.}}\qquad {\boldsymbol{A}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{T}} \\ {\boldsymbol{T}} \end{array}} \right] \geqslant {\boldsymbol{b}}, \\ \qquad \quad \,\,\, \left[{\boldsymbol{B}}\,\,\,{{{\boldsymbol{I}}_6}} \right]{\boldsymbol{x}} = \overline {\boldsymbol{\tau }} 。\\ \end{gathered} $ | (10) |
式中:
由于推进器的推力是有约束的,可采用可行方向法求取式 (10) 的最优解。可行方向法的主要思想是从可行点出发,沿着下降的可行方向搜索,求出使得目标函数下降的新的可行点,求解流程如图4 所示。
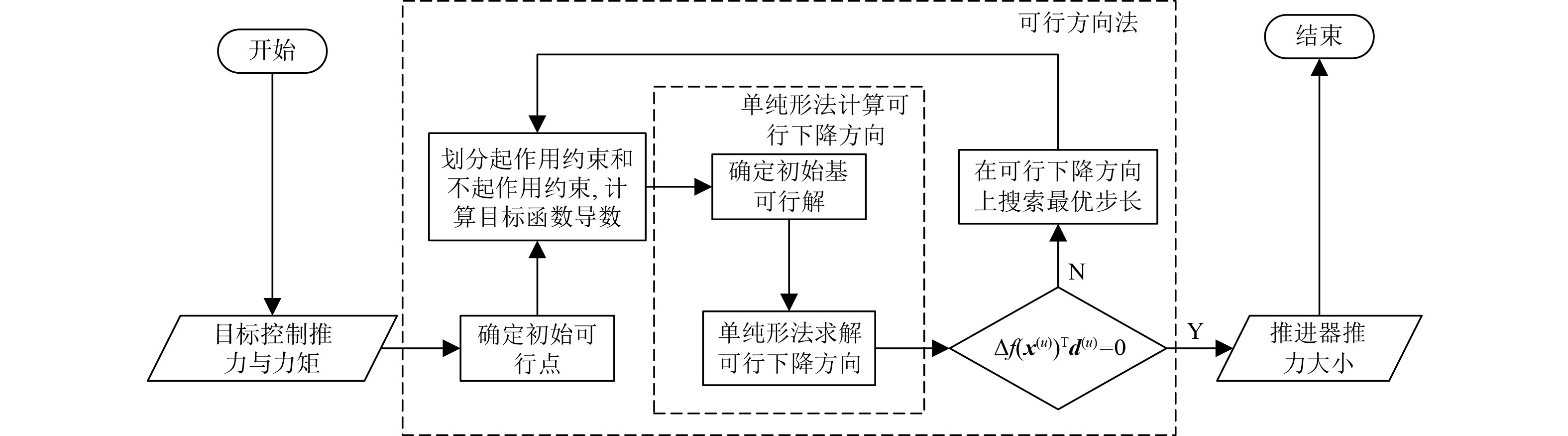
|
图 4 可行方向法流程图 Fig. 4 Flow chart of feasible direction method |
具体计算步骤[10]如下:
1)确定初始可行点
2)在点
3)求下降的可行方向
| $ \begin{gathered} \min \qquad \nabla f{({{\boldsymbol{x}}^{(u)}})^{\text{T}}}{\boldsymbol{d}} = [{{\boldsymbol{0}}_{n \times 1}}\;{{\boldsymbol{s}}^{\text{T}}}]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{\boldsymbol{H}} \end{array}} \right]{\boldsymbol{d}} ,\\ {\text{s}}{\text{. t}}{\text{.}}\qquad {{\boldsymbol{A}}_1}{\boldsymbol{d}} \geqslant {\boldsymbol{0}}, \\ \qquad \quad \,\,\, \left[{\boldsymbol{B}}\,\,\,{{{\boldsymbol{I}}_6}} \right]{\boldsymbol{d}} = {\boldsymbol{0}}, \\ \qquad \quad \,\,\, {- 1} \leqslant {d_j} \leqslant 1,j = 1, \cdots ,n + 6 。\\ \end{gathered} $ | (11) |
求解线性规划即得最优下降的可行方向
4)如果
5)找到下降的可行方向后,计算前进的步长
| $ {\lambda _{\max }} = \left\{ {\begin{array}{*{20}{l}} {\min \left\{ {\frac{{\widehat {{b_i}}}}{{\widehat {{d_i}}}}|\widehat {{d_i}} < 0} \right\},}&{\widehat {\boldsymbol{d}}\not \geqslant 0} ,\\ {\infty ,}&{\widehat {\boldsymbol{d}} \geqslant 0} 。\end{array}} \right. $ | (12) |
在
| $ \begin{gathered} \min \qquad f({{\boldsymbol{x}}^{(u)}} + \lambda {{\boldsymbol{d}}^{(u)}}) ,\\ {\text{s}}{\text{. t}}{\text{.}}\qquad 0 \leqslant \lambda \leqslant {\lambda _{\max }} 。\\ \end{gathered} $ | (13) |
得到最优解
6)置
对于式 (11) 所示的
| $ \begin{gathered} \min \qquad [{{\boldsymbol{0}}_{n \times 1}}\;{{\boldsymbol{s}}^{\text{T}}}]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{\boldsymbol{H}} \end{array}} \right]{\boldsymbol{\delta }} ,\\ {\text{s}}{\text{. t}}{\text{.}}\qquad - {{\boldsymbol{A}}_1}{\boldsymbol{\delta }} \leqslant - {{\boldsymbol{A}}_1} \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}, \\ \qquad \quad \,\,\, \left[{\boldsymbol{B}}\,\,\,{{{\boldsymbol{I}}_6}} \right]{\boldsymbol{\delta }} = \left[ {\boldsymbol{B}}\,\,\,{{{\boldsymbol{I}}_6}} \right] \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}, \\ \qquad \quad \,\,\, 0 \leqslant {\delta _j} \leqslant 2,j = 1, \cdots ,14。\\ \end{gathered} $ | (14) |
式中:
引进
| $ \begin{gathered} \min \qquad \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{0}}_{n \times 1}}}&{{{\boldsymbol{s}}^{\text{T}}}}&{{{\boldsymbol{0}}_{q \times 1}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}}&{\boldsymbol{0}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{\boldsymbol{H}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{\boldsymbol{0}}&{\boldsymbol{0}} \end{array}} \right]{\boldsymbol{\delta }} ,\\ {\text{s}}{\text{. t}}{\text{.}}\qquad \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - {{\boldsymbol{A}}_1}} \\ {{{\boldsymbol{I}}_{(n + 6)}}} \end{array}}&{{{\boldsymbol{I}}_q}} \end{array}} \right]{\boldsymbol{\delta }} = \left[ {\begin{array}{*{20}{c}} { - {{\boldsymbol{A}}_1} \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}} \\ {2 \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}} \end{array}} \right], \\ \qquad \quad \,\,\, {\text{ }}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{B}}&{{{\boldsymbol{I}}_6}}&{{{\boldsymbol{0}}_{q \times 6}}} \end{array}} \right]{\boldsymbol{\delta }} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{B}}&{{{\boldsymbol{I}}_6}} \end{array}} \right] \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}, \\ \qquad \quad \,\,\, {\text{ }}{\boldsymbol{\delta }} \geqslant {\boldsymbol{0}}。\\ \end{gathered} $ | (15) |
式中,
式 (15) 已经化为单纯形方法的标准形式。然而,使用单纯性法还有一个前提:找到初始基本可行解。为了寻找初始基本可行解,先寻找一个可行解,然后根据可行解通过变换得到基本可行解。
将式 (15) 改写为
| $ \begin{gathered} \min \qquad {\boldsymbol{c\delta }} ,\\ {\text{s}}{\text{. t}}{\text{.}}\qquad {{\boldsymbol{A}}_s}{\boldsymbol{\delta }} = {{\boldsymbol{b}}_s}, \\ \qquad \quad \,\,\,{\text{ }}{\boldsymbol{\delta }} \geqslant {\boldsymbol{0}}。\\ \end{gathered} $ | (16) |
式中:
| $ {{\boldsymbol{A}}_s} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - {{\boldsymbol{A}}_1}} \\ {{{\boldsymbol{I}}_{(n + 6)}}} \end{array}}&{{{\boldsymbol{I}}_q}} \\ {\begin{array}{*{20}{c}} {\boldsymbol{B}}\,\,\,\,\,\,{{{\boldsymbol{I}}_6}} \end{array}}&{{{\boldsymbol{0}}_{q \times 6}}} \end{array}} \right], $ | (17) |
| $ {{\boldsymbol{b}}_s} = \left[ {\begin{array}{*{20}{c}} { - {{\boldsymbol{A}}_1} \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}} \\ {2 \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}} \\ {\left[ {\begin{array}{*{20}{c}} {\boldsymbol{B}}&{{{\boldsymbol{I}}_6}} \end{array}} \right] \cdot {{\boldsymbol{I}}_{(n + 6) \times 1}}} \end{array}} \right]。$ | (18) |
将
| $ {{\boldsymbol{A}}_s} = \left[ {{{\boldsymbol{p}}_1},{{\boldsymbol{p}}_1}, \ldots ,{{\boldsymbol{p}}_{(n + l) + 6 + (n + l)}}} \right]。$ | (19) |
设
| $ \sum\limits_{i = 1}^s {{\gamma _i}{{\boldsymbol{p}}_i} = 0} ,$ | (20) |
构造一个点
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat \delta }_i} = {x_i} - \alpha {\gamma _i},}&{i = 1, \ldots ,s,} \\ {{{\hat \delta }_i} = 0,}&{i = s + 1, \ldots ,(n + l) + 6 + (n + l)。} \end{array}} \right. $ | (21) |
式中,
通过观察式 (15), 可以发现
| $ {\boldsymbol{\delta}} ={[\stackrel{(n+6)个1}{\overbrace{1,1,\dots ,1}},\stackrel{l个0}{\overbrace{0,0,\dots ,0}},\stackrel{(n+6)个1}{\overbrace{1,1,\dots ,1}}]}^{\text{T}} $ | (22) |
是一个可行解。利用式 (22) 所示的可行解,通过上述变换方法可以获得一个基本可行解。然后就可以利用单纯形法求解。式 (13) 所示的一元二次优化问题可以直接用求导的方法求解。
3 仿真验证 3.1 参数选取及目标值推力转换矩阵
根据目标推力与力矩,分别采用伪逆法和可行方向法求解每个推进器推力的大小,然后根据式 (7) 可以计算得到推力与力矩。
图5 为通过伪逆法和可行方向法计算得到的推进器推力。通过原始伪逆法计算得到的推进器推力会超出推进器的推力上下限,这里采用放缩法处理伪逆法的饱和问题。可以看出2种方法计算得到所有的推进器的推力都未超过其上下限。
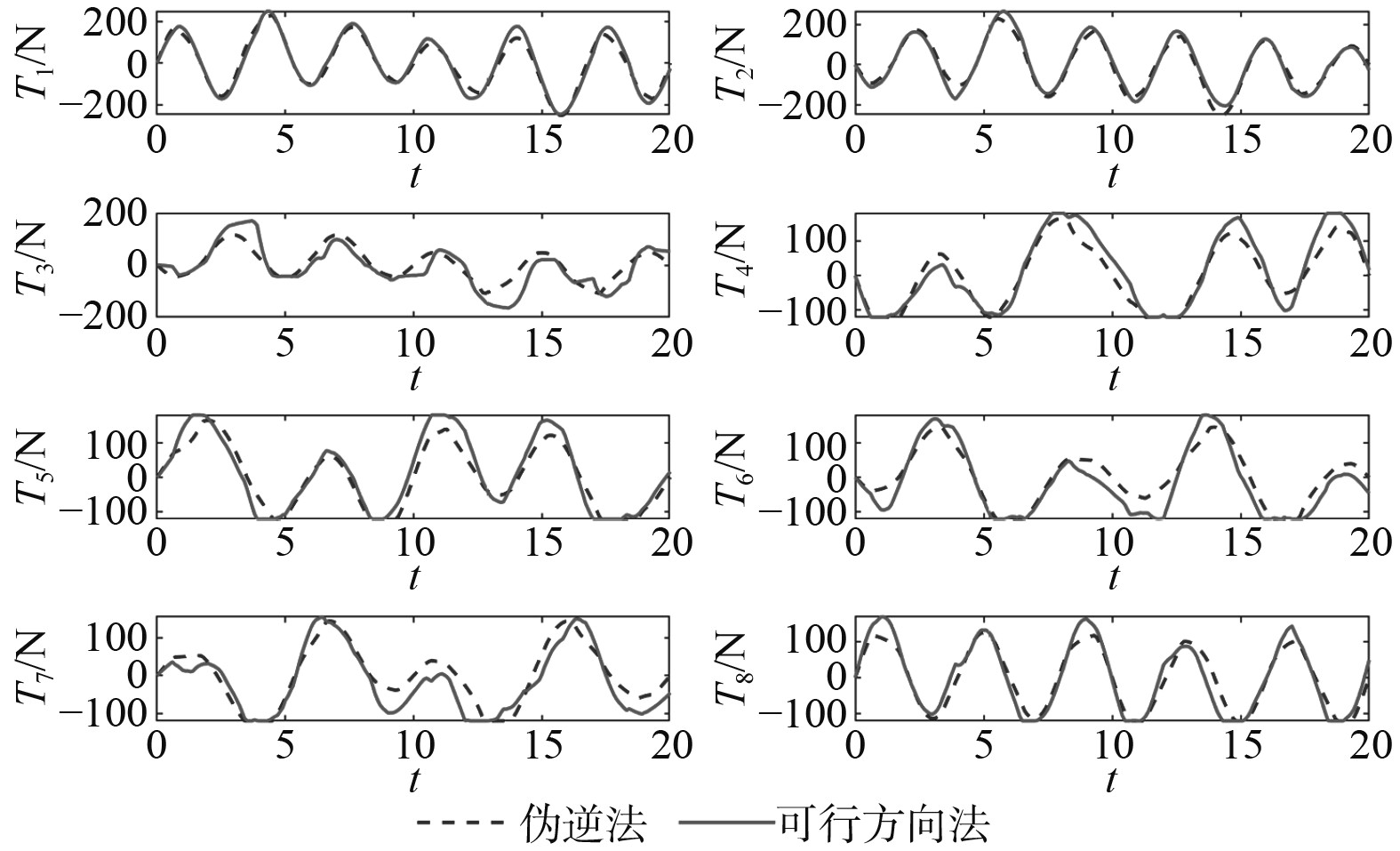
|
图 5 伪逆法与可行方向法得到的推进器推力 Fig. 5 The thruster thrusts obtained from pseudo inverse method and feasible direction method |
图6为用伪逆法与可行方向计算得到推进器推力合成得到推力与力矩
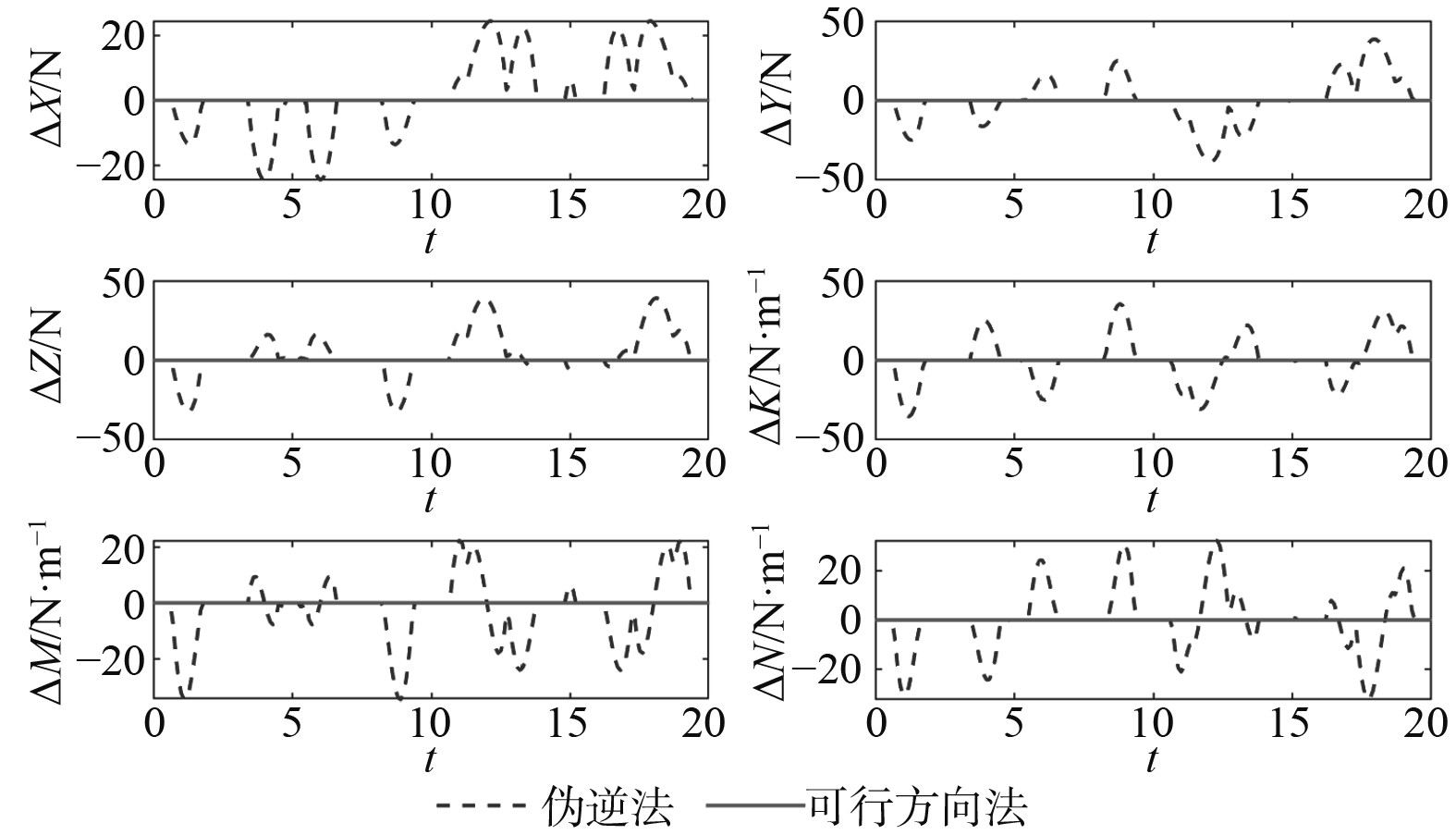
|
图 6 伪逆法与可行方向法的推力与力矩误差 Fig. 6 The thrust and torque error of pseudo inverse method and feasible direction method |
采用矩阵运算的方式,建立推进系统数学模型。在推力分配中,利用二次规划约束条件控制的优势,以最小化推力与力矩与目标值的差值建立二次规划问题,并以可行方向法进行求解。利用单纯形法求取可行的下降方向,并通过可行解转化为初始基本可行解作为单纯形法的输入,再通过一维搜索求取步长。为了验证本方法的有效性,模拟2组目标推力与力矩,比较了经过放缩处理的伪逆法和可行方向法推力分配的结果。结果表明,经过放缩处理的伪逆法和可行方向法得到的各个推进器的推力都未超出其上下限,可行方向法得到的推力与力矩更接近目标值,可行方向法可以克服饱和问题。
| [1] |
平伟, 马厦飞, 张金华, 等. “海马”号无人遥控潜水器[J]. 舰船科学技术, 2017, 39(15): 138-141+145. |
| [2] |
任峰, 张莹, 张丽婷, 等. “海龙Ⅲ”号ROV系统深海试验与应用研究[J]. 海洋技术学报, 2019, 38(2): 30-35. |
| [3] |
JOHANSEN T A, FOSSEN T I. Control allocation—A survey[J]. Automatica, 2013, 49(5): 1087-1103. DOI:10.1016/j.automatica.2013.01.035 |
| [4] |
李新飞, 马强, 袁利毫, 等. 矢量推进水下机器人的推力分配方法[J]. 哈尔滨工程大学学报, 2018, 39(10): 1605-1611. |
| [5] |
魏延辉, 陈巍, 杜振振, 等. 深海ROV伺服控制方法研究及其仿真[J]. 控制与决策, 2015, 30(10): 1785-1790. |
| [6] |
李新飞, 马强, 袁利毫, 等. 作业型ROV矢量推进建模及推力分配方法[J]. 船舶力学, 2020, 24(3): 332-341. |
| [7] |
JOHANSSON B, SIESJö J, FURUHOLMEN M. Seaeye Sabertooth A Hybrid AUV/ROV offshore system[C]//Oceans 2010 MTS/IEEE Seattle. 2010: 1–3.
|
| [8] |
FOSSEN T I. Marine control systems[M]. Trondheim: Tapir Trykkeri, 2002.
|
| [9] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons, Ltd, 2011.
|
| [10] |
陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2005.
|
 2022, Vol. 44
2022, Vol. 44
