船舶在静水或者航行中,受海浪、洋流以及船体自身螺旋桨运动作用的影响,会不可避免的发生多自由度运动,在这些摇荡运动形式中,横摇运动的危险性最大,也是船舶减摇设计重点针对的方向。传统的船舶减摇方式包括减摇水舱和减摇鳍2种,减摇水舱的工作原理是利用水在舱室中的惯性力产生的阻尼效应,但这种减摇方式体积大、成本高;减摇鳍也是一种相对成熟的减摇技术,它利用高速运动下海水在减摇鳍表面的流体动力特性,产生抵抗船舶横摇的力矩,从而保证船舶的稳定性。
目前,针对船舶高航速下的减摇鳍技术在业内广泛存在,但对于慢速或者零航速下的减摇鳍设计还相对较少。本文研究利用嵌入式技术实现减摇鳍的鳍型变化,实现慢速或者零航速下的减摇。详细介绍减摇鳍和船舶的流体动力学特性,并进行变鳍型减摇鳍的机械原理和性能仿真。
1 嵌入式变鳍型减摇鳍的水动力特性分析 1.1 减摇鳍原理与流体力学基本理论减摇鳍的形状改变直接影响其流体动力学性能,当船舶航行速度较高时,鳍表面与流体的相对速度高,此时鳍表面产生的作用力和力矩较大[1]。当航行速度较慢时,为了同样提升鳍表面产生的作用力和力矩,需要将鳍面进行顺时针转动,改变鳍面的截面形状。
减摇鳍的鳍型改变示意图如图1所示。
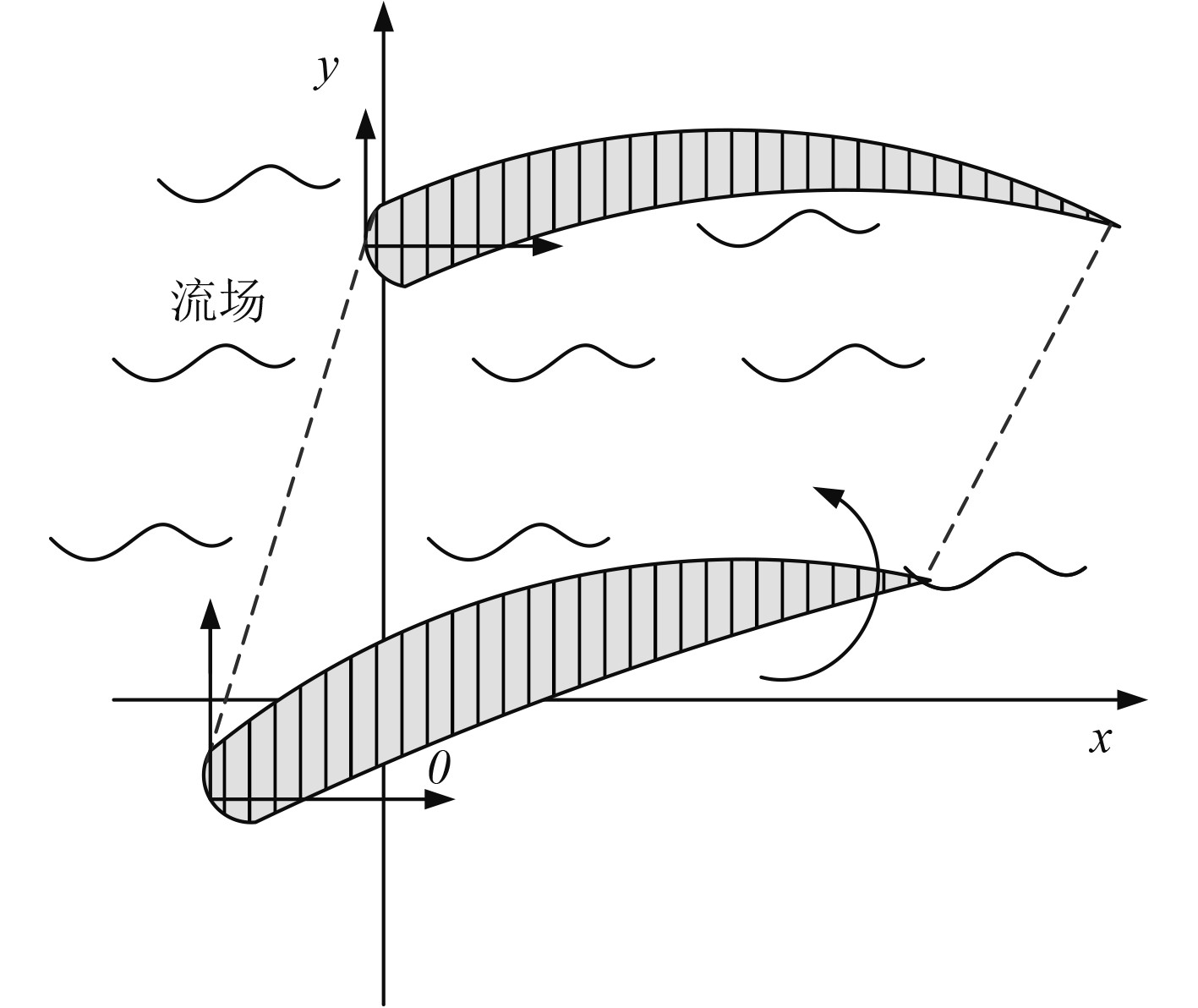
|
图 1 减摇鳍的鳍型改变示意图 Fig. 1 Schematic diagram of fin shape change of fin stabilizer |
在分析船舶减摇鳍的流体动力学特性前,首先需要针对船舶的流体动力学特性,尤其是船舶的横摇运动特性进行研究。在分析船舶流体动力学特性时,将舰船的速度分解2个方向分量,即
| $ u = {u_i} + {u_j} \text{,} $ |
海水的速度势分解为:
| $ \phi = {\phi _i} + {\phi _j} \text{。} $ |
建立RANS方程[2]为:
| $ \left( {\begin{array}{*{20}{c}} {\dfrac{{\partial {u_j}}}{{\partial t}} + \dfrac{\partial }{{\partial t}}(\rho {u_i}) = 0} ,\\ {\dfrac{{\rho \partial ({\phi _i})}}{{\partial t}} + \rho \dfrac{\partial }{{\partial t}}({u_i}{u_j}) = \dfrac{{\partial {\phi _j}}}{{\partial t}} + \mu \left[\dfrac{{\partial {u_i}}}{{\partial t}} + \dfrac{{{\partial ^2}{u_i}}}{{\partial {t^2}}}\right]}。\end{array}} \right. $ |
式中
定义船舶周围的海水为湍流,建立湍流模型为:
| $ \Delta {F_L} = \delta \left[\frac{{\partial {u_i}}}{{\partial {x_i}}} + \frac{{\partial {u_j}}}{{\partial {x_j}}}\right] - \frac{1}{3}\rho {Re} 。$ |
式中,
| $ {Re} = \frac{{{C_e}\rho {\eta ^4}\left(1 - \dfrac{\eta }{{{\eta _0}}}\right)}}{{1 + b{\eta ^4}}}\frac{{{\varepsilon ^3}}}{k} 。$ |
式中,
分析船舶减摇鳍及船舶横摇运动时,需要考虑以下2个边界条件:
1)流体动力学边界[3]
定义流体的不可压缩性,建立动力学边界条件如下式:
| $ \frac{{\partial \phi }}{{\partial t}} + \frac{1}{2}\nabla {\phi ^{^2}} + g\delta = 0 。$ |
式中:
2)运动学边界;
定义船舶运动方程为:
| $ F = f\left[ {x(t),y(t),t} \right] - z\left( t \right) = 0 \text{,} $ |
其中,
| $ \frac{{{\rm{d}}F}}{{{\rm{d}}t}} = \frac{{\partial F}}{{\partial t}}\frac{{dz}}{{dt}} + \frac{{\partial F}}{{\partial t}}\frac{{dy}}{{dt}} + \frac{{\partial F}}{{\partial t}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = 0 。$ |
建立船舶横摇模型为:
| $ \left\{ {\begin{array}{*{20}{c}} {\left( {{J_{}} + \Delta {J_{}}} \right)w + 2\kappa w + \dfrac{1}{2}Dh\theta = {T_0}},\\ {M\dfrac{{{\rm{d}}{u_i}}}{{{\rm{d}}t}}\sin \theta + M\dfrac{{{\rm{d}}{u_j}}}{{{\rm{d}}t}}\cos \theta = {F_0}} 。\end{array}} \right. $ |
式中:M为船舶重量;
船舶横摇角度与时间的关系曲线如图2所示。
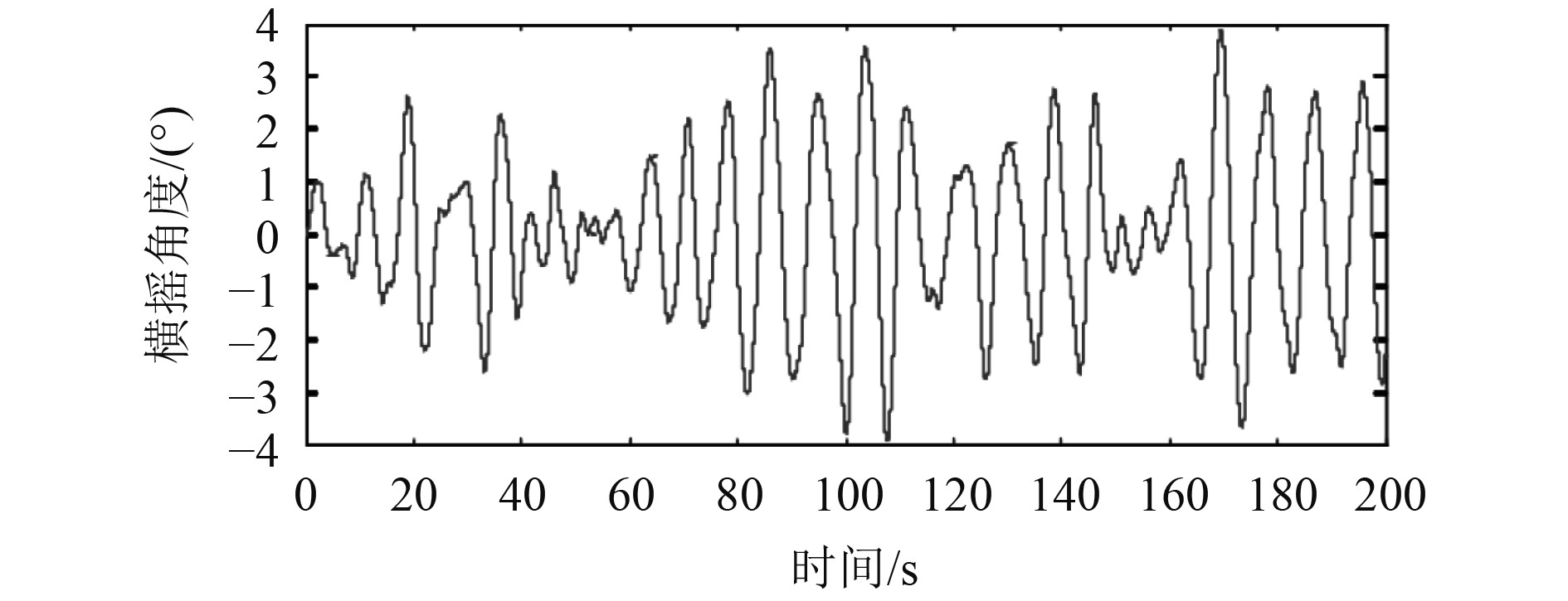
|
图 2 船舶横摇角度与时间的关系曲线 Fig. 2 Relation curve between ship rolling angle and time |
船舶减摇鳍为了抵消横摇力矩,必须要产生大小相同,方向相反的力和力矩,建立减摇鳍的抵抗力模型为:
| $ - {F_0} = {F_k} = \frac{1}{2}{\rho _{}}S \cdot \delta {u^2} \text{。} $ |
式中:
| $ - {T_0} = {T_s} = \frac{1}{2}h\sin \theta {F_k}\cos \beta \text{。} $ |
式中,
为了实现减摇鳍的鳍型改变,适应不同航行速度下的船舶减摇需求,设计收放式减摇鳍[4],转鳍机构的主动件运动均采用液压缸实现,图3为变鳍型减摇鳍的机械结构原理。
|
图 3 变鳍型减摇鳍的机械结构原理 Fig. 3 Mechanical structure principle of variable fin stabilizer |
本文设计的变鳍型减摇鳍采用翼型为NACA0025系列,其基本参数如表1所示。
|
|
表 1 减摇鳍翼型基本参数表 Tab.1 Basic parameters of fin stabilizer airfoil |
减摇鳍三维翼型改变通过收放、旋转和嵌套3种方式,根据原理图可知,减摇鳍旋转力矩与液压装置的关系为:
| $ {M_{\text{Z}}} = \frac{{\pi D_d^2Zp{R_0}{\eta _m}}}{{4{{\cos }^2}\alpha }} \text{。} $ |
其中:
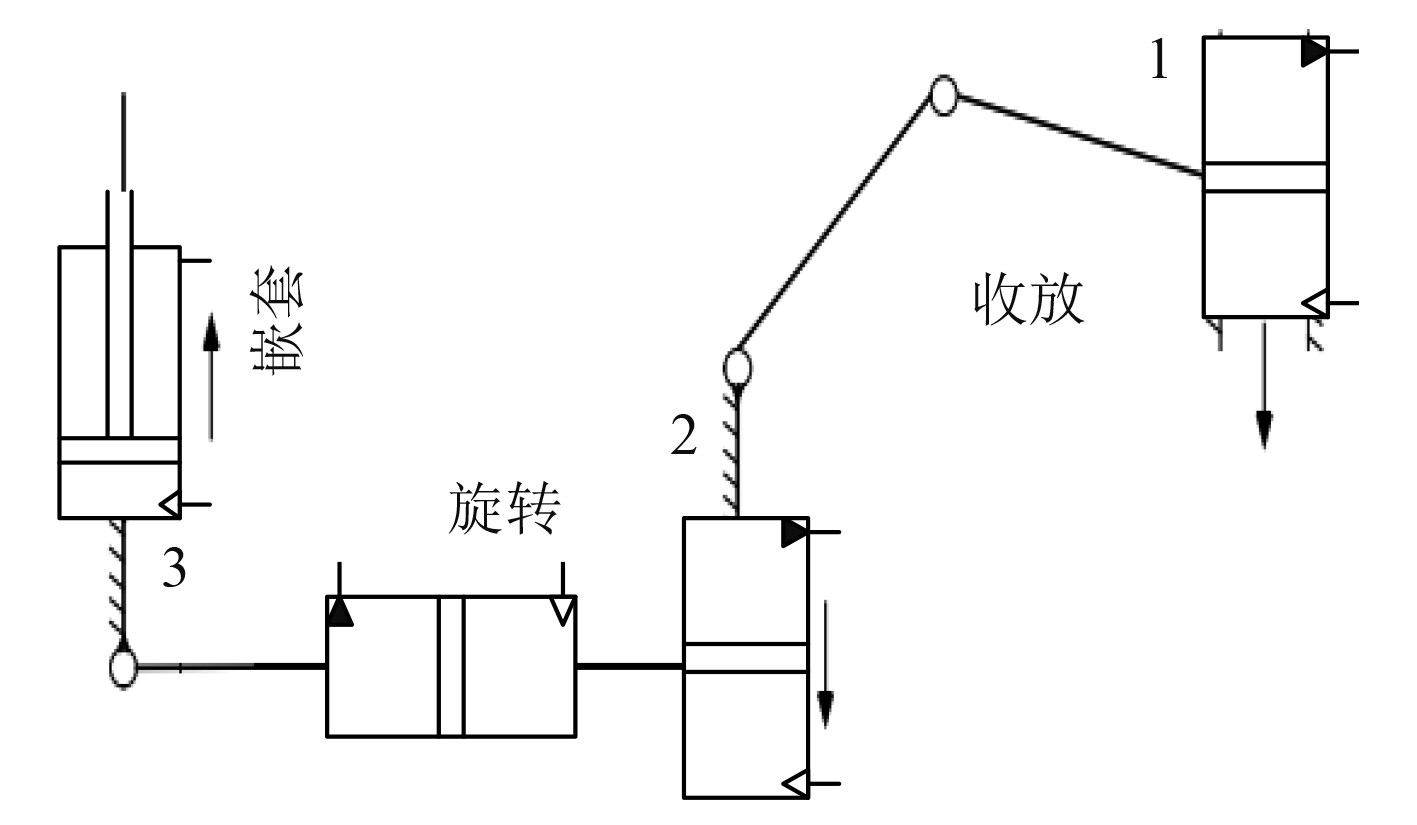
图4为变鳍型减摇鳍的液压缸系统原理。

|
图 4 变鳍型减摇鳍的液压缸系统原理 Fig. 4 Principle of hydraulic cylinder system for variable fin stabilizer |
当直径为50 mm,距离
| $ {p_{\max }} = \frac{{4{{\cos }^2}a{M_Z}}}{{\pi D_d^2Z{R_0}{\eta _m}}} = 3.441\;2\;{\text{MPa}} 。$ |
结合嵌入式控制技术,研究变鳍型减摇鳍的控制系统。采用非线性鲁棒性控制系统,控制系统原理如下:
定义减摇鳍非线性系统模型为
| $ f(t) = Ax\left( t \right) + By\left( t \right) \text{,} $ |
式中:
将减摇鳍控制系统进行分解,如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot f}_1}(t) = {{\boldsymbol{A}}_1}{x_1}\left( t \right) + {{\boldsymbol{B}}_1}{y_1}\left( t \right)} ,\\ {{{\dot f}_2}(t) = {{\boldsymbol{A}}_2}{x_2}\left( t \right) + {{\boldsymbol{B}}_2}{y_2}\left( t \right)} ,\\ {...} \\ {{{\dot f}_n}(t) = {{\boldsymbol{A}}_n}{x_n}\left( t \right) + {{\boldsymbol{B}}_n}{y_n}\left( t \right)} 。\end{array}} \right. $ |
式中:
建立嵌入式控制模态函数[6]为
| $ S(x,t) = Cx(t) = 0 \text{,} $ |
式中,
基于嵌入式的船舶减摇鳍控制器结构如图5所示。
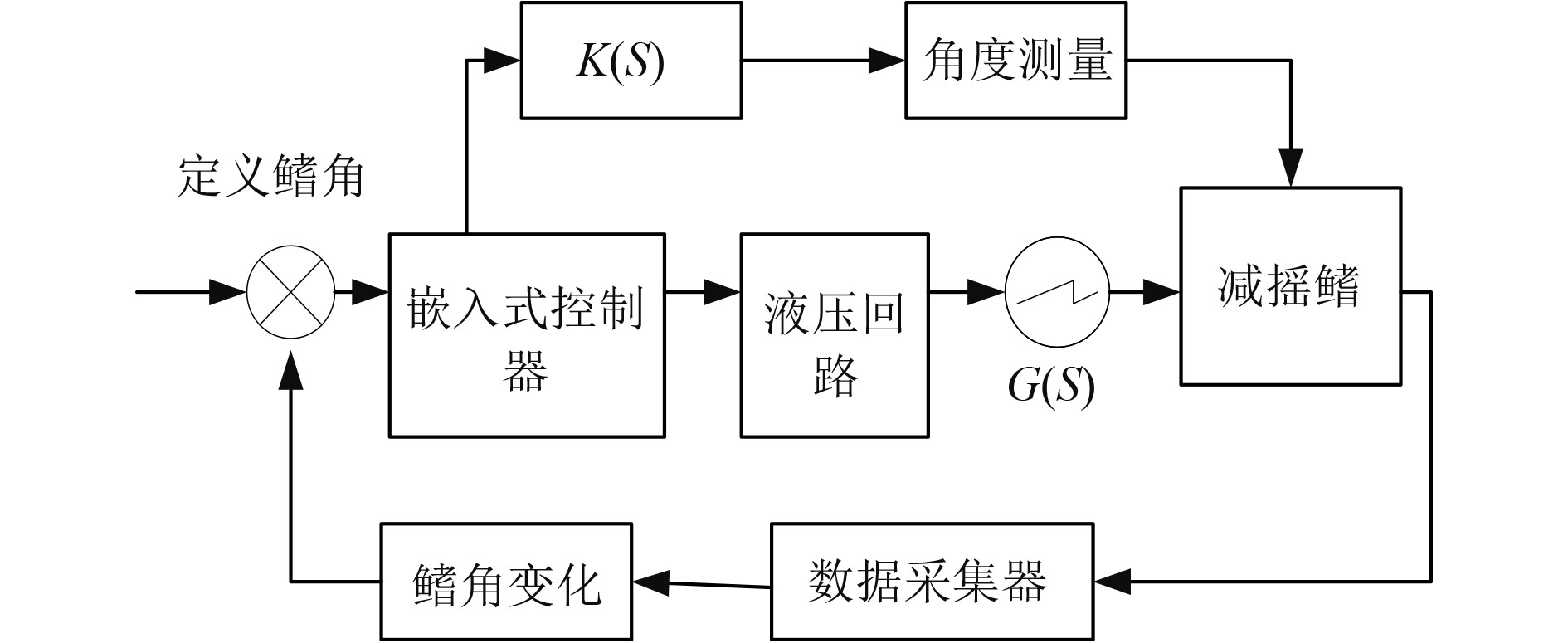
|
图 5 基于嵌入式的船舶减摇鳍控制器结构 Fig. 5 Structure of ship fin stabilizer controller based on embedded system |
该嵌入式控制器的传递函数为:
| $ G(s) = {k_1} + \frac{{{k_2}}}{\omega } + \frac{{{k_3}}}{{{\omega ^2}}}{s^2} \text{。} $ |
其中:
为了验证变鳍型减摇鳍的性能,建立减摇鳍控制的仿真系统,系统包括船舶模型、波浪模型、检测元件、放大器等,仿真系统采用为500 t标准散货船,基本参数如表2所示。
|
|
表 2 散货船参数表 Tab.2 Bulk carrier parameter table |
海浪是船舶减摇过程的关键扰动作用力,为了提高仿真的精度,对海浪的随机性、频谱特性进行研究,建立幅频模型为:
| $ \xi (t) = \sum\limits_{i = 1}^n {{\xi _0}(t)\cos ({k_1}\delta + {w_0}t + \varphi )} \text{。} $ |
式中:
定义义波高为1.95 m的波浪能谱密度公式[7]如下:
| $ \eta (\omega ) = \frac{{{k_1}}}{{{\omega ^3}}}\exp \left(\frac{{ - {k_2}}}{{{\omega ^4}}}\right) \text{。} $ |
其中:
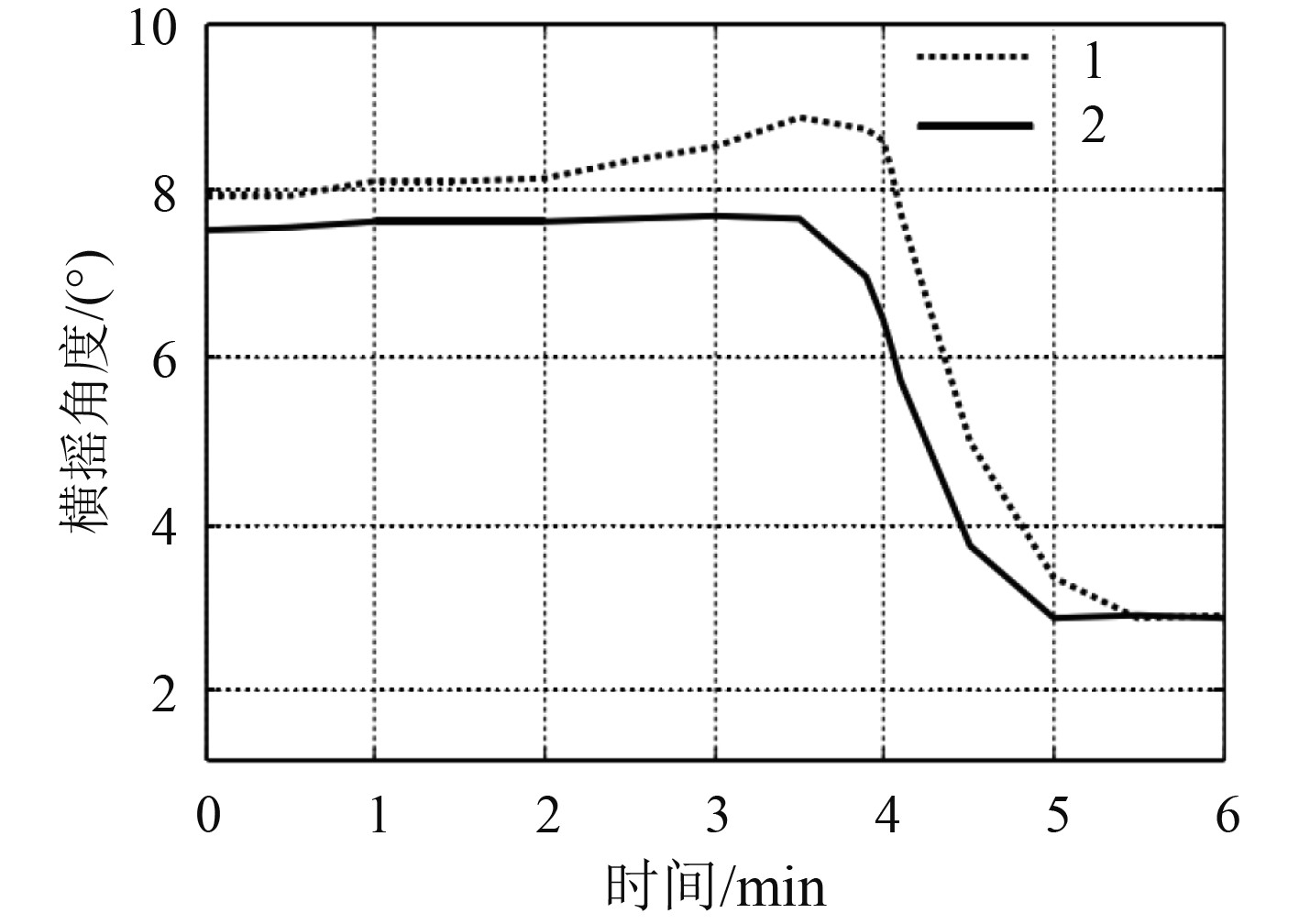
在Matlab中得到有无减摇鳍下的船舶横摇角度对比如图6所示。
|
图 6 有无减摇鳍下的船舶横摇角度对比 Fig. 6 Comparison of ship rolling angle with and without fin stabilizer |
图中,曲线1为未装配减摇鳍的船舶横摇角度,曲线2为装配变鳍型减摇鳍的船舶横摇角度。
3 结 语| [1] |
叶青云. 鳍—船体适配性及其低航速控制策略研究[D]. 哈尔滨: 哈尔滨工程大学, 2015: 32−38.
|
| [2] |
吉明, 叶青云, 袁聪. 减摇鳍与船体的适配性数值模拟[J]. 中国舰船研究, 2014, 9(3): 8-19+42. JI Ming, YE Qingyun, YUAN Cong. Research on the adaptability of fin to hull[J]. Chinese Journal of Ship Research, 2014, 9(3): 8-19+42. DOI:10.3969/j.issn.1673-3185.2014.03.002 |
| [3] |
马磊, 张显库. 基于混沌分析的船舶参数激励横摇运动及其减摇鳍控制研究[J]. 船舶力学, 2013, 17(7): 741-747. MA Lei, ZHANG xianku. Research on ship parameter excited rolling motion and fin stabilizer control based on chaos analysis[J]. Journal of Ship Mechanics, 2013, 17(7): 741-747. DOI:10.3969/j.issn.1007-7294.2013.07.004 |
| [4] |
徐世杰, 邢继峰, 彭利坤. 基于模糊理论的船舶减摇鳍控制系统研究[J]. 船舶, 2011, 22(3): 24-26. DOI:10.3969/j.issn.1001-9855.2011.03.005 |
| [5] |
罗德红. BP神经网络应用于船舶减摇鳍控制系统的仿真研究[J]. 电气自动化, 2011, 33(2): 25-27. LUO Dehong. Simulation study on the application of BP neural network in Ship Fin Stabilizer control system[J]. Electrical Automation, 2011, 33(2): 25-27. DOI:10.3969/j.issn.1000-3886.2011.02.009 |
| [6] |
刘维亭, 张冰, 姜建国. H_∞控制理论在船舶减摇鳍控制中的应用研究[J]. 工矿自动化, 2003(3): 16-19. LIU Weiting, ZHANG Bing, JIANG Jianguo. Application of H ∞ control theory in Ship Fin Stabilizer control[J]. Journal of Mine Automation, 2003(3): 16-19. DOI:10.3969/j.issn.1671-251X.2003.03.007 |
| [7] |
李晖, 郭晨, 李晓方. 基于MATLAB的船舶减摇鳍控制系统仿真[J]. 仪器仪表学报, 2002(S1): 295-296. LI Hui, GUO Chen, LI Xiaofang. Simulation of Ship Fin Stabilizer control system based on MATLAB[J]. Chinese Journal of Scientific Instrument, 2002(S1): 295-296. DOI:10.3321/j.issn:0254-3087.2002.z1.131 |
 2022, Vol. 44
2022, Vol. 44
