0 引　言

船舶在进行远距离航行时，为了最大程度降低燃油消耗，往往需要对船舶的航行方向、航速等进行较精确的控制，船舶的运动控制主要包括2个方面：一是船舶的航向保持性控制，主要目的是通过控制船舶的运动参数，抵抗来自海浪、海风等作用力的干扰，使船舶沿着既定航向运动；二是船舶的机动性，当船舶沿直线运动过程中，航线突然出现障碍物时，需要尽快调整船舶航行方向，实现避障，这种情况在船舶进出港或内河航道中经常出现。因此，提高船舶运动控制能力非常重要。

目前，船舶航向控制是通过动力系统螺旋桨和船舵共同实现的，船舵的性能与船舶吃水、舵与水流的相对速度、柴油主机动力特性、船舶阻力情况等密切相关。本文结合线性变参数（LPV）系统算法，对船舶的运动与参数控制进行数学建模，开发基于线性变参数（LPV）系统算法的船舶运动与参数控制器。

1 线性变参数（LPV）系统算法的基本理论 1.1 线性变参数（LPV）系统的原理

线性变参数（LPV）系统算法是一种变增益的系统稳定性控制算法，其核心是线性矩阵不等式，线性变参数（LPV）系统算法重点考虑了系统在线参数的变化与系统稳定性的关系，在稳定性、鲁棒性控制方面具有很大的应用潜力^[1]。

线性变参数（LPV）系统描述如下：

$ \begin{gathered} \frac{{\rm{d}}}{{{\rm{d}}t}}x(t) = A\left( {{\theta _t}} \right)x(t) + B\left( {{\theta _t}} \right)u(t)，\\ y(t) = C\left( {{\theta _t}} \right)x(t) + D\left( {{\theta _t}} \right)u(t)。\\ \end{gathered} $

式中： $ x(t) $ 为系统的状态参量； $ y(t) $ 为系统的输出参量； $ u(t) $ 为系统的控制输入； $ A\left( {{\theta _t}} \right) $ ， $ B\left( {{\theta _t}} \right) $ ， $ C\left( {{\theta _t}} \right) $ ， $ D\left( {{\theta _t}} \right) $ 分别为变参数 $ \left( {{\theta _t}} \right) $ 的仿射函数。分别表示如下：

$ \begin{gathered} A\left( {{\theta _t}} \right) = {A_0} + {\theta _{t,\lambda }}{A_1} + \cdots + {\theta _{t,s}}{{\boldsymbol{A}}_s}，\\ B\left( {{\theta _t}} \right) = {B_0} + {\theta _{t,\lambda }}{B_1} + \cdots + {\theta _{t,s}}{{\boldsymbol{B}}_s}，\\ C\left( {{\theta _t}} \right) = {C_0} + {\theta _{t,\lambda }}{C_1} + \cdots + {\theta _{t,s}}{{\boldsymbol{C}}_s}，\\ D\left( {{\theta _t}} \right) = {D_0} + {\theta _{t,\lambda }}{D_1} + \cdots + {\theta _{t,s}}{{\boldsymbol{D}}_s}，\\ \end{gathered} $

${{\boldsymbol{A}}_s}$ ， ${{\boldsymbol{B}}_s}$ ， ${{\boldsymbol{C}}_s}$ ， ${{\boldsymbol{D}}_s}$ $ \left( {s = 0,1,2,...,n} \right) $ 为LPV系统的常数矩阵，令

$ {\boldsymbol{S}}\left( {{\theta _t}} \right) = \left[ {\begin{array}{*{20}{l}} {A\left( {{\theta _t}} \right)}&{B\left( {{\theta _t}} \right)} \\ {C\left( {{\theta _t}} \right)}&{D\left( {{\theta _t}} \right)} \end{array}} \right] \text{，} $

${{\boldsymbol{S}}_i} = \left[ {\begin{array}{*{20}{c}} {{A_s}}&{{B_s}} \\ {{C_s}}&{{D_s}} \end{array}} \right]$ ，可将系统状态矩阵的LPV系统描述为：

$ {\boldsymbol{S}}\left( {{\theta _t}} \right) = {S_0} + {\theta _{t,1}}{S_1} + \cdots {\theta _{t,s}}{S_s} \text{，} $

当 ${\boldsymbol{S}}\left( {{\theta _t}} \right)$ 的取值位于多面体 $ {\alpha _i} $ 内部时，有

$ {\boldsymbol{S}}\left( {{\theta _t}} \right) = \left\{ {\sum\limits_{i = 1}^k {{\alpha _i}} {S_i},{\alpha _i} \geqslant 0,\sum\limits_{i = 1}^k {{\alpha _i}} = 1} \right\} \text{，} $

$ {{\boldsymbol{S}}_1} = \left[ {\begin{array}{*{20}{l}} {{A_1}}&{{B_1}} \\ {{C_1}}&{{D_1}} \end{array}} \right],{{\boldsymbol{S}}_2} = \left[ {\begin{array}{*{20}{l}} {{A_2}}&{{B_2}} \\ {{C_2}}&{{D_2}} \end{array}} \right] \cdots {{\boldsymbol{S}}_i} = \left[ {\begin{array}{*{20}{c}} {{A_i}}&{{B_i}} \\ {{C_i}}&{{D_i}} \end{array}} \right] \text{。} $

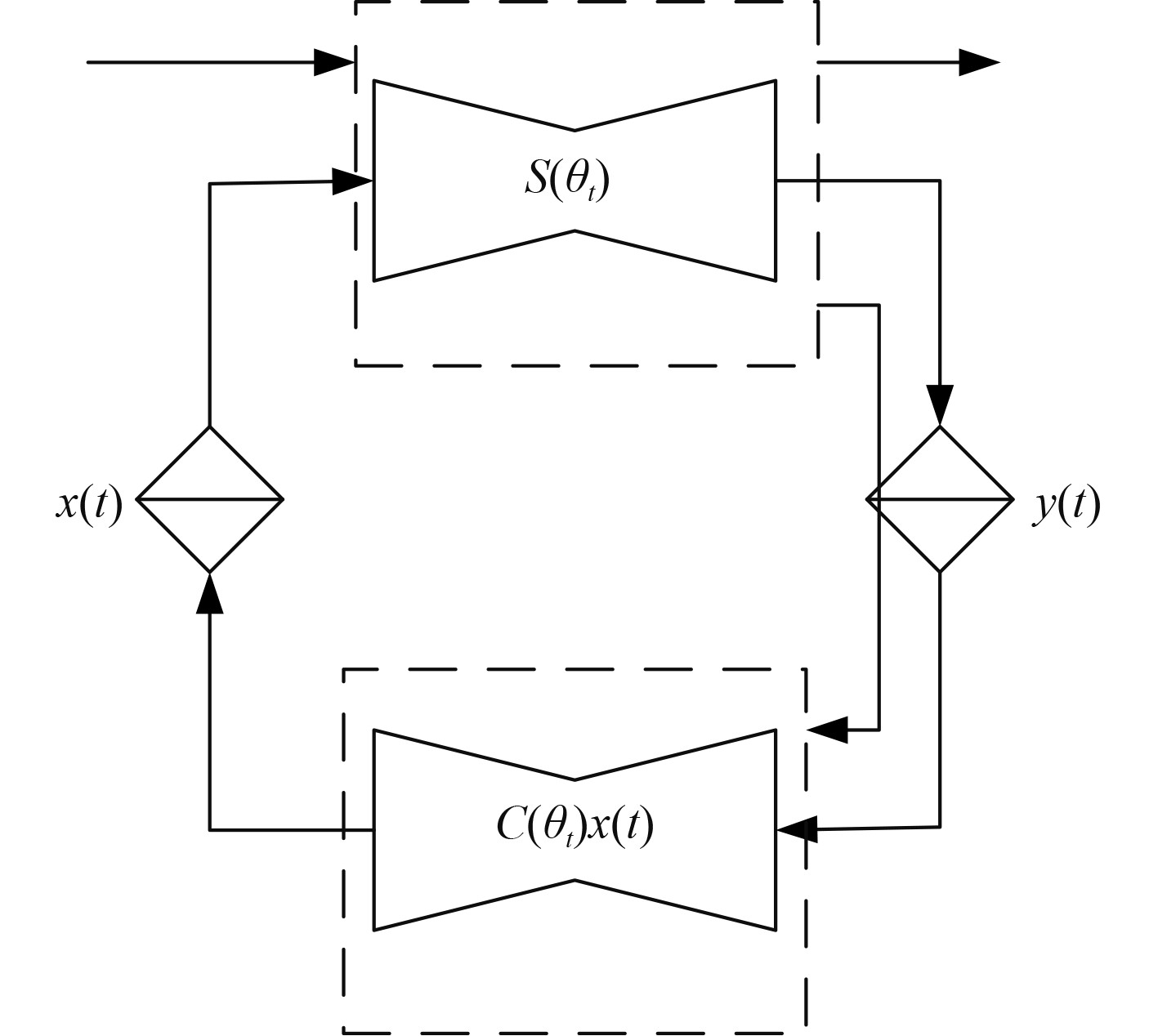
线性变参数（LPV）系统的原理图如图1所示。

1.2 线性变参数（LPV）系统算法的稳定性控制技术

在船舶运动参数控制领域，稳定性控制是一个非常重要的部分，本文采用的稳定性控制原理为Lyapunov理论。

假设有一个线性变参数（LPV）系统如下：

$ f\left( t \right) = A\left( {{\theta _t}} \right)x\left( t \right) \text{，} $

式中 $ x\left( t \right) $ 为系统的状态变量。

假设存在矩阵P，是一个正定矩阵，在LPV系统的 $ {\theta _t} $ 取值范围内满足：

$ A{\left( {{\theta _t}} \right)^{\rm{T}}} * P + Px\left( t \right) < 0 \text{，} $

则LPV系统具有稳定性。令 $ \delta \left( t \right) = A{\left( {{\theta _t}} \right)^{\rm{T}}} * P $ ，则系统的稳定性方程表示为：

$ e = \frac{{{\rm{d}}\left( {\delta \left( t \right)} \right)}}{{{\rm{d}}t}} < 0 。$

2 船舶运动与参数控制系统的函数建模 2.1 船舶动力系统主机与螺旋桨的函数建模

在建立基于线性变参数算法的船舶运动与参数控制系统之前，对船舶动力系统主机和螺旋桨进行数学建模。

1）柴油主机

建立柴油主机的扭矩方程为：

$ {M_0} - {M_1} = \frac{\pi }{{30}}{J_0}\frac{{{\rm{d}}n}}{{{\rm{d}}t}} \text{，} $

其中： $ {M_0} $ 为输出转距； $ M_{1} $ 为负载扭矩； $ {J_0} $ 为转动惯量。

柴油机动力装置输出转矩按下式计算：

$ {M_0} = \frac{{{H_g}g{n_0}}}{{2\text{π} }} \text{。} $

式中： $ {H_g} $ 为柴油的燃烧热值； $ {n_0} $ 为气缸个数；每个气缸输出的扭矩为 $ {T_{\text{e}}} $ ，如下式：

$ {T}_{\text{e}}\text=\frac{{M}_{0}}{{n}_{e}}={F}_{\text{e}}R\left(\text{sin}\alpha +\frac{\lambda \mathrm{sin}2\alpha }{2\sqrt{1-{\lambda }^{2}{\mathrm{sin}}^{2}{\alpha }^{}}}\right) 。$

式中： $ R $ 为气缸行程； $ {F_{\text{e}}} $ 为活塞作用于曲轴上的压力； $ \alpha $ 为活塞角度， $ \lambda $ 为扭矩系数^[2]。

2）.螺旋桨

螺旋桨的运动模型为：

$ nP - {F_r} = km\frac{{{\rm{d}}{V_0}}}{{{\rm{d}}t}} \text{。} $

式中： $ m $ 为总质量； $ n $ 为桨叶个数； $ P $ 为压力； $ {F_r} $ 为桨叶受到的阻力；k为相关系数； $ {V_0} $ 为转动线速度。

螺旋桨的功率方程如下：

$ {P_w} = \frac{{1\;000{F_r}}}{{m{V_0}}} , $

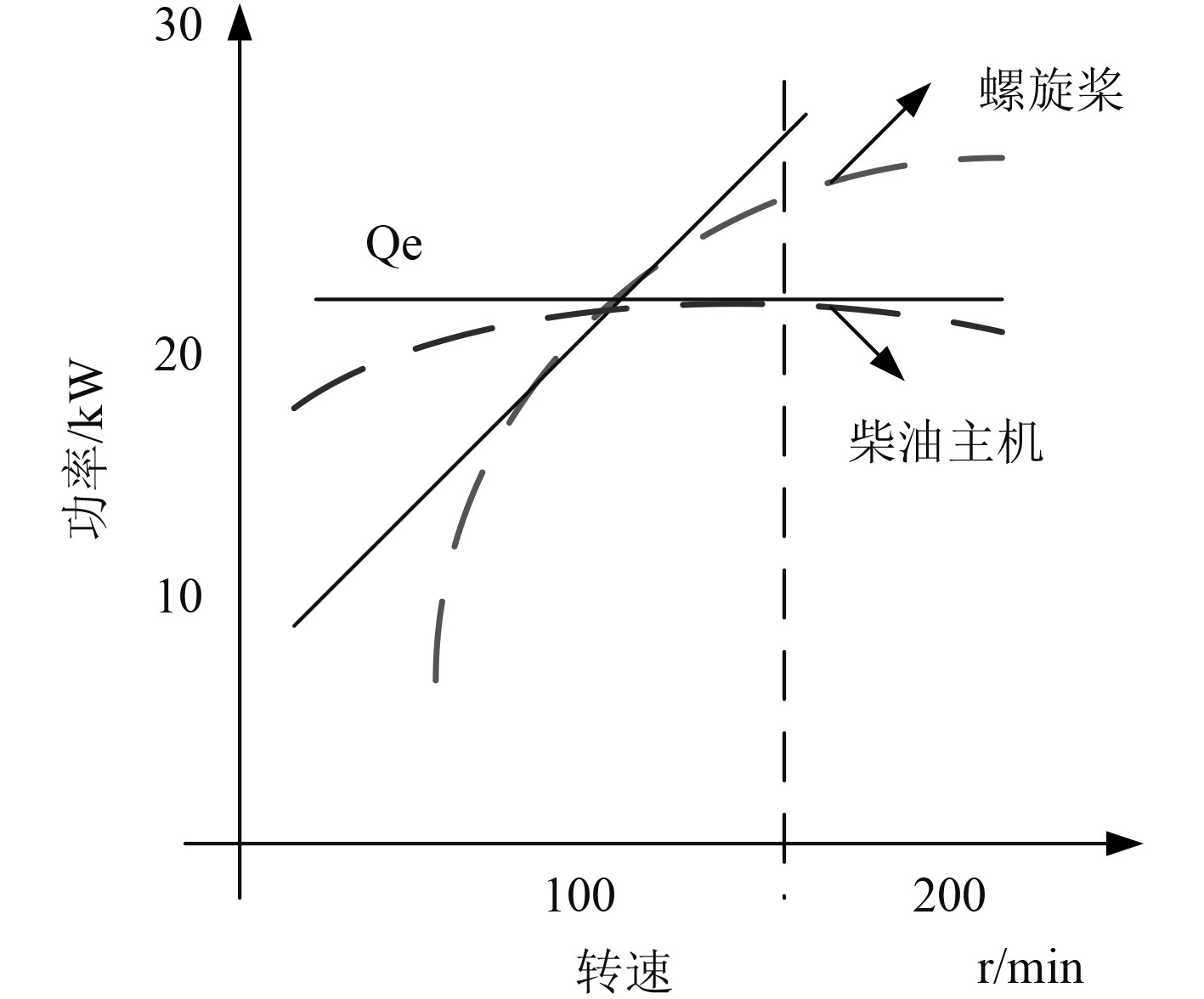
螺旋桨和柴油主机的功率与转速关系曲线如图2所示。

2.2 船-机-桨综合系统的函数建模

建立整个船舶-柴油主机-螺旋桨综合系统的函数模型，整个系统的负载转矩如下：

$ {T_P} = {K_P}\rho {n^2}{D_P}^5 。$

式中： $ \rho $ 为水的密度； $ n $ 为螺旋桨转速； $ {K_P} $ 为船体负载阻力； $ {D_P} $ 为负载阻力产生的力矩^[3]。

船舶-柴油主机-螺旋桨综合系统的平衡方程如下式：

$ \begin{gathered} {T_a} = \lambda \frac{{{F_0}}}{2}{v_a}，\\ {T_b} = {J_0}{\left( {\frac{{d\varOmega }}{t}} \right)^2}，\\ \end{gathered} $

式中： $ {T_a} $ ， $ {T_b} $ 分别为综合系统输入和输出转矩，满足

$ {T_a} - {T_b} = {T_p} \text{。} $

式中： $ {F_0} $ 为综合系统的等效推力； $ {v_a} $ 为船舶航行速度； $ \lambda $ 为转矩系数； $ {J_0} $ 为综合系统的转动惯量； $ \varOmega $ 为转动角度。

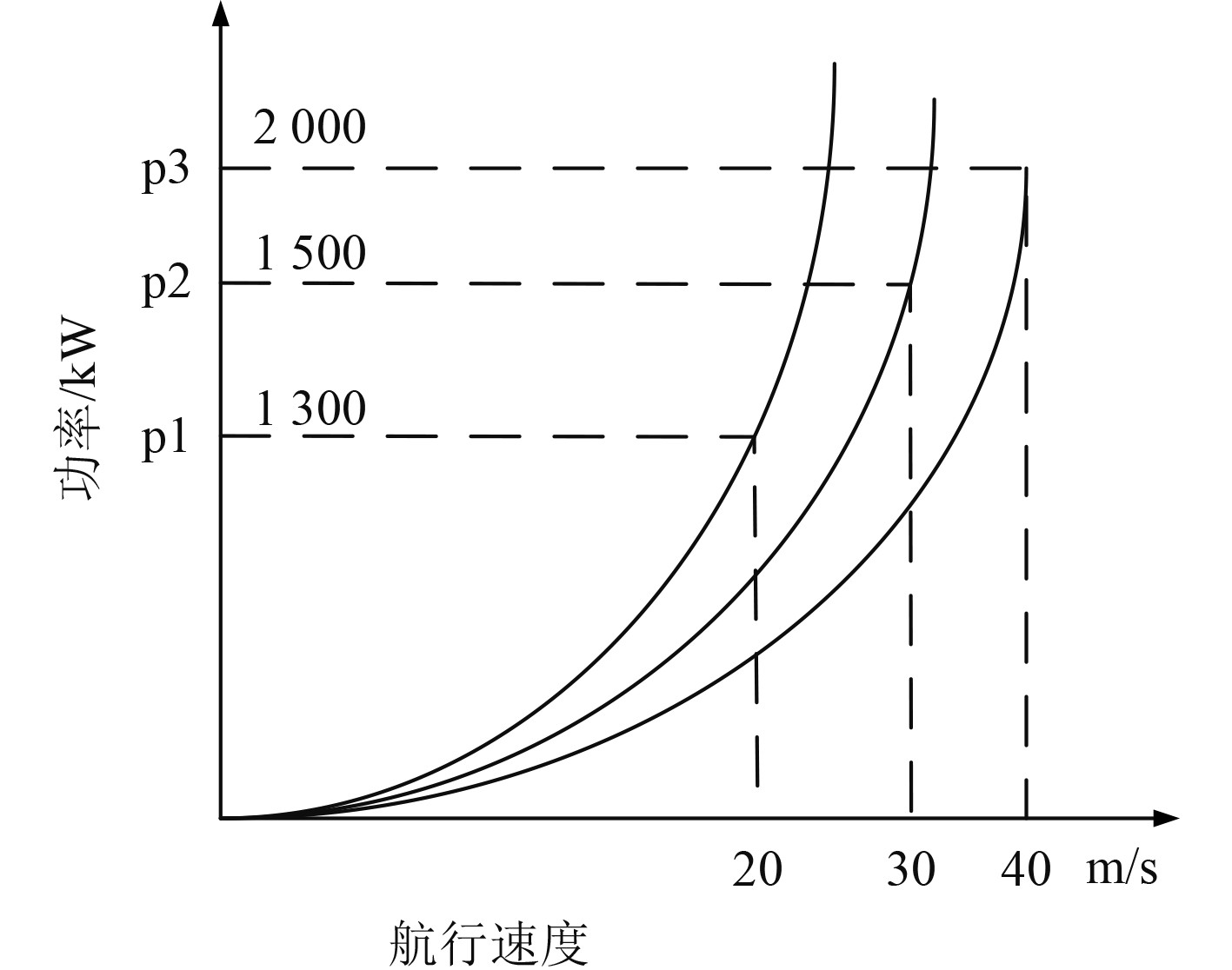
综合系统的功率与航行速度关系曲线如图3所示。

3 基于线性变参数的船舶运动与参数控制器设计 3.1 船舶运动与参数控制器的关键参数控制

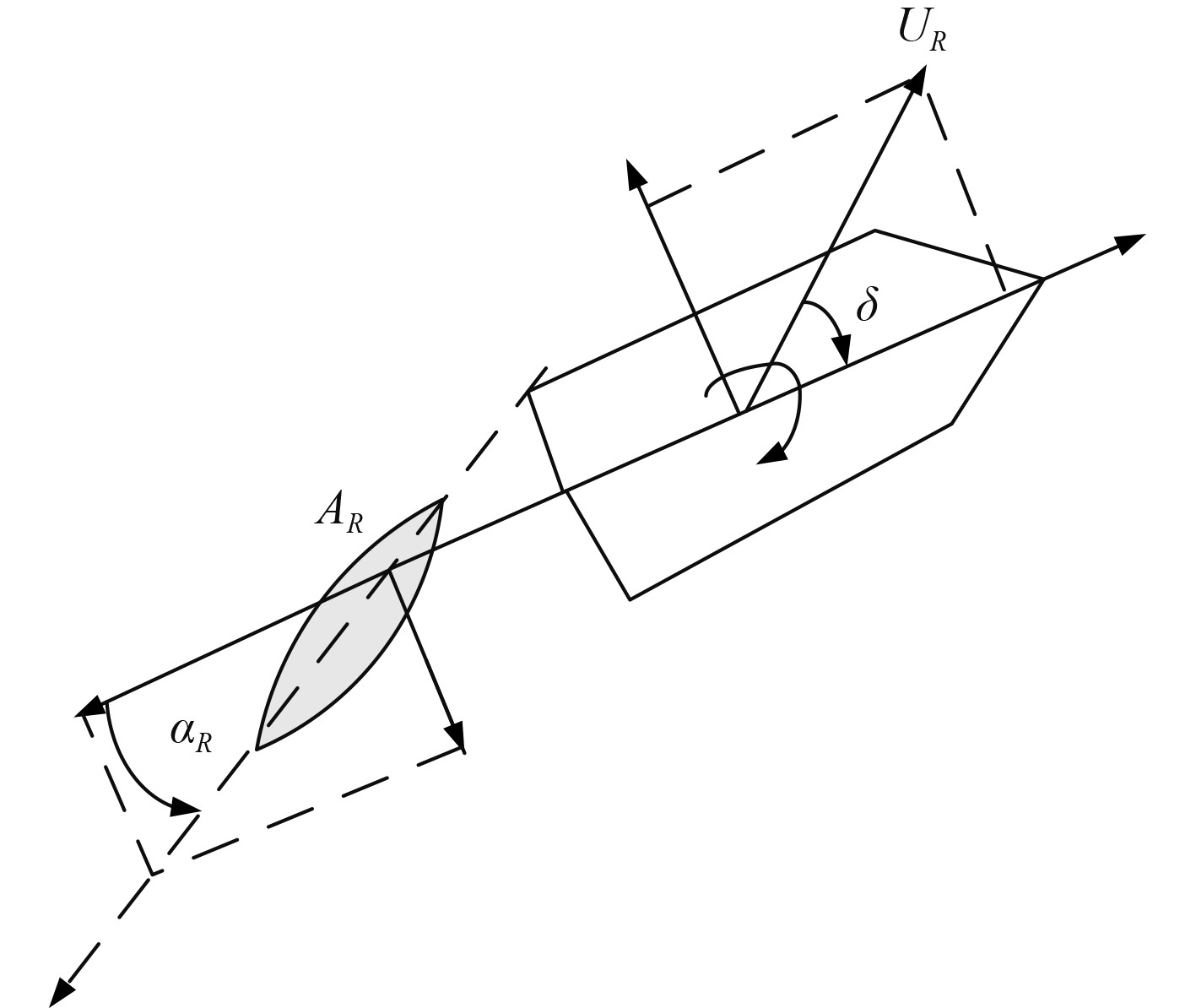
为了提高船舶运动参数的控制效率，结合建立的柴油机、螺旋桨和船-机-桨综合系统模型，将系统内的关键参数设定为船舵驱动力和力矩，建立船舵力学坐标系如图4所示。

船舵驱动力及力矩通过建模可知：

$ B(p(k)) \begin{gathered} {F_n} = {P_w}\frac{{1\;000}}{{m{V_0}}} \cdot \sin \delta \cdot {F_t}，\\ {T_R} = {T_p}\left( {1 + {a_H}} \right){F_n}\cos \delta 。\\ \end{gathered} $

其中： $ {a_H} $ 为船舵力矩的修正因子^[4]； $ \delta $ 为舵角； $ {F_t} $ 为船舵正压力，用下式计算：

$ {F_t} = - \frac{1}{2}\rho {A_R}{f_\alpha }U_R^{}\sin {\alpha _R} 。$

式中： $ {A_R} $ 为舵叶的面积； $ {f_\alpha } $ 为升力系数^[5]； $ {\alpha _R} $ 为船舵冲角； $ U_R^{} $ 为舵叶附近的有效流速。

3.2 船舶运动与参数控制器设计

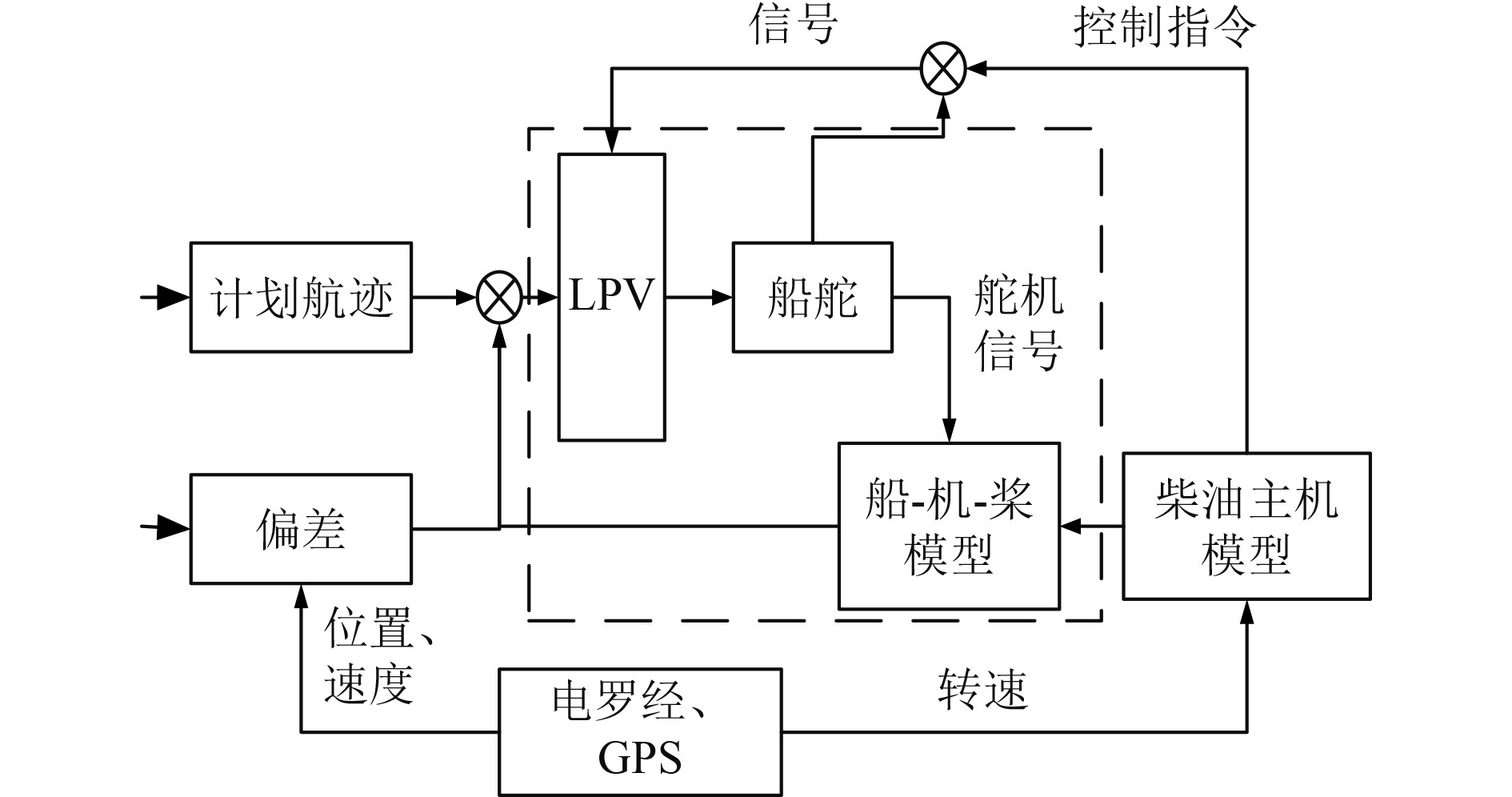
在船舶运动与参数控制领域，欠驱动船舶的运动控制是一个热门课题，结合线性变参数（LPV）系统，在船舶柴油主机、螺旋桨及船舵控制模型的基础上，建立控制器如图5所示。

船舶运动参数控制器模型为：

$ x(k + 1) = A(p(k))x(k) + B(p(k))u(k) \text{，} $

系统的输入信号为计划航迹 $ u(k) $ ，控制矩阵 $ A(p(k)) $ ， $ B(p(k)) $ 满足LPV状态参量方程如下：

$ A(p(k)) = \sum\limits_{j = 1}^t {{p_j}} (k){A_j},\quad B(p(k)) = \sum\limits_{j = 1}^t {{p_j}} (k){B_j} \text{。} $

3.3 基于LPV算法船舶运动与参数控制器仿真

仿真平台选用Matlab-Simulink^[6]，仿真对象为TEU集装箱船，船舶基本参数见表1。

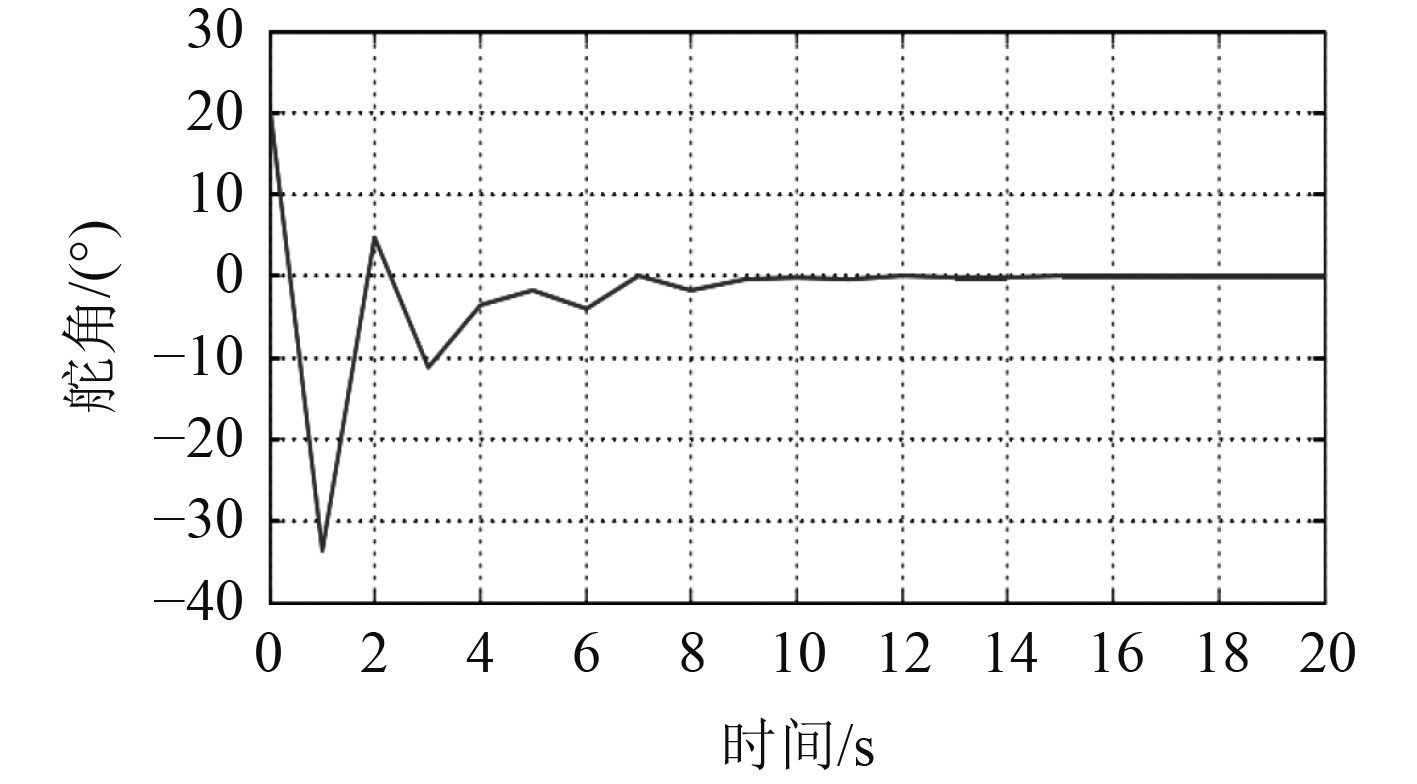
仿真条件设定为主机转速120 r/min，风速10 m/s，风向与船舶航行方向的夹角为25°，船舵的初始舵角为0°，得到船舶舵角在初始扰动下的仿真曲线如图6所示。

4 结　语

线性变参数（LPV）系统是一种时变系统，当系统中某个参数值随时间发生改变时，LPV系统的整体特性也随之改变，在稳定性控制方面有广泛应用。本文结合线性变参数（LPV）系统算法，在船舶动力主机、螺旋桨、船舵等函数模型的基础上，设计船舶运动与参数控制器，并进行原理分析和仿真试验，取得了良好的效果。