2. 辽宁行政学院,辽宁 沈阳 110161
2. Liaoning Academy of Governance, Shenyang 110161, China
船体结构一半以上是由加筋板和梁焊接而成的,焊接质量直接决定了船舶的使用寿命。一方面,船体结构的焊缝质量与船体的强度和刚度密切相关,一旦焊缝出现缺陷,则船舶整体极易发生破损;另一方面,焊缝中不可避免存在微裂纹,船舶结构焊缝在海浪、洋流等循环载荷作用下,微裂纹会不断的扩展,直至出现明显的裂缝,此时船体的焊接结构就会失效,导致严重事故。
循环载荷对于船体结构的破坏作用是一个不断累加的过程,基于miners疲劳损伤累加理论可以定性的进行分析。本文研究的船体舱壁结构在循环载荷作用下的极限强度特性,是指循环载荷下,船体结构的应变高于屈服应变,产生不可恢复的塑性变形,进而导致船体的失效。
首先分析船体舱壁结构的极限强度理论,基于Ansys软件,针对循环载荷下的船体结构极限强度进行有限元分析,对于改善船体舱壁结构设计有一定意义。
1 船体舱壁结构的极限强度基本理论在船舶舱室、甲板等区域,为了仿真船体结构在弯矩作用下不会发生破坏,往往在舱壁等位置设置多个筋板,筋板和船舶舱壁等结构共同构成了较大的应力截面,从而具有较高的抵抗弯矩和扭矩的特性。
在常规的力学模型里,当筋板和梁受到弯矩作用时,筋板和梁截面其中一侧受到压力时,另一侧必然会受到拉力的作用。对于受压一侧的结构,当应力达到屈服极限应力时,材料被压溃,产生塑性变形;对于受拉一侧,当应力达到屈服极限时,材料发生断裂,结构失效。
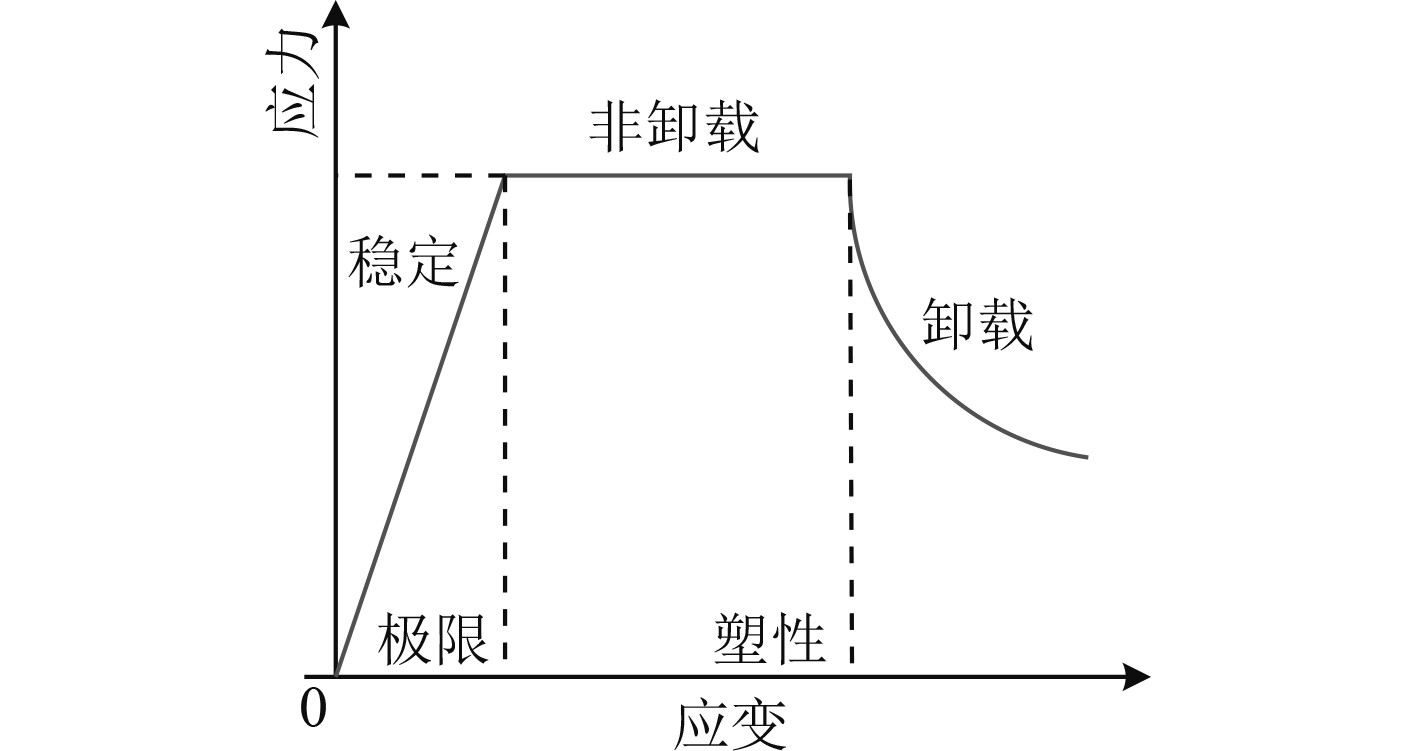
本文结合结构塑性变形理论,将船体舱壁结构应力应变关系划分为如图1所示的3个阶段。
|
图 1 船舶结构应力-应变关系曲线 Fig. 1 Stress-strain curve of ship structure |
将船体舱壁结构的应力-应变关系分为稳定区域、非卸载区域和卸载区域,其中,稳定区域为结构的弹性应变区域,其余2个区域为船体结构的塑性应变区域。
弹塑性阶段的区分按下式:
| $ {\sigma _x} = \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} \times E},&{{\varepsilon _x} \leqslant {\varepsilon _y}} ,\\ {{\sigma _y}},&{{\varepsilon _x} > {\varepsilon _y}} 。\end{array}} \right. $ |
式中:
1)稳定阶段
当船体舱壁结构的应力-应变关系处于稳定阶段时,结构的失效特性与结构的截面特性有关,此时,船体结构的应力-应变关系如下式:
| $ \sigma = \left\{ {\begin{array}{*{20}{l}} {E{\varepsilon _x}},&{{\text{ if }}{\sigma _{}} \leqslant {\sigma _y}} ,\\ {E{\varepsilon _x}\dfrac{{{A_r}}}{A}},&\,\,\,{{\rm{else}}}。\end{array}} \right. $ |
式中:
2)非卸载阶段
在非卸载阶段,船体舱壁结构受到的应力达到屈服应力,且在一段时间内保持不变,但此时船体舱壁结构的应变和挠度仍不断增加,挠度的增量可用下式计算:
| $ w = \frac{{2a}}{\text{π} }\sqrt {{\varepsilon _y} - {\varepsilon _x}} \text{,} $ |
此时,船体舱壁结构的截面仍旧承载弯矩,结构的轴向应力可用下式计算:
| $ {\sigma _x} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{M_p} - (1/8)q{a^2}}}{{{A_r}{w_T}}}},&{{\text{ if }}{\sigma _x} \leqslant {\sigma _y}},\\ {\dfrac{{{M_p} - (1/8)q{a^2}}}{{{A_r}{w_T}}}},&{{\text{ }}{\rm{else}}}。\end{array}} \right. $ |
式中:
| $ {\delta _0} = \frac{{5q{a^4}}}{{384EI}} 。$ |
循环载荷是指具有一定周期和频率的载荷,船舶结构受到的循环载荷以海浪载荷和动力系统振动载荷为主,在进行循环载荷下的船体结构极限强度分析时,首先建立以下假设:
1)船体舱壁结构的横截面受力产生的应变在截面高度方向上具有线性分布的特征;
2)忽略船体舱壁结构的剪力影响,将舱壁横截面的构件划分为一个个单元;
3)船体舱壁结构的材料模型为典型的弹塑性模型。
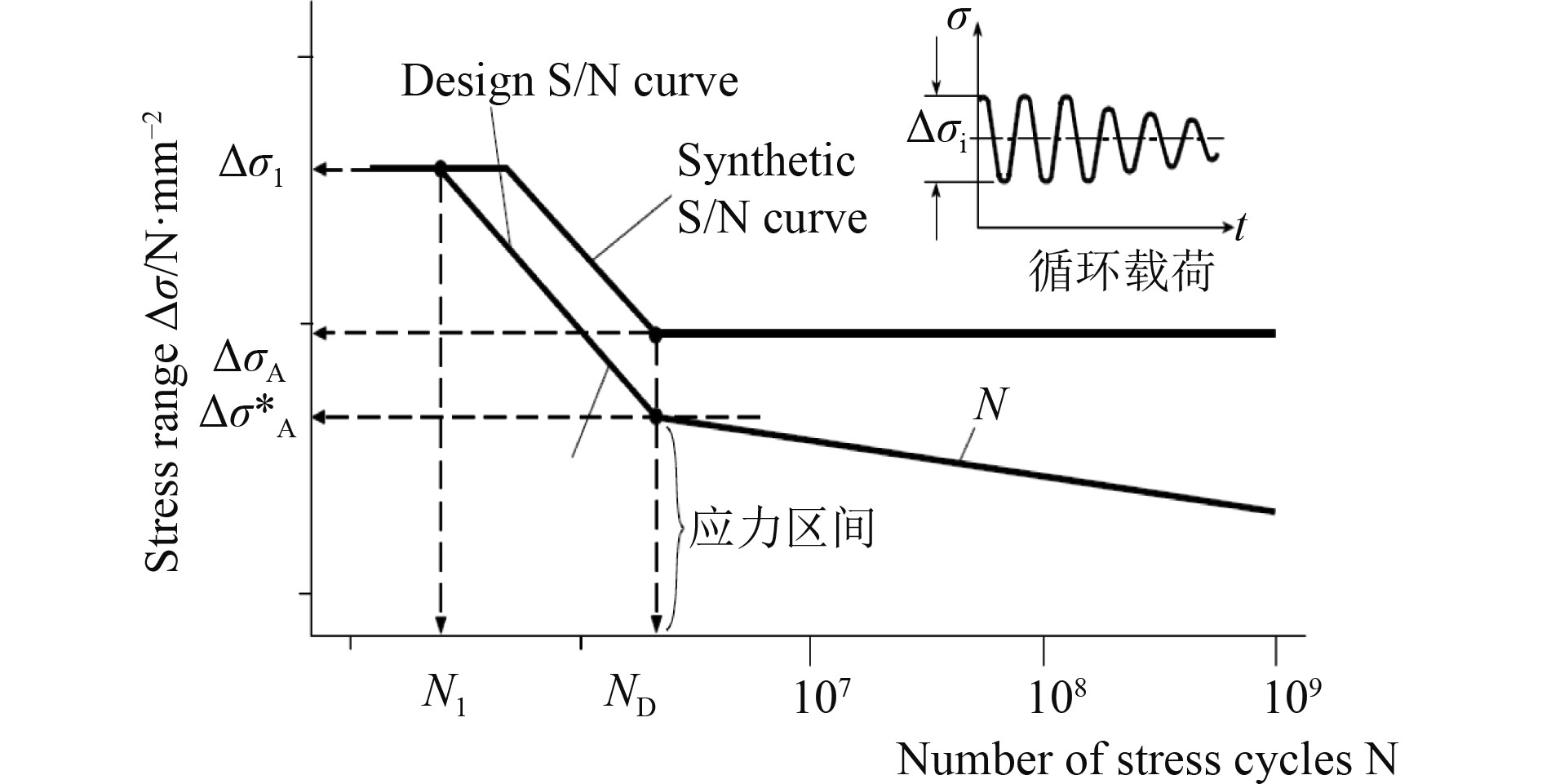
|
图 2 船体舱壁结构的循环载荷S-N曲线图 Fig. 2 Cyclic load S-N curve of hull bulkhead structure |
有限元法是利用数值模拟和工程算法,将连续的、复杂的问题进行离散处理,划分为由有限个单元组成的组合体,利用近似函数对结果进行拟合。基于有限元的船体结构强度计算过程中,需要准备的有限元模型数据包括:
1) 系统控制数据
比如需要定义有限元分析的类型,是静力学分析、弹塑性变形分析、模态分析还是热场、磁场分析等。
2) 有限元模型的基本材料属性定义
主要包括2个方面,一是有限元模型的材料定义,比如材料的密度、屈服强度、导热系数等,船体结构的主要承载部分以钢结构为主,其材料属性包括密度、屈服强度等;二是有限单元的材料特性,比如有限单元的泊松比、弹性模量[2]等。
3) 边界参数荷载数据
包括计算有限元模型时需要固定的自由度,有限元模型的载荷模式、载荷加载的方式和工况组合等,在船体结构的循环载荷极限强度分析中,需要定义船体结构在3个方向的自由度,船体受到的压力、弯矩等。
4) 单元拓扑结构的关系界定
在复杂的装配体有限元计算中,需要在有限元网格中确定装配零部件之间的相互关系,比如2个零部件模型相接的地方,如果需要传递力矩和力,那装配体的接触面就需要建立contact,采用的单元类型为contact 170和target171单元,分别表示接触面和目标面。此外,当需要向某一个面传递弯矩时,可以通过建立bonded关系传递弯矩,每一个bonded关系包括一个rigid point和一组节点集合[3]。
利用有限元软件Ansys,对船体舱壁结构在循环载荷下的极限强度进行了分析与仿真,整个过程如下:
1)有限元划分
有限元划分是进行强度计算的第一步,也是决定有限元分析精确性的关键,有限元模型划分的尺寸越小,整个有限元仿真的精度越高,同时会对Ansys求解器的内存带来一些压力[4],求解时间也相对较长;有限元模型的单元尺寸越大,计算结果越快,但与之相对应的计算精度越差。
因此,在进行有限元划分时,关键步骤是进行主体结构的网格化划分和局部网格的细化。通常,当模型较大时,主体网格的密度可放大到60~100 mm,局部细化的网络尺寸可细化到20~30 mm。
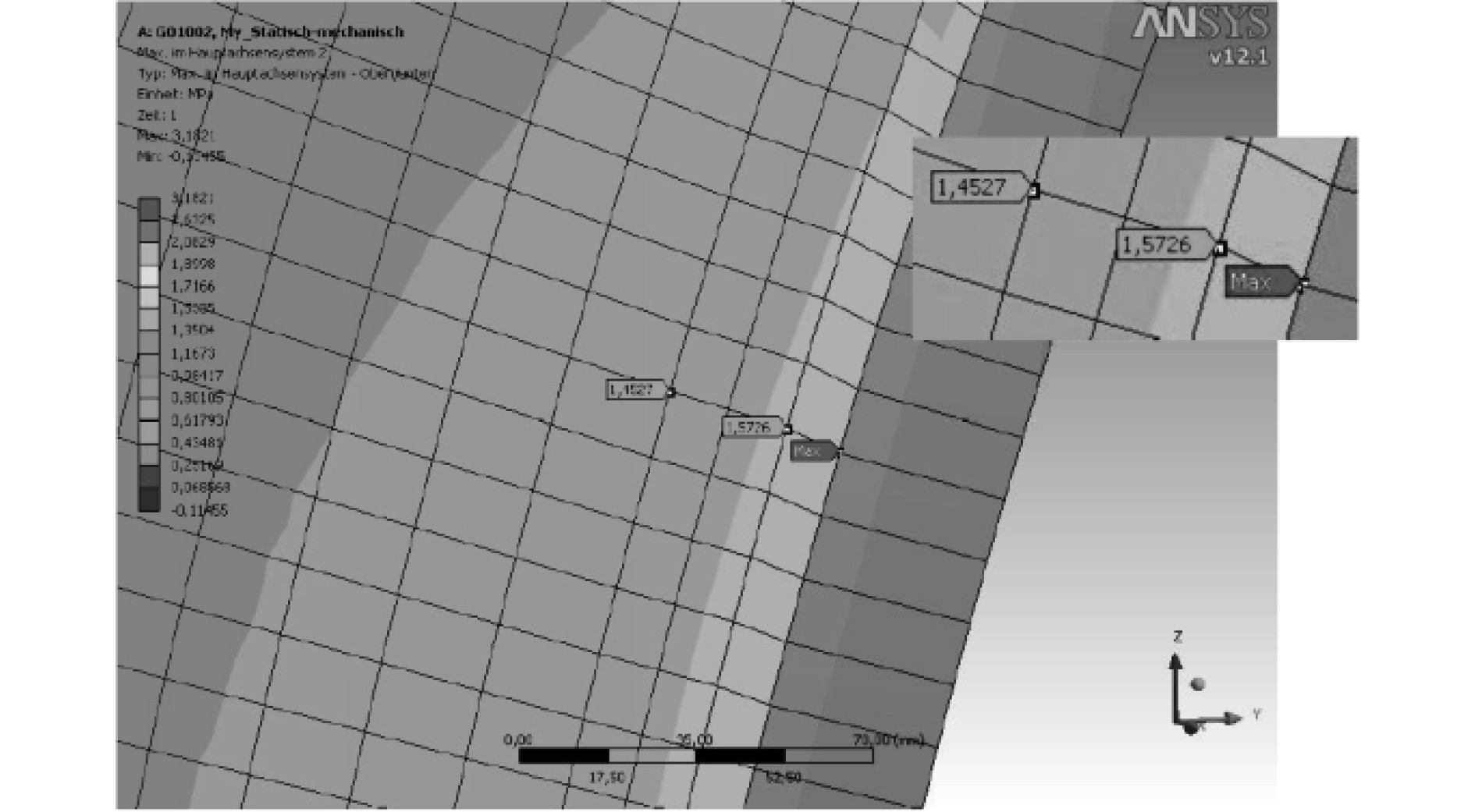
在舱壁结构的有限元划分时,对局部区域进行网格的细化,单元采用solid186单元[5],划分方式为六面体和四面体单元混合划分,图3为船舶舱壁局部区域的有限元模型示意图。
|
图 3 船舶舱壁局部区域的有限元模型示意图 Fig. 3 Schematic diagram of finite element model of local area of ship bulkhead |
2)确定舱壁有限元模型的材料属性
根据船级社对船体材料的规定,船舶用钢材的屈服强度在200~400 MPa区间内,因此,在定义有限元模型的材料属性时,选用弹性模量为
3)定义载荷
对船体舱壁结构的曲率
| $ \varphi = \min _{i = 1}^n\left\{ {\frac{{{{\left( {{\varepsilon _x}} \right)}_i}}}{{{y_i}}},\frac{{{\varepsilon _y}}}{{{y_i}}}} \right\} \text{。} $ |
式中:
定义船舶舱壁的循环弯矩载荷为:
| $ M = \sum\limits_{i = 1}^n {{\sigma _x}} \cdot {A_i} \cdot {y_i} \text{。} $ |
式中:
4)定义边界条件
在该船体仓壁结构极限强度分析中,边界条件为2个长边UX=0,即约束X方向的自由度;2个短边的RX=RY=0,即约束2个短边绕X和Y轴的转动自由度,释放水平自由度。
5)求解和后处理
施加循环载荷,在Ansys中对该有限元模型进行计算,获得船体结构的VON-MISES[6]有限元计算应力云图如图4所示。

|
图 4 船体结构VON-MISES有限元计算应力云图 Fig. 4 Von-mises finite element stress nephogram of hull structure |
船体结构在循环载荷下的强度特性具有重要意义,本文分析循环载荷下的极限强度理论,结合Ansys软件,对船体舱壁结构在循环载荷下的极限强度进行了分析和仿真。
| [1] |
郑玄亮, 林焰, 陈明, 等. 槽形舱壁Ansys有限元自动建模方法及程序实现[J]. 船舶设计技术交流, 2004(4): 23-26. |
| [2] |
王博, 王琳. 低强度循环载荷训练对髌骨髌腱结合部损伤和髌骨微细结构的影响[J]. 成都体育学院学报, 42(2): 5.
|
| [3] |
王艳巍, 李霞, 李中华. 有限元分析在钢网架屋盖结构设计中的应用研究[J]. 铁道工程学报, 2007, 24(0): 48-51,59. |
| [4] |
董琴, 杨平, 余志锋. 循环载荷下考虑累积塑性破坏的船体缺口板CTOD理论及数值模拟研究[J]. 船舶力学, 2018, 22(7): 865-872. DOI:10.3969/j.issn.1007-7294.2018.07.010 |
| [5] |
侯超. 基于ANSYS软件的船体局部强度计算模型[J]. 中国水运:下半月, 2008, 8(5): 20-21. |
| [6] |
杨树耕, 藤明清, 孟昭瑛, 等. 有限元分析软件ANSYS在海洋工程中的应用(续1) 第二讲采用ANSYS程序的导管架平台结构有限元分析[J]. 中国海洋平台, 2000(5): 42-48. |
 2022, Vol. 44
2022, Vol. 44
